随着现代隐身技术的发展,舰船航行时所产生的声信号、电磁信号的强度受到大幅削减,传统的使用声信号、静电场信号对舰船实施定位的方式难以满足舰船定位高精度的需求。使用新型的测量信号以及布阵方式实现水中目标定位具有较高的军事意义[1]。舰船在水中航行,会因电偶腐蚀,漏电流等原因产生静电场、工频电场,以及由阴极保护装置产生的保护电流与腐蚀电流共同经螺旋桨调制产生的轴频电场[2-3]。轴频电场因其不易衰减,传播距离远,规律性强的特点,正逐渐受到国内外研究学者的关注[4-6]。针对轴频电场的研究主要集中在反演推算、特性分析等方面[7-10]。
目前,国内外在目标定位技术中出现了较多采用阵列式探测系统的方法。其中,圆阵列在波达方向估计和被动式静电探测系统中应用的可行性、有效性已被证实[11-12]。上述研究领域使用的信号主要以声信号和静电场信号作为测量信号,易受到外界因素的干扰,衰减速度较快,实现远距离目标定位存在一定难度。本文探索了一种以轴频电场作为探测信号的圆阵列测量系统。舰船轴频电场频率约为1~7 Hz,可用同频率的水平时谐偶极子模拟轴频场源[13]。在海底布置2个以自身中点为轴旋转的连接杆,并在每个连接杆的两端分别布放电场三分量传感器,通过连接杆的旋转,模拟圆形阵列探测系统,测得不同角度下,直径上对称两点的电场强度差值。通过研究所测得的电场强度差值波形规律与舰船位置的关系,实现对舰船位置的定位。基于这种建模探测方法可对准近场目标进行探测,并具有较高的探测精度。
1 系统模型在3层介质中建立圆阵列测量系统,探测原理及电偶极子位置如图1所示

|
图 1 理论模型 Fig. 1 Theoretical mode |
建立O-xyz直角坐标系,原点位于水面,海水与空气、海水与海床分界面分别为z=0和z=D平面,z<0区域为空气介质,0<z<D区域为海水介质。以水平时谐偶极子对舰船轴频电场进行建模,其位置坐标为(x0,y0,z0)。在海底平面布置2个可绕其中点旋转的连接杆,连接杆两端各布置一个三分量电场传感器。两连接杆绕自身中点以速度v旋转,连接杆两端的传感器形成圆周运动轨迹。通过该方式实现对圆形阵列的模拟(圆1的圆心为(0,0,D),圆2圆心为(a,0,D),半径均为r)。旋转过程中,传感器可实现对圆周上关于圆心对称两点间的电场强度差值的扫描测量。
根据图1的几何关系,可计算得出两圆阵列上任意位置探测器的坐标,如下式:
| $ \begin{split} &\left\{ \begin{array}{l} {x_1} = {{r}} \cdot \cos {\theta _1},\\ {y_1} = {{r}} \cdot \sin {\theta _1},\\ {z_1} = D, \end{array} \right.\;\;\;\;\;\;\;\;\;\left\{ \begin{array}{l} x'_1 = {{r}} \cdot \cos ({\text{π}} + {\theta _1}),\\ y'_1 = {{r}} \cdot \sin ({\text{π}} + {\theta _1}),\\ z'_1 = D, \end{array} \right.\\ &\left\{ \begin{array}{l} {x_{\rm{2}}} = a + {{r}} \cdot \cos {\theta _{\rm{2}}},\\ {y_{\rm{2}}} = {{r}} \cdot \sin {\theta _{\rm{2}}},\\ {z_{\rm{2}}} = D, \end{array} \right.\;\;\left\{ \begin{array}{l} x'_2 = a + {{r}} \cdot \cos ({\text{π}} + {\theta _2}),\\ y'_2 = {{r}} \cdot \sin ({\text{π}} + {\theta _2}),\\ z'_2 = D\text{。} \end{array} \right. \end{split} $ | (1) |
在3层介质条件下,水平时谐电偶极子在空间某处产生的矢量磁位A及电场强度E满足的方程可根据麦克斯韦方程组推导得出,其矢量表达式为[14-15]:
| ${\nabla ^2}{{A}} + {k^2}{{A}} = - \mu {J_s}\text{,}$ | (2) |
| $E = - j\omega \left[ {{{A}} + \frac{1}{{{k^2}}}\nabla \left( {\nabla \cdot {{A}}} \right)} \right]\text{。}$ | (3) |
其中:
| $ \begin{array}{l} {\left. {\left[ {\dfrac{{\nabla \cdot {{{A}}_i}}}{{k_i^2}} - \dfrac{{\nabla \cdot {{{A}}_j}}}{{k_j^2}}} \right]} \right|_{{L_{ij}}}} = 0,\\ {\left. {\left[ {\dfrac{{{{{A}}_{in}}}}{{{\mu _i}}} - \dfrac{{{{{A}}_{jn}}}}{{{\mu _j}}}} \right]} \right|_{{L_{ij}}}} = 0,\\ {\left. {\left[ {\dfrac{\partial }{{\partial z}}\left( {\dfrac{{{{{A}}_{it}}}}{{{\mu _i}}} - \dfrac{{{{{A}}_{jt}}}}{{{\mu _j}}}} \right)} \right]} \right|_{{L_{ij}}}} = 0\text{。} \end{array}$ |
其中:Lij表示相邻不同介质中的分界面,对于3层介质而言,Lij表示z=0和z=D两个分界面。矢量磁位下标n、t分别表示法向和切向分量。
对于3层介质模型,由方程(2)可得不同介质中矢量磁位分别满足的约束方程为:
| $\left\{ \begin{array}{l} {\nabla ^2}{{{A}}_{1z}} + k_1^2{{{A}}_{1z}} = 0\text{,} \\ {\nabla ^2}{{{A}}_{2z}} + k_2^2{{{A}}_{2z}} = - \mu {J_s}\delta (\left| {R - R'} \right|)\text{,} \\ {\nabla ^2}{{{A}}_{3z}} + k_3^2{{{A}}_{3z}} = 0\text{,} \end{array} \right.$ | (4) |
为了简化运算,结合Sommerfeld积分公式求解,式(4)中不同介质下对应的解为[19]:
| $\left\{ \!\!\!\!\!\begin{array}{l} {{{A}}_{1z}} \!=\!\!\! \displaystyle\sum\limits_{m = - \infty }^\infty \!\!{\cos m\varphi \!\!\int_0^\infty \!\!\!\!{{J_m}} } (\rho \xi )\left[ {{a_1}(\xi ,m){e^{z{\upsilon _1}}} \!\!+\!\! {b_1}(\xi ,m){e^{ - z{\upsilon _1}}}} \right]{\rm{d}}\xi \text{,}\\ {{{A}}_{2z}} \!=\!\!\! \displaystyle\sum\limits_{m = - \infty }^\infty\!\! {\cos m\varphi \!\!\int_0^\infty \!\!\!\!{{J_m}} } (\rho \xi )\left[ {{a_2}(\xi ,m){e^{z{\upsilon _1}}} \!\!+\!\! {b_2}(\xi ,m){e^{ - z{\upsilon _1}}}} \right]{\rm{d}}\xi \!+ \\ \qquad\dfrac{{{\mu _2}Il}}{{4{\text{π}} }}\displaystyle\int_0^\infty {\dfrac{\xi }{{{\upsilon _2}}}{J_0}(\rho \xi ){e^{ - {\upsilon _1}\left| {z - {z_0}} \right|}}d\xi } \text{,}\\ {{{A}}_{3z}} \!=\!\!\! \displaystyle\sum\limits_{m = - \infty }^\infty \!\!{\cos m\varphi \!\!\int_0^\infty \!\!\!\!{{J_m}} } (\rho \xi )\left[ {{a_3}(\xi ,m){e^{z{\upsilon _1}}} \!\!+\!\! {b_3}(\xi ,m){e^{ - z{\upsilon _1}}}} \right]{\rm{d}}\xi \text{。}\\ \end{array} \right.$ | (5) |
其中:ai(ξ,m),bi(ξ,m)(其中i=1,2,3)分别表示待定系数,Jm表示m阶贝塞尔函数,
将式(5)代入边界条件可求得海水中矢量磁位表达式为:
| $\begin{split} {{{A}}_{2z}} =& \int_0^\infty {\left[ {{a_2}(\xi ,0){e^{z{\upsilon _1}}} + {b_2}(\xi ,0){e^{ - z{\upsilon _1}}}} \right]{J_0}(\rho \xi ){\rm{d}}\xi } \cdot {e_z} + \\ &\dfrac{{{\mu _2}Il}}{{4{\text{π}} }}\int_0^\infty {\frac{\xi }{{{\upsilon _2}}}{J_0}(\rho \xi ){e^{ - {\upsilon _1}\left| {z - {z_0}} \right|}}{\rm{d}}\xi } \cdot {e_z} \text{。}\\ \end{split} $ | (6) |
其中:
| $ \begin{split}& {a_2}(\xi ,0) = \frac{{\mu Il}}{{4{\text{π}} }}\xi \left( {\frac{{k_1^2{\upsilon _2} + k_2^2{\upsilon _1}}}{{k_2^2{\upsilon _2}}}K - \frac{1}{{{\upsilon _2}}}{e^{ - {\upsilon _2}{z_0}}}} \right),\\ &{b_2}(\xi ,0) = \frac{{\mu Il}}{{4{\text{π}} }}\frac{{\xi (k_1^2{\upsilon _2} - k_2^2{\upsilon _1})}}{{k_2^2{\upsilon _2}}}K,\\ &K = \frac{{k_2^2\left[ {H{e^{{\upsilon _1}(D - {z_0})}} - H'{e^{ - {\upsilon _1}(D - {z_0})}}} \right]}}{{(k_1^2{\upsilon _2} + k_2^2{\upsilon _1})H{e^{D{\upsilon _1}}} + (k_1^2{\upsilon _2} - k_2^2{\upsilon _1})H'{e^{ - D{\upsilon _1}}}}},\\ &H = k_2^2{\upsilon _3} + k_3^2{\upsilon _2},H' = k_2^2{\upsilon _3} - k_3^2{\upsilon _2}\text{。} \end{split} $ |
将式(6)代入式(3)即可求得海水中的圆阵列圆周上电场强度的分布。
对圆阵列上任意点处电场强度与其关于圆心对称点处的电场强度做差,即可得出任意位置处直径两端的电场强度差值波。
3 仿真计算 3.1 圆阵列上电场强度差值分布规律由于圆阵上直径两端电场强度差值均为同频率正弦波,现以任意位置处时谐偶极子在圆阵上直径端产生的场强差值波的幅值及相位随连杆位置角的变化规律作为轴频电场定位的研究对象。
假设空气的电性参数为σ0=0 S/m,ε0=1/36π×10−9 F/m,μ0=4π×10−7 H/m。海水的电性参数为σ1=4 S/m,ε1=80ε0,μ1=μ0。当水平时谐偶极子的频率为3 Hz,大小为1 A·m,圆1的圆心为(0,0,40),半径为5 m。对偶极子在(−3000,1000,5),(−1750,1000,5),(−500,1000,5)三个位置点在圆阵列上产生的轴频电场变化进行仿真。根据式(1)求解出圆阵列上不同位置处坐标,代入式(6)得到矢量磁位后,由式(3)对2个圆阵列圆周上的电场强度分布进行求解。由各方向直径两端的电场强度波作差值,得出差值波幅值与相位随测量角度变化的规律。仿真结果如图2所示。

|
图 2 圆阵列上的差值波分布规律 Fig. 2 Distribution of differenceial waves on circular arrays |
由图2可知,偶极子位于(−500,1000,5)位置点时,差值波相位变化率最大处位于26.57°,该位置同时为幅值最小的差值波产生的位置。而幅值最大差值波的位置位于116.57°,与幅值最小处相差90°,该范围内差值波的相位在0.8~0.9 rad间波动,且变化不明显,因此该处同时也是相位变化最慢的位置。此时,偶极子相对于圆阵列圆心的位置与x轴正向的夹角为116.57°,与图中幅值最大差值波的方位角一致。在准近场条件下,通过改变时谐偶极子的位置发现,所测得的差值波的幅值与相位始终符合上述变化规律,即幅值的最值的位置角随时谐偶极子的位置改变而变化。
由式(3)可知,圆阵列上电场强度与时谐偶极子位置坐标有关,在固定深度情况下,坐标信息等价于时谐偶极子与圆阵列在平面上的相对位置关系,由偶极子相对圆心的距离R和位置角Ф两个变量决定。保持2个变量中的一个不变,对另一个量改变时产生的电场差值变化规律进行研究。
固定方位角变量,研究电场强度分布随相对距离变化的规律。在相对方位角120°与150°两方向上,分别仿真计算出场强差值波幅值最大处位置角随相对距离的变化如图3所示。

|
图 3 幅值最大处位置角变化规律 Fig. 3 Variation of position angle at maximum amplitude |
由图3可知,偶极子在固定方向120°和150°上运动时,当距离分别超过897.3 m和612.2 m时,场强差幅值最大处的位置角变化值趋向于0°,并且与偶极子的相对位置角保持一致。由此可知,在某一固定相对方向上,随着测量阵列的相对距离值不断变大并超过一定极限范围时,圆阵直径端场强差幅值最大与相对方向角逐渐趋近一致,并且该极限范围随相对位置角的变化而不同。
计算相对方位角0°~180°范围内偶极子在不同位置下的情况得出极限距离在612.2~1237.7 m之间。固定相对距离变量,研究电场强度分布随方位角的变化发现,当场源位于各方向时,相对距离R>1237.7 m并继续增大,场强差幅值最大处位置角变化值∆Ф<0.001°并与测量阵列相对方位保持一致,满足定位需求。
研究结果表明,在固定场源参数情况下,当相对距离足够大时,相对位置角对电场强度分布产生的影响可忽略不计。此时,相对距离对电场强度影响增大,并成为主要影响因素。
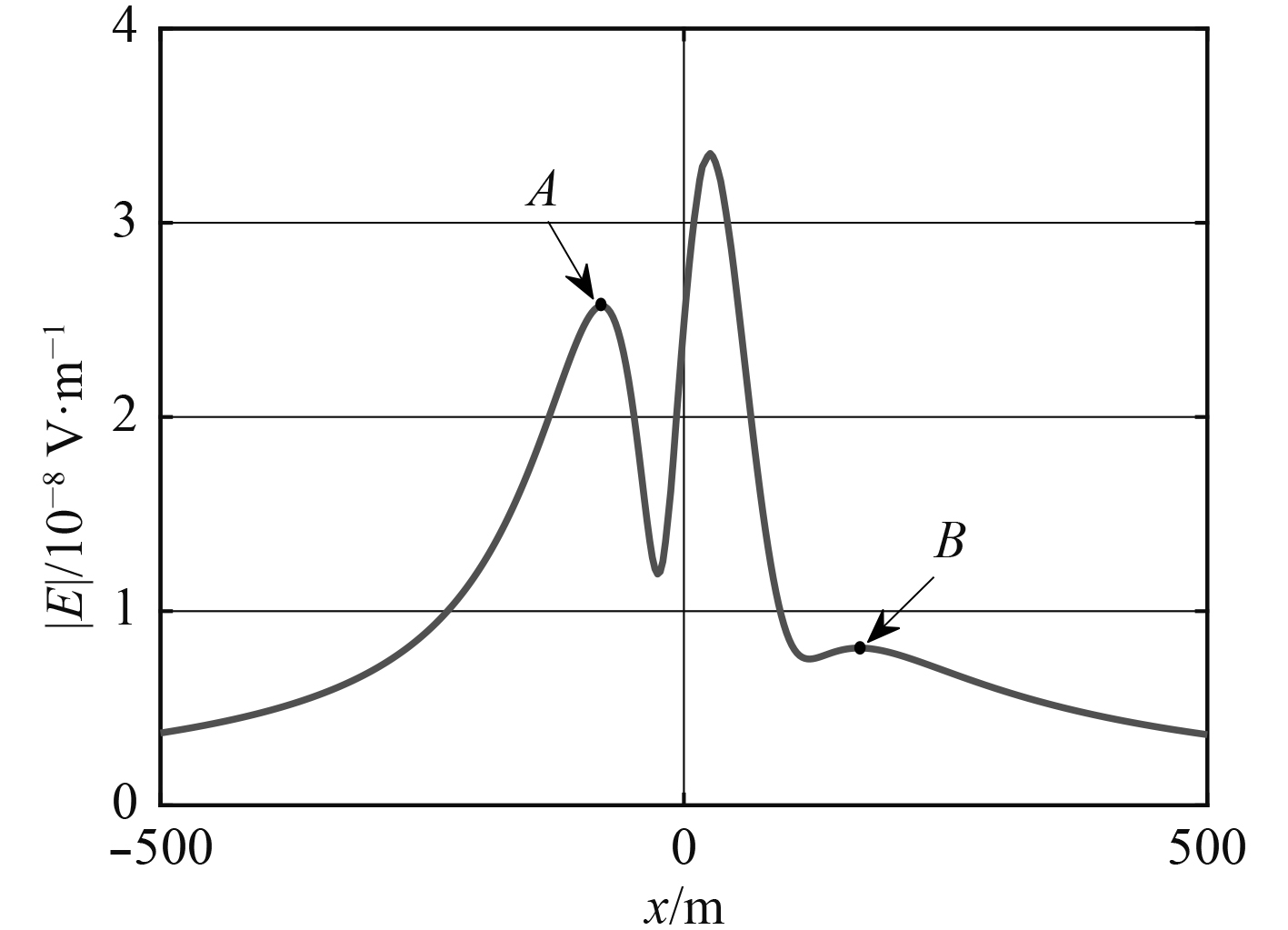
3.2 极限距离产生的原因分析3.1节结论中存在极限距离的原因,主要是与水平时谐偶极子电场在空间中的分布规律有关。对运动时谐偶极子在固定场点产生的电场强度进行仿真,根据位置相对关系,通过特性曲线即时谐偶极子在空间的电场分布状态[13]。假设场点位于(0,100,40),时谐偶极子沿x轴正向从(−500,0,5)运动到(500,0,5),场点上各分量电场强度幅值及总场强幅值随x坐标变化如图4和图5所示。

|
图 4 仿真电场分量信号 Fig. 4 Component signal of simulatedelectric field |
|
图 5 仿真电场模值信号 Fig. 5 Module signal of simulated electric field |
由图4可知,在准近场环境下,时谐偶极子电场强度各分量幅值随距离变化具有单调性。
由图5可知,时谐偶极子到达A点以前以及离开B点之后,在固定场点处产生的电场强度幅值随距离的变化具有单调性,距离越大,电场强度幅值越小。在A点与B点之间的范围内,场强幅值随距离的变化不再具有单调性,此时,偶极子与场点的相对方位角对电场的分布规律产生的影响不可忽略。
仿真结果表明,轴频场源在近距离环境下的分布规律决定于场点的相对距离和位置角,在准近场环境下,受相对方位角的影响减小,相对距离成为主要影响因素,电场模值呈现明显的单调性。因此,轴频电场的场源分布特性极限距离存在的主要原因。在大于极限距离的范围内测量电场时,圆阵列上沿场源所在方向上的直径两端点间距离差最大,所产生的电场强度差值的幅值最大。同时,与该方向垂直的直径两端点相对于场源的距离相等,距离差最小,产生的电场强度差值的幅值最小。
综上所述,在一定的距离范围,通过测量圆阵列上直径端电场强度差值的最值位置,可相应得出场源的方位,实现定位目的。
3.3 基于电场强度差值定位的计算由3.2节仿真结论可知,使用圆阵列上电场强度差值分布规律只能实现对时谐偶极子方位角的定位。测量点与源点之间相对距离的测算,可通过同一平面上,具有一定相对距离的2个圆形阵列上测得的最值位置角度以及两圆阵列的相对位置关系实现。系统在海底平面上的投影平面图如图6所示,两圆阵列在x轴方向上并列分布,时谐偶极子位置为(x0,y0)。

|
图 6 系统投影平面图 Fig. 6 Systematic projection plane |
根据图6中位置坐标关系可知,
| ${x_0} = a\tan {\theta _2}/(\tan {\theta _2} - \tan {\theta _1})\text{,}$ | (8) |
| ${y_0} = a\tan {\theta _1}\tan {\theta _2}/(\tan {\theta _2} - \tan {\theta _1})\text{。}$ | (9) |
通过测得的相对位置角θ1,θ2,以及圆阵相对距离a代入式(8)和式(9)可计算得出场源位置。仿真条件设定如下:圆1的圆心坐标(0,0,40),圆2的圆心坐标(20,0,40),连杆长10 m,则圆阵列半径均为5 m。对x=−1300~−800,y=1000航迹上的位置点进行仿真计算结果如表1所示。
|
|
表 1 偶极子位置真实值与仿真计算值对照表 |
由于轴频场源定位方法是基于轴频电场在空间的分布规律产生,因此验证该定位方法的正确性,关键在于验证时谐偶极子在空间的仿真分布模型的正确性。
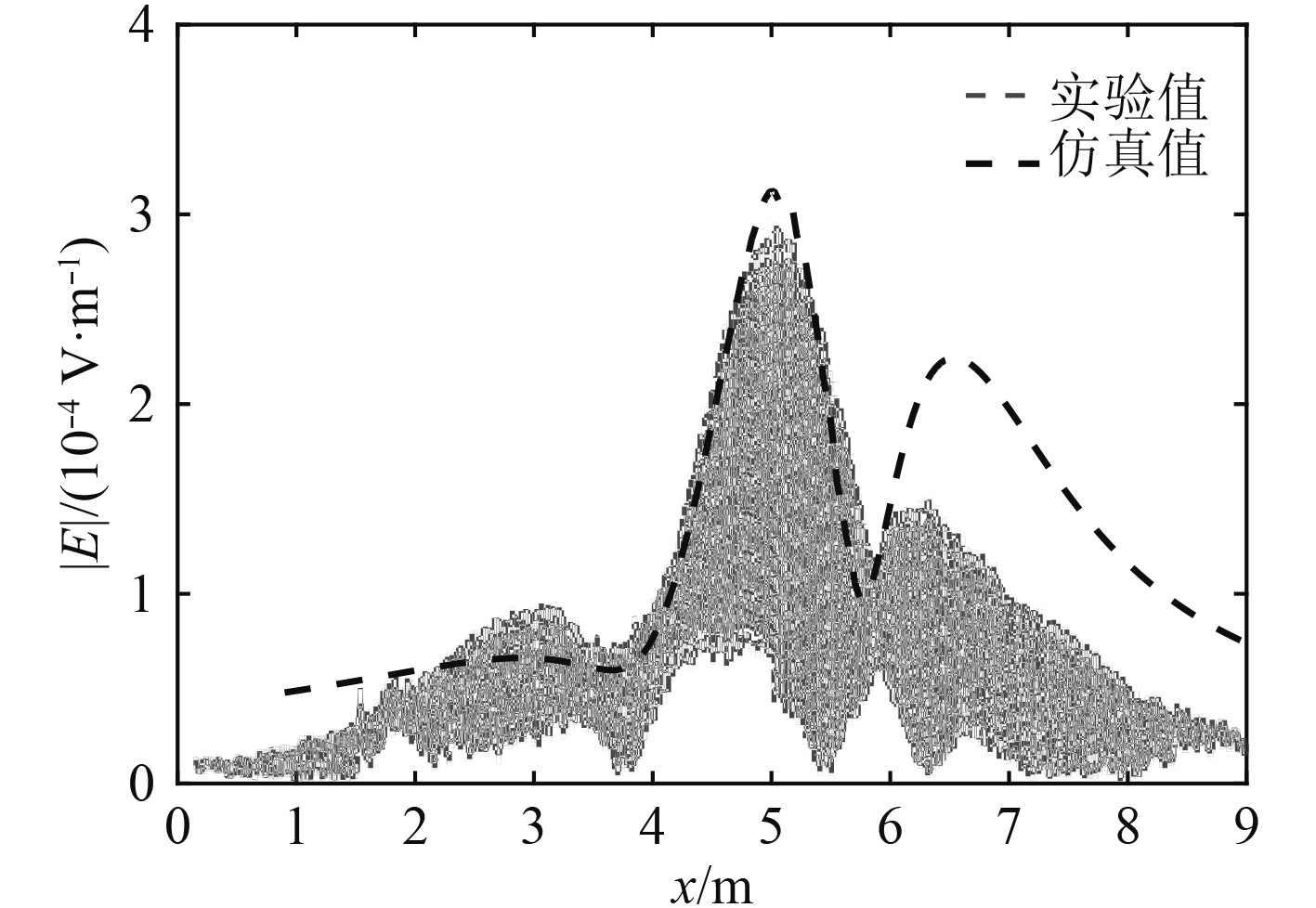
实验在15 m×10 m×1.5 m的水池中进行,使用工业盐配制成电导率为3.27 S/m的模拟海水,在水池中央底部布置10个Ag/AgCl电极,其中9个电极放置在垂直于水池长度的横截面上(可选取其中任意两对相互垂直的电极作为y,z方向电场分量的测量通道),剩余电极沿水池长度方向垂直于该平面放置,实现x分量场强的测量。以安装有5叶螺旋桨的船模产生的轴频电场作为场源,船模体与螺旋桨分别采用921A钢和B10铜制成,船长1.2 m。为增强测量信号强度,在船体上均匀布置8对牺牲阳极。步进电机拖动船模以0.1 m/s的速度沿水池匀速通过测量场点所在横截面。航线与测量点横向垂直距离1 m。实验结果与相同参数下仿真计算拟合结果如图7所示。
|
图 7 实测电场模值信号 Fig. 7 The measured signal of simulated electric field |
由图7可知,实验结果与仿真电场模在峰值附近拟合较好。在6~9 m位置处出现误差,主要是由于选取的三分量传感器正交性存在误差导致。从图中仍可看出实验在量级和波形上与仿真结果基本一致,验证了第3节中的轴频电场分布规律的正确性。证明了理论计算模型的正确性及系统定位方法的可行性。
5 结 语通过计算3层介质中时谐电偶极子在2个圆阵列上产生的电场强度分布规律,得到圆阵列直径上两端电场强度差值随场源不同位置变化的分布特性,并对该模型下的分布规律进行仿真计算与实验验证。
结果表明,可通过2个圆阵列上电场强度差值波形变化规律计算出电偶极子的位置,相对方位角误差小于0.005%,相对距离误差小于0.08%,在允许范围内。因此,用双圆阵列系统对3层介质当中的场源定位具有较高的精确度。
| [1] |
朱炜, 郭航. 现代舰船隐身技术的若干方法研究[J]. 舰船电子工程, 2014, 34(12): 22-26. ZHU Wei, GUO Hang. Research on the methods of warship stealthy technology[J]. Ship Electronic Engineering, 2014, 34(12): 22-26. |
| [2] |
JONES D L, BURKE C P. The DC filed components of horizontal and vertical electric dipole sources immersed in three-layered stratified media[J]. Annales Geophysicae, 1997, 15(4): 503-510. DOI:10.1007/s00585-997-0503-6 |
| [3] |
张建春. 海水中腐蚀相关轴频电场建模及特性分析[D]. 武汉: 海军工程大学, 2013. ZHANG Jianchun. The modeling and analysis about ship's shaft-rate electric field related to corrosion in seawater[D]. Wuhan: Naval University of Engineering, 2013. |
| [4] |
RASNOW B.. The effects of simple objects on the electric field of Apteronotus[J]. Journal of Comparative Physiiology A: Neuroethology, Sensory, Ne-ural, and Behavioral Physiiology, 1996, 178(3): 397-411. |
| [5] |
张华, 王向军, 单潮龙, 等. 基于目标静电场的水中兵器制导方法研究[J]. 电子学报, 2013, 41(3): 470-474. ZHANG Hua, WANG Xiangjun, SHAN Chaolong, et al. Research of guidance method based on the electrostatic field of target for underwater weapon[J]. Acta Electronica Sinica, 2013, 41(3): 470-474. |
| [6] |
SOLBERG J. R., LYNCH K. M., MACIVER M.. A active electrolocation for underwater target localization[J]. The International Journal of Robotics Research, 2008, 27(5): 529-548. DOI:10.1177/0278364908090538 |
| [7] |
卢新城, 龚沈光, 周骏, 等. 海水中时谐水平电偶极子的准近场定位[J]. 武汉理工大学学报, 2005, 29(3): 331-334. LU Xincheng, GONG Shenguang, ZHOU Jun, et al. Quasi-near field localization of a time-harmonic HED in sea water[J]. Journal of Wuhan University of Technology, 2005, 29(3): 331-334. |
| [8] |
CRAMPTON, W. G. R. Electric signal design and habitat preferences in a species rich assemblage of gymnotiform fishes from the Upper Amazon Basin[R]. Anais da Academia Brasileira de Ciências, 2008, 70(4 Part 2): 805–847.
|
| [9] |
FOX, D., THRUN, S., BURGARD, W., and DELLAERT, F. Particle filters for mobile robot localization[C]. Sequential Monte Carlo Methods in Practice. New York: Springer-Verlag, 2008, 42: 56-63.
|
| [10] |
谭浩, 陈聪, 蒋治国. 船舶水下电场的预测方法[J]. 国防科技大学学报, 2016, 38(6): 168-172. TAN Hao, CHEN Cong, JIANG Zhiguo. Electric field prediction method for ships at sea[J]. Journal of National University of Defense Technology, 2016, 38(6): 168-172. |
| [11] |
刘松, 杨士中. 均匀圆阵高效波达方向估计关键技术研究[D]. 重庆: 重庆大学, 2016. LIU Song, YANG Shizhong. Study on key tech-nologies of efficient direction-of-arrival estimati-on based on uniform circular array[D]. Chongq-ing: Chongqing University, 2016. |
| [12] |
陈曦, 徐立新, 毕军建, 等. 基于圆阵的被动式静电探测系统定位方法研究[J]. 北京理工大学学报, 2005, 25(2): 159-163. CHEN Xi, XU Lixin, BI Junjian, et al. Location method of round array based passive electrostatic detection system[J]. Transactions of Beijing Institute of Technology, 2005, 25(2): 159-163. |
| [13] |
熊露, 姜润翔, 龚沈光. 浅海中船舶轴频电场建模方法[J]. 国防科技大学学报, 2014, 36(1): 98-103. XIONG Lu, JIANG Runxiang, GONG Shenguang. Ship modeling method of shaft-ELFE in shallow sea[J]. Journal of National University of Defense Technology, 2014, 36(1): 98-103. |
| [14] |
卢新城, 龚沈光, 周骏, 等. 海水中极低频水平电偶极子电磁场的解析解[J]. 电波科学学报, 2004, 19(3): 290-295. LU Xingcheng, GONG Shenguang, ZHOU Jun, et al. Analytical expression of the electromagnetic fields produced by a ELF time-harmonic HED embedded in the sea[J]. Chinese Journal of Radio Science, 2004, 19(3): 290-295. |
| [15] |
毛伟, 张宁, 林春生. 在三层介质中运动的时谐水平偶极子产生的电磁场[J]. 电子学报, 2009, 37(9): 2077-2081. MAO Wei, ZHANG Ning, LIN Chunsheng. The EM Fields produced by a moving horizontally-directed time-harmonic dipole in three-layer medium[J]. Acta Electronica Sinica, 2009, 37(9): 2077-2081. |
| [16] |
张建春, 王向军. 水平电流元在深海中的电场强度算法研究[J]. 舰船科学技术, 2016, 38(1): 90-93. ZHANG Jianchun, WANG Xiangjun. Arithetic re-search about electric-field intensity of horizontal-harmonic current in the deep sea[J]. Ship Science and Technology, 2016, 38(1): 90-93. |
| [17] |
VANDERLINDE J. Classical electromagnetic tlieory[M]. 2th ed. London, LK: Springer, 2005: 33-35.
|
| [18] |
雷银照. 时谐电磁场解析方法[M]. 北京: 科学出版社, 2000.
|
| [19] |
姚端正, 梁家宝. 数学物理方法[M]. 武汉: 武汉大学出版社, 2011.
|
 2020, Vol. 42
2020, Vol. 42

