0 引　言

法兰式无键液压联轴器具有工作可靠、使用寿命长、装拆简便等优点，但法兰式无键液压联轴器安装过程中的径向油压和轴向推力都和联轴器外套的推入量相关^[1-4]。如果无键联轴器液压安装后实际的推入量较小，联轴器不能正常的传递扭矩力，严重时法兰式液压联轴器的无键联接可能会突然失效松脱，造成尾轴和螺旋桨的停转。如果无键联轴器液压安装后实际的推入量较大，联轴器外套的等效应力也随之增大，当等效应力超过联轴器材料的屈服极限时，联轴器可能会被撑裂而报废^[5-7]。为此以正云1号船舶作为研究对象，根据船级社规范进行理论计算，运用有限元法对液压安装过程中的推入量和油压进行仿真分析。通过理论值和仿真值的对比分析，检验选取推入量的理论值是否合理，获得液压安装过程中的p-S（油压-推入量）曲线，提出一种无键螺旋桨液压安装方案，为无键螺旋桨液压安装的控制提供理论依据。

1 计算原理 1.1 推入量的计算公式

船舶轴系的液压联轴器在安装的初期，要有一个初始推入量，设初始推入量为S，则初始的推入量的取值范围为S₁<S<S₂，其中S₁和S₂的计算公式如下^[8]：

$\begin{split} {S_1} = & \frac{1}{K}\left[ {47750 \times {{10}^4}\frac{{{N_{\rm{e}}}}}{{A{n_e}}}\left( {\frac{{{C_1}}}{{{E_1}}} + \frac{{{C_2}}}{{{E_2}}}} \right) + } \right.\\ & \left. {({a_2} - {a_1})(35 - t){d_1} + 0.03} \right]\text{，} \end{split}$

(1)

${S_2} = \frac{1}{K}\left[ {0.7{\sigma _s}d{}_1\frac{{K_2^2 - 1}}{{\sqrt {3K_2^4 + 1} }}(\frac{{{C_1}}}{{{E_1}}} + \frac{{{C_2}}}{{E{}_2}}) - ({a_2} - {a_1}){d_1}t} \right]\text{。}$

(2)

式中：K为轴套的锥度（其中 ${K_1} = {{{d}}_0}/{d_1}$ ， ${K_2} = {{{d}}_2}/{d_1}$ ）；Ne为传递到尾轴的额定功率；A为轴内套和外套的接触面积；d₁为尾轴的直径；n_e为轴工作时的转速；a₁，a₂分别为尾轴材料和轴套材料的线膨胀系数； ${\sigma _s}$ 为轴套材料的屈服强度；t为轴套安装时的环境温度；E₁，E₂分别为尾轴和轴套材料的弹性模量； ${C_1} = \displaystyle\frac{{1 + K_1^2}}{{1 - K_1^2}} - {\upsilon _1}$ ， ${C_2} = \displaystyle\frac{{1 + K_2^2}}{{K_2^2{\rm{ - }}1}}{\rm{ + }}{\upsilon _2}$ 。

1.2 液压安装的基础力

当在室温的环境下安装时，联轴器外套和内套接触面的表面最小压力为P，当联轴器的外套和内套紧密结合时，定义此时的轴向推力为F₀，P和F₀的计算公式如下：

$P = \frac{{{S_F}T}}{{A{B_1}}}\left( { - \frac{{{S_F}K}}{2} + \sqrt {\mu _1^2 + {B_1}{{\left( {\frac{{{F_V}}}{T}} \right)}^2}} } \right)\text{，}$

(3)

${F_0} = A\left( {0.002 + \frac{K}{{20}}} \right) \cdot \left[ {{P_{35}} + \frac{{18}}{{{B_2}}}({\alpha _2} - {\alpha _1})} \right]\text{。}$

(4)

式中：S_F为防止滑移的安全摩擦系数；T为联轴器受到的推力；FV为联轴器外套和内套接触面上的切向力； ${\mu _1}$ 为联轴器外套和内套接触面间的摩擦系数。

1.3 轴向推力和径向油压

联轴器在安装的过程中所施加的轴向推力为：

${F_1} = Ap\left( {{\mu _2} + K/2} \right)\text{，}$

(5)

式中， ${\mu _2}$ 为联轴器安装过程中的接触面间的摩擦系数（0.03）。在液压联轴器安装过程中的径向油压必须大于联轴器内套和外套接触面上的压力，一般情况下的径向油压为接触压力的1.1倍。因此径向油压的计算公式如下：

$P = 1.1SK/({d_1}{B_2})\text{。}$

(6)

1.4 应力的计算

如果液压联轴器内套和外套的等效应力过小，在船舶运行过程中，液压联轴器容易滑移脱落；如果应力过大，液压联轴器塑性变形也会滑移脱落。因此为了检验无键液压联轴器安装后的可靠性，必须计算液压联轴器内套和外套的等效应力。等效应力的计算公式如下：

$\begin{split} \sigma = & \sqrt {\frac{1}{2}\left[ {{{\left( {{\sigma _1} - {\sigma _2}} \right)}^2} + {{\left( {{\sigma _2} - {\sigma _3}} \right)}^2} + {{\left( {{\sigma _3} - {\sigma _2}} \right)}^2}} \right]} = \\ & 0.9p\left[ {\sqrt {3K_2^4 + 1} /\left( {K_2^4 - 1} \right)} \right]\text{。} \end{split}$

(7)

式中： ${\sigma _1}$ ， ${\sigma _2}$ ， ${\sigma _3}$ 分别为接触面间的3个主应力。

2 实例计算分析

以正云1号船舶上的无键液压联轴器的安装为例，表1为实例分析中用到的主要数据。

2.1 模型的网格划分和约束的施加

根据以上提供的数据建立液压联轴器的安装三维模型和抗冲击性能分析的三维模型，并且将三维模型进行有限元的六面体网格划分，设置网格划分的全局尺寸为0.02 mm，有限元网格划分如图1所示。

为了实现准确的有限元计算，安装三维模型包括尾轴和联轴器，安装时将尾轴端部位置和联轴器内套进行全约束，因为联轴器外套处于安装状态，所以联轴器外套处于纵向活动状态。抗冲击性能分析的三维模型包括尾轴、联轴器和中间轴，因为这时的各个部件已经安装完毕，因此将尾轴、中间轴以及轴承位置进行部分约束，使轴处于旋转状态。

2.2 等效应力

选取联轴器外套的内表面为接触面，以联轴器的内套外表面为目标面，对液压联轴器进行缓慢定速安装，选取理论计算的最大推入量34.87 mm进行仿真分析，安装后仿真分析的结果如图2所示。

由图可知，液压联轴器外套安装后的最大仿真应力为162.49 MPa，联立式（6）和式（7）理论计算联轴器外套的等效应力理论值为157 MPa，压力的分布不均匀，最大应力在液压联轴器的外套内表面中部。由于实际安装过程中的边缘等效应力的奇异性，外套边缘位置具有应力集中的现象，联轴器的法兰盘和外套的过渡区域应力偏大，因此仿真的计算结果要大于理论计算的值。液压联轴器安装后的极大等效应力值小于联轴器的屈服强度，因此该液压联轴器可以正常的工作。

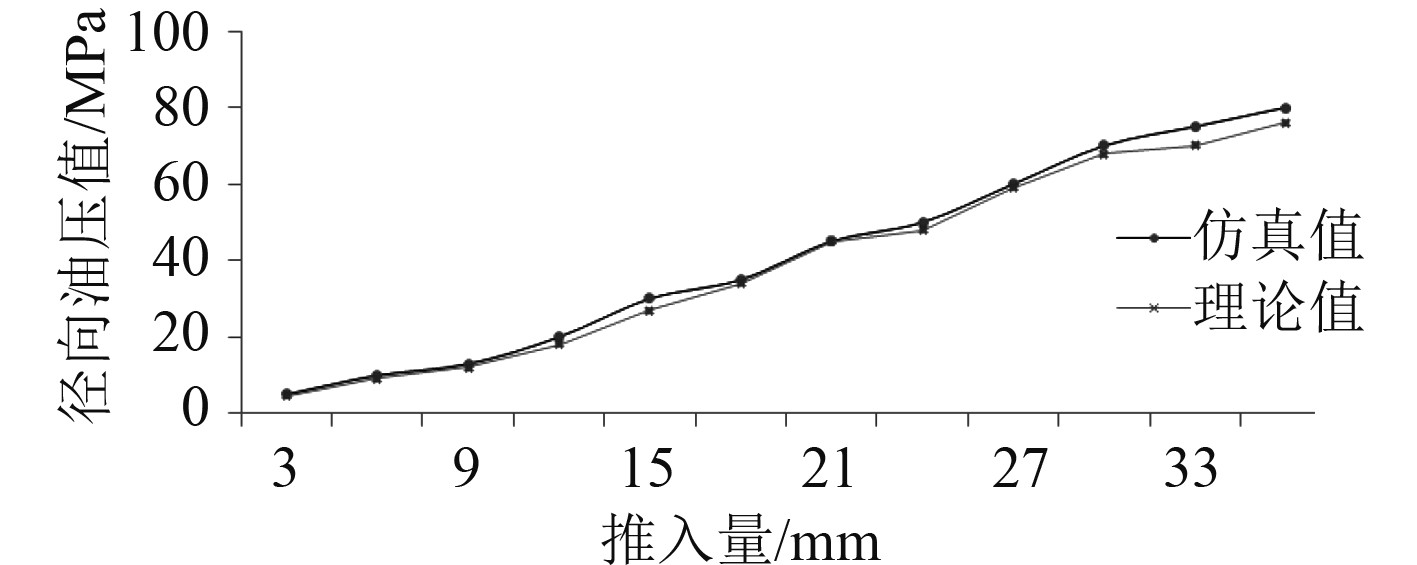
2.3 径向油压

在液压联轴器推入过程中（S=0～34.87 mm），选取其中的12组油压的数据，并且和式（6）计算的理论油压值进行比较。液压联轴器安装过程中径向油压的仿真值和理论值对比曲线如图3所示。

由图可知，联轴器液压安装过程中径向油压的仿真值和理论值基本都是呈线性增大，两者相差不大。从推入量到达27 mm以后，仿真值和理论计算值偏差开始增大；径向油压的理论计算值几乎都小于有限元的仿真值，其中理论值与仿真值的最大差值为2.31 MPa，理论值和仿真值的最大误差为6.7%，满足船级社钢制海船入级规范中的7%的要求，通过对比验证，说明了仿真计算结果的正确性。

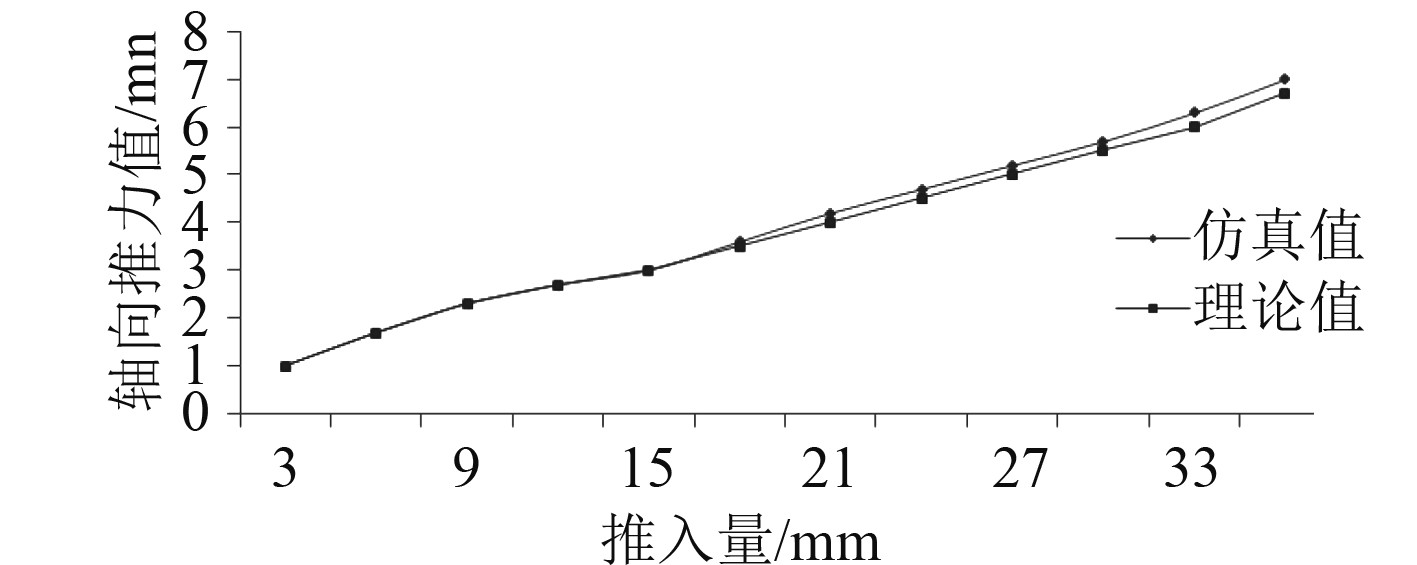
2.4 轴向推力

利用workbench后处理功能，将所有节点纵向的力做和处理，根据力的平衡原理，仿真计算的纵向总力就是近似安装的纵向推力，利用式（5）计算纵向推力的理论值，理论值和仿真分析的计算结果如图4所示。

由图可知，联轴器液压安装过程中轴向推力的仿真值和理论计算值基本都是呈线性增大，两者相差不大。从推入量到达18 mm左右以后，由于实际安装过程中的边缘等效应力的奇异性，接触的边缘位置具有应力集中的现象，接触面的摩擦力比理论值大，导致实际的轴向推力仿真值增大，仿真值和理论计算值偏差开始增大；其中理论值与仿真值的最大差值为70 3456 N，理论值和仿真值的最大误差为5.63%，满足船级社钢制海船入级规范中7%的要求。通过对比验证，说明了仿真计算结果的正确性。

2.5 无键联轴器液压安装方案

在无键联轴器液压安装前，对液压安装的重要参数进行理论计算，建立联轴器-轴无键联接的三维模型，运用有限元分析方法进行无键液压安装的仿真分析，获得液压安装过程中的轴向油压和径向油压与推入量之间的关系曲线，实际安装时的油压随推入量的数值按照给定的关系曲线进行加载。在联轴器无键液压安装过程中，对油压的数值进行实时的监测，并对监测的实际曲线设定波动范围。如果监测的实际曲线在给定曲线的设定偏差范围内波动，无键联轴器可以进行液压安装；如果监测的实际油压曲线超出给定油压曲线的设定范围，为防止联轴器和螺旋桨轴等部件被破坏，需停液压安装，进一步分析无键联轴器液压安装过程中出现故障的原因。

3 联轴器的稳定性分析

无键法兰式液压联轴器安装好以后，为了验证在极限工作状态下的稳定性，对在最大扭矩（3600 kNm）工况下的液压联轴器的应力分布进行仿真分析，仿真结果如图5所示。

从图可知，液压联轴器的外套最大应力为165.39 MPa，由于法兰螺栓链接盘和外套的连接过渡位置出现应力集中现象，因此过渡部位的应力比其他部位偏大。液压联轴器内套的最大应力要比外套的小一个等量级。但是由于受到边缘等效应力集中现象的影响，内套的最大应力出现在边缘位置，联轴器承内套的薄弱环节出现在两端。但是液压联轴器内套和外套的应力都小于材料屈服强度，故联轴器内外套均符合抗冲击的要求。

4 结　语

经过对正云1号船舶液压联轴器的安装和安装后稳定性的分析可知，按照理论计算的推入量不仅可以满足液压联轴器正常运行的需要，还符合液压联轴器内外套抗冲击性的要求。

1）由于液压联轴器实际安装过程中边缘等效应力的奇异性，接触的边缘位置具有应力集中的现象，接触面的摩擦力异常增大。当推入量达到一定的值以后，轴向推力仿真的计算结果大于理论计算的值。为了保证液压联轴器正常的工作，安装后的极大等效应力值应该小于联轴器的材料屈服强度。

2）联轴器液压安装过程中径向油压和轴向推力的仿真值和理论值基本都是呈线性增大，当推入量达到某位置以后，仿真值和理论计算值偏差开始增大，并且径向油压的理论计算值几乎都小于有限元的仿真值。为了保证液压联轴器正常的工作，径向油压和轴向推力理论值与仿真值的最大误差要低于船级社钢制海船入级规范中的7%的要求。

3）在液压联轴器运行稳定的情况下，液压联轴器内套的应力小于外套，由于受到边缘等效应力集中现象的影响，内套的最大应力出现在边缘位置，联轴器承内套的薄弱环节出现在两端。