2. 武汉第二船舶设计研究所,湖北 武汉 430064
2. Wuhan Second Ship Design and Research Institute, Wuhan 430064, China
冰区加强船舶不需要自主破冰,通常需要在破冰船已经开辟的航道中航行,即在碎冰区域航行。船舶在冰水混合的碎冰区航行时,航行阻力与开敞水域有明显不同。关于船舶在冰水混合流动中的阻力性能预报,通常有理论计算、经验公式估算、数值模拟和船模试验等方法。理论计算及经验公式估算受船型尺度等限制,通常只针对特定船型且精度较差。
在数值模拟方面,国内外开展的相关研究并不多。目前应用最多的是离散元法(DEM)、有限元法(FEM)以及光滑粒子流体动力学方法(SPH)等。Jungyong Wang等[1]基于Ls-dyna软件模拟了碎冰条件下Terrry Fox号破冰船的阻力性能,分析了碎冰密集度对阻力性能的影响。Moon-Chan Kim等[2]对一艘冰区加强型散货船的碎冰区阻力性能进行了数值模拟,通过与试验结果的对比验证了数值结果的准确性,其数值结果与试验值误差在20%左右。郭春雨等[3]同样采用Ls-dyna软件计算各种工况下的船舶航行阻力特性,并与试验值进行了对比。王超等[4]基于离散元模型结合欧拉多相流对碎冰区船舶的冰阻力进行了数值模拟,得到了碎冰阻力随航速等的变化规律。在自编程计算方面,李紫麟[5]基于离散元理论,采用三维圆盘模拟海冰单元,对不同航速碎冰作用于船体的力进行了数值模拟。J.Tuhkuri等[6]对DEM方法应用于冰水船相互作用的研究进行了系统的评述。总的来说,碎冰区域航行船舶的阻力性能数值预报仍需要提高精度。
在船模试验方面,冰水池船舶试验通常分为冻结模型冰试验和非冻结模型冰试验。随着冰水池技术的发展,国内外冰池船模试验技术迅速发展,并取得了较多研究成果。首次破冰船阻力试验是在1964年,Corlett和Snaith[7]以石蜡代替冰,对1艘小型破冰船进行了阻力试验。随后德国、芬兰、韩国、加拿大、俄罗斯等冰水池相继在船舶冰区阻力、操纵性等方面开展了大量的模型试验。在国内,郭春雨等[8-9]依托哈尔滨工程大学常温拖曳水池采用非冻结模型冰进行了一系列的船-冰相互作用试验。黄焱等[10-11]在天津大学冰力学实验室,开展了碎冰和平整冰阻力试验。
本文采用STARCCM+商用软件,基于离散元方法,结合拉格朗日方法的颗粒接触动力学模型,建立船-冰-水的CFD-DEM耦合数值计算模型,对一艘冰区加强型集装箱船在碎冰区航行的阻力特性进行研究。参照冰水池试验结果,选取不同的颗粒形状进行数值模拟,将数值计算现象与试验现象进行对比,对不同航速、不同冰厚下的阻力特性进行分析。
1 理论基础 1.1 数值计算方法计算模型中,流体满足不可压缩及连续性方程,同时忽略各相之间的热传递过程[12]。基于VOF方法捕捉自由液面,湍流模型为SST-K-omege模型。为防止出流边界处的流体反射对船体周围流场的影响,对出流边界附近采用Choi方法进行数值消波[13]。数值离散方法采用离散元方法。
离散元方法在20世纪70年代初由Cundalland Strack[14]首次提出。离散元方法将研究对象离散成一系列的单元,单元之间通过节点进行连接。其求解过程一般为:1)将研究对象离散为单元颗粒,选定合理的单元连接形式,给定初始条件;2)根据接触条件判断单元之间是否发生接触,若发生接触则根据单元间的本构模型,计算单元之间相互作用力,从而得到各单元之间的相对速度和位移,更新单元信息。通过对计算域内所有单元的物理量的求解,可以得到整体的研究对象的变形及运动情况。
1.2 离散项接触力模型两单元之间接触作用模型如图1所示,在离散元中接触力公式实际是弹簧-阻尼器模型的一种变形。弹簧产生排斥力将颗粒分开,而阻尼器表示粘性阻尼并允许模拟除完全弹性外的碰撞类型。作用在接触点处的接触力可以看做是一对弹簧-阻尼器振子。
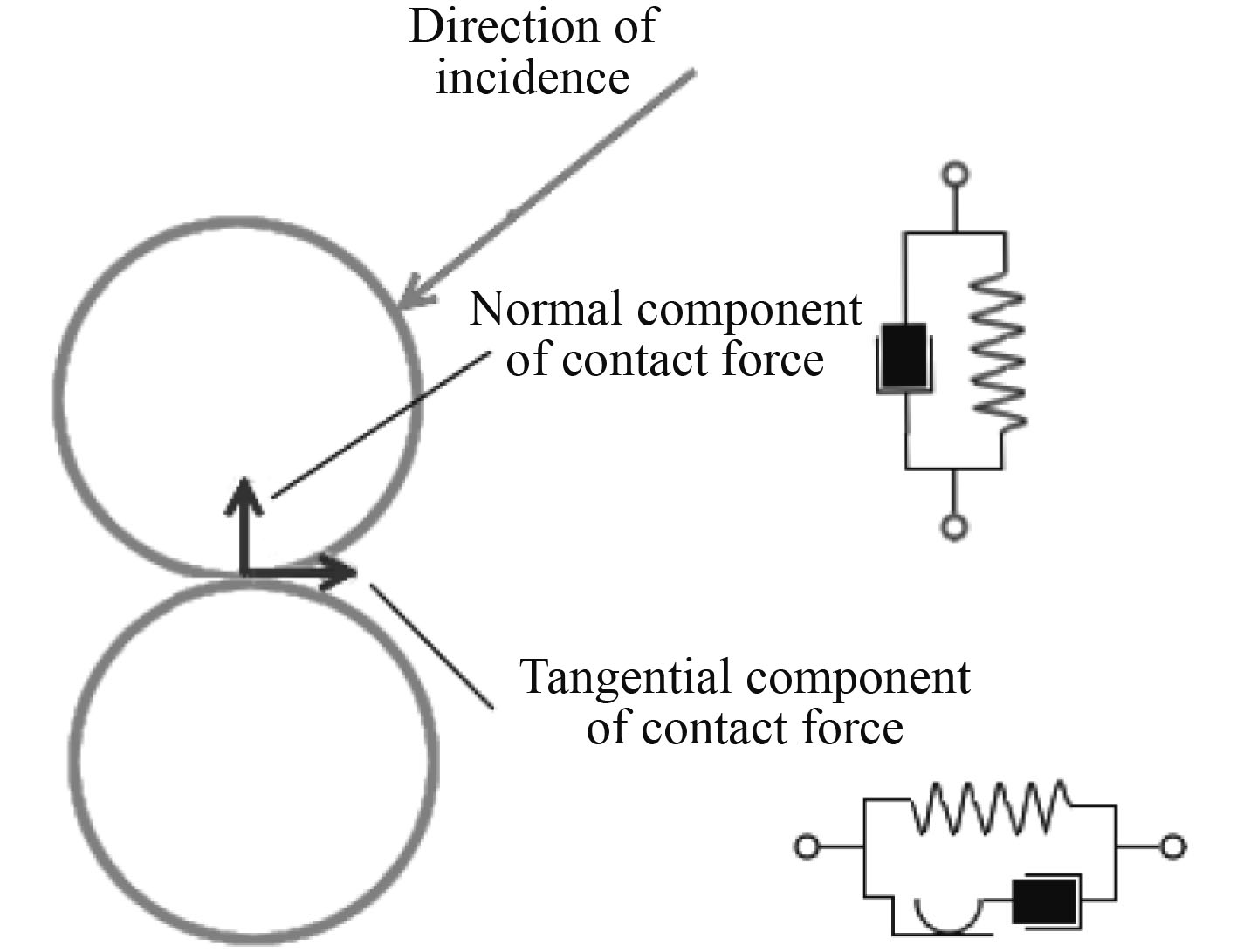
|
图 1 接触力模型 Fig. 1 Model of contact force |
Hertz-Mindlin无滑移接触模型是一种非线性弹簧-阻尼器接触模型的变形[15]。作用在2个单元A和B之间的力可表示为:
| ${F_{contact}} = {F_n} + {F_t}{\text{。}}$ | (1) |
其中:
法向力分量可以写成:
| $\begin{split} {F_n} = & - {K_n}{d_n} - {N_n}{v_n}{\text{,}} \\ {K_n} = & \frac{4}{3}{E_{eq}}\sqrt {{d_n}{R_{eq}}}{\text{,}} \\ {N_n} = & \sqrt {(5{K_n}{M_{eq}})} {N_{n\; damp}}{\text{;}} \end{split} $ | (2) |
切向力分量可以写成:
| $\begin{split} {F_t} = & \frac{{\left| {{K_n}{d_n}} \right|{C_{fs}}{d_t}}}{{\left| {{d_t}} \right|}} {\text{,}} \\ {K_t} = & 8{G_{eq}}\sqrt {{d_n}{R_{eq}}} {\text{,}} \\ {N_t} = & \sqrt {(5{K_t}{M_{eq}})} {N_{t\; damp}} {\text{。}} \end{split} $ | (3) |
其中:
| $\begin{split} {M_{eq}} = & \frac{1}{{\frac{1}{{{M_A}}} + \frac{1}{{{M_B}}}}} {\text{,}} \\ {E_{eq}} = & \frac{1}{{\frac{{1 - v_A^2}}{{{E_A}}} + \frac{{1 - v_B^2}}{{{E_B}}}}} {\text{,}} \\ {G_{eq}} = & \frac{1}{{\frac{{2(2 - {v_A})(1 + {v_A})}}{{{E_A}}} + \frac{{2(2 - {v_B})(1 + {v_B})}}{{{E_B}}}}} {\text{。}} \end{split} $ | (4) |
对于单元-壁面碰撞,上述公式保持不变,将壁面半径和质量设定为
离散项冰粒子的建模参照冰水池试验的碎冰图像,碎冰粒子表现为一系列的圆球组成的复合粒子,碎冰粒子形状选取为金字塔形和不规则棱柱形,如图2所示。冰的密度为917 kg/m3。冰的弹性模量为E=9 GPa,根据冰属性的缩尺比关系[16],冰粒子模型的弹性模量为300 MPa,泊松比为0.3。
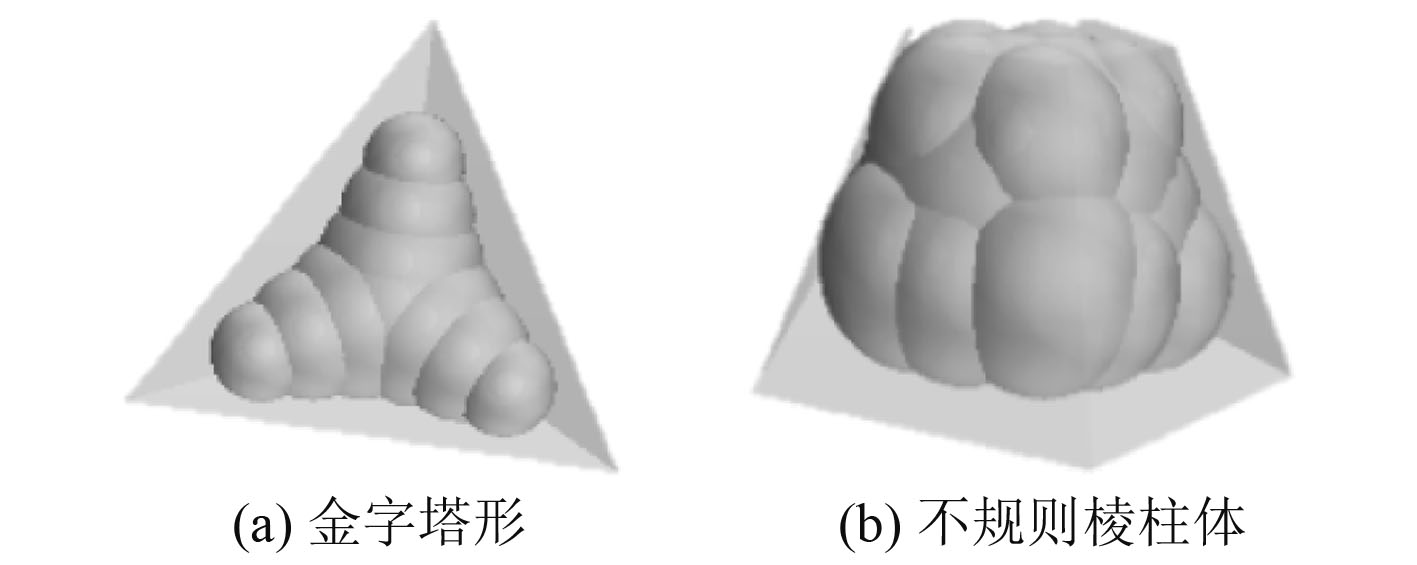
|
图 2 碎冰几何形状 Fig. 2 Geipetric shape of crushed ice |

|
图 3 数值航道中的碎冰粒子 Fig. 3 Ice particles in numerical channels |
根据北极地区碎冰尺寸统计数据,碎冰尺寸大致服从对数正态分布规律,其分布形式为:
| $F(D) = \frac{1}{2}\left[ {1 + erf\left( {\frac{{\ln D - \ln \bar D}}{{\sigma \sqrt 2 }}} \right)} \right]{\text{。}}$ | (5) |
其中:D为冰块直径;
本文数值模拟中,颗粒(2种碎冰模型)、流体(水)和壁面(船体壁面、航道边界壁面)多相之间会产生碰撞等相互作用,在计算中考虑7种相互作用类型,如图4所示。其中,船-冰之间的摩擦系数为0.1,冰-冰之间的摩擦系数为0.1,动摩擦系数为0.3。冰粒子采用喷射器的形式进入流场,喷射器定义冰粒子进入的速度、位置及方式等。
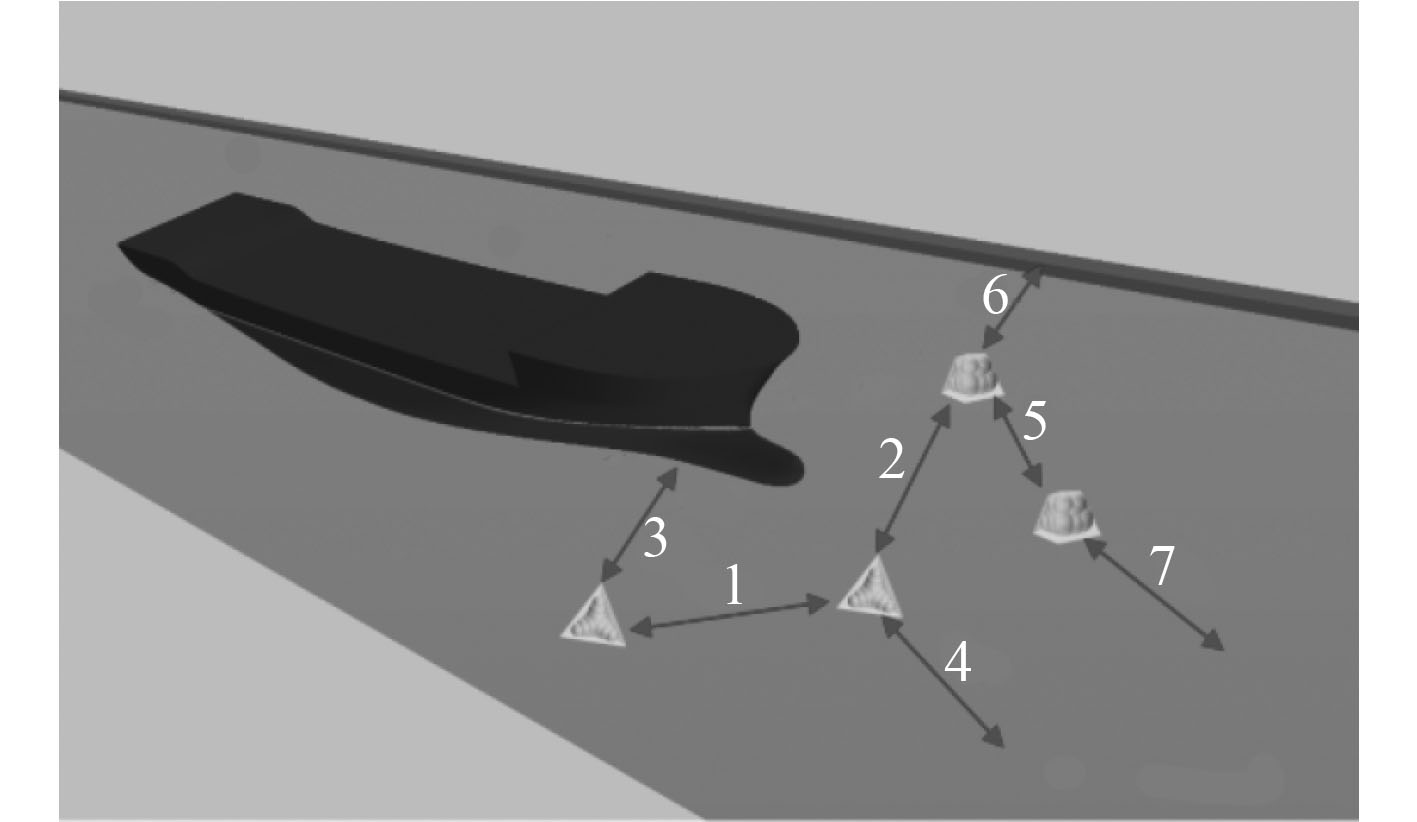
|
图 4 多相相互作用示意图 Fig. 4 Schematic diagram of mutiphase interaction |
本文计算模型为1艘典型冰区加强型集装箱船,模型缩尺比为30,实船及模型主尺度参数如表1所示。
|
|
表 1 船体主尺度参数 Tab.1 The main parameters of ship |
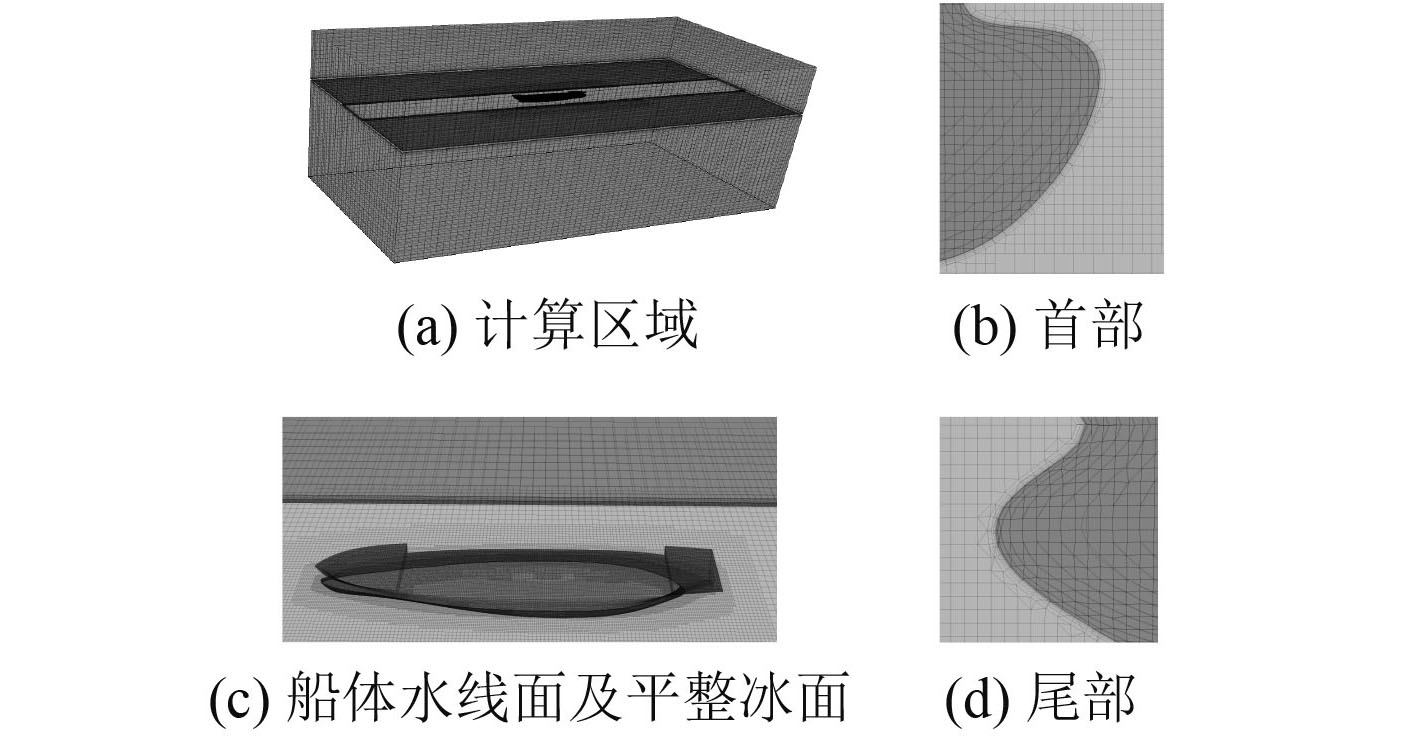
碎冰航道计算域以船体为中心,船体前后距计算域边界距离均为8 L,船体两侧距计算域边界距离均为1.5 Lpp,在垂直方向上计算域尺寸为−1.5 Lpp~2.0 Lpp。船体、平整冰及计算域的4个壁面均为无滑移壁面边界条件,速度入口及压力出口边界如图5所示。本文计算域分为空气域和水域,计算过程中船体保持不动,通过改变速度入口处的速度调节船舶的航速。为准确捕捉自由液面位置、船体周围流场等,在相应的区域进行网格加密处理,边界层网格形式为棱柱形边界层,边界层采用y+壁面处理,y+值范围为30~60。船体表面网格尺度为5 mm,船体表面第1层网格厚度为2 mm,计算域中等网格总数约为212万,图6为网格划分结果。
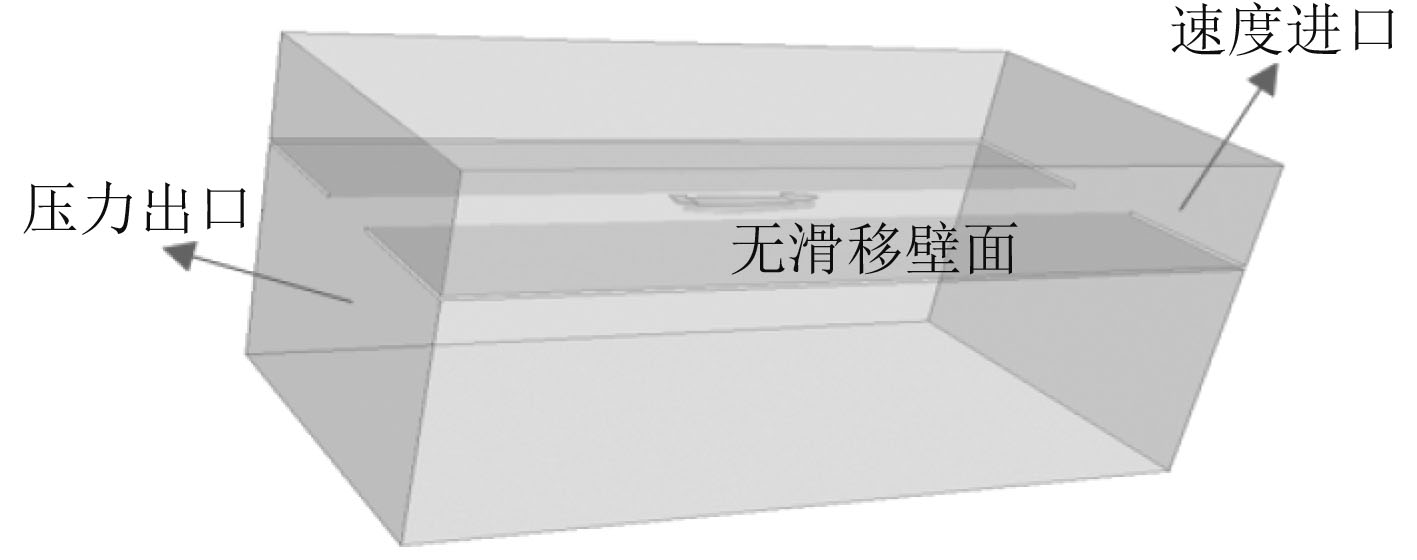
|
图 5 计算域及边界条件 Fig. 5 Calculation domain and boundary conditions |
|
图 6 网格划分结果 Fig. 6 Result of meshing |
图7为汉堡冰水池进行的某冰区加强型散货船的碎冰阻力试验图像[17]。船舶在碎冰区域航行时,碎冰在与船舶发生碰撞时会发生翻转现象,而随着船舶的航行,在船体首部区域会发生碎冰堆积现象,同时一部分碎冰运动到船体底部或舷侧随船体滑移。在这个过程中,碎冰之间以及碎冰与船体之间会发生碰撞。从图7可以看出数值计算现象与试验现象吻合度较好,证明本文采用的碎冰粒子模型及数值方法可以有效模拟碎冰区船舶与碎冰接触时的现象。

|
图 7 船-冰碰撞现象模拟 Fig. 7 Simulation of ship-ice collision |
船舶在碎冰区域航行时,碎冰与船体之间的碰撞、摩擦等作用产生的阻力是船体阻力的重要成分。分析船体周围碎冰的运动状态对阻力特性的预报十分重要。计算V=0.563 m/s时船体周围碎冰分布如图8所示。可以看出碎冰在船体首部发生碰撞后堆积,碎冰与船体间的相对速度骤降。而在船体尾部,由于船体尾流的作用使得碎冰分布较为分散,聚集在螺旋桨周围的碎冰较少,这可以有效减少冰-桨接触,有利于螺旋桨的推进效率。从图9也可以看出,随着航速的增加,船体周围的兴波已经较为明显,兴波可以有效地将船体周围的碎冰排开。同时可以看到,在船体尾部形成了一条浮冰很少的航道,该航道宽度大致相当于船体的宽度,这会有效降低船体-冰之间的接触力。

|
图 8 船体周围碎冰的运动状态 Fig. 8 Movement position of crushed ice around hull |

|
图 9 不同航速碎冰状态对比 Fig. 9 Movement position of crushed ice in different speed |
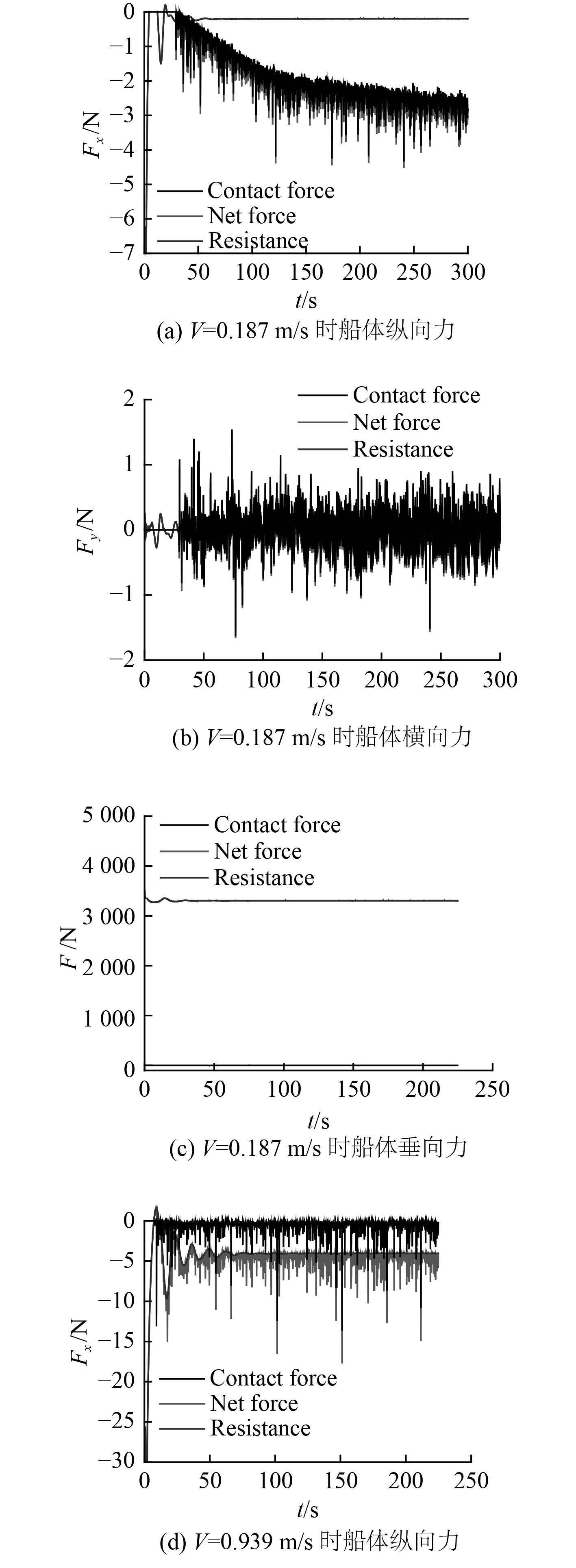
船舶在敞水区域航行时,航速对船体阻力的影响很大。计算航速分别为0.187 m/s,0.376 m/s,0.563 m/s,0.751 m/s和0.939 m/s(分别对应实船航速2 kn,4 kn,6 kn,8 kn和10 kn)时,船体受到的冰阻力时历曲线如图10所示。时历曲线中阻力分为3部分,contact force为船-冰接触力,resistance为水阻力,net force为船体受到的总阻力。可以看出船-冰接触力随着航速的增大而增大,同时接触力有强烈的震荡特性。接触力的3个分量中,纵向力以某一基准值为下限震荡;侧向力则在0值附近上下震荡,这是由于船体左右两舷对称的原因;而垂向力基本为0,这表明船-冰碰撞基本为水平方向碰撞。低速航行时,纵向接触力震荡下限远大于水阻力;航速较高时,纵向接触力的震荡下限小于水阻力。这说明随着航速的增大,水阻力在船体总阻力中所占的比重越来越高。
|
图 10 低速和高速时船体阻力分量时历曲线 Fig. 10 Time history curve of hull resistance at low speed and high speed |
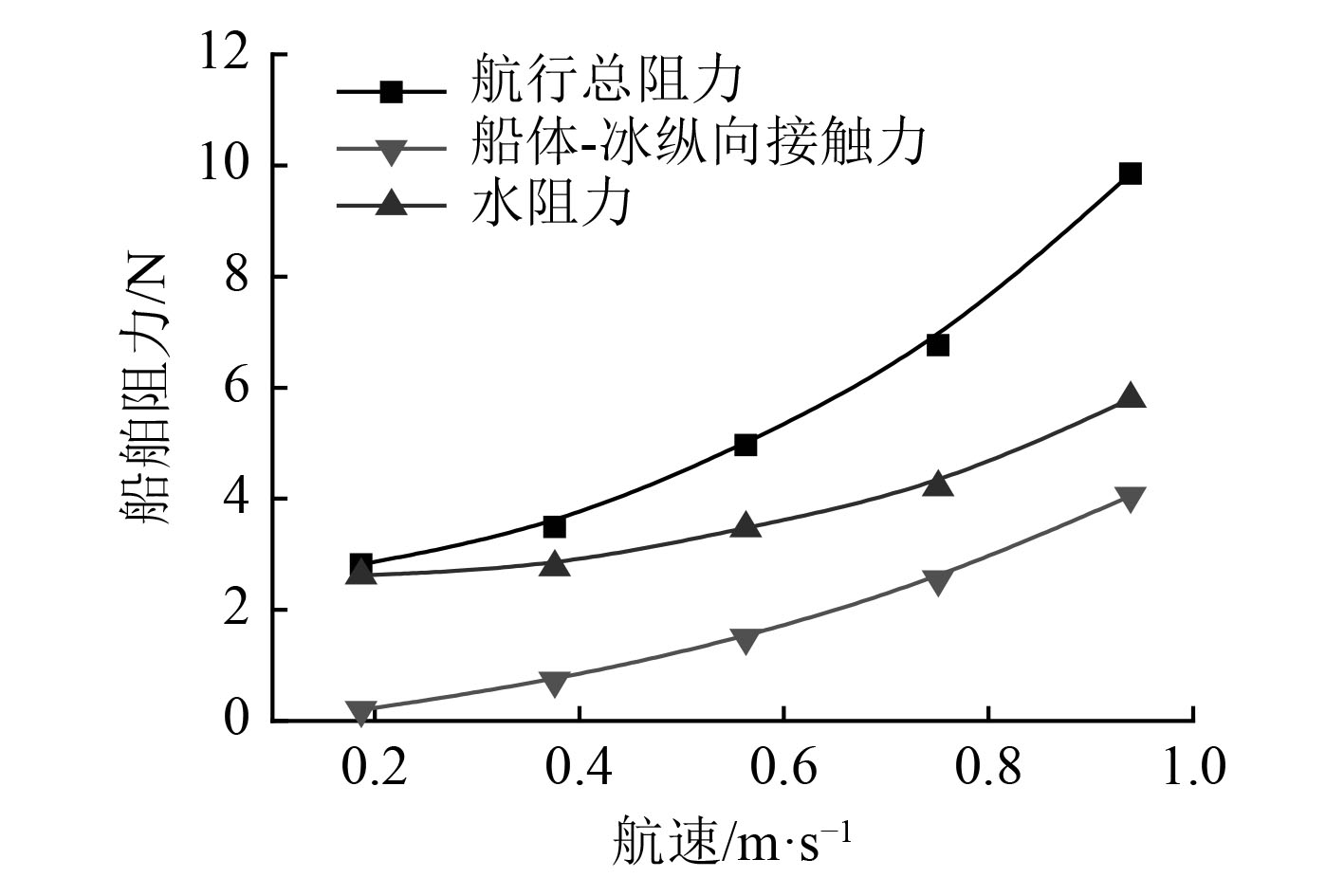
对船体阻力的各个分量取稳定段时间平均即得到各航速下的船体阻力分量如图11所示。可以看出,船体总阻力及各分量均随航速的增大而增大,这与敞水航行阻力的规律类似。在航速从0.187 m/s增大到0.939 m/s时,航速变为原来的5倍,总阻力增大为原来的3.5倍,纵向接触力增大为原来的2.2倍,水阻力增大为原来的20.4倍,说明随着航速的增大,水阻力的增大速度远高于船-冰接触力的增大速度。但在航速增大的过程中,纵向接触力占总阻力的比例越来越小,航速为0.939 m/s时比重约为59%;水阻力占总阻力的比例越来越大,航速为0.939 m/s时比重约为41%。
|
图 11 船体总阻力及分量随航速变化曲线 Fig. 11 Comparision of resistance components |
为进一步解释航速增大而船-冰接触力增大不明显的现象,图12给出2种航速下船体表面与碎冰接触力的分布。可以看出,在低航速时,碎冰在船体周围聚集使得船体与碎冰的接触面积较大;而高航速时,高航速及船体的兴波等使得船体排开碎冰的效果更明显,船体周围聚集的碎冰数量明显减少,因此船体与碎冰的接触面积变小,因此航速增大后接触力的增长不明显。

|
图 12 不同航速船体表面接触力分布 Fig. 12 Contace force distribution of hull surface in different speed |
本文以1艘典型冰区加强型集装箱船为研究目标,建立DEM和CFD相结合的数值模拟方法对碎冰区航行船舶的船-冰-水耦合作用进行研究。讨论了船体周围碎冰的运动状态、航行阻力特性分析以及航速对船体航行阻力的影响等,结论如下:
1)基于CFD-DEM结合的数值方法可以有效模拟船舶在碎冰区航行的过程,对碎冰在船体附近的堆积、翻转等运动状态可以有效模拟,采用该方法进行船-冰-水耦合作用分析是有效可行的。
2)碎冰在与船体接触作用后会在首部形成一个明显的减速区,使得碎冰在首部堆积。首部的碎冰一部分沿着船体侧边或底部滑行。在尾部区域,由于尾流的作用会在船体尾部形成一条碎冰数量较少的航道,而随着航速的增大,该航道碎冰变得更少,同时船体左右两侧的兴波使得船体排开碎冰的作用更加明显。
3)航速对碎冰区航行船舶阻力有重要影响,碎冰区航行阻力与敞水航行阻力曲线特性一致。随着航速的增大,水阻力的增大速度远高于船-冰接触力的增大速度,水阻力占总阻力的比重随着航速的增大而增大明显。
| [1] |
WANG J, DERRADJI A A. Numerical prediction for resisitance of Canadian icebreaker CCGS Terry Fox in level ice[C]// ICSOT 2009: Ice Class Vessels, 2011: 72.
|
| [2] |
KIM M C, LEE S K, LEE W J, et al. Numerical and experimental investigation of the resistance performance of an icebreaking cargo vessel in pack ice conditions[J]. International Journal of Naval Architecture and Ocean Engineering, 2013, 5(1): 116-131. DOI:10.2478/IJNAOE-2013-0121 |
| [3] |
郭春雨, 李夏炎, 王帅, 等. 冰区航行碎冰阻力预报数值模拟方法[J]. 哈尔滨工程大学学报, 2016, 37(2): 145-156. GUO C Y, LI X Y, WANG S, et al. A numerical simulation method for resistance prediction of ship in pack ice[J]. Journal of Harbin Engineering University, 2016, 37(2): 145-156. |
| [4] |
王超, 封振, 李兴, 等. 航行于碎冰区船舶冰阻力与冰响应探析[J]. 中国舰船研究, 2018, 13(1): 73-78. WANG C, FENG Z, LI X, et al. Analysis on ice resistance and ice response of ships sailing in brash ice[J]. Chinese Journal of Ship Research, 2018, 13(1): 73-78. |
| [5] |
李紫麟, 刘煜, 孙珊珊, 等. 船舶在碎冰区航行的离散元模型及冰载荷分析[J]. 力学学报, 2013, 45(6): 868-877. LI Z L, LIU Y, SUN S S, et al. Analysis of ship maneuvering performances and ice loads on ship hull with discrete element model in broken-ice fields[J]. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(6): 868-877. |
| [6] |
TUHKURI J, POLOJÄRVI A. A review of discrete element simulation of ice-structure interaction[J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 218, 376(2129).
|
| [7] |
CORLETT E C B, SNAITH G R. Some aspects of icebreaker design[J]. Trans. RINA, 1964, 1064(4): 389-413. |
| [8] |
郭春雨, 谢畅, 王帅. 碎冰条件下冰区船阻力性能试验研究[J]. 哈尔滨工程大学学报, 2016, 37(4): 481-486. GUO C Y, XIE C, WANG S. Resistance of ships in pack ice conditions[J]. Journal of Harbin Engineering University, 2016, 37(4): 481-486. |
| [9] |
郭春雨, 王帅, 田太平, 等. 波浪-浮冰作用下冰区船舶阻力性能试验[J]. 哈尔滨工程大学学报, 2017, 38(10): 1511-1517. GUO C Y, WANG S, TIAN T P, et al. Experiment research on ice-going ship resistance performance under combined wave-ice effect[J]. Journal of Harbin Engineering University, 2017, 38(10): 1511-1517. |
| [10] |
黄焱, 李伟, 王迎晖, 等. 大型运输船极地浮冰去航行阻力的模型试验[J]. 中国造船, 2016, 27(3): 26-35. HUANG Y, LI W, WANG Y H, et al. Model tests on the resistance of a large transport ship in arctic region with pack ice[J]. Shipbuliding of China, 2016, 27(3): 26-35. |
| [11] |
黄焱, 孙剑桥, 季少鹏, 等. 大型运输船极地平整冰区航行阻力的模型试验[J]. 中国造船, 2016, 57(3): 36-44. HUANG Y, SUN J Q, JI S P, et al. Model tests of resistance of transport vessel navigating under level ice conditions in polar region[J]. Shipbuliding of China, 2016, 57(3): 36-44. |
| [12] |
STEPHEN B P. Turbulent flows[M]. United Kindom: Cambridge University Press, 2010.
|
| [13] |
CHOI J, YOON S B. Numerical simulations using momentum source wave-maker applied to RANS equation model[J]. Coastal Engineering, 2009, 56(10): 1043-1060. DOI:10.1016/j.coastaleng.2009.06.009 |
| [14] |
CUNDALL P A, STRACK O D L. A discrete numerical model for granular assemblies[J]. Geotechnique, 1979, 29(1): 47-65. DOI:10.1680/geot.1979.29.1.47 |
| [15] |
Di RENZO A, Di MAIO F P. Comparison of contact-force models for the simulation of collisions in DEM-based granular flow codes[J]. Chemical Engineering Science, 2004, 59(3): 525-541. DOI:10.1016/j.ces.2003.09.037 |
| [16] |
TIMCO G W. Ice forces on structures: physical modelling techniques[C]// Second IAHR State-of-the-Art Report on Ice and Arctic Engineering. Canada, Newfoundland, 2015.
|
| [17] |
Brash ice tests for a Panmax bulker with ice class 1B: HSVA Report[R]. 2012.
|
 2020, Vol. 42
2020, Vol. 42
