2. 中国舰船研究设计中心 船舶振动噪声重点实验室,湖北 武汉 430063;
3. 武汉理工大学 交通学院,湖北 武汉 430063;
4. 武汉理工大学 理学院,湖北 武汉 430063
2. China Ship Development and Design Center, National key Laboratory on Ship Vibration and Noise, Wuhan 430063, China;
3. Wuhan University of Technology, School of Transportation, Wuhan 430063, China;
4. Wuhan University of Technology, School of Science, Wuhan 430063, China
在船海工程的减振领域,机械设备的减振技术经历了早期的刚性安装、单层隔振、双层隔振和浮筏隔振等几个主要阶段[1]。传统的浮筏隔振系统是将多组设备共同固定在一个公共筏架平台上,筏架平台与安装基础通过隔振器弹性连接。浮筏隔振系统能有效抑制设备的机械振动,减少噪声的传递,有利于保证设备的精度,因此得到了广泛的应用[2-5]。随着浮筏隔振技术的发展,对其大型化、集成化的要求也越来越高,浮筏结构开始与舰船舱室结合,形成了舱筏结构。舱筏内由于人员和重要设备的存在,对其隔振和抗冲击性能提出了更高的要求。传统形式的浮筏结构已很难满足这种性能要求,因此需要设计一些新型浮筏结构。桁架式箱体浮筏系统是一种基于多级隔振理念设计出的新型隔振装置。这种浮筏结构将舱室与隔振设施融为一体,克服了传统浮筏结构体积大、空间利用率差的特点,同时因为采用桁架式结构,在保证足够刚度和抗冲击能力的前提下,能够大大减轻浮筏的总体质量。
对于浮筏结构而言,隔振器的布置直接关系到隔振效果的好坏[6]。对浮筏结构的隔振器配置进行合理的选型及优化,有助于提高浮筏系统的减振和抗冲击性能。学者们在对浮筏系统隔振器选型和布置优化等方面,已有一定的研究成果。张华良[7],张衡[8]和张辉[9]等以弹簧单元模拟隔振器,分别用力传递率法、功率流理论和振级落差法,评估了隔振器的隔振效果。结果表明,隔振器刚度的增加会对隔振效果会产生不利影响,而增大隔振器的阻尼会提高浮筏系统的隔振效果。祝华[10]的研究表明,隔振器刚度中心与质量承载中心纵向偏差不超过两隔振器间距的3%时,对隔振效果无明显影响。杜奎[11]利用导纳原理分析了双层减振装置隔振器上下对齐安装和不对齐安装方案的传递功率流,认为不对齐安装更有利于降低宽频率振动的传递,提高隔振效果。杨本磊[6]分析了4种不同隔振器组合布置形式浮筏模型的模态和隔振效果,认为下层隔振器的布置位置对浮筏隔振系统的模态影响不大,而下层隔振器两侧布置时,会有较好的隔振效果。
本文针对某种新型桁架式箱体浮筏舱筏结构,建立有限元模型,并对隔振器配置了3种方案,对各种方案下浮筏结构的静力、抗冲击效果以及隔振效果进行比对分析。
1 浮筏数值模型及方案布置本文研究对象为某新型桁架式箱体浮筏,筏架主体部分长、宽、高分别为8 m,6.08 m和2.1 m。上、下面板厚度0.012 m。浮筏总质量为23.84 t,材料为Q345钢,密度为7.85×103 kg/m3,弹性模量E=2.06×1011 N/m2,泊松比σ=0.3。浮筏上层的主要设备有:显控台、操作台、雷达机柜等,下层主要用作生活舱室使用,主要设备有集成冷柜和厨房设备,每台设备均使用4个隔振器与浮筏连接,设备总质量9.79 t。
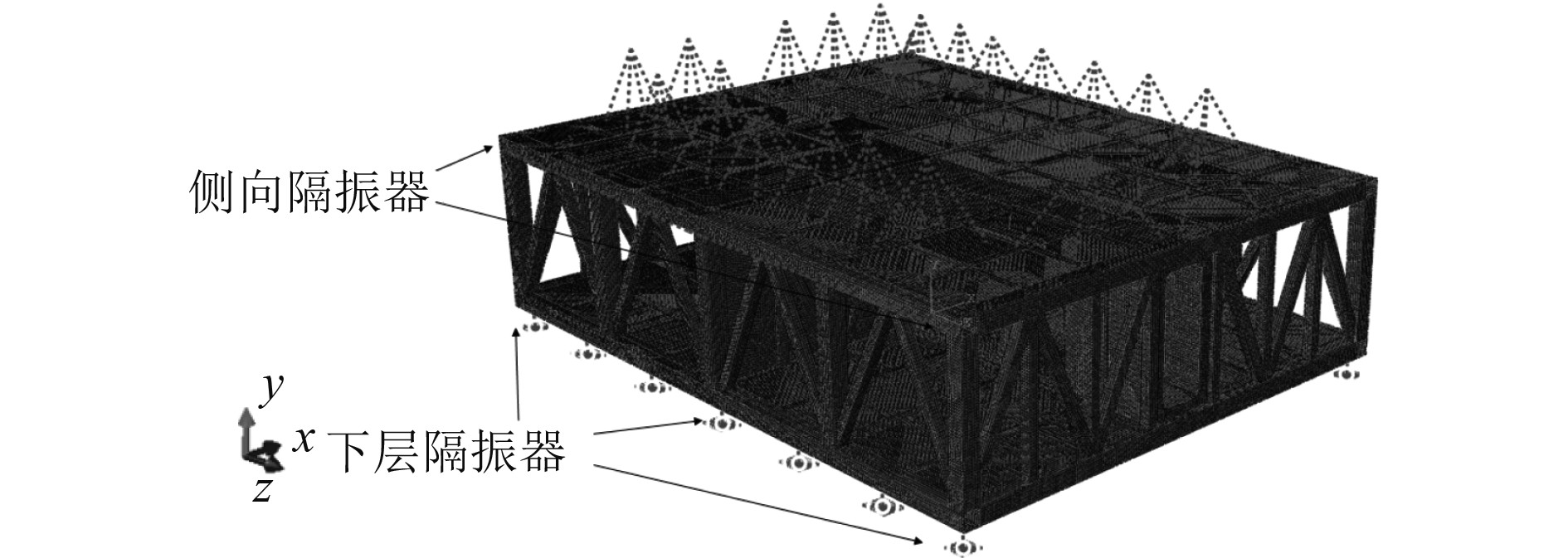
采用有限元软件Abaqus对筏架进行建模,筏架结构采用板单元建模,由于隔振器质量较小,忽略其内部结构,用三向弹簧单元模拟隔振器,以弹簧单元两端位移差值代表隔振器变形量。对于筏架上的设备,由于其尺度和筏架相比要小的多,故采用质量点的方式模拟设备,质量点与弹簧单元上端点之间采用多点约束(Multi-point constraint,MPC)的方式进行刚性约束。对浮筏系统进行1∶1 建模,模型的坐标系方向为Z轴正向指向艇体纵向首部,Y轴正向为铅垂向上,X轴正向指向艇体右舷。坐标原点设在筏架下面板几何中心。结合工程项目的实际需求,以及隔振器的性能参数,选用大变形KB系列隔振器并设计了3种方案。不同方案的隔振器配置方式及隔振器参数如表1~表3所示。考虑到浮筏结构与船体倾斜摇摆状态下可能与侧壁擦碰,又布置了6个刚度较小的侧向隔振器,侧向及下层隔振器均为左右对称分布,大致位置如图1所示。
|
|
表 1 桁架式箱体浮筏隔振器布置方案 Tab.1 Arrangement scheme of truss box floating raft isolator |
|
|
表 2 KB隔振器型号及各向刚度参数 Tab.2 Model and isotropic stiffness parameter of KB isolator |
|
|
表 3 KB隔振器的冲击参数 Tab.3 Shock parameters of KB isolator |
|
图 1 浮筏系统隔振器布置示意图 Fig. 1 Arrangement of vibration isolator for floating raft system |
舰船在航行时,会出现不同程度的倾斜,因此需要对浮筏结构在不同倾斜状态下的应力和位移进行评估。在桁架式浮筏隔振系统有限元模型建立的基础上,对桁架浮筏在正浮、横倾30°和纵倾15°的结构响应进行分析。浮筏系统总静刚度如表4所示。将下层隔振器的刚度设置为静刚度,隔振器下端节点采用固定约束边界条件,限制其在6个方向上的自由度。在计算时,仅考虑设备和筏架自身的重量,对模型施加重力场进行计算。艇体在正浮时,重力加速度在垂向(Y向)和横向(X向)的分量分别为Gy=9810 mm/s2,Gx=0 mm/s2。艇体在横倾30°状态下重力加速度在Y向和X向的分量为:Gy=8494.5 mm/s2,Gx=4905 mm/s2。艇体在纵倾15°状态下重力加速度在Y向和Z向的分量为:Gy=9475 mm/s2,Gz=2539 mm/s2。
|
|
表 4 不同方案隔振系统总静刚度/N·mm−1 Tab.4 Total static stiffness of vibration isolation system with different schemes |
静力计算结果如表5所示。在正浮、横倾30°和纵倾15° 三种状态下,各种方案的隔振器变形值为负数,表示在重力的作用下,隔振器处于压缩状态。且各种状态下方案1的下层隔振器变形最大,方案3最小,这是由方案1的总静刚度最小,方案3的总静刚度最大决定的。对于筏架的最大位移值,可以得到同样的结论,即浮筏的最大位移随着隔振系统的总静刚度的增加而减小。另外,对比筏架的最大位移值和下层隔振器的变形值,可以发现筏架的要大些,这是因为筏架位移除了下层隔振器的变形值外,筏架作为弹性体还有自身的形变量。筏架的最大应力,相对来说都非常小,值都在21.8~38.75 MPa范围内,远小于材料的屈服极限。
|
|
表 5 三种方案静力计算结果 Tab.5 Static calculation results of three schemes |
本文冲击环境基于GJB1060.1-91中冲击设计输入,参考德国BV043-85标准将浮筏系统的设计冲击响应关于频率的冲击谱等效转化为系统的冲击载荷-时间变化曲线[12-13]。已知浮筏系统总质量为33.63 t,设备抗冲击能力设计为A级,浮筏安装在艇体基座上,安装形式为弹性安装。设计的浮筏系统的垂向冲击载荷输入如图2所示。

|
图 2 浮筏系统垂向冲击加速度时域曲线 Fig. 2 Time-domain curve of vertical impact acceleration of floating raft system |
计算浮筏的抗冲击效果时,采用瞬态动力学显式分析的方法,将加速度冲击波曲线作为动载荷施加到浮筏系统上直接计算浮筏系统在冲击荷载下的动态响应。计算时,将隔振器刚度统一设置为冲击刚度,冲击计算时间为1 s。由于浮筏是通过隔振器与船体相连接。冲击载荷通过船体作用于整个系统,因此,将冲击载荷加于筏架下层隔振器的底端和侧向隔振器的外端。
筏架结构在冲击的作用下,隔振器由于阻尼的原因会反复震荡衰减,冲击能量逐渐耗散,如图3所示。由于垂向冲击,筏架下层隔振器的垂向变形量远大于其他2个方向,变形量因阻尼的作用呈现明显的周期性变化,且振幅逐步衰减。桁架箱体浮筏不仅承载了设备,还作为人员活动舱室,保护设备和人员的安全,其上、下面板的峰值加速度须小于人体的承载极限(约为12 g)。方案3的筏架结构上、下面板加速度如图4所示。由于设备和人员的存在,筏架又非刚体结构,所以在冲击作用下,筏架上、下面板的加速度并不是处处相等的。且此时上、下面板的峰值加速度值约为13.25 g,大于人体承载极限(约12 g),表明方案3配置下的浮筏系统抗冲击性能较差。

|
图 3 垂向冲击作用下下层隔振器变形量随时间衰减曲线(方案3) Fig. 3 Attenuation curve of deformation of lower-layer isolator with time under vertical impact(Scheme 3) |

|
图 4 垂向冲击作用下筏架上、下面板加速度云图(方案3) Fig. 4 Acceleration clouds of the upper and lower panels of the raft under vertical impact(Scheme 3) |
冲击作用下的结果如表6所示。3种方案下的应力的最大值为103.3 MPa,小于材料的许用极限。不同方案下层隔振器的最大变形量为19.40 mm,根据表3数据可知,当下层隔振器形变量不超过30 mm时,下层隔振器的形变量均在线性范围内。由此可计算出,3种方案对应的冲击总刚度分别为50400 N/mm,46000 N/mm和55200 N/mm。
|
|
表 6 不同方案下筏架在垂向冲击作用下的结果统计 Tab.6 Result statistics of raft under different impacts under different schemes |
由于方案2和方案3的隔振器个数和布置形式相同,其中方案3冲击总刚度较大,从而造成方案3的隔振器的变形量及筏架的最大位移较小,筏架的最大应力及上、下面板的峰值加速度较大。对比方案1和方案2的结果,筏架最大位移和隔振器变形量的变化与冲击总刚度变化并不完全一致,原因是方案1使用了较多的隔振器,其布置形式与方案2不同,从而导致方案1隔振器最大变形量较方案2的大。根据式(1)可计算得方案1的隔振器吸收的能量约为9484 J,方案2隔振器吸收的总能量约为8541 J。
| $ U = \frac{1}{2}k\Delta {x^2}\text{。} $ | (1) |
式中:
在方案1的总冲击刚度大于方案2的前提下,由于隔振器个数和布置形式的关系,隔振器吸收的能量反而越多,上、下面板的峰值加速度反而越小。由此可见,决定上下面板峰值加速度的因素除隔振器冲击总刚度外,还有隔振器个数和布置形式。
4 隔振效果分析对筏架模型进行隔振效果分析,将模型中隔振器的刚度都设置为动刚度,筏架下层隔振器下端节点处设置等效的弹簧单元代替浮筏的基座,等效基座的底部采用固定边界条件,限制其在6个方向上的自由度。在计算时,在上层设备处施加1个垂直向下的100 N正弦激励力,采用固定边界条件,计算频率范围为0~1000 Hz。
评估隔振效果的常用方法有:力传递率、插入损失、振级落差、振动烈度和功率流[14]。同其他方法相比,振级落差的测量更为简单方便,本文选用振级落差的方式来评价浮筏系统的隔振效果。加速度振级落差是指弹性系统两端加速度比值的对数的20倍。计算时,从能量传递的角度考虑,常用加速度的平方
| $ {D_a} = 10\lg \left( {\dfrac{{\dfrac{1}{N}\displaystyle\sum\limits_{i = 1}^N {{{\left| {a_i^t} \right|}^2}} }}{{\dfrac{1}{N}\displaystyle\sum\limits_{i = 1}^N {{{\left| {a_i^b} \right|}^2}} }}} \right) = 10\lg \left( {\dfrac{{\displaystyle\sum\limits_{i = 1}^N {{{\left| {a_i^t} \right|}^2}} }}{{\displaystyle\sum\limits_{i = 1}^N {{{\left| {a_i^b} \right|}^2}} }}} \right)\text{。} $ | (2) |
式中:
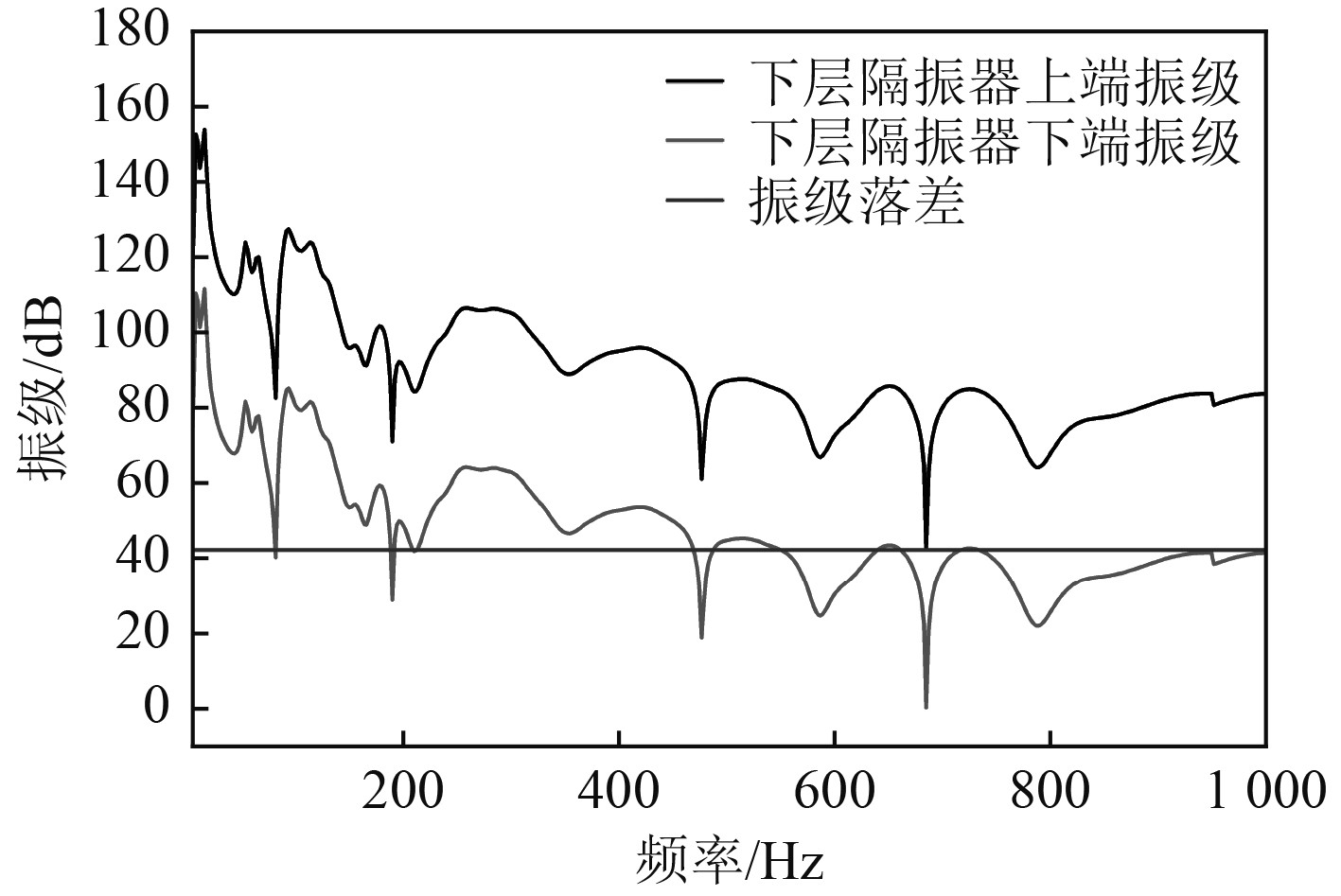
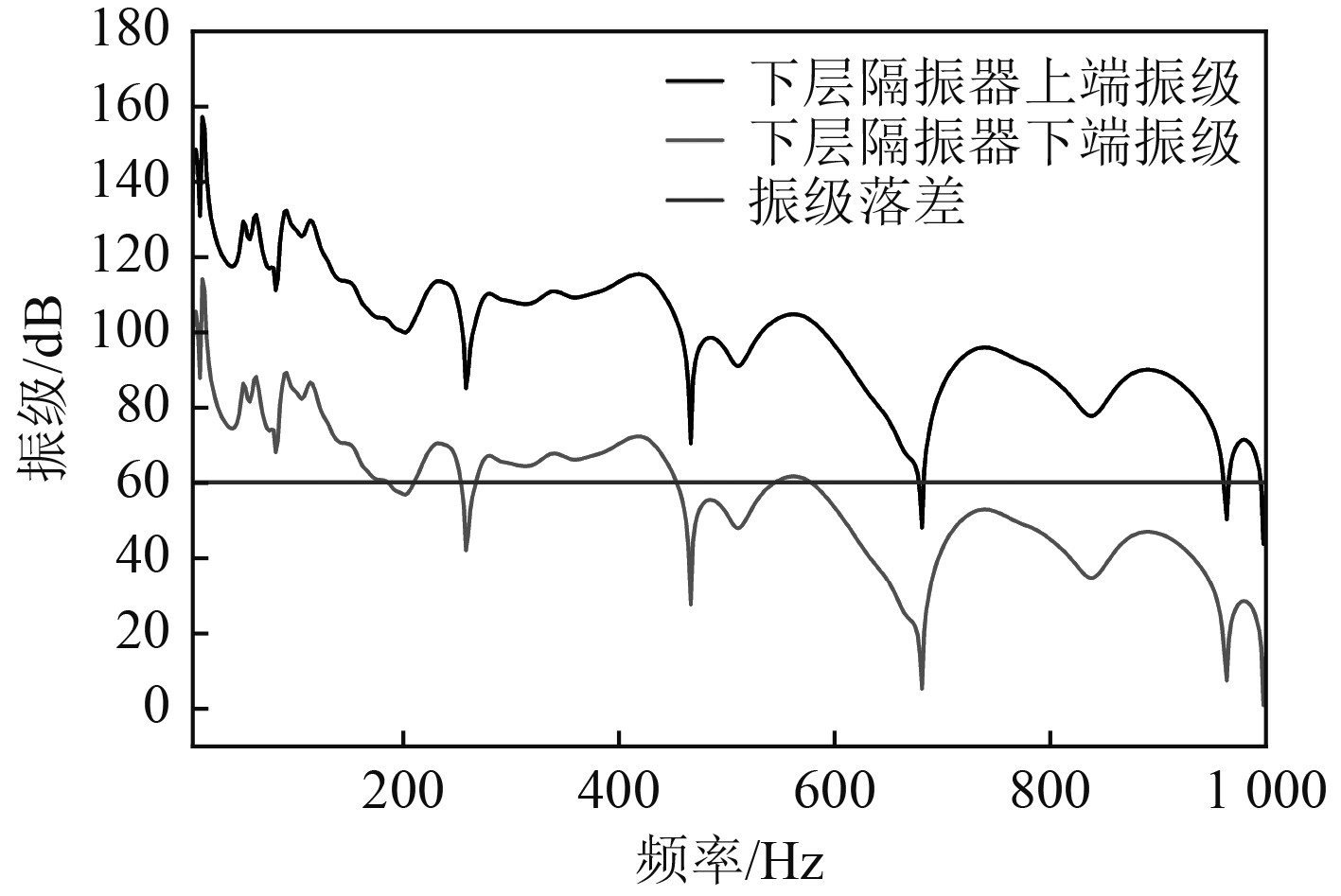
下层隔振器振级和振级落差曲线如图5~图7所示。对比方案1和方案2的曲线图,在0~14 Hz内,筏架的振级急剧增大并达到峰值。在14~400 Hz的区间,筏架振级处于大幅波动状态,并在波动中快速下降,且隔振器动刚度越大,波动范围就越大。在400~1000 Hz的中高频段,浮筏振级处于比较平缓的箱体波动中,波动范围的大小与隔振器动刚度变化保持一致,动刚度越大,波动范围也越大。3种方案隔振器的振级落差都维持在比较稳定的状态,方案1的下层隔振器振级落差为47.6 dB,方案2和方案3下层隔振器两端的振级落差均为42.3 dB。由此可见,隔振器动刚度较小时,浮筏系统拥有更好的隔振效果。
|
图 5 下层隔振器振级和振级落差曲线(方案1) Fig. 5 Vibration level and vibration level drop curve of lower layer isolator(Scheme 1) |

|
图 6 下层隔振器振级和振级落差曲线(方案2) Fig. 6 Vibration level and vibration level drop curve of lower layer isolator(Scheme 2) |
|
图 7 桁架浮筏结构下层隔振器振级和振级落差曲线(方案3) Fig. 7 Vibration level and vibration level drop curve of lower layer isolator(Scheme 3) |
本文对新型桁架式箱体浮筏结构设计了3种隔振器配置方案,且对3种配置方案下的浮筏系统在静力状态、抗冲击性能及隔振效果的差异进行了比对分析,主要结论如下:
1)在静力状态下,3种隔振器配置方案的应力、位移都较小,满足设计要求。浮筏的最大位移和下层隔振器变形量随隔振器总静刚度的增加而减小。
2)在垂向冲击作用下,浮筏的隔振器形变量因阻尼作用会随时间产生周期性衰减。同等个数和布置形式下,隔振器冲击总刚度越大,浮筏的抗冲击效果越差,认为隔振器冲击总刚度及个数和布置形式都会对上下面板峰值加速度产生影响。
3)浮筏结构振级在低频段快速下降,在中高频段,振级的波动范围会随动刚度的增大而增大,浮筏系统的隔振效果相对稳定,较小的动刚度具有更好的隔振效果。
4)基于3种方案下的静力、抗冲击及隔振效果分析,优先选择方案1对当前浮筏进行隔振器配置。
| [1] |
余永丰, 彭旭, 刘远国. 整舱浮筏全频段能量传递数值分析研究[J]. 舰船科学技术, 2006(S2): 77-80. |
| [2] |
PININGTON R. J., WHITE R. G.. Damping by a nearly continuous distribution of nearly undamped oscillatiors: linear analysis[J]. Journal of Sound And Vibration, 2001, 240(4): 711-731. |
| [3] |
SCIULLY D., INMAN D. J.. Isolation design for a flexible system[J]. Journal of sound and vibration, 1995, 212(2): 251-267. |
| [4] |
TRUMPER D L, SATO T. A vibration isolation platform[J]. Mechatronics, 2002, 12(2): 281-294. DOI:10.1016/S0957-4158(01)00068-X |
| [5] |
沈密群, 严济宽. 舰船浮筏装置工程实例[J]. 噪声与振动控制, 1994(1): 21-23. |
| [6] |
杨本磊. 船舶浮筏隔振系统振动特性分析[D]. 大连: 大连海事大学, 2011.
|
| [7] |
张华良, 瞿祖清, 傅志方. 浮筏隔振系统各主要参数对系统隔振性能的影响[J]. 振动与冲击, 2000(2): 7-10+6+92. |
| [8] |
张衡. 框架式浮筏隔振系统设计及隔振特性研究[D]. 杭州: 浙江工业大学, 2012.
|
| [9] |
张辉. 船舶浮筏隔振系统的性能分析及参数优化匹配研究[D]. 武汉: 华中科技大学, 2016.
|
| [10] |
祝华, 胡明, 王强, 等. 隔振布置偏差对双层隔振系统整体性能的影响研究[J]. 噪声与振动控制, 1996(5): 7-10. |
| [11] |
杜奎. 浮筏隔振系统隔振器最佳布置方案研究[J]. 海军工程大学学报, 2005, 17(2): 92-94. |
| [12] |
刘林炜. 浮筏隔振系统静动态响应直接计算法研究[D]. 武汉: 华中科技大学, 2018.
|
| [13] |
GJB1060.1-91, 舰船环境条件要求—机械环境[S]. 北京: 国防科学技术工业委员会, 1991.
|
| [14] |
朱石坚, 楼京俊, 何其伟等. 振动理论与隔振技术[M]. 北京: 国防工业出版社, 2006
|
 2020, Vol. 42
2020, Vol. 42
