2. 中国舰船研究院,北京 100192;
3. 哈尔滨工程大学,黑龙江 哈尔滨 150001
2. China Ship Research and Development Academy, Beijing 100192, China;
3. Harbin Engineering University, Harbin 150001, China
船舶结构在机械设备不平衡激扰力和不平衡激扰力矩作用下,会产生多种形式的振动,从而引起结构向外辐射噪声,不仅对船舶声学性能产生负面影响,而且对船载机械设备的正常运行以及人员的舒适性带来极大威胁[1-3]。
船舶结构振动声辐射特性与其所受到的激励载荷密切相关,如何明确设备对船舶结构的激励载荷输入[4]与减小船舶结构振动声辐射一直以来都是国内外研究人员着力解决的问题[5-7]。早期专家学者对机械设备结构振动特性的分析,大多是采用互易原理和等效力方法经测量换算后获得的[8-10]。随着研究的深入,逐渐采用设备输入到船体结构的功率来表示机械设备结构振动特性的基本参数[11-12]。王振鸿[13]系统介绍了船舶结构中能量的传递以及设备激振力获取的问题。俄罗斯中央科学研究院[14]建立了“设备—隔振器—基座结构”强迫振动系统的一般求解方程,形成了分析系统激励载荷的理论。马建强[15]等采用数值方法分析了典型船舶基座结构的阻抗特性,并研究了基座结构参数与结构形式对舱段声振特性的影响,
综上所述,目前国内外所进行的研究工作大多数只是探究了在单一载荷形式对于船舶结构振动声辐射特性的影响,一定程度上忽略了船舶结构振动声辐射特性与激励载荷形式因素之间的关系,因此本文将开展在设备不平衡激扰力、不平衡激扰力矩、不平衡激扰力与力矩联合作用下船舶结构振动声辐射特性分析,并归纳总结不同激励载荷对于船舶结构振动声辐射的影响。
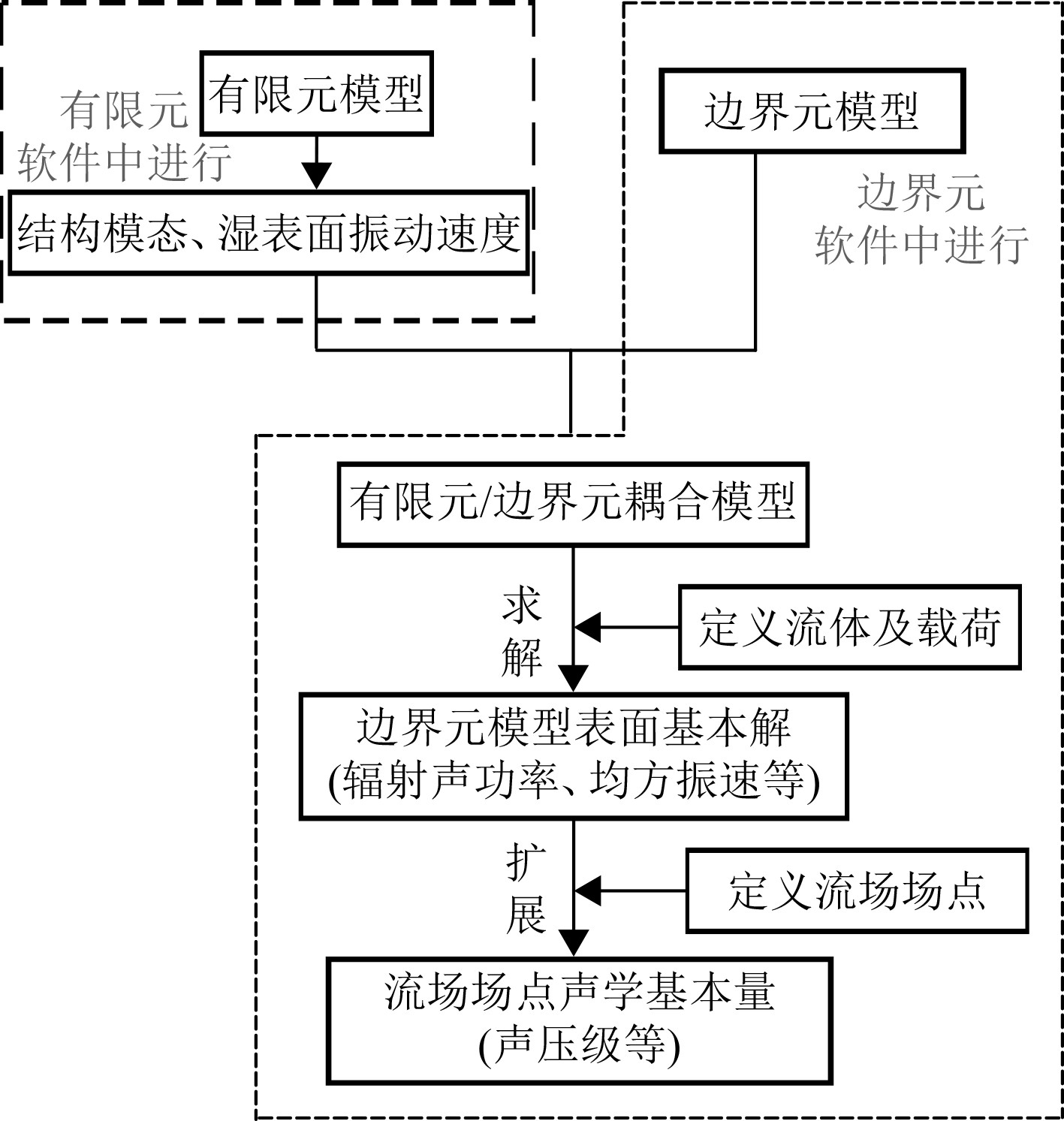
1 船舶结构振动声辐射理论分析 1.1 声固耦合理论基础船舶结构振动产生的声辐射声场与船舶结构之间相互耦合,这种耦合作用相比空气噪声源与空气的耦合作用更为复杂,所以针对船舶这种大型复杂结构且考虑到船舶振动多是低频激励源,有限元/边界元法是较适合解决船舶结构振动声辐射的方法。声固耦合有限元法计算船舶结构振动声辐射计算流程如图1所示。
|
图 1 声固耦合有限元法计算流程图 Fig. 1 Acoustic-structure coupling finite element method calculation flowchart |
假定流体为理想声学介质,流场中声波的波动方程为:
| ${\nabla ^2}p = \frac{1}{{{c^2}}}\frac{{{\partial ^2}p}}{{\partial {t^2}}}\text{。}$ | (1) |
其中:p为瞬时声压;t为时间;c为声速;
约去声压变分,得到流体区域内声场的有限元方程矩阵如下:
| ${{{M}}_f}\ddot P + {{{K}}_f}P + {\rho _f}{{R}}\ddot U = 0\text{。}$ | (2) |
式中:
当考虑在流体区域边界Σ上和流体与船体结构的交界面S上有阻尼吸声材料时阻尼时,矩阵方程式为:
| ${{{M}}_f}\ddot P + {{{C}}_f}\dot P + {{{K}}_f}{{P}} + {\rho _f}{{R}}\ddot U = 0\text{。}$ | (3) |
式中:
类似的,有结构阻尼舱段结构振动的有限元方程为:
| ${{{M}}_s}\ddot U + {{{C}}_s}\dot U + {{{K}}_s}{{U}} = {{{F}}_s}\text{。}$ | (4) |
式中:
船舶结构与声场耦合振动矩阵方程为:
| ${{{M}}_s}\ddot U + {{{C}}_s}\dot U + {{{K}}_s}{{U}} = {{{F}}_s} + {{{F}}_f}\text{。}$ | (5) |
式中:
将以上两式联立得:
| $\begin{split} & \left( {\begin{array}{*{20}{c}} {{{{M}}_s}}&0\\ {{\rho _f}{{R}}}&{{{{M}}_f}} \end{array}} \right)\left\{ {\begin{array}{*{20}{l}} {\ddot U}\\ {\ddot P} \end{array}} \right\} + \left( {\begin{array}{*{20}{c}} {{{{C}}_s}}&0\\ 0&{{{{C}}_f}} \end{array}} \right)\left\{ {\begin{array}{*{20}{l}} {\dot U}\\ {\dot P} \end{array}} \right\} + \\ & \quad \quad \left( {\begin{array}{*{20}{c}} {{{{K}}_s}}&{ - {{{R}}^{\rm{T}}}}\\ 0&{{{{K}}_f}} \end{array}} \right)\left\{ {\begin{array}{*{20}{l}} {{U}}\\ {{P}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{l}} {{{{F}}_s}}\\ 0 \end{array}} \right\}\text{。} \end{split}$ | (6) |
根据上式,可以得到船体结构表面节点处的位移和声压,当流场边界无声波反射时,可以看作无限流体域结构与流体的耦合振动和声辐射问题。
1.2 船舶结构分析模型建立 1.2.1 舱段结构基准模型选取综合考虑本文研究目的旨在探索不同类型激励载荷作用下结构振动声辐射特性规律,因此设置本文研究目标模型为某船舶典型机舱舱段结构。舱段模型几何尺寸为4×2.4×2 m,舷侧舱壁结构沿纵向布设有7根加强筋,相邻加强筋间距0.5 m,舷侧舱壁结构沿纵向布设有7根加强筋,相邻加强筋间距0.5 m,肋骨选用尺寸0.14×0.12×0.008×0.01 m T型材,舱壁厚度为0.01 m;舱室上甲板与舱室内底板同样布设有加强结构,顶部肋板2.1×0.006×0.1 m,底部肋板1.8×0.008×0.2 m;基座安装在舱室底板的局部式基座,属水平方向上的中央位置,主要由面板、腹板及肘板组成,舱段结构原模型的基座结构面板厚度0.006 m、腹板厚度0.006 m、肘板厚度0.006 m。
1.2.2 声固耦合分析模型建立在开展舱段结构振动特性分析之前,首先建立内外流场,定义物理属性,然后根据计算的频率范围确定流场单元尺寸,最后将结构和流场之间相互耦合。为保证计算结果的正确性,在板架结构中一个波长范围内必须包含至少4~5个节点,可以根据下式确定最大网格尺寸。
| $x \leqslant 0.4{\text{π}} {\left( {{\rm{D}}/\rho h} \right)^{1/4}}{\omega ^{ - 1/2}}\text{。}$ | (7) |
基于上述理论,建立船舶典型舱段结构有限元分析模型,结构网格尺寸λ=0.04 m。结构面单元数46000个,有限元模型单元总数46000个,边界元模型单元总数5000个,如图2所示。

|
图 2 舱段结构基准模型有限元/边界元模型 Fig. 2 Finite element/boundary element model of cabin structure benchmark model |
船用机械设备按照振动机理不同,可分为往复类、旋转类及流体动力类等,有些设备在运行过程中会产生不平衡激扰力或不平衡激扰力矩,如推进电机、汽轮发电机等设备。因此本文在分析设备对安装基础激励特性的过程中,分为设备不平衡力单独作用,设备不平衡激扰力矩单独作用以及联合作用3种工况分别进行讨论。考虑到机械设备产生的激振载荷主要处于低频段,所引起结构辐射噪声也主要处于低频范围,因此计算频段选定为1~200 Hz。
2.1 设备不平衡力激励作用 2.1.1 设备对基座激励力分析设备对安装基础的激励载荷与设备自身以及安装方式密切相关,为便于研究,采用常见安装方式即设备通过隔振器与基座相连接的方式,分析基座所受到的激励载荷。
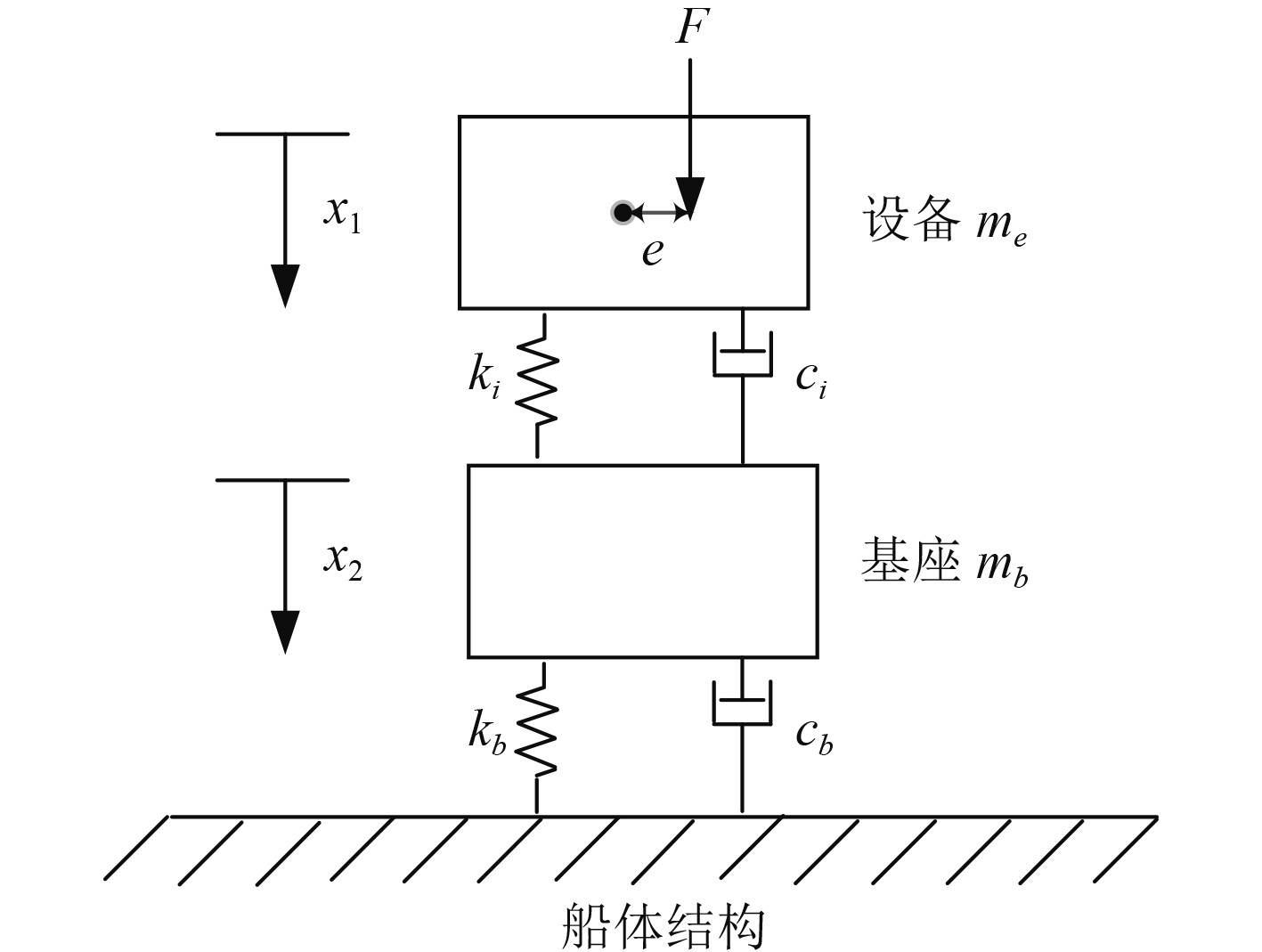
当仅有不平衡激扰力作用在设备上时,设备-基座耦合模型简化为一维振动模型,如图3所示。
|
图 3 不平衡力作用下设备与基座耦合模型图 Fig. 3 Coupling model diagram of equipment and base under unbalanced force |
根据强迫振动理论[16],不平衡激扰力单独作用情况下的振动系统的运动方程为:
| $\left\{ \begin{array}{l} {m_e}{{\ddot x}_1} + {c_i}\left( {{{\dot x}_1} - {{\dot x}_2}} \right) + {k_i}\left( {{x_1} - {x_2}} \right) = {F_0}{e^{j\omega t}}\text{,} \\ {m_b}{{\ddot x}_2} + \left( {{c_i} + {c_b}} \right){{\dot x}_2} - {c_i}{{\dot x}_1} + \left( {{k_i} + {k_b}} \right){x_2} - {k_i}{x_1} = 0 \text{。}\\ \end{array} \right.$ | (8) |
经求解,基座受到的激励载荷为:
| ${F_T} = {k_i}\left( {{x_1} - {x_2}} \right) + {c_i}\left( {{{\dot x}_1} - {{\dot x}_2}} \right) = \left( {{k_i} + j{c_i}\omega } \right)\left( {{x_1} - {x_2}} \right)\text{。}$ | (9) |
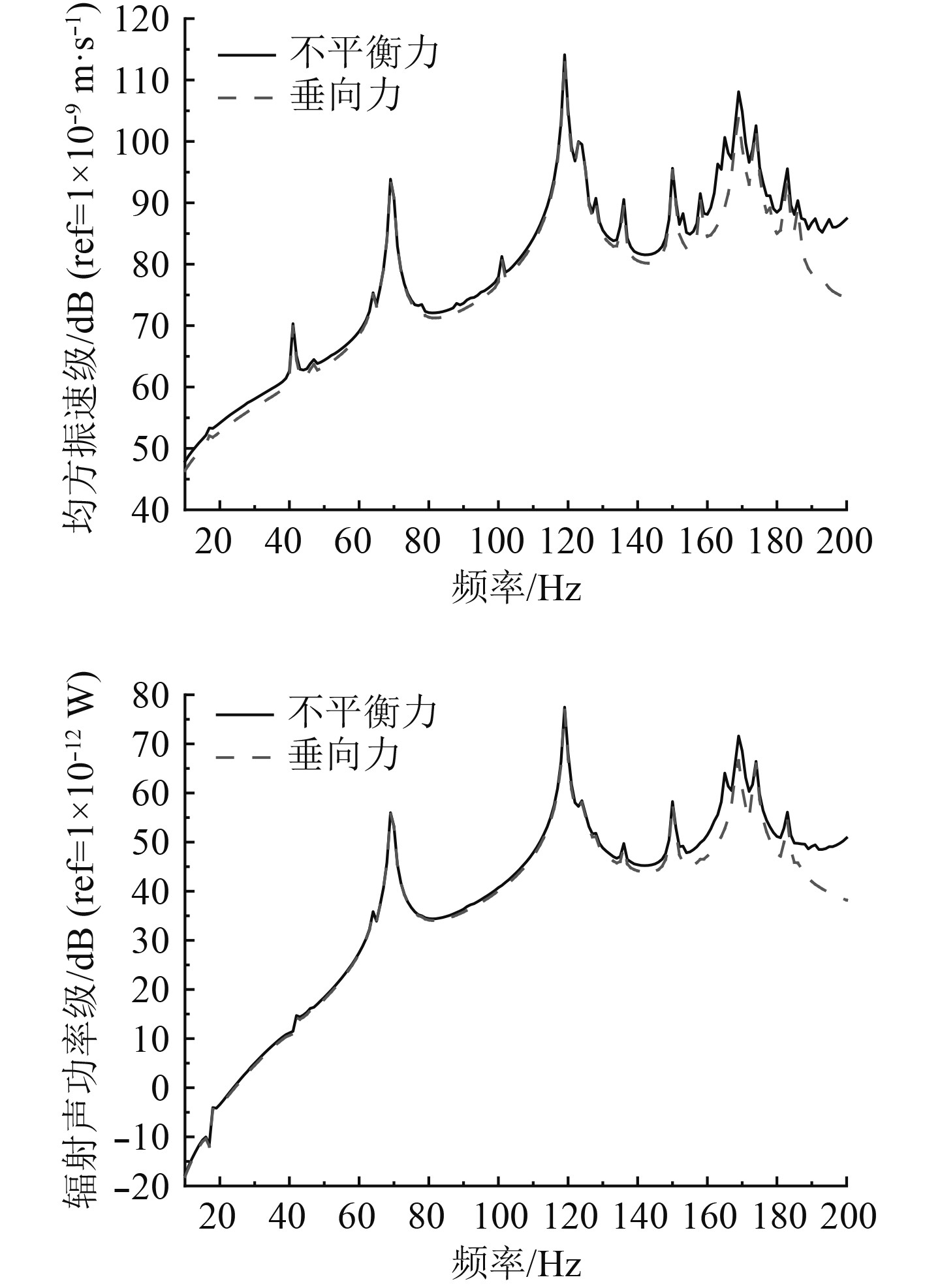
如果设备主要因为自身不平衡力产生对外部的激励,此设备自身的不平衡力既有垂向力(垂直于基座面板)又有水平力,且两者幅值大小相当。因此在分析设备不平衡力作用下,在设备质心处施加垂向与水平方向单位力,舱段结构在不平衡力作用下振动声辐射计算结果如图4所示。
|
图 4 不平衡力作用下舱段结构振动声辐射特性 Fig. 4 Vibration and sound radiation characteristics of cabin structure under unbalanced force |
可以看出,舱段结构在不平衡激振力载荷作用下相应曲线趋势与垂向力作用下响应曲线趋势基本一致,振动峰值所对应的频率基本相同,且在所计算频段范围内,只考虑垂向力的计算结果与不平衡力计算结果在大多数频点处响应值相差3 dB以内,由此可知,不平衡力作用下,垂向载荷起到主导作用。随着频率的升高,振动频谱特性更加丰富,小的振动峰出现频率增大。部分典型振动峰值频率下结构振型图如图5所示。

|
图 5 峰值频点处振动响应云图对比 Fig. 5 Contrast of vibration response cloud images at peak frequency points |
由结构振动位移响应云图可以发现,69 Hz时结构振型均表现为甲板结构的1阶振动,119 Hz处表现为甲板2阶振动,侧面舱壁主要表现为板格中心振动,随着频率的升高,结构主要表现为板格中心振动。
2.2 设备不平衡力矩激励作用 2.2.1 设备对基座激励力分析当设备受到不平衡激扰力矩作用时,设备-基座耦合振动系统会出现平面内扭转运动,因此基座受到的载荷会发生相应改变。
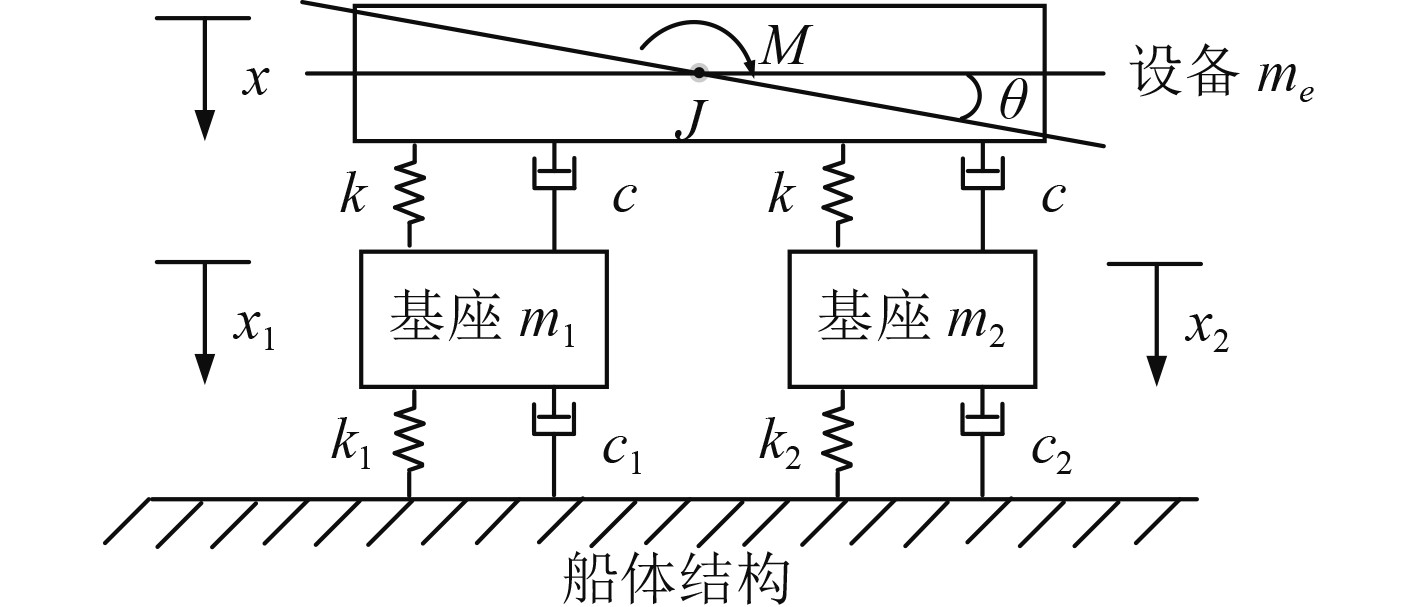
假设设备的不平衡激扰力矩的作用点为设备的质心,隔振器对称布置在设备几何中心两侧;由于设备将发生扭转振动,两侧基座受到的激励大小不同,因此分析模型分为左右两基座进行讨论,耦合振动系统计算模型如图6所示。
|
图 6 不平衡力矩作用下设备与基座耦合模型图 Fig. 6 Coupling model diagram of equipment and base under unbalanced moment |
对设备与基座联立振动方程组,则设备通过隔振器向安装基础所传递的激励力可表示为:
| $\begin{split} &{F_{TL}} = k\left( {x - a\theta - {x_1}} \right) + c\left( {\dot x - a\dot \theta - {{\dot x}_1}} \right)\text{,} \\ &{F_{TR}} = k\left( {x - b\theta - {x_2}} \right) + c\left( {\dot x - b\dot \theta - {{\dot x}_2}} \right)\text{。} \end{split} $ | (10) |
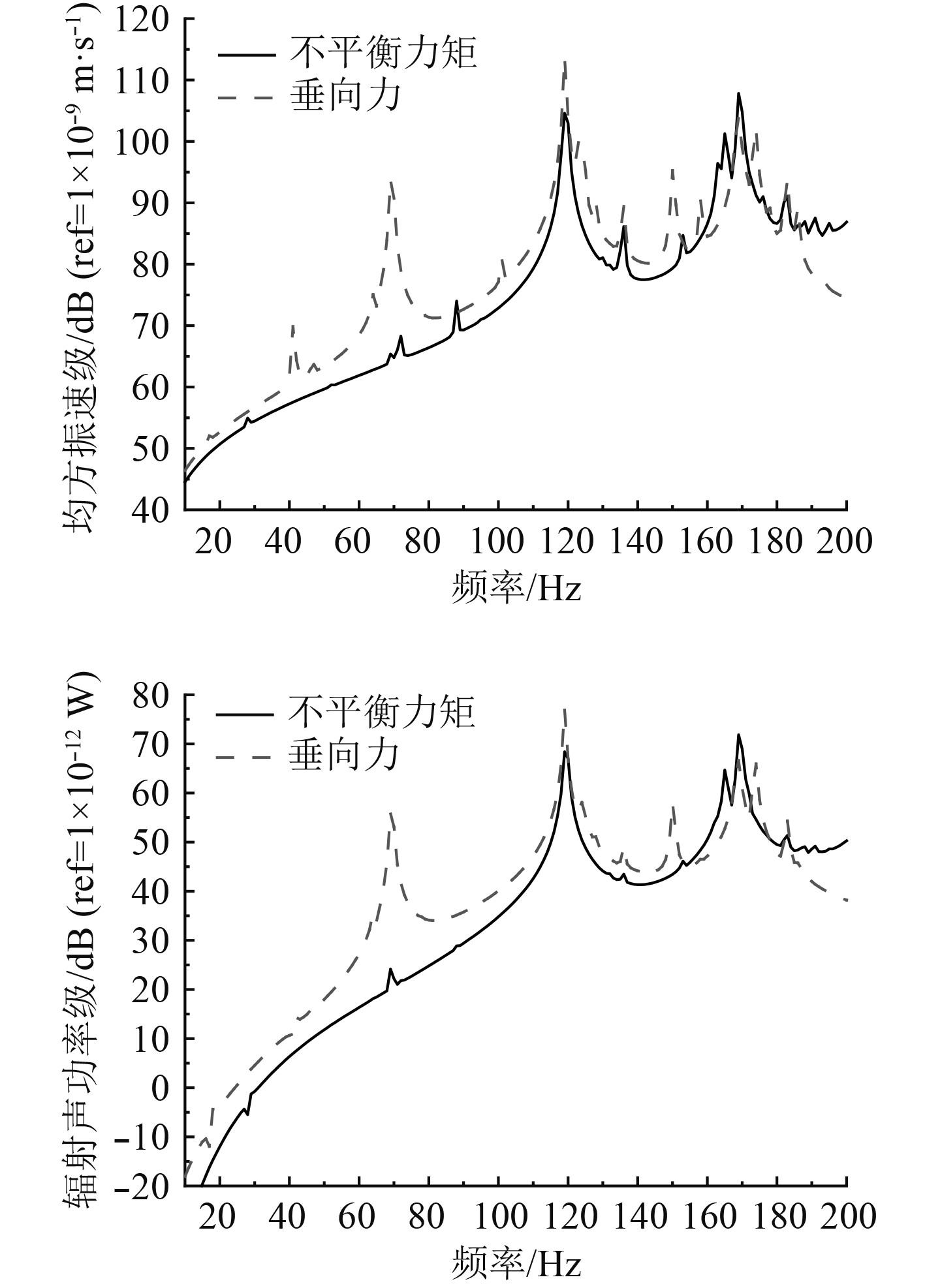
以设备产生的不平衡力矩为输入载荷,分析计算结构的声振特性。如果设备主要因为自身不平衡弯矩对外发出激励,此设备以自身转动为主。因此在分析设备不平衡力矩作用下,在设备质心处施加单位力矩,舱段结构在不平衡弯矩作用下振动声辐射计算结果如图7所示。
|
图 7 不平衡力矩作用下舱段结构振动声辐射特性 Fig. 7 Vibration and sound radiation characteristics of cabin structure under unbalanced moment |
可以看出,舱段结构在不平衡激振力矩载荷作用下,响应曲线趋势与垂向力作用下曲线趋势基本一致,在低频处出现明显振动峰值,但波峰数量以及峰值大小较不平衡力载荷作用时均有减小。在计算频段内,舱段结构声振特性曲线在大多数频点相差5 dB以内,且在垂向力作用下结构响应值较不平衡弯矩作用下响应值偏大,由此所计算出的结果可以认为是偏于安全的,所以对于以不平衡弯矩载荷为主的机械设备来说,将其等效为垂向力作用是可行的。随着频率的升高,振动频谱特性更加丰富,小的振动峰出现频率增大。部分典型振动峰值频率下结构振型图如图8所示。
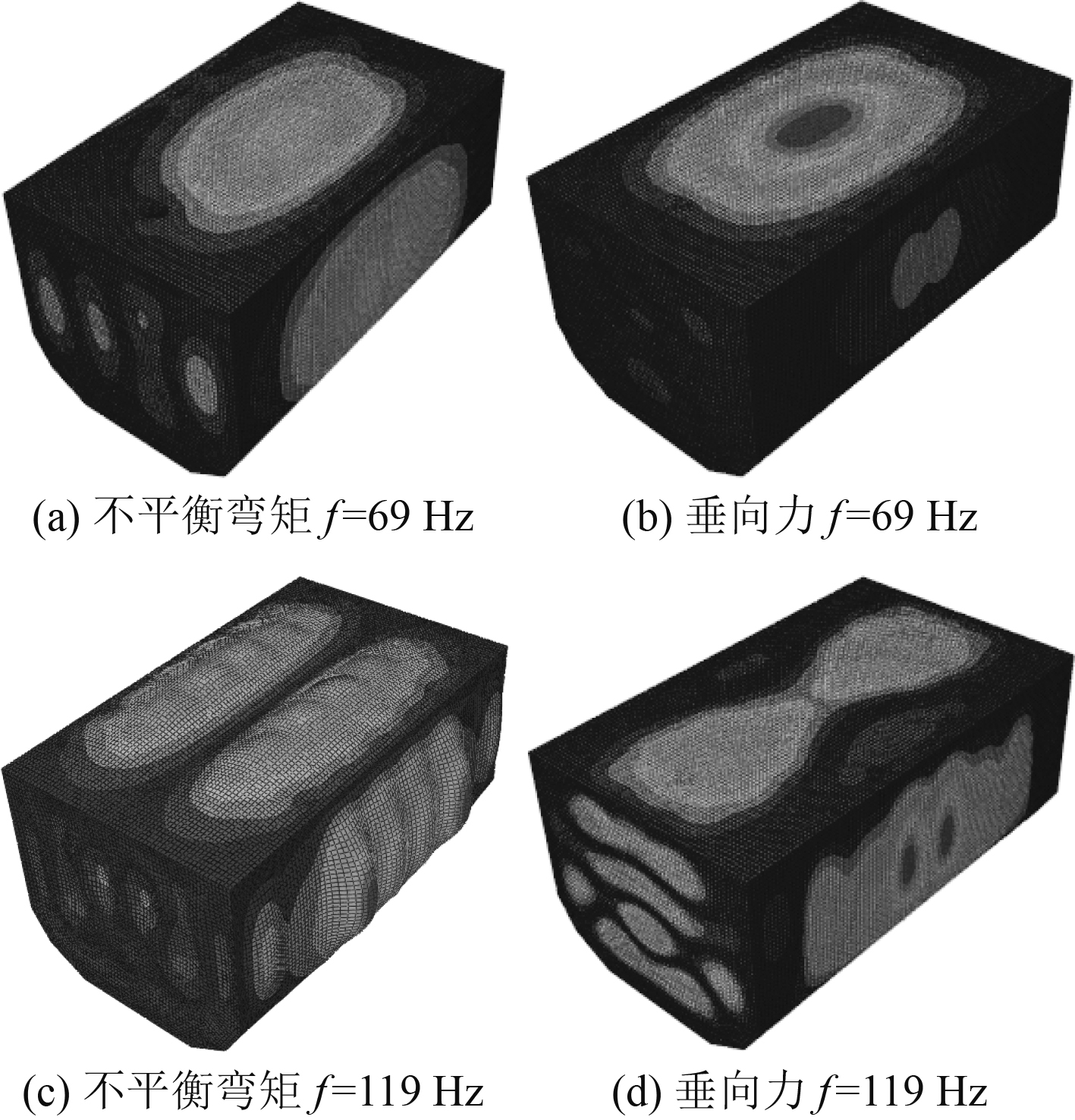
|
图 8 峰值频点处振动位移响应云图 Fig. 8 Vibration displacement response cloud diagram at peak frequency |
由结构振动位移响应云图可以发现,69 Hz频率时结构振型均表现为舱壁结构的1阶振动,119 Hz处表现为甲板横向2阶振动,侧面舱壁主要表现为板格中心振动,随着频率的升高,结构主要表现为板格中心振动。
2.3 设备不平衡力与力矩联合激励作用 2.3.1 设备对基座激励力分析当设备是不平衡激扰力和不平衡激扰力矩共同作用的情况时,该振动系统会同时出现上述所描述的激扰力方向的振动以及平面内的扭转振动,仍按上述思路分析基座所受的载荷。
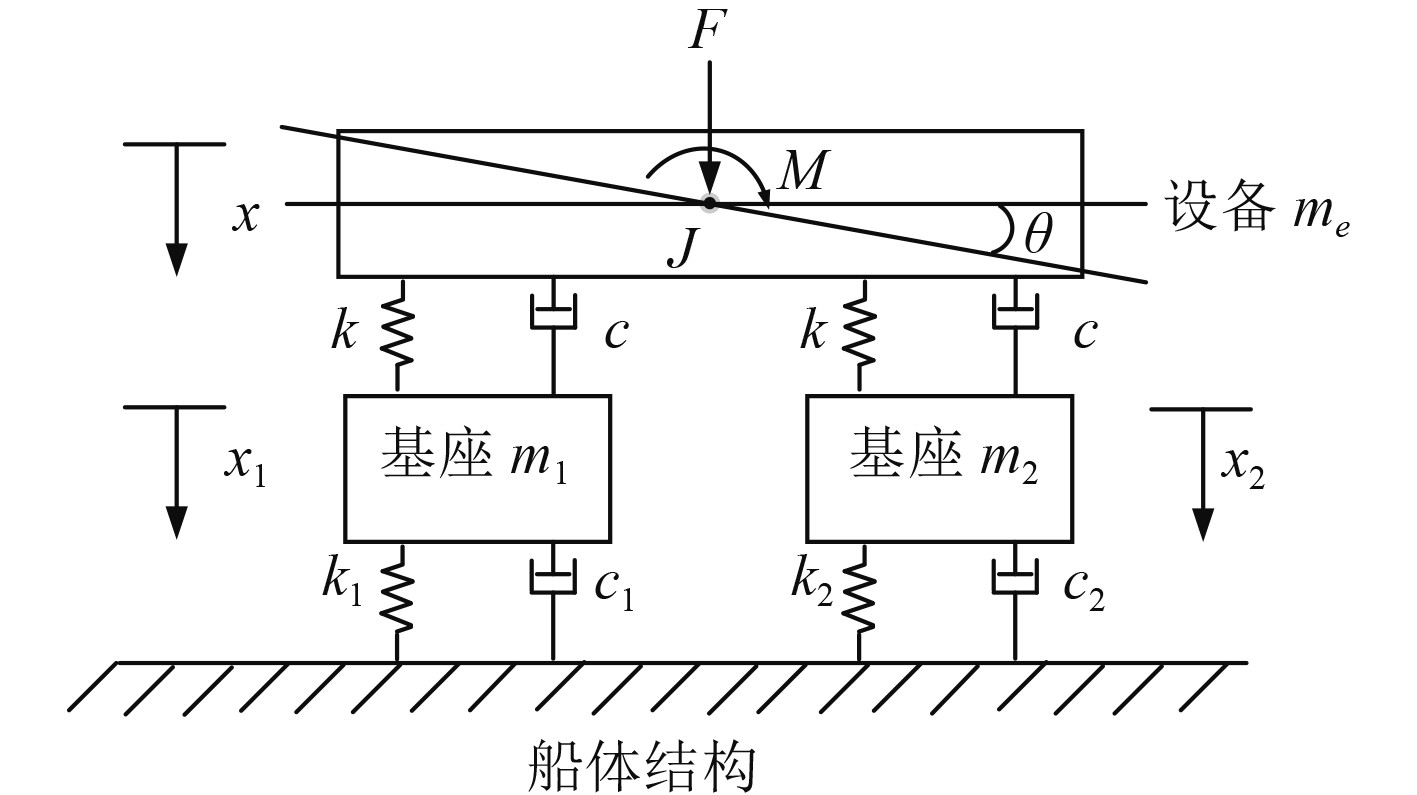
假设设备的不平衡激励力和不平衡激扰弯矩的作用点为设备的质心,耦合系统分析模型进行简化,如图9所示。
|
图 9 不平衡力与力矩联合作用下设备与基座耦合模型图 Fig. 9 Coupled model diagram of equipment and base under the combined action of unbalanced force and moment |
对设备基座联立振动方程组,根据平衡条件,则设备通过隔振器向安装基础所传递的激励力可表示为:
| $\begin{split} & {F_{TL}} = k\left( {x - a\theta - {x_1}} \right) + c\left( {\dot x - a\dot \theta - {{\dot x}_1}} \right)\text{,} \\ &{F_{TR}} = k\left( {x - b\theta - {x_2}} \right) + c\left( {\dot x - b\dot \theta - {{\dot x}_2}} \right) \text{。} \end{split} $ | (11) |
当设备激励既有不平衡力又有不平衡力矩时,在设备质心处施加不平衡单位力与不平衡单位力矩,舱段结构在不平衡力与不平衡力矩联合作用下振动声辐射计算结果如图10所示。

|
图 10 不平衡力与不平衡力矩联合作用下舱段结构振动声辐射特性 Fig. 10 Vibration and sound radiation characteristics of cabin structure under the combined action of unbalanced force and unbalanced moment |
可以看出,舱段结构在不平衡激振力与激振力矩载荷联合作用下,在低频处出现明显振动峰值,且峰值数量较不平衡力单独作用或不平衡弯矩单独作用时更为丰富,幅值也较载荷单独作用时有一定增加;与垂向力单独作用相比较,不平衡力与力矩联合作用情况下结构响应略微增大,在大多数频点响应值相差4 dB以内,但在舱段结构固有频率所对应的频点处,峰值大小相差较小,响应值相差小于1 dB,可见在不平衡力与力矩等效为垂向载荷作用时,仍能有效地反映出结构振动特性。随着分析频率的增大,振动频谱特性更加丰富,小的振动峰出现频率增大。部分典型振动峰值频率下结构振型图如图11所示。
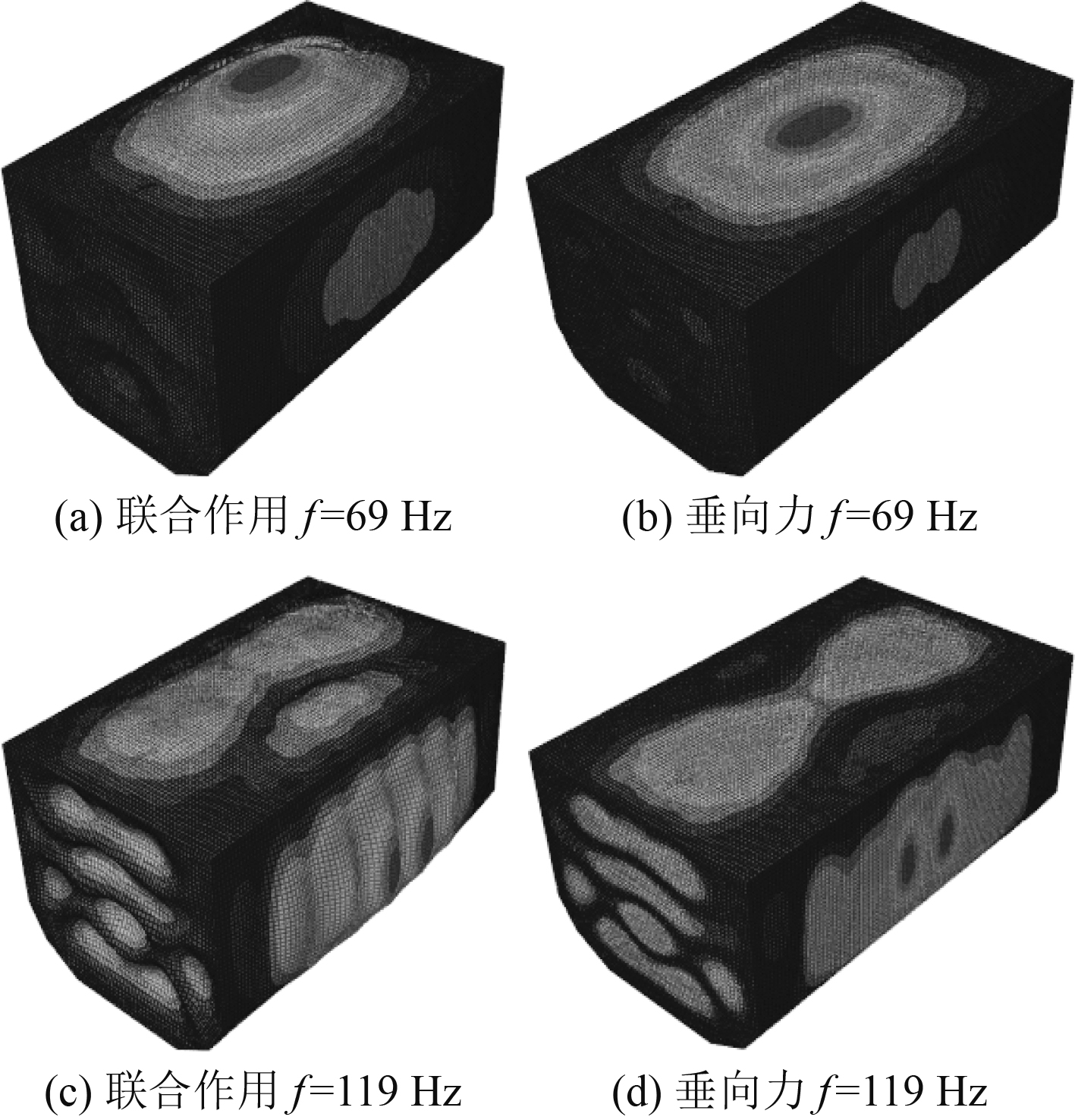
|
图 11 峰值频点处振动位移响应云图 Fig. 11 Vibration displacement response cloud diagram at peak frequency |
由结构振动位移响应云图可以发现,69 Hz频率时结构受迫振动振型均表现为甲板结构的1阶振动,119 Hz处表现为甲板2阶振动,侧面舱壁主要为板格中心振动,随着频率升高,结构模态信息更为丰富,主要表现为板格中心振动。
3 结 语本文首先对声固耦合方法进行简单阐述,在此基础上,从“设备-基座-船舶结构”系统耦合振动角度出发,针对设备不平衡激扰力、不平衡激扰力矩、不平衡激扰力与力矩联合作用等典型设备激励载荷,以船舶结构振动与辐射噪声为考核量,探究舱段结构在设备不同典型设备激励载荷作用下辐射噪声的影响变化,得出如下主要结论:
1)舱段结构在不平衡激振力载荷作用下相应曲线趋势与垂向力作用下响应曲线趋势基本一致,振动峰值所对应的频率基本相同。对于以不平衡力载荷为主的机械设备来说,垂向载荷起到主导作用。随着频率的升高,振动频谱特性更加丰富,小的振动峰出现频率增大。
2)舱段结构在不平衡激振力矩载荷作用下,响应曲线趋势与垂向力作用下曲线趋势基本一致,在低频处出现明显振动峰值,但波峰数量以及峰值大小较不平衡力载荷作用时均有减小。对于以不平衡弯矩载荷为主的机械设备来说,将其等效为垂向力作用是可行的。随着频率的升高,振动频谱特性更加丰富,小的振动峰出现频率增大。
3)舱段结构在不平衡激振力与激振力矩载荷联合作用下,在低频处出现明显振动峰值,且峰值数量较不平衡力单独作用或不平衡弯矩单独作用时更为丰富,幅值也较载荷单独作用有一定增加。可见在不平衡力与力矩等效为垂向载荷作用时,仍能有效反映结构振动特性。随着分析频率的增大,振动频谱特性更加丰富,小的振动峰出现频率增大。
| [1] |
孙增华, 王丹, 于洋, 等. 船舶舱室噪声的工程预报方法[J]. 船舶工程, 2014(S1): 246-251. |
| [2] |
钱江, 李楠, 史文强. 复合材料在国外海军舰船上层建筑上的应用与发展[J]. 舰船科学技术, 2015(1): 233-237. |
| [3] |
吴刚. 海洋工程结构振动与声学特性计算[D]. 上海: 上海交通大学, 2008.
|
| [4] |
魏来. 基于台架试验的实船设备激励载荷计算方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2017.
|
| [5] |
黎胜. 结构振动声辐射的数值分析方法和优化设计研究进展[C]. 船舶水下噪声学术讨论会. 2015.
|
| [6] |
俞孟萨, 吴有生. 舰船声弹性及声辐射理论研究概述[J]. 船舶力学, 2008, 12(4): 669-676. |
| [7] |
何祚镛. 水下噪声及其控制技术进展和展望[J]. 应用声学, 2002, 21(1): 26-34. |
| [8] |
VERHEIJ J W. Acoustic modeling of machinery excitation[J]. Inter Sym. Shipboard Acoustics 76’Proceeding[C]. Ed by Janssen JH, 1976.
|
| [9] |
STEENHOCK H F. The riciprocal measurement of mechanical-acoustic transfer function[J]. Acoustica, 1970, 23: 301. |
| [10] |
JANSSEN M H A. The use of an equivalent forces method for the experimental quantification of structural sound transmission in ship[J]. Journal of Sound and Vibration, 1999, 226(2): 305-328. DOI:10.1006/jsvi.1999.2303 |
| [11] |
GOYDER HGD, WHITE RG. Vibrational power flow from machines into built2up structures Part3: Power flow through isolation systems[J]. Journal of Sound and Vibration, 1980, 68(1): 97-117. DOI:10.1016/0022-460X(80)90454-X |
| [12] |
PETERSON B, PLUNT J. On effective mobilities in the prediction of structure borne-sound transmission between a source structure and a receiving structure, theoretical ground and basic experimental studies[J]. Journal of Sound and Vibration, 1982, 82(4): 517-529. DOI:10.1016/0022-460X(82)90405-9 |
| [13] |
王振鸿, 机械噪声控制技术—机械阻抗与能量传递[R]. 中国船舶科学研究中心科技报告, 1997.
|
| [14] |
俄罗斯联邦克雷洛夫中央科学研究院. 船舶声学特性的物理基础[R], 2001.
|
| [15] |
马建强, 贾地, 王雪仁, 等. 基座阻抗均匀化对加筋柱壳水下辐射噪声的影响[J]. 噪声与振动控制, 2017, 37(1): 98-102. |
| [16] |
季文美, 方同, 陈松淇. 机械振动[M]. 北京: 科学技术出版社, 1985.
|
 2020, Vol. 42
2020, Vol. 42
