0 引　言

小水线面双体船（Small Waterplane Area Twin Hull Ship，SWATH）是近年来发展起来的一种高性能船型，由于具有优良的耐波性、宽敞而规整的甲板面积等显著优点而日益受到重视，在军用和民用领域得到了广泛应用与快速发展^[1-2]。我国自20世纪末开始SWATH船的设计研究，并于2001年建造了国产第1艘230吨级的SWATH船。中国船级社（CCS）也于2005年颁布了《小水线面双体船指南》（以下简称《指南》），为设计者进行构件尺寸设计、屈服屈曲强度校核、疲劳评估等提供了有效参考^[3]。

SWATH船船型特殊，具有较宽的横向接触面积和特殊的横剖面几何形状，所受波浪载荷情况明显。与常规单体船不同，SWATH船的横向波浪的诱导载荷达到相当的量级，引起船体结构出现高应力^[4]，导致SWATH船上层建筑下围与甲板相交处常规腹板加强十字焊接型节点结构疲劳强度问题特别突出，有必要进行疲劳强度评估及结构抗疲劳优化设计。

《指南》对钢制材料的S-N曲线选取仅参见CCS规范要求，而随着规范版本的不断更新^[5]，对焊接节点的S-N曲线选取原则发生变化，使得疲劳理论评估结果缺乏有效验证分析。此外，目前对SWATH船结构疲劳问题的研究主要依据规范和直接计算分析方法，少量的疲劳试验也是基于标准试件^[6-8]，针对实板厚结构模型的疲劳试验较少^[9]。因此，针对小水线面双体船上层建筑的疲劳典型节点，采用模型试验的方法确定该部位的S-N曲线特性十分必要，能够准确评价节点的疲劳特性。

本文基于某小水线面双体船整船有限元计算结果，确定疲劳问题严重的部位；根据受疲劳影响区域的结构情况，设计实板厚的节点疲劳强度试验模型；模拟典型工况下的载荷情况，开展疲劳强度试验，获取在不同加载水平下的疲劳失效循环次数，拟合S-N曲线，并对该节点部位进行疲劳强度评估。

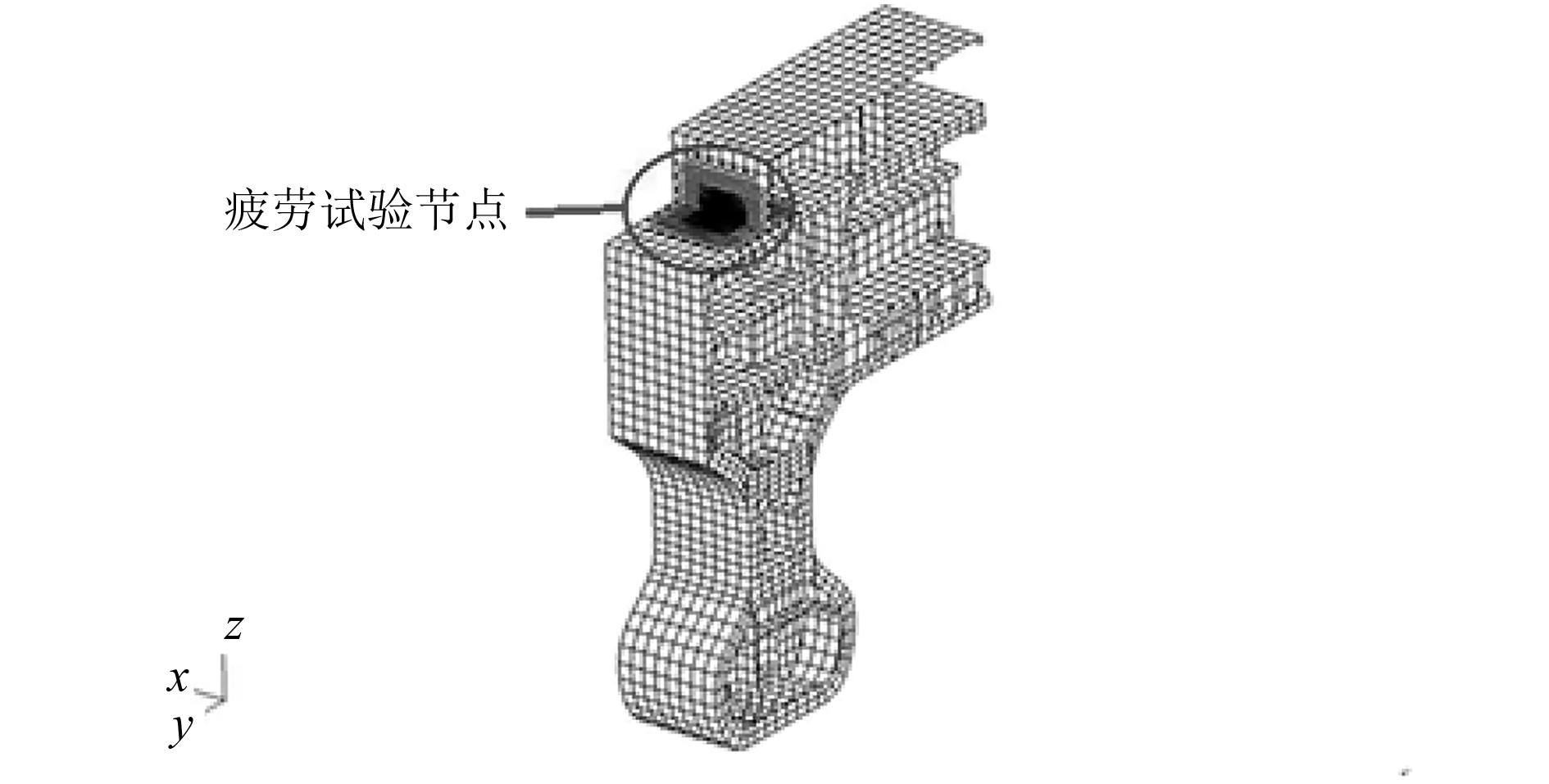
1 疲劳强度试验设计 1.1 试验模型设计

鉴于双体船结构的特殊性，采用更为精确的谱分析法进行全船疲劳强度计算。结果表明，横浪工况下的疲劳损伤占主导地位，其横向开力引起船中附近01甲板与上层建筑外侧壁交汇处应力集中现象明显，选取船中FR92处作为试验部位，如图1所示。

为模拟该节点的受力状态，保证试件与目标船高应力区域一致及高应力区域的应力分布相似，并考虑试验限制条件，对目标船结构做相应的简化处理。将目标船01甲板下横舱壁高度进行缩减，并补焊高厚度板材，确定模型尺寸（长×宽×高）为 ${\rm{2}}{\rm{.4\;m}} \times {\rm{0}}{\rm{.4\;m}} \times {\rm{1}}{\rm{.56\;m}}$ 。模型所选材料及焊接形式与实船保持一致。节点1为校核部位优化前的腹板加强十字焊接接头，校核热点位于接头焊缝处；节点2为优化后的一般焊接接头，校核热点位于肘板焊缝趾端，模型如图2所示。

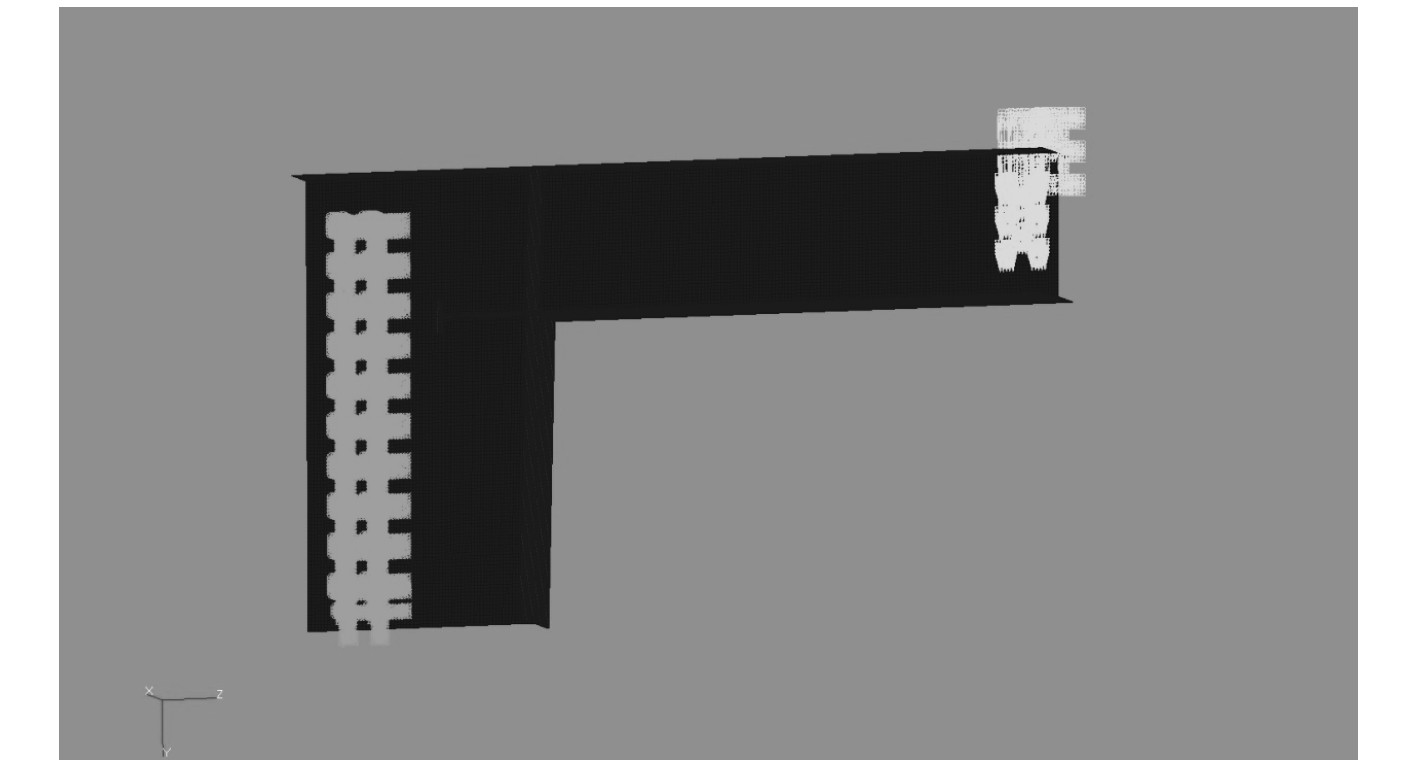
2种节点的试验件均采用一端刚性固定，另一端沿Y向施加力，模拟横浪工况下的横向对开力引起的横向弯矩，边界条件及加载如图3所示。

将试件加载后的有限元应力分布结果与实船局部细化有限元模型计算结果对比，应力云图如图4和图5所示，热点位置及应力分布梯度基本一致。

1.2 试验情况概述

试验设备主要采用MTS加载试验系统和DH5902动态信号采集分析系统，模型疲劳试验时的应力状态利用电阻应变片测得。电阻应变片布置前应将测点附近打磨光滑，消除表面光洁度的影响。试验加载采用应力比 R =－1的正弦波。选取监测点处裂纹穿透壁厚作为疲劳破坏标准，记录此时的循环次数。

2种节点的模型各制作6个试验件，分别选取3个载荷工况。由于加载形式，边界条件比较复杂，需要根据疲劳试验模型设计配套的工装。

在疲劳试验前，进行静应力分布测试，确认热点附近的应力梯度，找出热点位置，再从中抽取需要的点做动态应变测量。节点1的热点应力测量考虑腹板的影响，在腹板及面板上均布置电阻应变片。节点2的模型试件在肘板上端焊趾根部布置电阻应变片。

试验载荷加载时应结合经济性和实验数据分散性原则，最终确定加载水平，如表1所示。

2 疲劳强度试验结果分析 2.1 试验结果

通过试验发现，节点1试件的疲劳破坏部位均在该十字接头的面板焊缝处，未在腹板焊缝处发现裂纹，位置较理想，疲劳裂纹从焊缝根部扩展贯穿角焊缝。节点2的疲劳破坏部位在肘板焊趾处，位置较理想，为预计危险点，疲劳裂纹起始于焊趾处缺陷，并从焊趾扩展进母材。

热点应力水平由与裂纹扩展方向垂直的45°范围内的主应力插值得到。因此，测点处主应力按下述公式计算：

$\begin{split} {\sigma _{1,2}} =& \frac{E}{2}\left[ {\frac{{{\varepsilon _0} + {\varepsilon _{90}}}}{{1 - \mu }} \pm } \right.\\& \left. {\frac{1}{{1 + \mu }}\sqrt {{{\left( {{\varepsilon _0} - {\varepsilon _{90}}} \right)}^2} + {{\left( {2{\varepsilon _{45}} - {\varepsilon _0} - {\varepsilon _{90}}} \right)}^2}} } \right]\text{。} \end{split}$

(1)

式中： ${\varepsilon _0}$ ， ${\varepsilon _{45}}$ ， ${\varepsilon _{90}}$ 为直角应变片测得的3个方向的应变。

再按下式插值，计算得到热点处的应力：

${\sigma _h} = \frac{{3{\sigma _{0.5t}} - {\sigma _{1.5t}}}}{2}\text{。}$

(2)

式中： ${\sigma _{0.5t}}$ ， ${\sigma _{1.5t}}$ 为测点最大主应力, $t$ 为板厚。

试验结果如表2和表3所示。

2.2 S-N曲线拟合

鉴于试验件数目有限，试验数据分散性较大，统计分析结果无法作为疲劳曲线的真实斜率，因此本文采用定斜率的极大似然法进行S-N曲线拟合。参考类似结构来确定S-N曲线的斜率m，参照新版规范^[5]的S-N曲线选取原则，本试验选取的2种焊接节点可采用定斜率m=3。

实践经验表明，对数疲劳寿命在中等疲劳寿命区都遵循正态分布。在双对数坐标系下，中值S-N曲线可用线性关系表示，即

$\lg N = \lg A - m\lg S\text{。}$

(3)

式中：A与m为待定常数。

假定在任意应力水平 ${S_i}$ 下，对数疲劳寿命的母体平均值和母体标准差分别为 ${\mu _i}$ 和 ${\sigma _i}$ 。采用极大似然法，只需通过子样估计 ${\lg _A}$ 便可拟合中值S-N曲线。

设似然函数为：

$L = \prod\limits_{i = 1}^n {\left\{ {\frac{1}{{{\sigma _i}\sqrt {2{\text{π}} } }}\exp \left[ { - \frac{1}{{2\sigma _i^2}}{{\left( {\lg {N_i} - {\mu _i}} \right)}^2}} \right]} \right\}} ,$

(4)

参数 ${\lg _A}$ 的估计值为：

$\lg \mathop A\limits^ \wedge = \frac{1}{n}\sum\limits_{i = 1}^n {\lg {N_i}} - \frac{m}{n}\sum\limits_{i = 1}^n {\lg {S_i}} \text{。}$

(5)

根据如上方法对试验数据进行处理，可得节点1和节点2的定斜率中值S-N曲线，如表4所示。

根据疲劳可靠性理论，船体结构的疲劳是一个受到大量因素影响的复杂现象，需要引入存活概率p保证疲劳实际寿命大于设计寿命的概率不能过低。一般采用成组试验方法得到各个应力水平下的对数疲劳寿命的均值和标准差^[10-11]。在船舶及海洋工程中，对一般构件常取p=97.72% ( ${\mu _P} = - 2.0$ )，挪威船级社和法国船级社将标准差统一取为定值。标准差 ${S_{\lg A}}$ 参阅规范取为0.2^[12]，P-S-N曲线表达式为：

$\lg N = \lg {A_p} - m\lg S\text{。}$

(6)

式中： $\lg {A_p} = \lg \mathop A\limits^ \wedge + {\mu _p}{S_{\lg A}}$ 。

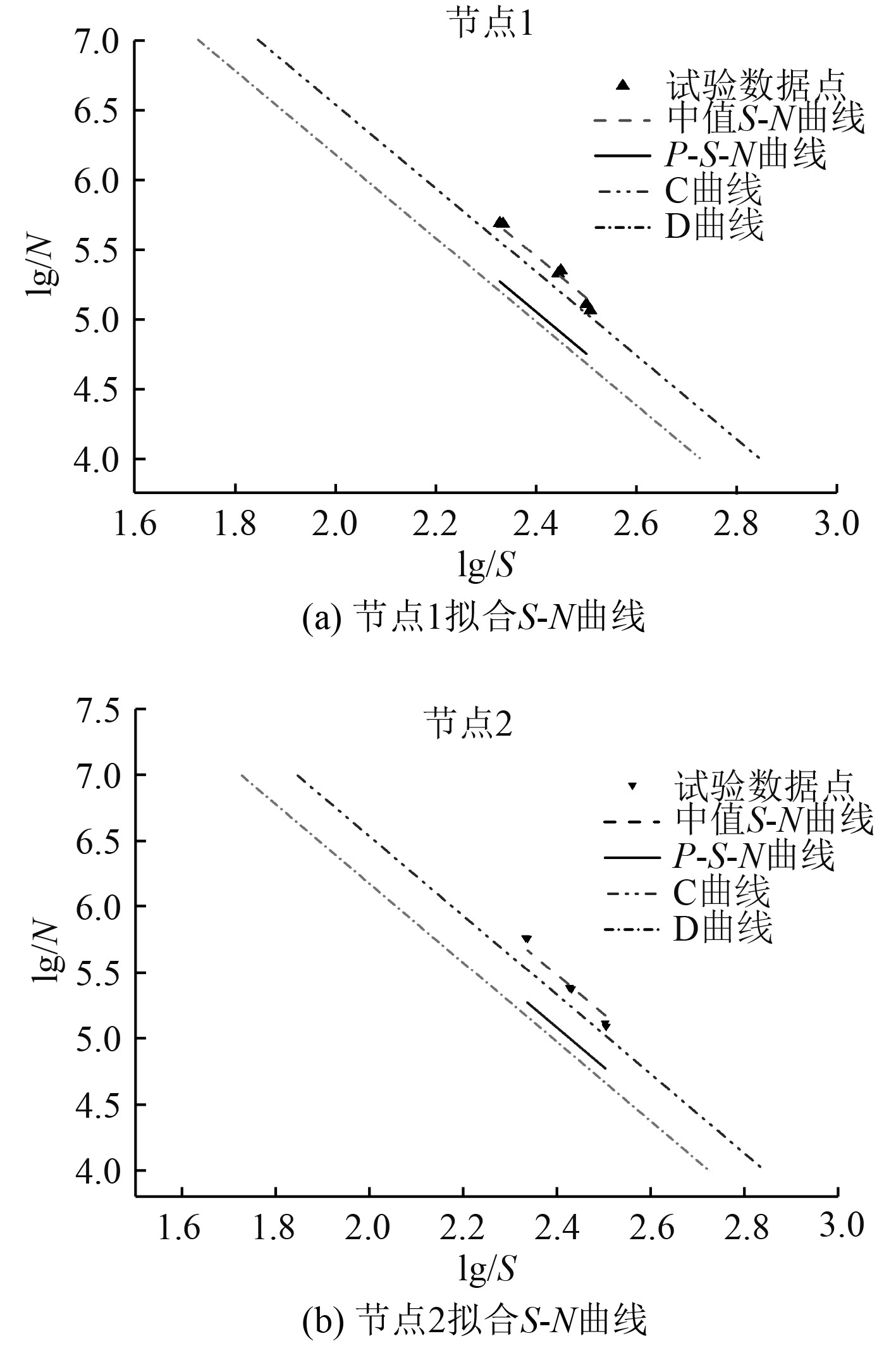
根据上述理论，对节点1和节点2的试验数据进行处理，最终拟合结果如表5和图6所示。

拟合结果表明，上述2种焊接节点的疲劳特性较为接近，中值S-N曲线均超出规范中的C曲线，P-S-N曲线位于C曲线和D曲线之间，且更为接近D曲线。

3 实船疲劳寿命计算

采取谱分析法对上述校核节点分别采用CCS新版规范要求的D曲线和试验曲线进行疲劳寿命计算。对校核节点进行疲劳网格细化，如图7所示。就上述试验疲劳破坏位置的构件和焊缝进行应力响应传递函数的计算，再选取全球海况作为计算海况，得到各短期分布的应力响应谱，叠加得到总损伤和寿命，如下式：

$\begin{split} D =& \frac{{{T_d}}}{{\mathop a\limits^ - }}\Gamma \left(1 + \frac{m}{2}\right)\sum\limits_{n = 1}^{{N_{load}}} {{p_n}} \cdot {\sum\limits_{i = 1}^{{n_S}} {\sum\limits_{j = 1}^{{n_H}} {{p_i}{p_j}{\nu _{ijn}}(2\sqrt {2{m_{0ij}}} )} } ^m} =\\ &\frac{{{\nu _0}{T_d}}}{{\mathop a\limits^ - }}\Gamma \left(1 + \frac{m}{2}\right)\sum\limits_{n = 1}^{{N_{load}}} {{p_n}} \cdot {\sum\limits_{i = 1}^{{n_S}} {\sum\limits_{j = 1}^{{n_H}} {{p_i}{p_j}{r_{ijn}}(2\sqrt {2{m_{0ij}}} )} } ^m} , \end{split} $

(7)

${T_f} = {T_d}/D\text{。}$

(8)

式中： ${T_d}$ 为实船设计使用寿命，为20年；其余各项参数参见文献[4]。

计算结果表明，采用试验所得P-S-N 曲线计算时所得疲劳寿命较大，按规范计算偏安全。此外，节点1的计算疲劳寿命明显小于设计使用寿命，节点2的计算疲劳寿命为节点2的4倍多，满足船体疲劳设计要求。

4 结　语

本文进行小水线面双体船上层建筑下围与甲板相交处的实板厚疲劳强度试验，得到该部位优化前后2种焊接形式节点的疲劳曲线特性，验证了船舶结构节点实板厚模型疲劳试验的可行性，以及优化方案的有效性，得出以下结论：

1）试验所得的P-S-N曲线均略高于规范给出的D曲线，因此，腹板加强十字焊接型节点或一般焊接型节点在疲劳计算评估时采用新版规范的D曲线偏安全，可用于小水线面双体船该类型焊接节点的疲劳强度评估；

2）该腹板加强十字焊接型节点的疲劳破坏位置均发生在面板焊缝处，可为疲劳强度有限元计算时应力插值以及试验测点布置提供参考；

3）小水线面双体船上层建筑侧壁与甲板相交采用肘板优化后的应力集中明显减小，疲劳累积损伤较小，该抗疲劳设计优化方案较为合理。