2. 中国舰船研究院,北京 100192;
3. 哈尔滨工业大学电气工程及自动化学院,黑龙江 哈尔滨 150001
2. China Ship Research and Development Academy, Beijing 100192, China;
3. School of Electrical Engineering and Automation, Harbin Institute of Technology, Harbin 150001, China
在理论上,可以通过船上主、子惯导的多种参数进行匹配实现传递对准[1]。根据匹配参数性质的不同,可将传递对准匹配方法分为2类:一类是利用惯导计算的导航参数进行传递匹配,称为计算参数匹配法;另一类是利用惯性元件测量参数进行传递匹配,称为测量参数匹配法。一般来说,测量参数法由于方法直接,其快速性优于计算参数法,但载体结构挠曲运动比计算参数法要敏感,即在同等条件下,其精度低于计算参数法。为解决这一问题,Kain J E和Cloutier J首次提出了“速度”+“姿态”匹配法,它克服了传统速度匹配法的缺陷,载体只要做特定运动即可实现传递对准,从而大大缩短了对准时间,极大地提高了惯导系统的反应速度;Ross C C使用实际的实验数据,研究了在更新频率为1 Hz时,速度匹配、积分速度匹配和双积分速度匹配的性能,研究结果表明:3种方法在估计俯仰角和横滚角的误差时,效果基本相同,但在估计方位角误差时,速度匹配要优于积分及双积分速度匹配;Rogers R M使用“速度”+“角速率”匹配法进行快速传递对准。该方法与“速度”+“姿态”匹配法一样都能缩短对准时间,但对振动噪声的敏感性要比“速度”+“姿态”匹配法大[2-3]。
虽然从理论上来说,“速度”+“姿态”匹配传递对准有载体机动方式简单、对准精度较高的特点,但相关的方案设计及仿真研究较少,影响了方案的实际应用因此,所以,本文从工程应用角度出发,提出一种工程化的传递对准误差评估方法,并设计了相关的传递对准方案,在此基础上结合实际应用开展了仿真分析,为后续研究奠定基础。
1 传递对准误差评估方案设计首先设计加工一个大的安装连接托板,将母、子2套惯导系统同时安装于托板上,并且2套系统之间保留有一定的距离。2套系统之间的姿态基准由托板加工面确定,为了验证所设计方案对姿态误差估计的正确性,2套系统之间人为设定一定的姿态偏差和航向偏差。方案验证时采用载体特定运动来完成传递对准过程,即载体在进入传递对准状态后,首先航向角向左运动一定角度,之后再向右运动一定角度,之后保持匀速直航,传递对准过程即已完成。对准结束后,通过判断2套惯导系统机体系之间的安装误差角估值的均值是否与事先设定的安装偏角相等评估所设计方案对姿态及航向误差的估计准确度情况,各误差角的估值方差(即重复性)为对准精度。
2 传递对准误差评估算法设计 2.1 姿态量测方程构造设主惯导输出的载体姿态矩阵为
| ${{C}}_{{b_m}}^{{b_s}} = \left[ {{{I}} - \left( {{{\lambda}} \times } \right)} \right]\text{,}$ | (1) |
| ${\hat{ C}}_{{b_m}}^n = \left[ {{{I}} - \left( {{{{\varphi}} _m} \times } \right)} \right]{{C}}_{bm}^n\text{,}$ | (2) |
| ${\hat{ C}}_n^{{b_s}} = {{C}}_n^{{b_s}}\left[ {{{I}} + \left( {{{\varphi}} \times } \right)} \right]\text{。}$ | (3) |
构造如下矩阵:
| $\begin{split} {{\bf{Z}}_{DCM}} &= {\hat{\bf C}}_{{b_m}}^n{\hat{ C}}_n^{{b_s}} = \\& \left[ {{{I}} - \left( {{{{\varphi}} _m} \times } \right)} \right]{{C}}_{{b_m}}^n{{C}}_n^{{b_s}}\left[ {{{I}} + \left( {{{\varphi}} \times } \right)} \right] = \\& \left[ {{{I}} - \left( {{{{\varphi}} _m} \times } \right)} \right]{{C}}_{{b_m}}^n\left[ {{{I}} - \left( {{{\lambda}} \times } \right)} \right]{{C}}_n^{{b_m}}\left[ {{{I}} + \left( {{{\varphi }} \times } \right)} \right] = \\& {{I}} - \left( {{{{\varphi}} _m} \times } \right) - \left[ {\left( {{{C}}_{{b_m}}^n{{\lambda }}} \right) \times } \right] + \left( {{{\varphi}} \times } \right) \text{。} \end{split} $ | (4) |
由(4)式可知,
| $\left\{ \begin{array}{l} {Z_x} = \left( {{{{Z}}_{DCM}}\left( {3,2} \right) - {{{Z}}_{DCM}}\left( {2,3} \right)} \right)/2\text{,} \\ {Z_y} = \left( {{{{Z}}_{DCM}}\left( {1,3} \right) - {{{Z}}_{DCM}}\left( {3,1} \right)} \right)/2 \text{,}\\ {Z_z} = \left( {{{{Z}}_{DCM}}\left( {2,1} \right) - {{{Z}}_{DCM}}\left( {1,2} \right)} \right)/2 \text{,} \end{array} \right.$ | (5) |
其中,
| ${{{Z}}_\theta } = {{\varphi }} - {{C}}_{{b_m}}^n{{\lambda}} + {{V}}\text{。}$ | (6) |
式中,
选取系统状态量为
| $\left\{ {\begin{aligned} & {{\dot{\bf \varphi }} = - {\bf{\omega }}_{in}^n \times {\bf{\varphi }} - {{C}}_{{b_s}}^n{\bf{\varepsilon }}_b^{{b_s}} - {{C}}_{{b_s}}^n{\bf{\varepsilon }}_w^{{b_s}}} \\ & \delta {\dot{ V}}_e^n = \left( {{{C}}_{{b_s}}^n{{f}}_s^{{b_s}}} \right) \times {\bf{\varphi }} - \left( {2{\bf{\omega }}_{ie}^n + {\bf{\omega }}_{en}^n} \right) \times \\& \qquad \quad \delta {{V}}_e^n + {\bf{C}}_{{b_s}}^n\nabla _b^{{b_s}} + {\bf{C}}_{{b_s}}^n\nabla _w^{{b_s}} \\& \dot \lambda = 0 \\ & {{\dot{\bf \varepsilon }}_b^{{b_s}} = {{0}}} \\ & {\dot \nabla _b^{bs} = {{0}}} \end{aligned}} \right.$ | (7) |
写成矩阵形式如下:
| ${\dot{ X}} = {{FX}} + {{GW}}\text{,}$ | (8) |
式中:
量测方程为:
| $\begin{split} Z & =\left[ {\begin{array}{*{20}{c}} {{{{Z}}_\theta }} \\ {{{{Z}}_V}} \end{array}} \right]= \\ & \left[ {\begin{array}{*{20}{c}} {{I_{3 \times 3}}}&{{0_{3 \times 3}}}&{ - {\bf{C}}_{{b_m}}^n}&{{0_{3 \times 3}}}&{{0_{3 \times 3}}} \\ {{0_{3 \times 3}}}&{{I_{3 \times 3}}}&{{0_{3 \times 3}}}&{{0_{3 \times 3}}}&{{0_{3 \times 3}}} \end{array}} \right]{{X}} + {{V}} \text{,} \end{split} $ | (9) |
式中:
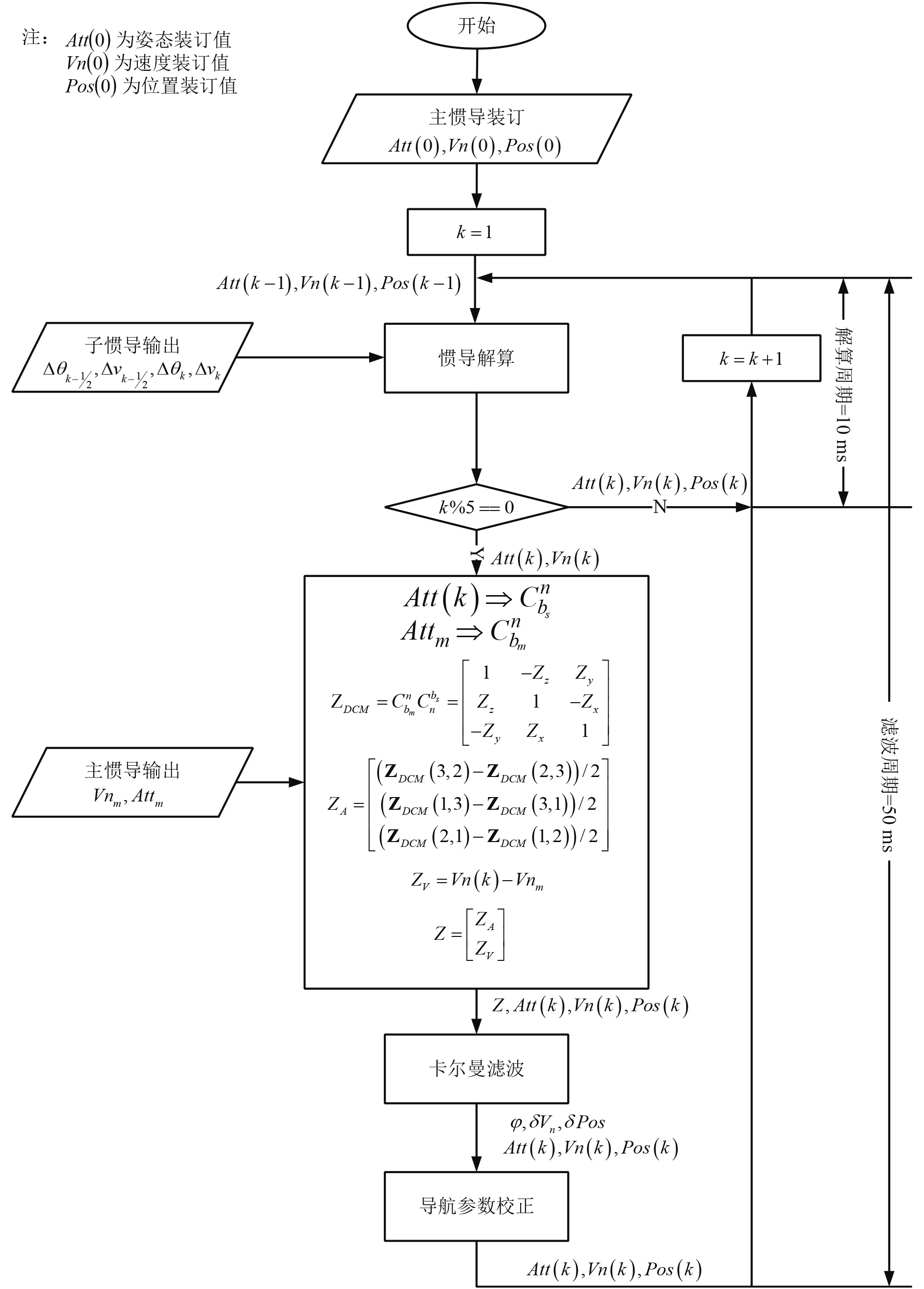
综上,设计传递对准误差评估方案流程图如图1所示。
|
图 1 传递对准误差评估方案流程图 Fig. 1 Flow chart of transfer alignment error evaluation scheme |
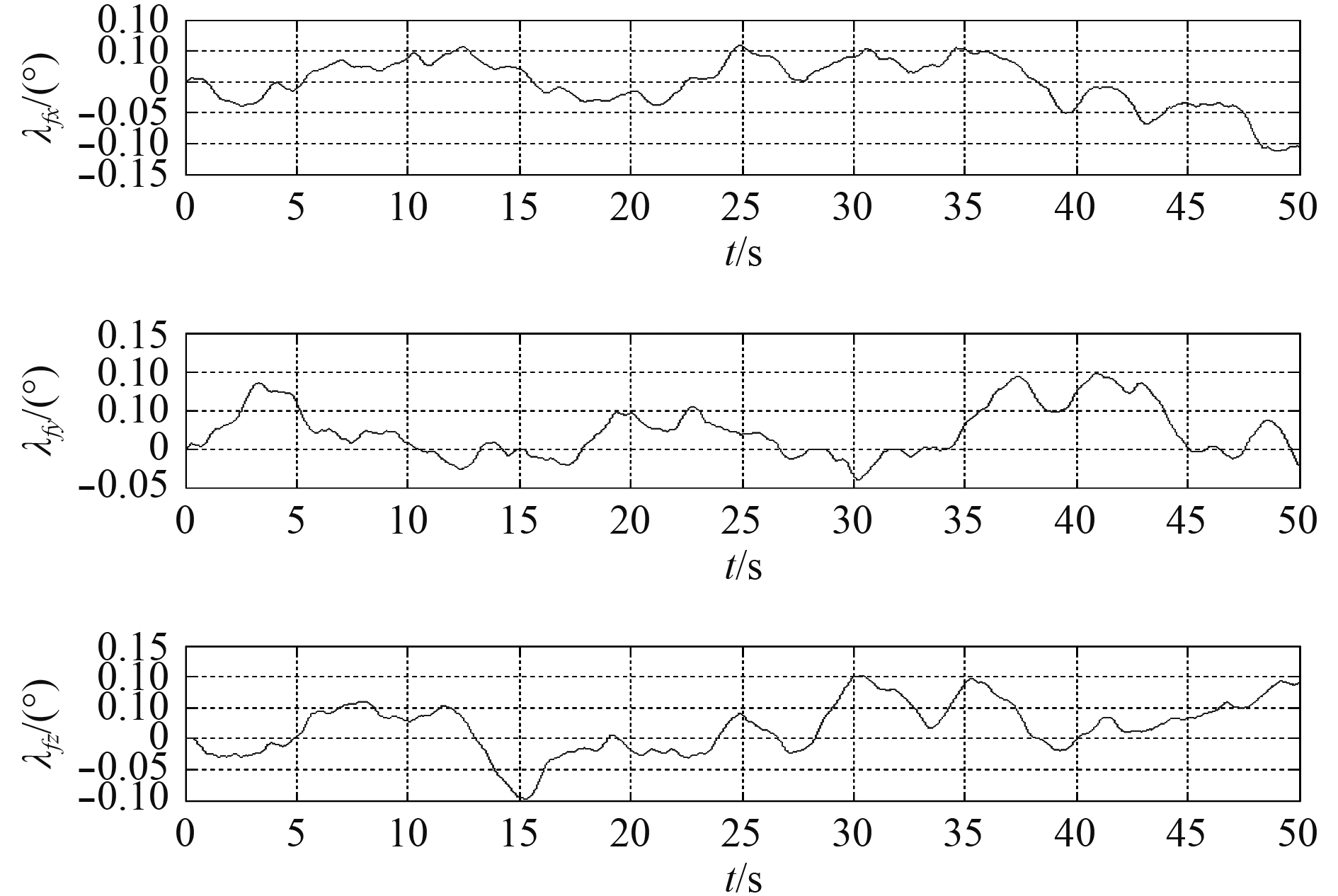
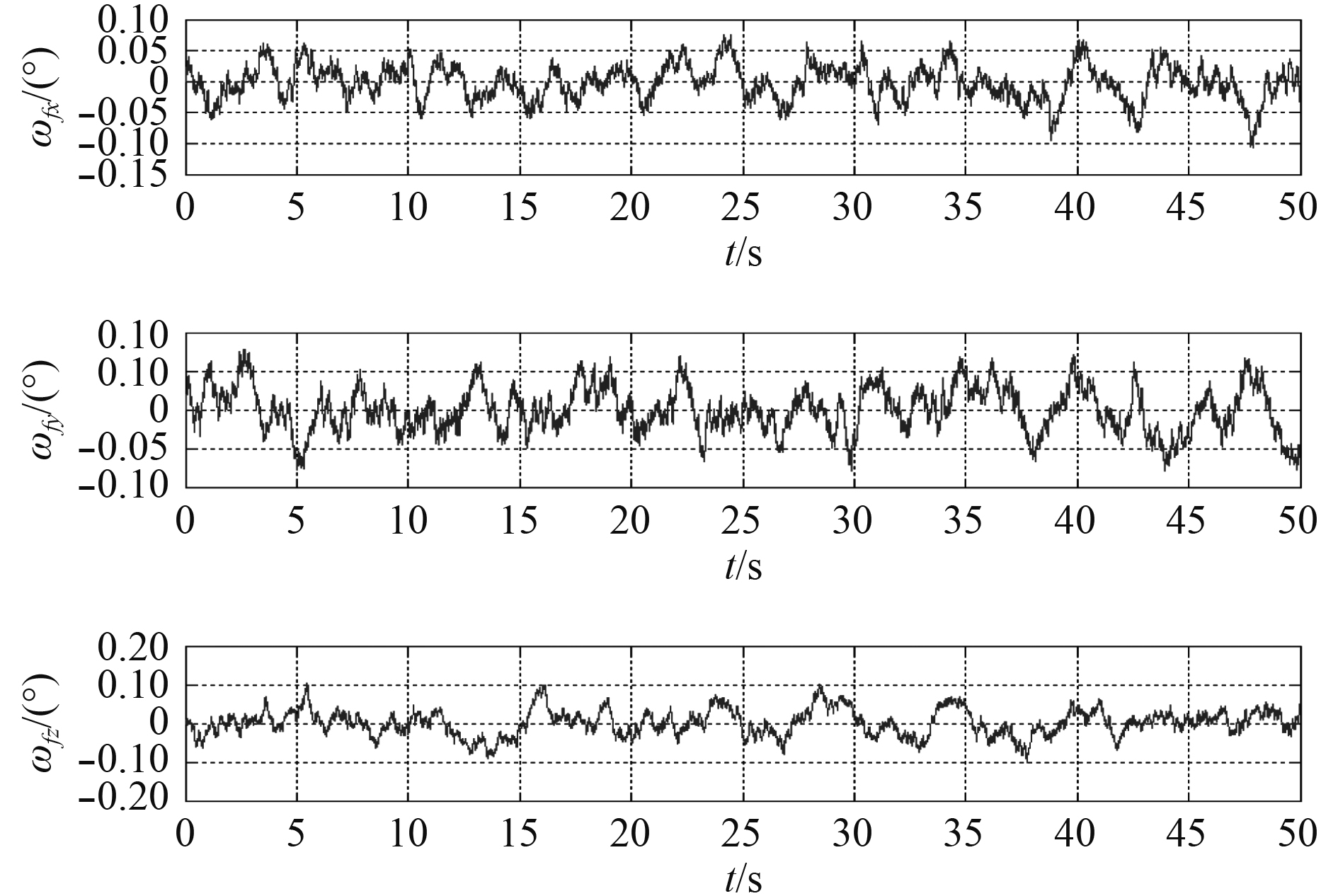
仿真条件如表1所示,载体运动轨迹如表2和表3所示,挠曲变形参数分别为
|
|
表 1 仿真条件 Tab.1 The simulation conditions |
|
|
表 2 轨迹1 Tab.2 Track 1 |
|
图 2 挠曲变形角 Fig. 2 Deflection angle |
|
|
表 3 轨迹2 Tab.3 Track 2 |
|
图 3 挠曲变形角速度 Fig. 3 Angular velocity of deflection |
1)仿真1
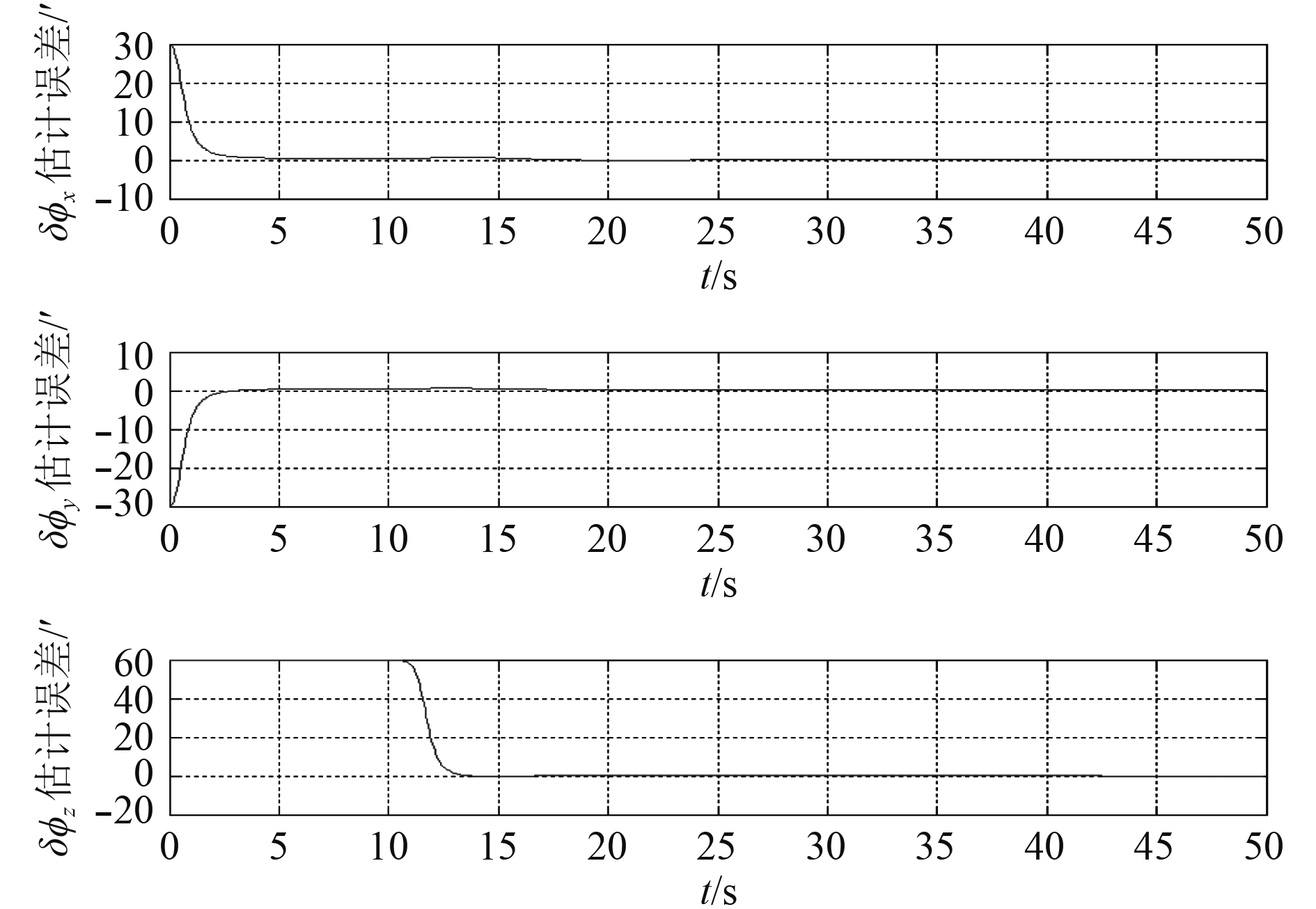
不考虑杆臂与挠曲变形,载体按轨迹1运动,选取0.005°/h的陀螺仪进行仿真,仿真结果如图4所示。
|
图 4 传递对准误差 Fig. 4 Transfer alignment error |
2)仿真2
不考虑杆臂与挠曲变形,载体按轨迹1运动,选取0.1°/h的陀螺仪进行仿真,仿真结果如图5所示。

|
图 5 传递对准误差 Fig. 5 Transfer alignment error |
3)仿真3
不考虑杆臂与挠曲变形,载体按轨迹2运动,选取0.005°/h的陀螺仪进行仿真,仿真结果如图6所示。
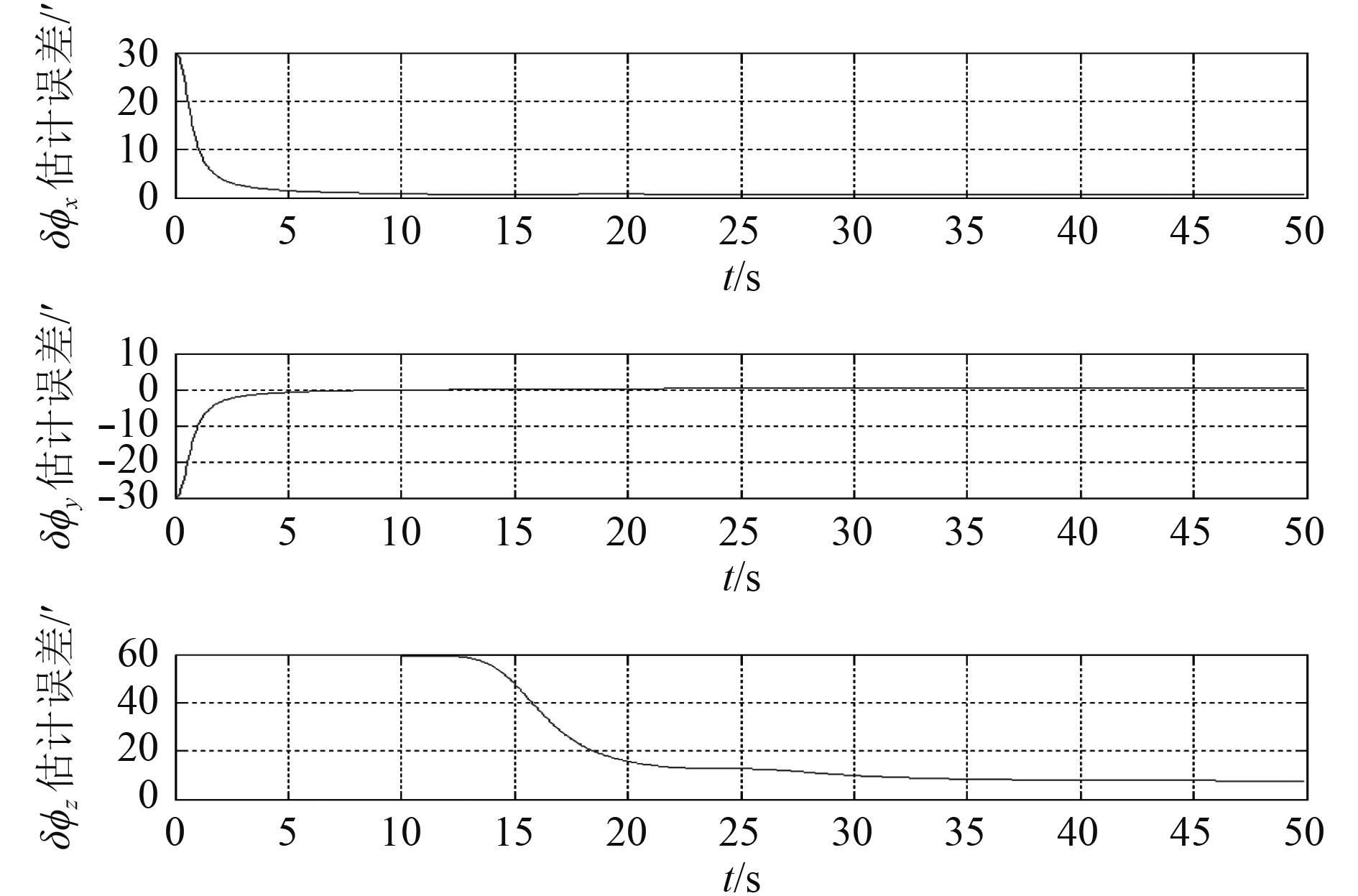
|
图 6 传递对准误差 Fig. 6 Transfer alignment error |
4)仿真4
不考虑杆臂与挠曲变形,载体按轨迹2运动,选取0.1°/h的陀螺仪进行仿真,仿真结果如图7所示。
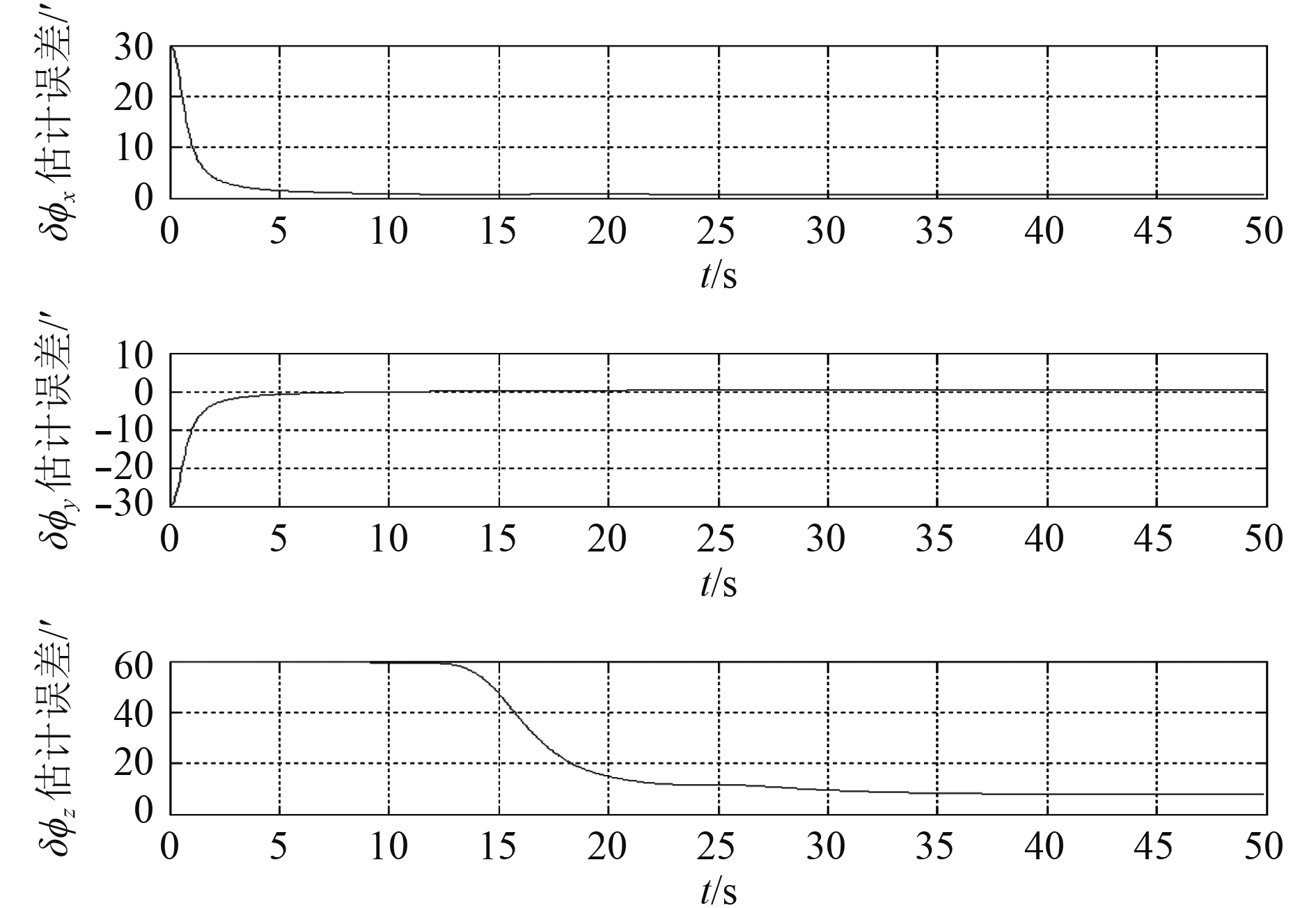
|
图 7 传递对准误差 Fig. 7 Transfer alignment error |
从上述仿真结果可以看出,在不考虑挠曲和杆臂的情况下,水平安装误差角估计可以迅速收敛且与机动状态关系不大,经过10 s钟的对准后,水平安装误差角误差小于1′。航向安装误差角对准精度和对准速度主要取决于机动的大小,经过20 s的机动后轨迹1的航向安装误差角的对准精度较高小于1′,而对于轨迹2由于航向角速度太小,经过20 s的机动后航向安装误差角误差约为8′。由于安装误差角可以事先准确标定,所以安装误差角的估计精度能说明失准角的估计角度。
3.3 考虑杆臂与挠曲变形仿真1)仿真5
设载体按轨迹1运动,选取0.005°/h的陀螺仪进行仿真,仿真结果如图8所示。
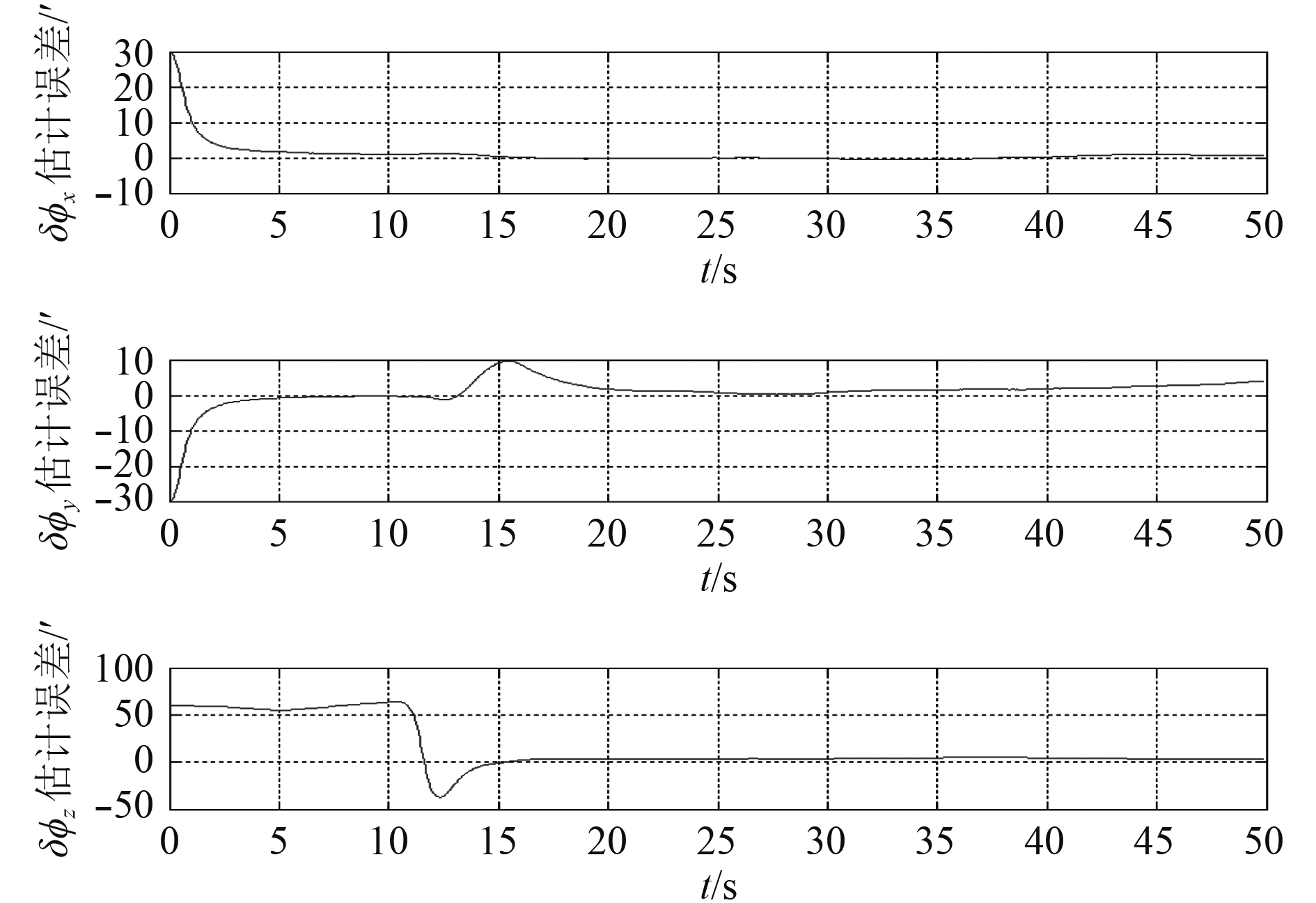
|
图 8 传递对准误差 Fig. 8 Transfer alignment error |
2)仿真6
设载体按轨迹1运动,选取0.1°/h的陀螺仪进行仿真,仿真结果如图9所示。
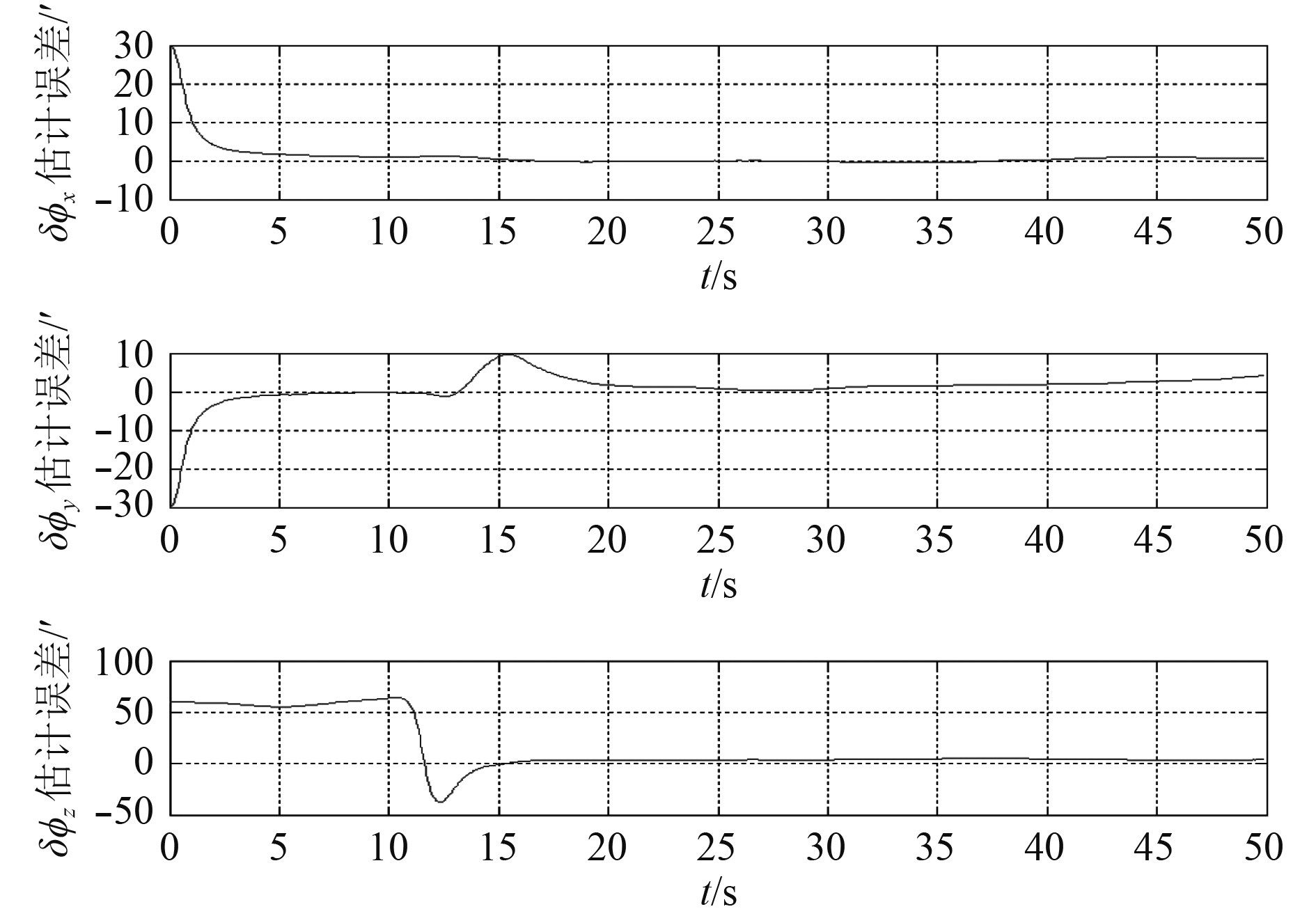
|
图 9 传递对准误差 Fig. 9 Transfer alignment error |
3)仿真7
设载体按轨迹2运动,选取0.005°/h的陀螺仪进行仿真,仿真结果如图10所示。
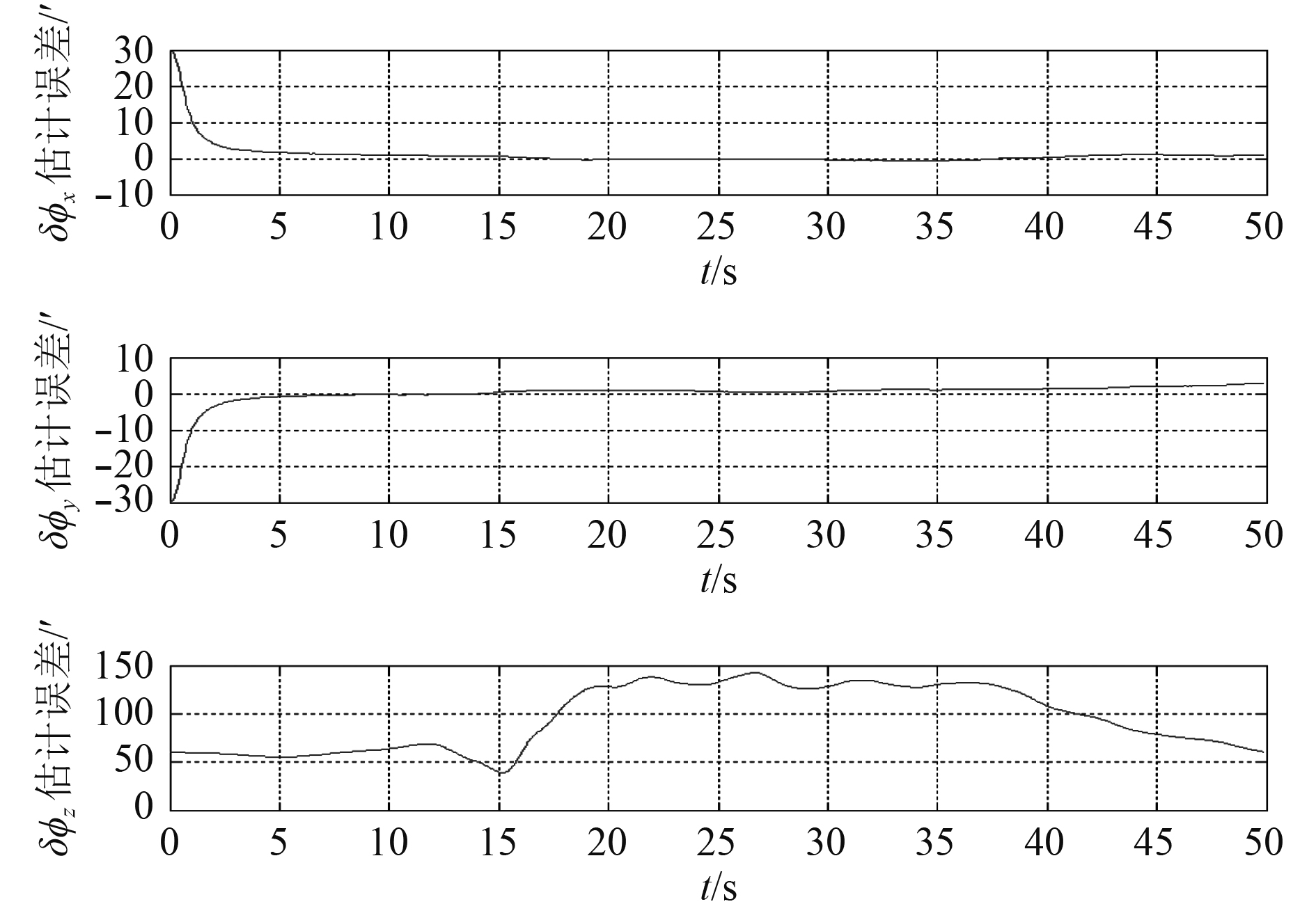
|
图 10 传递对准误差 Fig. 10 Transfer alignment error |
4)仿真8
设载体按轨迹2运动,选取0.1°/h的陀螺仪进行仿真,仿真结果如图11所示。
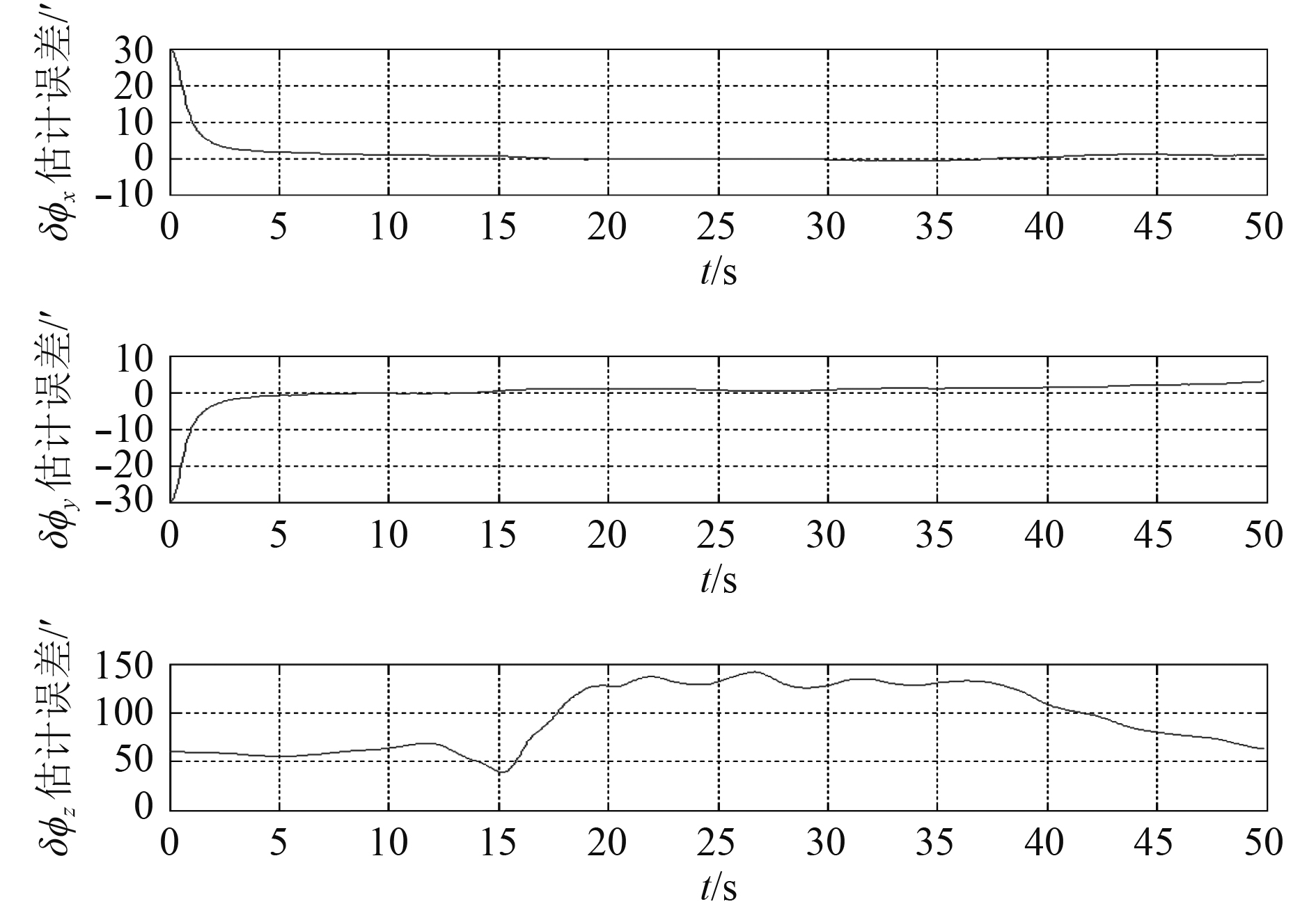
|
图 11 传递对准误差 Fig. 11 Transfer alignment error |
从仿真5~仿真8可以看出,当存在杆臂和挠曲变形时,与不考虑杆臂和挠曲变形的情况相比传递对准精度受到严重影响,这是因为当存在挠曲变形时姿态量测受到挠曲变形的污染而变差。但是对于相同的挠曲变形的情况下,轨迹中角速度越大则对准效果越好,这是因为角速度越大越有利于提高姿态量测得信噪比,有助于提高传递对准的精度。因此,在考虑挠曲变形的情况下尽量选择较大的机动来提高对准精度。
4 结 语本文在分析“速度”+“姿态”匹配传递对准方式的基础上,从工程应用角度出发,提出一种工程化的传递对准误差评估方法,并设计相关的传递对准方案,在此基础上结合实际应用开展考虑/不考虑杆臂与挠曲变形仿真分析。试验结果表明,所提方法能有效的实现传递对误差评估,为后续应用奠定基础。
| [1] |
王司, 邓正隆. 惯导系统动基座传递对准技术综述[J]. 中国惯性技术学报, 2003. |
| [2] |
秦永元. 惯性导航[M]. 北京: 科学出版社, 2006.
|
| [3] |
秦永元, 张洪钺, 汪叔华. 卡尔曼滤波与组合导航原理[M]. 西安: 西北工业大学出版社, 1998.
|
 2020, Vol. 42
2020, Vol. 42
