2. 天津航海仪器研究所,天津 300131
2. Tianjin Navigation Instruments Research Institute, Tianjin 300131, China
舰船组合导航系统组合不同特点的导航设备与导航方法,应用信息融合技术对导航信息进行综合处理,以提高系统数据精度和可靠性。常用卡尔曼滤波方法对多传感器数据进行滤波融合[1],但由于其依赖于系统数学模型而带来模型误差。借助神经网络技术对卡尔曼滤波估计进行误差补偿,可提高卡尔曼滤波器的自适应性与估计精度。航行安全问题一直是航海界关注解决的重大课题,基于航海避碰理论和人工智能技术,研究建立航海避碰决策系统,有利于提高航行安全和减轻航海人员负担。现代化舰船导航设备的集成化和智能化程度不断提高[2],不但要为舰船操控和武器系统等提供实时准确的导航信息,还要求具备故障识别和状态预测的能力,因而研究具有联想记忆和逻辑推理能力的智能诊断系统具有重要意义。
1 舰船组合导航系统随着舰船导航技术的发展,各导航设备的功能特点和性能优劣已基本稳定,单一传感器的导航系统已无法满足在数据精度和可靠性等多方面的要求。为此,基于多传感器信息融合技术的舰船组合导航系统应运而生。
舰船组合导航系统主要分为传感器、数据处理中心和决策控制终端3个部分。传感器一般包括惯导、卫导和计程仪等设备,其作为导航系统的信息源,主要提供舰船位置、航向和航速等信息。数据处理中心以高速计算机为载体,应用卡尔曼滤波器和最优化统计理论,对各传感器导航信息进行融合处理,从而给出各导航参数的最优解。决策控制终端是导航参数的应用端,主要包括信息显示、操控指挥和武器作战等系统设备。基于多传感器信息融合的组合导航系统,不仅有效提高了导航数据精度和可靠性,同时为实现舰船的航海避碰、故障诊断和综合决策等智能化应用奠定了重要基础。
2 人工智能技术人工智能作为计算机科学的一个分支,致力于智能行为的自动化[3]。人工智能领域的研究主要包括神经网络、模糊逻辑和专家系统3个方面。
人工神经网络是对人脑结构和功能进行简化模拟,通过神经元的广泛互连和一定的学习机制,确立系统输入与输出间的非线性映射关系,进而能够依据外部信息进行动态响应的信息处理系统。建立系统神经网络模型的过程如图1所示。首先分析系统的需求背景和功能模型,设定神经网络结构;然后基于大量样本数据对神经网络模型进行训练,使模型更加贴近系统工作实际;最后评价检验权值满足要求后,便建立了系统输入与输出间的网络化动态关系;神经网络模型在工作过程中继续学习,得到不断优化。
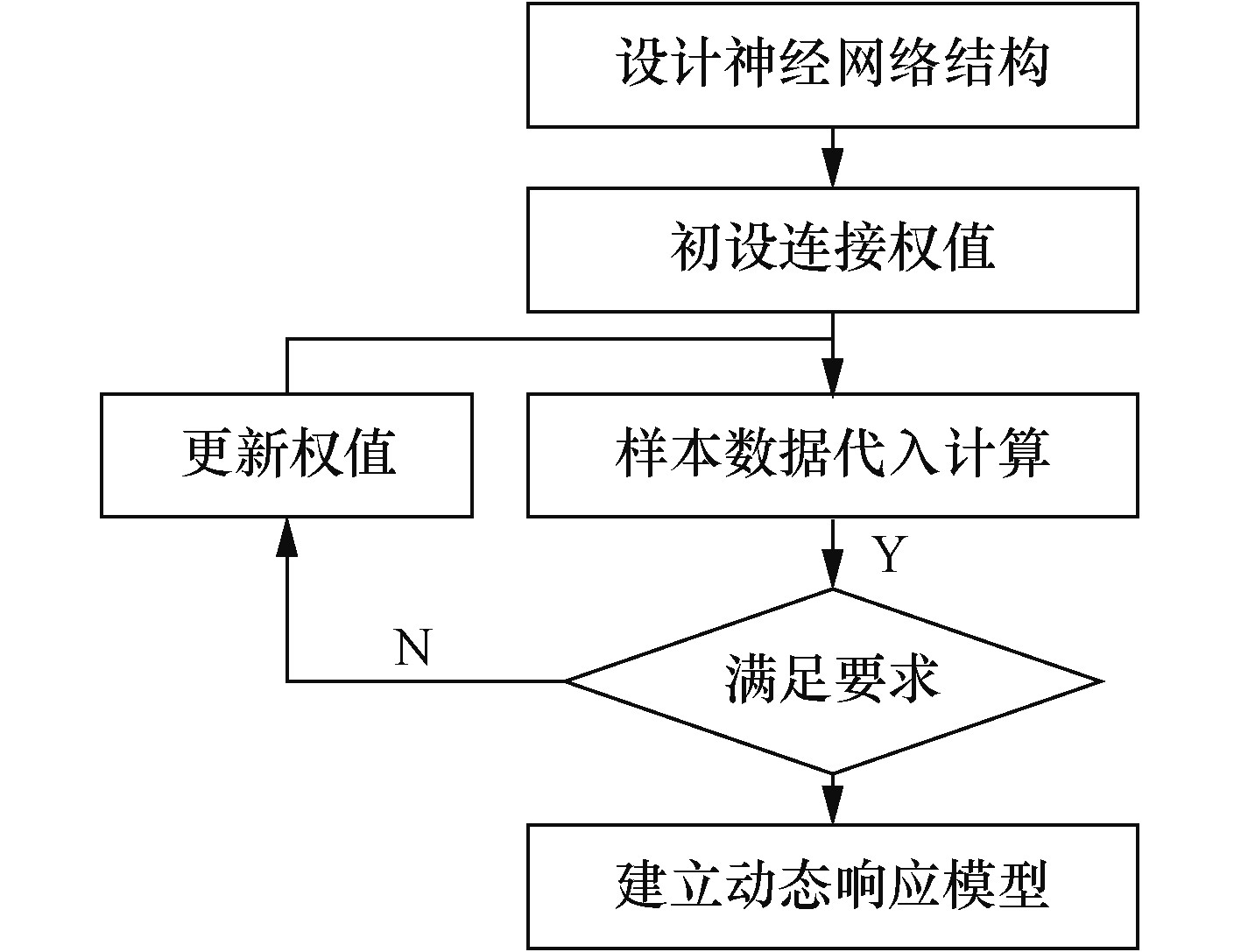
|
图 1 神经网络模型的建立过程 Fig. 1 The learning process of neural networks |
由于客观事物不断变得复杂,常用一些模糊性语言来概括事物的某种属性,并采用不确定性推理来描述模糊事物之间的关系。模糊逻辑推理是一种常用的不确定性推理手段,其推理机制包含如下几步:1)将模糊命题中的不定性元素表示成定性值的形式构成模糊集合,根据模糊元素与模糊集和的关系推导出隶属度函数;2)专家基于问题中的模糊关系制定模糊规则,应用模糊规则建立操作模糊集的数学模型;3)将模糊集合、隶属度函数、模糊规则和模糊集操作模型,按照一定的数学表达方式构建专家知识库;4)基于专家知识库中的模糊逻辑关系,建立模糊命题与推论之间的数学联系。
专家系统是利用专家知识组建成知识库,针对问题特征在知识库中进行搜索匹配,并通过推理手段来解决特定问题的程序系统。专家系统的组成结构如图2所示。首先基于专家知识和经验方法,按照一定的数据存储形式创建系统知识库;推理模块根据问题信息的特征在知识库中搜索匹配,并根据需要继续向用户索要补充信息,经推理分析后给出问题解答。最后,用户可根据理解需要向专家系统寻求解释,专家知识库依据问题解决情况自动对系统知识补充更新。

|
图 2 专家系统的组成结构 Fig. 2 General structure of an expert system |
卡尔曼滤波是由Kalman提出的一种线性最小方差估计,离散卡尔曼滤波算法的系统状态方程和量测方程表达式为[4]:
| $\left\{ \begin{array}{l} {X_k} = { \phi _{k,k - 1}}{X_{k - 1}} + { \varGamma _{k,k - 1}}{W_{k - 1}} , \\ {Z_k} = {{ H}_k}{X_k} + {V_k}, \\ \end{array} \right.$ | (3-1) |
式中:
| $\left\{ \begin{array}{l} E\left[ {{W_k}} \right] = 0,E\left[ {{W_k}W_j^{\rm T}} \right] = {Q_k}{\delta _{kj}} {\text{,}} \\ E\left[ {{V_k}} \right] = 0,E\left[ {{V_k}V_j^{\rm T}} \right] = {R_k}{\delta _{kj}} {\text{,}} \\ E\left[ {{W_k}V_j^{\rm T}} \right] = 0 {\text{。}} \\ \end{array} \right.$ | (3-2) |
式中:
| $\left\{ \!\!\! \begin{array}{l} {{\vec X}_k} = {{\vec X}_{k,k - 1}} + { K_k}\left[ {{Z_k} - {H_k}{{\vec X}_{k,k - 1}}} \right], \\ {K_k} = {P_{k,k - 1}}H_k^{\rm T}{\left[ {{H_k}{P_{k,k - 1}}H_k^{\rm T} + {R_k}} \right]^{ - 1}} = {P_k}H_k^{\rm T}R_k^{ - 1}\text{。} \end{array} \right.$ | (3-3) |
式中:
基于多个子卡尔曼滤波器组合成联邦卡尔曼滤波器,可实现多个数据融合得到最优结果。以2个子滤波器(N=2)为例对数据融合过程进行说明。设
| ${\vec X_g} = {\left[ {P_1^{ - 1} + P_2^{ - 1}} \right]^{ - 1}}(P_1^{ - 1}{\vec X_1} + P_2^{ - 1}{\vec X_2})\text{。}$ | (3-4) |
分析式(4)可以看出,若
在组合导航系统中,惯导系统一般作为参考公共系统,即将其输出值作为系统观测值
由于环境噪声影响造成的系统模型误差,降低了数据融合精度和稳定性。根据系统输入输出关系和环境动态影响过程,建立自适应性神经网络模型,实现对卡尔曼滤波器融合结果的动态补偿,从而有效降低了模型误差对滤波精度的影响。
应用神经网络辅助卡尔曼滤波的基本原理如图3所示:1)对系统模型和输入输出样本进行分析,建立神经网络结构和初始参数;2)将联邦卡尔曼滤波器的输出
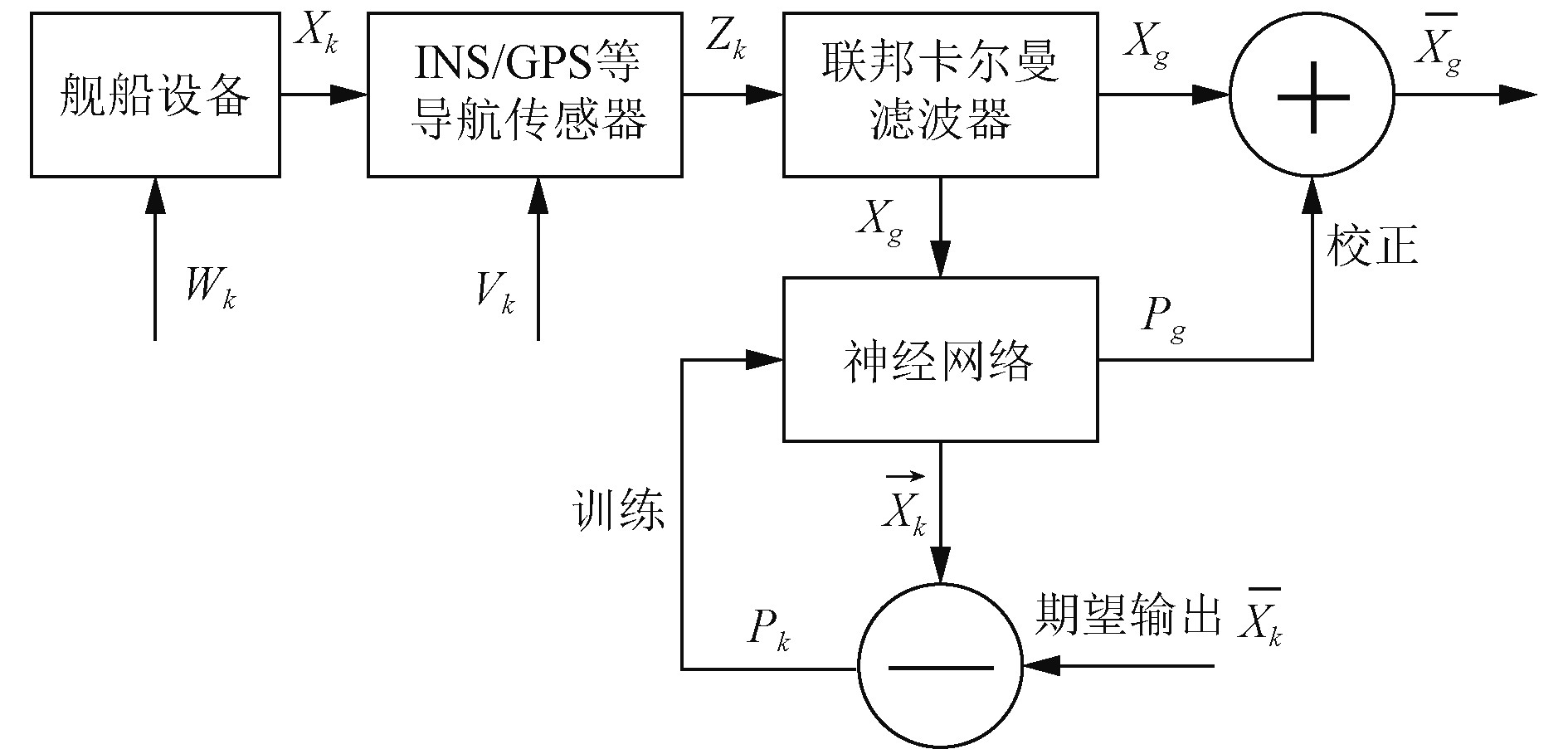
|
图 3 神经网络辅助卡尔曼滤波原理框图 Fig. 3 Block diagram of neural network-assisted Kalman filtering |
航海智能避碰专家系统采用探测传感器对危险目标进行探测,通过无线网络接收指挥中心和其他舰船直接发来的航行信息,基于航行专家知识库中的知识案例进行计算推理,判断是否会出现碰撞等危险情况,然后决策给出避让行动方案。
航海智能避碰专家系统设计方案如图4所示。在判别碰撞危险度阶段,系统依据目标运动状态和海洋环境信息,基于碰撞危险度模型计算出碰撞危险度;在判断碰撞危险态势阶段,系统依据两船的相对位置和航行信息,对当前的碰撞态势进行匹配识别;在舰船避让决策阶段,系统基于碰撞危险度和碰撞态势,依据专家知识和经验进行综合推理,在此过程中可通过人机交互接口获取补充信息或者传递解释信息,最终确定避碰策略和行动方案;在知识库更新阶段,系统基于新产生的碰撞案例和处理经验,通过一定的信息描述机制对知识库内容进行完善。
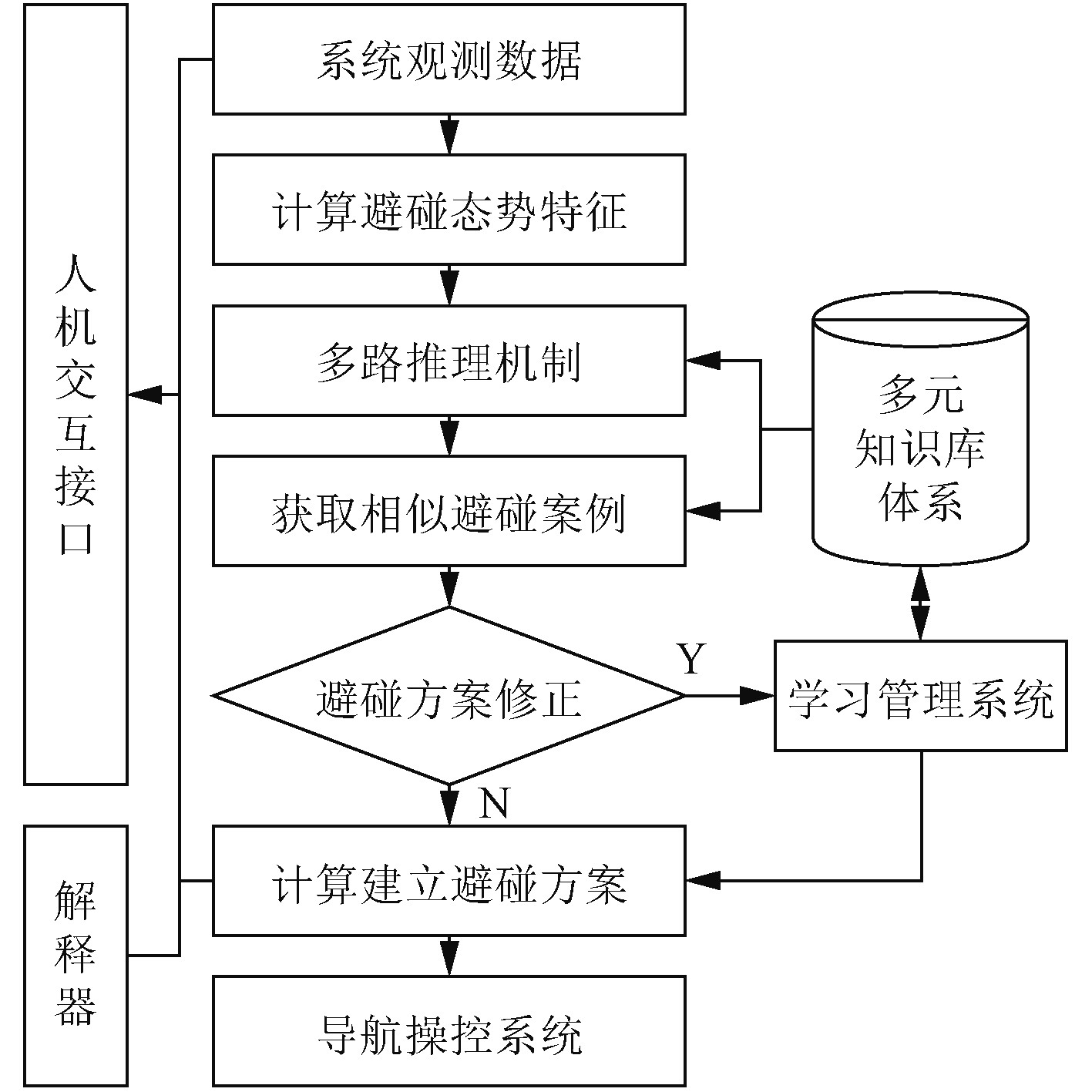
|
图 4 航海专家避碰系统设计方案 Fig. 4 Design scheme of collision avoidance system for marine experts |
以DCPA(D,最小会遇距离)、TCPA(T,最小会遇时间)和Range(R,船舶与目标距离)为主要因素建立碰撞危险度模型,如下式[5]:
| $\left\{ \begin{array}{l} {d_1} = \left( {{K_1} \cdot DLA + T \cdot {V_R} \cdot {F_1}} \right) \cdot {F_2} \cdot {F_3}\text{,}\\ {F_1} = \left\{ \begin{array}{l} \displaystyle\frac{{{{360}^ \circ } - DE}}{{{{360}^ \circ }}}{\rm{ }}DE \leqslant {180^ \circ }\text{,}\\ \displaystyle\frac{{DE}}{{{{360}^ \circ }}}{\rm{ }}DE > {180^ \circ }\text{,}\\ \end{array} \right.\\ DE = \left\{ \begin{array}{l} {\text{目标当前方位}} DCPA \leqslant 0.5\;{\rm nm}\text{,}\\ {\text{目标}}CPA{\text{点的方位}} DCPA > 0.5\;{\rm nm}\text{,} \end{array} \right.\\ {d_2} = {K_2} \cdot {d_1}\\ {\mu _A} = {a_D} \cdot {\mu _{AD}}(D) + {a_T} \cdot {\mu _{AT}}(T) + {a_R} \cdot {\mu _{AR}}(R)\text{。} \end{array} \right.$ | (4-1) |
式中:
舰船基于最小会遇距离和衡量距离,判断本船与危险目标间的碰撞危险度。当DCPA<
在本船与目标船的会遇过程中,根据航海避碰规则一般将会遇局面分成:对遇(左、右)、小角度交又(左、右)、大角度交叉(左、右)、追越和被追越等,在每一种会遇局面里边包含了多种会遇状态。根据以往的航行会遇态势判别经验,通常将航向交叉角C和目标船舷角Q作为主要判别依据。
基于神经网络建立舰船会遇态势推理模型的基本结构如图5所示。首先建立推理模型的网络结构,子网NN1,NN2用于舷角Q和航向交叉角C的信息输入,Vr为系统外部误差,NN3用于对会遇态势进行模糊推理;将专家结论和航行经验通过一定的数学语言进行描述,确定网络模型的权值参数,并在工作中对其不断修正。最后,模型根据弦角Q和交叉角C信息进行推理,得出会遇态势结果。

|
图 5 态势网络推理模型 Fig. 5 Situational Network Reasoning Model |
当两船构成碰撞危险时,两船中的一船或者两船都要采取避让行动。舰船根据碰撞危险度、会遇态势、运动状态和海洋环境等因素,采取不同的避让策略和行动。航海规则中将两船会遇的避让行动分为采取避让行动、碰撞危险、紧迫局面和紧迫危险共4个阶段[6]。因此,舰船避碰决策问题就转化为判别避让行动阶段的问题。将舰船碰撞危险度、会遇态势、运动状态和外界环境作为模型的4个模糊因子,综合应用专家理论和历史避碰案例等建立避碰规则库,通过推理分析和匹配算法,得到当前危险局势与避碰行动策略之间的非线性逻辑关系。将当前的会遇信息进行量化,依据避碰规则和神经网络进行匹配推理,确定当前所处的避碰行动阶段,并按照阶段要求确定避碰行动方案。
5 基于神经网络的导航故障诊断专家系统 5.1 系统组成结构故障诊断专家系统是基于舰船航行和排故经验组建知识库,应用神经网络的逻辑推理能力,解决带有随机性和突发性故障问题的智能诊断系统。故障诊断专家系统原理如图6所示。首先基于专家资料和排故案例,计算神经网络连接权值并组建成知识库;专家系统对舰船设备进行自动诊断,当设备功能失调或者数据异常时,推理故障原因并对其发展趋势进行预测;当用户向诊断系统发出诊断请求时,系统依据请求征兆信息进行案例匹配和推理,并依据需要向用户索要补充信息;最后得出诊断结果并解释说明。如果在排故中得出新的诊断经验,系统自动对知识库进行补充。
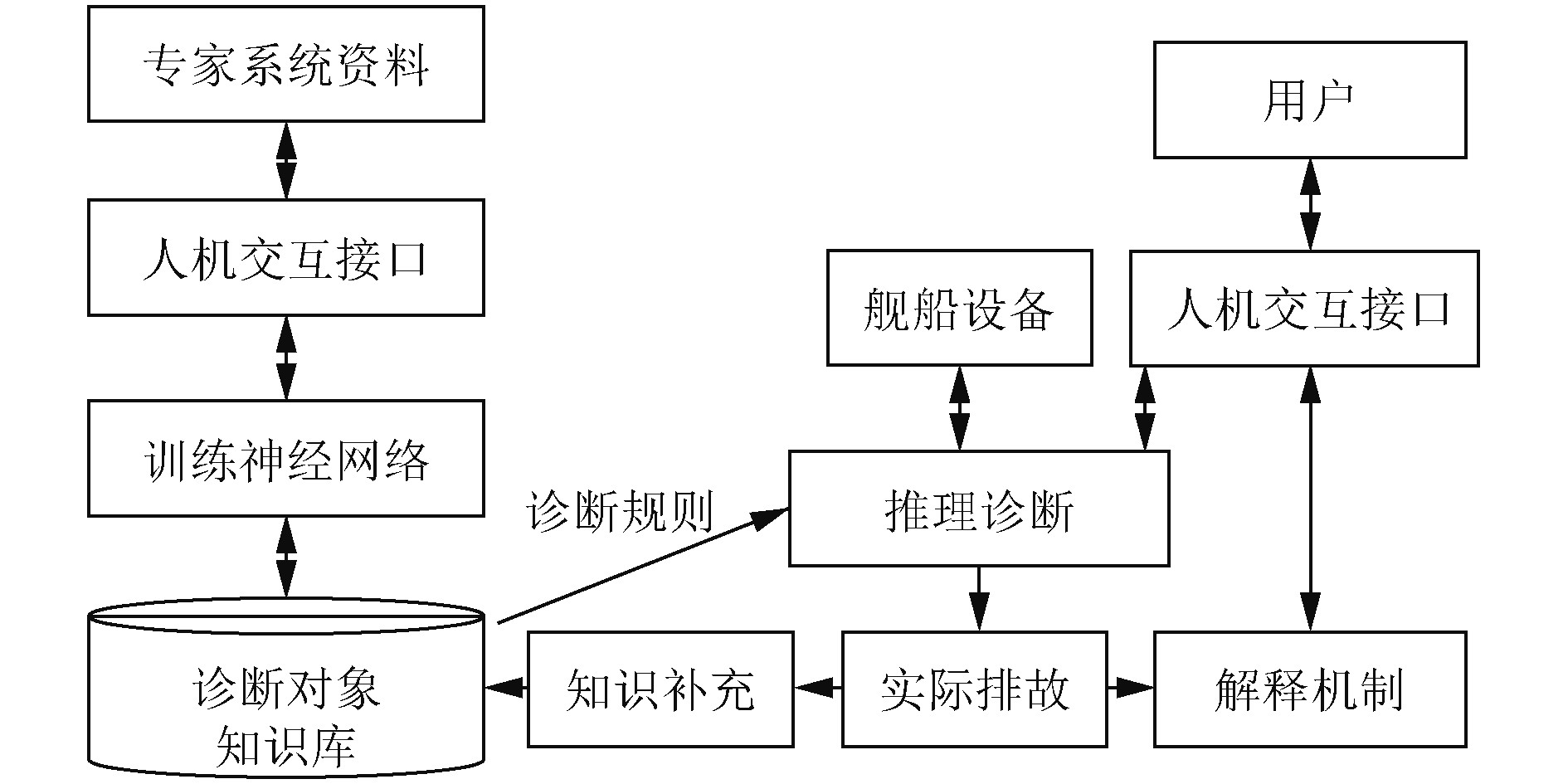
|
图 6 故障诊断专家系统结构图 Fig. 6 Structure chart of fault diagnosis expert system |
知识库是组建故障诊断专家系统的关键 [7],其知识数量和质量决定了专家系统的技术水平。故障问题的求解过程就是通过模拟人类专家思维,基于知识库中的知识案例,对故障特征信息进行推理解释的过程。组建步骤为:1)分析诊断对象的故障知识结构,确定神经网络模型;2)选择故障诊断样本对神经网络进行训练,计算输入层与隐含层、隐含层与输出层之间的连接权值,建立故障征兆与故障原因之间的数学推理关系;3)存储连接权值建立知识库。
5.3 系统的神经网络设计用于故障检测的神经网络设计如图7所示,其结构可分为样本输入层、隐含层和结果输出层共3个部分。INS,GPS,计程仪等传感器构成了系统输入层,每个传感器信息变量都对应着输入层的一个节点;隐含层由神经元组成,隐含层的层数和神经元的个数基于输入输出关系、学习速度和推理能力确定;输出层接收经隐含层计算得到的故障诊断数值结果,基于专家知识库进行匹配推理,给出最终诊断结果。神经网络的设计关键在于计算网络间的连接权值。首先根据系统网络模型对连接权值进行预设;接着输入样本信息沿着特定的神经元路径进行计算,将计算结果传向输出层;如果计算输出值与经验理论期望值不符,则将两者的差值沿原来的连接通道反向传播,修改连接权值直至满足期望目标。
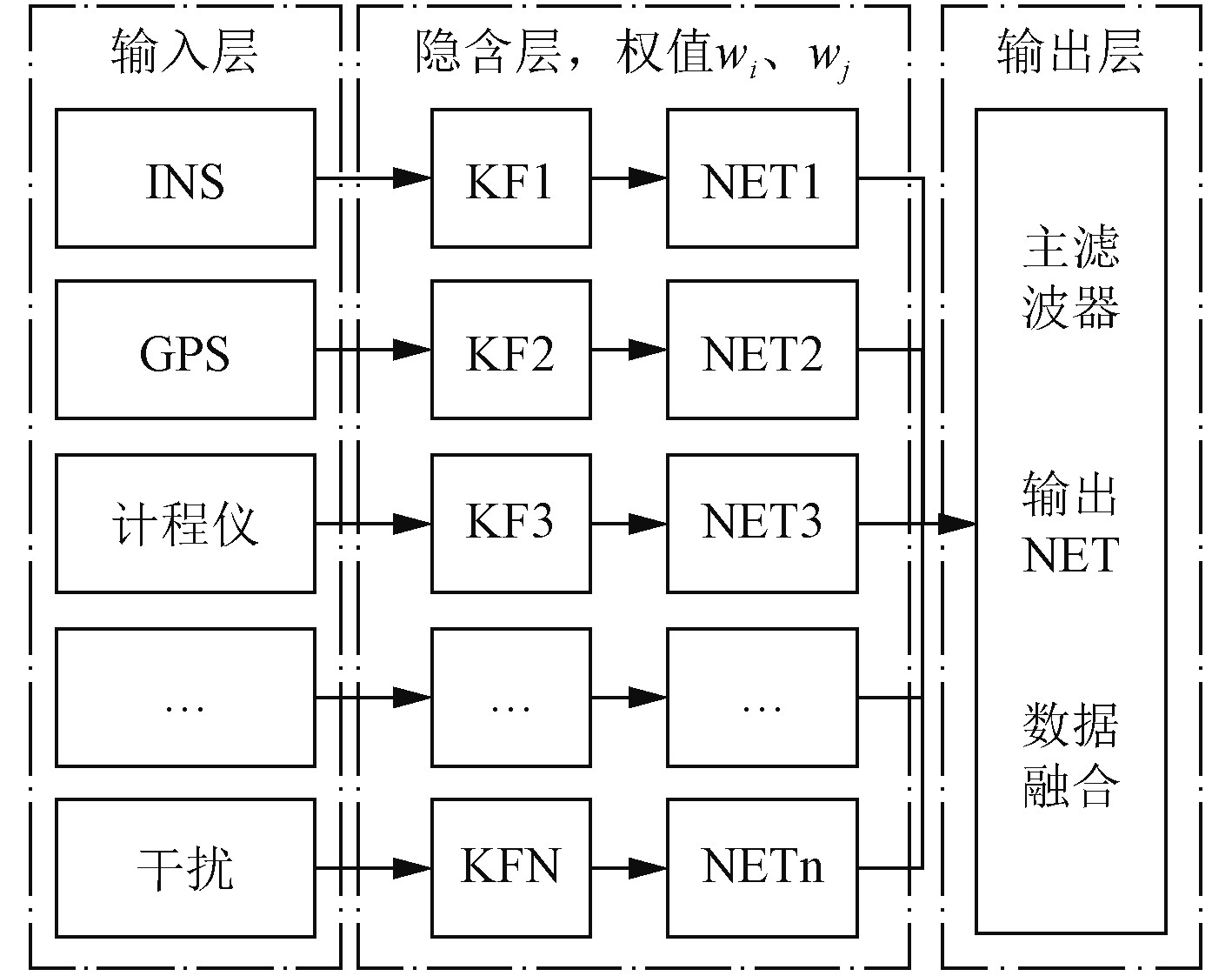
|
图 7 用于故障检测的神经网络设计 Fig. 7 Neural network design for fault detection |
故障诊断专家系统依据知识库中的数学逻辑关系,基于神经网络模型对故障征兆信息进行匹配推理,最终得到诊断问题的结果。系统推理机制包含正向推理,反向推理和混合推理3种。正向推理是己知故障征兆信息,借助神经网络计算和知识库匹配得到故障诊断结果;反向推理是根据故障征兆假设出一个故障诊断结果,然后对诊断结果进行反向神经网络计算,验证计算结果与故障征兆是否一致;混合双向推理是己知部分故障征兆信息,依据征兆信息提出一个可能故障,然后验证假设是否成立,若成立则诊断结束,否则基于诊断情况作出新的假设继续验证。
6 结 语在应用卡尔曼滤波器进行导航信息融合的过程中,依据神经网络模型对估计结果进行动态误差补偿,能有效提高数据融合精度和可靠性。基于专家系统和模糊神经网络,建立舰船的碰撞危险度计算、会遇态势分类和避让决策模型,给出了舰船与危险目标会遇时的避碰策略和最优化方案。应用专家神经网络的推理能力与匹配算法,建立系统故障征兆与诊断结果之间的对应联系,进而实现了导航系统故障的智能化诊断。随着机器学习、图像处理等新兴技术不断发展,具有更高精度、可靠性和智能性的舰船组合导航系统将迎来更大的应用前景。
| [1] |
蒋恩松, 李孟超, 孙刘杰. 一种基于神经网络的卡尔曼滤波改进方法[J]. 电子与信息学报, 2007, 29(9): 2073-2076. |
| [2] |
杨跃轮. 智能导航系统研究[D]. 哈尔滨: 哈尔滨工程大学, 2002: 1-5.
|
| [3] |
王礼军. 模糊神经网络专家系统在发动机故障诊断中的应用研究[D]. 重庆: 重庆交通大学, 2012: 7-34.
|
| [4] |
王峰. 基于联邦卡尔曼滤波的车载组合导航算法研究[D]. 哈尔滨工程大学, 2018: 25-29.
|
| [5] |
鲍宏杨. 舰船自动智能避碰数学模型及其仿真研究[J]. 舰船科学技术, 2017, 39(10): 164-169. |
| [6] |
胡甚平. 船舶会遇过程中避碰阶段的划分与量化[J]. 中国航海, 2001, 2(49): 83-87. |
| [7] |
司景萍, 马继昌, 牛家骅, 等. 基于模糊神经网络的智能故障诊断专家系统[J]. 振动与冲击, 2017, 36(04): 164-171. |
 2020, Vol. 42
2020, Vol. 42
