0 引　言

随着航天活动的日趋频繁，在轨卫星数量越来越多，特别是美国在轨侦察卫星多达数十颗，可对我海上舰船目标进行大范围、全天候、高时效的侦查探测和海洋监视，为有效规避其侦察监视或对其实施干扰抗击，对其卫星轨道进行预测十分必要。目前，国际上主要通过经典力学模型对卫星轨道进行预报。北美防空司令部（North American Aerospace Defense，NORAD）提供的两行轨道根数（Two-Line Elements，TLE）结合解析模型进行轨道预报是目前针对卫星轨道预报的主流方法。NORAD的TLE需要在简化常规扰动（Simplified General Perturbation Version4, SGP4）解析模型中进行计算^[1]，SGP4适用于近地空间目标轨道周期小于225 min的卫星^[2]。对卫星轨道预报精度的研究，一方面集中在TLE初值，另一方面集中在对各摄动力模型优化。尽管传统方法相对成熟，但是卫星轨道预测模型仍存在一定局限性、预报精度还有待提高。首先，现有的理想化的摄动力模型偏差相对较大；其次，所谓的摄动力是考虑影响卫星轨道的影响因素，这些因素放到一个模型里可能考虑不全甚至说不清楚；再次，由于很难获取他国卫星的轨道数据，无法及时修正轨道，数学模型在长期轨道预报中存在误差发散现象^[3]。针对上述不足，本文提出基于神经网络的轨道预报算法，使用卫星的历史TLE数据作为神经网络的学习样本，通过对大量数据的学习，得出卫星轨道运行的规律，预报卫星轨道。

1 卫星轨道数据

根据TLE两行数据，卫星的轨道根数核心数据包括6个积分常数，即开普勒轨道六要素^[4]，卫星的轨道根数确定后，便可确定卫星任一时刻的空间位置，国际上采用较多的是美国全球观测网（SSN）发布的TLE根数形式，该根数形式提供开普勒根数中的轨道偏心率e，卫星运动轨道面与赤道面的夹角i，卫星轨道升交点赤经Ω，近地点极角ω。此外还提供了平近点角M₀和平均运动n₀，这2个参数可以推算出开普勒轨道根数中的卫星过近地点时刻ξ和轨道半长轴a。因此，本文将上述的6个参数e，i，Ω，ω，M₀，n₀，统称为TLE两行轨道的六要素。

SSN每天不定时会发布一条针对卫星的TLE轨道数据，随着时间T变化，TLE两行轨道六要素也发生改变，直观上来看，TLE轨道六要素的变化和时间T之间应存在某种对应关系。TLE轨道六要素的物理含义详细说明见表1，使用神经网络进行轨道预测将使用六要素，如表1所示。

2 基于神经网络的轨道预报算法 2.1 构建LSTM预测模型

使用神经网络算法对卫星轨道预报分为两部分：一是对TLE轨道数据核心要素的预报；二是对卫星位置和速度进行预报。对卫星的核心要素进行预报是指针对TLE轨道六要素进行预报，通过训练历史TLE数据，得到六要素随时间的变化趋势预报模型，可对1 d，3 d，5 d，10 d后的轨道六要素进行预报，进而可以生成完整的TLE数据。对卫星的位置和速度进行预报，是指通过训练TLE的六要素和卫星位置速度的对应关系，形成预报模型，预报过程中，通过提供卫星的TLE六要素，可得到卫星在任意时刻的位置和速度。

基于神经网络的LSTM算法适合处理时序数据，使用循环神经网络LSTM预报卫星轨道TLE，同时在预报过程中结合数据的特征使用线性回归对部分数据进行拟合。本文根据TLE数据的特点及其物理含义，在TLE轨道六要素的基础上增添TLE数据获取时间戳T以及相邻TLE数据之间的时间间隔D，用以构建适用于TLE数据预测的TLE预报八要素^[5]：

var = {e，i，Ω，ω，M₀，n₀，T，D}。

鉴于神经网络训练多个参数的复杂度，对轨道六要素分别进行训练和预报。根据对TLE轨道六要素的时序变化分析^[6]，轨道六要素中的轨道倾角i、轨道离心率e以及平均运动n₀三个可以直接用神经网络进行训练，针对这3个要素分别构建基于LSTM的预测算法。

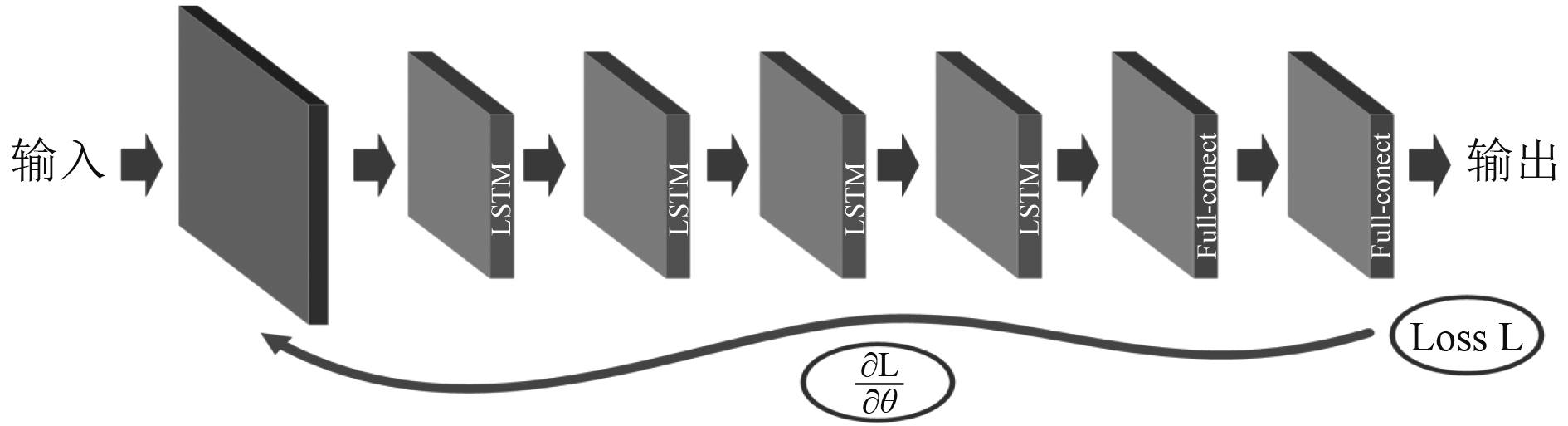
基于LSTM的预测模型由4部分组成，如图1所示。

1）输入层：TLE轨道预报八要素数据。

2）LSTM层：获取TLE轨道预报八要素数据的高维度特征。

3）全连接层（Full-connect）：对获取到的高维度特征进行整合。

4）输出层：计算目标要素的预测值并输出。

以轨道倾角i的预测模型为例。首先，以历史连续的N条数据作为输入x，以相应的第N+1条TLE数据中轨道倾角i的值作为输出y，构建轨道要素预报数据。在模型的训练过程中，模型的输入层接受输入数据x。通过LSTM层学习依赖于N条TLE数据较长时间跨度内的高维度特征，在全连接层对获取到的高维度特征进行微调和整合，给出回归向量 $ {R}^{*} $ 。最后，在输出层对回归向量 $ {R}^{*} $ 进行线性组合得到相应的要素预测 $ \tilde {y} $ 。

使用均方根误差（RMSE，Root Mean Squard Error）作为损失函数，即使用轨道要素真实值y与相应的模型预测值 $ \tilde {y} $ 之间的平方损失来衡量模型预测的好坏程度^[7]。模型的损失函数如下：

$ J\left(\theta \right) =\sqrt{\frac{1}{m}\sum\limits _{i=1}^{m}{({y}_{i}-{\tilde {y}}_{i})}^{2}} {\text{。}}$

其中：θ为神经网络模型中的权重参数；m为训练过程中预测的样本数量。在训练过程中，通过梯度下降法迭代更新参数θ完成最小化 $ \mathrm{J}\left(\mathrm{\theta }\right) $ 的目标，从而得到轨道参数基于LSTM较为准确的预测模型。

对于轨道六要素中的其他3个：升交点赤经 $ {\Omega } $ 、近地点角距ω以及平近点角 $ {M}_{0} $ ，根据其数据的时序变化特点和仿真结果，假定这3个要素在较短时间跨度内与时间呈近似线性关系，故基于线性回归（Linear Regression）算法分别针对这3个要素构建预测模型^[8]。以升交点赤经Ω的要素预测模型为例，以轨道预报八要素中的时间戳T与升交点赤经Ω分别作为模型的输入，并用其输出值进行模型的准确度评估，该预报问题可定义为：

给定m个变量 $ \{\left({{t}}_{1},{{y}}_{1}\right),\left({{t}}_{2},{{y}}_{2}\right),\cdots ,({{t}}_{{m}},{{y}}_{{m}}\left)\right\} $ ，其中 $ {t}\in {{R}}^{{n}},{y}\in {R} $ ，目标是找到一个最合适的函数F(t): $ f:{{R}}^{{n}}\to {R} $ 。

因为y与t呈近似线性关系，其关系可表示为：

$ f\left({w}_{1},\cdots ,{w}_{n},b\right)=y=w\cdot t+b+\epsilon \text{。}$

其中：w为系数；b为截距。

为了找到最佳函数，在基于线性回归的预测算法中，同样采用均方根误差 $ {J}\left({\theta }\right) $ 作为模型预测好坏程度的评价指标，其中θ表示神经网络模型中的权重参数，在训练过程中通过梯度下降法迭代更新参数θ，使得 $ {J}\left({\theta }\right) $ 最小。

2.2 构建LSTM-CNN网络模型

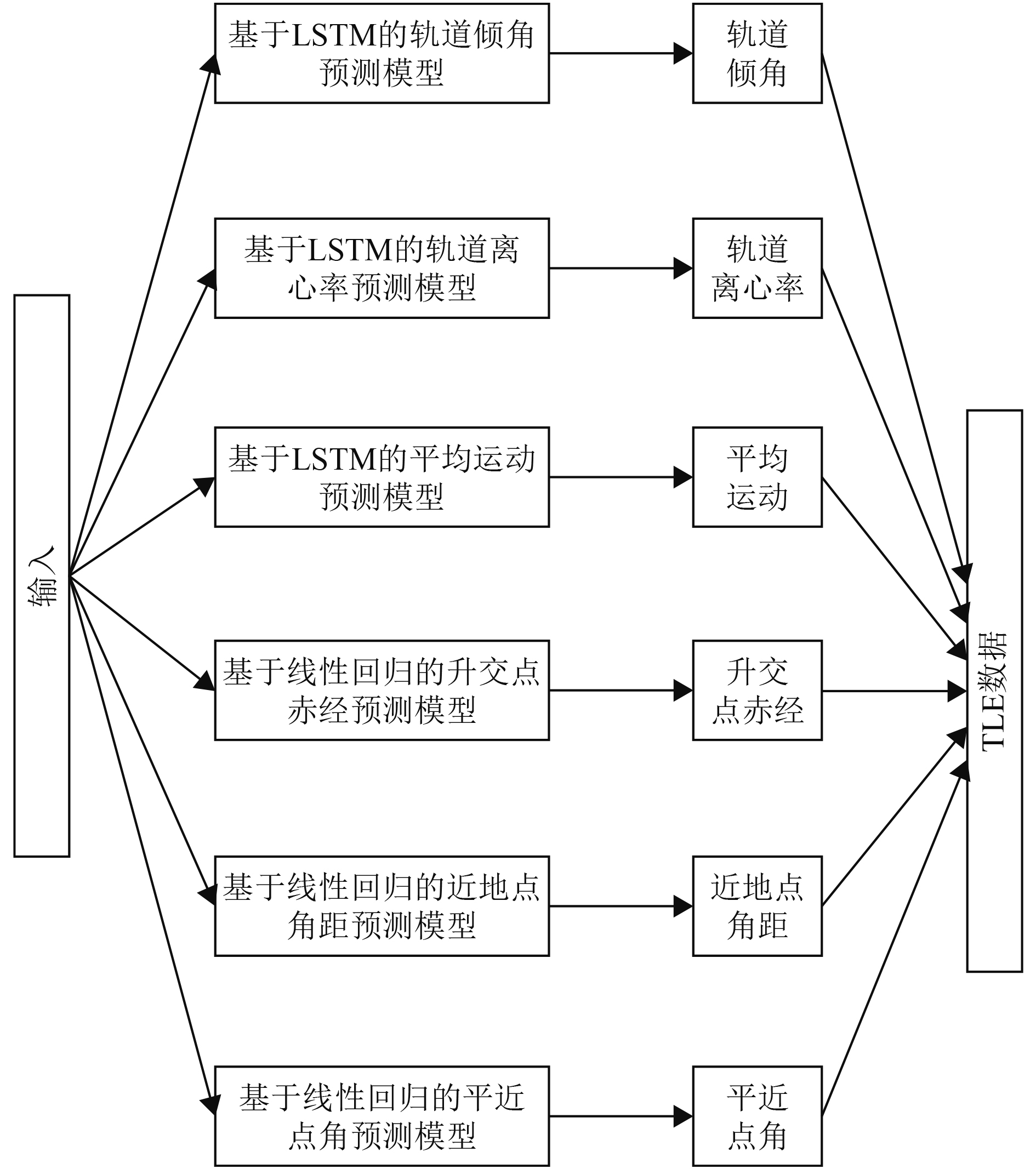
为了验证卷积神经网络模型的加入有助于轨道预报精度的提高，在原有的LSTM模型的基础上，添加了卷积神经网络来获取TLE数据之间的短期时序依赖关系，其模型框架如图2所示。

具体而言，给定训练数据 $ {{T}{L}{E}}_{0}^{\mathrm{m}} $ 和预测的时间戳 $ {{t}}_{{m}+1} $ ，首先对训练数据分割来获取末端n个TLE数据 $ {{t}{l}{e}}_{{s}} $ ，用此来预测未来时刻起始的TLE数据，其形式化表示为：

$ {{t}{l}{e}}_{{s}}={TLE}_{m-n-1}^{m}\text{，} $

$ {{T}{L}{E}}_{{m}}=\{{{i}}_{{m}},{\omega }_{m},{M}_{m},{i}_{m},{e}_{m},{n}_{m},{t}_{m},\Delta {t}_{m}\}\text{，} $

$ \Delta {{t}}_{{m}}={t}_{m+1}-{t}_{m}\text{。} $

特别注意第m个TLE数据 $ {{T}{L}{E}}_{{m}} $ ，也就是训练数据中的最后一个TLE数据，其时间间隔 $ \Delta {{t}}_{{m}} $ 是根据预测的时间戳 $ {{t}}_{{m}+1} $ 和其当前时间戳 $ {{t}}_{{m}} $ 求差得到的。

之后将 $ {{t}{l}{e}}_{{s}} $ 分别输入到TLE数据中每个元素各自对应的模型，得到第m+1时刻TLE数据的6个要素，注意第m+1时刻的TLE数据是在测试集，测试集被视为空间飞行物未来时刻的数据，形式化表示如下:

$ {\tilde {{i}}}_{{m}+1}=LSTM\_CN{N}_{1}\left({TLE}_{m-n-1}^{m}\right)\text{，} $

$ {\tilde {{e}}}_{{m}+1}=LSTM\_CN{N}_{2}\left({TLE}_{m-n-1}^{m}\right)\text{，} $

$ {\tilde {{n}}}_{{m}+1}=LSTM\left({TLE}_{m-n-1}^{m}\right)\text{，} $

$ {\tilde {{\Omega }}}_{{m}+1}=LR\left({TLE}_{m-n-1}^{m}\right) \text{，}$

$ {\tilde {{\omega }}}_{{m}+1}=LR({TLE}_{m-n-1}^{m}\text{，} $

$ {\tilde {{M}}}_{{m}+1}=LR\left({TLE}_{m-n-1}^{m}\right) \text{。}$

其中： $ {L}{R} $ 为线性回归模型； $ {L}{S}{T}{M} $ 为长短时记忆网络模型；CNN为卷积神经网络模型； ${L}{S}{T}{M}\_{C}{N}{N}$ 为联合LSTM和CNN的轨道预报模型。

接着将预测到的第 $ {m}+1 $ 时刻TLE数据中不同的元素拼接起来构成新的TLE数据：

$ \begin{split} & {\tilde {{T}{L}{E}}}_{{m}+1}=\{{\tilde {{i}}}_{{m}+1},{\tilde {\omega }}_{m+1},{\tilde {M}}_{m+1},{\tilde {i}}_{m+1},{\tilde {e}}_{m+1},{\tilde {n}}_{m+1},{t}_{m+1},\Delta {t}_{m+1}\}\\ &\Delta {{t}}_{{m}+1}={t}_{m+2}-{t}_{m+1*} \text{，}\\[-10pt] \end{split} $

其中， $ {{t}}_{{m}+2} $ 是第m+2时刻的时间戳。

最后将预测的第m+1时刻的TLE数据 $ {\widetilde {{T}{L}{E}}}_{{m}+1} $ 和第m-n-2时刻到第m时刻的TLE数据 $ {{T}{L}{E}}_{m-n-2}^{m} $ 进行拼接，从而得到模型下一轮预测的输入数据 $ {{T}{L}{E}}_{m-n-2}^{m+1} $ ，

$ {{T}{L}{E}}_{m-n-2}^{m+1}={{T}{L}{E}}_{m-n-2}^{m}\oplus {\widetilde {{T}{L}{E}}}_{m+1} \text{。}$

不断重复上述步骤，直到完成指定未来预测的天数为止。

2.3 模型衡量指标

1）根据模型预测的TLE数据和真实的TLE数据的绝对误差作为衡量指标，来衡量模型预测TLE数据的精度:

$ {{m}{e}{t}{r}{i}{c}}_{1}=\left|\right|{{T}{L}{E}}_{{p}}-{{T}{L}{E}}_{{t}}\left|\right| \text{，}$

其中 $ {{T}{L}{E}}_{{p}} $ 表示模型预测TLE数据， $ {{T}{L}{E}}_{{t}} $ 表示真实的TLE数据。

2）传统的动力学模型的衡量指标是在同一时刻模型预测空间飞行物体的状态，例如速度和位置，与星历数据观察值的绝对误差，绝对误差越小说明其精度越高。为了能和传统的动力学模型比较，采用速度和位置的绝对误差作为模型的另一衡量指标。

$ {metric}_{2}^{position}=\sqrt{{\left({p}_{x}^{t}-{p}_{x}^{p}\right)}^{2}+{\left({p}_{y}^{t}-{p}_{y}^{p}\right)}^{2}+{\left({p}_{z}^{t}-{p}_{z}^{p}\right)}^{2}} \text{，}$

$ {metric}_{2}^{velocity}=\sqrt{{\left({v}_{x}^{t}-{v}_{x}^{p}\right)}^{2}+{\left({v}_{y}^{t}-{v}_{y}^{p}\right)}^{2}+{\left({v}_{z}^{t}-{v}_{z}^{p}\right)}^{2}} \text{。}$

其中： $ {p}_{x}^{t} $ ， $ {p}_{y}^{t} $ 和 $ {p}_{z}^{t} $ 分别为星历数据在位置x轴、y轴和z轴上的观察值； $ {p}_{x}^{p} $ ， $ {p}_{y}^{p} $ 和 $ {p}_{z}^{p} $ 分别表示模型预测的TLE数据经过转化之后在位置x轴、y轴和z轴上的预测值； $ {v}_{x}^{t} $ ， $ {v}_{y}^{t} $ ， $ {v}_{z}^{t} $ ， $ {v}_{x}^{p} $ ， $ {v}_{y}^{p} $ 和 $ {v}_{z}^{p} $ 表示速度各个维度在星历数据上的观察值和模型的预测值。

3 初步实验结果 3.1 实验数据

告密者1（Informator 1）是Koskon（空间转换）全球空间通信系统的一颗原型通信卫星，选择从1991年6月17日到2003年2月8日由其有效载荷AO-21生成的共10550条TLE数据，按照时间先后排序之后，将前80%的TLE数据作为训练集，将后20%的TLE数据，其详细统计数据如表2所示。

3.2 模型参数设置

为了能和LSTM模型有比较，因此我们设置网络训练的参数与LSTM模型相同，LSTM_CNN模型在LSTM模型的基础上引入了CNN模型来获取TLE时序数据的局部特征。

一开始尝试LSTM模型对应的3个元素全部用LSTM_CNN模型替换，并记录相应的实验结果。为了更加深入地研究LSTM_CNN模型对位置预报精度的影响，将线性回归预测的3个变量的实验参数设置和LSTM对应相同。

3.3 实验结果与分析

1）LSTM_CNN模型替换LSTM模型

将LSTM模型对应的3个元素使用LSTM_CNN模型来训练和预测，分别记录在20 d内轨道离心率、轨道倾角和平均运动的误差及在20 d内速度位置上的误差。

首先比较LSTM_CNN模型和LSTM模型对TLE元素的预测结果发现，LSTM模型对轨道离心率、轨道倾角和平均运动的误差分别控制在0.333，2.34和0.22，而LSTM_CNN模型对轨道离心率、轨道倾角和平均运动的误差分别控制在0.17，1.68和0.53。上述现象的原因是轨道离心率、轨道倾角随着时间呈现比较复杂的变化曲线，而平均运动时间呈现比较缓慢的变化，增加模型的复杂度对轨道离心率和轨道倾角的预测精度有所提高，而对于平均运动则会存在过拟合的问题，导致其在训练数据集上表现效果好，而在测试数据集上误差高。

其次比较LSTM_CNN模型和LSTM模型对位置上的误差，发现LSTM_CNN模型在轨道离心率和轨道倾角上的精度提高，在平均运动上的预报精度下降，导致在位置上的总体误差从LSTM模型的100 km升高到了200 km，由此说明平均运动的精度和位置上的预报精度成正比。为了让结论更加有说服力，分别构建在3个元素不同预报精度下对位置误差的影响。

其中“真实值”表示采用预测数据的真实值，不采用LSTM模型或者LSTM_CNN模型的预测值。通过灵敏度分析可知，平均运动的预报模型宜采用LSTM模型，轨道倾角和轨道离心率的预报模型为宜采用LSTM_CNN模型，这样预测的三要素误差值最小。观察表中的实验结果，比较序号1和序号2，在保持轨道倾角和轨道离心率不变的情况下，其中序号1中平均运动的误差低，同时序号1的整体位置误差比序号2低，由此可充分说明平均运动的预报精度和对空间飞行物位置上的整体预报精度成正比关系。除此之外，比较序号3、序号4和序号5中轨道倾角的误差分别为1711，6716和0，而位置上的整体误差控制在98 km左右，充分说明了轨道倾角的预报精度对位置上的误差影响较小。最后观察序号3和序号6上的轨道离心率的误差分别在16816和0，而位置上的整体误差控制在97 km左右，由此说明轨道离心率对轨道预报模型精度的影响较小。

4 结　语

通常，其他国家的卫星特别是有军事用途的卫星实时信息是严格保密不易获取的。本文建立仅依赖历史数据的卫星轨道预测模型，针对不同的预测参数采用不同的神经网络模型算法，可以最大可能地减少预测误差、提高预测精度，同时该预测模型支持长时间跨度的卫星轨道预测，最长可以对20 d的卫星数据进行预测，位置误差控制在100 km以内，基本能够满足使用要求。后续，考虑增大训练集合规模，采用不同时序处理算法开展下阶段研究，以期进一步提高预测精度。