在鱼雷声自导技术中,主动声自导性能与信号发射波形密切相关,其发射波形的设计与选择直接影响声自导系统的分辨率、测量精度以及抗混响能力等主要性能,是主动声自导系统设计的重要内容。
目前鱼雷声自导中常用的主动声信号仍以CW与FM信号2种常规信号形式为主。但由于矩形脉冲信号(CW)不能同时获得较高的时间分辨力和频率分辨力,线性调频信号(LFM)的时频分辨力可以单独调整,但当速度和距离均未知时,存在距离-速度二维耦合,测量会带来附加误差。这种常规信号波形体制在鱼雷的目标定位、识别及海洋环境的适应性能力还非常有限[1-3]。
近年来,组合信号形式的研究得到广泛关注。由于在信号波形设计中,相对于常规单一信号形式,组合信号及若干复杂信号在目标分辨力以及抗混响性能上具有明显优势,在声呐技术中得到一定研究[4-5]。但在声自导技术中,该研究还处于起步阶段。为提高声自导能力及抗混响性能,本研究采用组合信号等复杂信号形式,以优化声自导波形设计而提高声自导能力,在声自导新技术研究方面具有重要意义。
另一方面,在海洋环境下的鱼雷目标探测过程中,鱼雷本身是高速运动体(速度高达数十节),主动声自导方式下,主动发射信号的混响干扰将远高于海洋环境的噪声影响,已成为声自导的主要噪声干扰。因此,声自导复杂信号波形的抗混响性能是需要研究的另一重要内容[6-10]。
随着水声技术的发展特别是换能器技术与信号处理技术的发展,复杂信号形式的产生与信号处理已不再是水声工程技术的难点,这为复杂信号在鱼雷自导及声呐中的应用提供了可能性。本文在关注单一信号形式特点研究的基础上着重探讨了CW-CW,FM-FM,CW-LFM,Costas等多种复杂信号特性及在声自导中应用的可能性,并详细分析了鱼雷混响产生机理及复杂信号抗混响性能。本文将为声自导目标探测识别及环境适应性新技术的研究提供一定的技术参考。
1 几种声自导复杂信号模型常规单一信号体制下的目标探测及抗混响能力还非常有限。如果将单一信号组合起来,充分利用其各自不同特点,则可以提高目标的检测性能。以下是几种可用于声自导的复杂组合信号波形形式。
1.1 CW-CW组合信号单一CW信号不能同时提高距离分辨力和速度分辨力,所以依次发射不同频率的CW信号可形成CW-CW组合信号,以2个频率组合信号为例(以下同理),观察其性能。组合CW信号数学表达式为:
| $s(t) = \left\{ {\begin{array}{*{20}{c}} {rec\left(\dfrac{t}{T}\right){e^{j2{\text{π}} {f_1}t}}} \text{,}&{0 \leqslant t \leqslant 0.05} \text{,}\\ {rec\left(\dfrac{t}{T}\right){e^{j2{\text{π}} {f_2}t}}} \text{,}&{0.05 < t < 0.1} \text{。} \end{array}} \right.$ | (1) |
其中:
线性调频(LFM)信号是主动声自导使用最为广泛的发射信号形式之一,可单独调整时延分辨力或频移分辨力,但当距离速度全部未知时,会存在一定程度的二维耦合。其主要参数包括中心频率、调频斜率、带宽和脉宽。矩形包络的LFM信号也称Chirp信号。
同CW-CW组合信号一样,LFM-LFM组合信号是依次发射不同中心频率的LFM信号,其信号数学表达式为:
| $s(t) = \left\{ {\begin{array}{*{20}{c}} {rec\left(\dfrac{t}{T}\right){e^{j2\pi ({f_1}t \pm \frac{K}{2}{t^2})}}} \text{,}&{0 \leqslant t \leqslant 0.05}\text{,} \\ {rec\left(\dfrac{t}{T}\right){e^{j2\pi ({f_2}t \pm \frac{K}{2}{t^2})}}} \text{,}&{0.05 < t \leqslant 0.1} \text{。} \end{array}} \right.$ | (2) |
其中:
在绝大多数情况中,对检测目标的速度并不了解,如果把CW,LFM两种波形融合起来,充分利用它们各自不同的特点,就可以提高检测性能。CW-LFM组合信号就是CW信号与LFM信号组合成一个信号形式,为了方便比较,选择优先发射CW信号,之后再发射LFM信号。CW-LFM组合信号数学表达式为:
| $s(t) = \left\{ {\begin{array}{*{20}{c}} {rec\left(\dfrac{t}{T}\right){e^{j2{\text{π}} {f_1}t}}} \text{,}&{0 \leqslant t \leqslant 0.05} \text{,}\\ {rec\left(\dfrac{t}{T}\right){e^{j2{\text{π}} ({f_2}t \pm \frac{K}{2}{t^2})}}} \text{,}&{0.05 < t \leqslant 0.1} \text{。} \end{array}} \right.$ | (3) |
频率调制脉冲信号具有带宽大、距离分辨率高、发射功率谱密度捷变、脉内调制复杂的特点,有良好的低截获概率特性,Costas编码是一种典型的频率调制脉冲编码[11-13]。
设Costas信号脉冲宽度为T,码元宽度
| $s(t) = \frac{1}{{\sqrt {N{t_b}} }}\sum\limits_{m = 1}^M {{u_m}[t - (m - 1){t_b}]} \text{,}$ | (4) |
式中:
| $ {s_m}(t) = \left\{\!\! {\begin{array}{*{20}{c}} {\exp \;(j2\text{π} {f_m}t)}\text{,}&{0 \leqslant t \leqslant {t_b}}\text{,}\\ 0\text{,}&{\text{其他}}\text{,} \end{array}} \right. $ | (5) |
| $ {f_m} = {a_m} \cdot t_b^{ - 1}\text{。} $ | (6) |
为有效分析上述声自导复杂信号的目标分辨能力,采用模糊函数[14-15]对复杂信号进行分析。
信号
| $\left| {\varPsi (\tau ,\xi )} \right| = \left| {\int_{ - \infty }^{ + \infty } {s(t){s^*}(t + \tau ){e^{ - j2{\text{π}} \xi t}}{\rm{d}}t} } \right|\text{,}$ | (7) |
模糊度函数具有以下3个特点:1)对原点的对称性;2)体积不变性;3)可实现性。
CW-CW组合信号参数为:信号幅值
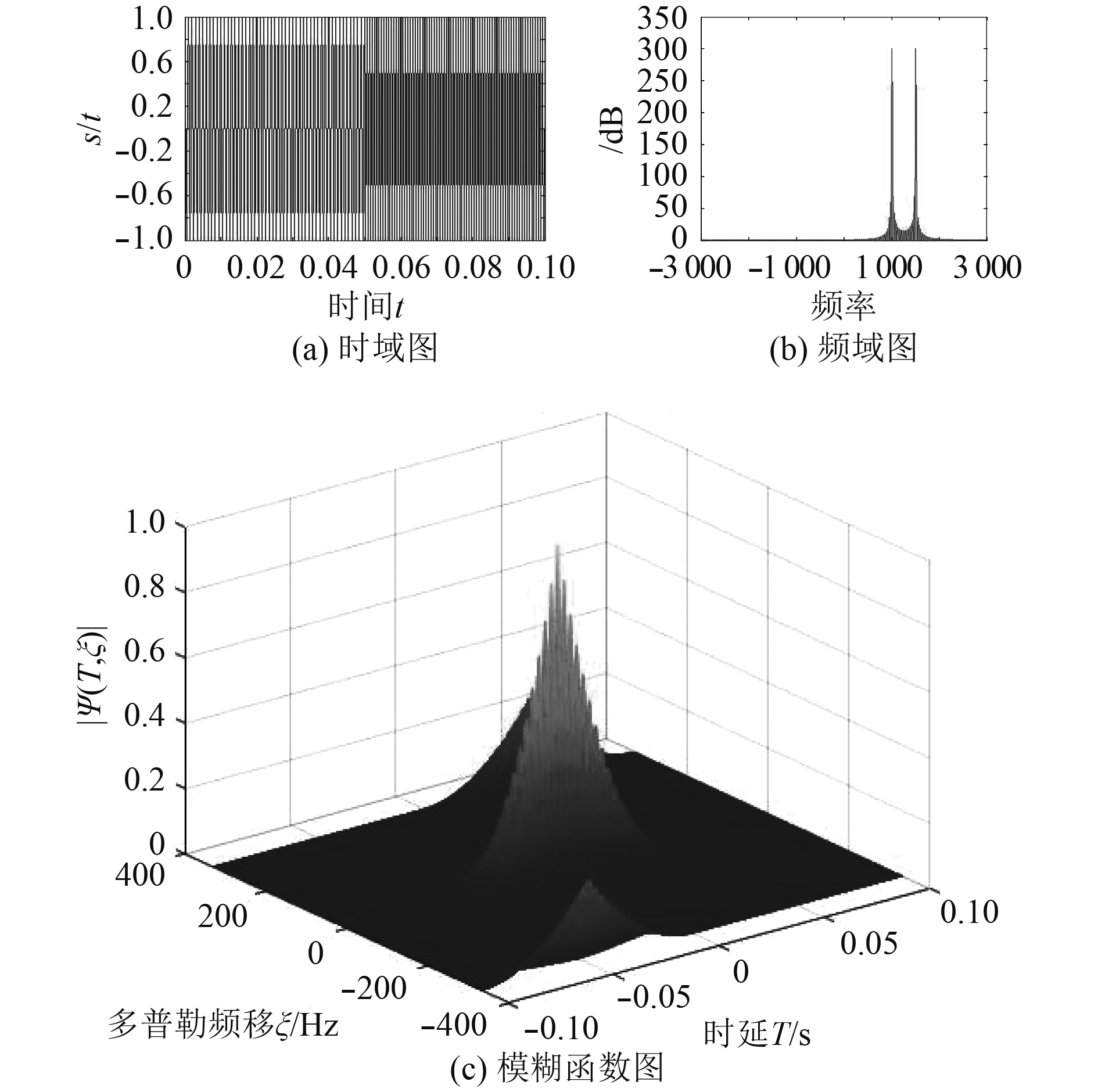
|
图 1 CW组合信号 Fig. 1 CW combined signal |
为了方便信号之间形成对比,LFM组合信号采用CW组合信号相同的信号幅值(A)、采样频率(

|
图 2 LFM组合信号 Fig. 2 LFM combined signal |
CW-LFM组合信号采用CW-CW组合信号的第1个CW信号和LFM-LFM组合信号中第2个LFM信号,时域、频谱、模糊函数图如图3所示。
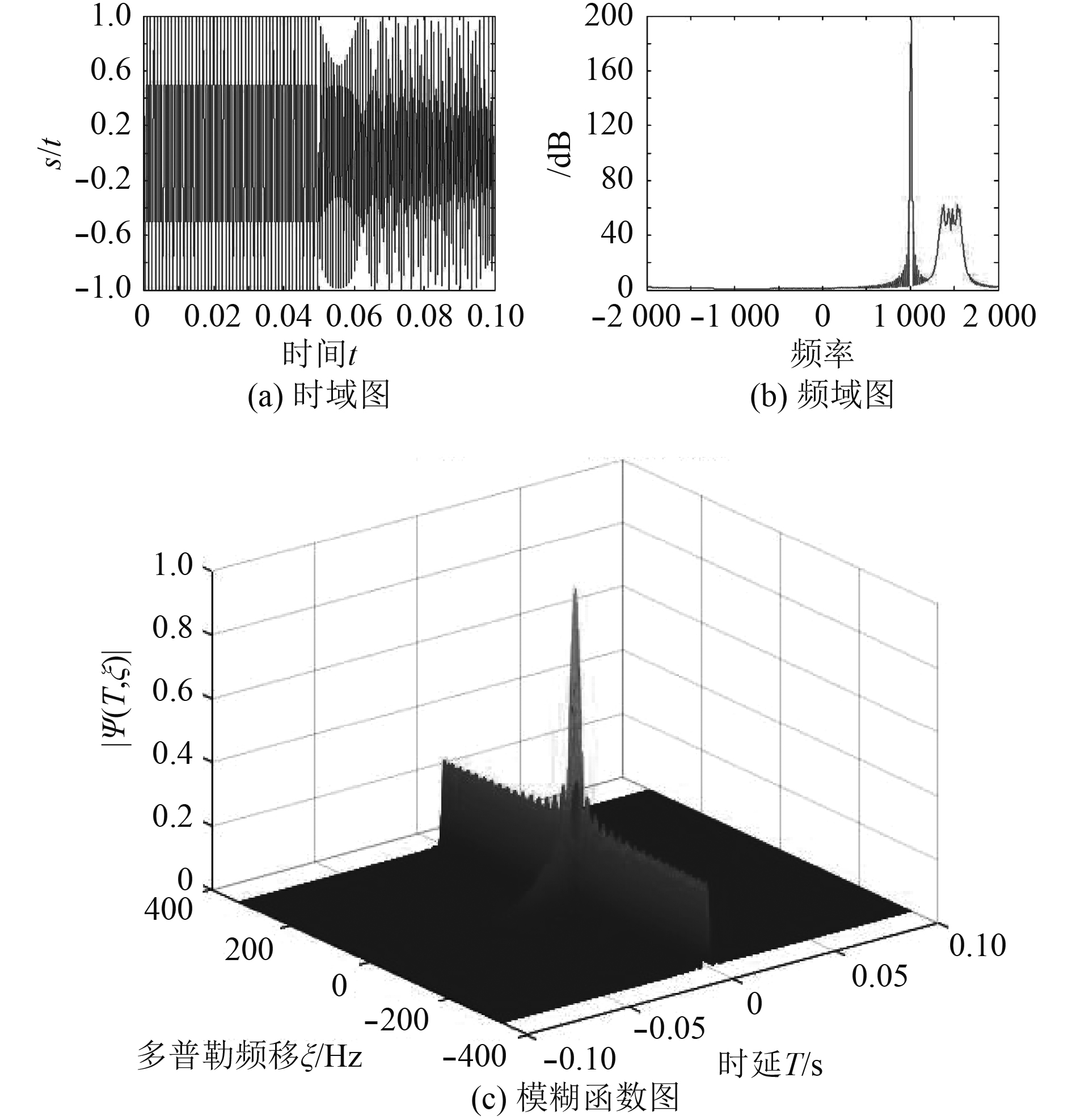
|
图 3 CW-LFM组合信号 Fig. 3 CW-LFM combined signal |
设频率编码序列长度为6,编码序列为[8 1 5 3 9 6],可以得出Costas编码信号的模糊函数为:
| $\begin{split} \chi (\tau ,\mu ) = &\frac{1}{M}\sum\limits_{m - 1}^M {\exp [j2{\text{π}} (m - 1)\mu {t_b}\{ \Phi (\tau ,\mu )} + \\ & \sum\limits_{n = q,m \ne 1}^M {{\Phi _{mn}}[\tau - (m - n){t_b},\mu ]} \} ]\text{,} \end{split}$ | (8) |
式中:
| ${\varPhi _{mn}}(\tau ,\mu ) = (1 - \frac{{\left| \tau \right|}}{{{t_b}}})\frac{{\sin \alpha }}{\alpha }\exp ( - j\beta - j2{\text{π}} {f_n}\tau ),\left| \tau \right| \leqslant {t_b}\text{,}$ | (9) |
| $\alpha = {\text{π}} ({f_m} - {f_n} - \mu )({t_b} - \left| \tau \right|)\text{,}$ | (10) |
| $\beta = {\text{π}} ({f_m} - {f_n} - \mu )({t_b} + \left| \tau \right|)\text{。}$ | (11) |
Costas编码信号的时域、频谱、模糊函数如图4所示。

|
图 4 Costas信号 Fig. 4 Costas signal |
模糊函数图的主瓣宽度代表信号的时频分辨力,主瓣宽度越小,时频分辨力越好;而旁瓣数量的多少以及高度表示信号在混响限制下分辨多目标的能力。CW-CW组合信号模糊函数图具有较高的旁瓣,不具备分辨多目标能力;较单一CW信号而言同样具有良好的频移分辨力,并且时延轴离散化,有很明显的改善。
LFM-LFM组合信号模糊函数图具有较尖锐的主瓣,具有较好的时频分辨力,其旁瓣区也较低,可用于进行多目标检测,但距离-速度二维耦合并没有得到改善。
CW-LFM组合信号模糊函数图较CW-CW组合信号,时延轴下降速率变快,但频移轴旁瓣有所上升;相比于LFM-LFM,CW-LFM组合信号,减弱了距离-速度二维耦合,得出CW-LFM组合信号在模糊度、时间分辨率以及频率分辨率都具有很好的普遍适用性。虽然牺牲了某些最优性能,但作为一种次优发射信号,具有更高的稳定性。
Costas模糊函数图具有较窄的主瓣,说明Costas信号有很好的时频联合分辨率,并且其旁瓣非常低,很适合于混响条件下多目标检测。
从以上复杂信号模糊函数图可以看出:在鱼雷声自导过程中,CW-CW组合信号比较适合于鱼雷远程、中程声自导过程;LFM-LFM组合信号比较适合于鱼雷中、近程声自导的目标探测;Costas信号可用于声自导末程的发射信号。
为对比不同信号下系统的检测性能,图5给出了各复杂信号检测概率随输入信噪比变化的关系曲线(ROC曲线)。

|
图 5 各信号ROC曲线图 Fig. 5 ROC curve of each signal |
可以看出,在相同信噪比的情况下,CW-LFM信号检测概率最高,其次是Costas信号、HFM-HFM组合信号、LFM-LFM组合信号、CW-CW组合信号。说明CW-LFM组合信号的抗混响能力最优,可见本文所给出的各复杂信号的检测性能均优于单一信号(CW,FM)的性能。
3 抗混响性能分析 3.1 声自导信号混响模型如前所述,鱼雷本身是高速运动体(速度高达数十节)。主动声自导方式下,主动发射信号的混响远大于海洋环境的噪声影响,是声自导的主要噪声干扰。
设发射信号的中心频率为
| ${f_T} = {f_0}\left(1 + \frac{{2{V_s}}}{c}\cos {\theta _s} - \frac{{2{V_T}}}{c}\cos {\theta _T}\right)\text{,}$ | (12) |
混响源相对声自导系统夹角为
| ${f_R} = {f_0}\left(1 + \frac{{2{V_s}\cos {\theta _R}}}{c}\right)\text{。}$ | (13) |
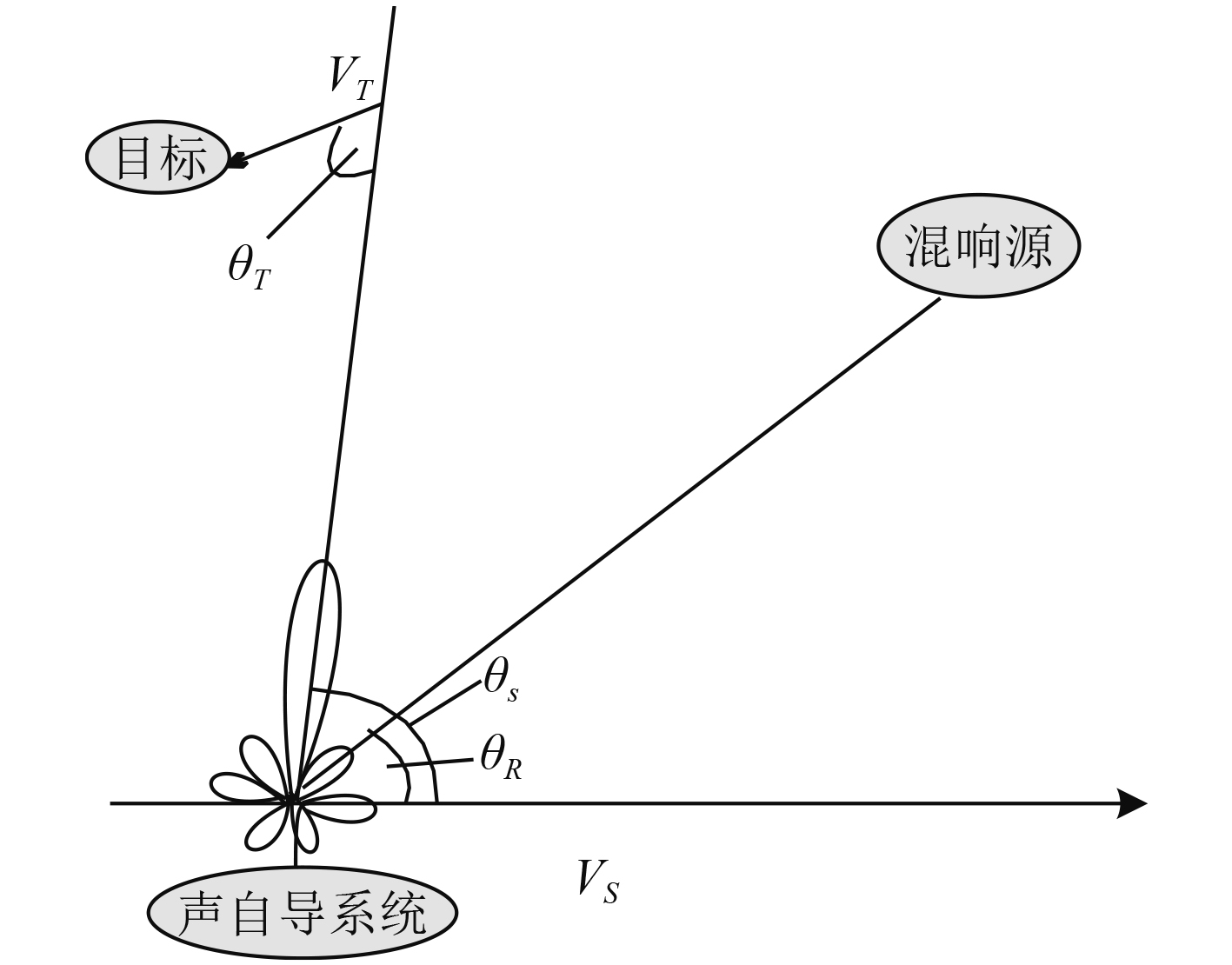
|
图 6 声自导载体运动模型 Fig. 6 Acoustic self-guided carrier motion model |
由上式可知,混响干扰与鱼雷载体的速度、发射信号频率及方位有关。波束除主瓣因素外,旁瓣越小抑制混响效果也越明显。
3.2 信号—混响原理图对于主动声自导,特别是在浅海情况,混响是一种主要的背景干扰。在混响环境中,信号的检测性能与所选的波形有重要的关系。一般可用检测指数d作为衡量接收机性能的一个重要指标。在高斯白噪声中,经过一系列推导后可得[16]:
| $d \approx \frac{{\sigma _t^2}}{{\int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {{\varphi _{hh}}(\omega ,\tau ){c'}({\tau _t} - \tau ,{\omega _d} - \omega )\dfrac{1}{{2{\text{π}} }}{\rm{d}}\omega {\rm{d}}\tau } } }}\text{。}$ | (14) |
式中:
可看出,在混响限制条件下,随着发射信号能量的增加,目标反射能量与混响能量同样会增加,并不会使输出信噪比得到改善。因此要改善信噪比,可以减少信号的模糊函数与信道散射函数的重叠部分。
当
信号—混响原理图可以分析波形的混响抑制能力。图7为发射脉冲
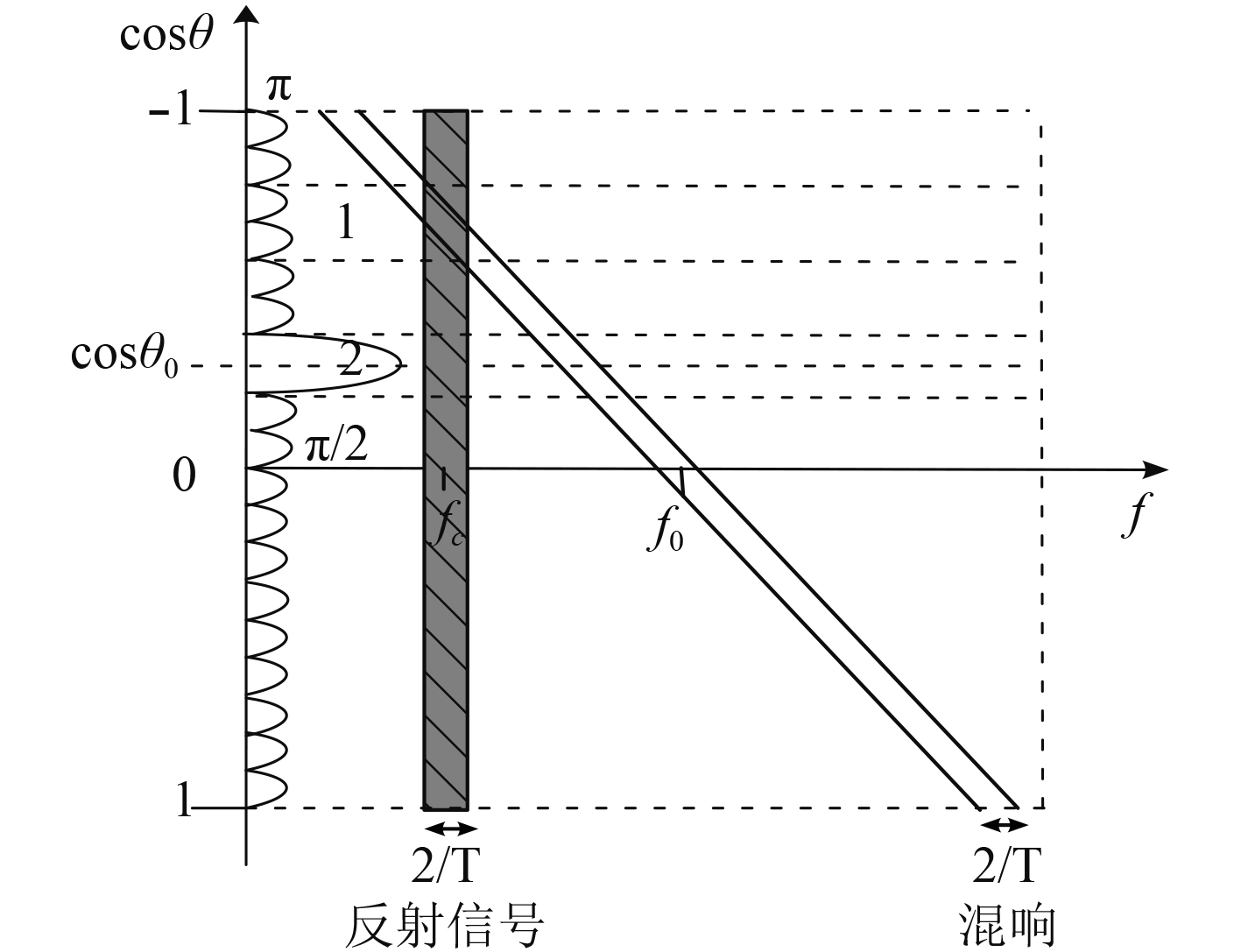
|
图 7 CW信号—混响原理图 Fig. 7 Signal-reverberation schematic of CW signal |
图8为宽带信号的混响原理图,可看出由于频带较宽,其混响分布在整个频带内,减弱了混响对于主瓣的影响。

|
图 8 FM信号—混响原理图 Fig. 8 Signal-reverberation schematic of FM signalπ |
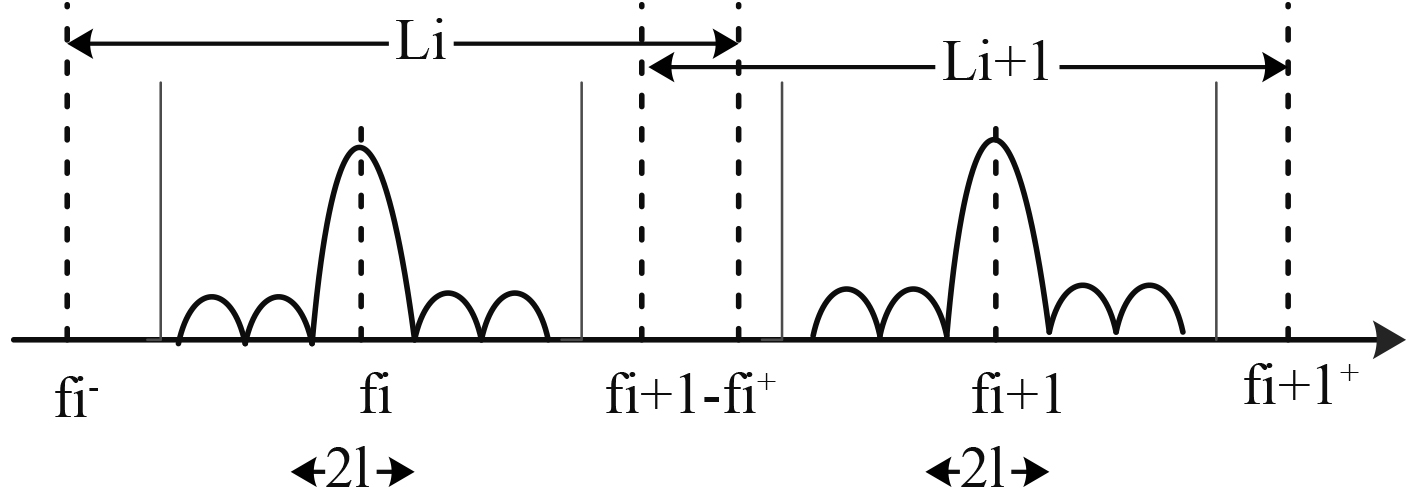
由于部分复杂信号含有不止一个频率,就会面临一个频率选择问题。为了防止其余频率发射信号所产生的混响对此相邻信号产生干扰,需对每个声自导发射频率有限制条件:各脉冲经多普勒频移后的回波信号的频率应在其他脉冲引起的混响的频带之外,如图9所示。
|
图 9 相邻脉冲发射模型 Fig. 9 Adjacent pulse emission model |
若声自导系统载体速度为
| $f_i^ + = (1 + 2{{{V_0}} / C})({f_i} + l)\text{。}$ | (15) |
式(15)表示
| $f_i^ + \leqslant (1 - 2{{{V_0}} / C})({f_{i + 1}} - l)\text{。}$ | (16) |
同理,目标反射脉冲
| $f_{i + 1}^ - \geqslant (1 + 2{{{V_0}}/ C})({f_i} + l)\text{。}$ | (17) |
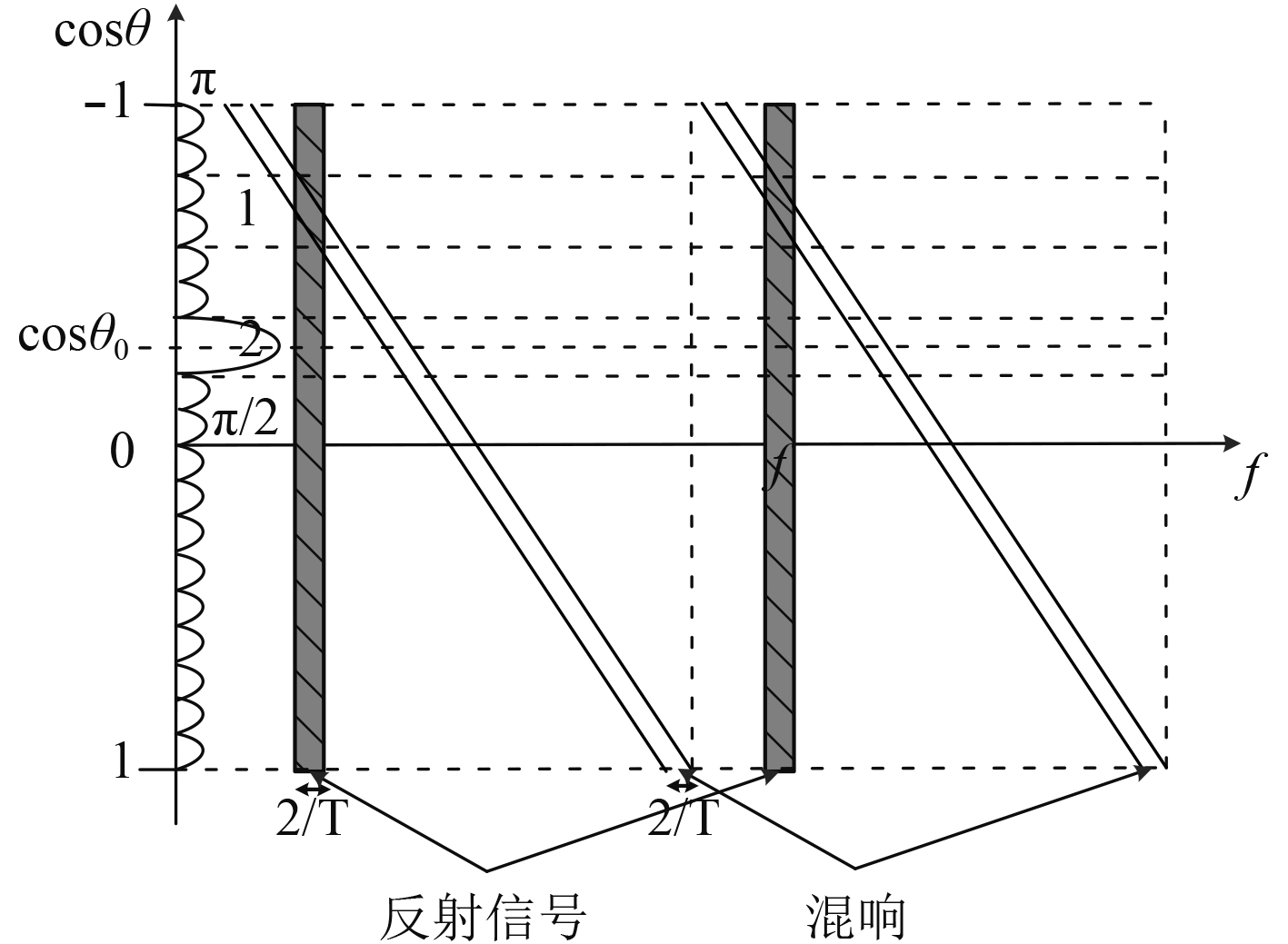
根据式(16)和式(17)可以给出CW-CW组合信号-混响原理图如图10所示。
|
图 10 CW组合信号—混响原理图 Fig. 10 Signal-reverberation schematic of CW combined signal |
Q函数是度量声呐波形混响输出的一个标准,是衡量信号抗混响性能标准之一。模糊函数延
| $Q(\xi ) = \int {{{\left| {\varPsi (\xi ,\tau )} \right|}^2}{\rm{d}}\tau } \text{,}$ | (18) |
其中,
根据式(18)得出以上各复杂信号的Q函数。
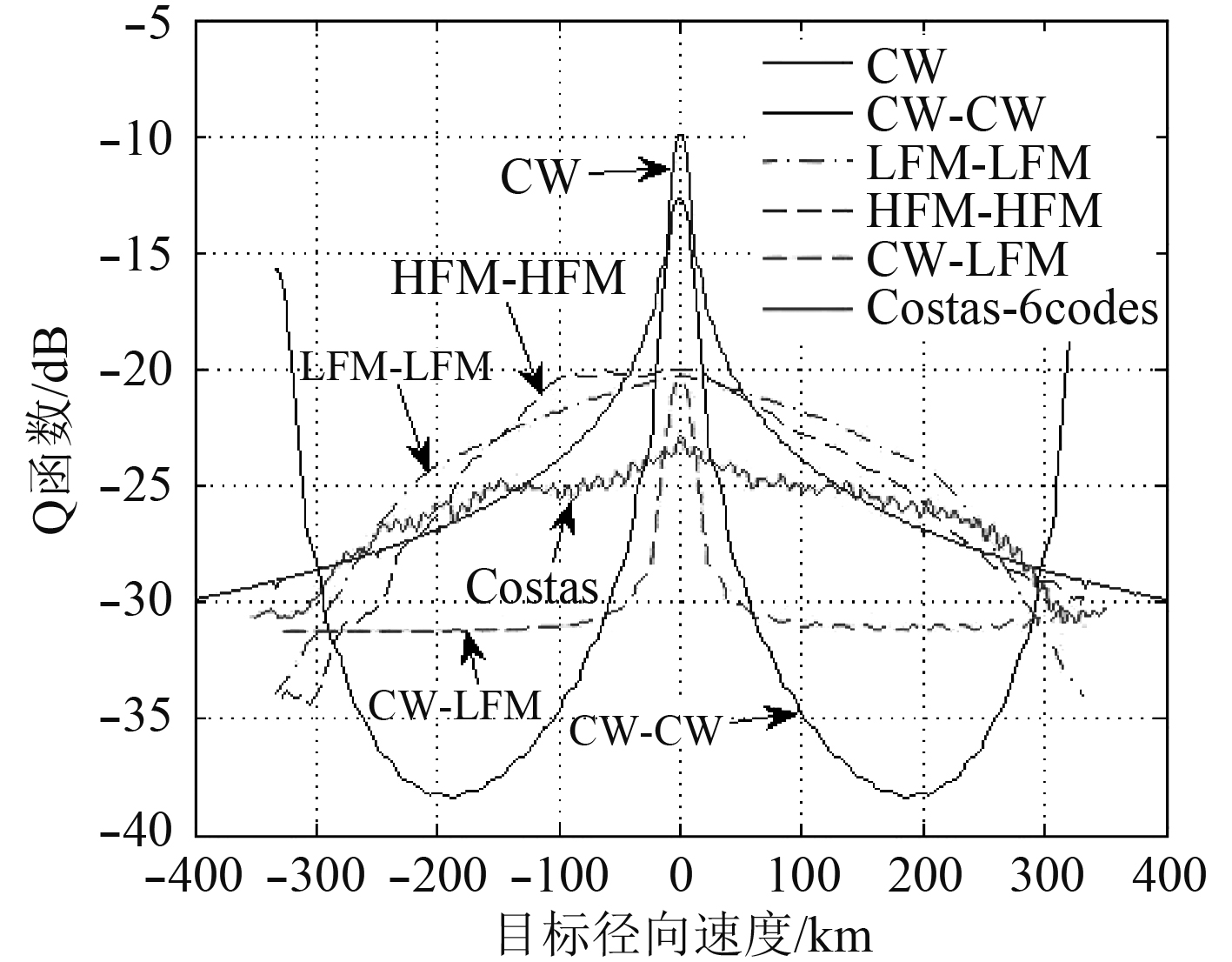
由图11可以看出:
|
图 11 各种信号的Q函数 Fig. 11 Q function of various signals |
1)信号位于0多普勒时,Costas信号Q函数值最低,CW-LFM,LFM-LFM,HFM-HFM组合基本相同,Costas信号在0多普勒区域抗混响能力更优;
2)当信号位于低多普勒时,CW-LFM与CW-CW组合信号的Q函数值最低,CW信号最高,说明 CW-CW,CW-LFM组合信号在低多普勒时为最优选择信号;
3)当信号位于中高多普勒时,Q函数最低的是CW-CW组合信号,CW-LFM组合信号次之,说明CW-CW组合信号在中多普勒频移时抗混响性能最好;
4)CW-LFM组合信号、Costas信号和HFM-HFM在较广的多普勒频移范围内的Q函数均值较低,具有普遍适用性。再通过CW-LFM组合信号的Q函数看出,其抗混响兼顾了CW-CW组合信号和LFM-LFM组合信号的特点,在零多普勒频率时,和CW-CW组合信号类似,有较高的Q函数峰值,但随着多普勒频率的增加,其抗混响性能又具有LFM-LFM组合信号的特点,具有平滑的Q函数图。
5 结 语本文探讨多种可用于声自导的复杂信号特点及抗混响特性,并进行仿真验证分析。研究结果表明:CW-CW,LFM-LFM,CW-LFM,Costas等各复杂信号较单一CW,LFM信号形式有更尖锐的模糊函数图主瓣,其速度-距离分辨力有明显的改善;ROC曲线分析表明各复杂信号检测性能较常规单一信号形式具有更优的性能。在抗混响能力方面,0多普勒时,Costas组合信号抗混响最好;低多普勒时,CW-LFM组合信号具有更高的抗混响性能。CW-LFM与Costas信号具有在较广速度范围内目标的检测能力。另外,HFM-HFM信号也具有良好的抗混响性。由此可见,本文所给出的复杂信号较常规信号具有更优的性能,在声自导中具有较好的工程应用前景。
实际中,可根据鱼雷自导的远、中、近、末不同阶段任务需求选择不同的复杂信号形式,如何在声自导中选择具体的波形组合与实时信号处理算法等都将是值得研究的课题。
| [1] |
金凤来, 马梦博, 田振. 主动声纳侦察中的LFM信号参数估计方法[J]. 舰船电子工程, 2017, 37(4): 112-115, 121. DOI:10.3969/j.issn.1672-9730.2017.04.028 |
| [2] |
徐钧, 凌国民. 水面舰艇声呐新技术评述[J]. 声学与电子工程, 2003(3): 1-8. |
| [3] |
李启虎. 声呐信号处理引论[M]. 北京: 海洋出版社, 1985.
|
| [4] |
郭瑞. 主动声纳组合波形设计技术的发展现状和趋势[A]. 中国声学学会水声学分会. 中国声学学会水声学分会2015年学术会议论文集[C]. 中国声学学会水声学分会:, 2015: 4.
|
| [5] |
杨崇林, 姚蓝. 探测高速小目标的声纳信号波形设计[J]. 声学技术, 1999(3): 16-19. |
| [6] |
章业成. 水声目标识别技术的现状与发展[J]. 电子技术与软件工程, 2019(18): 97-98. |
| [7] |
郝程鹏, 施博, 闫晟, 等. 主动声纳混响抑制与目标检测技术[J]. 科技导报, 2017, 35(20): 102-108. |
| [8] |
陈洁丽. 多普勒频移环境下的水声信号检测[D]. 广州: 华南理工大学, 2012.
|
| [9] |
YAN S. WILLETT P. LYNCH R. Waveform fusion for sonar detection and estimation[C]//2002 IEEE International Conference on Acoustics, Speech, and Signal Processing. IEEE, 2003, 3: 2973-2976.
|
| [10] |
刘贯领, 凌国民, 严琪. 主动声纳检测技术的回顾与展望[J]. 声学技术, 2007(2): 335-340. DOI:10.3969/j.issn.1000-3630.2007.02.035 |
| [11] |
肖靖, 杨文军. 线性调频-Costas频率步进信号分析及宽带合成处理[J]. 现代雷达, 2015, 37(3): 11-14. DOI:10.3969/j.issn.1004-7859.2015.03.004 |
| [12] |
张鑫, 艾勇军, 黄宇. Costas编码信号的循环谱特征分析与参数估计[J]. 海军航空工程学院学报, 2011, 26(04): 427-428, 430-431, 499. DOI:10.3969/j.issn.1673-1522.2011.04.016 |
| [13] |
罗贤全, 尚朝轩, 何强. 基于Costas编码跳频雷达信号分析及成像研究[J]. 电光与控制, 2007(6): 176-179. DOI:10.3969/j.issn.1671-637X.2007.06.045 |
| [14] |
王爽. 基于时频分析和模糊函数的LPI雷达波形识别算法研究[D]. 哈尔滨: 哈尔滨工程大学, 2019.
|
| [15] |
孙亚东. 雷达信号模糊函数理论研究与仿真[D]. 武汉: 武汉理工大学, 2007.
|
| [16] |
李峻年, 孟士超, 佘亚军. 主动声呐发射波形设计研究[J]. 舰船科学技术, 2014, 36(4): 108-113. DOI:10.3404/j.issn.1672-7649.2014.04.022 |
 2020, Vol. 42
2020, Vol. 42
