舰船综合电力系统将舰船的动力和电力两大系统整合为一个系统,提高了能量的综合利用率,具有简化动力系统结构、降低舰船噪声、优化总体布置、提高发电机运行效率、降低能耗等优势,提高了解决舰船动力系统发展瓶颈的技术方案[1-2]。
第2代综合电力系统以整流发电机为电源,以中压直流电网作为输电网络,采用直流区域配电系统为配电网络供电。区域配电变流器具有隔离潮流的作用,使得第2代综合电力系统输电网络潮流和配电网络潮流具有解耦的特点,可以实现输配电网络潮流的分别调整控制。直流输配电的网络结构使得系统不传输无功功率,只需考虑有功潮流的调整控制。上述特点使得第2代综合电力系统潮流调控相对简单且手段较多。直流系统并联发电机的运行中,主要通过调节发电机励磁实现有功功率的输出控制[3]。
目前国内船舶能量优化调度策略一般采用增减机原则。增机原则是指设定储备功率为恒值,如果系统储备功率小于相应的给定值,增加1台发电机组。减机原则是指如果1台发电机解列,发电机平均功率小于相应的设定值,则解列1台发电机组[4-5]。这种能量调度策略虽然可以避免系统储备功率不足和发电机运行在轻载的高耗能状态,但是并未考虑原动机的燃油耗量特性,无法实现综合电力系统的燃油经济性优化调度。
直流系统整流发电机功率输出有主从控制、电压偏差控制、对等控制3种控制方法。主从控制是指选定1台发电机为主发电机,控制直流母线电压为给定值,其余发电机作为从发电机,控制输出功率为给定值。主发电机作为平衡机,调节其输出功率以维持直流母线电压恒定。船舶运行需要电力系统要有一定的储备功率,以满足重要负载功率需求,此时系统抵抗负荷扰动的任务由主发电机承担,使得系统的抗扰能力大为下降。主从控制对通讯的依赖较强,对系统安全稳定运行有不利的影响。
电压偏差控制相当于主从控制的改进,在主发电机故障失去电压控制能力后,后备定发电机可以检测到电压偏移,转换为主发电机控制电压,保证系统继续稳定运行。电压偏差控制的偏差值选取较为困难,响应速度也较慢,同时未解决只有主发电机承担系统功率平衡任务的问题,各后备定发电机优先级的设置也增加了系统的设计复杂度。
对等控制是指所有的整流发电机在控制上都具有相同的地位,各控制器之间不存在主从关系,每个配电电源均根据接入系统点的电压和频率信息进行本地控制,共同维持系统电压和频率稳定,下垂控制是对等控制的主要方法。与主从控制方式相比,采用对等控制的发电机不依赖于某台主发电机,可以方便地实现发电机即插即用,可以避免主从控制模式中因主控发电机故障而导致系统崩溃的情况,同时降低了对通信系统的依赖,提高了配电系统运行的可靠性[3]。但传统下垂控制的并联发电机负载功率按其额定功率比例分配,不能直接用来实现整流发电机的优化运行。
本文针对综合电力系统运行需求,采用典型的中压直流综合电力系统作为研究对象,建立综合电力系统燃油经济性优化调度模型,提出基于改进下垂控制的综合电力系统燃油经济性优化调度方法,并通过仿真试验验证所提出方法的有效性。
1 综合电力系统燃油经济性优化调度方法在图1所示的典型第2代综合电力系统模型中,由整流发电机供电,整个系统包括中压直流、低压直流和区域交流配电3个子系统,由n1台整流发电机组并联为中压直流母线供电,中压直流母线给n2台DC/DC变流器、n3台推进负载PM供电。每台DC/DC变流器通过低压直流母线向DC/AC逆变器供电,DC/AC逆变器对交流配电系统进行配电,为了提高用电负荷的供电连续性和可靠性,区域交流配电系统配有辅助同步发电机[3]。
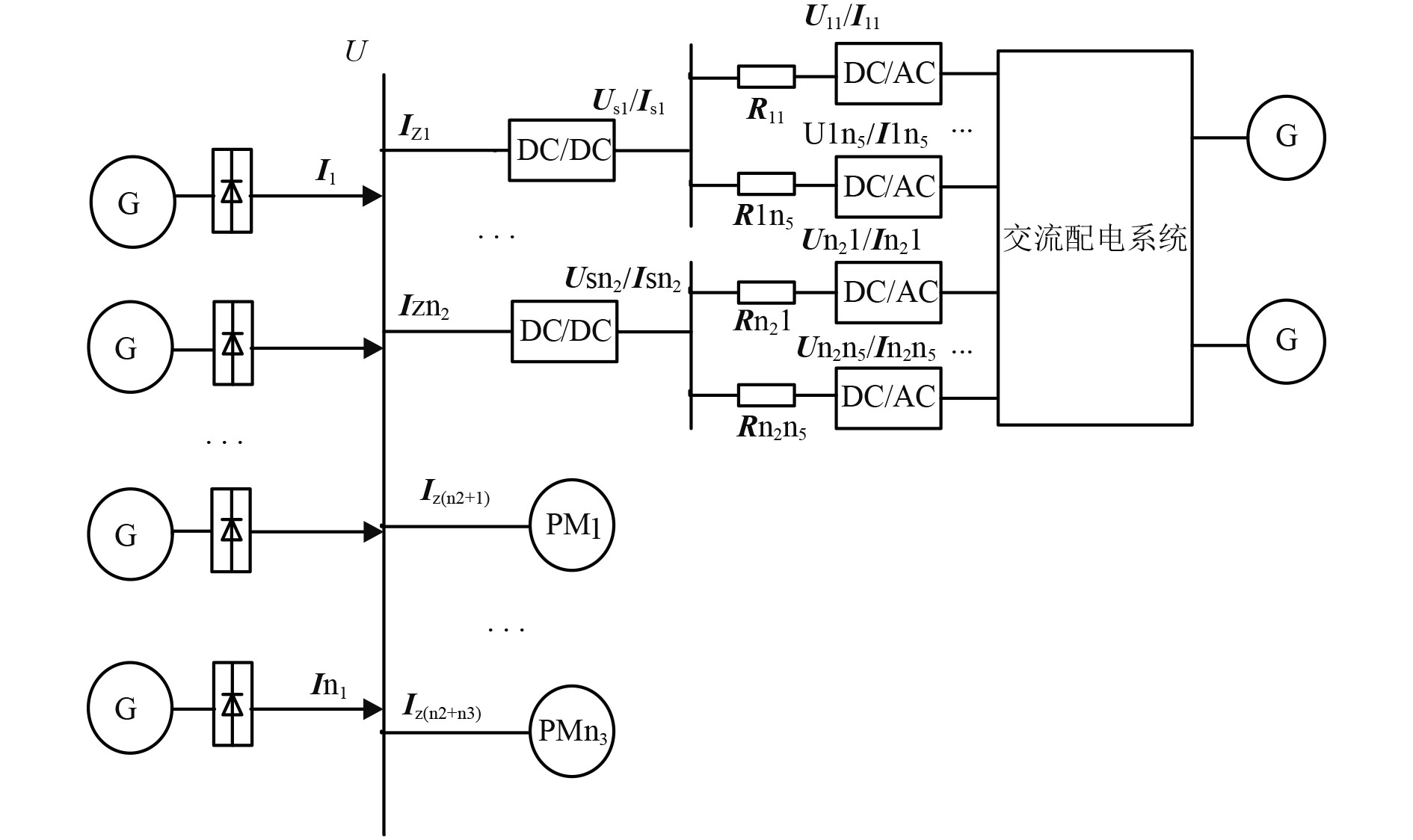
|
图 1 综合电力系统模型 Fig. 1 The model of integrated power system |
交流电力系统是通过调节原动机转速实现有功功率的输出控制,通过调节发电机励磁实现无功功率的输出控制。与此不同,提高中压直流综合电力系统发电机的励磁电势,其交流输出电压就会升高。由于发电机通过整流二极管并联,这台发电机整流二极管导通时间的比例就会提高,其输出电流就会增加,输出电磁功率也就随之增加。增大的电磁功率必将导致原动机转速下降,由于原动机调速系统的控制目标是维持其转速为额定,原动机就会逐渐提高输出功率直到其转速达到额定。因此,调整整流发电机的励磁控制就可以调节其输出功率。
1.1 整流发电机励磁的传统下垂控制环的控制参数的整定第i台整流发电机励磁的双环控制如图2所示,包括传统下垂控制环和改进下垂控制环。
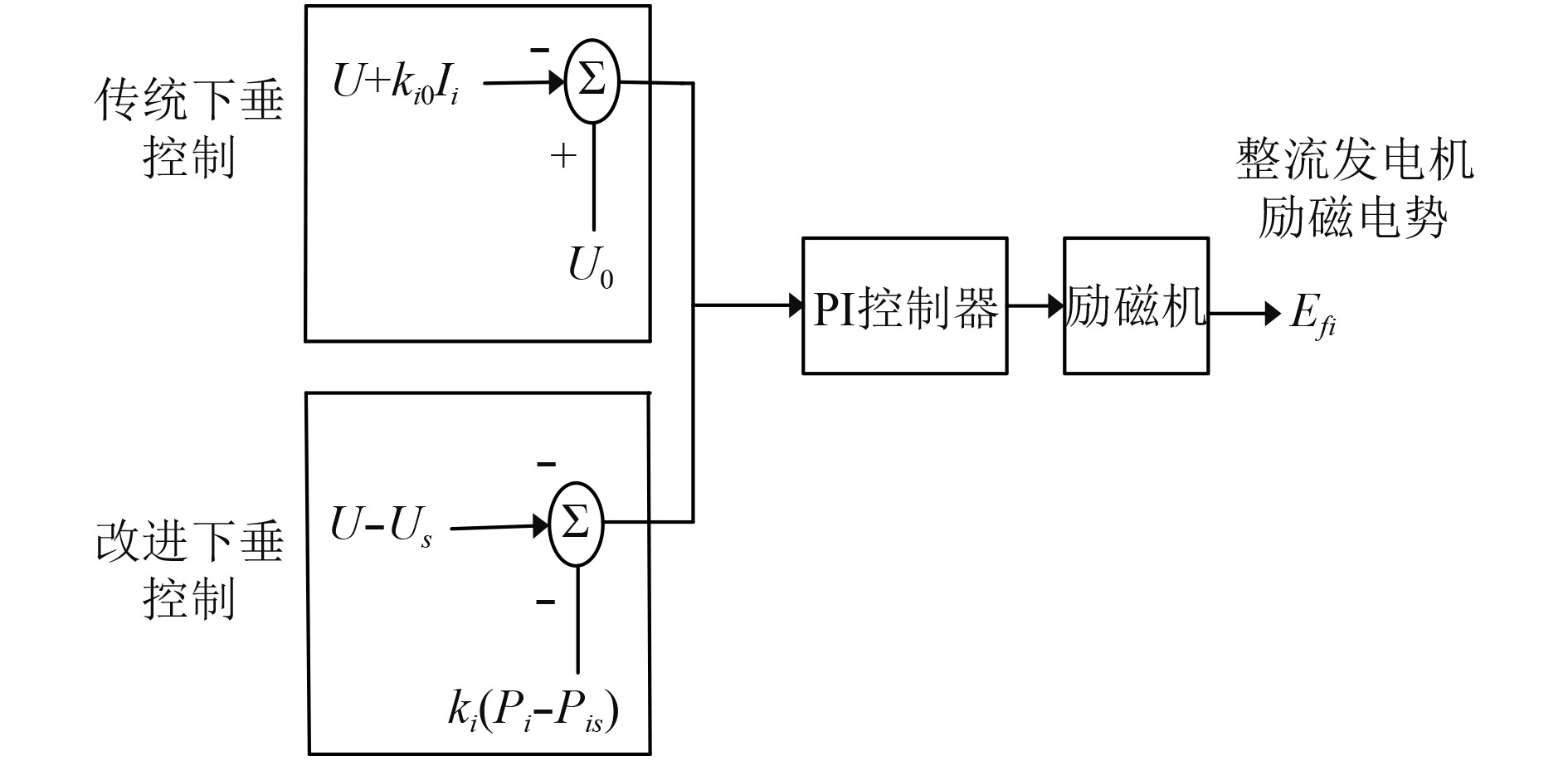
|
图 2 整流发电机励磁双环控制 Fig. 2 Rectifier generator excitation double loop control |
设n1台发电机的额定功率分别为P1r,P2r,
| $U + {k_{i0}}{I_i} = {U_0},\;\;i = 1, \cdots ,{n_1}\text{,}$ | (1) |
式中:U为发电机直流电压;Ii为第i台发电机的输出直流电流;控制参数有ki0和U0两个;ki0为第i台发电机励磁控制的下垂系数;U0为发电机的截距系数,数值上等于空载直流电压。
传统下垂控制的控制参数整定方法如下式:
| $\begin{split} & {k_{i0}} = \frac{{2\alpha {U_r}}}{{{I_{ir}}}},i = 1, \cdots ,{n_1}\text{,}\\ & {U_0} = {U_r}(1 + \alpha )\text{。} \end{split}$ | (2) |
由此可实现发电机输出电流按额定电流比例分配如下式:
| ${I_1} :{I_2}:\; \cdots \;:{I_{{n_1}}} = {I_{1r}}:{I_{2r}}:\; \cdots \;:{I_{{n_1}r}}\text{。}$ | (3) |
式中:直流空载电压为Ur(1+α),额定负载时直流电压为Ur (1-α),满足系统的运行要求。
采用传统下垂控制,发电机输出功率按照各发电机额定功率的比例均分,不需要更新系统运行状态,不会出现一台发电机达到额定功率时,其他发电机没有达到额定额定功率的情况,控制系统鲁棒性好。运行在最优点的电力系统出现发电机跳闸时,这时优化调度的给定值不再是最优点,可能出现发电机过载现象,这时需要将改进下垂控制环切换到传统下垂控制环,等待下一个优化调度周期,再切换到改进下垂控制环。
1.2 综合电力系统燃油经济性优化调度模型设船舶在出发前已安排好多个时间段的不同负荷任务,由于不同时间段系统总负荷的变化,在保证燃油经济性前提下,投入的发电机组数量可能会改变,发电机组存在启停问题,此时需要引入启停变量,并假设系统只在负荷变化时启停机组。直流系统呈献辐射状供电,直流线路传输功率与其用电设备的输入功率一致,因而不会发生直流线路传输功率越限。故综合电力系统燃油经济性调度问题中可以不用考虑潮流方程和直流电压和功率的越限。考虑到输电网和配电网的解耦关系,可将配电网等效为一个负荷。据此建立考虑机组启停的综合电力系统燃油经济性优化调度模型如下式:
| $\begin{split} & \mathop {\min }\limits_{{u_i}(t)} \sum\limits_{t = 1}^T {(\mathop {\min }\limits_{{P_{Gi}}(t)} \sum\limits_{i = 1}^{{n_1}} {[{u_i}(t){f_i}({P_{Gi}}(t),t)} } + \\ & (1 - {u_i}(t - 1)){u_i}(t){M_i}]) \text{,} \\ & {\rm{s}}.{\rm{t}}.\sum\limits_{i = 1}^{{n_1}} {{P_{Gi}}(t) = {P_D}} (t),t = 1, \cdots ,T \text{,} \\ & {P_{Gi1}} \leqslant {P_{Gi}}(t) \leqslant {P_{Gi2}},i = 1, \cdots ,{n_1},t = 1, \cdots ,T \text{,}\\ & \sum\limits_{i = 1}^{{n_1}} {{P_{Gi2}}} - {P_D}(t) \geqslant {P_b}(t),t = 1, \cdots ,T \text{。} \end{split} $ | (4) |
该模型的优化变量为PGi(t),即机组i在t时刻的输出功率;目标函数fi(PGi(t),t)为机组i在t时刻出力为PGi(t)时对应的燃油耗量,一般为发电机输出功率的二次函数,可由发电机耗量实验曲线经过二次函数拟合得到;T为计算时段数;n1为机组集合总数;ui为0,1整数变量,为0时表示t时段第i台机组停机,为1时表示开机;Mi为机组i停机时段t之后开机的启动费用[6-8];通过实时数据采集系统得到系统总的负荷功率PD(t),忽略直流输电网络损耗,系统总发电量等于总负荷功率PD(t)。约束条件为发电机和负载的功率平衡约束、发电机输出功率的上下限约束和系统储备功率约束,第i台发电机的功率上下限分别为PGi1和PGi2,系统储备功率为Pb(t)。
考虑到实际情况中船舶不会频繁更换运行状态,故不考虑机组的爬坡速率及最小开停机时间约束。上述问题是一个包含离散变量和连续变量的离散、非凸的动态混合整数非线性优化问题。在问题规模较小时可采取穷举法求解,并可得到全局最优解;在问题规模较大时可采取动态规划法或整数规划法求解[9]。本文采用穷举法对模型进行求解,即先根据不同时段的系统总负荷及功率上下限约束列举出所有的机组组合,再考虑系统储备功率约束,由此可得到全局最优解。
1.3 整流发电机励磁的改进下垂控制环的控制参数的整定假设燃油经济性优化调度模型给出系统最优运行点P1s,P2s,
| $U - {U_s} + {k_i}\left( {{P_i} - {P_{is}}} \right) = 0,i = 1, \cdots ,{n_1}\text{。}$ | (5) |
控制参数有ki、Us和Pis三个。其中ki为第i台发电机励磁的改进下垂控制的下垂系数且ki>0。Pi为第i台发电机输出功率,将上述方程与功率平衡方程联立如下式:
| $\sum\limits_{i = 1}^{{n_1}} {{P_i} = {P_D}}\text{。} $ | (6) |
方程未知数为(P1,P2,
| $\left[ {\begin{array}{*{20}{c}} {{k_1}}&{}&{}&{}&1 \\ {}&{{k_2}}&{}&{}&1 \\ {}&{}& \ddots &{}&1 \\ {}&{}&{}&{{k_{{n_1}}}}&1 \\ 1&1& \cdots &1&0 \end{array}} \right]{\text{。}}$ |
其行列式为
| $ - \sum\limits_{i = 1}^{{n_1}} {\frac{1}{{{k_i}}}} \left( {\prod\limits_{i = 1}^{{n_1}} {{k_i}} } \right) \ne 0\text{,}$ | (7) |
故方程不奇异,存在唯一解(P1s,P2s,…,Pn1s,Us),这样可以使系统运行在最优点。
引进新变量第i台发电机的功率增量为∆Pi=Pi-Pis,第i台发电机的剩余功率为∆Pil=Pir−Pis。
整流发电机励磁的改进下垂控制的控制参数整定方法如下式:
| $\begin{split} & {k_1} = \frac{{{k_{10}}}}{{{U_r}}}\text{,}\\ & {k_i} = \frac{{{k_1}\Delta {P_{1l}}}}{{\Delta {P_{il}}}},i = 2, \cdots ,{n_1}\text{。} \end{split}$ | (8) |
采用这种整定方法可以使得每台发电机的功率增量按其剩余功率分配,即满足
| $\Delta {P_1} :\Delta {P_2}:\; \cdots \;:\Delta {P_n} = \Delta {P_{1l}} :\Delta {P_{2l}}:\; \cdots \;:\Delta {P_{nl}}\text{。}$ | (9) |
改进下垂控制函数参照传统下垂控制U-I线性关系其等效下垂系数为k1U,∙∙∙,kiU ,等效截距系数为(Us+kiPis)。若P1s: P2s: ∙∙∙:Pn1s=∆P1l: ∆P2l: ∙∙∙: ∆Pn1l,由于U接近于Ur,则2种整定方法基本一致,故改进下垂控制方法为传统下垂控制方法的扩展[12]。如果P1s: P2s: ∙∙∙:Pn1s≠∆P1l: ∆P2l: ∙∙∙: ∆Pn1l,对第1台发电机,改进下垂控制的等效下垂系数与传统下垂控制的下垂系数相比基本一致,其他等效下垂系数和等效截距系数变化不大,实现了整流发电机励磁控制环切换时扰动尽可能小的目标[13-15]。
在系统运行中每一个调度周期开始时,重新测量系统的总负荷PD,并重复1.2节和1.3节的内容,使系统在每个调度周期内都运行在最优点,系统负荷增减时各发电机的功率增减量按发电机剩余功率的比例分配,不会出现发电机过载的运行状态,共同维护系统运行状态的安全稳定,系统总的储备功率为所有发电机的剩余功率之和,且系统运行点变化时,整流发电机励磁的改进下垂控制的参数变化不大,使得系统运行状态切换时扰动尽可能小。
2 算例及仿真假定直流母线上有6台柴油发电机,其中4台8 MW和2台13.5 MW,发电机耗量特性曲线为一条二次曲线,各参数取值及系统运行条件如表1所示。
|
|
表 1 综合电力系统参数与运行状态 Tab.1 The integrated power system parameters and operating conditions |
假定系统负荷为29.5 MW,为系统总负荷的50%,并假设1号发电机组处于停机检修状态。在穷举法的基础上采用二次规划算法,系统燃油经济性策略如表2所示,系统储备功率Pb(t)为4 MW。
|
|
表 2 50%总负荷时燃油经济性策略 Tab.2 Fuel economy strategy at 50% total load |
由表2可知,当1号机组停机检修,在系统总负荷为50%时,2~6号机组采取2,4号机组停机,3,5,6号机组开机方案时系统燃油消耗量最小。
首先整定整流发电机励磁的传统下垂控制环的控制参数。直流母线额定电压为Ur=6 kV,直流电压调整率为2α=0.04。10 s前发电机采用传统下垂控制,其输出功率按额定功率比例分配,由传统下垂控制的控制参数整定方法,可得传统下垂控制的控制参数如表3所示。
|
|
表 3 传统下垂控制环控制参数 Tab.3 Traditional droop control loop control parameters |
根据本文上述综合电力系统燃油经济性优化调度模型,求解出系统的最优运行点。然后整定整流发电机励磁的改进下垂控制环的控制参数。10 s时希望的直流母线电压为Us=6 kV,根据1.3节整流发电机励磁的改进下垂控制的控制参数整定方法,可得改进下垂控制环的控制参数如表4所示。
|
|
表 4 10s时改进下垂控制环控制参数 Tab.4 Improved droop control loop control parameters at 10s |
20 s时系统负荷突加4 MW,3台发电机的剩余功率分别为3.87 MW,0.36 MW,1.27 MW,3台发电机的新增功率满足∆P3:∆P5:∆P6=∆P3l: ∆P5l: ∆P6l分配,即∆P3=2.82 MW,∆P5=0.26 MW,∆P6=0.92 MW。3台发电机新的输出功率分别为6.95 MW、13.40 MW、13.15 MW,3台发电机按其剩余功率共同承担系统负荷功率的增减。
在新的调度周期,更新系统的输入数据,重复1.2节和1.3节内容,使系统在新的调度周期内能满足系统的优化运行需求。20 s时系统负荷发生变化,虽然3台发电机共同承担了系统负荷功率的增加,但系统不满足优化运行条件。在30 s时新的调度周期开始,更新系统负荷PD=33.5 MW,由优化模型可求得发电机最优输出功率,计算得到改进下垂控制环的控制参数如表5所示。
|
|
表 5 30 s时改进下垂控制环控制参数 Tab.5 Improved droop control loop control parameters at 30 s |
综上所述,系统的动态响应过程中运行点变化如表6所示。10 s前整流发电机励磁采用传统下垂控制,10 s由发电机传统下垂控制切换到改进下垂控制,系统控制方式变化时,系统能够运行在最优点。20 s时系统负荷变化,所有发电机按其剩余功率共同承担系统负荷功率的增减,且负荷变化时,动态响应性能较好。30 s时新的调度周期开始,系统运行状态切换到新的最优点。
|
|
表 6 系统的稳态运行点 Tab.6 Steady-state operating point of the system |
系统响应过程在Matlab/Simulink中的模型如图3所示。图3中上半部分为励磁机外框模型,下半部分为三相整流发电机模型(三相发电机通过二极管整流后与负载端相连),其中励磁机外框模型里的励磁机具体仿真模型如图4所示。励磁机的输入Efdex为图2中双环控制切换后通过PI控制器得到的电压值,而励磁机的输出励磁电流Ifdex又作用于PI控制器,由此构成闭环反馈。
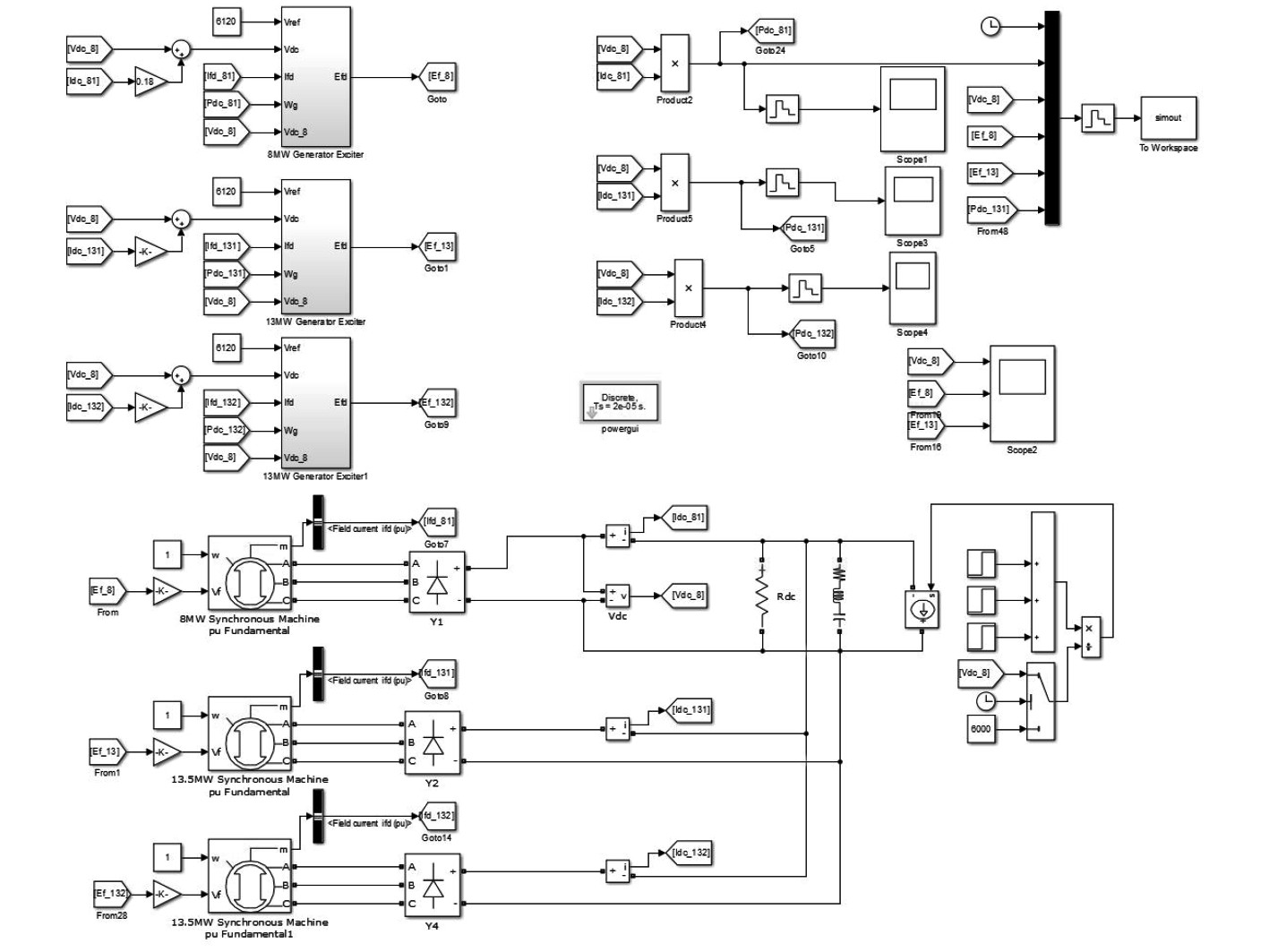
|
图 3 系统仿真模型 Fig. 3 The simulation model of the system |
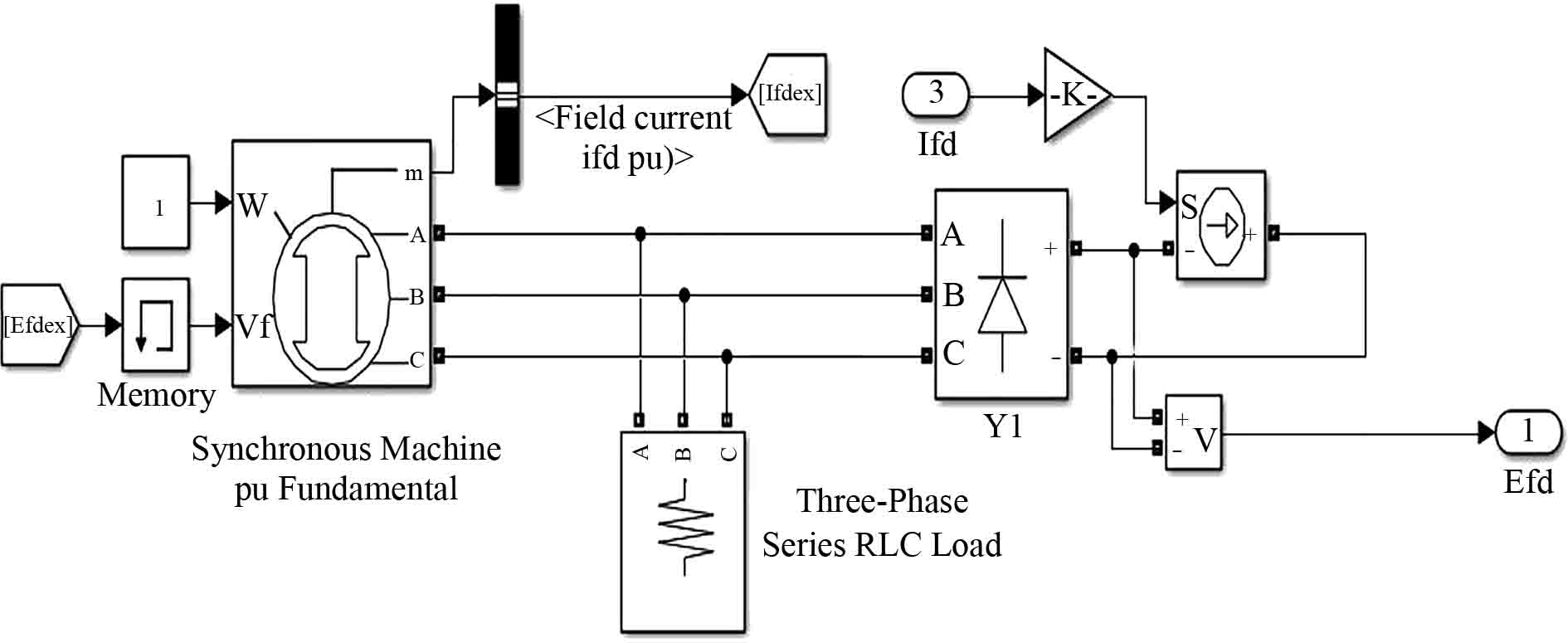
|
图 4 励磁机仿真模型 Fig. 4 Exciter simulation model |
系统响应过程在Matlab/Simulink中的仿真如图5 ~ 图6所示。
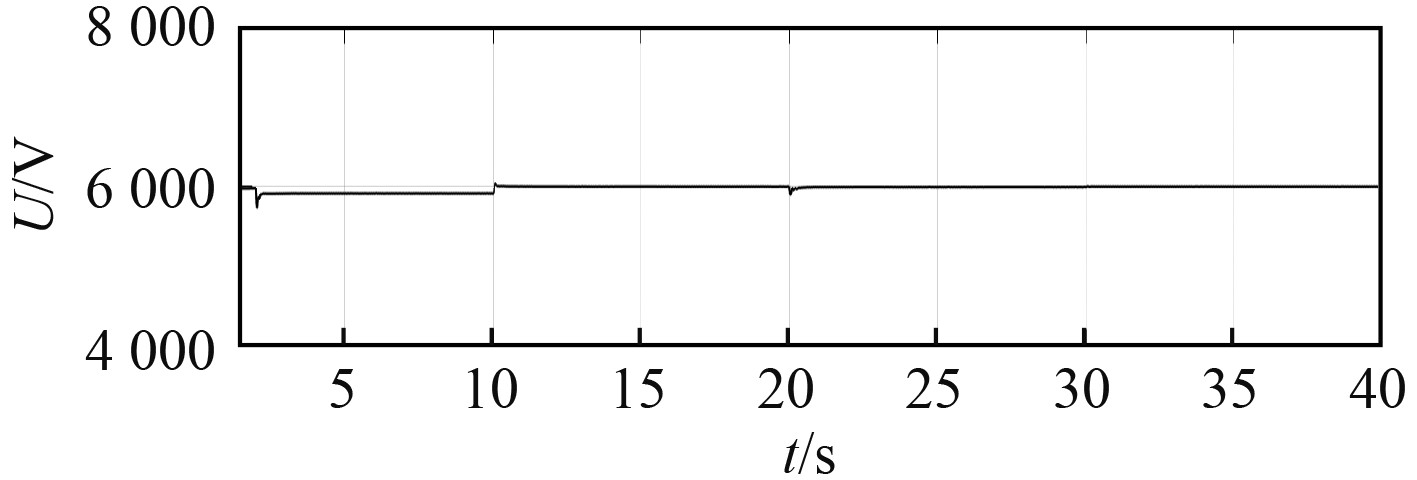
|
图 5 直流母线电压 Fig. 5 DC bus voltage |
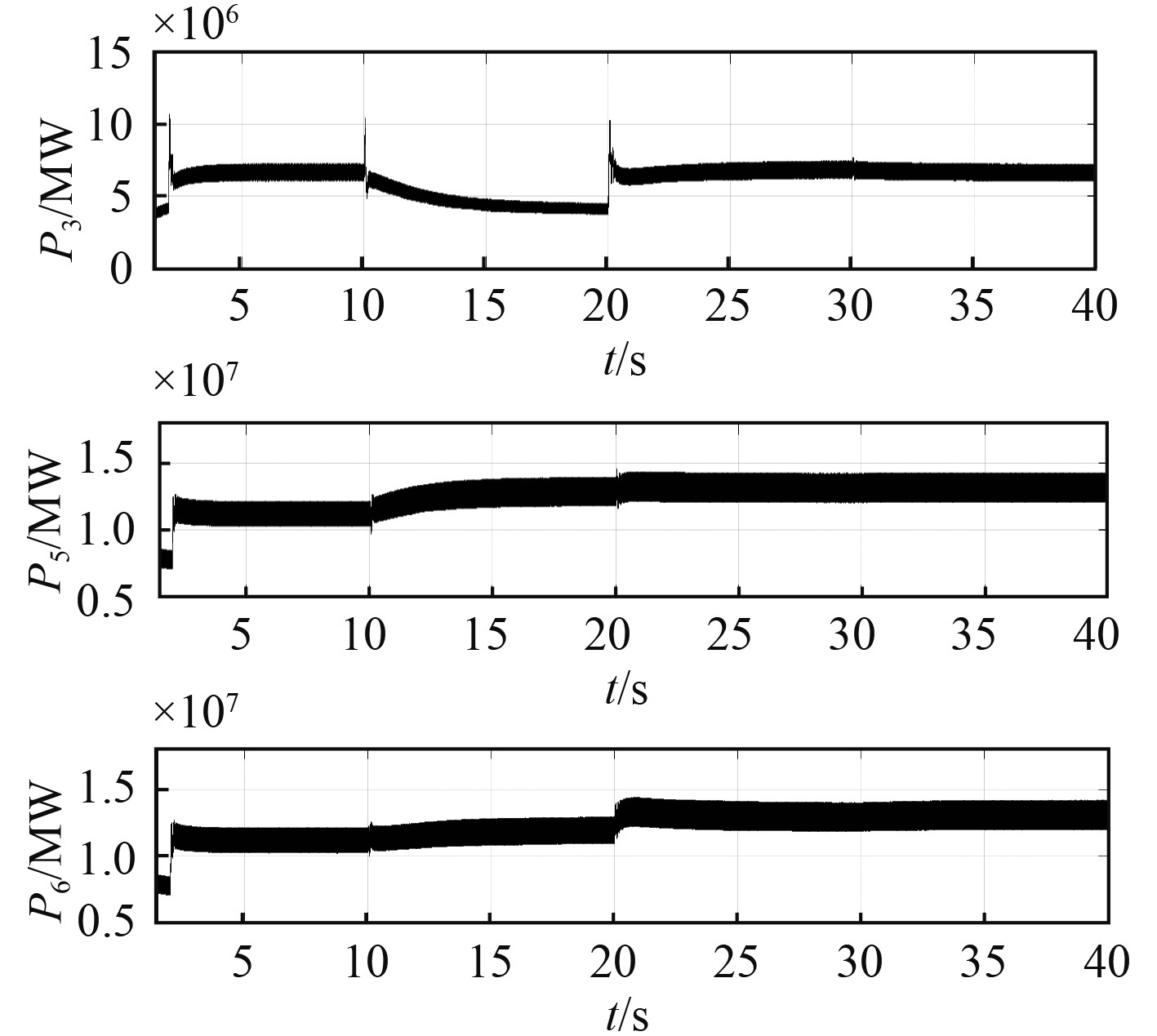
|
图 6 机组输出功率 Fig. 6 Unit output power |
可见,各运行时段系统直流母线电压及发电机组输出功率均符合系统的运行要求。
3 结 语本文针对中压直流综合电力系统燃油经济性运行要求和能量调控手段的特点,提出基于改进下垂控制的综合电力系统燃油经济性优化调度方法。根据综合电力系统运行在最优点,发电机按剩余功率比例输出,发电机励磁控制环切换时扰动尽可能小的运行需求,通过系统燃油经济性模型计算出系统运行最优点,给出希望的直流母线电压值,整定发电机励磁的改进下垂控制环的控制参数,实现了综合电力系统燃油经济性的优化调度,并通过仿真试验验证了所提出方法的有效性。
| [1] |
MA Weiming. A survey of the second-generation vessel integrated power system[C]//The International Conference on Advanced Power System Automation and Protection. Beijing, China: IEEE, 2011: 1293-1302.
|
| [2] |
MA Weiming. Development of vessel integrated power system[C]// The 14th International Conference on Electrical Machines and Systems. Beijing, China: IEEE, 2011.
|
| [3] |
肖润龙, 王刚, 李子梦, 等. 中压直流输电直流区域配电综合电力系统静态状态估计方法研究[J]. 电工技术学报, 2018, 33(13): 3023-3033. |
| [4] |
龚喜文, 郑元璋, 石林龙. 船舶PMS控制器设计及关键技术研究[J]. 上海船舶运输科学研究所学报, 2010, 33(2): 83-87. DOI:10.3969/j.issn.1674-5949.2010.02.001 |
| [5] |
石林龙, 龚喜文, 郭晨, 等. 综合电力舰船能量动态优先管理技术[J]. 中国航海, 2013, 36(3): 19-22. DOI:10.3969/j.issn.1000-4653.2013.03.005 |
| [6] |
ZAHEDI. B, NORUM. L. E, LUDVIGSEN. K. B. Ludvigsen. Optimized efficiency of all-electric ships by DC hybrid power systems[J]. J. Power Sources, 2014, 255: 341-354. DOI:10.1016/j.jpowsour.2014.01.031 |
| [7] |
BENATMANE M, MALTBY R. Integrated electric power and propulsion system on land an overview[C]//IEEE Electric Ship Technology Symposium, Arlington, USA, 2007: 7-13.
|
| [8] |
DAMIR R. Integrated control of marine electrical power systems[D]. Department of Marine Technology, Norwegian University of Science and Technology, 2008.
|
| [9] |
VIANA A, PEDROSO J P. A new MILP-based approach for unit commitment in power production planning[J]. Electrical Power and Energy Systems, 2013, 44(1): 997-1005. DOI:10.1016/j.ijepes.2012.08.046 |
| [10] |
冉晓洪, 苗世洪, 吴英杰, 等. 基于最优功率分配的多端直流网络改进下垂控制策略[J]. 电工技术学报, 2016, 31(9): 16-24. DOI:10.3969/j.issn.1000-6753.2016.09.003 |
| [11] |
徐玉琴, 马焕均. 基于改进下垂控制的逆变器并联运行技术[J]. 电力系统保护与控制, 2015, 43(7): 103-107. DOI:10.7667/j.issn.1674-3415.2015.07.016 |
| [12] |
TAO Y, LIU Q, DENG Y, et al. Analysis and mitigation of inverter output impedance impacts for distributed energy resource interface[J]. IEEE Transactions on Power Electronics, 2015, 30(7): 3563-3576. DOI:10.1109/TPEL.2014.2339849 |
| [13] |
ZHONG Q. Robust droop controller for accurate proportional load sharing among inverters operated in parallel[J]. IEEE Transactions on Industrial Elec-tronics, 2013, 60(4): 1281-1290. DOI:10.1109/TIE.2011.2146221 |
| [14] |
李浩然, 杨旭红, 冯成臣. 多逆变器并联下的输出阻抗分析和改进下垂控制策略研究[J]. 电力系统保护与控制, 2015, 43(20): 29-35. DOI:10.7667/j.issn.1674-3415.2015.20.005 |
| [15] |
薛潺. 基于改进下垂控制的多微网并联运行控制策略研究[D]. 北京: 北京工业大学, 2018.
|
 2020, Vol. 42
2020, Vol. 42
