行星齿轮传动装置中的行星轮滑动轴承与平行轴齿轮传动装置中的滑动轴承,从承载条件到结构形式均有很大的不同。目前,行星轮轴承采用滚动轴承的居多,尤其像风电[1]、农业机械及工具机械等领域几乎均采用滚动轴承,但在大型船舶行星齿轮传动装置中,多采用滑动轴承。
当前关于行星轮轴承对行星传动系统均载技术的影响、滑动轴承—行星齿轮耦合系统动力学特性研究较多[2-5],但对于行星传动装置中行星轮滑动轴承性能的研究较少,而实践证明,行星轮滑动轴承性能的优劣关系到整个传动装置运转性能,同时也对传动系统的安全性具有重要影响。
本文首先对行星轮滑动轴承性能进行理论分析,然后以某型两级行星传动装置行星轮滑动轴承为例,分别分析了两级行星轮轴承需要重点关注的影响轴承安全的特性。最后进行测点温度试验,理论计算与试验温度趋势一致,验证了船舶行星传动装置行星轮滑动轴承性能分析方法和判据的准确性。
1 行星轮滑动轴承计算模型分析 1.1 行星轮滑动轴承特点行星轮滑动轴承与普通平行轴滑动轴承具有不同的特点,主要表现在以下几个方面:
1)结构方面
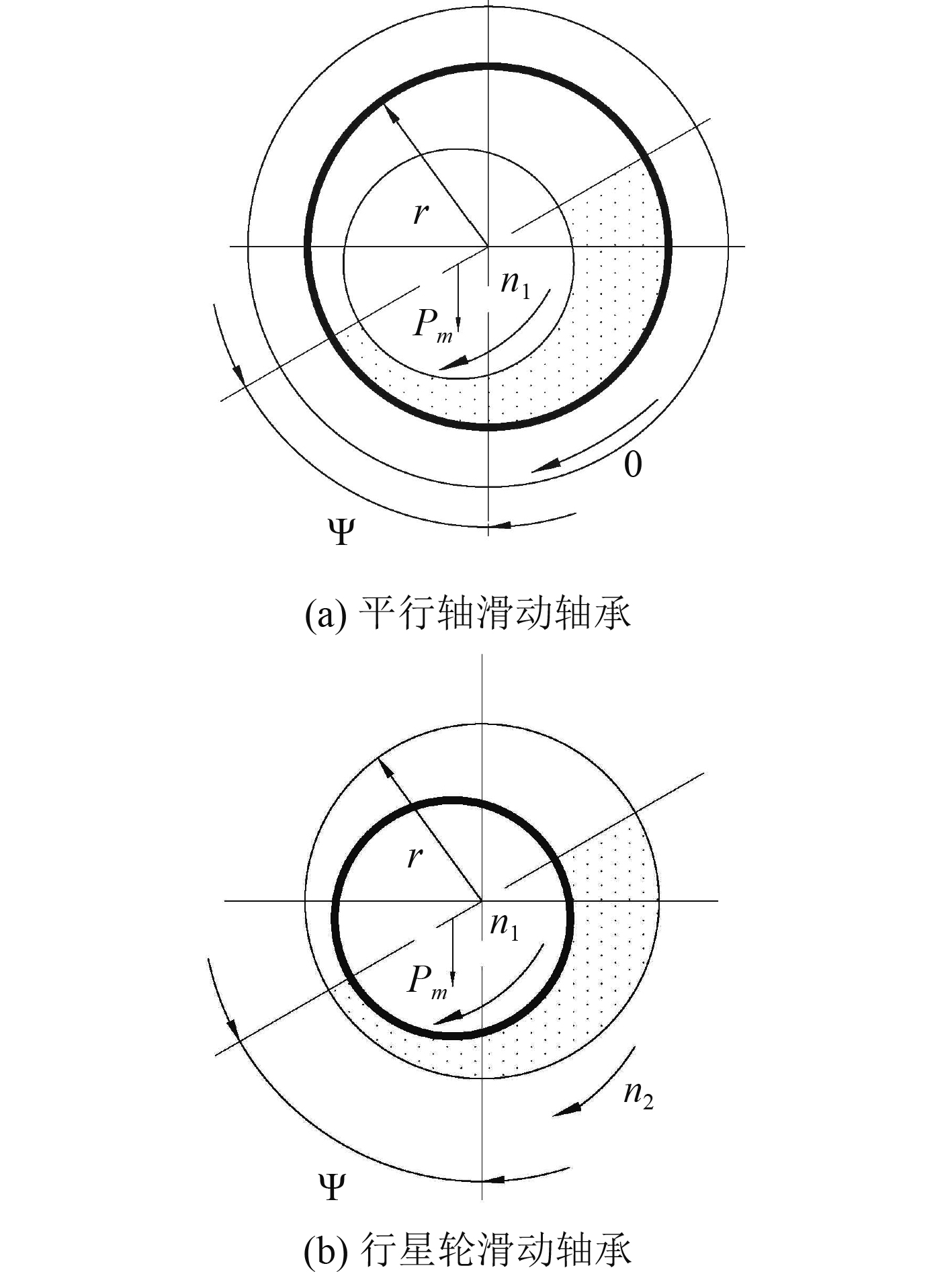
行星轮滑动轴承一般与普通滑动轴承结构不同,如图1所示,由于结构与加工限制,行星轮轴承合金一般采用静止浇注法[6]浇注在行星轮轴承外部,与行星轮一起形成承载油膜。此种结构可以节约空间,减小行星传动装置外形尺寸。
|
图 1 滑动轴承工作状态简图 Fig. 1 Working state diagram of journal bearing |
2)相对运动方面
行星轮轴承与普通滑动轴承相比,其安装在行星架中,同行星架进行公转,这就使形成油膜的2个相对运动构件均处于运动状态。
3)承载条件方面
在行星传动装置中,行星轮相当于惰轮,行星轮轴承承载力较大,又由于公转的存在,行星轮轴承除了承受行星轮重力,齿轮啮合力外,还承受离心力。
4)供油条件方面
由于公转的存在,行星轮轴承供油方式采用轴承内部供油。
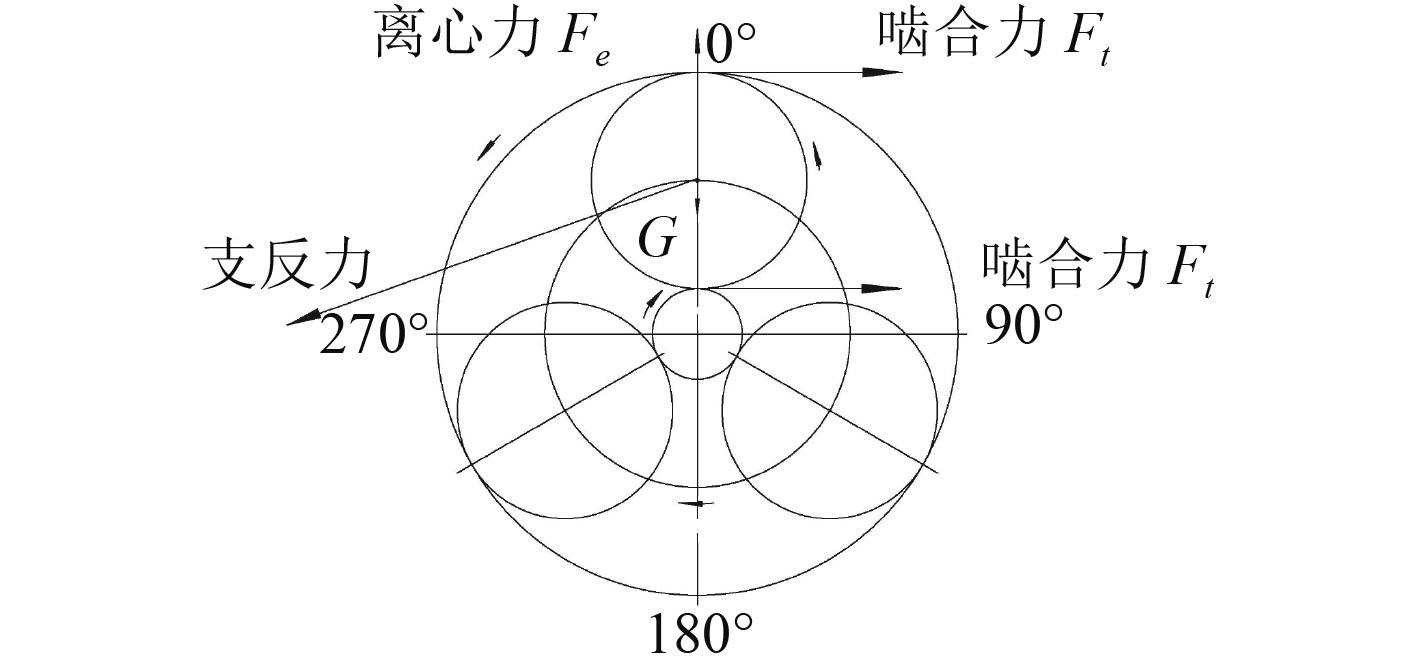
1.2 行星轮滑动轴承载荷分析图2以布置3个行星轮为例,对行星轮轴承所承受载荷进行分析。
|
图 2 行星轮轴承载荷分析 Fig. 2 Load analysis of planetary gear bearing |
以行星轮为研究对象,分析受力,行星轮所受到的切向力、重力及离心力的合力与行星轮轴承提供的支反力大小相等,方向相反。行星轮轴承载荷为:
| $F = 2{{{F}}_t} + {{{F}}_e} + {{G}}{\text{。}}$ |
其中:
从图2可以看出,行星轮轴承相当于惰轮,承受两倍的啮合力,并且由于离心力和重力的存在,行星轮轴承每旋转一周,轴承所受的载荷大小方向均变化,但一般变化范围有限,尤其对于功率较高工况,行星轮轴承旋转一周载荷大小方向变化在5%以内,因此工程上可作为静载荷处理。
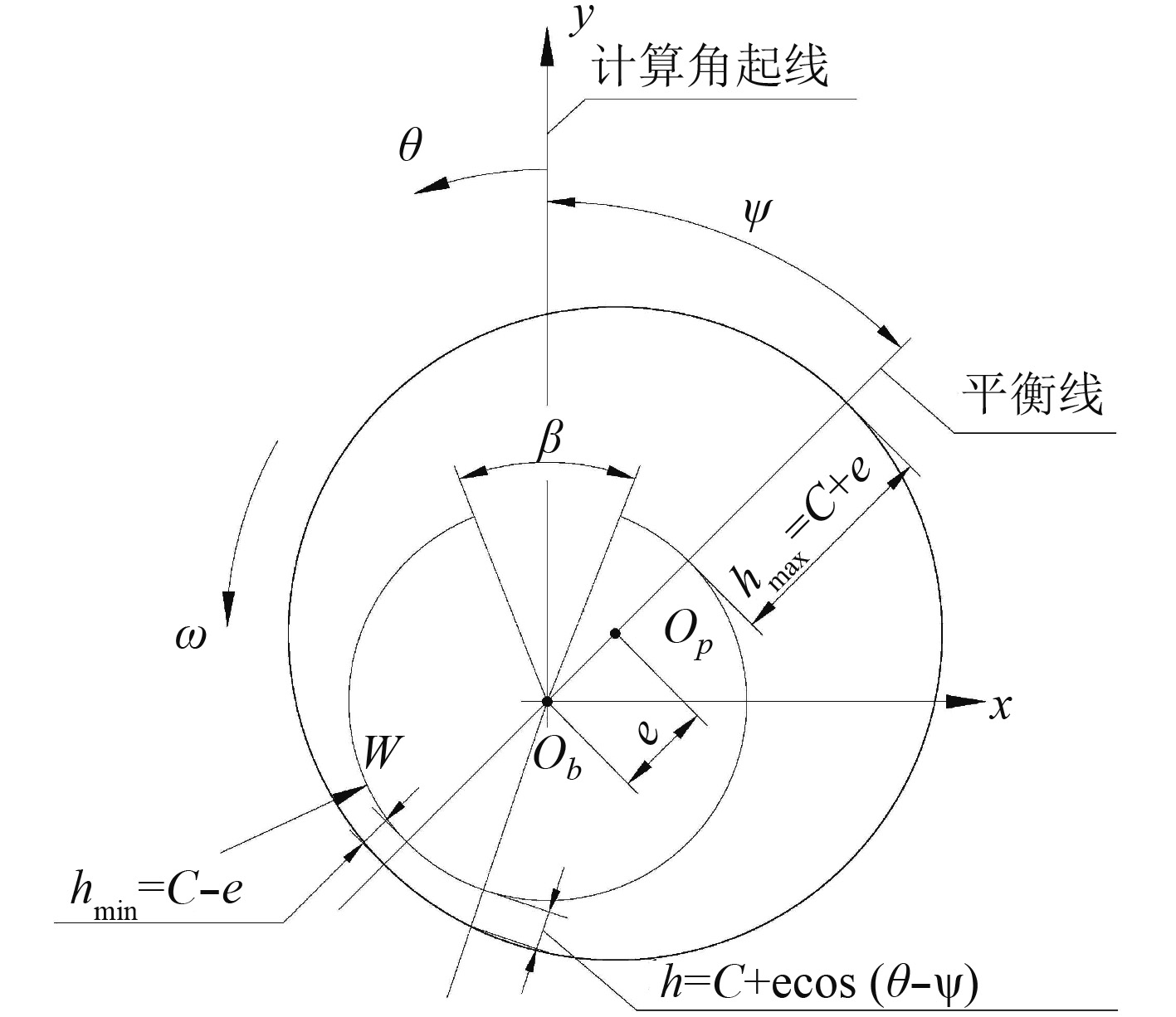
1.3 行星轮轴承性能计算模型行星轮轴承安装在行星架上,随着行星轮旋转和行星架公转,行星轮中心与行星轮轴承中心不再重合,而具有一定的偏心距和偏位角,与普通平行轴滑动轴承不同,普通平行轴滑动轴承偏心是处于内部的轴相对于轴承运动,而行星轮轴承偏心是处于外部的行星轮相对于行星轮轴承运动。计算时,行星轮轴承参数定义如图3所示。应用流体力学方程求解行星轮轴承性能。
|
图 3 轴承参数 Fig. 3 Bearing parameters |
图中:
1)雷诺方程
| $ \frac{\partial }{{\partial {{x}}}}\left( {{{{G}}_{{x}}}\frac{{{{{h}}^3}}}{{\rm{\mu }}}\frac{{\partial p}}{{\partial {{x}}}}} \right) + \frac{\partial }{{\partial {{z}}}}\left( {{{\rm{G}}_{{y}}}\frac{{{{{h}}^3}}}{{\rm{\mu }}}\frac{{\partial p}}{{\partial {\rm{z}}}}} \right) = \frac{{{U}}}{2}\frac{{\partial {{h}}}}{{\partial {{x}}}} + \frac{{\partial {{h}}}}{{\partial {{t}}}}{\text{。}} $ |
其中:p为油膜压力;
2)能量方程
| $\begin{split} & {\rm{\rho }}\left[{{v_x}}\frac{{\partial ({{c_v}}T)}}{{\partial x}} + {{v_y}}\frac{{\partial ({{{c_v}}}T)}}{{\partial y}} + {{v_z}}\frac{{\partial ({{c_v}}T)}}{{\partial z}}] = \right. \\& \left. {\rm{\mu [}}{\left( {\frac{{\partial {{v_x}}}}{{\partial y}}} \right)^2} + {\left( {\frac{{\partial {{v_z}}}}{{\partial y}}} \right)^2}\right] {\text{。}} \end{split} $ |
其中:ρ为密度;
3)温粘关系
| $\mu = {A}{{\rm{e}}^{ - {B}T}}{\text{。}}$ |
式中:T为温度;A,B可以由已知温度油膜粘度计算获得;μ为油膜粘度。
为模拟实际应用,计算中考虑温度分布的影响。联立求解3个方程获得压力和温度分布,由压力分布进而求得轴承性能。
2 行星轮滑动轴承性能判定依据分析行星轮轴承性能指标包括温度、油膜厚度、流量、功耗等,在工程应用中,判断行星轮轴承性能可靠与否主要关注下面2个指标,一是轴承最高油膜温度不要超出材料的许用温度,二是最小油膜厚度大于许用最小油膜厚度。因此本文将着重对行星轮滑动轴承上述2个指标的判据进行分析。
1)轴承许用最高油膜温度
轴承最高油膜温度小于合金要求使用温度100 ℃[7]。超过此温度,轴承合金的强度将明显降低,轴承承载能力下降,甚至导致烧瓦。
2)许用最小油膜厚度
工程上,轴承许用的最小油膜厚度[8]为:
| $ \left[ {{h_{{\rm{min}}}}} \right] = \xi \cdot \left( {{R_{a1}} + {R_{a2}}{\rm{ + }}{y_1} + {y_2}} \right){\text{。}}$ |
其中:
行星轮轴承结构是一根空心轴,总长度为直径的两倍以上,又由于行星轮轴承所受的载荷很大,使得行星轮轴承挠度
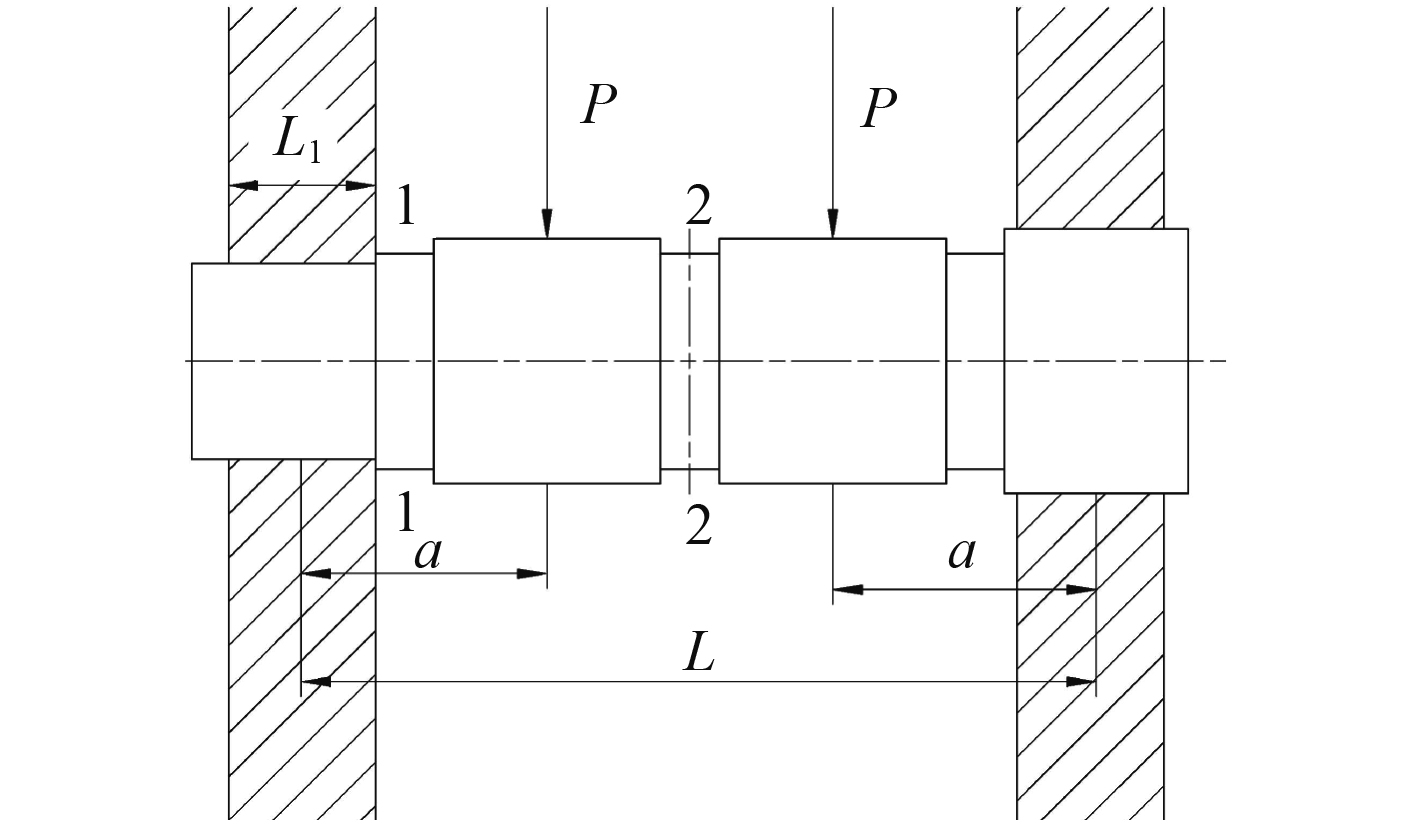
采用有限元方法进行行星轮轴承挠度计算,行星轮轴承安装简图见图4,建立行星轮轴承模型,考虑轴承内孔尺寸,如图5所示。行星轮轴承两侧安装在行星架上,通过行星架安装宽度对其施加约束。计算行星轮轴承应力应变,进而计算行星轮轴承允许的最小油膜厚度。
|
图 4 行星轮轴承安装简图 Fig. 4 Installation diagram of planetary gear bearing |

|
图 5 有限元模型 Fig. 5 Finite element model |
以两级行星齿轮传动装置为例,两级行星轮轴承工况如表1所示。
|
|
表 1 行星轮轴承运行工况 Tab.1 Operation condition of Planetary gear bearing |
其中Ⅰ级行星轮轴承有效尺寸:D×L:320 mm×460 mm;内孔:170 mm;Ⅱ级行星轮轴承有效尺寸:D×L:320 mm×540 mm;内孔:180 mm;滑油采用L-TSA68(GB11120-2011),进油温度40 ℃。
3.2 轴承性能分析从表2可以看出,同一工况下,Ⅰ级行星轮轴承最高温度及测点温度均高于Ⅱ级行星轮轴承,而Ⅱ级行星轮轴承最小油膜厚度明显低于Ⅰ级行星轮轴承。
|
|
表 2 行星轮轴承性能 Tab.2 Performance of Planetary gear bearing |
行星轮轴承载荷与测点如图6所示。
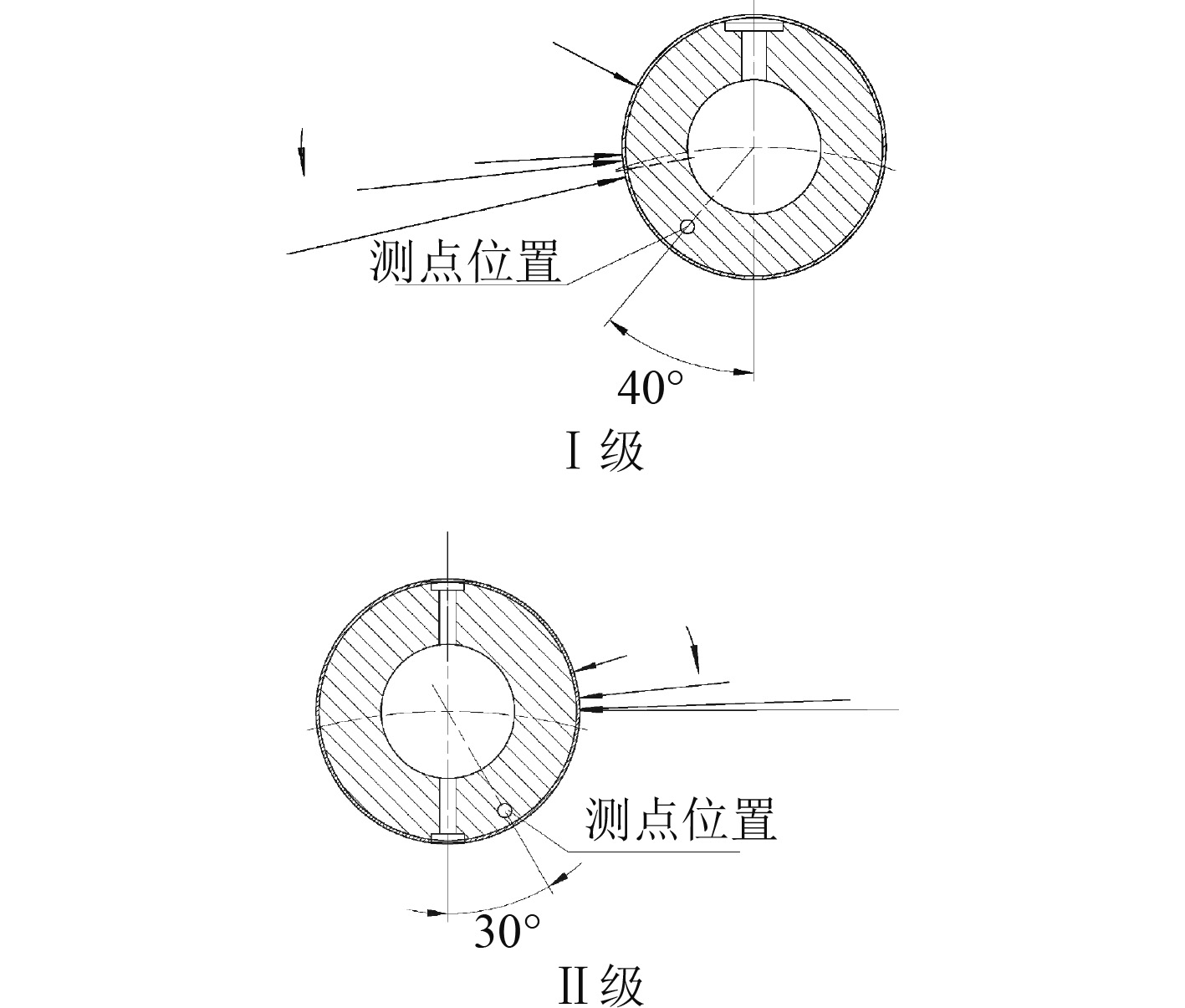
|
图 6 载荷分布与测点位置 Fig. 6 Load distribution and measuring point location |
最大工况(工况4)下,Ⅰ级、Ⅱ级行星轮轴承挠曲变形与计算结果如图7和图8所示,Ⅰ级行星轮轴承最大变形0.0108,最大应力为29.8 MPa,Ⅱ级行星轮轴承最大变形0.015,最大应力为32 MPa。
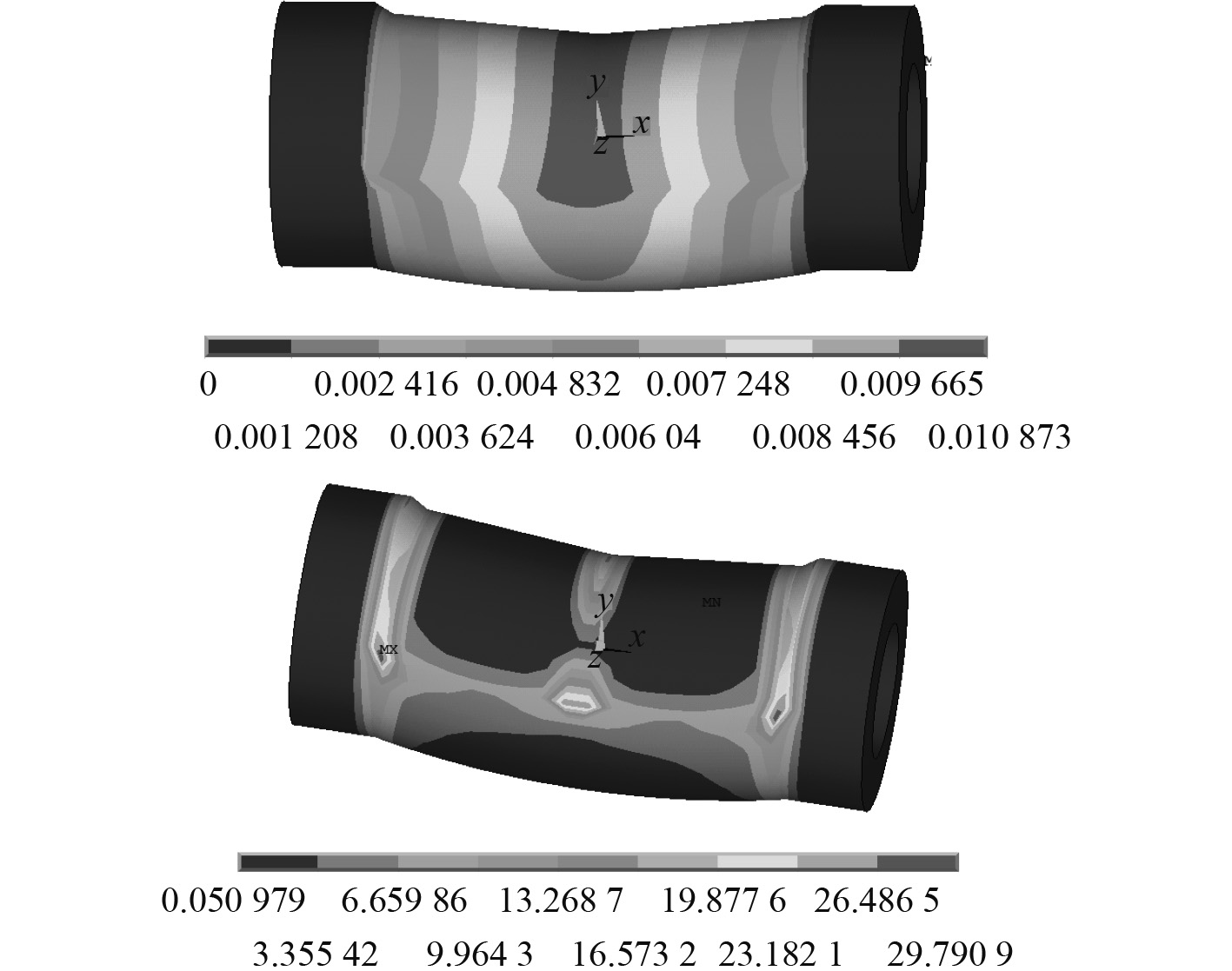
|
图 7 Ⅰ级行星轮轴承变形及应力 Fig. 7 Deformation and stress of I stage planetary gear bearing |
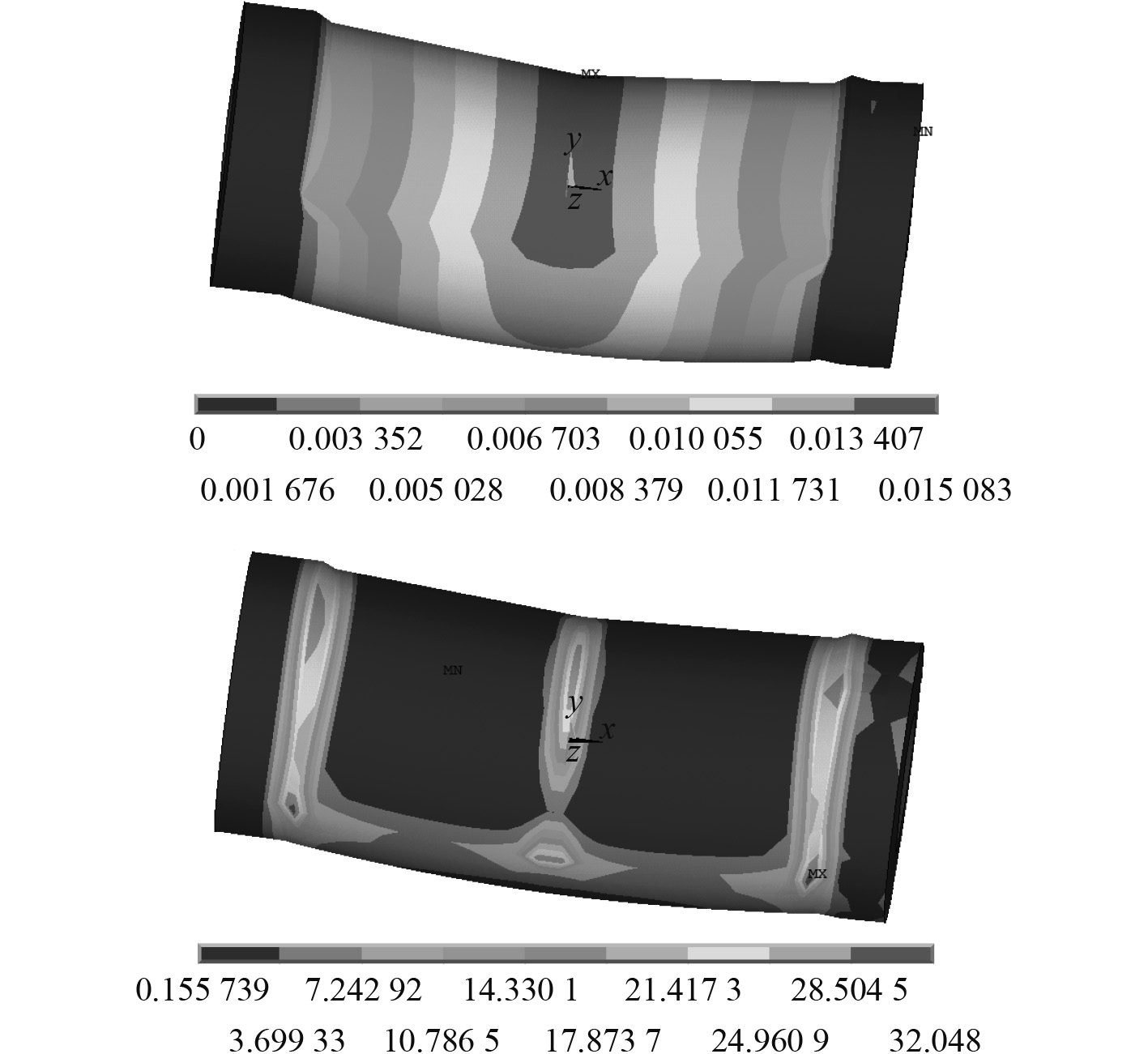
|
图 8 Ⅱ级行星轮轴承变形及应力 Fig. 8 Deformation and stress of Ⅱ stage planetary gear bearing |
按照最大工况计算轴承允许的最小油膜厚度。
| $ \begin{split} {\left[ {{h_{{\rm{min}}}}} \right]_1} &= {\xi ^ \cdot }\left( {{R_{a1}}{\rm{ + }}{{\rm{R}}_{a2}}{\rm{ + }}{y_1}{\rm{ + }}{y_2}} \right)= \\& 1.5\times (0.001\;6 + 0.000\;8 + 0.010\;8)= \\& 0.019\;8{\text{,}}\\ {\left[ {{h_{{\rm{min}}}}} \right]_2} &= {\xi ^ \cdot }\left( {{R_{a1}}{\rm{ + }}{{\rm{R}}_{a2}}{\rm{ + }}{y_1}{\rm{ + }}{y_2}} \right)= \\& 1.5\times (0{\rm{.001\;6 + 0}}{\rm{.000\;8 + 0}}{\rm{.015)}}= \\& 0{\rm{.026\;1}}{\text{。}} \end{split} $ |
Ⅰ级、Ⅱ级行星轮轴承最小油膜厚度和最高温度均在允许的范围内,但数值有很大不同,重点关注的判据不同,Ⅰ级行星轮轴承最高计算温度比Ⅱ级高,最小油膜厚度较大,因此,Ⅰ级行星轮轴承主要由判据1油膜温度判断,而Ⅱ级行星轮轴承温度不高,但最小油膜厚度较小,Ⅱ级行星轮轴承主要由判据2允许的最小油膜厚度判断。
4 行星轮滑动轴承运行温度测试分析本类型行星齿轮传动装置Ⅰ级行星传动具有3个行星轮轴承,Ⅱ级行星传动具有5个行星轮轴承,对行星轮轴承进行温度测量。测得的轴承温度如表3和表4所示。通过数据整理得到Ⅰ、Ⅱ级行星轮滑动轴承温度变化曲线如图9所示。
|
|
表 3 Ⅰ级行星轮轴承测点温度 Tab.3 Temperature of Ⅰ stage planetary gear bearing measuring point |
|
|
表 4 Ⅱ级行星轮轴承测点温度 Tab.4 Temperature of Ⅱ stage planetary gear bearing measuring point |
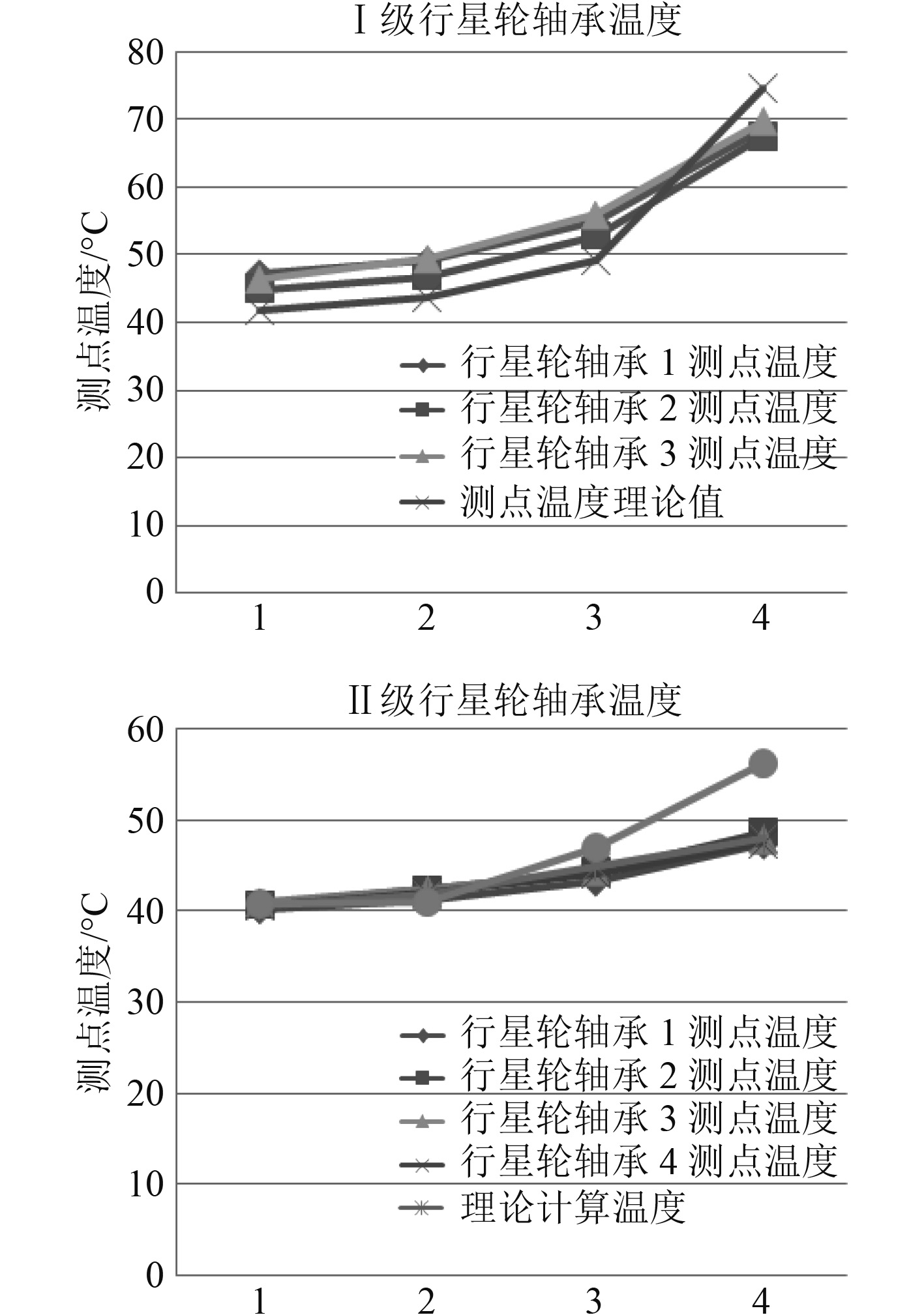
|
图 9 行星轮轴承测点温度 Fig. 9 Temperature of planetary gear bearing measuring point |
行星轮轴承计算测点温度与试验测点温度相近,随工况变化趋势相同,计算方法有效;在高工况下,计算测点温度略高于实际测点温度;Ⅰ级行星轮轴承实际测量温度高于Ⅱ级行星轮轴承,Ⅰ级行星轮轴承应重点关注温度。按性能计算方法和2个判据设计的两级行星轮轴承运行平稳,温度稳定,可用于船舶行星轮轴承设计。
5 结 语1)行星轮轴承与普通平行轴滑动轴承应用特点和结构均不同,轴承设计时要考虑离心力、供油条件及运动关系等的影响。行星架旋转一周,轴承载荷在有限的范围内变化,工程上可以作为静态力处理。
2)在行星轮轴承性能判断时,要考虑许用最高油膜温度和由行星轮轴承挠曲变形计算得出的允许的最小油膜厚度两个判据,计算温度及油膜厚度较高的Ⅰ级行星轮轴承重点关注油膜温度,对于Ⅱ级行星轮轴承重点关注最小油膜厚度。
3)从理论和实际测点温度对比看,趋势相近,轴承运行平稳,性能计算结果可以指导船舶行星轮轴承设计,设计判据安全可靠。
| [1] |
曾雨田, 李金库, 胡云波, 等. 风电齿轮箱行星轮轴承跑圈失效分析[J]. 机械工程师, 2019(4): 178-180. ZENG Yutian, LI Jinku, HU Yunbo, et al. Analysis on running ring fault of planetary wheel bearing in wind turbine gearbox[J]. Mechanical Engineer, 2019(4): 178-180. DOI:10.3969/j.issn.1002-2333.2019.04.061 |
| [2] |
胡升阳, 方宗德. 行星传动均载及动载系数定义改进与分析[J]. 西安交通大学学报, 2019, 53(8): 40-46.
|
| [3] |
ERITENEL T, PARKER R G. Model properties of three dimensional helical planetary gears[J]. Journal of Sound and Vibration, 2009, 325(1-2): 397-420. DOI:10.1016/j.jsv.2009.03.002 |
| [4] |
PARKER R G, WU X. Parametric instability of planetary gears having elastic continuum ring gears[J]. Journal of Vibration &Acoustics, 2012, 134(4): 1002-1010. |
| [5] |
王均刚, 杨士男, 刘燕德, 等. 行星齿轮主要涉及理论与分析方法及均载特性综述[J]. 华东交通大学学报, 2019, 36(2): 111-116. WANG Jungang, YANG Shinan, LIU Yande, et al. The theory and analysis method of planetary gear and its load sharing characteristics[J]. Journal of East China Jiaotong University, 2019, 36(2): 111-116. |
| [6] |
马军, 张文灼, 段永彬, 等. 巴氏合金轴瓦的浇注工艺. 金属铸锻焊技术. 2011(8): 206-207. MA Jun, ZHANG Wenzhuo, DUAN Yongbin, et al. Pouring technology of Babbitt axle bush. Casting. Forging. Welding. Aug. 2011: 206-207 |
| [7] |
GB/T 1174-1992铸造轴承合金标准 [S] 1992. GB/T 1174-1992 Standard for cast bearing alloy [S] 1992. |
| [8] |
机械设计手册第06篇轴承 [M]. 化学工业出版社, 2004.
|
 2020, Vol. 42
2020, Vol. 42

