0 引　言

大力发展舰用燃气轮机是近几十年以来的趋势。当前对燃气轮机性能的评估标准均为ISA（International Standard Atmosphere，环境温度15 ℃，大气压力101325Pa）条件下，不同季节、地域的环境条件（包括温度和湿度等）将对其性能产生很大影响。由于当前研究的燃机较多处于含湿量较小的陆地环境中，因此更多研究着眼于温度对燃机出力及循环效率的影响。

舰用燃气轮机长时间运行在高盐高湿度的大含湿量环境中。燃机性能计算对工质的热力学参数有很强的依赖，湿空气的热力学参数（例如比热、气体常数、比热比）不同于干空气条件，湿度越大，干、湿两类条件下的性能差异越大。同时，燃机性能测试精度要求不断提高，受空气湿度的影响带来的误差，可能会使测量超出误差带导致测试失效，令测试可重复性较差^[1]。综合考虑上述影响，需要将湿度纳入性能的影响因素之中。

20世纪20～50年代，NACA^[2-5]进行了一系列湿度相关的发动机性能实验研究，得到了若干湿度修正图表及公式。Bird等^[6]指出湿空气对动力循环性能有如下影响：1）利用理想气体工质计算部件效率与湿空气工质相差可达2%～3%；2）增加发动机耗油率；3）增加燃料量；4）改变发动机推力或者出功。AGARD报告^[7]汇总了前人研究成果并给出了具体的空气湿度修正系数的表达式。

压气机作为燃气轮机三大部件之一，亦受到湿度的影响。湿度会使得压气机压比、效率等参数降低^[8]，偏移的特性会影响燃机部件间的匹配使得运行效率降低，因此探讨空气湿度对压气机部件的影响可以给燃气轮机可靠的总体性能设计提供研究依据。

王国钦等^[9]引入析水系数对压气机排气量进行修正。Tomita等^[10]利用流线曲率法计算了湿空气对某轴流压气机性能的影响，温比、压比和效率较理想空气条件下均有所恶化。Smith等^[11]在普渡大学三级轴流压机实验台上进行空气湿度修正公式验证，实验结果与理论公式相吻合。吴闻彭等^[8]指出绝对湿度是影响折合流量和折合转速的关键参数，当绝对湿度为1%时，压气机折合转速需要提高0.25%才能达到指定性能。

综合目前的研究进展，关于空气湿度对压气机性能影响的研究均仅关注湿空气与理想空气热力学参数的不同导致压比、效率等参数的误差。湿空气物性的变化导致其输运特性（如粘性、导热系数、扩散系数等）与理想空气也不尽相同^[12-13]，输运特性的不同会导致流场结构的差异。尽管从性能差异上来看只有1%～2%数量上的区别，但是对于叶顶流场来说细微的流场变化，会对压气机裕度有较大的影响^[14]。而裕度是考量压气机性能的另一重要指标，但目前尚无公开文献探讨空气湿度对压气机稳定运行范围的影响。

本文分析了湿度对热力学参数的作用并讨论其对压气机性能的影响。通过三维数值模拟方法，以某舰船微型燃气轮机用对置式两级离心压气机为例，研究不同空气湿度条件对压气机压比、效率及裕度的影响并阐述原因。

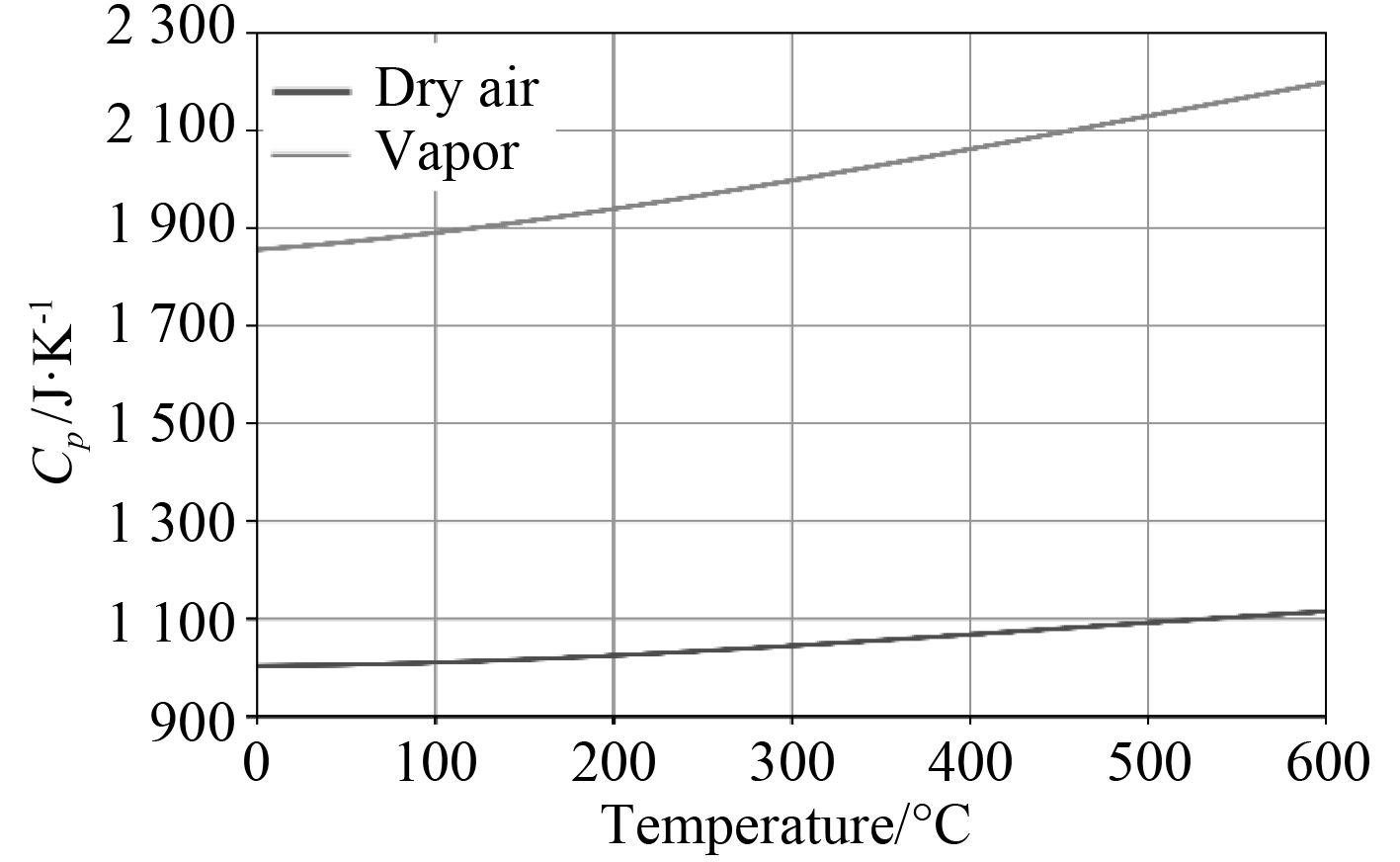
1 空气湿度的影响 1.1 湿空气对热力学参数的影响

本文采用五系数变比热公式^[15]分别计算干空气和水蒸气的定压比热，系数见表1，公式如下：

$ \frac{{{C_p}}}{R} = \alpha + \beta T + \gamma {T^2} + \delta {T^3} + \varepsilon {T^4}{\text{。}} $

(1)

式中：对干空气气体常数 ${R_{dry}}$ 取287.05 J/kg∙K，水蒸气气体常数 ${R_{vapor}}$ 取461.5 J/kg∙K。图1为根据上式在0～600 ℃范围内绘制出的水蒸气及干空气定压比热曲线，温度的上升会引起定压比热的上升且水蒸气受温度的影响变化速率更快。

在压气机性能计算过程中，需要用到的湿空气的热力学参数主要包括定压比热、气体常数和比热比，计算公式如下：

$ {C_{p,humid}} = \frac{{{C_{p,dry}} + d \times {C_{p,vapor}}}}{{1 + d}}\text{，} $

(2)

$ {R_{humid}} = \frac{{{R_{dry}} + d \times {R_{vapor}}}}{{1 + d}}\text{，} $

(3)

$ {k_{humid}} = \frac{{{C_{p,humid}}}}{{{C_{p,humid}} - {R_{humid}}}}\text{，} $

(4)

式中下标humid，dry和vapor分别代表湿空气、干空气和水蒸气， ${C_p}$ 为定压比热， $R$ 为气体常数， $d$ 为含湿量， $k$ 为比热比。

计算式（2）～式（4）中湿空气较干空气条件下各热力学参数的相对变化量，得到：

$ \Delta {C_p} = \frac{{{C_{p,humid}} - {C_{p,dry}}}}{{{C_{p,dry}}}} = \frac{d}{{1 + d}}\left( {\frac{{{C_{p,vapor}}}}{{{C_{p,dry}}}} - 1} \right)\text{，} $

(5)

$ \Delta R = \frac{{{R_{humid}} - {R_{dry}}}}{{{R_{dry}}}} = \frac{d}{{1 + d}}\left( {\frac{{{R_{vapor}}}}{{{R_{dry}}}} - 1} \right)\text{，} $

(6)

$\begin{split} \Delta k = & \frac{{{k_{humid}} - {k_{dry}}}}{{{k_{dry}}}} = \left( {{k_{dry}} - 1} \right)\left( {\Delta R - \Delta {C_p}} \right){\kern 1pt} {\kern 1pt} = \\ & \frac{{\left( {{k_{dry}} - 1} \right)d}}{{1 + d}}\left( {\frac{{{R_{vapor}}}}{{{R_{dry}}}}{\rm{ - }}\frac{{{C_{p,vapor}}}}{{{C_{p,dry}}}}} \right)\text{。} \end{split}$

(7)

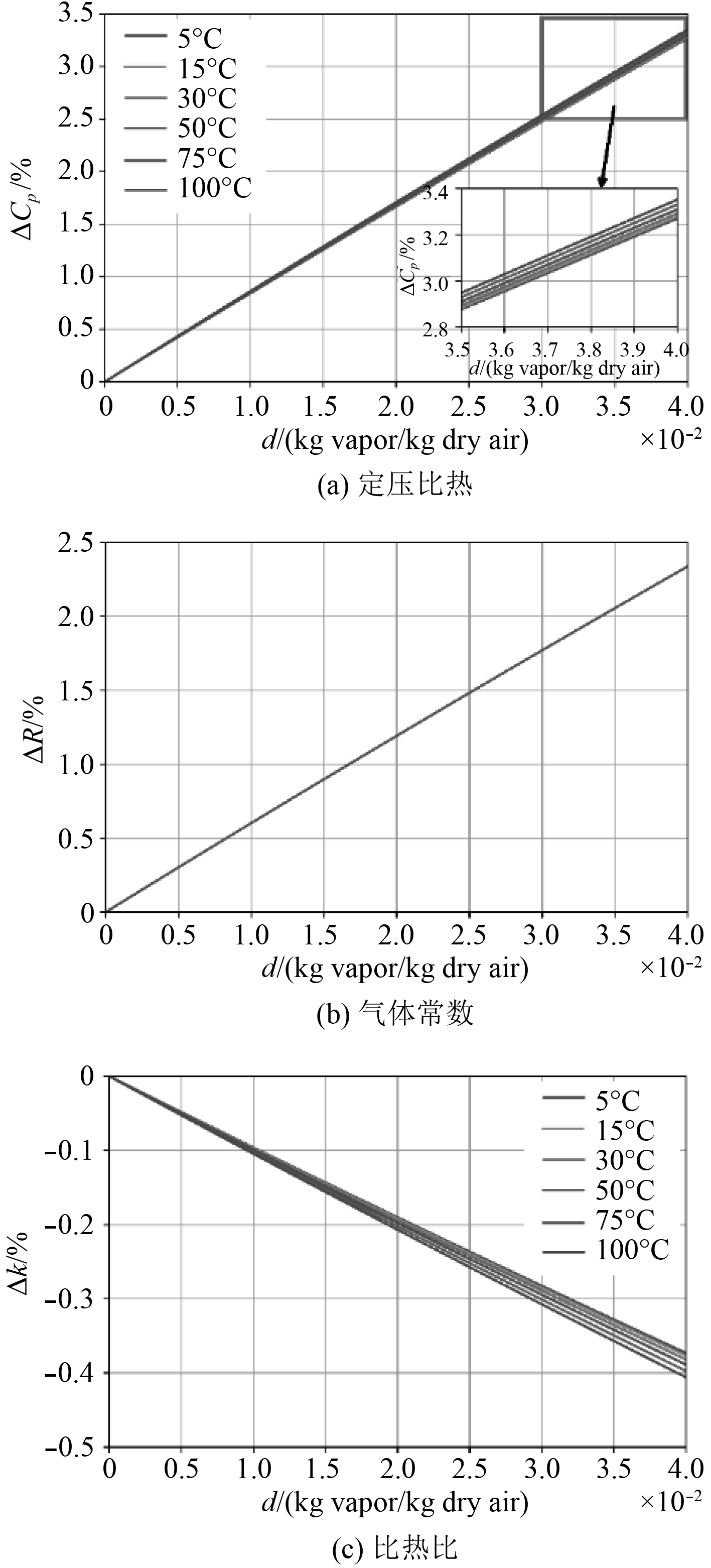
图2分别展示了定压比热、气体常数及比热比相对变化随着含湿量增大皆呈现出近线性关系。

在含湿量为0.04时，气体温度为5 ℃和100 ℃时，干湿情况下定压比热的相对变化量分别为3.27%和3.35%，相差不大。定压比热相对变化总体受温度影响较小，在小含湿量下，温度基本无影响，随着含湿量的增加，定压比热变化量呈近线性增加，气体温度越高，差量的增加速率更高，如图2（a）所示。

气体常数变化随着含湿量上升而增加。在含湿量为0.04时，干湿情况下的气体常数相差可达2.4%，如图2（b）所示。

含湿量总体对比热比影响较小，在小含湿量下温度影响较小。随着含湿量的增加，比热比变化增大，且湿空气温度越高比热比相对减少的越多，如图2（c）所示。

在压气机效率计算过程中经常使用等熵效率及多变效率，公式如下：

$ {\eta _{Isen}} = \frac{{TP{R^{\frac{{k - 1}}{k}}} - 1}}{{TTR - 1}}\text{，} $

(8)

$ {\eta _{Poly}} = \frac{{k - 1}}{k}\frac{{\ln \left( {TPR} \right)}}{{\ln \left( {TTR} \right)}}\text{。} $

(9)

式中： ${\eta _{Isen}}$ 和 ${\eta _{Poly}}$ 分别为等熵效率和多变效率，TPR（Total Pressure Ratio）和TTR（Total Temperature Ratio）分别为总压比和总温比。

等熵效率计算中 $TP{R^{\frac{{k - 1}}{k}}}$ 变量还需考虑压比的影响，随着含湿量的增加，比热比降低，等熵效率减少，且压气机本身压比越高，等熵效率减少的越多。现忽略效率计算公式中湿度对压比和温比的影响，当含湿量为0.04，比热比为1.394，压气机压比为20时，湿空气下的等熵效率较干空气下减少了约1.6%。

在多变效率计算中，效率随着比热比的减小而减少，其值的干湿差异计算与压气机参数无关。类似地，得到多变效率与含湿量的关系：随着含湿量的增加，比热比降低，多变效率减少。例如含湿量为0.04，比热比为1.394的条件下，湿空气下的多变效率较干空气下减少了约1.1%。

综上，随着湿空气的含湿量增加，气体的定压比热和气体常数增加，比热比减少，压气机效率降低。

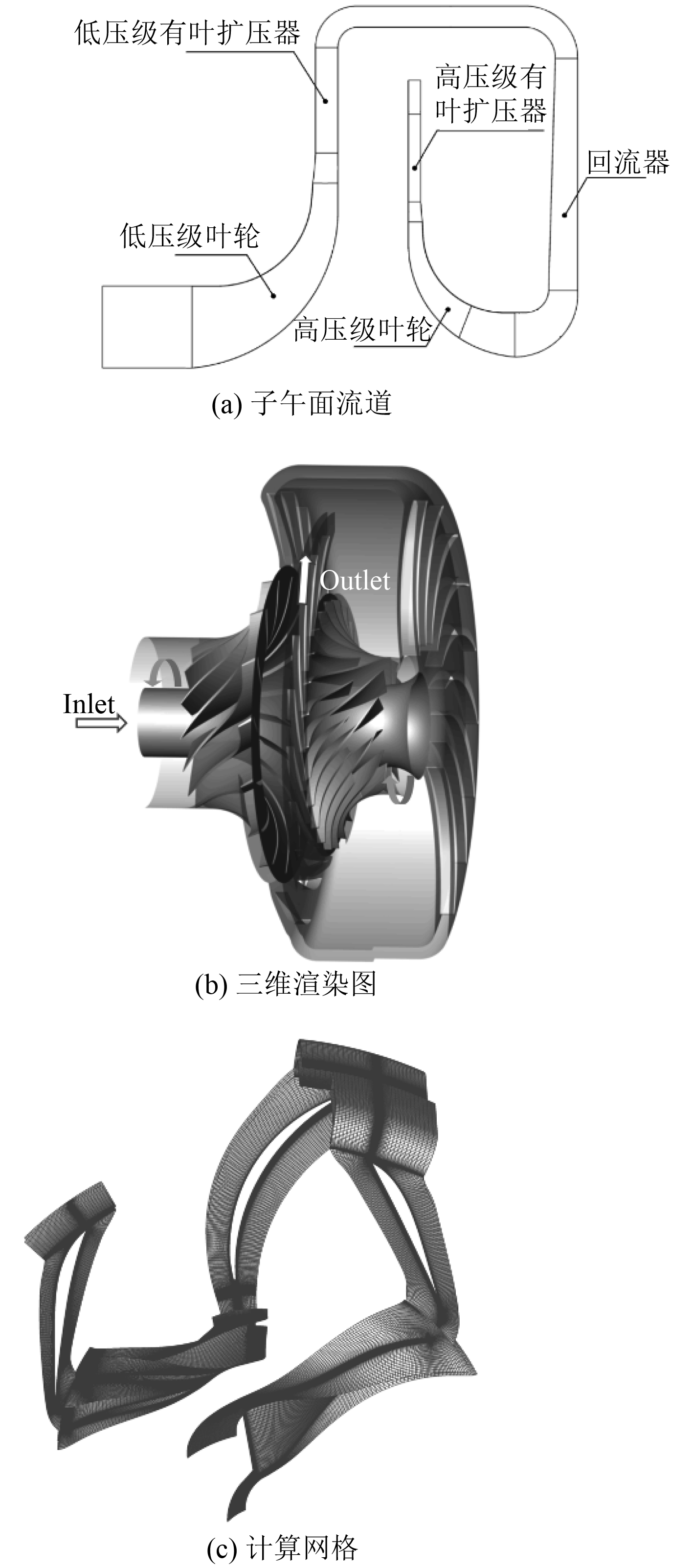
2 物理模型及数值计算方法 2.1 物理模型

本文对某两级对置式离心压气机进行研究，几何结构如图3所示。主要部件有5个：1）低压级叶轮；2）低压级有叶扩压器；3）回流器；4）高压级叶轮；5）高压级有叶扩压器。表2为压气机的关键设计参数，低压级（LP）与高压级（HP）安装在两根转轴上，转速分别为14000 r/min和28000 r/min。压气机名义设计点流量4.8 kg/s，设计时给定1.04的流量裕度，实际设计流量为4.97 kg/s，详细设计信息见文献[16]。

2.2 网格无关性验证

本文利用Ansys CFX软件进行三维数值计算，数值方法验证对象选取NASA压比为4的单级离心压气机，具体验证结果可参见文献[16]。计算网格采用多块结构化网格，划分采用HOH拓扑。选取每个部件中单排通道进行数值计算。

为保证数值计算的准确性及可靠性，本文选取3套计算网格，数量分别为162万（稀），300万（中等）及500万（密），针对工质为干空气情况进行网格无关性验证。定常计算选取k-ε湍流模型，设计工况下Y⁺最大值为15。模拟过程中，边界条件设置为压气机进口给定总压101325 Pa、总温288.2 K，气体轴向进气；出口条件改变静压；部件间利用混合平面法传递数据。

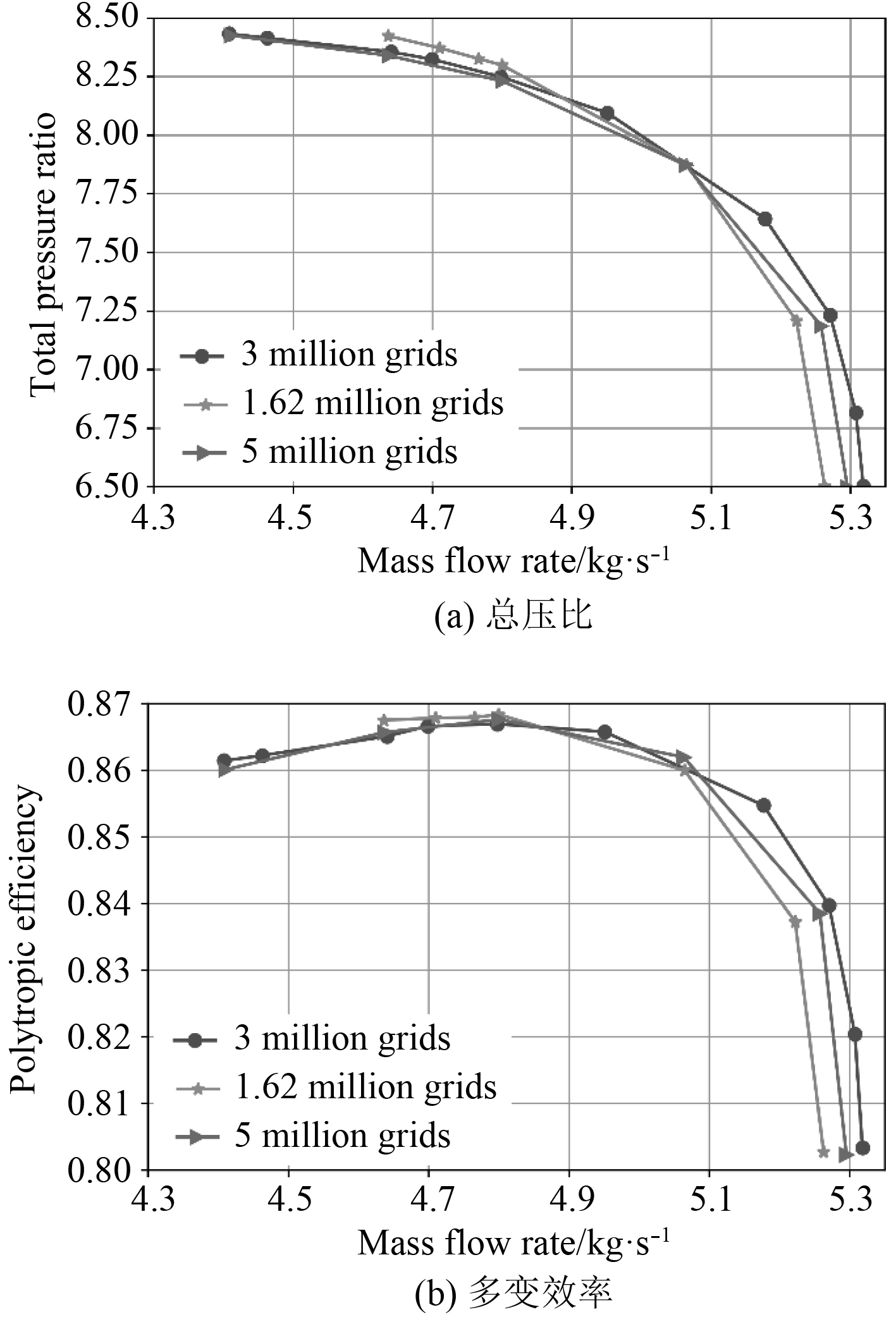
采用3种网格计算所得压气机特性如图4所示。稀网格所得失速点流量明显大于其他2种网格结果，中等密度网格和密网格所得结果在全流量范围内吻合较好，仅在堵塞点附近稍有差异。如表3所示，以300万网格为基准，对比给出了堵塞流量、失速点流量、设计流量点压比和效率的差异。在设计点流量下，稀、密网格多变效率及总压比最大误差最大约1%，但稀网格在裕度上，与基准相比，范围缩减5.48%，误差较大。失速裕度（ $SM$ ）及裕度变化量（ $\Delta SM$ ）定义如下：

$ S\!M = \left[ {\left(\frac{{{{\text{π}} _{NS}}}}{{{{\dot m}_{NS}}}}\right)\Big/\left(\frac{{{{\text{π}} _{D{\rm{esi}}gn}}}}{{{{\dot m}_{De{\rm{s}} ign}}}}\right) - 1} \right] \times 100{\text{%}}\text{，} $

(10)

$ \Delta {S\!M} = {S\!M} - {{S\!M}_{baseline}}\text{。} $

(11)

稀网格在非设计工况下，性能曲线较其余二特性线有所偏置，对非设计点大分离工况捕捉还不够精确。而300万网格和500万密网格特性线基本重合，为了节约计算成本，本文选取300万网格作为下文湿空气计算的基础网格。

2.3 数值计算方法

本文在计算过程中对湿空气采取工质为干空气和水蒸气理想混合物，湍流模型为两方程标准 $k - \varepsilon $ 模型，近壁面区采用自适应壁面函数（Scalable Wall Function），部件间通量交换采用混合平面法，空间离散采用二阶迎风格式，时间离散采用二阶向后欧拉法，基于多组分稳态雷诺平均Navier-Stokes方程组隐式求解计算^[17]。

2.4 边界条件设置

压气机进口采用轴向进气，总压101325 Pa，总温288.2 K，各湿度工况条件（不同相对湿度及含湿量）如表4所示。部件间采用混合平面法交换数据；出口条件为截面平均静压，通过增加背压模拟压气机运行中的节流过程得到压气机特性线。

3 数值计算结果 3.1 总体性能分析 3.1.1 特性参数

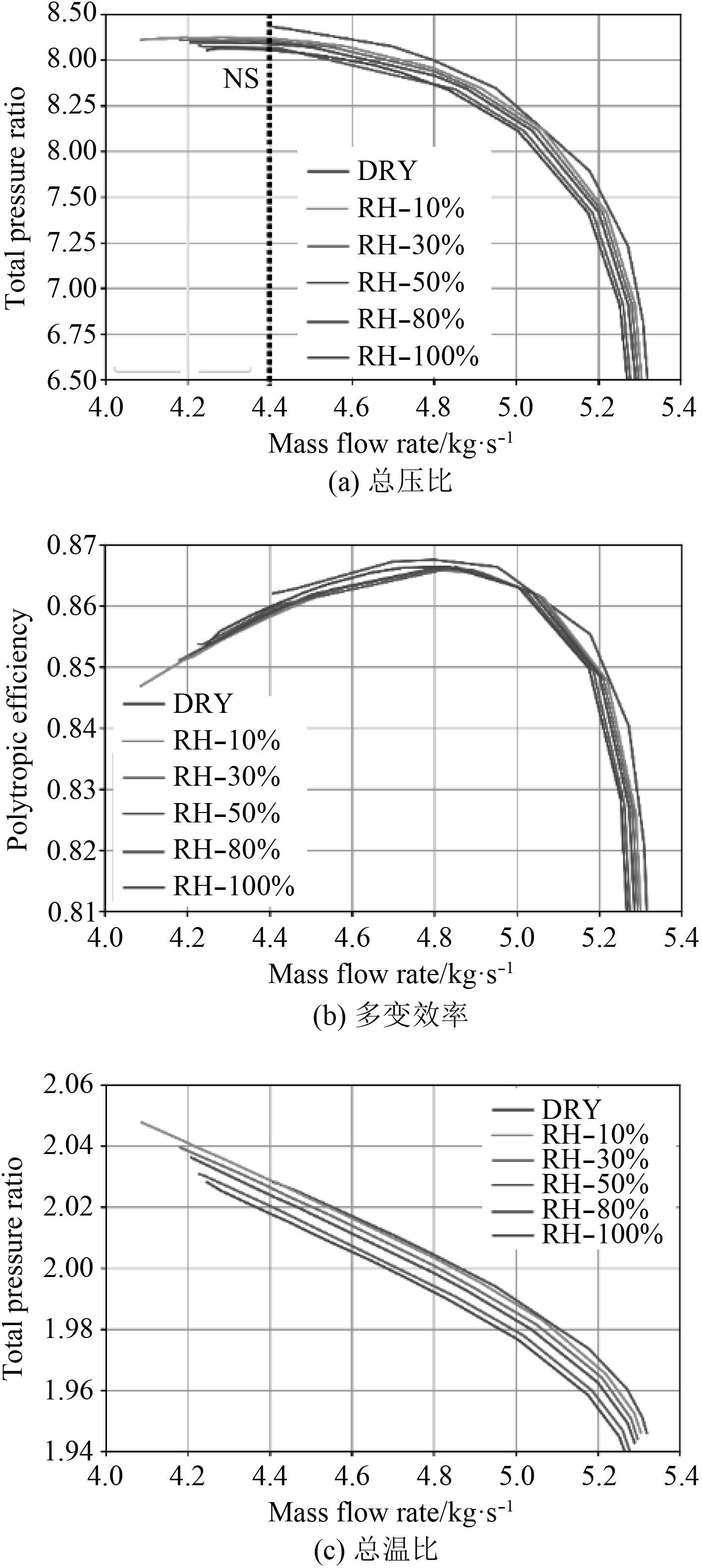
图5分别展示了两级压气机的压比、多变效率及温比。图中，压气机堵塞点流量随着湿度的增加而减少，而压气机特性线形状基本保持不变，总体表现为特性线随着湿度的增加，向小流量、低压比、低效率方向偏移；随着含湿量的增加，水蒸气含量增加，由于水蒸气的分压比重增加，压气机总压比恶化；温比在节流过程中逐渐增大，随着湿度的增加温比较干空气条件下降低；根据式（9）得到多变效率，计算过程中受气体热力学参数及压气机自身性能（包括压比和温比）的影响，而本文研究对象在改变湿度过程中，比热比、压比及温比均下降，较难分出主要影响参数，最终体现结果为多变效率随着湿度的增加而下降。

3.1.2 裕度

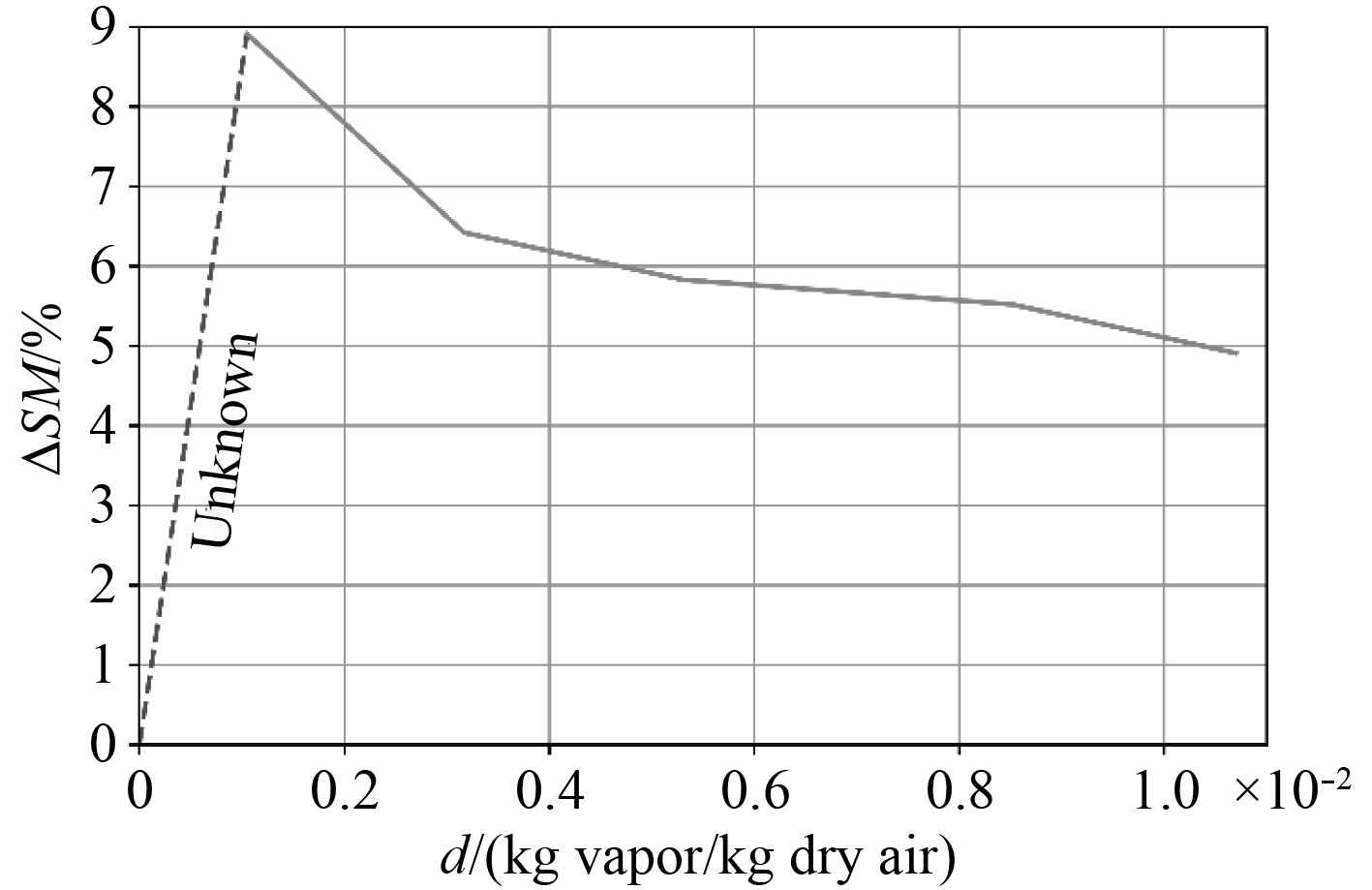
根据式（10）和式（11）计算得到压气机裕度及裕度改变量，如表5所示。图6绘制了含湿量约0～0.01范围内与裕度变化量的关系。湿空气条件下，压气机稳定性有显著提升，随着湿度的改变，压气机裕度增量约在5%～9%范围内变化。湿度增大，裕度改善量呈现减少的趋势。另外，本文还未开展对于极小含湿量（0～0.001）范围内的研究，因此在该范围内的裕度增量变化规律尚未知，在图6中以虚线表示。

3.2 压气机流场分析

如图5（a）中黑色虚线所示，本文选取干空气条件下近失速工况点（Near Stall，NS）为比较基准点，对比研究不同湿度对压气机流场的影响。如上节所述，干湿工况下压气机裕度有显著区别。找到本文压气机的失速原因，找出湿空气如何改善了流场，从而使得压气机稳定运行范围增加是本节的目的。

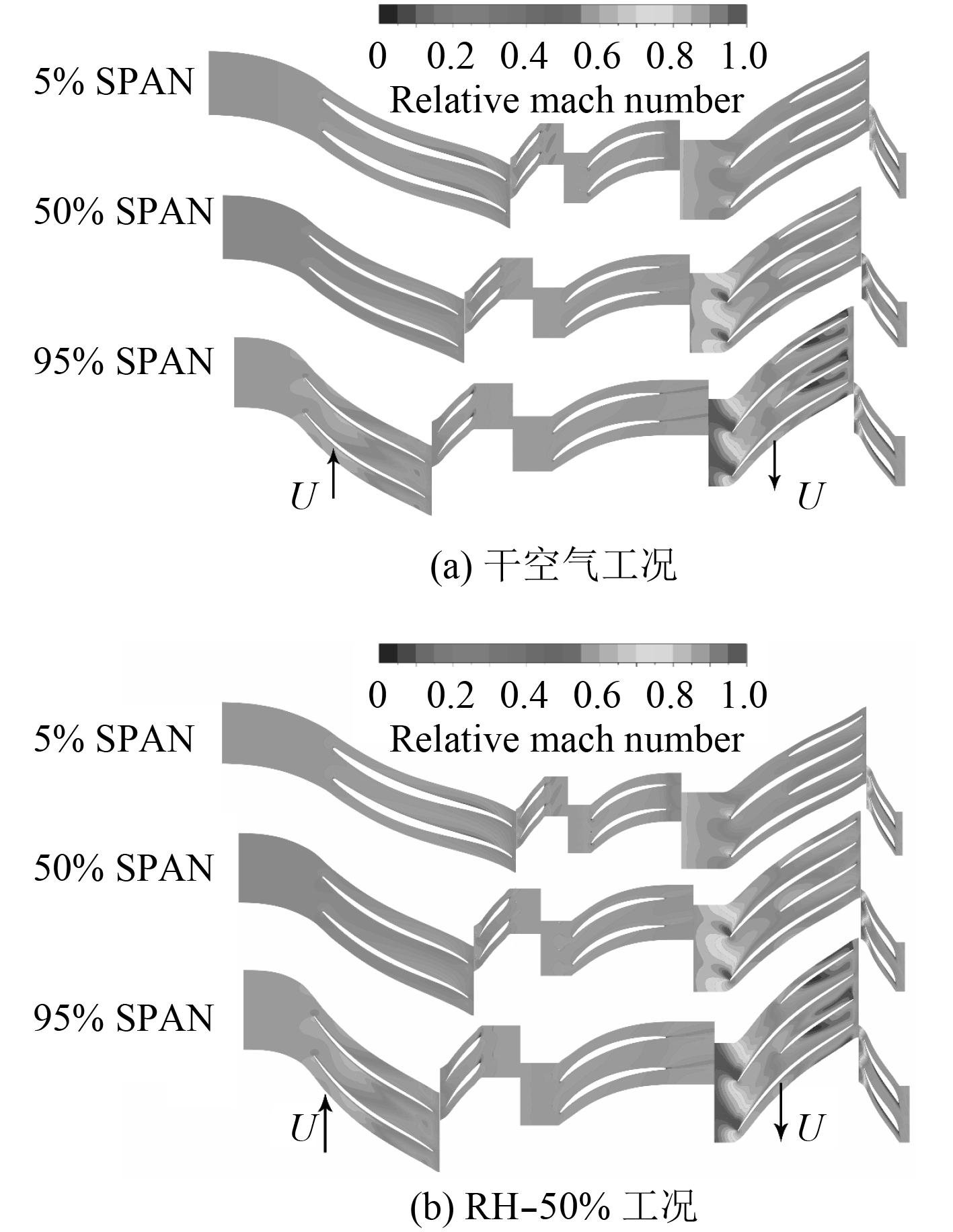
图7以干空气及RH-50%工况为例，展示了两级压气机5%，50%及95%展向位置的相对马赫数云图。气流在高压级扩压器喉部产生了强烈的激波，气流在激波后压力突增而速度骤降并在吸力面产生了较大的低速分离区，为本文研究对象失速发生原因。

在湿空气工况下，马赫数分布总体与干空气一致，湿度的变化并不影响压气机失速发生的机理，针对高压级扩压器研究湿度对其内部流动的影响。

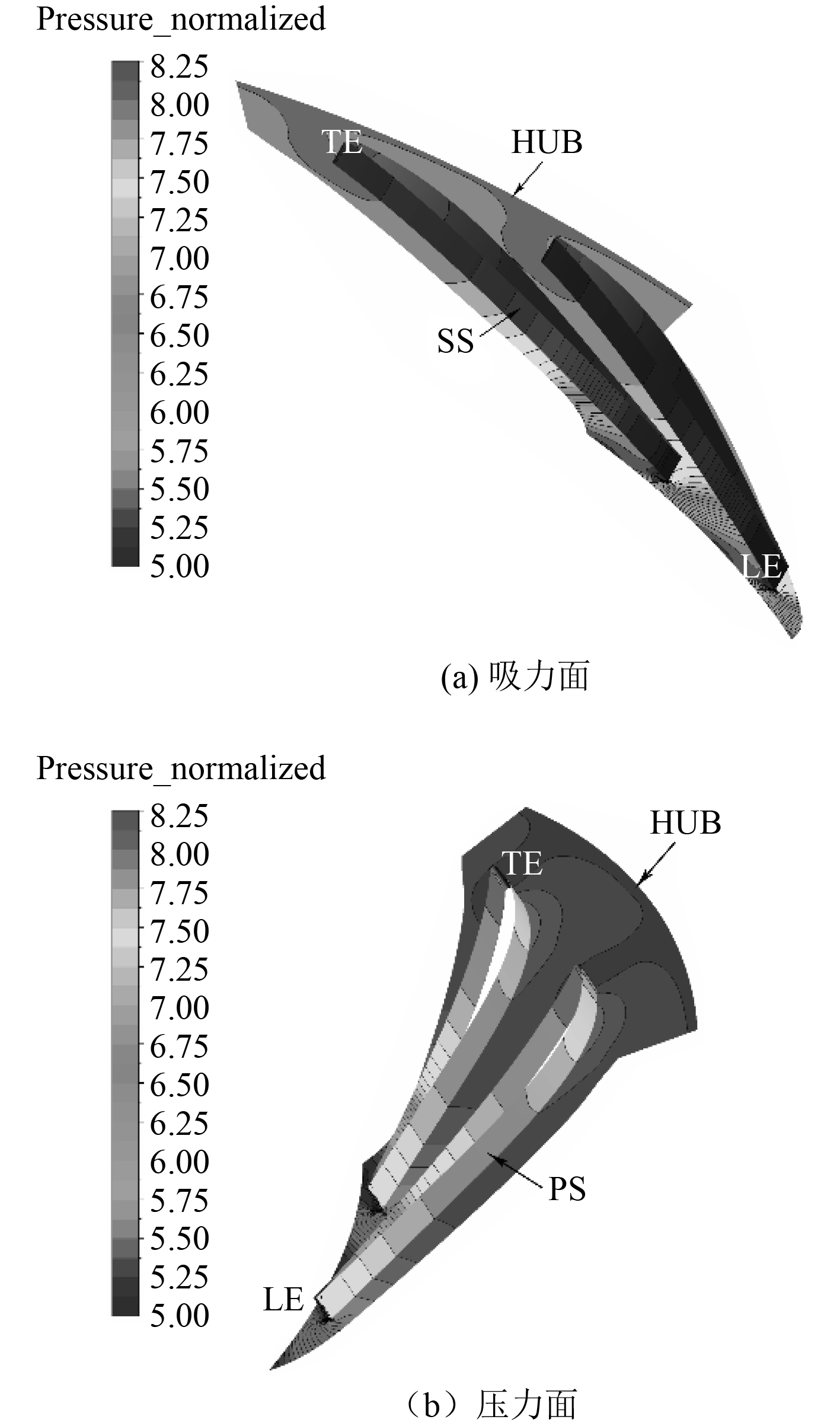
图8为干空气条件近失速工况下扩压器叶片表面正规化静压云图，扩压器吸力面叶身前侧有较大的低压区而压力面侧压力相对较高且变化平缓；叶身后侧吸力面叶表静压略高于压力面。

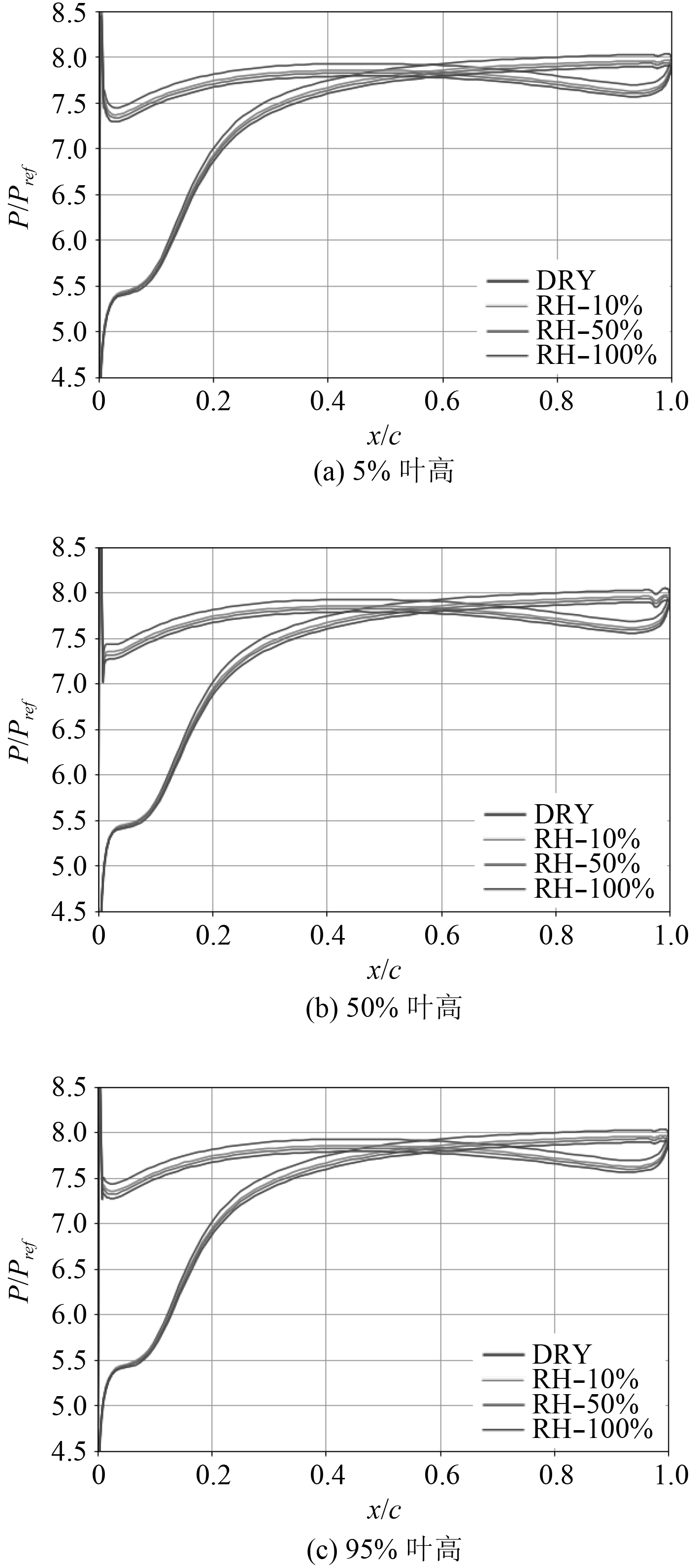
图9为RH-10%，RH-50%和RH-100%工况与干空气在高压级扩压器叶片表面正规化静压沿叶展方向的对比。由于上游叶轮出口速度不均匀，在扩压器前缘静压分布有微小差别；随着湿度的增加，水蒸气分压增加，混合气体压力下降，导致叶表静压下降，但分布规律基本保持一致。在叶片吸力面5%～20%弦长位置处，因激波产生了压力突跃且受湿度影响较小，而相应区域的压力面静压降低，使叶身头部区域负荷小于干空气。

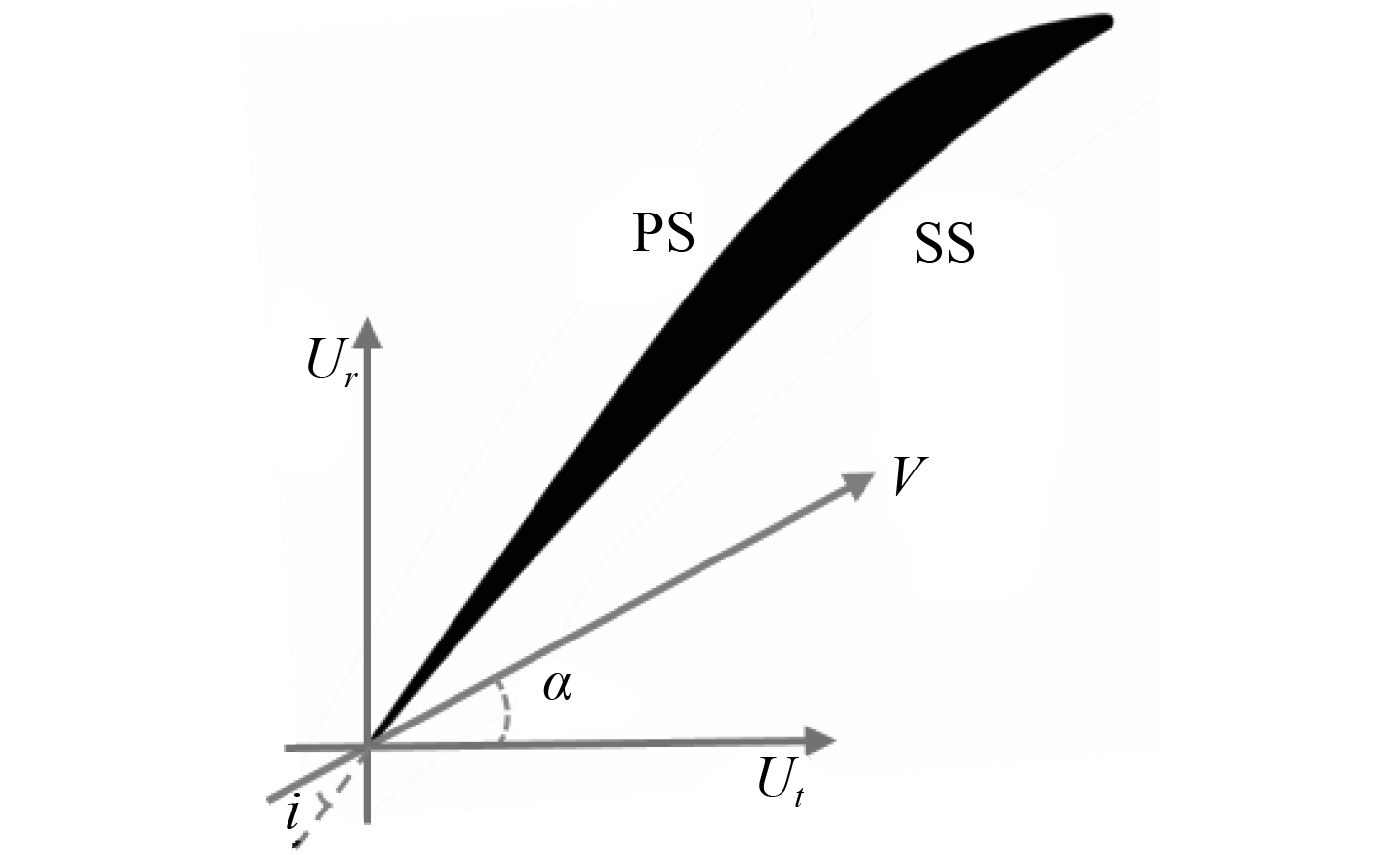
本文气流角的定义为气流与切向速度方向的夹角，如图10中的 $\alpha $ 所示，气流角计算采用周向面积平均。 $i$ 为气流与叶型前缘中弧线切线的夹角，即攻角。由图可得，气流角增加，攻角减小。

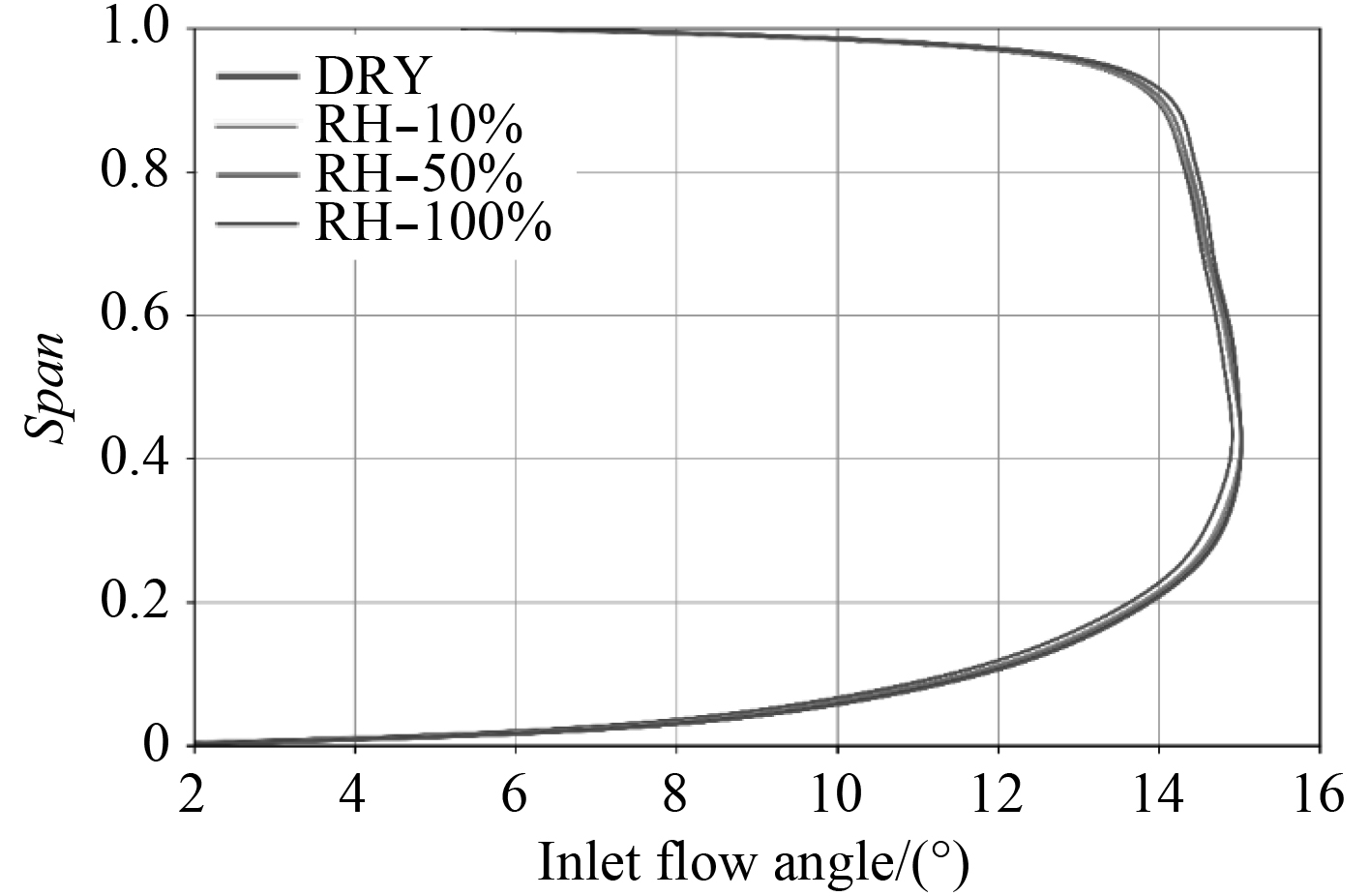
图11为RH-10%，RH-50%和RH-100%工况与干空气在高压级扩压器进口气流角沿展向的分布规律。湿空气条件下，进气角在10%～90%展向位置均大于干空气条件，湿度越大，进气角越大。根据本文气流角定义可得：湿度增大，气流的攻角减小，降低了叶片前缘的负荷，使得气流流向更加吻合叶片通道，减少吸力面的流动分离。在20%～60%展向位置，湿空气工况较干空气进气角平均增加约0.2°，但不同含湿量之间进气角差异较小。

综上，湿空气条件下，压气机高压级扩压器叶片前缘载荷下降，正攻角减小，改善了流动；由于水蒸气的引入，随着湿度的增加，叶表静压总体减少。

4 结　语

本文分析了空气湿度对热力学参数的影响并给出对压气机效率计算的变化规律；以某对置式离心压气机为例，分析了含湿量在0～0.01范围内共计6个工况下压气机的性能，结论如下：

1）随着空气中含湿量的增加，气体的定压比热和气体常数增加，比热比减少，压气机效率降低。

2）压气机特性线随着湿度的增加，向小流量、低压比、低效率方向偏移；总压比、多变效率及温比随着含湿量的增加而减少；湿空气条件下，裕度较干空气有明显的改善，随着湿度的增加，裕度增量减少。

3）湿度条件不改变压气机失速机理；随着湿度的增加，高压级扩压器叶片表面静压总体下降，前缘载荷降低，气流正攻角减少因而缓解了吸力面的流动分离。