2. 江苏科技大学 土木工程与建筑学院,江苏 镇江 212003
2. School of Civil Engineering and Architecture, Jiangsu University of Science and Technology, Zhenjiang 212003 China
我国从20世纪60年代起开始在渤海勘探和开发海上油气资源,目前已建成海洋平台100余座[1]。海洋平台作为海洋油气资源开采的重要设施,其造价昂贵、工艺复杂、设备布置集中、作业环境恶劣,一旦发生爆炸和火灾事故,后果不勘设想。大量的海洋平台事故统计[2]表明爆炸和火灾事故是导致海洋平台结构失效的主要原因之一,不仅造成人员伤亡和经济损失,而且对周边环境造成严重的污染和破坏。因此,对海洋平台结构进行爆炸和高温作用下的动态响应分析及结构毁伤研究是十分必要的。
目前国内外的主要研究方向是爆炸载荷作用下结构力学性能及毁伤机理研究,而对火灾对其结构毁伤过程的影响研究较少。Yin Qun[3]对不同形式爆炸载荷作用下舱壁结构的破坏模式及毁伤特性进行了数值模拟研究,提出新型箱型梁防护结构。Y. L. Liu[4]考虑流体与船体结构之间采用非线性耦合方法,对水面舰船在水下爆炸时的整体响应进行了数值模拟研究,建立了考虑相互作用的FSI模型。于文静[1]基于有限元软件Ansys/Ls-dyna,采用考虑应变率效应的材料本构模型,研究爆炸对导管架海洋平台结构抗高温性能的影响。
本文采用显式非线性有限元软件MSC.Dytran对海洋平台结构在爆炸和高温作用下的毁伤过程进行数值仿真研究,分析了海洋平台结构的破损模式,研究了爆炸和火灾事故对平台结构动态响应的影响,得到海洋平台结构塑性变形及冲击环境受爆炸和高温影响的变化规律,为海洋平台的设计和建造提供参考依据。
1 空中爆炸理论爆炸是能量快速释放的过程。当炸药爆炸时,爆炸产物迅速膨胀,周围气体受到猛烈压缩,在波头产生压力突跃,从而形成冲击波。冲击波形成初期压力较高,随后冲击波波阵面在向外传播的过程中压力不断衰减,当爆炸产物膨胀到某一特定体积,它的压力降至初始压力

|
图 1 空中爆炸冲击波传播原理图 Fig. 1 Schematic diagram of air explosion shock wave propagation |
Henrych在《爆炸动力学及其应用》[5]介绍了空中爆炸现象、空中爆炸载荷传播规律及其应用,提出空中爆炸冲击波载荷的Henrych经验公式。以TNT球形药包为例,冲击波瞬时压力与时间的关系为:
| $\Delta p(t) = \Delta {p_m}\left(1 - \frac{t}{\tau }\right){e^{ - \alpha t/\tau }},$ | (1) |
| $ \begin{split}\frac{\tau }{{\sqrt[3]{W}}} =& {10^{ - 3}}(0.107 + 0.444\overline R + 0.264{\overline R ^2} - 0.129{\overline R ^3} +\\ &0.0335{\overline R ^4}),\;\;\;0.05 \leqslant \overline R \leqslant 3,\end{split} $ | (2) |
| $ {{\Delta }{p_m} \!=\! \frac{{14.0717}}{{\bar R}} \!+\! \frac{{5.5397}}{{{{\bar R}^2}}} \!-\! \frac{{0.3572}}{{{{\bar R}^3}}} \!+\! \frac{{0.00625}}{{{{\bar R}^4}}},\;0.05 \!\leqslant\! \bar R \!\leqslant\! 0.3}, $ | (3) |
| $ {{\Delta }{p_m} = \frac{{6.1938}}{{\bar R}} - \frac{{0.3262}}{{{{\bar R}^2}}} + \frac{{2.1324}}{{{{\bar R}^3}}},\;\;\;\;\;\;\;\;\;0.3 \leqslant \bar R \leqslant 1}, $ | (4) |
| $ {\Delta }{p_m} = \frac{{0.662}}{{\bar R}} + \frac{{4.05}}{{{{\bar R}^2}}} + \frac{{3.288}}{{{{\bar R}^3}}},\;\;\;\;\;\;\;\;\;1 \leqslant \bar R \leqslant 10{\text {。}} $ | (5) |
式中:
采用日本学者[6]提出的等效TNT方法,将泄漏气体等效为相应TNT质量:
| ${M_{ET}} = 6.4 \times {10^{ - 6}}M \cdot {H_c}{\text{。}}$ | (6) |
式中:
实践中经常使用非TNT的炸药。只要知道炸药的比爆热
本文利用有限元分析软件MSC.Patran建立海洋平台有限元模型,有限元模型共包含238860个节点、257088个单元。本文在不影响仿真结果的基础上,对模型进行适当简化。为了数值模拟的准确性,模型的单元尺寸均不大于0.3 m×0.3 m。炸药设在舷侧边舱内,距甲板2.25 m,距舷侧2 m,距横舱壁4.5 m,如图2所示。海洋平台结构关于中纵剖面对称,图3为平台结构半剖面厚度分布示意图。本文将海底泥线以下桩腿结构采用四周刚性固定,约束节点的6个自由度(δx=δy=δz= 0,θx=θy=θz=0),如图4所示。

|
图 2 炸药位置示意图 Fig. 2 Sketch map of explosive location |
|
图 3 厚度分布示意图(半剖) Fig. 3 Distribution of thickness of platform(semi-section) |

|
图 4 有限元模型的约束条件示意图 Fig. 4 Boundary conditions of finite element model |
为真实模拟爆炸冲击波与平台结构之间的相互作用,数值模拟过程中采用考虑耦合面失效的多欧拉耦合算法。舷侧边舱、相邻各舱室及平台外表面均设定耦合面(COUPLE1卡),与耦合面对应的空气欧拉域采用box定义,如图5(a)~图5(c)所示。考虑爆炸舱室可能出现破损失效,故与舷侧边舱相邻的舱室均设定失效模式(PARAM FASTCOUP FAIL卡),当耦合面发生失效,欧拉材料会从失效处穿过耦合面流向另一侧。整体有限元计算模型中的欧拉域包含平台外的空气域和各个小耦合面内的空气域。其中平台外部空气域主要分布在结构周围半径为80 m的球形区域内,在空气域边界定义流入、流出边界,以防止冲击波在欧拉域边界发生反射现象,如图5(d)所示。
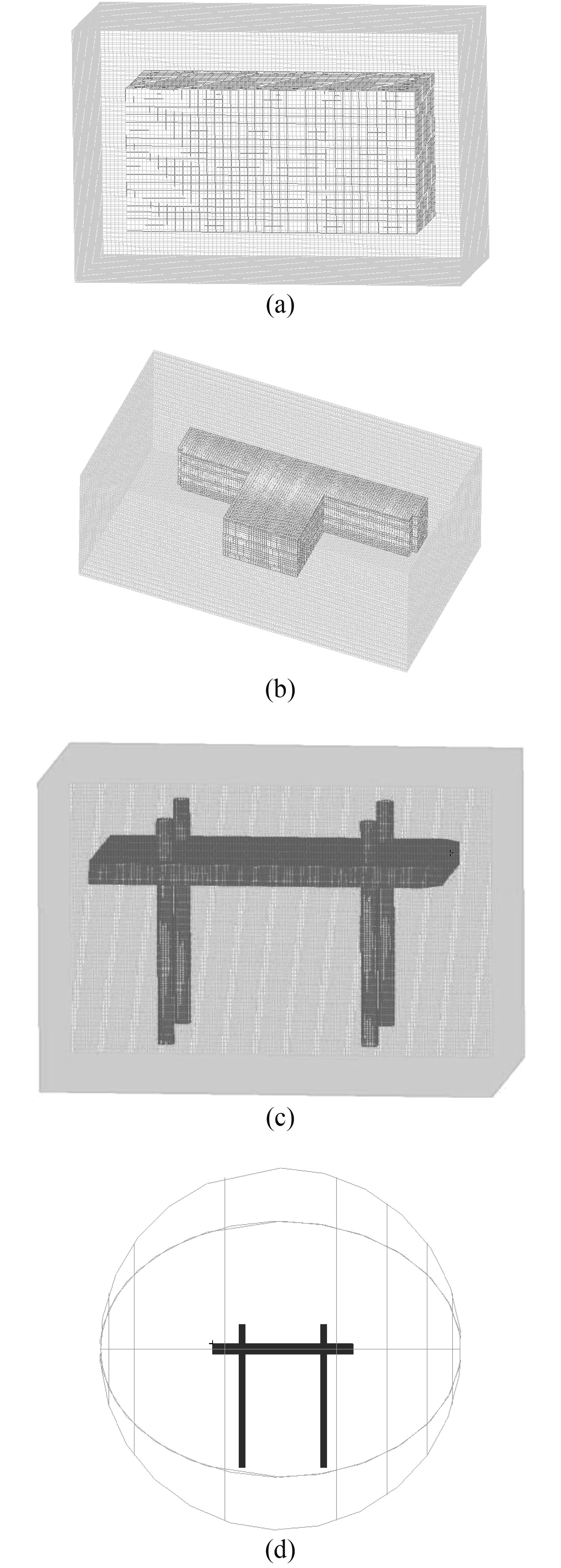
|
图 5 多欧拉域的有限元模型 Fig. 5 Finite element model of multi-euler domain |
在爆炸和高温载荷作用下需要考虑应变率强化效应和高温软化效应对钢材力学性能的影响。本文通过钢结构抗火设计规范[7]和Cowper-Symonds本构关系模型综合考虑高温的软化效应和爆炸的应变率效应。平台主体结构均采用一般强度船用钢,材料的泊松比为0.3,密度为7800 kg/m3,弹性模量为2.1
| $\sigma {}_y = \left[ {\left. {1 + {{\left( {\frac{{\dot \varepsilon }}{D}} \right)}^{1/q}}} \right]} \right.\left( {{\sigma _0} + \beta {E_p}\varepsilon _p^{eff}} \right){\text{。}}$ | (7) |
式中:
炸药和空气材料通常采用JWL状态方程和Gamma律状态方程设定,因本文采用欧拉求解器的近似黎曼算法(ROE算法)不支持多欧拉材料的算法,因此,本文采用Gamma律状态方程EOSFAM来定义空气和炸药材料,Gamma律状态方程为:
| $P = \left( {\gamma - 1} \right)\rho e{\text{。}}$ | (8) |
式中:e为单位质量比内能。其中空气比内能2.1×105 J/kg,炸药采用高能密度空气压缩球来进行模拟,比内能4.4×106 J/kg;
根据温度对钢材力学性能的影响,本文将温度工况分为:低温段(20 ℃~200 ℃),在此温度范围内钢材的力学性能受温度的影响不大,主要考虑应变率强化效应;高温段(200 ℃~500 ℃),在此温度范围内需要考虑温度软化效应和应变率强化效应;温度软化段(﹥500 ℃),此阶段钢的屈服强度只有常温下的20%左右,由于钢材截面应力不可能只有屈服强度的1/5,因此本文不考虑此阶段。根据燃气泄漏速率[9]将爆炸工况(气体泄漏1 min的泄漏量)分为:小规模泄漏(m<1 kg/s),中等规模泄漏(1 kg/s<m<10 kg/s),大规模泄漏(m>10 kg/s),m为燃气泄漏速度,如表1所示。
|
|
表 1 计算工况 Tab.1 Calculation conditions |
高温使钢材发生软化效应,爆炸冲击波使钢材强度提高,两种荷载对钢材的影响相反,当爆炸和火灾事故同时发生,增加了平台结构毁伤变形的分析难度。本文将爆炸和高温载荷作用下的平台结构的毁伤变形、冲击环境和塑性变形能吸收进行逐一比较分析。
3.1 毁伤变形分析本文以50 kg中等规模燃气泄漏量的计算结果为例,分析舱室结构在爆炸和高温载荷作用下的毁伤变形情况,如图6所示。爆炸所产生的冲击波集中于舱室内部,因其空间相对密闭,能量大部分由舱室结构吸收。在爆炸和高温作用下,舱壁板出现塑性变形,变形区域集中在爆点附近,说明密闭空间爆炸具有局部效应。变形量和高应力区域随着温度的升高而增大,舱室内部冲击波能量在舱室角隅处汇聚,舱壁板缝线处出现应力集中现象,加大舱室结构的毁伤失效。
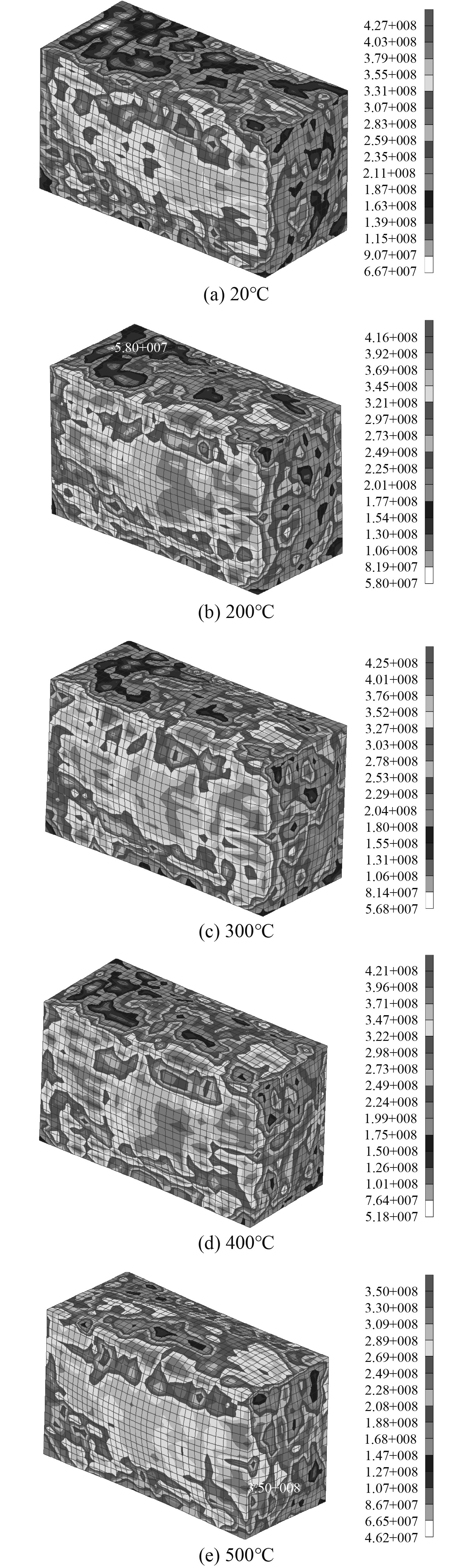
|
图 6 不同温度舱室结构毁伤应力图 Fig. 6 Structural damage stress diagram of bursting cabin at different temperatures |
将平台结构在不同温度工况下的应力变化情况统计于表2,并与相应工况的静态屈服应力结果相比较。在低温段,平台结构毁伤变形受应变率强化效应影响较大,温度载荷对平台结构毁伤变形影响不明显;当温度超过400 ℃后,
|
|
表 2 不同温度下应力对比表 Tab.2 Comparison table of stress at different temperatures |
不同温度下爆炸舱室结构最大变形量如图7所示,舱壁板的塑性变形量随着温度的升高而增大。在300 ℃~400 ℃之间时,材料发生“塑性流动”,钢材因“蓝脆”现象表现出温度“硬化”效应,此时位错被溶质原子气团束缚而使塑性形变困难,因此变形量没有明显变化。当温度超过400 ℃之后,钢材的力学性能随温度的升高而出现断崖式下降,塑性阶段材料强度随应变率的增加而降低,呈现应变率“软化”效应,舱壁板的塑性变形量增幅明显。

|
图 7 不同温度舱室结构最大变形图 Fig. 7 Maximum structure deformation of explosion chamber at different temperatures |
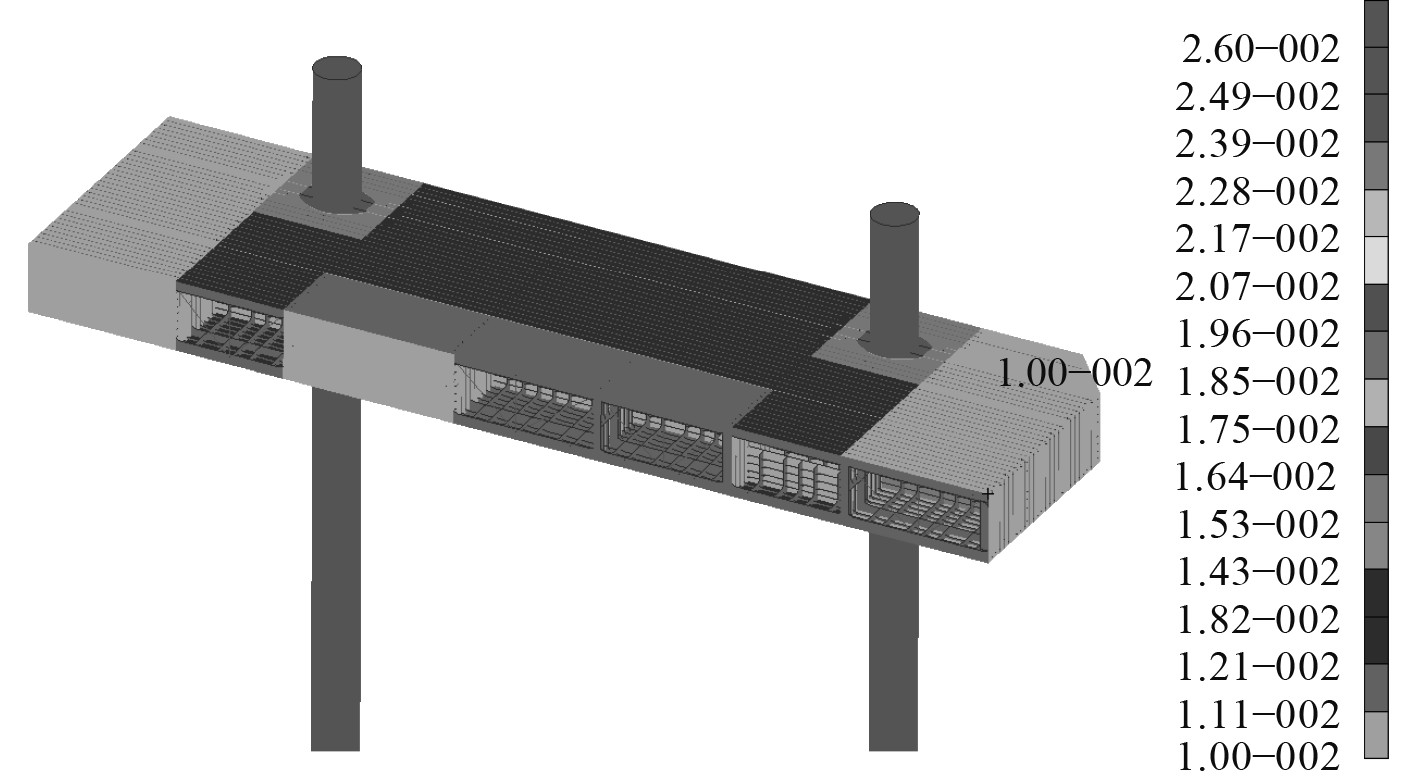
海洋平台上甲板布置密集的精密机械设备,冲击环境是设备抗冲击研究需考虑的重要因素。爆炸冲击波不仅会对仪器设备带来直接伤害,因冲击波而引发的振动现象还会对设备造成二次损伤。选取爆炸舱室上甲板结构距爆源中心点4.5 m处为测点,可以更好反映上甲板结构受振动影响的变化规律。本文以50 kg中等规模燃气泄漏量的计算结果为例进行分析,图8为不同温度上甲板中心点时间历程曲线。
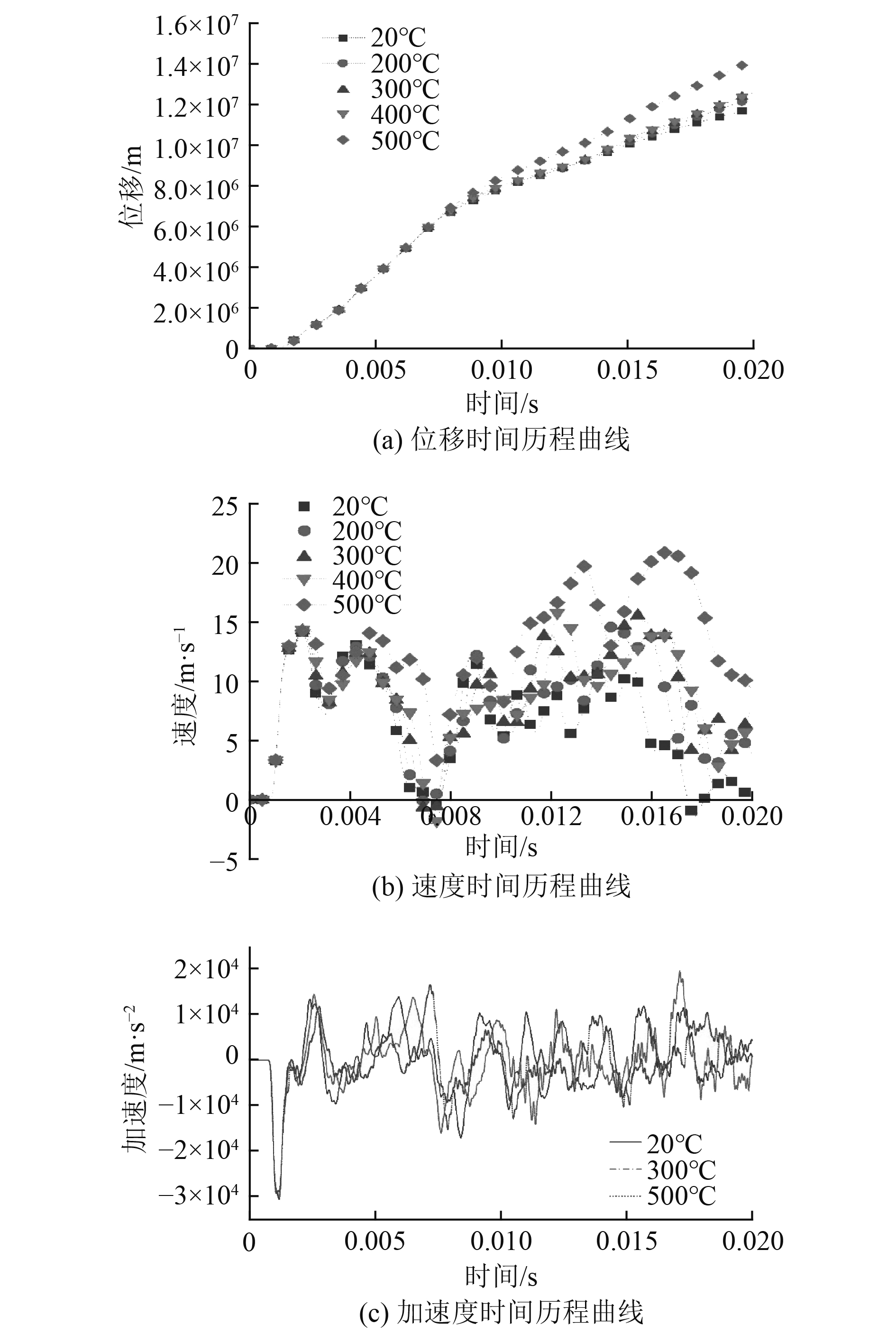
|
图 8 不同温度上甲板中心点时间历程曲线 Fig. 8 Time history curve of upper deck center at different temperature |
爆炸和火灾事故发生初期(t<4.2 ms),冲击波形成初期压力最大,甲板中心点位移开始快速增加;冲击波在扩散的过程中,在结构的失效变形吸能的作用下,冲击波能量出现衰减,位移增长速率开始放缓,测点位移整体近似呈线性增加;在温度不大于400 ℃阶段,不同温度下的甲板中心点最大位移增幅较小;受“蓝脆”现象影响,300 ℃和400 ℃的位移曲线几乎是重合的;当温度大于400 ℃,钢材的塑性指标降幅较大,甲板中心点位移出现明显的增幅。从图8(b)可以看到,当爆炸冲击波到达甲板后,不同温度载荷测点速度分布随着冲击波在舱室内反射而呈波浪式变化;当温度超过400 ℃,测点速度分布和周期有明显的增加。从图8(c)可以看到,舱室内部发生爆炸时,爆炸冲击波使测点加速度迅速达到极值,随后呈波浪式衰减,振荡周期随着温度载荷的增加而增加;高温使得钢材的塑性指标降低,结构变形吸能量增加,爆炸冲击波能量迅速衰减,测点速度整体呈上升趋势,加速度波动范围减小。
3.3 吸能分析海洋平台结构的塑性变形能是平台结构毁伤程度的重要指征参数之一,可以准确真实反映出平台结构的毁伤变形情况。本文以50 kg中等规模燃气泄漏量的计算结果进行分析。
对比分析不同温度工况下平台结构对应的各个结构吸能趋势:爆炸和火灾事故发生0.7 ms时,距爆点最近的纵舱壁结构吸能迅速增加,冲击波传播4.2 ms后,爆炸舱室不同构件吸能均开始上升,20 ms后,平台各结构吸能趋于平稳。横、纵舱壁是爆炸舱室结构的主要吸能结构;爆炸舱室不同构件的塑性变形能吸收量随着温度的升高而升增加,但各构件吸能比值没有明显变化,舱室结构总吸能提升26.9%。对比分析不同温度海洋平台结构吸能发现,甲板和纵舱壁结构吸能量增率最明显,海洋平台结构总吸能提升20%以上(见图9)。为了量化海洋平台各个结构在不同温度工况下的吸能情况,将平台结构各构件吸能量统计于表3,并与常温下的吸能结果进行比较分析。
|
|
表 3 不同温度平台结构吸能表 Tab.3 Energy absorption table with different temperature platform structure |

|
图 9 不同温度结构吸能时间历程曲线 Fig. 9 Time-history curve of structure energy absorption at different temperatures |
温度小于400 ℃阶段,随着温度的升高,平台不同构件吸能有小幅度增加;受高温软化影响,钢材塑性增加,甲板和底板结构变形加大,横、纵舱壁吸能和占比有所下降;300 ℃和400 ℃工况的吸能数值受“蓝脆”现象影响而没有明显变化。当温度高于400 ℃后,钢材的各项力学性能快速下降,舱室不同构件的吸能出现明显的增长,爆炸舱室结构吸能占比持续增加。
4 结 语本文应用非线性数值仿真软件MSC.Dytran,采用多欧拉耦合方法对海洋平台在爆炸和高温载荷作用下的动态响应进行研究,得到平台结构在爆炸和高温载荷作用下的毁伤变形、冲击环境和能量吸收等方面的变化规律,通过比较和分析得出以下结论:
1)温度载荷对结构应变率强化效应影响不大,
2)温度对结构冲击环境影响较大,速度和加速度的振荡周期随着温度载荷的增加而增大;当结构温度超过400 ℃后,高温软化效果使得结构塑性变形能力增加,结构速度分布整体呈上升趋势,加速度波动范围减小。
3)当结构温度在低温阶段时,温度载荷增加对平台结构抗毁伤能力和冲击环境没有太大影响,主要考虑爆炸冲击波对其造成的毁伤破坏。
4)结构在“蓝脆”阶段整体表现较为稳定;但当温度载荷继续增加,平台结构抗爆、抗毁伤能力出现大幅削减,此阶段结构强度受高温载荷影响较大。
| [1] |
于文静. 导管架海洋平台钢结构在爆炸和火灾作用下的力学性能研究[D]. 上海: 上海交通大学. 2012.
|
| [2] |
ZOHRA S. HALIM, JANARDANAN S., FLECHAS T., et al. In search of causes behind offshore incidents: Fire in offshore oil and gas facilities[J]. Journal of Loss Prevention in the Process Industries. 2018.54: 254-265.
|
| [3] |
YIN Qun; CAO Guangbo; XIE Renjie. et al. Research on a ship bulkhead structure under the combined load. Hydraulic Engineering V - Proceedings of the 5th International Technical Conference on Hydraulic Engineering[C], CHE 2017.
|
| [4] |
Y. L. LIU, A. M. ZHANG, Z. L. TIAN, et al.. Numerical investigation on global responses of surface ship subjected to underwater explosion in waves[J]. Ocean Engineering, 2018, 161: 277-290. DOI:10.1016/j.oceaneng.2018.05.013 |
| [5] |
HENRYCH J, ABRAHAMSON G R. The dynamics of explosionand its use[M]. Amsterdam Elsevier Scientifi Pub. 1979.
|
| [6] |
EMI Yohiko. Research on the Safety of Liquid Gases [A]. Proceedings of the Japan Shipbuilding Association[C], No. 156, Showa 59.
|
| [7] |
NEN-EN1993-1-2. Eurocode3: Design of Steel Structures Part1-2: General Rules Structural Fire Design. Brussels: European Committee for Standardization, 2005.
|
| [8] |
王培涛. FPSO油气爆炸性能评估及抗爆结构设计研究[D]. 镇江: 江苏科技大学. 2016.
|
| [9] |
胡云昌, 黄海燕, 余建星. 基于概率影响图的海洋平台安全风险评估方法[J]. 中国造船, 1998, 1429(3): 38-46. |
 2020, Vol. 42
2020, Vol. 42
