对于长期处于海洋环境中的钻井平台而言,其受力情况十分复杂。在各种环境载荷(如风、浪、流)作用下,极易导致平台局部结构失效,进而导致平台整体结构失效,造成经济损失,人员伤亡等[1]。而极限强度是结构安全性评估的重要指标,为了获得安全的结构设计,提高平台结构极限状态下的生存能力,需要精确评估主要结构的极限强度[2-3]。
目前,极限强度常用的方法包括逐步破坏法[4-6]、数值仿真法[7-8]、模型试验法[9]等。本文以第七代钻井平台薄弱结构撑杆为研究对象,开展撑杆结构在压缩载荷作用下极限强度模型试验研究,数值仿真研究等。通过本文的研究,建立第七代钻井平台撑杆结构模型试验技术,掌握该结构力学特性,给出结构应力分布和变形特征情况,为该结构的进一步优化设计提供支撑。同时通过模型试验与数值仿真的对比验证,促进数值仿真方法的进一步发展。
1 试验对象本次试验对象为第七代钻井平台结构的部分平台立柱结构以及撑杆。其中立柱的高度为25 m,长度为19.25 m,宽度为18.5 m,转角半径为4.55 m,撑杆结构长度约为33.29 m,直径为3.2 m,立柱和撑杆结构原型仿真模型如图1和图2所示。
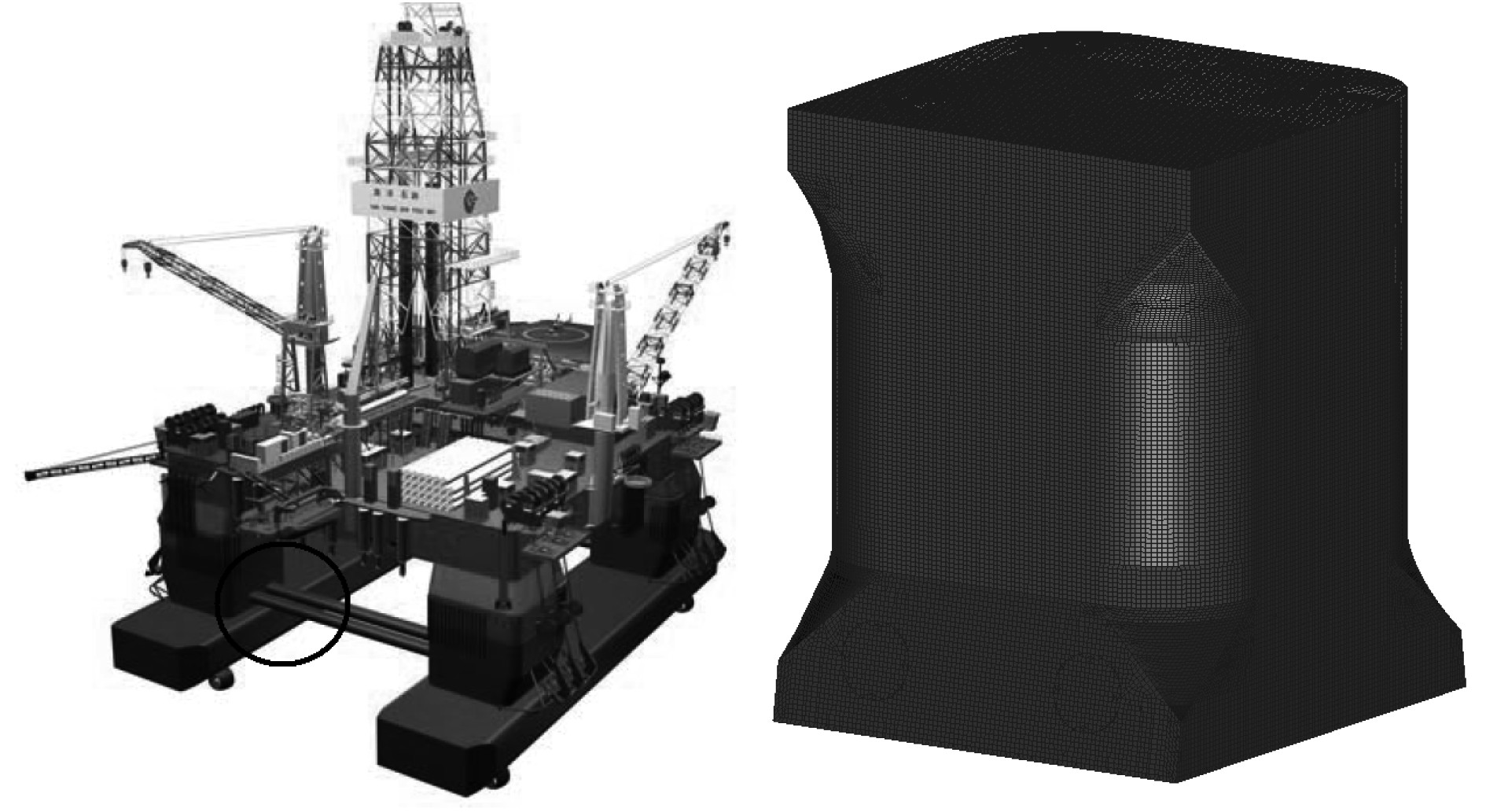
|
图 1 模型试验区域及有限元结构 Fig. 1 Test area and finite element model of column prototype |

|
图 2 撑杆原型有限元模型 Fig. 2 Finite element model of struct |
为了便于模型设计及加工,试验采用材料屈服应力为310 MPa(根据材料试验得出)的船用材料,主尺度及板厚缩尺比均为
| $\frac{{{F_s}}}{{{F_m}}} = \lambda \cdot \lambda \text{。}$ | (1) |
其中:
根据相应的计算结果以及试验室加载等情况综合考虑,选定主尺度及板厚缩尺比为6。图3和图5为实际结构与等效模型的数值仿真模型,其中简化模型仅采用一根撑杆结构,立柱结构按照舱壁将其简化成1/4的模型,即模拟立柱半宽,撑杆结构内部的T型骨材采用扁钢进行模拟。图4和图6为极限状态下实际结构和等效模型的应力分布情况,可以看出简化后的结果与实际结构的应力分布大体一致。图7和图8为撑杆结构数值仿真得到的失效模式,通过对比可以发现,2模型的撑杆结构的失效模式基本一致,应力分布大体相似。图9为整个结构的载荷位移曲线,通过计算得出实际撑杆结构的极限压缩载荷为1.60×108 N,试验模型的极限压缩载荷为4.57×106N,转换为实际结构后得出的压缩载荷为1.64×108N,与原型极限载荷误差为2.5%。通过对比可以发现,本方案的试验模型设计合理。

|
图 3 原型结构数值仿真计算模型 Fig. 3 Finite element model of prototype |

|
图 4 原型结构数值仿真计算模型极限状态 Fig. 4 Limit state stress tensor of prototype |

|
图 5 简化后试验模型 Fig. 5 Simplied model |

|
图 6 简化后试验模型极限状态计算结果 Fig. 6 Limit state stress tensor of simiplied model |
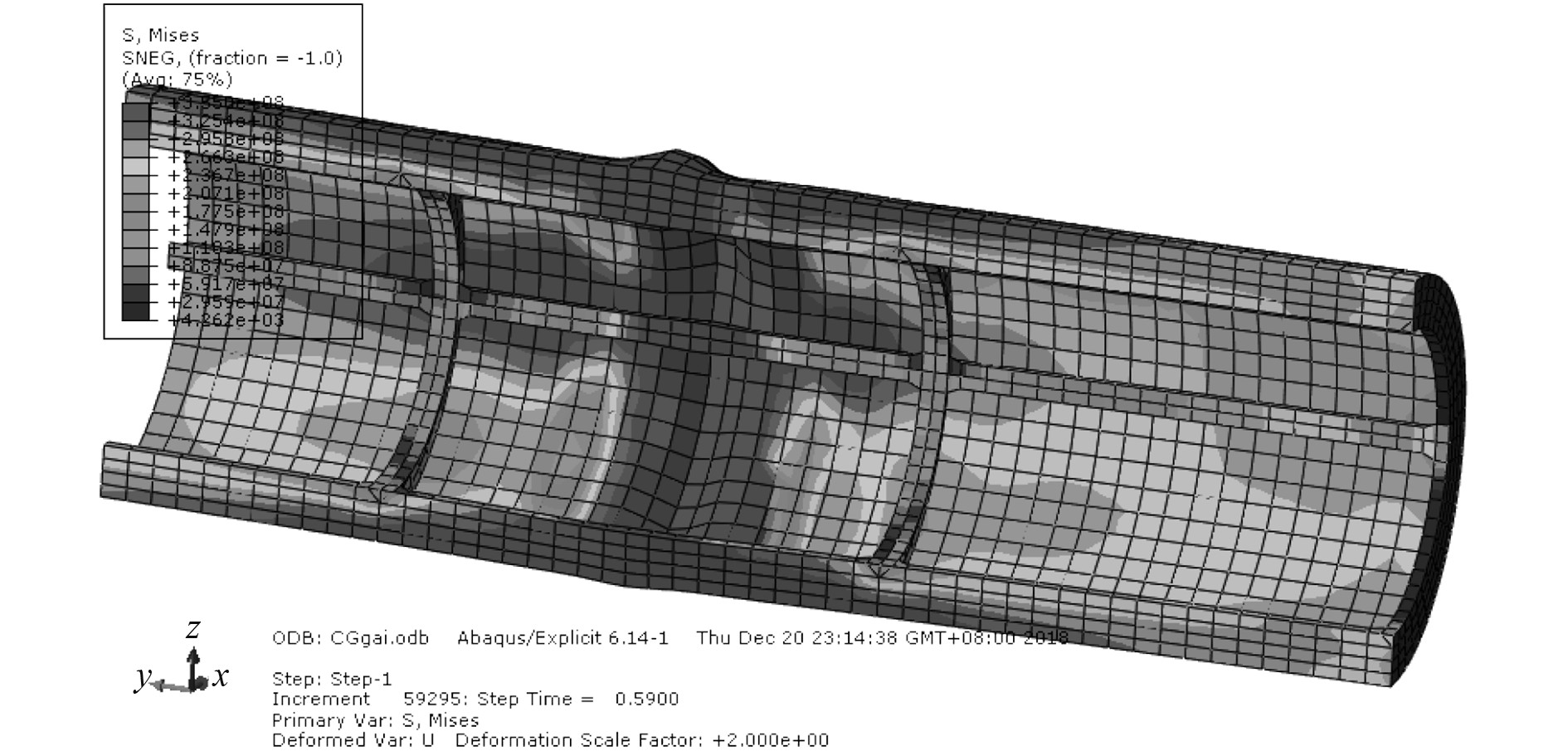
|
图 7 撑杆原型极限状态失效模式 Fig. 7 Limit state stress tensor of struct prototype |

|
图 8 简化模型极限状态失效模式 Fig. 8 Limit state stress tensor of simplied model |
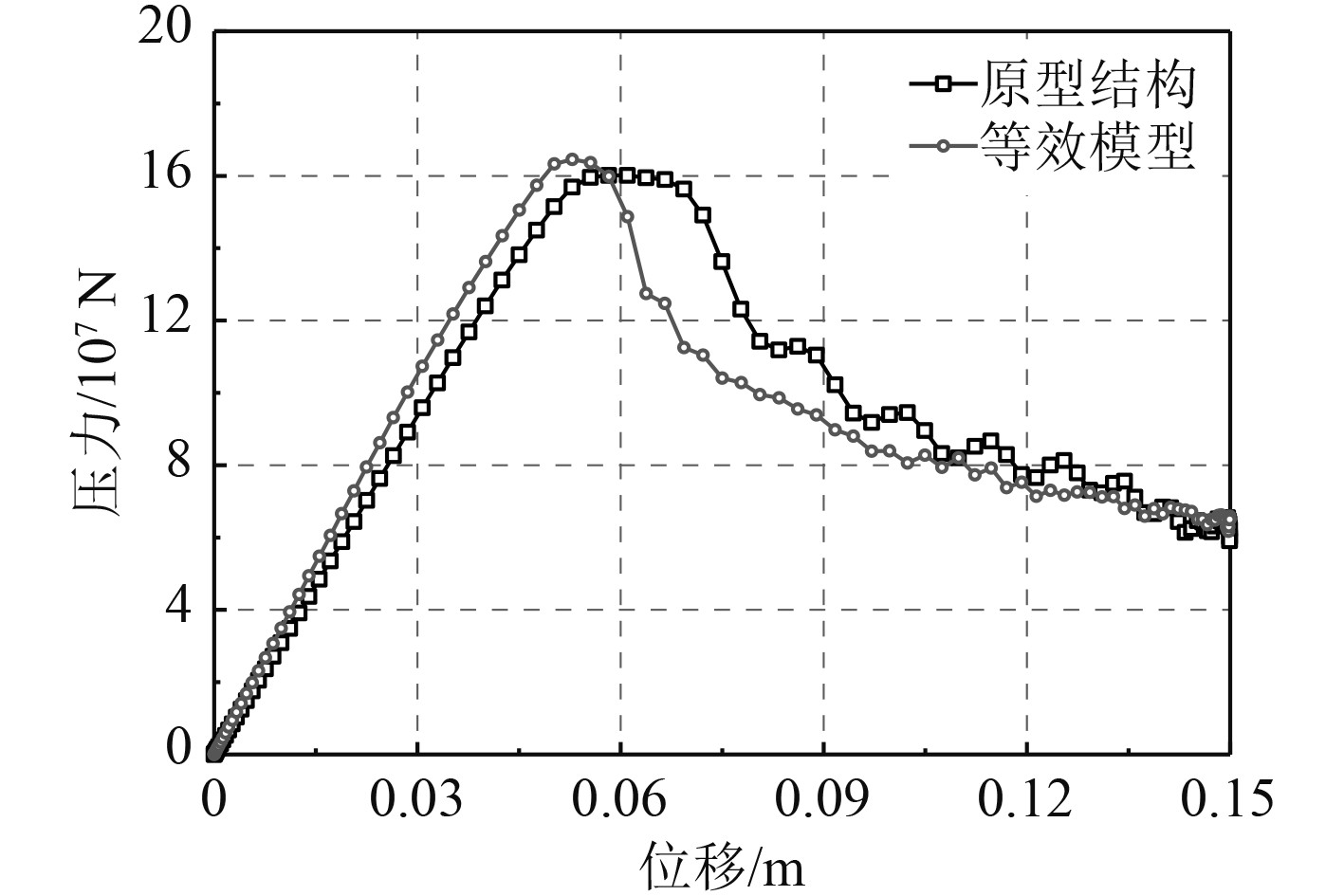
|
图 9 载荷-位移曲线 Fig. 9 Load-displacement curve |
模型试验测试仪表包括静态应变仪、位移传感器、应变片等。图10为模型试验各测点布置情况,沿撑杆各跨布置20个测点,沿撑杆纵向布置,并在撑杆加载端布置位移传感器,同时在剖面1、剖面2、剖面3布置位移传感器。
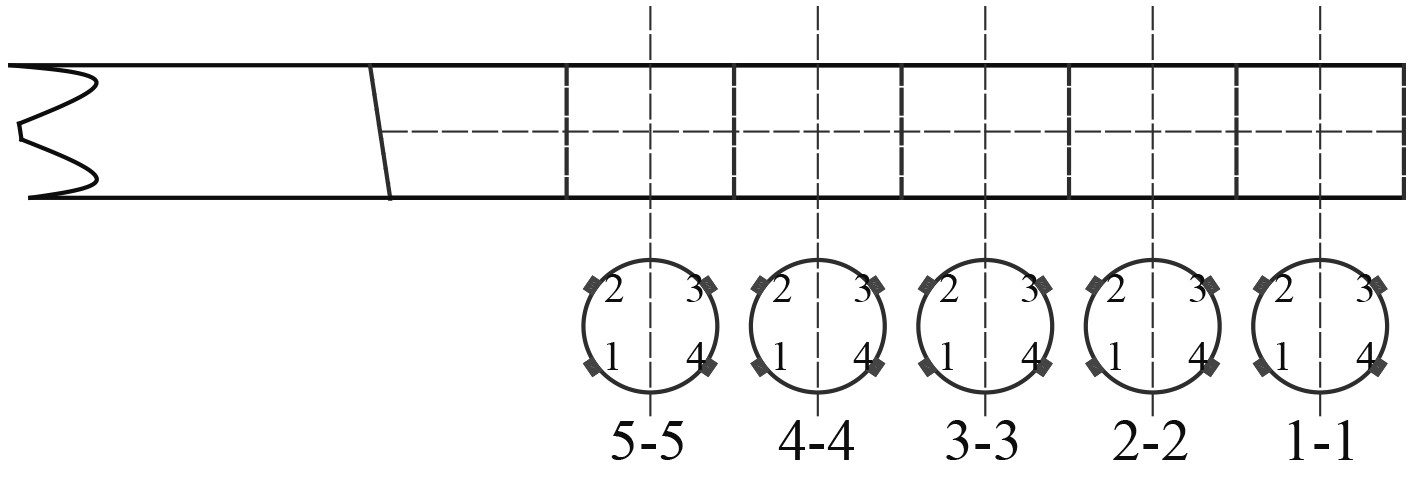
|
图 10 应变测点位置 Fig. 10 Location of measure points |
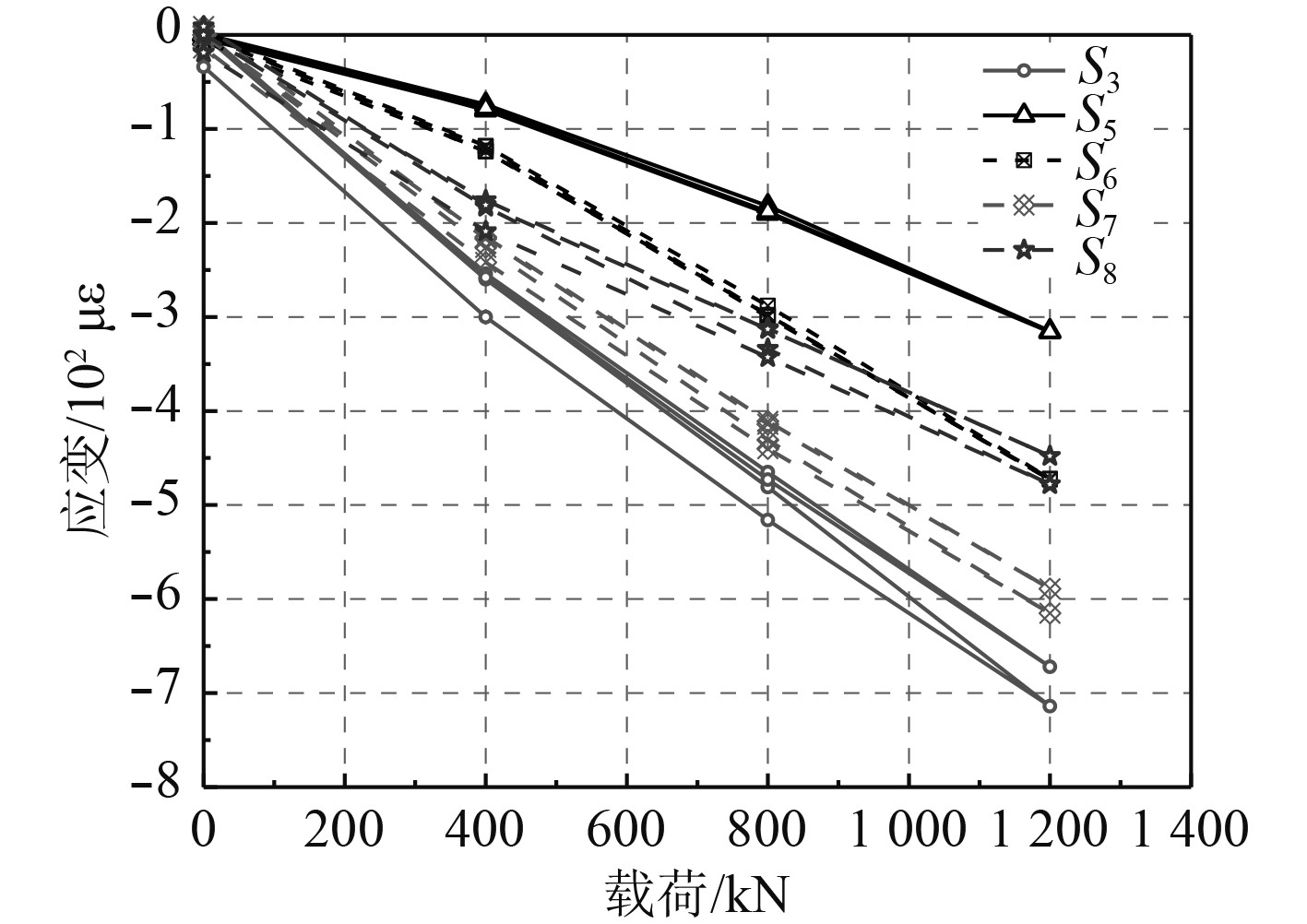
压缩载荷作用下的弹性范围内模型试验主要是通过多次的加载消除模型加载装置以及工装之间的间隙。本次试验在弹性范围内加载3次,应变曲线如图11所示。可以看出,测点的应力变化基本处于线性状态,且其加载3次前后的变化基本一致。
|
图 11 弹性状态载荷应变曲线 Fig. 11 Load-strain curve of elastic state |
图12为结构极限状态下的失效模式,图13为本次试验得到的载荷位移曲线。可以看出,模型试验中极限载荷为3200 kN。该载荷与设计阶段的4570 kN存在较大的差异,且失效部位与数值仿真结果存在差异,极限载荷差异主要因为试验模型的材料屈服极限约为310 MPa,相比于设计阶段的极限载荷355 MPa而言略小,且其撑杆外壳的板厚与理论值相比为负公差。因此,试验结果小于其设计模型结果。

|
图 12 极限状态失效模式 Fig. 12 Collaspe mode of limit state |

|
图 13 载荷-位移曲线 Fig. 13 Load-displacement curve |
为验证数值仿真方法得出结果的可靠性,采用试验模型的参数为基准,建立有限元模型,开展压缩载荷作用下的结构极限承载能力仿真计算。图14为仿真计算获得的撑杆结构失效模式,图15为仿真计算获得的压缩载荷位移曲线。可以得出撑杆结构压缩极限载荷为3435 kN,与试验结果相差7.3%左右,该数值仿真结果中尚未计及初始变形以及焊接残余应力的影响,因此,本数值仿真结果精度可以满足工程要求。

|
图 14 仿真计算失效模式 Fig. 14 Collpase mode of numerical simulation |

|
图 15 载荷-位移曲线 Fig. 15 Load-dislpacement curve |
本文对模型试验进行研究,首先开展撑杆结构模型参数设计,通过数值仿真分析验证缩比模型设计的正确性;然后,对模型相应的弹性试验及极限承载能力试验进行相应的分析,通过分析主要得出以下结论:
1)本文根据相似关系进行的模型设计合理;
2)通过弹性范围内模型试验可以发现,模型的应变为线性状态;
3)通过极限强度模型试验可以看出,整个结构的失效是由撑杆结构失效所引起的;
4)本文的分析方法可为我国第七代钻井平台撑杆结构设计优化等提供技术支撑。
| [1] |
王杰. 半潜式钻井平台甲板结构极限强度分析[D]. 镇江: 江苏科技大学, 2014. WANG Jie. Ultimate strength analysis of semi-submersible drilling platform deck structure[D]. Zhenjiang: Jiangsu University of Science and Technology, 2014. |
| [2] |
赵南. 复杂载荷作用下超大型浮体结构极限强度研究[D]. 北京: 中国舰船研究院, 2015. ZHAO Nan. Study on the ultimate strength of very large floating structure under complex loads[D]. Beijing, China Ship Research and Development Academy, 2015. |
| [3] |
赵南, 顾学康, 祁恩荣, 等. 复杂载荷作用下连接器基座加强区结构极限强度研究[J]. 船舶力学, 2018, 7(22): 854-864. ZHAO Nan, GU Xue-kang, QI En-rong, et al. Theoretical and experimental study in the ultimate strength of the VLFS connector foundation support reinforcing area structure under complex loads[J]. Journal of Ship Mechanics, 2018, 7(22): 854-864. |
| [4] |
何福志, 万正权. 船体结构总纵极限强度的简化逐步破坏分析[J]. 船舶力学, 2001, 5(5): 21-35. HE Fu-zhi, WAN Zheng-quan. A simplified progressive collapse analysis of ultimate longitudinal strength of ship structures[J]. Journal of Ship Mechanics, 2001, 5(5): 21-35. |
| [5] |
GANNON L, LIU Y, PEGG N, et al. Effect of welding-induced residual stress and distortion on ship hull girder ultimate strength[J]. Marine Structures, 2012(28): 25-49. |
| [6] |
PAIK J K, KIM B J. Progressive collapse analysis of thin-walled box columns[J]. Thin-Walled Structures, 2008(46): 541-550. |
| [7] |
AMLASHI H K K, MOAN T. Ultimate strength analysis of a bulk carrier hull girder under alternate hold loading condition-A case study Part 1: Nonlinear finite element modelling and ultimate hull girder capacity[J]. Marine Structures, 2008(21): 327-352. |
| [8] |
GU Hai-ying, FENG Jia-quan, TANG Ming-gang, et al. Study on ultimate strength of braced structure of Very Large Floating Structure[J]. Journal of Ship Mechanics, 2018, 22(7): 845-856. |
| [9] |
XU M C, SOARES C G. Comparisons of calculations with experiments on the ultimate strength of wide stiffened panles[J]. Marine Structures, 2017(31): 82-101. |
 2020, Vol. 42
2020, Vol. 42
