近年来,随着水下机器人在巡检、摄像、水下对接等场景的需求不断增长,对水下机器人位置和姿态控制的稳定性和灵活性提出了更为苛刻的要求。而在水下机器人的各种控制算法中,滑模控制具有对参数变化和系统未建模部分的不敏感性和极强的抗干扰性而成为水下机器人控制的有效方案之一[1]。在水下机器人的控制上,已有学者将滑模变结构控制应用在水下机器人的位置追踪和姿态控制上[2-5],也有学者将反演法与滑模控制结合起来,取得了良好的控制效果[6-9]。然而在实际过程中,由于受限于执行器的动作时间、饱和限制等,实际控制效果尚有待考究。因此,本文考虑输入饱和的反演滑模控制器,试图对其实际控制效果及工程应用进行进一步的探究。
1 系统建模水下机器人的建模主要包括运动学建模和动力学建模。水下机器人的目标轨迹和目标姿态需在地面坐标系下给出,而表征力和运动的动力学方程是在载体坐标系下进行的。因此运动学即表示2个坐标系下运动量的转化关系。
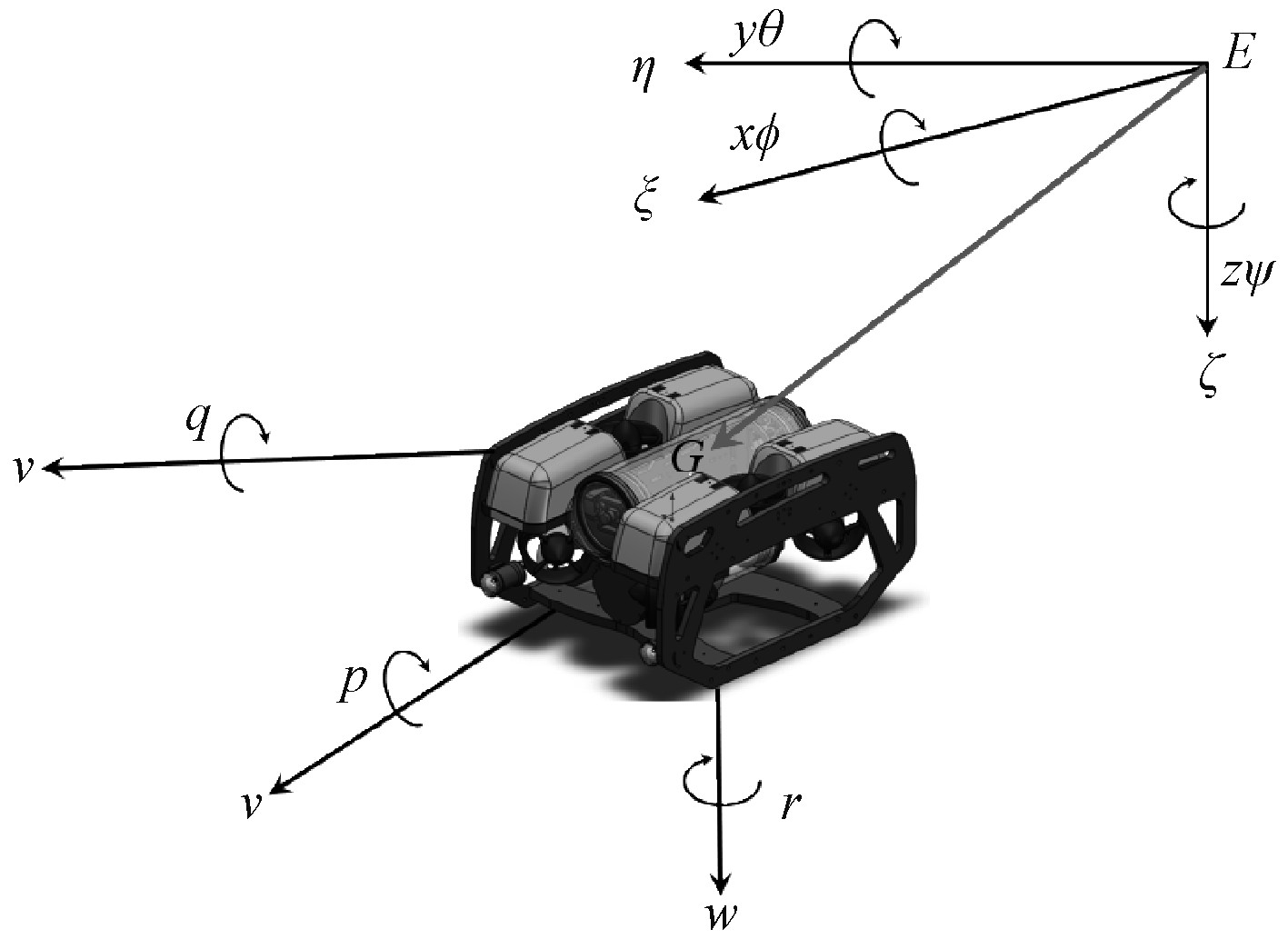
1.1 运动学建模按照国际拖曳水池(ITTC)推荐的坐标系以及轮机工程学会(SNAME)术语公报的体系[10 − 11],建立地面坐标系(E系)和载体坐标系(G系),如图1所示。
|
图 1 水下机器人的地面坐标系与载体坐标系 Fig. 1 Earth-fixed and body-fixed coordinate system |
按照特定的旋转顺序(Oζ-Oy1-Ox),则表示运动量从运载体坐标系到地面坐标系的转换矩阵可以唯一表示为:
| ${ J}(\eta )=\left[ {\begin{array}{*{20}{c}} {{{ J}_1}(\eta )}&{{0_{3 \times 3}}} \\ {{0_{3 \times 3}}}&{{{ J}_2}(\eta )} \end{array}} \right]\text{,}$ | (1) |
| ${{ J}_1}(\eta )\!\!=\!\!\left[\!\!\! {\begin{array}{*{20}{c}} {c\psi c\theta }&{c\psi s\theta s\phi - s\psi c\phi }&{c\psi s\theta +s\psi s\phi } \\ {s\psi c\theta }&{s\psi s\theta s\phi +c\psi c\phi }&{s\psi s\theta c\phi +c\psi s\phi } \\ { - s\theta }&{c\theta s\phi }&{c\theta c\phi } \end{array}}\!\!\! \right]\text{,}$ | (2) |
| $ {{ J}_2}(\eta ){\rm{=}}\left[ {\begin{array}{*{20}{c}} 1&{t\theta s\phi }&{t\theta c\phi } \\ 0&{c\phi }&{ - s\phi } \\ 0&{s\phi /c\theta }&{c\phi /c\theta } \end{array}} \right]\text{,} $ | (3) |
于是,运动学方程可以描述为:
| $\dot \eta =J(\eta )v\text{。}$ | (4) |
式中,
动力学是在运载体坐标系下描述水下机器人力和运动之间的关系。作用在航行器上的力和力矩主要包括[11 − 12]:1)航行器所受到的静力−重力和浮力;2)航行器所受到的水动力;3)推进器所产生的推力和推力矩;4)由风浪流产生的干扰力和干扰力矩。
水下机器人的动力学模型可以表示为:
| $\begin{split} {{ M}_{RB}}\dot \nu +{{ C}_{RB}}(\nu )\nu =& - {{ M}_{AM}}\dot \nu - {{ C}_{AM}}(\nu )\nu - \\ & { D}(\nu )\nu - { g}(\eta )+{\tau _E}+\tau \text{,}\\ \end{split} $ | (5) |
进一步整理可得:
| ${ M}\dot \nu +{ C}(\nu )\nu +{ D}(\nu )\nu +{ g}(\eta )={\tau _E}+\tau \text{。}$ | (6) |
式中,M=MAM+MRB,其中MRB和MAM分别为质量矩阵和附加质量矩阵;C=CRB+CAM,其中CRB和CAM分别为科氏向心力矩阵和附加向心力矩阵;D为阻尼矩阵;g(η)为恢复力矩阵;τE为慢变干扰力;τ为六自由度控制力和控制力矩。
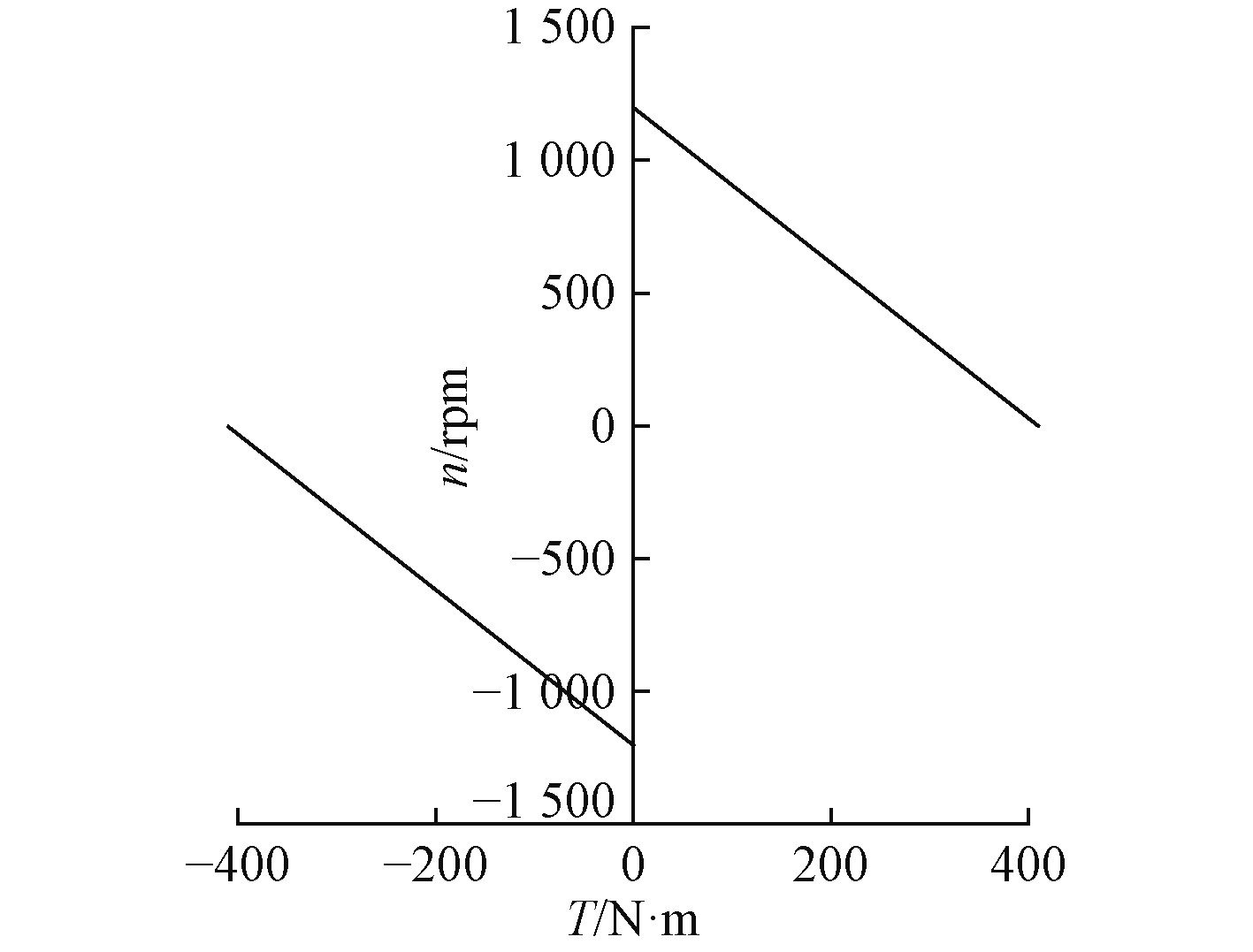
1.3 执行器建模本文中,直流电机连接螺旋桨构成水下机器人的推进器,直流电机的转速即为系统的控制输入量。直流电机机械特性的一般表达式为[13]:
| $n=\frac{U}{{{K_e}\Phi }} - \frac{{{R_a}}}{{{K_e}{K_T}{\Phi ^2}}}T\text{。}$ | (7) |
式中:U为电动机供电电源电压;Φ为磁通量;Ke为电动机的反电动势系数;Kt为转矩系数;Ra为电枢电阻;T为电动机转矩。
电动机铭牌数据为:PN=3.8 kW,UN=220 V,IN=20.6 A,nN=1100 r/min;假设额定工况下电动机的铜耗约为总损耗的50%,则由此计算可得:
1)电动机最高转速为1200 r/min;
2)电动机最大输出转矩为409 N·m;
3)电动机转速和转矩之间的关系满足:
T>0时,n=1200-2.92927*T;
T<0时,n=−1200-2.92927*T。
上述条件即为电动机的输出受限条件。
|
图 2 直流电机的固有机械特性 Fig. 2 Mechanical characteristics of DC motor |
反演法作为一种回归设计方法,将Lapunov函数的选取与控制器的设计相结合,通过采用引入虚拟控制的方式,从系统微分方程的最低阶次开始,一直后推来设计满足要求的虚拟控制,从而设计出最终的控制律,使系统达到期望的性能指标[14]。
滑模变结构控制本质上是一种非线性控制,其最大的特点是控制的不连续性。滑模控制通过切换函数来实现非线性控制,根据系统状态偏离滑模的程度来切换控制器参数,从而使系统状态按照滑模规定的“滑动模态”轨迹运行的控制方法。滑模控制具有物理实现简单,对系统参数变化不敏感无需在线辨识,抗外界干扰的优点[15]。
将反演法与滑模控制相结合,并考虑控制器的输出饱和,控制器的设计步骤如下:
1)定义位置误差函数z1和角度误差函数z2
| ${z_1}={\eta _d} - \eta\text{,} $ | (8) |
| ${z_2}=\nu - \alpha\text{,} $ | (9) |
式中:ηd为目标位置;η为实际位置;ν为实际速度;α为虚拟控制量,可以看做是ν的估计值,α的取值将直接影响系统的稳定性,此处选取
2)定义Lyapunov函数V1和V2
| ${V_1}=\frac{1}{2}z_1^{\rm T}{z_1}\text{,}$ | (10) |
对V1求导可得:
| ${\dot V_1}=z_1^{\rm T}{\dot z_1}=z_1^{\rm T}(\dot \eta - {\dot \eta _d})=z_1^{\rm T}(J(\eta )v - {\dot \eta _d})\text{,}$ | (11) |
为使
| ${V_2}={V_1}+\frac{1}{2}z_2^{\rm T}M{z_2}\text{,}$ | (12) |
由于质量矩阵M正定,故V2正定,对V2求导可得:
| $\begin{split} {{\dot V}_2}= & {{\dot V}_1}+z_2^{\rm T}{ M}{{\dot z}_2}={{\dot V}_1}+z_2^{\rm T}M(\dot v - \dot \alpha )= \\ & z_2^{\rm T}(\tau +{\tau _E} - { g}(\eta ) - { D}(v)v - { C}(v)v+{J^{\rm T}}{z_1})+ \\ & z_2^{\rm T}{ M}\dot \alpha - z_1^{\rm T}{z_1}\text{,} \\ \end{split} $ | (13) |
3)设计滑模面s=z2
为保证
| $\begin{split} \tau =& - {J^{\rm T}}{z_1} - { M}\dot \alpha - {\tau _E}+{ g}(\eta )+{ D}(\nu )\nu + \\ &{ C}(\nu )\nu - \chi sat({z_2}) \text{。} \end{split} $ | (14) |
式中,
| ${\rm {sat}}(s)=\left\{ \begin{array}{l} \begin{array}{*{20}{c}} {} \end{array}1,\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}s>\Delta \\ s\dfrac{1}{\Delta },\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}|s| \leqslant \Delta ,\begin{array}{*{20}{c}} {} \end{array}\Delta \in R,\begin{array}{*{20}{c}} {} \end{array}\Delta >0 \\ - 1,\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}\begin{array}{*{20}{c}} {} \end{array}s< - \Delta \\ \end{array} \right.\text{。}$ | (15) |
控制对象采用框架式水下机器人KAMBARA,其质量为117 kg,浮力为1158 N;以重心G为运载体坐标系原点,浮心的坐标为rb=[-0.017,0,-0.015]T,其他模型参数如下:
| $ \begin{split} & {M_{RB}} = {\rm diag}\{ 117,117,117,117,117,117\} \text{,} \\ & {M_{AM}} = {\rm diag}\{ 58.4,23.8,23.8,3.38,1.18,2.67\} \text{,} \\ & D(v) = {\rm diag}\{ 120 + 90|u|,90 + 90|v|,150 + 120|w|, \\ & \quad \quad \quad 15 + 10|p|,15 + 12|q|,18 + 15|r|\} \text{。} \end{split} $ |
在原有模型的基础上增加一个侧向推进器,从而使其成为全驱动水下机器人,其推力布置矩阵如下式[12]:
| $ { B}=\left[ {\begin{array}{*{20}{c}} 1&1&0&0&0&0 \\ 0&0&0&0&0&1 \\ 0&0&{ - 1}&{ - 1}&{ - 1}&0 \\ 0&0&{ - 0.28}&{0.28}&0&{0.05} \\ { - 0.05}&{ - 0.05}&{ - 0.32}&{ - 0.32}&{0.43}&0 \\ {0.47}&{ - 0.47}&0&0&0&0 \end{array}} \right]\text{。} $ |
设定六自由度水下机器人的初始状态和目标状态,如表1所示。
|
|
表 1 目标轨迹、姿态与初始状态设定 Tab.1 Target trajectory,attitude and initial state |
反演滑模控制器中,∆取0.05,
在输入饱和的情况下,可以看到:在x,y方向的位置跟踪上,输入饱和的反演滑模控制器能够从初始位置迅速跟踪上目标轨迹,并且保持高精度跟随;在z方向上,从初始位置跟踪至目标轨迹的时间稍长于x,y方向,但在经过初始调整阶段后依然能保持高精度的跟踪。

|
图 3 输入饱和控制器的位置跟踪效果 Fig. 3 Input saturation controller path tracking results |
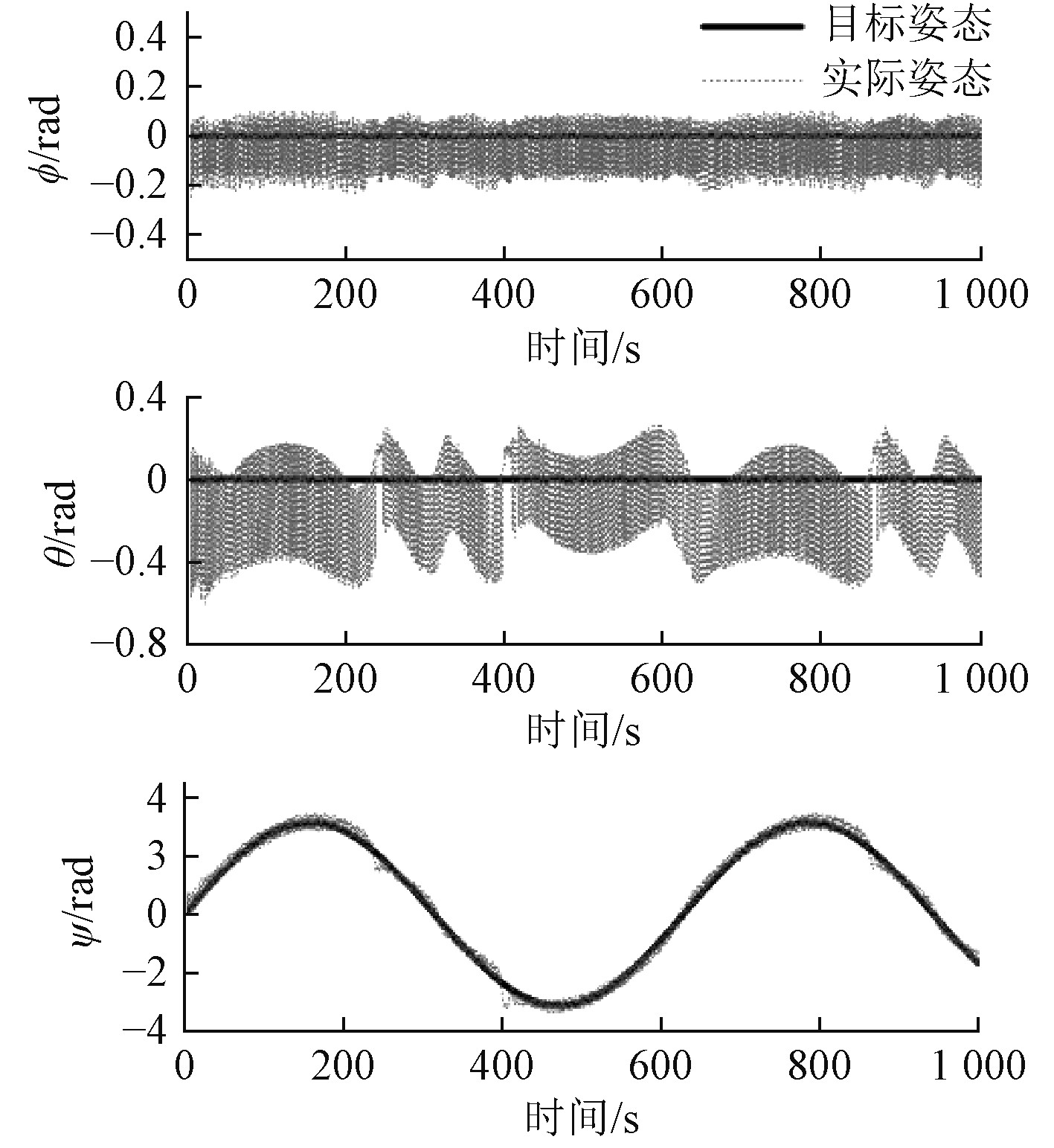
在姿态跟踪上,由推力布置矩阵B可知,角度的控制至少由3个推进器耦合协同完成,由于强耦合关系使得ϕ,θ,ψ的控制精度逊色于位置控制。但从工程角度讲,ϕ的平均偏差约为0.05 rad,最大偏差约为0.2 rad;ψ的平均误差约为0.02 rad/s,已经满足大多数场合的控制要求;θ的偏差较大的原因在于:θ由5个推进器协同控制,存在着强耦合关系,后续可以尝试改进KAMBARA的推进器布置以得到更高的控制精度。
|
图 4 输入饱和控制器的姿态控制结果 Fig. 4 Input saturation controller attitude control results |
最终的控制量为直流电机的转速,在输入受限的条件下,6个推进器对应的直流电机的转速曲线中,第1,2,6号电机存在着明显的阶段特征,而第3,4,5号电机则持续性地在转速上下限之间变动;从推力分配矩阵B的系数来看,第1,2,6号电动机在同时影响水下机器人多个自由度的运动时,均有明显的主次之分,而第3,4,5号电动机的对六自由度的运动影响权重区别并非十分明显,因此造成了频繁的抖动。

|
图 5 直流电机的速度曲线 Fig. 5 Speed curve of DC motor |
在实际工程应用中,由于推进电机不能超越最大转速,且转速不能突变,因而实际控制力并不能达到理想效果。而根据上述计算分析表明,在考虑执行器输入饱和的情况下,若推力布置合理,反演滑模控制方法在水下机器人的轨迹跟踪和姿态控制上依然能够得到较好的结果,从而验证了该理论方法的实际可行性。同时可以推断出所选电机的动力响应越迅速,越能满足实际工程需求;针对精度需求十分高的场合,可以尝试优化推进器的分布,尽量消除推进器之间的耦合关系,使得单一推进器影响尽量少的自由度运动。
| [1] |
戴学丰, 边信黔. 6自由度水下机器人运动轨迹滑模控制[J]. 计算技术与自动化, 2000(02): 68-71. DOI:10.3969/j.issn.1003-6199.2000.02.017 |
| [2] |
邓威. 带缆遥控水下机器人三维运动滑模控制研究[D]. 广州: 华南理工大学, 2011.
|
| [3] |
史文韬. 基于DSP的水下机器人嵌入式控制系统设计[D]. 哈尔滨: 哈尔滨工程大学, 2010.
|
| [4] |
梁凇. 水下检测与作业机器人ROV控制系统研制及动力定位研究[D]. 镇江: 江苏科技大学, 2017.
|
| [5] |
徐璐瑜. 智能水下机器人运动规划研究[D]. 镇江: 江苏科技大学, 2014.
|
| [6] |
肖涛. 基于Backstepping方法的水下机器人自适应滑模控制技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2009.
|
| [7] |
尹强. 基于反演滑模的欠驱动AUV的路径跟踪控制研究[D]. 大连: 大连海事大学, 2016.
|
| [8] |
万磊, 崔士鹏, 张国成, 等. 欠驱动水下机器人航迹跟踪控制[J]. 电机与控制学报, 2013, 17(02): 103-111. DOI:10.3969/j.issn.1007-449X.2013.02.016 |
| [9] |
崔士鹏. 微小型水下机器人运动控制[D]. 哈尔滨: 哈尔滨工程大学, 2013.
|
| [10] |
国际船模试验池会议船舶水动力学辞典[M]. 北京: 中国造船编辑部, 1981.
|
| [11] |
严浙平, 周佳加. 水下无人航行器控制技术[M]. 北京: 国防工业出版社, 2015.
|
| [12] |
高剑. 无人水下航行器自适应非线性控制技术[M]. 西安: 西北工业大学出版社, 2016.
|
| [13] |
周永鹏, 李浚元, 秦忆. 电力拖动基础[M]. 武汉: 华中科技大学出版社, 2004.
|
| [14] |
胡跃明. 非线性控制系统理论与应用[M]. 北京: 国防工业出版社, 2001.
|
| [15] |
王康玲. 不确定参数条件下水下机器人的定深和轨迹跟踪控制方法研究[D]. 济南: 山东大学, 2018.
|
| [16] |
乔继红. 反演控制方法与实现[M]. 北京: 机械工业出版社, 2011.
|
 2020, Vol. 42
2020, Vol. 42
