2. 江苏海洋大学 机械与海洋工程学院,江苏 连云港 222002;
3. 江苏科技大学 海洋装备研究院,江苏 镇江 212000
2. The Department of Mechanical and Ocean Engineering of Jiangsu Ocean University, Lianyungang 222002, China;
3. Institute of Marine equipment, Jiangsu University of Science and Technology, Zhenjiang 212000, China
水下机器人(Underwater Vehicle)主要分为有缆水下机器人(Remotely Operated Vehicle,ROV)和自治水下机器人(Autonomous Underwater Vehicle,AUV)。作为一种探索海洋的智能工具,水下机器人在水产养殖、水下石油勘探、大巴检测以及军事等领域扮演着重要的角色[1-2]。但由于外部水流的干扰,以及自身各刚体间的耦合,水下机器人难以稳定地在水下进行运动,因此,对于水下机器人控制系统的研究至关重要[3-5]。
为有效控制水下机器人的运动,目前许多控制方法被使用,如自适应控制[6-8]、滑模控制[9-11]、模糊控制[12-13]、欠驱动控制[14]等。其中,欠驱动控制可以有效地控制水下机器人的运动,同时减少推进器的数量,降低能耗,但这种控制方法极为复杂,一般都是通过消除非线性项来解决,这会严重降低系统的鲁棒性[15]。
作为一种非线性控制方法,滑模控制具有结构简单、响应快速、鲁棒性强以及对外界干扰不灵敏等特点[16],备受广大研究人员青睐。但经典滑模控制方法存在严重抖动问题,对于水下机器人而言,这会导致推进器能量消耗过大,甚至损坏推进器[17]。因此,如何解决抖动问题成为近几年滑模控制研究的焦点。
经典滑模控制中的抖动,主要是由于控制规律中不连续的切换控制项引起的。针对这一问题,Soylu等[18]提出一种无抖动滑模控制方法,其方法主要是设计自适应控制项代替不连续的切换控制项,自适应控制项可以持续补偿系统模型不确定影响,从而消除抖动。但这种方法较为复杂,控制参数设置较多,在实际中难以实现;Liu等[19]提出了一种全局滑模控制方法,采用饱和函数替代了常用的符号函数。这种方法简单有效,但设计时并未考虑水下机器人模型不确定因素的影响;Huang等[20]采用了双闭环滑模控制方法,用以提高ROV运动时地抗干扰能力,在减小滑模控制抖动问题方面,则是通过设计一种连续的函数作为切换控制项。但此方法同样未考虑ROV模型不确定因素的影响。
为了解决经典滑模控制中的抖动问题以及ROV运动时地模型参数不确定性问题,本文针对一类小型观测级ROV的四自由度运动,提出一种基于径向基函数神经网络(Radial Basis Function Neural Network,RBFNN)自适应滑模控制方法。针对ROV运动时模型不确定因素的干扰问题,采用RBF神经网络算法,实现对ROV模型的补偿;用反正切函数替换符号函数,减小了经典滑模控制的抖动。
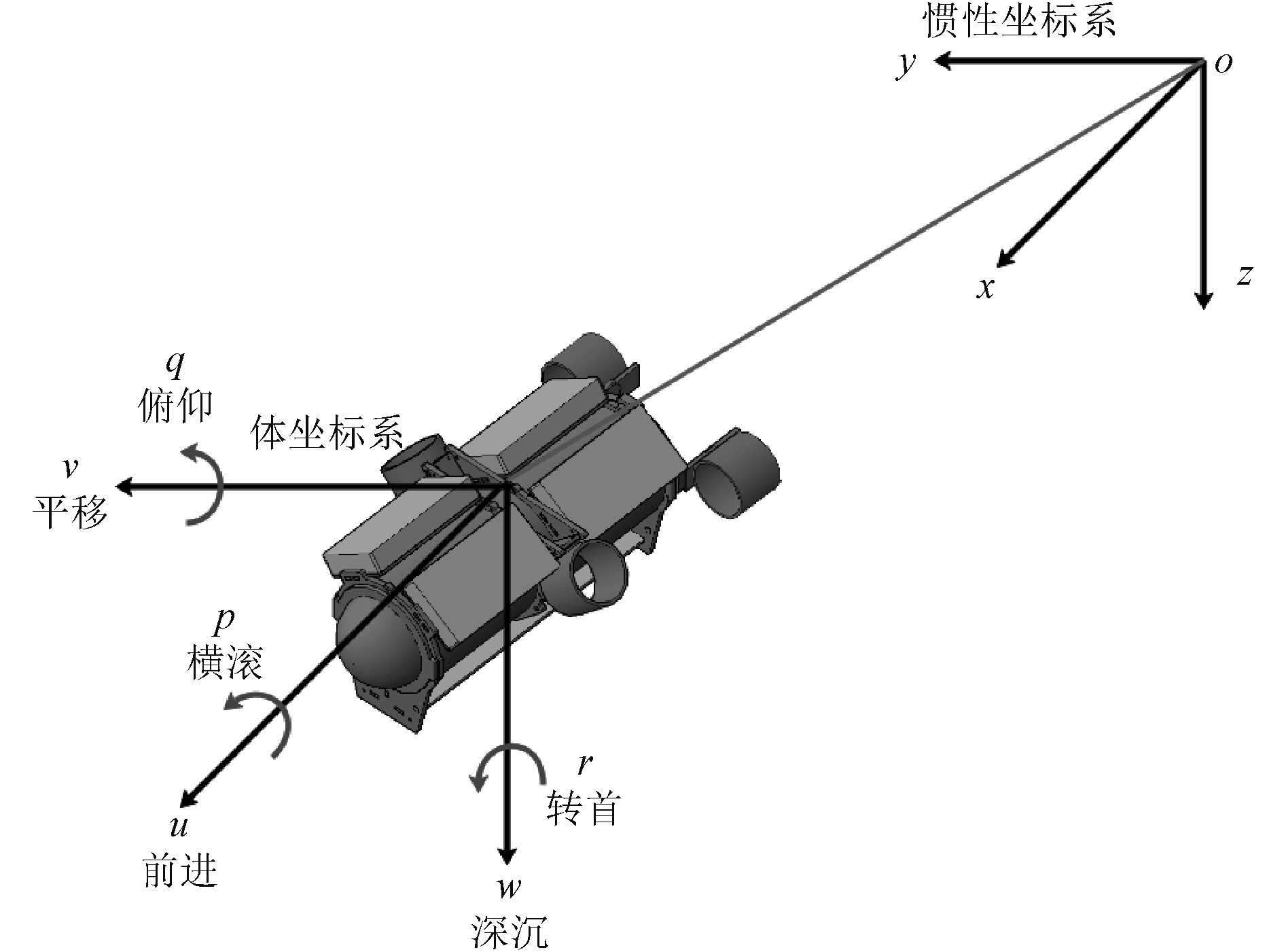
1 ROV模型数学描述 1.1 ROV运动学模型本文针对一类小型观测级ROV进行设计,这类ROV一般配备4个推进器,主要实现前后、平移、深沉和转首四自由度的运动,如图1所示。
|
图 1 小型观测级ROV模型 Fig. 1 The model of small monitoring ROV |
在ROV中,通常采用惯性坐标系(Inertial frame)和体坐标系(body-fixed frame)来描述ROV的运动。相对于体坐标系的速度向量可以表示为νT=[ν1 ν2],其中,ν1T=[u v w]代表ROV的线速度向量,u,v,w分别为前进、平移、深沉3个方向的速度;v2T=[p q r]为ROV角速度向量,p,q,r分别代表横倾、俯仰、转首3个方向的速度。相对惯性坐标系的位姿向量表示为ηT=[η1 η2],其中,η1T=[x y z]表示ROV在惯性坐标系中的运动位置向量,x,y,z分别为前进、平移、深沉3个方向的位置;η2T=[φ θ ψ]表示ROV在惯性坐标系中的运动姿态向量,φ,θ,ψ分别代表横倾、俯仰、转首3个方向的姿态。速度向量与位姿向量的转换可以写为如下形式:
| $\dot \eta = J(\eta )\nu\text{,} $ | (1) |
其中,J(η)为雅可比矩阵,定义为:
| ${ {J}}({ {\eta}} ) = \left[ {\begin{array}{*{20}{c}} {{J_1}(\eta )}&{{0_{3 \times 3}}} \\ {{0_{3 \times 3}}}&{{J_2}(\eta )} \end{array}} \right]\text{,}$ | (2) |
式中,J1(η)和J2(η)分别定义为:
| $\begin{split}{J_1}(\eta ) = & \left[ {\begin{array}{*{20}{c}} {\cos \psi }&{ - \sin \psi \cos \varphi + \cos \psi \sin \theta \sin \varphi }&\\ {\sin \psi \cos \theta }&{\cos \psi \cos \varphi + \sin \varphi \sin \theta \sin \psi }&\\ { - \sin \theta }&{\cos \theta \sin \varphi }& \end{array}} \right. \\ & \left. \begin{array}{l} \sin \psi \sin \varphi + \cos \psi \cos \varphi \sin \theta \\ - \cos \psi \sin \varphi + \sin \theta \sin \psi \cos \varphi \\ \cos \theta \cos \varphi \end{array} \right]\text{,}\\[-25pt]\end{split}$ | (3) |
| ${J_{\rm{2}}}(\eta ) = \left[ {\begin{array}{*{20}{c}} {\rm{1}}&{\sin \varphi \tan \theta }&{\cos \varphi \tan \theta } \\ 0&{\cos \varphi }&{ - \sin \varphi } \\ 0&{\sin \varphi /\cos \theta }&{\cos \varphi /\cos \theta } \end{array}} \right]\text{。}$ | (4) |
因为本文只讨论ROV前后、平移、深沉和转首4个自由度的运动,所以横倾角φ和俯仰角θ的变化都为0。因此,式(1)可以写为:
| $\left[ {\begin{array}{*{20}{c}} x \\ y \\ z \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \psi }&{ - \sin \psi }&0&0 \\ {\sin \psi }&{\cos \psi }&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} u \\ v \\ w \\ r \end{array}} \right]\text{。}$ | (5) |
针对四自由度的ROV,其动力学模型表示为[21]:
| $ {{M}}\dot \nu + {{C}}(\nu )\nu + {{D}}(\nu )\nu + g(\eta ) = \tau + {\tau _d}\text{,} $ | (6) |
式中,M∈R4×4为惯性矩阵,定义为:
| $M = {\rm{diag}}\{\!\! \begin{array}{*{20}{c}} {m - {X_{\bar u}},}&{m - {Y_{\bar v}},}&{\begin{array}{*{20}{c}} {m - {Z_{\bar w}},}&{{I_z} - {N_{\bar r}}} \end{array}} \!\! \end{array}\} \text{,}$ | (7) |
其中:m为ROV质量;Iz为ROV关于Z轴的转动惯量;
C(v)∈R4×4为科氏力和向心力矩阵,定义为:
| ${{C}}(\nu ) = \left[ {\begin{array}{*{20}{c}} 0&0&0&{ - (m - {Y_{\bar v}}v)} \\ 0&0&0&{ - (m - {X_{\bar u}}u)} \\ 0&0&0&0 \\ { - (m - {Y_{\bar v}}v)}&{ - (m - {X_{\bar u}}u)}&0&0 \end{array}} \right]\text{,}$ | (8) |
D(v)∈R4×4为阻尼系数矩阵,定义为:
| $ \begin{split} {{D}}(\nu ) =& - {\rm{diag}}\{ {{X_u} + {X_{u\left| u \right|}}\left| u \right|,}\qquad{{Y_v} + {Y_{v\left| v \right|}}\left| v \right|,}\\ & {{Z_w} + {Z_{w\left| w \right|}}\left| w \right|,}\qquad{{N_r} + {N_{r\left| r \right|}}\left| r \right|} \}\text{。} \end{split}$ | (9) |
其中:
g(η)∈R4为ROV恢复力和力矩向量,定义为:
| $g(\eta ) = \left[ {\begin{array}{*{20}{c}} 0 \\ 0 \\ { - (W - {W_B})} \\ 0 \end{array}} \right]\text{。}$ | (10) |
其中:W,WB分别为ROV的重心和浮心。
τ∈R4和τd∈R4分别为ROV的控制输入以及外部干扰。
根据式(1)和式(6),ROV的动力学模型可以改写为:
| ${{{M}}_\eta }(\eta )\ddot \eta + {{{C}}_\eta }(\nu ,\eta )\dot \eta + {{{D}}_\eta }(\nu ,\eta )\dot \eta + {g_\eta }(\eta ) = {\tau _T} + d\text{。}$ | (11) |
式中:
为了便于后面部分ROV的稳定性分析,假设ROV的动力学模型具有如下性质:
性质1 惯性矩阵Mη(η)为正定对角矩阵,即
性质2 矩阵
在经典滑模控制器设计中,首先设计一个滑模函数S,然后再设计一个控制规律τ。当系统的状态轨迹在外部干扰下偏离滑模面时,控制规律会迫使系统的状态轨迹重新沿着滑模面向平衡点运动。
针对四自由度ROV系统,定义ROV的期望位姿为
| $S = {\dot {\tilde \eta}} + \Lambda \tilde \eta \text{,}$ | (12) |
其中,S∈R4,Λ=diag{k1, k2, k3, k4},ki>0且ki为常数,i=1,
一般情况下,滑模控制规律设计为:
| ${\tau _T} = {\tau _{eq}} + {\tau _{sw}}\text{,}$ | (13) |
其中,τeq为等效控制项,τsw为切换控制项。等效控制项用于补偿系统模型。切换控制项则是为了提高系统的抗干扰能力,一般设计为τsw=−Ksgn(S),其中K为常数且K>0,sgn(·)代表符号函数。
对滑模函数求1阶导数:
| $\dot S = {\ddot{\tilde \eta}} + \Lambda {\dot{\tilde \eta}} \text{,}$ | (14) |
结合等式(11)、等式(12)和等式(14)可得:
| $\begin{split} {{{M}}_\eta }\dot S = & - {{{C}}_\eta }S - {{{D}}_\eta }S + {{{M}}_\eta }({\ddot \eta _d} + \Lambda {\dot{\tilde \eta}} ) + {{{C}}_\eta }({\dot \eta _d} + \Lambda \tilde \eta ) + \\ & {{{D}}_\eta }({\dot \eta _d} + \Lambda \tilde \eta ) + {g_\eta } - {\tau _T} - d\text{,} \end{split}$ | (15) |
如果ROV系统动力学模型中各参数都是不变的,则式(15)中控制规律τT可设计为:
| $\begin{split}{\tau _T} = & {{{M}}_\eta }({\ddot \eta _d} + \Lambda {\dot{\tilde \eta}} ) + {{{C}}_\eta }({\dot \eta _d} + \Lambda \tilde \eta ) + {{{D}}_\eta }({\dot \eta _d} + \Lambda \tilde \eta ) + \\ & {g_\eta } + {K_d}S - K{\rm{sgn}} (S)\text{。}\end{split}$ | (16) |
其中,Kd为常数。
然而在实际应用中,由于ROV自身的非线性特性以及环境的影响,ROV系统动力学模型中的各参数是变化的,因此经典滑模控制方法并不能有效实现ROV的运动控制。
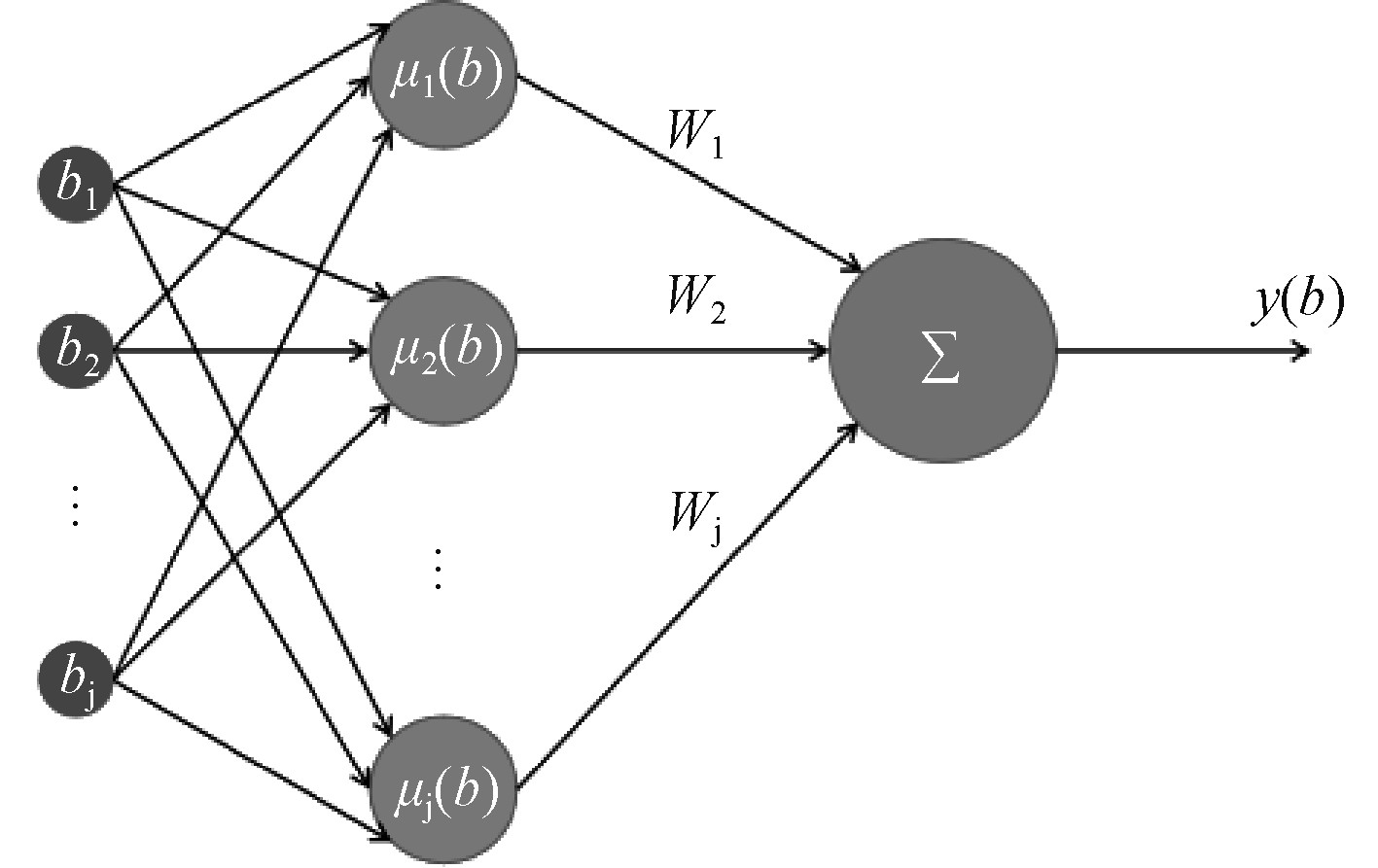
2.2 RBF神经网络自适应滑模控制器设计为解决ROV模型参数不确定性问题,目前神经网络算法被广泛使用。然而,传统的神经网络算法收敛速度慢,并不适用于实时的在线计算,如BP(Back Propagation)神经网络算法。RBF神经网络作为一种前馈式网络,具有结构简单,训练速度快等优点。因此,本文将采用RBF神经网络算法解决ROV模型不确定性问题。RBF神经网络算法逼近公式为:
| $y(b) = {W^{ * {\rm{T}}}}\mu (b) + \varepsilon \text{。}$ | (17) |
其中:b∈Rj是输入向量;W*∈Rj是网络的最优权值向量;μ(b)代表径向基函数,μ(b)=[μ1(x)μ2(x)
|
图 2 RBF神经网络结构图 Fig. 2 The structure diagram of RBF neural network |
根据式(15),定义ROV模型不确定项为:
| $y(b) = {{{M}}_\eta }({\ddot \eta _d} + \Lambda {\dot{\tilde \eta}} ) + {{{C}}_\eta }({\dot \eta _d} + \Lambda \tilde \eta ) + {{{D}}_\eta }({\dot \eta _d} + \Lambda \tilde \eta ) + {g_\eta }\text{,}$ | (18) |
则本文中神经网络结构输入层节点有4个,表示为
| ${\mu _j}(b) = \exp ( - \frac{{{{\left\| {b - {C_j}} \right\|}^2}}}{{2{B^2}_j}}),\begin{array}{*{20}{c}} {}&{j = 1,\cdots,4} \end{array}\text{。}$ | (19) |
其中,Cj和Bj分别为高斯函数的中心和宽度。
定义RBF神经网络对ROV模型不确定项逼近函数为:
| $\hat y(b) = {\hat W^{\rm{T}}}\mu (b) + \varepsilon \text{,}$ | (20) |
式中,
| ${\dot{\hat W}} = \mu (b){S^{\rm{T}}}\text{。}$ | (21) |
在本文中,将RBF神经网络部分作为等效控制项。此外,用反正切函数arctan(·)替换切换控制项中的符号函数sgn(·),则ROV的控制规律设计为:
| ${\tau _T} = {\hat W^{\rm{T}}}\mu (b) - {K_d}S - K\arctan (S)\text{。}$ | (22) |
RBF神经网络自适应滑模控制的框图如图3所示。

|
图 3 RBF神经网络自适应滑模控制框图 Fig. 3 Block diagram of RBF neural network based adaptive sliding mode control |
考虑引入控制规律
| $V(S,\tilde W) = \frac{1}{2}{S^{\rm{T}}}{{{M}}_\eta }S + \frac{1}{2}{\left\| {\tilde W} \right\|^2}\text{,}$ | (23) |
对Lyapunov函数求导,并将式(15)代入得:
| $\begin{split} \frac{{{\rm d}V(S,\tilde W)}}{{{\rm d}t}} = & {S^{\rm{T}}}[ - {{{C}}_\eta }S - {{{D}}_\eta }S + \hat y(b) - d - {\tau _T}] + \\ & \frac{1}{2}{S^{\rm{T}}}{\dot {{M}}_\eta }S - {\tilde W^{\rm{T}}}{\dot{\hat W}}\text{,} \end{split}$ | (24) |
将控制规律式(22)代入,则式(24)可写为:
| $ \begin{split} &\frac{{{\rm d}V(S,\tilde W)}}{{{\rm d}t}} = \frac{1}{2}{S^{\rm{T}}}({\dot {{M}}_\eta } - {{{C}}_\eta })S - {S^{\rm{T}}}{{{D}}_\eta }S - {S^{\rm{T}}}{K_d}S +\\ & \;\;\;\;\;\;\;\;{\tilde W^{\rm{T}}}[\mu (b){S^{\rm{T}}} - {\dot{\hat W}}] + {S^{\rm{T}}}[\varepsilon - d - K\arctan (S)]\text{。} \end{split} $ | (25) |
将自适应规律式(21)代入,并根据性质2,等式可以简化为:
| $\frac{{{\rm d}V(S,\tilde W)}}{{{\rm d}t}} = - {S^{\rm{T}}}{{{D}}_\eta }S - {S^{\rm{T}}}{K_d}S - K\left\| S \right\| - {S^{\rm{T}}}(\varepsilon - d)\text{。}$ | (26) |
其中,外界干扰
为验证本文提出的RBF神经网络自适应滑模控制器能有效控制四自由度ROV的运动,采用Matlab/Simulink软件进行仿真实验,比较RBF神经网络自适应滑模控制器与切换控制项分别为符号函数sgn(·)、饱和函数sat(·)的滑模控制器的性能。ROV的水动力参数如表1所示。
|
|
表 1 ROV水动力参数表 Tab.1 Hydrodynamic parameters of the ROV |
实验中,设定仿真时间t=60 s,选择cos(·)余弦函数作为外部干扰,ROV的初始位姿与期望位姿如表2所示。
|
|
表 2 ROV初始位姿与期望位姿 Tab.2 Initial position and desired position of the ROV |
仿真结果如图4~图8所示。其中,图4为RBF神经网络对ROV模型不确定项的逼近,图中虚线代表目标函数,实线代表逼近函数。可以看出,RBF神经网络可以有效地逼近ROV模型的不确定项,逼近误差大约在0.312~0.667,如表3所示。
|
|
表 3 RBF神经网络逼近误差 Tab.3 The approximation errors of RBF neural network |

|
图 4 RBF神经网络逼近ROV模型不确定项 Fig. 4 The RBF neural network approximates the ROV model uncertainties |
|
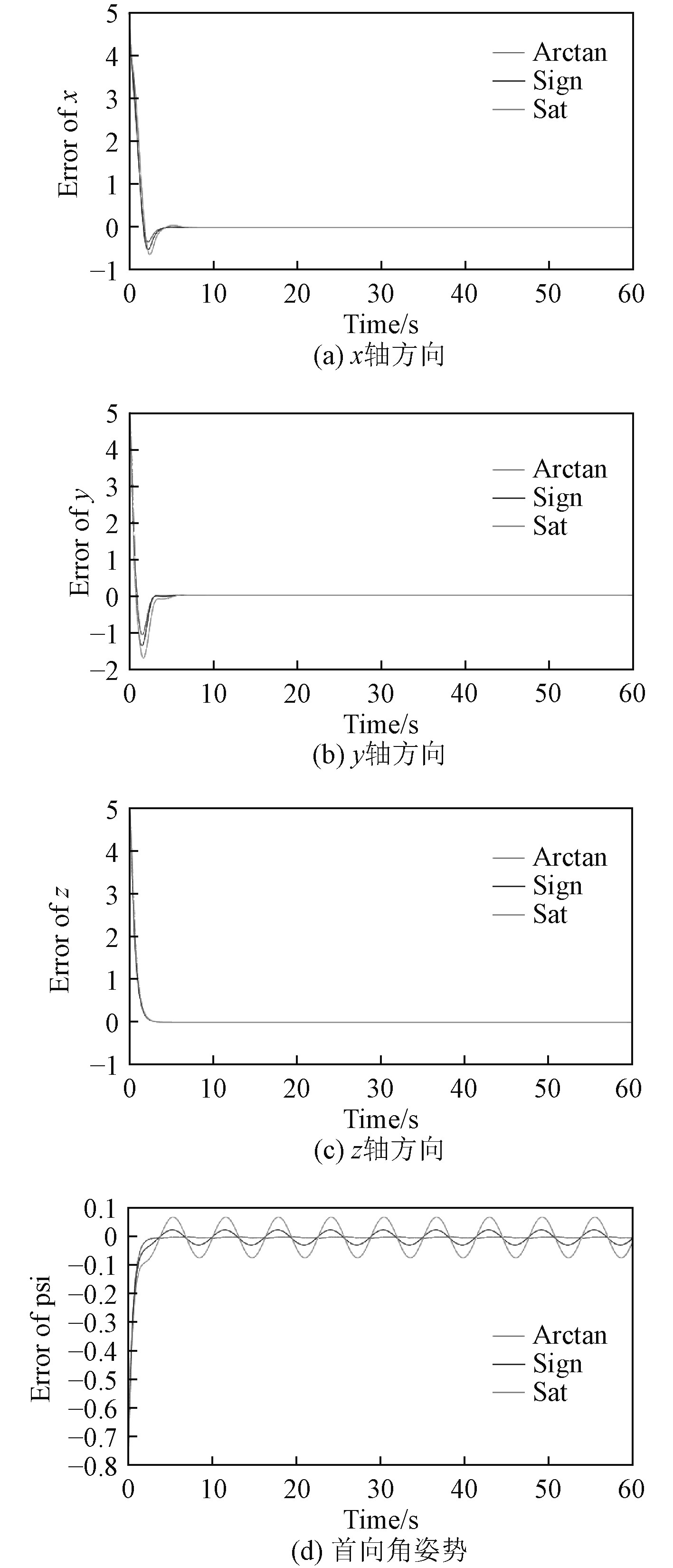
图 8 ROV位姿轨迹跟踪误差 Fig. 8 Tracking errors of ROV position and attitude |
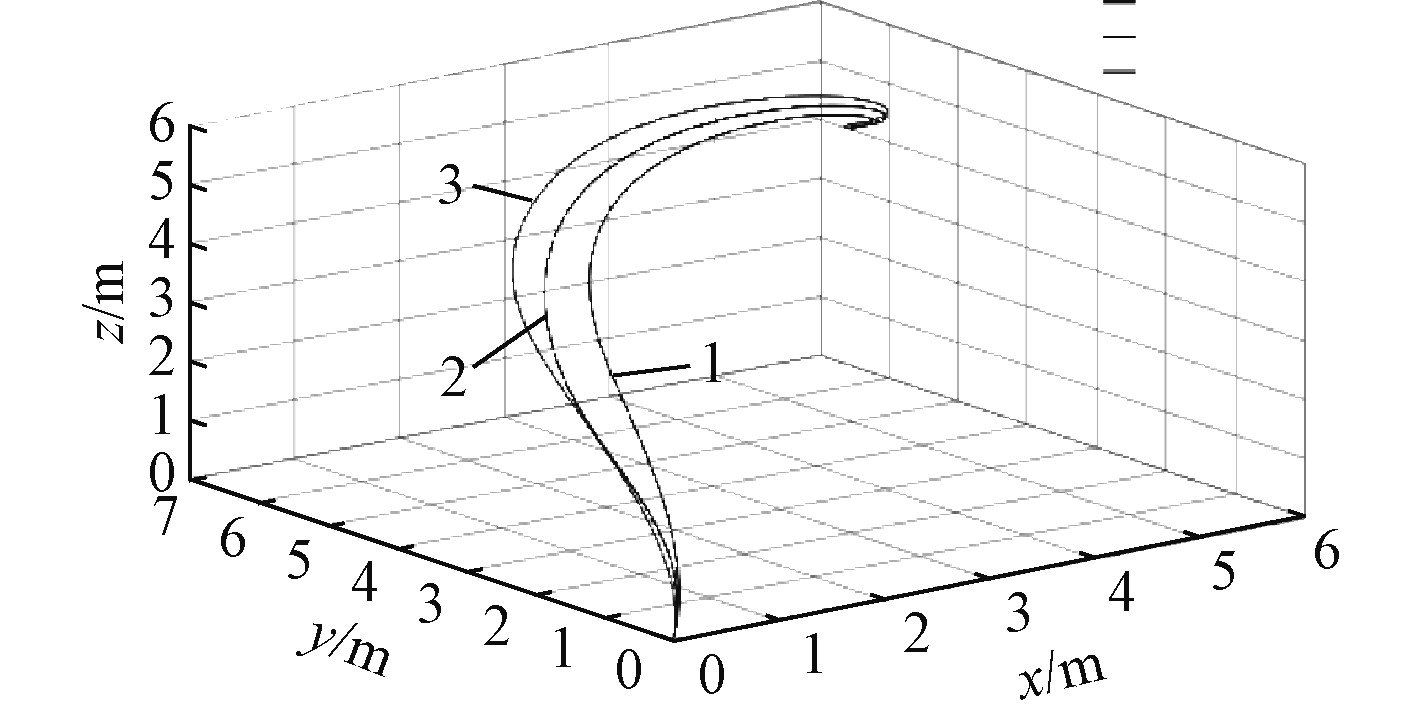
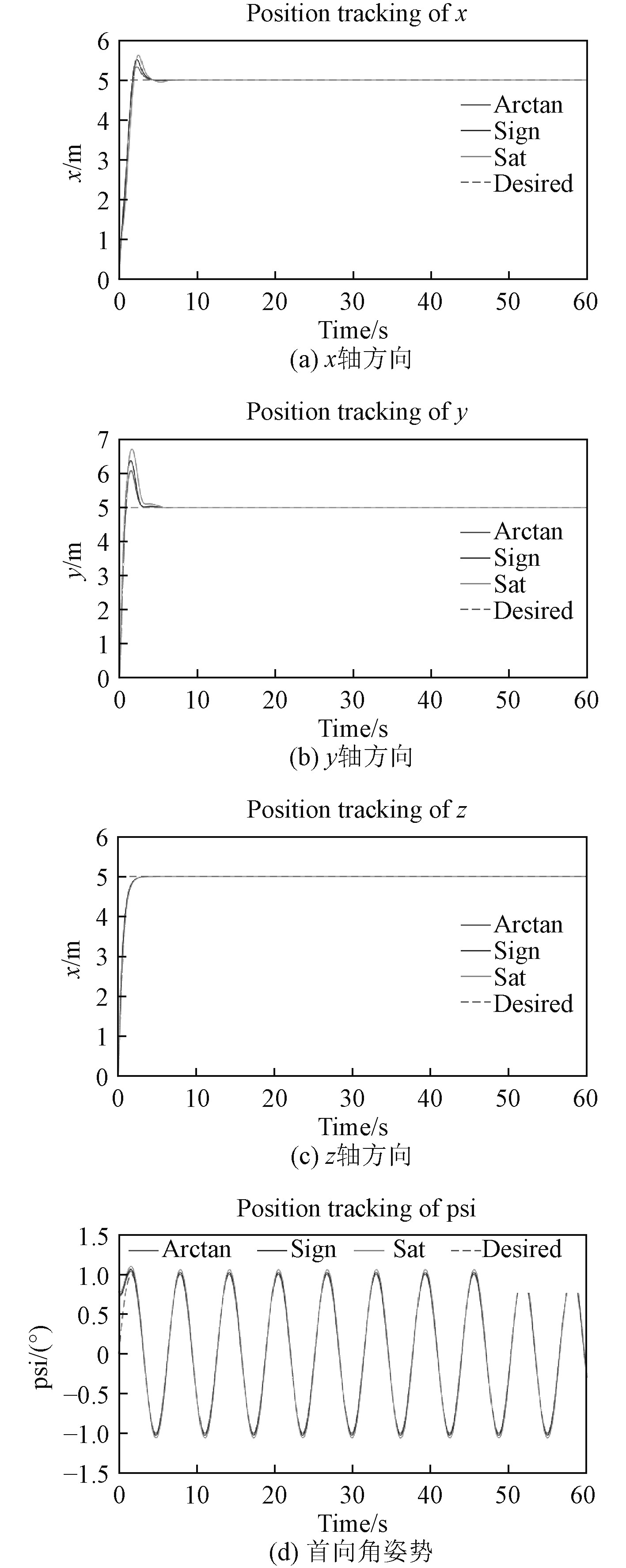
为了便于比较分析,图5~图8使用3条曲线代表各控制方法的仿真结果。其中,曲线1代表本文提出的控制方法,曲线2和曲线3分别代表切换控制项为sgn(·)和sat(·)的滑模控制。
|
图 5 ROV三维轨迹跟踪 Fig. 5 Position tracking results of ROV in xyz plot |
图5为ROV在3种控制方法下的三维运动轨迹。可以看出,在3种控制方法下,ROV都可以运动到期望位姿,但采用RBF神经网络自适应滑模控制的ROV运动效果更好,抗干扰能力更强。ROV的相轨迹图如图6所示。可以看出,ROV在采用切换控制项为sgn(·)的滑模控制方法时,相轨迹图存在着明显的抖动,在采用切换控制项为sat(·)的滑模控制方法时,在x,y,z轴方向上的相轨迹图都较为平滑,并最终都趋近于稳定点,但在对转首角的控制上,却出现了极限环,这是不允许的,如图6(d)所示。在采用RBF神经网络自适应滑模控制方法时,ROV的相轨迹都较为平滑,并且最终都趋近于稳定点。图7为ROV四自由度的轨迹跟踪图。由图7(a)~图7(c)可以看出,3种控制方法均可快速的跟踪到目标轨迹,但在x轴和y轴方向上,RBF神经网络自适应滑模控制方法的超调量小于其他2种控制方法。在转首角姿态上,RBF神经网络自适应滑模控制方法几乎0误差跟踪ROV的运动轨迹,而其他2种方法都存在着误差,如图7(d)所示。ROV的轨迹跟踪误差如图8所示。从图8(d)可以看到,在转首姿态上,切换控制项为sgn(·)的滑模控制方法的跟踪误差在0.03左右,切换控制项为sat(·)的滑模控制方法的跟踪误差在0.07左右。因此,综合上述实验结果,可以证明本文提出的RBF神经网络自适应控制方法具有很好的综合性能,有效地减小了经典滑模控制的抖动问题以及解决了ROV模型不确定性问题,能够实现控制ROV在外部干扰下稳定地运动。

|
图 6 ROV位姿相轨迹图 Fig. 6 Phase portrait of ROV position and attitude |
|
图 7 ROV位姿运动轨迹跟踪 Fig. 7 ROV position and attitude tracking results |
本文针对四自由度ROV,提出一种基于RBF神经网络的自适应滑模控制方法,主要解决了经典滑模控制中存在的抖动问题,以及ROV模型不确定性问题。首先考虑了ROV在运动时,受自身模型不确定因素的干扰,引入RBF神经网络算法,用以持续补偿ROV模型不确定项。RBF神经网络中的权值则是通过自适应控制方法给出。其次,为了解决经典滑模控制中存在的抖动问题,采用反正切函数作为切换控制项,这种方法简单有效,可以最大化减小滑模控制的抖动,使系统的状态轨迹平滑地沿着滑模面运动到平衡点。最后,根据Lyapunov稳定性定理验证了被控系统是全局渐进稳定的。通过仿真实验,将本文提出的控制方法与2种经典滑模控制方法进行了比较,仿真结果证明该控制方法具有更好的控制效果。
| [1] |
HOSSEINI M, SEYEDTABAII S. Improvement in ROV horizontal plane cruising using adaptive method[C]// 2016 24th Iranian Conference on Electrical Engineering (ICEE). IEEE, 2016.
|
| [2] |
MOON, G, JOO, et al. An autonomous underwater vehicle as an underwater glider and its depth control[J]. International Journal of Control, Automation& Systems, 2015, 13(5): 1-9. |
| [3] |
OSEN O L, SANDVIK R I, ROGNE V, et al. A novel low cost ROV for aquaculture application[C]//OCEANS 2017-Anchorage. IEEE, 2017: 1-7.
|
| [4] |
KHADHRAOUI A, BEJI L, OTMANE S, et al. Stabilizing control and human scale simulation of a submarine ROV navigation[J]. Ocean Engineering, 2016, 114: 66-78. DOI:10.1016/j.oceaneng.2015.12.054 |
| [5] |
TEAGUE J, ALLEN M J, SCOTT T B. The potential of low-cost ROV for use in deep-sea mineral, ore prospecting and monitoring[J]. Ocean Engineering, 2018, 147: 333-339. DOI:10.1016/j.oceaneng.2017.10.046 |
| [6] |
SARHADI P, NOEI A R, KHOSRAVI A. Model reference adaptive PID control with anti-windup compensator for an autonomous underwater vehicle[J]. Robotics and Autonomous Systems, 2016, 83: 87-93. DOI:10.1016/j.robot.2016.05.016 |
| [7] |
SHOJAEI K, AREFI M M. On the neuro-adaptive feedback linearising control of underactuated autonomous underwater vehicles in three-dimensional space[J]. IET Control Theory & Applications, 2015, 9(8): 1264-1273. |
| [8] |
XIANG X, LAPIERRE L, JOUVENCEL B. Smooth transition of AUV motion control: From fully-actuated to under-actuated configuration[J]. Robotics and Autonomous Systems, 2015, 67: 14-22. DOI:10.1016/j.robot.2014.09.024 |
| [9] |
CHIN C S, LIN W P. Robust genetic algorithm and fuzzy inference mechanism embedded in a sliding-mode controller for an uncertain underwater robot[J]. IEEE/ASME Transactions on Mechatronics, 2018, 23(2): 655-666. DOI:10.1109/TMECH.2018.2806389 |
| [10] |
ELMOKADEM T, ZRIBI M, YOUCEF-TOUMI K. Terminal sliding mode control for the trajectory tracking of underactuated Autonomous Underwater Vehicles[J]. Ocean Engineering, 2017, 129: 613-625. DOI:10.1016/j.oceaneng.2016.10.032 |
| [11] |
LIU S, LIU Y, WANG N. Nonlinear disturbance observer-based backstepping finite-time sliding mode tracking control of underwater vehicles with system uncertainties and external disturbances[J]. Nonlinear Dynamics, 2017, 88(1): 465-476. DOI:10.1007/s11071-016-3253-8 |
| [12] |
LONDHE P S, PATRE B M. Adaptive fuzzy sliding mode control for robust trajectory tracking control of an autonomous underwater vehicle[J]. Intelligent Service Robotics, 2019, 12(1): 87-102. DOI:10.1007/s11370-018-0263-z |
| [13] |
CHEN J W, ZHU H, ZHANG L, et al. Research on fuzzy control of path tracking for underwater vehicle based on genetic algorithm optimization[J]. Ocean Engineering, 2018, 156: 217-223. DOI:10.1016/j.oceaneng.2018.03.010 |
| [14] |
YAN Z, WANG M, XU J. Robust adaptive sliding mode control of underactuated autonomous underwater vehicles with uncertain dynamics[J]. Ocean Engineering, 2019, 173: 802-809. DOI:10.1016/j.oceaneng.2019.01.008 |
| [15] |
WANG L, ISIDORI A, SU H, et al. Nonlinear output regulation for invertible nonlinear MIMO systems[J]. International Journal of Robust and Nonlinear Control, 2016, 26(11): 2401-2417. DOI:10.1002/rnc.3454 |
| [16] |
LIU J K. Sliding mode control design and matlab simulation[M]. Tsinghua University Press, 2005.
|
| [17] |
SLOTINE J J E, LI W. Applied nonlinear control[M]. Prentice hall, 1991.
|
| [18] |
SOYLU S, BUCKHAM B J, PODHORODESKI R P. A chattering-free sliding-mode controller for underwater vehicles with fault-tolerant infinity-norm thrust allocation[J]. Ocean Engineering, 2008, 35(16): 1647-1659. DOI:10.1016/j.oceaneng.2008.07.013 |
| [19] |
LIU C, XU G H, WANG G X, et al. Global sliding mode depth control of abdominal operating ROV[J]. Techniques of Automation and Applications, 2018, 37(3): 11-17. |
| [20] |
HUANG B, YANG Q. Double-loop sliding mode controller with a novel switching term for the trajectory tracking of work-class ROVs[J]. Ocean Engineering, 2019, 178: 80-94. DOI:10.1016/j.oceaneng.2019.02.043 |
| [21] |
FOSSEN T I. Guidance and control of ocean vehicles[M]. New York: Wiley, 1994.
|
 2020, Vol. 42
2020, Vol. 42
