为了提升潜水器的水下作业能力以胜任各种不同的作业要求,水下观察系统越来越受关注。观察窗作为载人潜水器耐压球壳上的开口构件之一,其强度和变形等问题一直是水下工程研究的重点之一。目前,国内针对大开口型球扇型观察窗的研究相对较少,但是潜水器对于更加宽阔的视野的客观要求不断提升,这也促进着这方面研究的深入。
国内外学者对球扇型观察窗和有机玻璃进行了广泛的研究,并取得了丰富的成果。文献[1]对有机玻璃进行了不同温度和应变率下的单轴准静态拉伸试验,基于ZWT模型结合实验数据拟合出有机玻璃的本构关系式;文献[2]运用有限元数值计算方法对锥边球扇型观察窗进行了结构与协调性分析;文献[3]利用有限元软件探讨了不同摩擦系数对观察窗力学性能的影响;文献[4]通过对球扇型观察窗结构的理论分析,得到其在简化的边界条件下径向应力的理论公式;文献[5]通过计算分析和试验分析对观察窗的强度、蠕变、边界条件的影响进行了研究;文献[6]利用 Abaqus 中粘弹性材料定义的有机玻璃松弛模量多项式的 Prony 级数对有机玻璃在加热过程中的材料特性进行了有限元模拟分析;文献[7]根据有机玻璃材料的蠕变试验提出了针对有机玻璃蠕变的时间-温度-应力叠加原理应用方法。美国海军实验室Jerry Stachiw[8]的著作作为潜水器观察窗领域的参考标准,提供了丰富的数据资料。
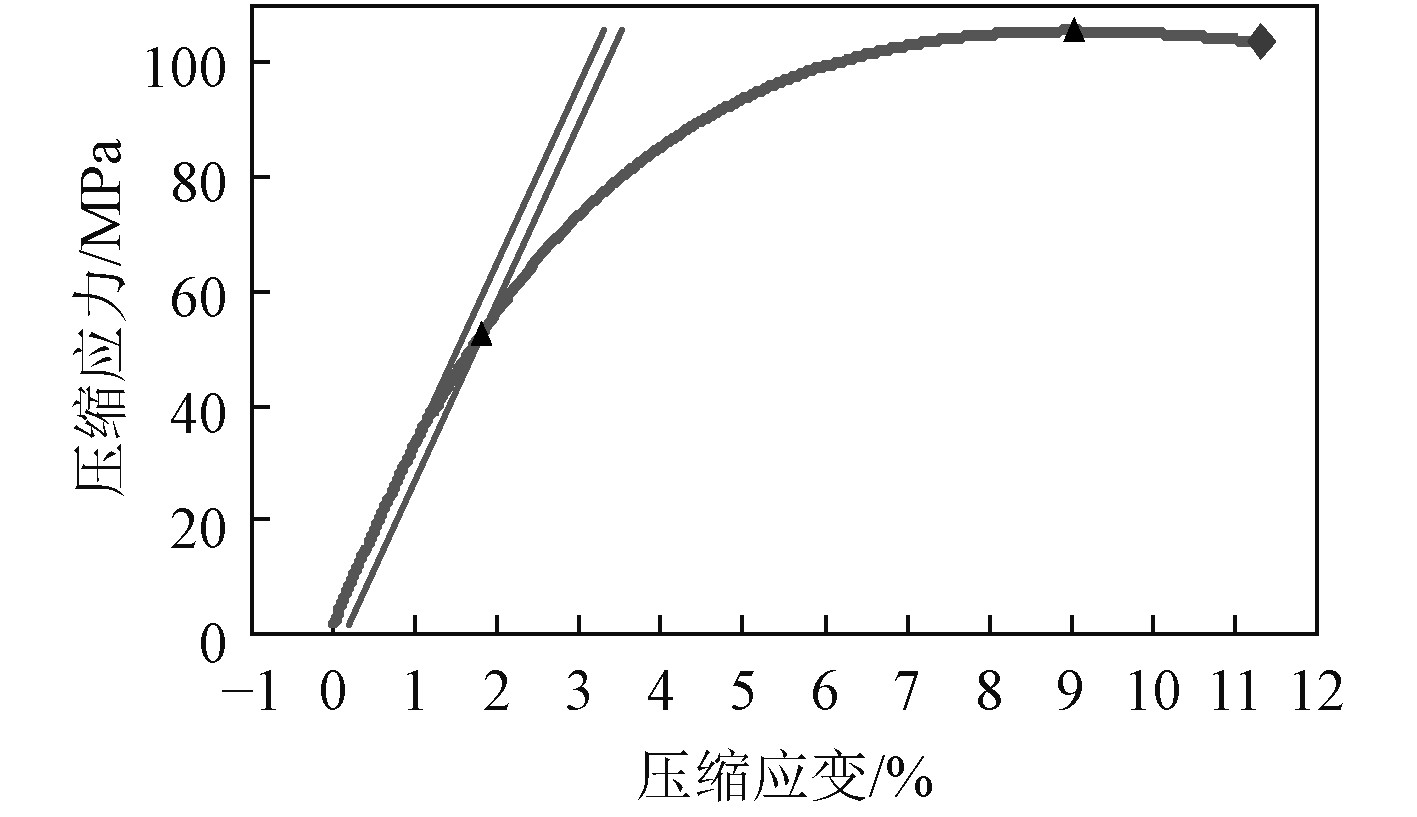
1 有机玻璃的力学特性有机玻璃作为一种高分子材料,具有典型的粘弹性,其压缩载荷下的应力-应变曲线如图1所示,其具体力学性能见表1。根据应力-应变曲线可以看出,压缩载荷作用下有机玻璃的线弹性特征不明显,应力和应变仅在应力0~40 MPa的范围内保持了较为良好的线性关系,线性拟合此范围内的应力应变数据,得到弹性模量为3121 MPa,结合文献[5]可以看出,有机玻璃的力学性能存在一定程度的离散性。在短期载荷的作用下,可以较为精确地预测有机玻璃的静力学行为,但要精准地预测长期载荷和循环载荷下的力学行为就十分困难了。
|
图 1 室温下有机玻璃压缩应力-应变曲线 Fig. 1 Compression stress - strain curve of PMMA at room temperature |
|
|
表 1 有机玻璃材料的力学性能[5] Tab.1 Mechanical properties of PMMA |
目前针对于描述高分子聚合物本构关系的粘弹性模型有很多,较为经典的粘弹性模型有弹性元件和阻尼元件串联形成的Maxwell模型,弹性元件和阻尼元件并联形成的Kelvin模型,弹性元件和Kelvin元件串联形成的标准线性固体模型,以及用这些模型构造的更加复杂的Kelvin链和广义Maxwell模型。本文参考文献[6]的经验方法,将采用广义Maxwell模型描述有机玻璃的粘弹性性能。该模型由多个Maxwell元件和一个弹性元件并联形成,在有限元Ansys软件中可以输入材料的蠕变试验数据曲线,Ansys将根据数据利用Prony级数自动拟合出材料的粘弹性模型。
有机玻璃的拉伸弹性模量与压缩弹性模量差距较小,一般大于2760 MPa,其弹性模量受温度和应变率影响较大,温度越低、应变率越大弹性模量越大,此外压缩弹性模量还受多轴压缩应力场的影响,在多轴压缩应力场下压缩弹性模量增大。有机玻璃的泊松比和弹性模量相似,受温度、应变率和多轴压缩应力场的影响,但该值还受到施加的压应力水平的影响,应力水平越高,泊松比越大[8]。
2 观察窗及耐压试验的设计本文进行试验的载人潜水器观察窗按照《Safety Standard for Pressure Vessels for Human Occupancy》2016(以下简称“PVHO-1-2016”)规范设计计算而得。观察窗属于大角度球扇型观察窗,观察窗厚度为90 mm,球冠内半径755 mm,开角为90°,金属球壳厚度为26.5 mm。窗玻璃通过压环压紧安装在窗座上,通过36个法兰螺栓与窗座法兰连接,观察窗密封通过密封圈实现。观察窗采用的有机玻璃材料性能满足“PVHO-1-2016”规范标准,金属球壳采用316L不锈钢材料。
加压试验分别在观察窗上A,B,C三个点贴上双向应变片(见图2),但经验证分析只有观察窗外部顶点A的应变值准确有效。加压试验实行分步加载,从0分步加压至3.75 MPa,试验环境温度5 ℃左右。

|
图 2 观察窗结构与应变片粘贴位置 Fig. 2 Viewport structure and pasting position of strain gauges |
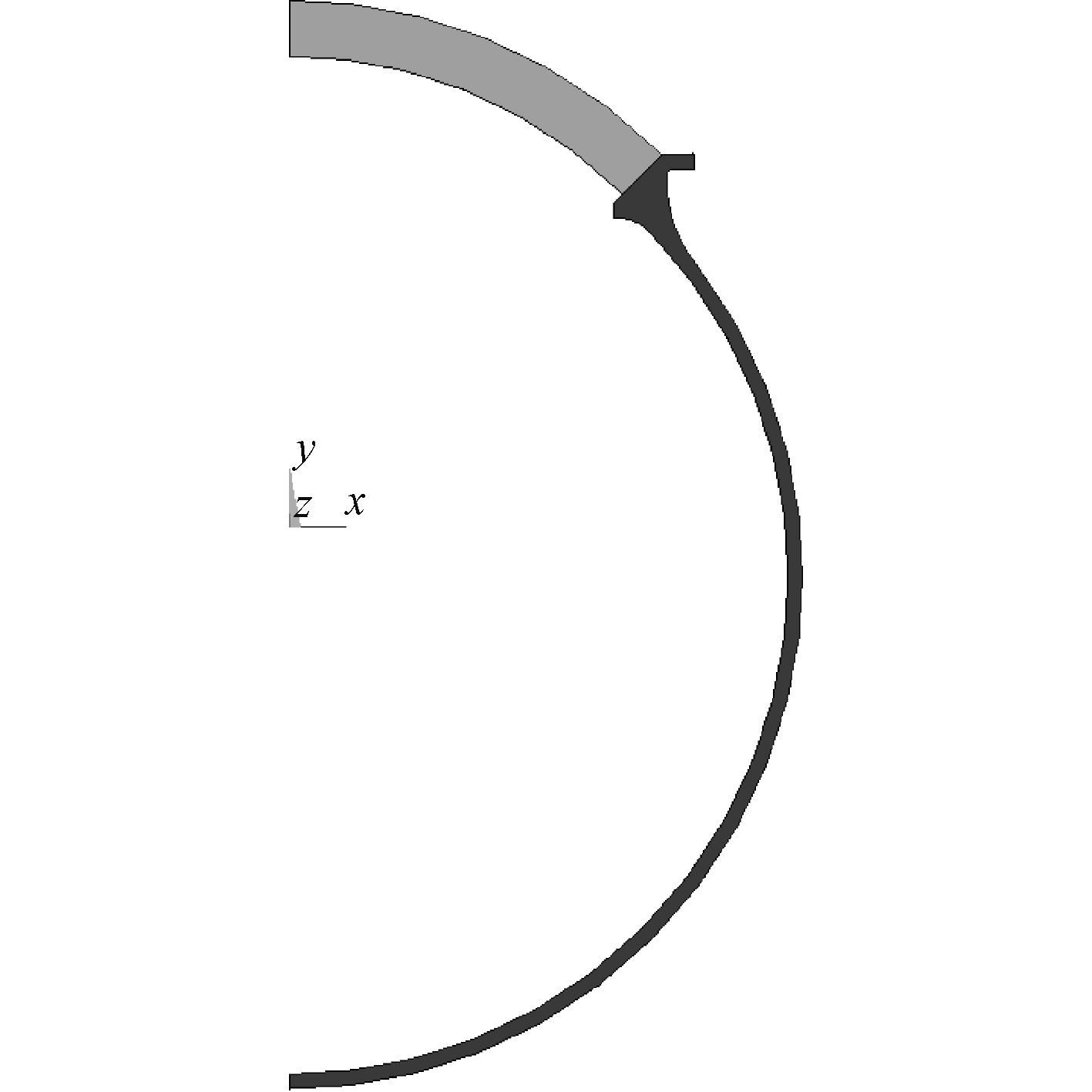
大开口球扇型观察窗的具体结构如图2所示,根据其结构尺寸建立的2D模型如图3所示。其中对金属壳体窗座处凸出的直角结构进行倒角处理,以防有限元计算失败。因为结构和载荷的对称性,本文取1/2模型进行有限元分析。
|
图 3 观察窗与球壳的有限元模型 Fig. 3 The finite element model of the viewport and hull |
本文采用PLANE183单元,该单元可以用作平面单元或者轴对称单元,具有计算塑性、蠕变、应力刚度、大变形和大应变的能力。因为属于旋转体轴对称结构,外载也为对称的均布外压,故单元行为设置为轴对称Axisymmetric。
根据材料手册及相关文献[5],有机玻璃弹性模量取业界公认允许的最小值2760 MPa,泊松比取0.38;不锈钢弹性模量206 GPa,泊松比0.3。
3.3 划分网格和定义接触对及边界条件划分网格时,根据结构形状特征采用不同划分方法,有机玻璃形状规则,采用映射网格划分,金属壳体较复杂采用自由网格划分,网格尺寸的确定基本遵循接触非线性分析中接触主面网格尺寸大于从面的原则,划分结果大致如图4所示。

|
图 4 有限元网格划分结果 Fig. 4 The finite element meshing result |
选取接触面定义面-面接触,窗座面因其刚度大,作为主面,观察窗作为从面,二者之间相互接触摩擦,取摩擦系数为0.1,接触对实常数设置:FKN取1,FTOLN取0.1。
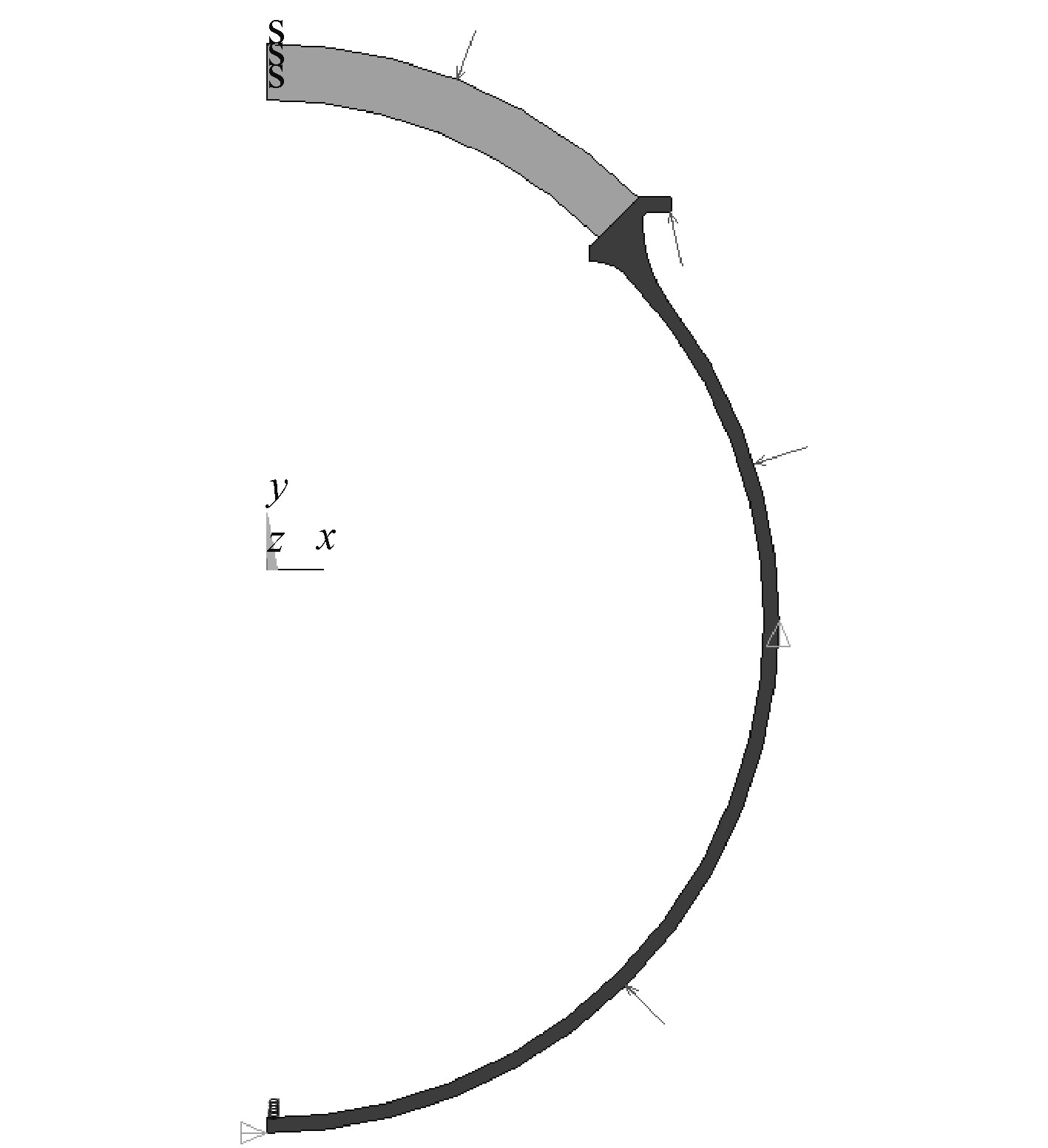
位移边界条件的设定:对称轴上设定轴对称约束,金属壳体最低点x方向位移为0,右侧面最外点y方向位移为0;载荷边界条件设定:在有机玻璃观察窗及金属壳体外表面轮廓线上施加压力载荷,模拟外部均布静水压力载荷,如图5所示。
|
图 5 边界条件 Fig. 5 The boundary conditions |
对有限元模型收敛性进行分析,调整单元网格尺寸并使用相同的网格划分方法,以改变网格的稀疏程度,保持软件的其他设置不变,最后提取不同网格尺寸下的结果对比分析,其计算结果如表2所示。当玻璃网格尺寸小于0.03 mm时,应变和位移结果都一直保持在稳定的水平,同时网格尺寸大于4 mm的各种情况下有限元计算速度并没有明显差异,故结合计算速度和结果精度综合考虑,玻璃网格尺寸取5 mm,壳体网格尺寸取10 mm。
|
|
表 2 不同网格尺寸的有限元结果 Tab.2 The finite element results for different element sizes |
在有限元分析中,通过设置载荷步对模型逐步加载,分别提取每个载荷步下模型的有限元结果,与压力试验的测量结果对比,观察窗外顶点的应变结果,如图6所示。可以看出,随着外载的增大,无论是有限元结果还是试验数据,其应变值也随之增大,二者的变化趋势及幅度基本一致。但二者的差异也显而易见,相较于试验数据,有限元结果明显偏大,由于结构整体仍旧处于小应变、低应力的状态,材料的塑性非线性行为尚未发生,结合有机玻璃的特性,其材料属性受温度影响较大,故推测误差较大的原因主要是输入的材料参数不准确及有机玻璃的粘弹性引发的蠕变行为,需要调正材料参数,引入粘弹性模型修正结果。因此可以得出结论,本文建立的有限元模型网格收敛性良好,但需重新定义材料模型及其参数以保证有限元模型的有效性。图7为观察窗在外载3 MPa下的应力云图,可以发现观察窗整体处于低应力水平,观察窗的最大等效应力点出现在与窗座接触的内侧点。

|
图 6 计算应变值与试验数据对比 Fig. 6 The calculated strain value compared with the test data |

|
图 7 观察窗的应力云图 Fig. 7 The stress contour plot of the viewport |
在验证完毕有限元模型网格收敛性的基础上,为保证有限元模型的有效性,提高有限元计算的准确性,开展有机玻璃的材料参数化分析,主要分析不同弹性模量和不同泊松比下,保持其他有限元模型参数及计算方法一致,单一变量弹性模量或者泊松比与有限元结果应变之间的关系。
文献[8]指出,有机玻璃的弹性模量和泊松比对温度非常敏感,温度提升10 ℃,弹性模量大约降低300~400 MPa;泊松比的变化范围在0.35~0.5之间,随着温度的升高,其变化趋势呈“S”型增长,先增大再保持水平,然后再增大。
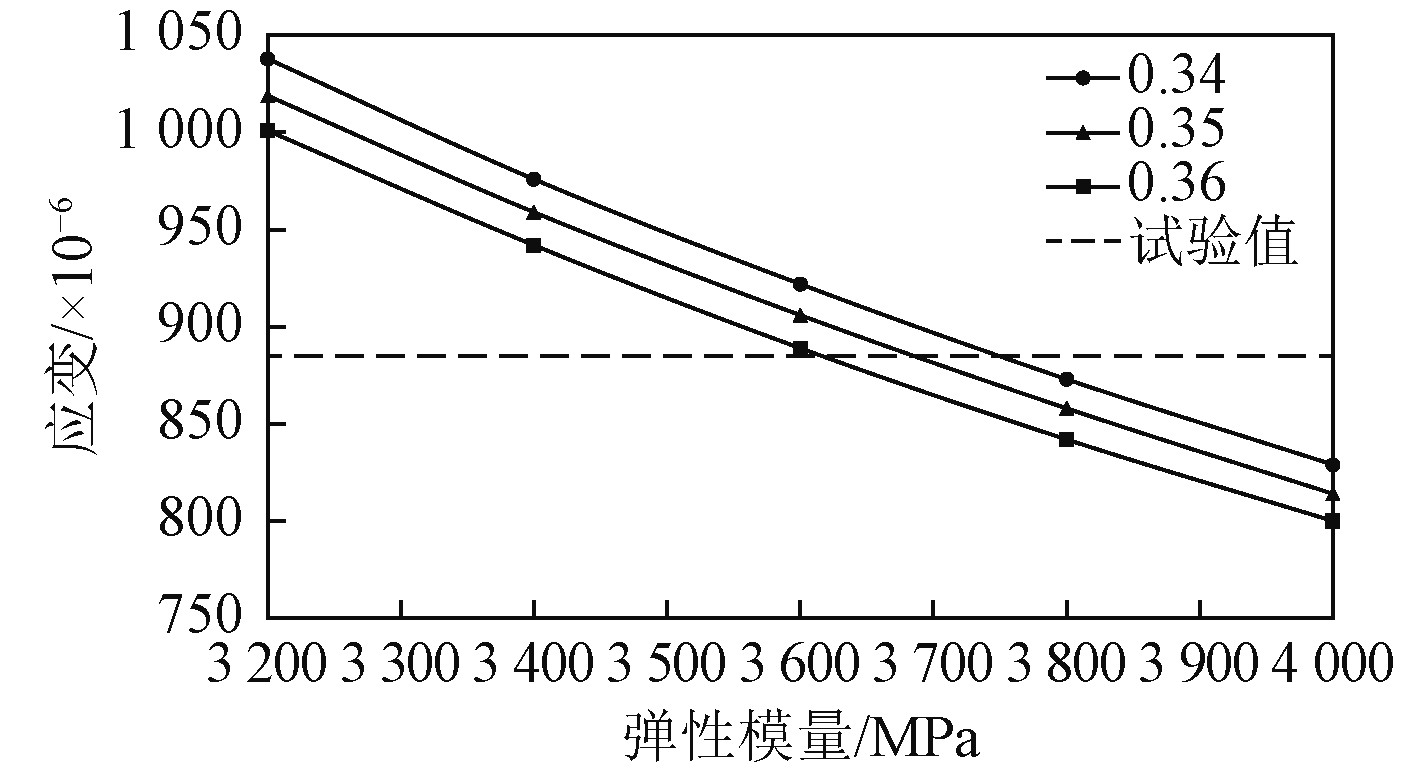
本文根据试验环境的温度划定了有机玻璃材料参数的变化范围,将泊松比分为了0.34,0.35,0.36三个系列,每个系列中将弹性模量分成了3200,3400,3600,3800,4000 MPa五组,分别用有限元统计计算外压为1 MPa时各系列各组的应变值,并与1 MPa时的试验应变值对比,结果如图8所示。
|
图 8 不同弹性模量和泊松比下有限元计算结果 Fig. 8 The finite element calculation results under different elastic modulus and poisson’s ratio |
根据各条曲线与水平试验值标准线的交点,得到了与试验结果相匹配的几组有机玻璃材料参数(0.34,3620),(0.35,3690),(0.36,3750)。由文献[8]中有机玻璃泊松比-温度变化曲线和弹性模量-温度变化曲线确定第2组材料参数(0.35,3690)为本此试验中有机玻璃的有效材料参数,该组参数既能保证有限元结果的准确性,又与试验温度下对应的材料参数值相匹配。
为计算使用方便,四舍五入后确定有机玻璃新的材料参数为(0.35,3700),并用有限元重新计算,与试验数据的对比如图9所示。虽然,根据外载为1 MPa时的试验数据所推得的材料模型新参数在1 MPa附近的应变误差很小,但随着外载的加大,很明显看出有限元结果与试验数据的偏差越来越大。这是由于随着加压时间的不断增长,有机玻璃累积的蠕变值越来越大,故计算结果的偏差也越来越大。
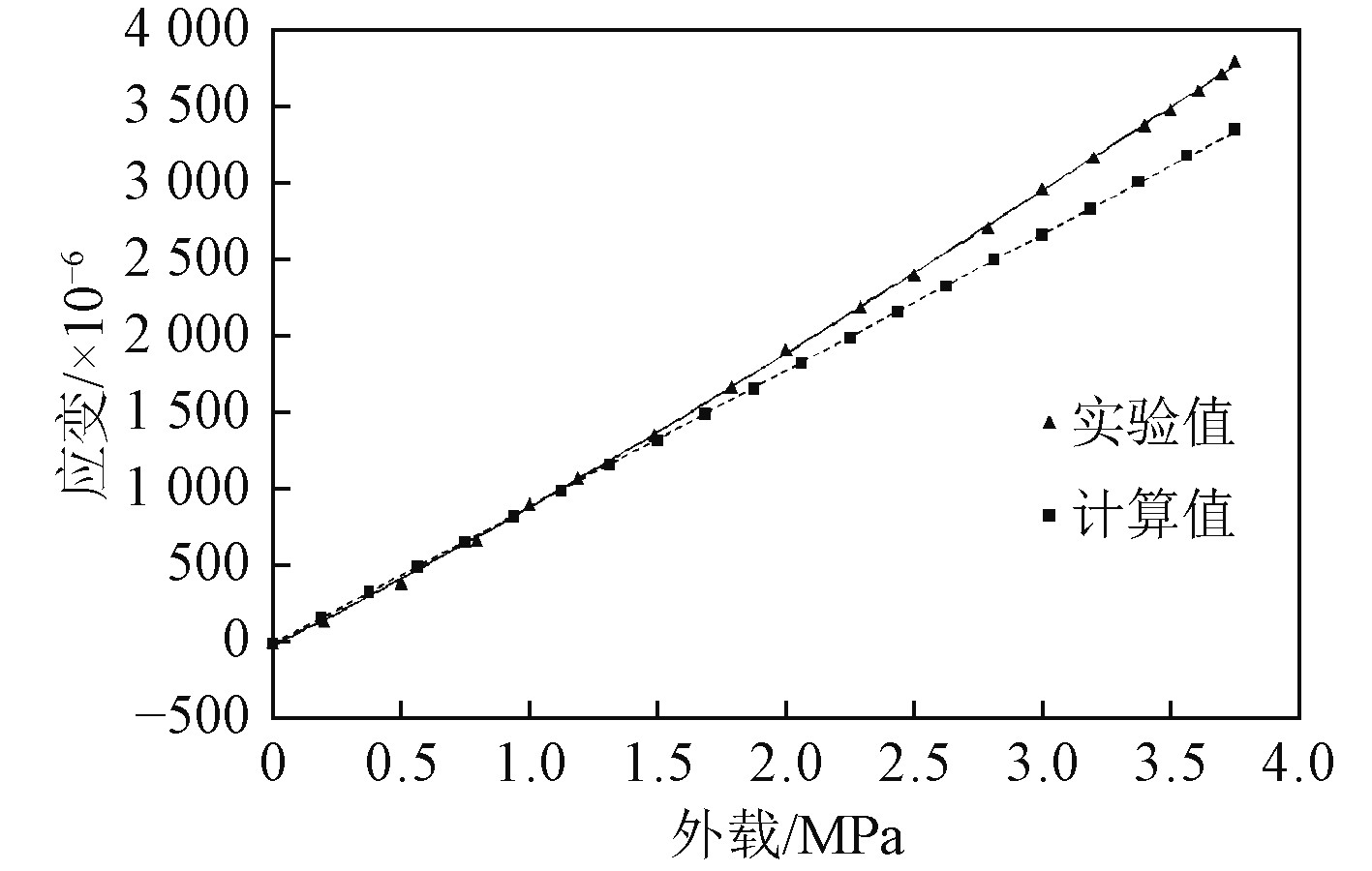
|
图 9 材料参数(0.35,3700)下的计算值与试验值的对比 Fig. 9 The calculated value under the material parameters(0.35, 3700) compared to the test value |
目前Ansys软件可以根据材料蠕变试验数据利用Prony级数拟合生成对应材料的粘弹性模型。文献[7]对有机玻璃材料进行了多组不同温度、不同应力水平下的蠕变试验,探讨了粘弹性材料有机玻璃的短期蠕变力学行为的温度和应力影响效应,发现其松弛时间与温度或应力水平呈负相关,蠕变柔量是应力和温度的函数,提出了针对有机玻璃蠕变的时间-温度-应力叠加原理应用方法。本文提取了该文献中有机玻璃的蠕变试验数据,通过计算将其转化成松弛模量对时间的数据点。根据线性粘弹性模型的原理,假定材料泊松比不变,材料的切变模量和体积模量与材料弹性模量呈线性一一对应关系,故可得切变模量和体积模量对时间的数据点。将这2组数据点输入Ansys软件,选定好用于拟合的Prony级数阶数和初始迭代参数,最后Ansys自动拟合生成用于模拟材料粘弹性的Prony级数参数,代入瞬时松弛模量表达公式:
| $E\left( t \right) = {E_0}\left[ {1 - \sum\nolimits_i {{a_i}} \left( {1 - {{\rm{e}}^{ - \frac{t}{{{\tau _i}}}}}} \right)} \right]\text{。}$ | (1) |
式中,
|
|
表 3 Prony级数拟合参数 Tab.3 Prony series fitted parameters |
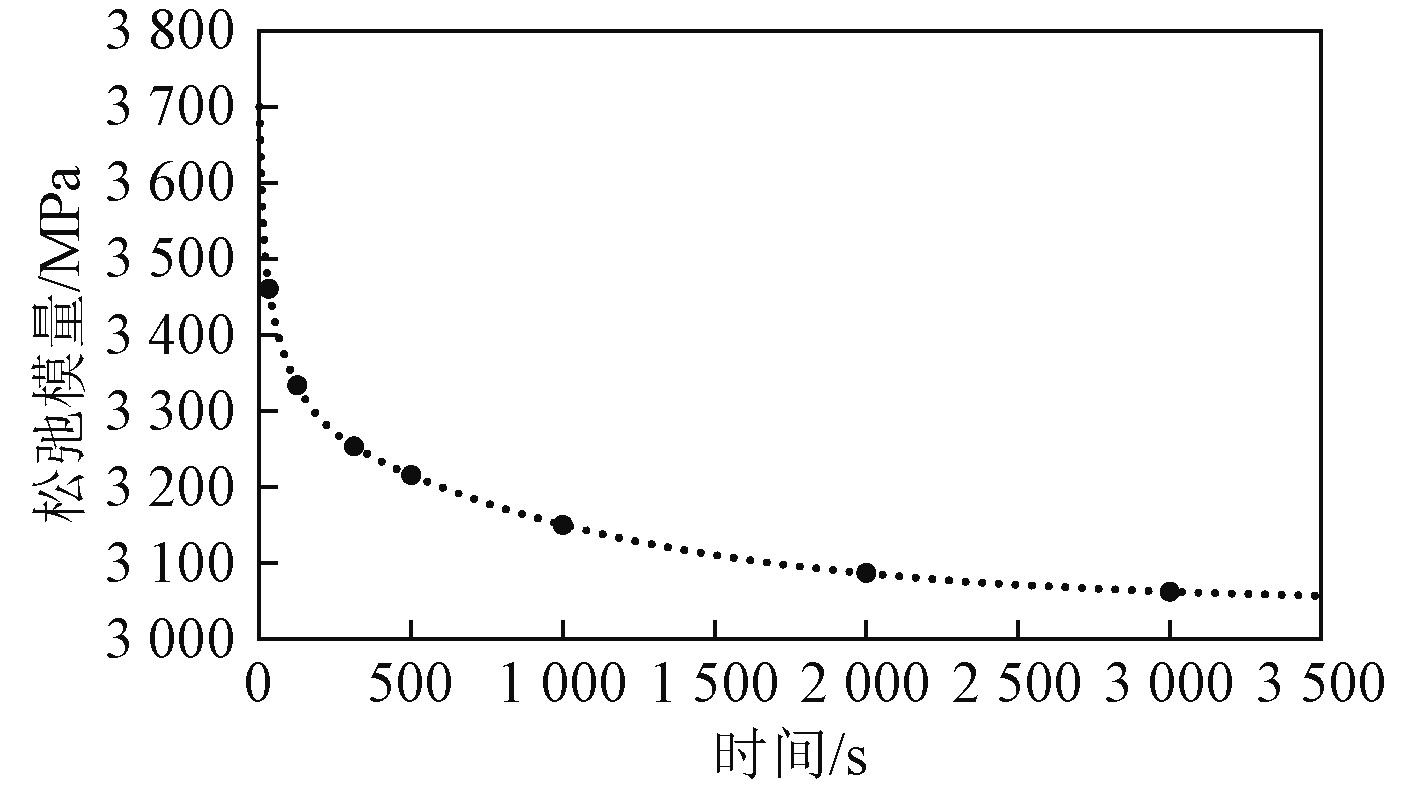
|
图 10 Prony级数拟合曲线与蠕变实验数据的比对 Fig. 10 Prony series fitted curve compared to the creep test data |
利用上述拟合参数建立有机玻璃的线性粘弹性模型,根据加载时长确定载荷步数,重新计算整个加载过程中观察窗的力学响应。计算结果如图11所示,引入有机玻璃粘弹性模型后的有限元计算结果明显与试验数据更加吻合,这进一步证明,在小变形、低应变的情况下,相较于线弹性模型,用Prony级数模拟的线性粘弹性模型能够更良好的预测有机玻璃的力学行为。但是,与试验数据相比,计算结果仍旧偏大。这是由于文献[7]中蠕变试验环境与本文试验环境不完全相符,本文试验环境略低于参考文献试验温度,而温度越低,粘弹性材料的松弛时间越长,蠕变效应越缓慢,故计算结果会比实际数值大。

|
图 11 粘弹性模型的有限元计算结果 Fig. 11 The finite element calculation results of viscoelastic model |
本文通过有限元计算分析的方法成功预测了大开口球扇型有机玻璃观察窗在外压下的力学行为,经过数据分析对比得出以下结论:
1)线性粘弹性模型相较于线弹性模型,能够获得更精确的有限元计算结果。但是由于线性粘弹性模型的局限性,本文忽略了不同应力水平对材料粘弹性和泊松比的影响,后续需要进一步研究探讨。
2)由于有机玻璃属于粘弹性材料,其材料力学性能参数受温度和应力水平影响很大,因此在用有限元计算其响应时,注意到耐压结构的不同工作环境(温度及压力)下材料参数的不同,适当变化材料参数能有效提高计算结果的准确度。
3)有机玻璃本身的力学性能离散性较大,在结构耐压试验之前,通过试件的拉压等其他试验取得材料对应的力学性能参数,对于提高有限元计算精度有重要意义。
| [1] |
范瑞鹤. 基于有机玻璃拉伸试验的本构关系拟合及有限元实例分析[D]. 哈尔滨: 哈尔滨工业大学, 2012.
|
| [2] |
杜青海, 王嫘, 崔维成. 锥边球扇形观察窗结构的协调性分析[J]. 船舶力学, 2011, 15(1-2): 101-108. |
| [3] |
廉俊盛. 深海载人潜水器球壳及观察窗力学行为的有限元分析[D]. 呼和浩特: 内蒙古工业大学, 2016.
|
| [4] |
施东春, 王帅, 张美荣, 等. 水下运载器球扇形观察窗结构的应力分析[J]. 四川兵工学报, 2014, 35(7): 139-142. |
| [5] |
刘道奇, 胡勇, 王芳, 等. 深海载人潜水器观察窗的蠕变特性[C]//2009年船舶结构力学学术会议暨中国船舶学术界进入ISSC30周年纪念会论文集. 中国造船工程学会, 2009: 50-59.
|
| [6] |
白杰. 超声振动辅助PMMA微压印成形工艺研究[D]. 哈尔滨: 哈尔滨工业大学, 2016.
|
| [7] |
LUO Wenbo, WANG Chuhong, ZHAO Rongguo. Application of Time- Temperature-Stress Superposition Principle to Nonlinear Creep of Poly(methyl methacrylate)[J]. Key Engineering Materials, 2007, 340-341: 1091-1096. DOI:10.4028/www.scientific.net/KEM.340-341.1091 |
| [8] |
J. D. Stachiw. Handbook of Acrylics for Submersibles, Hyperbaric Chambers and Aquaria[M]. US: Best Publishing Company, 2003.
|
 2020, Vol. 42
2020, Vol. 42
