随着全球集装箱航运市场行情趋稳,全球集装箱航运市场行情将继续改善,对于集装箱船的需求也逐渐释放[1],同时对于集装箱船的需求也呈现出大型化的趋势。与常规运输船相比,超大型集装箱船由于其较大的受风面积风阻研究变得更为必要[2]。
刘强[3]利用OpenFOAM对不同集装箱布置形式进行了数值计算,研究了通过经验公式计算难以得到的上层建筑形式风载荷的差别,分析空气绕流场的流动状态与船舶所受风载荷的关系。蔡文山[4]采用数值方法对不同的集装箱进行了研究,并对风洞试验的结果进行验证,结果吻合较好的基础上优化布置形式以减小风阻。罗少泽[5]在验证敞开式风场风阻试验的基础上对集装箱船的布置研究,通过数值计算有效地优化集装箱的风阻。Anderson[6]研究了1艘巴拿马型集装箱船在多种集装箱布置下的风阻和力矩,分析了风阻的影响因素并提供了优化方案。魏可可[7]利用数值手段研究了水面舰艇水面以上船体的风载,同时也根据经验公式对其风载荷进行估算,与试验值相比,数值方法和经验公式都存在一定的误差。刘亚冲[8]对16 000箱集装箱船船体水线以上结构表面风场风压进行数值模拟,得到风载荷系数,并与规范方法和Isherwood方法进行比较,为船舶初期的稳性设计提供数据参考。
综上所述,对于集装箱船的研究集中于数值方法以及经验公式,但对于数值方法的精确性有待进一步验证。风洞试验通过模拟实际环境中的风为试验模型提供外部风环境,人为控制风环境以对结构物风效应进行再现。风洞试验是目前计算风阻最为有效精确的手段,同时也能够为其他计算方法提供可靠的数据,作为估算风载荷的依据[9,10]。然而风洞试验因其较为昂贵的费用和较长周期,在计算船舶风阻方面的试验较少。本文通过集装箱空载吃水和设计吃水2种工况的风洞试验得到数据,计算得到风阻系数,并分析不同工况下风阻系数和力矩特点,并为后期风阻优化提供参考依据。
1 试验模型 1.1 船型简介集装箱船模型由船体和集装箱组成,集装箱船模型缩比为1:200,并采用3D打印的方式进行模型的加工制作。将水线与甲板之间船体和上层建筑、集装箱分开制作,其中船底、船侧平边、尾封板和甲板采用3 mm玻璃钢板材料加工,而上层建筑和集装箱用3D打印材料(聚乳酸)加工。模型主要参数见表1。
|
|
表 1 集装箱船模型参数 Tab.1 Parameters of the container ship |
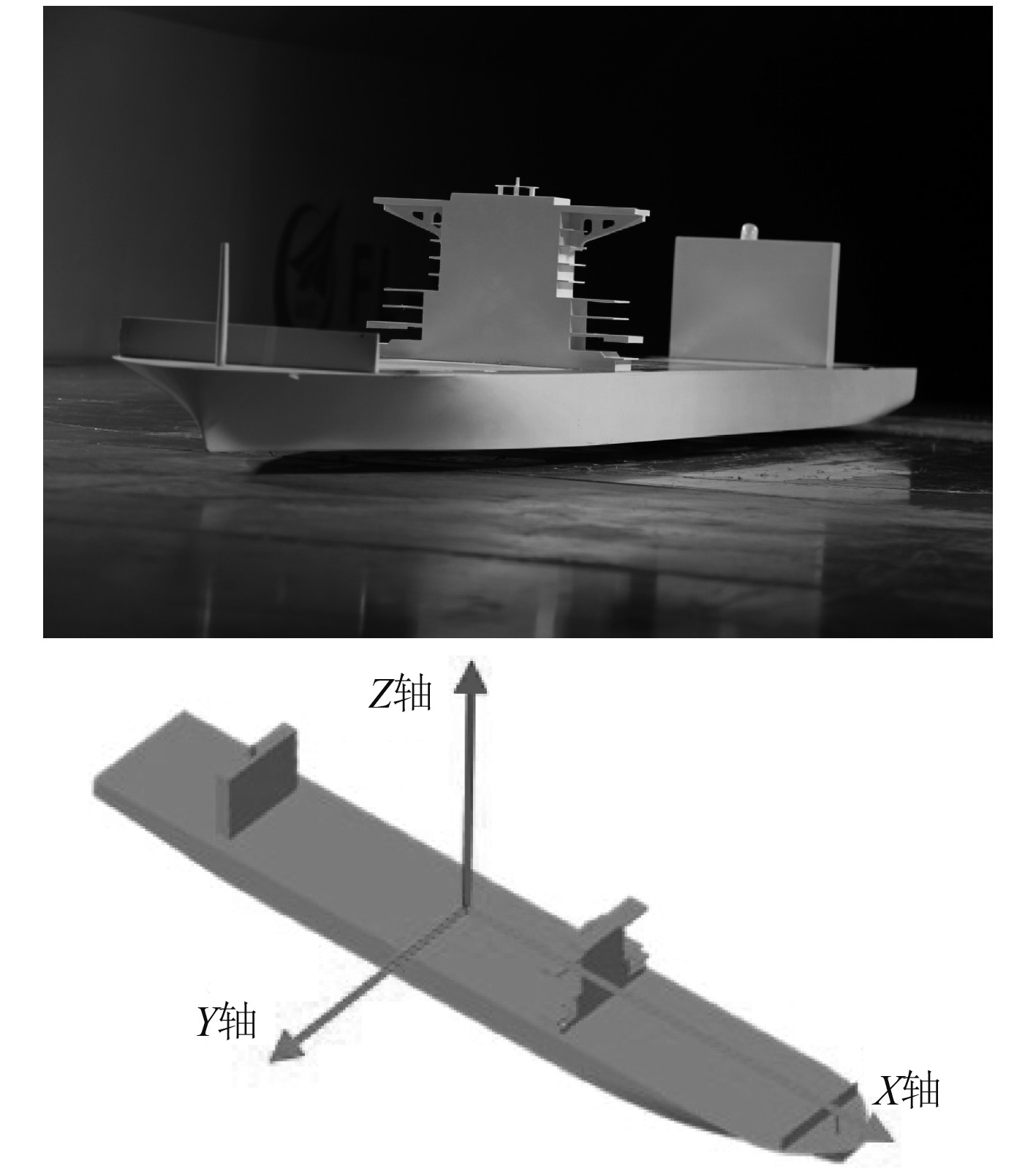
|
图 1 试验模型及坐标系 Fig. 1 Test model and coordinate system |
本次试验于中国航空工业空气动力研究院(哈尔滨)FL-8风洞进行。该风洞为低速单回路闭口风洞,试验段截面为切角矩形,其主要参数见表2。
|
|
表 2 风洞模型参数 Tab.2 Parameters of the tunnel |
风洞试验测力采用单支杆腹部支撑系统,该系统主要由迎角机构、侧滑角机构和支杆机构组成。采用该系统支撑的模型可实现两自由度方向的旋转功能,即模型的迎角和侧滑角。试验时,模型连接到天平上,天平连接到支撑系统上。本次试验用地板模拟水面,为防止试验过程中模型震颤碰到地板,地板与集装箱船船底之间的距离为20 mm。试验时,针对模型的各个状态,阶梯式改变模型的侧滑角对模型气动力及力矩进行测量。0°~180°每15°改变一次角度,共13个角度。试验风速为25 m/s。
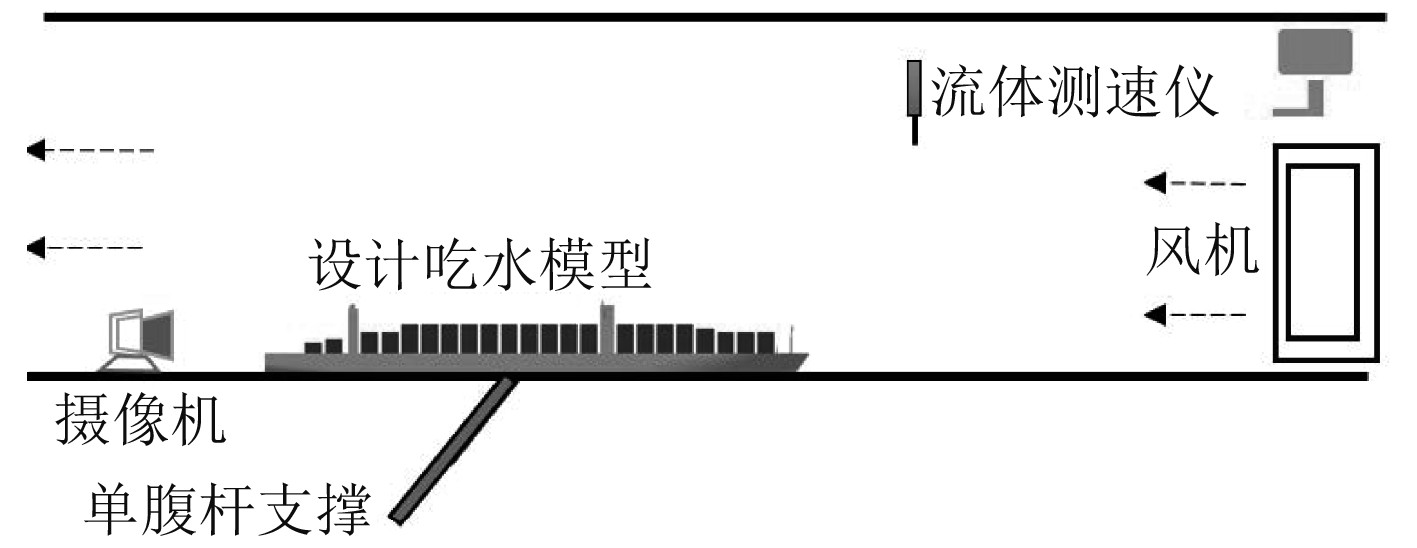
|
图 2 集装箱设计吃水风阻试验 Fig. 2 Draft design resistance tunnel test of container ship |
对模型气动力及力矩进行测量。定义力系数:
| $ C{F_X} = {F_X}/(\rho {A_f}{u^2}/2)\text{,} $ | (1) |
| $ C{F_Y} = {F_Y}/(\rho {A_c}{u^2}/2)\text{,} $ | (2) |
| $ {C_N} = N/(\rho {A_f}{u^2}L/2)\text{。} $ | (3) |
式中:船舶所受风阻包括沿船长方向的纵向力(阻力)FX;船宽方向上的横向力(侧向力)FY;偏航力矩CN;ρ为空气密度;u为风洞来流速度,β为迎风角。
由图3可以看出,随风向角的阶梯式改变,空载吃水和设计吃水2种工况的纵向风阻系数都呈现出接近正弦曲线变化的趋势,同时存在2个方向相反的阻力峰。在风向角接近β=45°和β=135°时二者的风阻系数值都达到机极值;当β=0°时,由于船舶受到正横风的作用,在纵向上并不存在风阻分量,所以沿船长方向的纵向风阻系数为0。
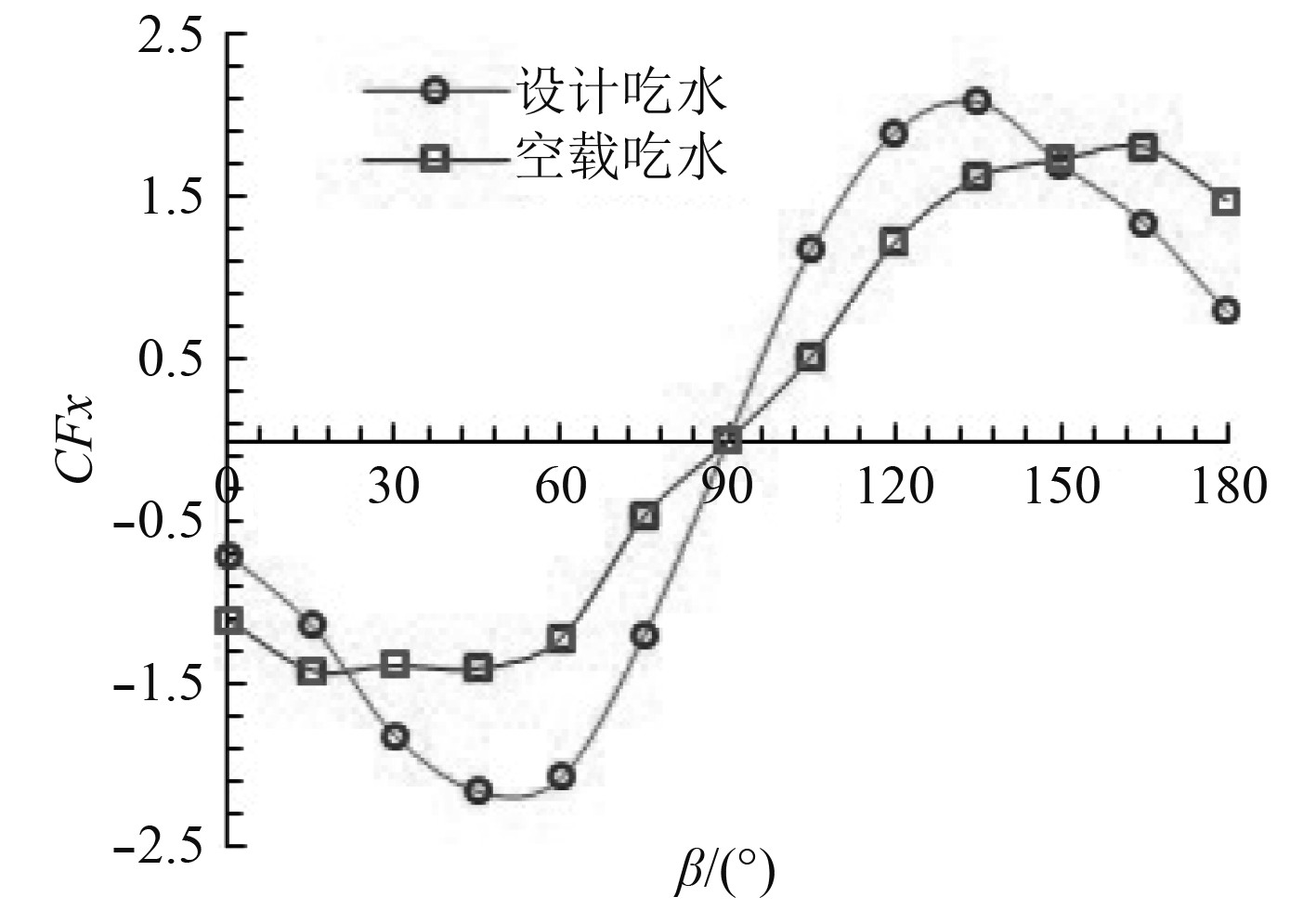
|
图 3 不同风向角下纵向风阻系数曲线 Fig. 3 Longitudinal wind resistance coefficient curves under different wind direction |

|
图 4 不同风向角下横向风阻系数曲线 Fig. 4 Transverse wind resistance coefficient curves under different wind direction |
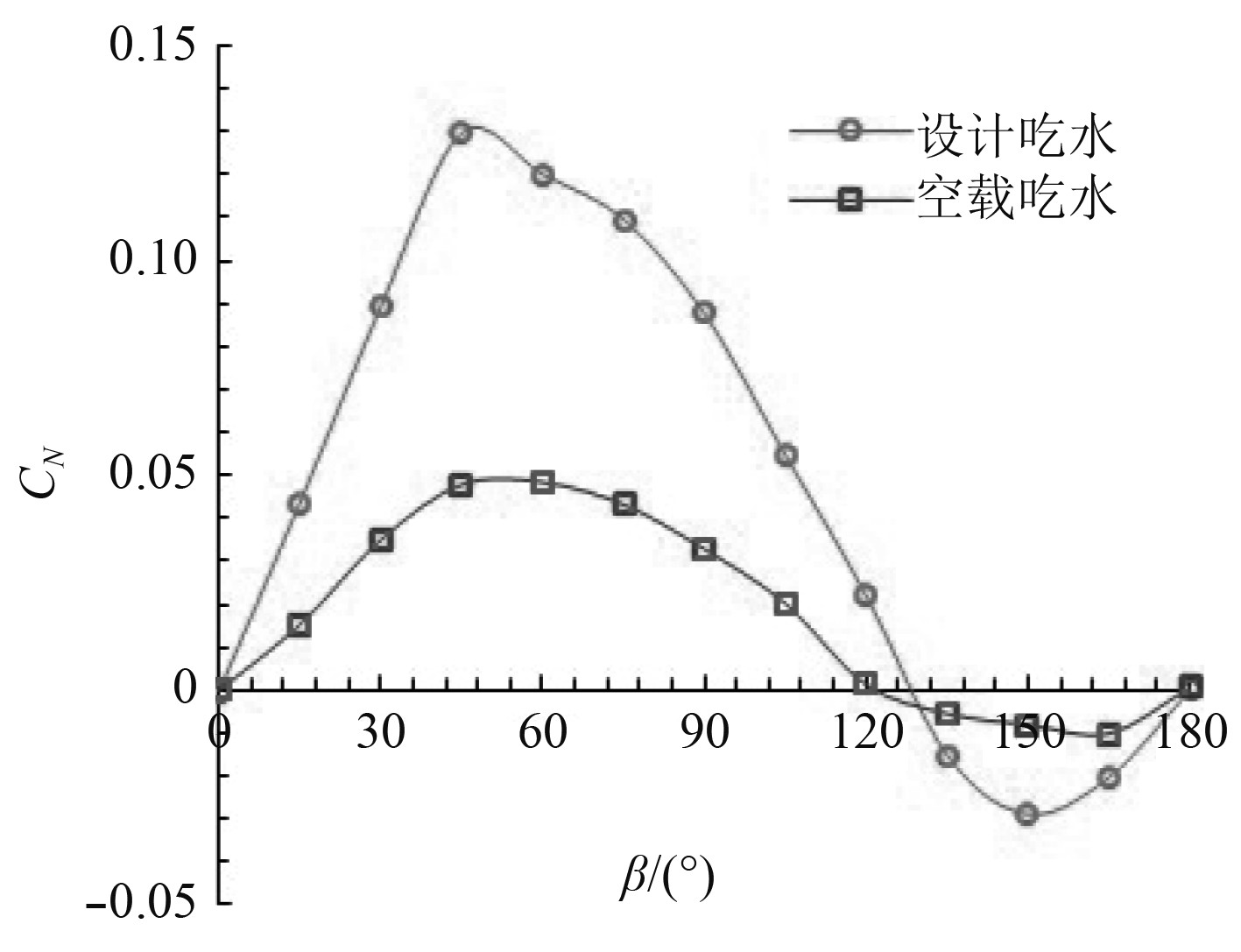
|
图 5 不同风向角下力矩曲线 Fig. 5 Moment curves under different wind direction |
对于空载吃水和设计吃水的横向风阻系数,在风向角β=0°和β=180°,船舶正迎风状态和正顺风状态时,船舶受到的风力横向分量为0。随着风向角由正迎风转到正横风后再过渡到正顺风时,风力的横向分量也随之先增大后减小,表现在横向风阻系数曲线即呈现出接近余弦曲线变化规律的趋势。在船舶处于遭遇横风状态时,设计吃水的横向风阻阻力系数较大,空载时由于上层建筑在纵剖面的投影较小,对风的阻滞作用降低,导致在正横风时曲线有一个下降的凹点,其余风向角二者阻力系数相差不大。同时由于设计吃水甲板上布置较多集装箱,所以在改变风向角时迎风面投影面积的变化较空载吃水状态缓和,表现在风阻系数曲线上即设计吃水的纵向和横向风阻系数曲线较为平滑。
空载吃水和设计吃水2种工况的力矩曲线有着明显的差别,空载时上层建筑在纵剖面的投影较小,所以前者力矩曲线数值要远远低于后者,同时由于集装箱船重心处于中后位置,上层建筑结构并不关于中横剖面对称,偏航力矩也并不完全遵循正弦曲线变化的规律,当遭遇风向角在50°附近时首摇力矩最大。
3 结 语本文通过风洞试验对集装箱船的设计吃水状态和空载吃水状态进行风场模拟,并对风阻系数进行分析。在试验风向角区间内,纵向风阻系数曲线形状近似于正弦曲线,存在方向相反的阻力极值,空载吃水时的曲线较为平缓且纵向风阻系数较小;横向风阻系数曲线类似抛物线,遭遇正横风时设计吃水的风阻系数最大,空载吃水状态由于上层建筑投影面积降低有局部极小值;集装箱的布置对于船舶的力矩曲线影响较大,需要对其布置进行深入研究。
| [1] |
蔡敬伟. 2017年全球集装箱船市场回顾与展望[J]. 世界海运, 2018, 41(3): 12-17. |
| [2] |
沈群章. 大型集装箱船外高桥水域强风中的调头靠泊操纵[J]. 世界海运, 2016, 39(6): 26-29. |
| [3] |
刘强, 谢伟, 段文洋, 等. 四种不同布置形式集装箱船风载荷计算研究[J]. 华中科技大学学报(自然科学版), 2013, 41(10): 95-99. |
| [4] |
蔡文山, 马卫星, 邓锐, 等. 不同集装箱布置下船舶风载荷数值仿真[J]. 中国航海, 2018, 41(2): 91-96. DOI:10.3969/j.issn.1000-4653.2018.02.019 |
| [5] |
罗少泽, 马宁, 平川嘉昭, 等. 大型集装箱船拖曳水池敞开式风场中风阻试验与数值计算[J]. 上海交通大学学报, 2016, 50(3): 389-394. |
| [6] |
ANDERSEN I M V. Wind loads on post-panamax container ship[J]. Ocean Engineering, 2013, 58: 115. DOI:10.1016/j.oceaneng.2012.10.008 |
| [7] |
魏可可, 高霄鹏. 水面舰船风载荷系数研究[J]. 舰船科学技术, 2018, 40(17): 27-31+38. WEI Ke-ke, GAO Xiao-peng. Research on wind load factor of a surface ship[J]. Ship Science and Technology, 2018, 40(17): 27-31+38. |
| [8] |
刘亚冲, 胡安康, 韩凤磊, 等. 超大型集装箱船风载荷系数研究[J]. 武汉理工大学学报, 2014, 36(4): 80-85. |
| [9] |
TOSHIFUMI Fujiwara, MICHIO Ueno, TADASHI Nimura. An estimation method of wind forces and moments acting on ships[C]//Mini Symposium on Prediction of Ship manoeuvring Performance. Tokyo: Japan Marine Dynamics Research Sub-Committee, 2001: 83−92.
|
| [10] |
HADDARA M R, GUEDES Soares C. Wind loads on marine structures[J]. Murine Structures, 1999, 12: 199-209. DOI:10.1016/S0951-8339(99)00023-4 |
 2020, Vol. 42
2020, Vol. 42

