2. 江苏现代造船技术有限公司,江苏 镇江 212003
2. Jiangsu Modern Shipbuilding Technology, Ltd., Zhenjiang 212003, China
随着陆地上不可再生能源的日益匮乏,节能减排在各行各业越来越受到重视。在海上运输领域,节能减排不仅能提高能源的利用率,亦可降低运输成本、提高经济效益。船舶在航行区域航行时多数是在波浪海况下航行,由于波浪的作用会使船舶阻力增加明显。船舶辅助推进装置就是以水翼在自由液面以下随波浪产生升沉和纵摇的周期性震荡运动,水翼震荡运动会产生水平方向的推力,进而为船舶推进提供辅助动力[1-3],降低船舶主机的输出功率,从而达到节能减排的目的。
一般而言,辅助推进装置多应用于低速船、无人艇等小型船舶上,震荡水翼沿船舶横向布置,宽度为船舶型宽的0.8~2.5倍。为了防止水翼在升沉运动处于波谷时不出水,还要确保水翼有一定的入水深度。诸多实验数据表明[4 − 6],对低速小型船舶加装辅助推进装置对船舶节能是行之有效的,并且也有完全由震荡水翼提供动力的实船在海上航行成功。然而,传统震荡水翼推进性能有以下缺点:
1)传统水翼在大角度震荡时水翼表面会产生涡脱落,脱落的涡会带走一部分能量从而降低水翼在来流中采集的能量,进而降低水翼产生的推力。
2)震荡水翼一般安装在自由液面以下一定深度来保证水翼处于波谷时不出水,而波动能量随水深的增加呈指数衰减,水翼采集的能量减少造成推进效率低下。
本文针对上述被动式震荡水翼缺点进行以下改进:
1)在传统水翼前缘增加凸起改善水翼在大攻角时的水动力性能,减少翼面涡脱落现象;
2)带有前缘凸起的水翼与自由液面处的浮子结合,以自由液面处浮子的升沉运动来带动水翼的升沉运动增加水翼运动的幅值。
综上所述,提出如图1所示浮子与前缘凸起水翼的组合装置。

|
图 1 水翼浮子耦合示意图 Fig. 1 Hydrofoil float coupling diagram |
本文基于CFD方法,使用STAR CCM+仿真软件对NACA0015水翼模型进行数值模拟,并将仿真结果与试验数据进行对比,验证模型与仿真方法的正确性。其次对本文提出的两点改进分步进行仿真计算:1)对前缘凸起水翼进行数值模拟,并将结果与前缘无凸起的水翼进行对比,分析前缘凸起水翼的水动力性能;2)讨论凸起在水翼前缘分布的长度[7 − 8]这一参数对水翼性能的影响。最后对前缘凸起水翼与浮子耦合进行数值模拟,分析浮子对水翼水动力性能的影响。
1 数值波浪水池 1.1 控制方程及离散格式数值波浪水池的数学模型以连续性方程和N-S方程为控制方程:
| $\frac{{\partial \rho }}{{\partial {\rm{t}}}} + \frac{{\partial (\rho {u_i})}}{{\partial {x_i}}} = 0 \text{,}\;\;\; \left( {i = 1,2,3} \right)\text{,}$ | (1) |
| $\begin{split} & \frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}{u_j}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\mu \left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)} \right] -\\ & \frac{{\partial p}}{{\partial {x_i}}} + \rho {f_{i }} \text{,}\;\;\; \left( {i,j = 1,2,3} \right)\text{。} \end{split}$ | (2) |
其中;
本文使用湍流模型为Realizable k-ε模型、有限体积法离散控制方程,采用SIMPLE方法求解压力耦合方程组,选择三维隐式不定常求解器与欧拉多相流模型;采用Volume Of Fluid(VOF)方法处理自由液面,主要采用网格单元中流体的体积与网格总体积的比值函数来确定自由液面的位置和形状,其方程为:
| $\frac{{\partial {a_q}}}{{\partial t}} + \frac{{\partial \left( {{u_i}{a_q}} \right)}}{{\partial {x_i}}} = 0 \text{,}\;\;\; \left( {q = 1,2} \right)\text{。}$ | (3) |
其中;
数值造波目前有3种方法:1)源造波法;2)仿物理造波法;3)直接输入法。本文采用精度高、易模拟实现的直接输入造波法来造一阶线性规则波,其波形方程为:
| $\zeta = {A_m}\cos \left( {kx - \omega t} \right)\text{,}$ | (4) |
当水深h与波长
| $\varphi = \frac{{{A_m}g}}{\omega }{e^{kz}}\sin \left( {kx - \omega t} \right)\text{,}$ | (5) |
则其速度场为:
| $\left\{ \begin{array}{l} u = {A_m}\omega {e^{kz}}\cos \left( {kx - \omega t} \right)\text{,} \\ v = 0\text{,} \\ w = {A_m}\omega {e^{kz}}\sin \left( {kx - \omega t} \right) \text{。}\\ \end{array} \right.$ | (6) |
其中,
进行数值模拟之前,需要在虚拟波浪水池中实现波的传播。在认为是无限水深的条件下共模拟验证了4个不同波长的规则波。
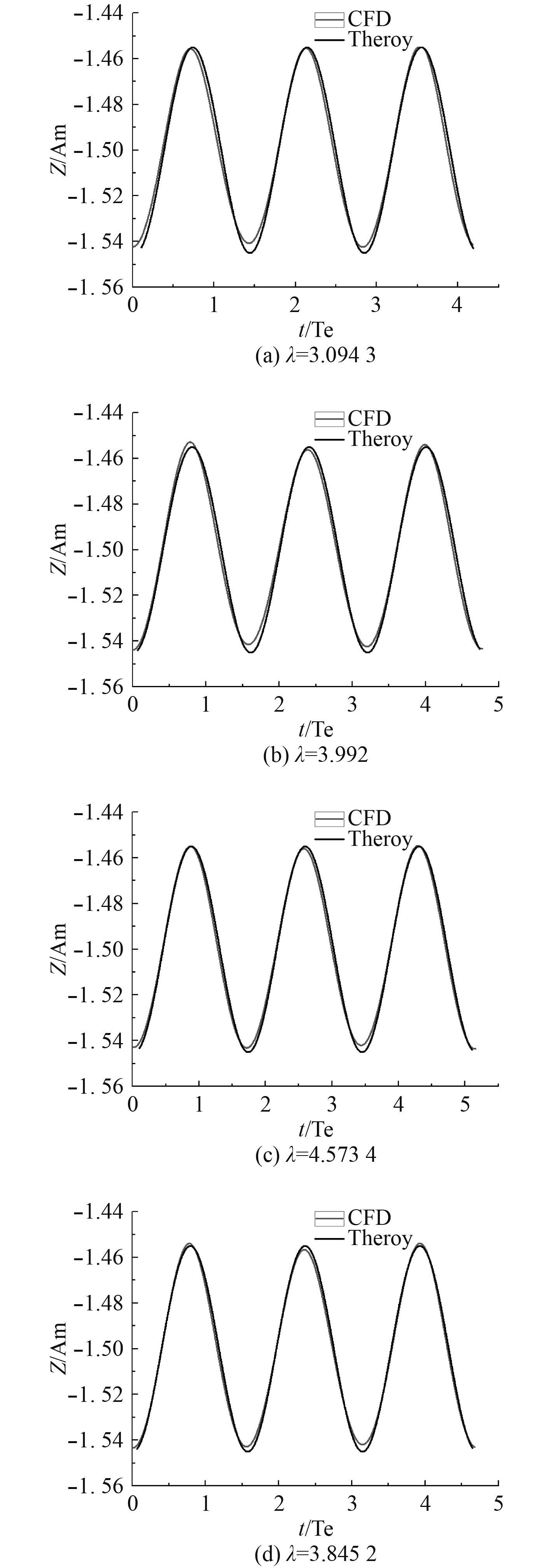
在三维数值水池中进行规则波模拟。为了减小数值耗散引起的波浪幅值衰减,采用波高方向20个网格单元,波长方向的网格尺寸为波高方向网格尺寸的8倍。通过设置在数值波浪水池中的浪高仪来监测获取4个不同波长入射波的薄面变化时间历程,如图2所示。可以看出,本文所模拟的规则波波幅与1阶Stokes波理论波幅基本吻合。
|
图 2 各波长监测点波高的时历曲线 Fig. 2 Time-history curve of wave height at each wavelength monitoring point |
消波是在数值水池出口区域设置消波区,防止波浪的反射对计算区域的波形和计算造成影响。在数值波浪水池压力出口处设置长度约为入射波长的1.5~2.0倍波长的人工阻尼消波区,如图3所示。可以看出,数值水池中的自由液面在靠近压力出口处波面逐渐恢复平静。

|
图 3 波浪自由液面 Fig. 3 Wave free surface |
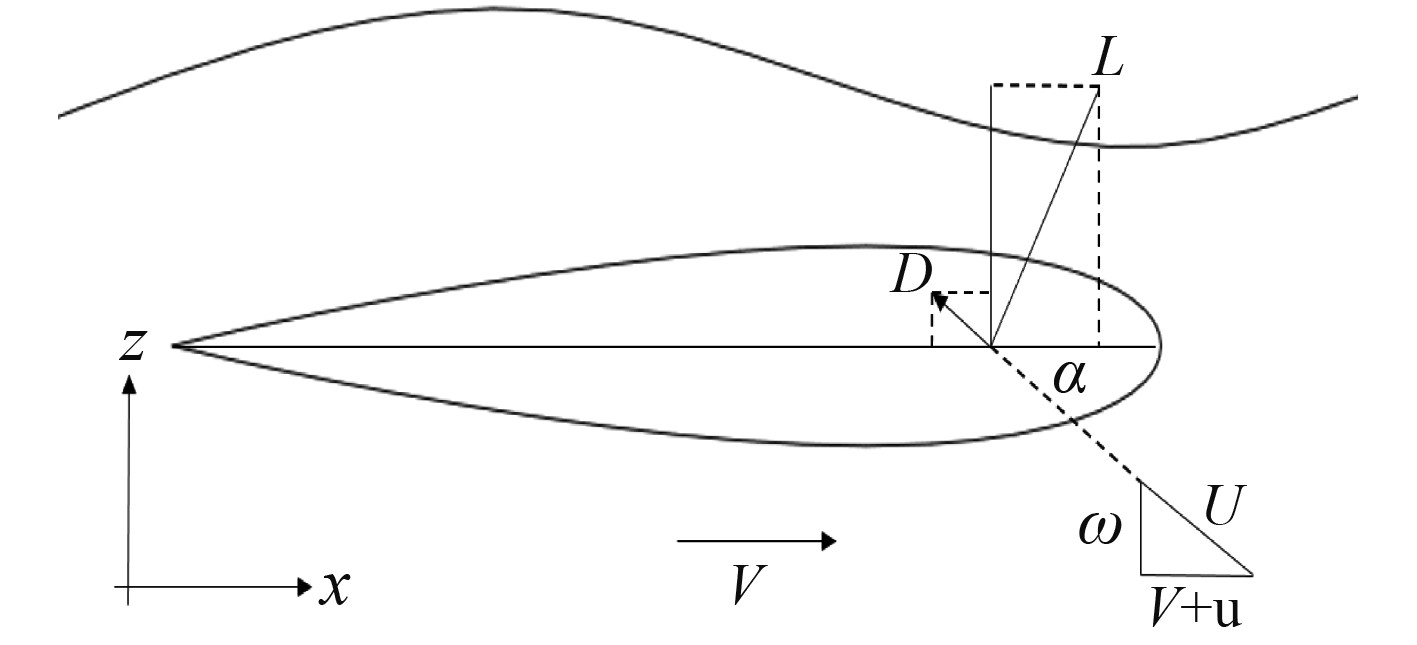
无限水深波浪中,水翼以水平速度V运动,如图4所示。
|
图 4 自由波面下水翼受力图 Fig. 4 Infinite water depth wave hydrofoil force diagram |
V+u是水翼与来流之间的水平相对速度,ω为垂向相对速度。则水翼与来流之间的相对速度为V+u与ω的矢量和设为U,设攻角为α,则有:
| $\sin \alpha = \frac{\omega }{{\left| U \right|}}\text{,}$ | (7) |
| $\cos \alpha {\rm{ = }}\frac{{V + u}}{{\left| U \right|}}\text{,}$ | (8) |
| $\tan \alpha = \frac{\omega }{{V + u}}\text{,}$ | (9) |
由机翼理论可得水翼生力为:
| $L = {C_L} \times 0.5\rho {U^2}S\text{,}$ | (10) |
水翼受到的阻力为:
| $D = {C_D} \times 0.5\rho {U^2}S\text{,}$ | (11) |
对于固定翼型,当其攻角在小范围内变化时其升力系数
水翼水平方向的合力为:
| $\begin{split} Fx =& D\cos \alpha - L\sin \alpha =\\& {C_D} \times 0.5\rho {U^2}S \times \frac{{V + u}}{{\left| U \right|}} - {C_L} \times 0.5\rho {U^2}S \times \frac{\omega }{{\left| U \right|}} =\\& 0.5\rho \left| U \right|S\left[ {{C_D} \times \left( {V + u} \right) - {C_L} \times \omega } \right]\text{。} \end{split} $ | (12) |
水翼竖直方向的合力为:
| $\begin{split} Fz =& D\sin \alpha + L\cos \alpha =\\& {C_D} \times 0.5\rho {U^2}S \times \frac{\omega }{{\left| U \right|}} + {C_L} \times 0.5\rho {U^2}S \times \frac{{V + u}}{{\left| U \right|}} =\\& 0.5\rho \left| U \right|S\left[ {{C_D} \times \omega + {C_L} \times \left( {V + u} \right)} \right]\text{,} \end{split} $ | (13) |
若使水翼产生其运动方向的推力即水翼水平方向的合力沿其运动方向,则需:
| $Fx = 0.5\rho \left| U \right|S\left[ {{C_D} \times \left( {V + u} \right) - {C_L} \times \omega } \right] < 0\text{,}$ | (14) |
要使式(14)成立则需满足:
| ${C_D} \times \left( {V + u} \right) - {C_L} \times \omega < 0\text{,}$ | (15) |
即升阻比
| $\frac{{{C_L}}}{{{C_D}}} > \frac{{V + u}}{\omega }\text{。}$ | (16) |
其中:
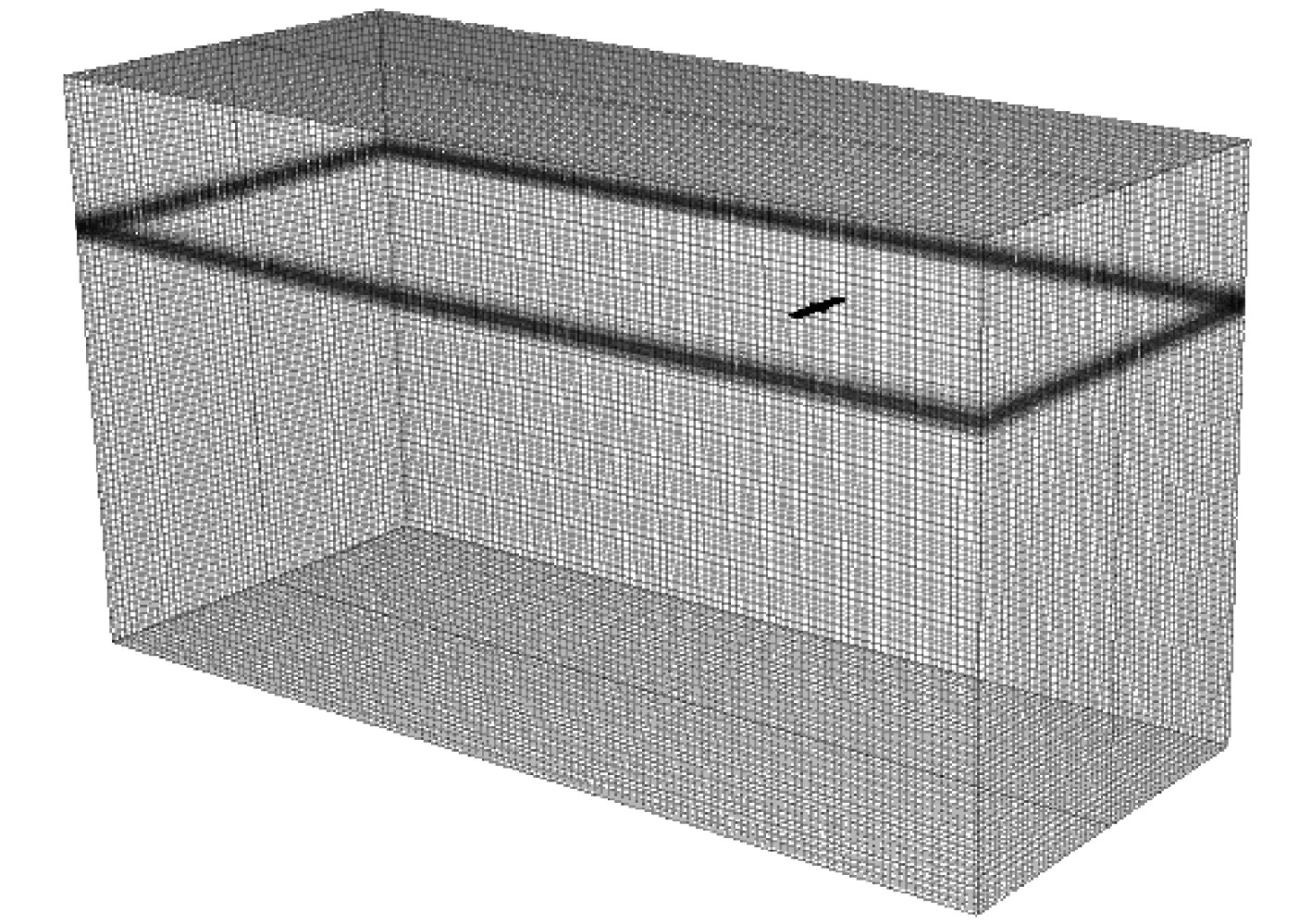
计算域的选取要保证对流场信息的准确捕捉,又要保证较少的网格数量以便节省计算成本。本文选用NACA0015翼型由于翼型来流方向为水翼弦长,水翼弦长较小所以以水翼展长L为基准来选取计算域,并结合相关文献选取计算区域为
|
图 5 数值水池与网格划分 Fig. 5 Numerical pool and meshing |
网格划分的合理性是影响计算结果准确性的关键因素,网格的划分即要考虑网格的质量又要考虑流长的流动特性,同时又要控制生成体网格的数量。综上所述,本文采用重叠网格技术。
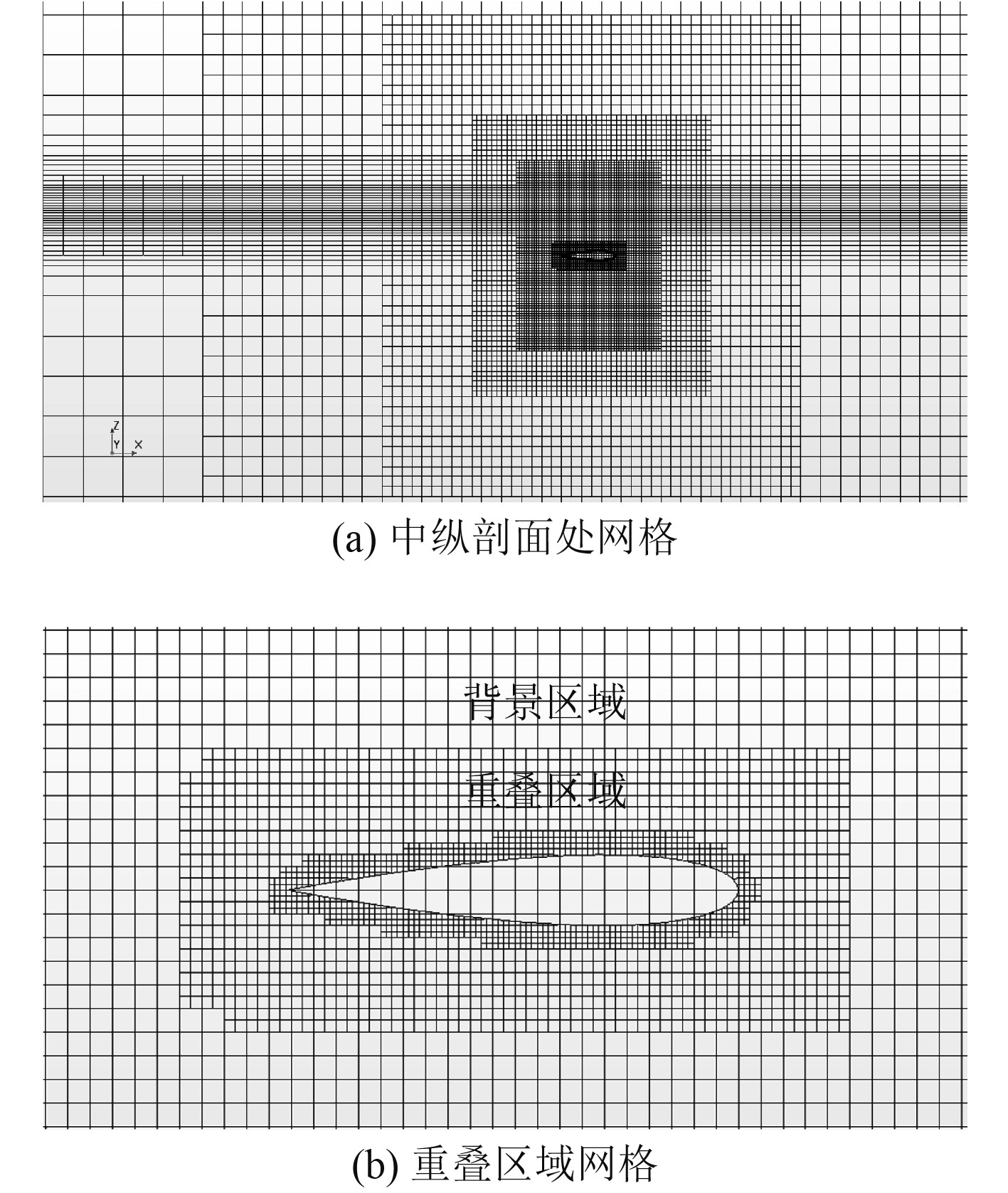
2.2 重叠网格技术重叠网格[9 − 10]技术需要将计算域划分为计算流场中的2个或多个子域,然后使用子域的运动来模拟边界的移动。这些子域和背景区域重叠,不论什么情况下,这些域之间都可以通过重叠网格交换信息。子域包含整个运动体,边界的形状由特定子域边界形状和运动体的运动确定。这种状态下子域和背景区域彼此独立。子域和背景区域由子域和背景区域的重叠部分耦合,因此耦合区域为两者之间的虚拟边界,每个子域和背景区域的网格是独立生成的。在耦合之后背景区域的一部分网格被“挖”,在“挖”的过程中子域网格与背景区域网格之间通过插值进行信息交换。
|
图 6 重叠网格方法 Fig. 6 Overlapping grid method |
1)仿真计算不同工况下NACA0015水翼产生的平均推力,与实验值进行对比验证模型与仿真方法的可行性;
2)水翼前缘凸起作为本文提出的新形式中的重要改进,对前缘凸起水翼进行数值模拟,分析有无凸起对水翼水动力性能的影响,并对凸起在水翼前缘分布长度这一参数对水翼性能的影响进行对比分析;
3)对耦合浮子的前缘凸起水翼进行数值模拟,计算在浮子作用下水翼产生的平均推力与无浮子凸起水翼以及无浮子NACA0015水翼产生的平均推力进行比较。分析浮子作为本文新形式中的第二点改进其对水翼性能的影响。
3.1 NACA0015模型与计算工况NACA0015模型及仿真方法验证。

|
图 7 NACA0015模型 Fig. 7 NACA0015 model |
本文选取NACA0015模型主尺度如表1所示。
|
|
表 1 NACA0015主尺度 Tab.1 NACA0015 main scale |
波浪计算工况分别取波长λ为1.55 m,2.31 m,3.1 m,3.8 m,4.3 m的规则波5种工况进行计算。对于计算结果在软件中采用报告监测绘图来实时监测水翼产生的推力,监测点选取整个模型表面,力选项选择压力和剪切,方向为波传播的负方向,即水翼前进方向。推力曲线如图8所示。可以看出,水翼的推力是程周期性变化的,其周期与图2(d)波长为3.8452的波浪周期基本一致。

|
图 8 λ=3.8452水翼推力时历曲线 Fig. 8 λ = 3.8452 hydrofoil thrust time curve |
由于水翼产生的推力是一个成周期变化的力,用瞬时推力来衡量水翼的推进性能时有很大的局限性并没有意义,水翼的推进性能用平均推力来衡量更合理。
假设水翼的瞬时推力为函数
| $\overline F = \frac{1}{{{t_2} - {t_1}}}\int_{{t_1}}^{{t_2}} {f\left( t \right){\rm{d}}t}\text{。} $ | (17) |
其中:
NACA0015水翼在1阶规则波波幅为0.045 m条件下推力仿真数据如表2所示。仿真结果与试验值基本吻合,初步判定仿真方法的可行性。
|
|
表 2 水翼在不同波长下的平均推力 Tab.2 Average thrust of hydrofoil at different wavelengths |
参阅相关文献提出水翼前缘凸起[7-10]作为本文新形式中的一项改进,如图9所示。研究凸起对水翼推进性能的影响,并讨论分析凸起在水翼前缘分布长度这一参数对水翼推进性能的影响。
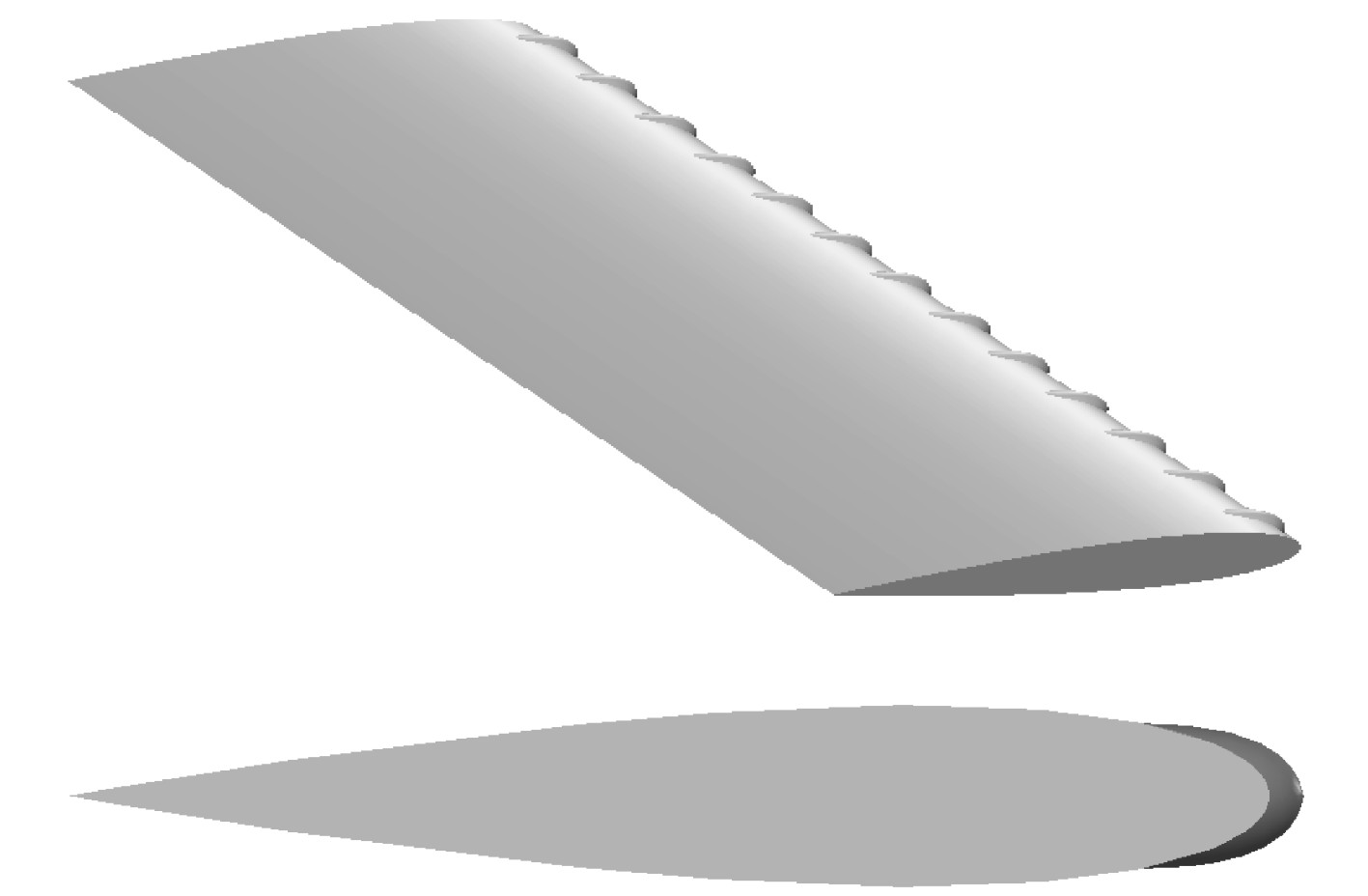
|
图 9 前缘凸起翼段 Fig. 9 Front raised hydrofoil |
研究表明海龟及座头鲸等海洋生物的鳍在大角度摆动时具有很高的推进效率,研究发现座头鲸前鳍上的凸起结构可以减小在拍动过程中的失速现象,这种结构大大提高了座头鲸前鳍的推进效率。本文在NACA0015机翼基础上在翼前缘加凸起作为新形式中的一项改进,通过与没有加凸起的翼型对比分析其推进性能。并分析凸起在翼前缘分布长度这一参数对水翼推进性能的影响。
当水翼前缘整个展长全部分布有仿生凸起,间距为1/25 L时,设波浪波长λ与水翼弦长C的比值为波弦比,其不同波弦比下平均推力与光滑翼平均推力对比如表3所示。
|
|
表 3 不同波弦比下两种机翼平均推力对比 Tab.3 Comparison of average thrust of two wings under different chord ratios |
可以看出,在4种波弦比工况下,前缘凸起水翼所产生的平均推力相较与光滑水翼产生的平均推力都有不同程度的提升。图10所示不同时间点下的水翼表面压力分布图可以一定程度上解释前缘凸起水翼平均推力产生的原因。
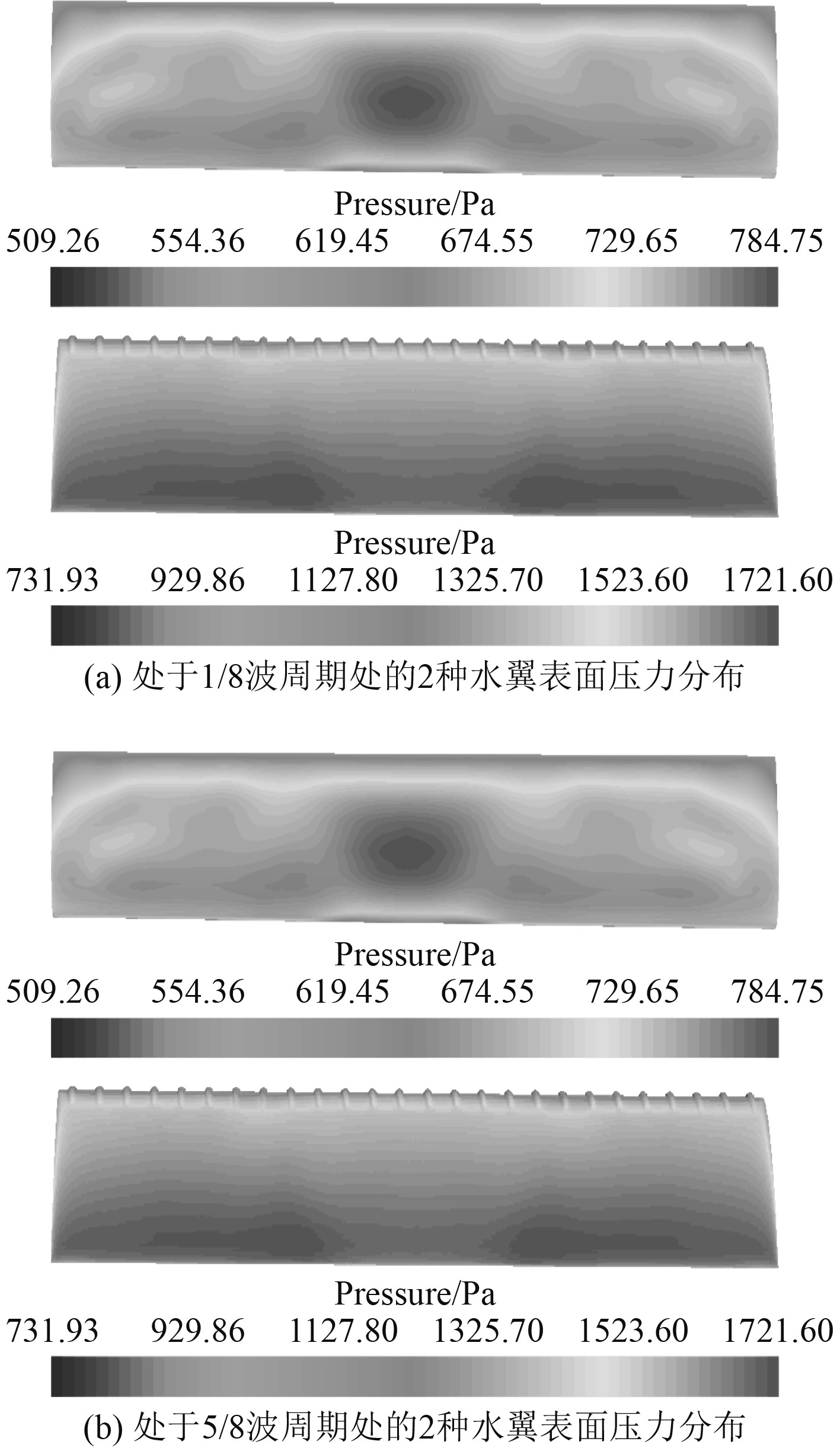
|
图 10 不同时间点下翼表面压力分布 Fig. 10 Lower wing surface pressure distribution at different time points |
可以看出,光滑翼表面压力分布较集中于翼段中部和翼两端部,而前缘凸起翼段表面无论是高压区还是低压区相较于光滑翼段分布更均匀,且分布面积更广。正是分布更均匀分布面积更广的正反面的压力差使得有凸起翼比光滑翼更容易产生升力,升力沿水平方向的分力即为水翼产生的推力。水翼前缘的凸起改善了来流中翼表面的压力分布,增加了最大与最小压力分布面积,增大了最大最小压差值,从而增加了平均推力的产生,改善了水翼的推进性能。
在相同工况下对翼段前缘凸起分布对水翼推进性能的影响进行探究,分别计算整个翼段展长前缘分布有凸起的全段翼、1/2展长前缘分布有凸起的1/2翼和1/3展长前缘分布有凸起的1/3翼,其推力计算结果如图11所示。可以看出,全段翼的平均推力要大于另外2种翼所产生的平均推力,且翼段前缘分布凸起的长度越长对增加产生的平均推力效果越好。这是因为前缘凸起可以改善翼表面的压力分布,使压力分布更均匀高压和低压区的面积更大增大了翼表面上下的压力差,使水翼产生更大的升力,从而提升了水翼产生的推力。而1/2,1/3翼只有部分区域分布有凸起,没有分布凸起的区域还是常规翼段,其表面压力分布没有得到改善,且当波弦比为43时1/2和1/3翼在处于波峰和波谷交换的时间点上,前端没有凸起的翼表面上产生了空泡,降低了水翼的推力如图11(b)所示,这也解释了图11(a)其推力曲线在波弦比43处骤降。

|
图 11 三种翼平均推力与翼表空泡图 Fig. 11 Three-wing average thrust and airfoil bubble diagram |
综上,翼段前缘凸起可以改善水翼上下表面的压力分布,增大上下翼面的压力差、增加水翼升力的产生,进而增加平均推力的产生。而凸起在翼前缘的分布也对平均推力的产生有影响,其沿翼前缘分布长度越长对平均推力的增加越好,整个翼前缘全部分布有凸起对提升平均推力效果最佳。
3.3 耦合浮子前缘凸起翼段推进性能研究本文提出新形式中的第2项改进是前缘带有凸起的水翼与浮子耦合。位于自由液面上的浮子与自由液面下的水翼耦合以浮子的升沉运动带动水翼的升沉和转动。
浮子在自由液面上在波浪作用下做升沉运动,通过浮子的升沉运动带动水翼的升沉和转动,解决随水深的增加波动能量指数衰减的问题。耦合浮子的水翼在波浪中产生的推力其峰值较无浮子的水翼有很大提升,其平均推力也有所增加。有无浮子的水翼其水翼推力时历曲线如图12所示。

|
图 12 相同工况下2种水翼推力曲线 Fig. 12 Two hydrofoil thrust curves under the same working conditions |
由图12可知,在有浮子的条件下水翼产生的推力、阻力峰值都明显增加,但推力峰值增加更显著。只有平均推力为正时水翼才有推进效果,虽然阻力峰值有所增加,但推力峰值的增加不仅抵消了阻力的增加还提高了平均正推力,增加了水翼的推进效果。
由图13两组对比图可以看出,在相同入水深度、相同波浪参数下水翼的升沉和纵摇幅值都有很大程度的增加。波动能量随入水深度增加呈指数下降的问题由于浮子的存在得到改善,浮子带动水翼升沉和转动随着水翼运动幅值的增加,水翼所产生推力峰值也随之增加,最终提高水翼平均推力。
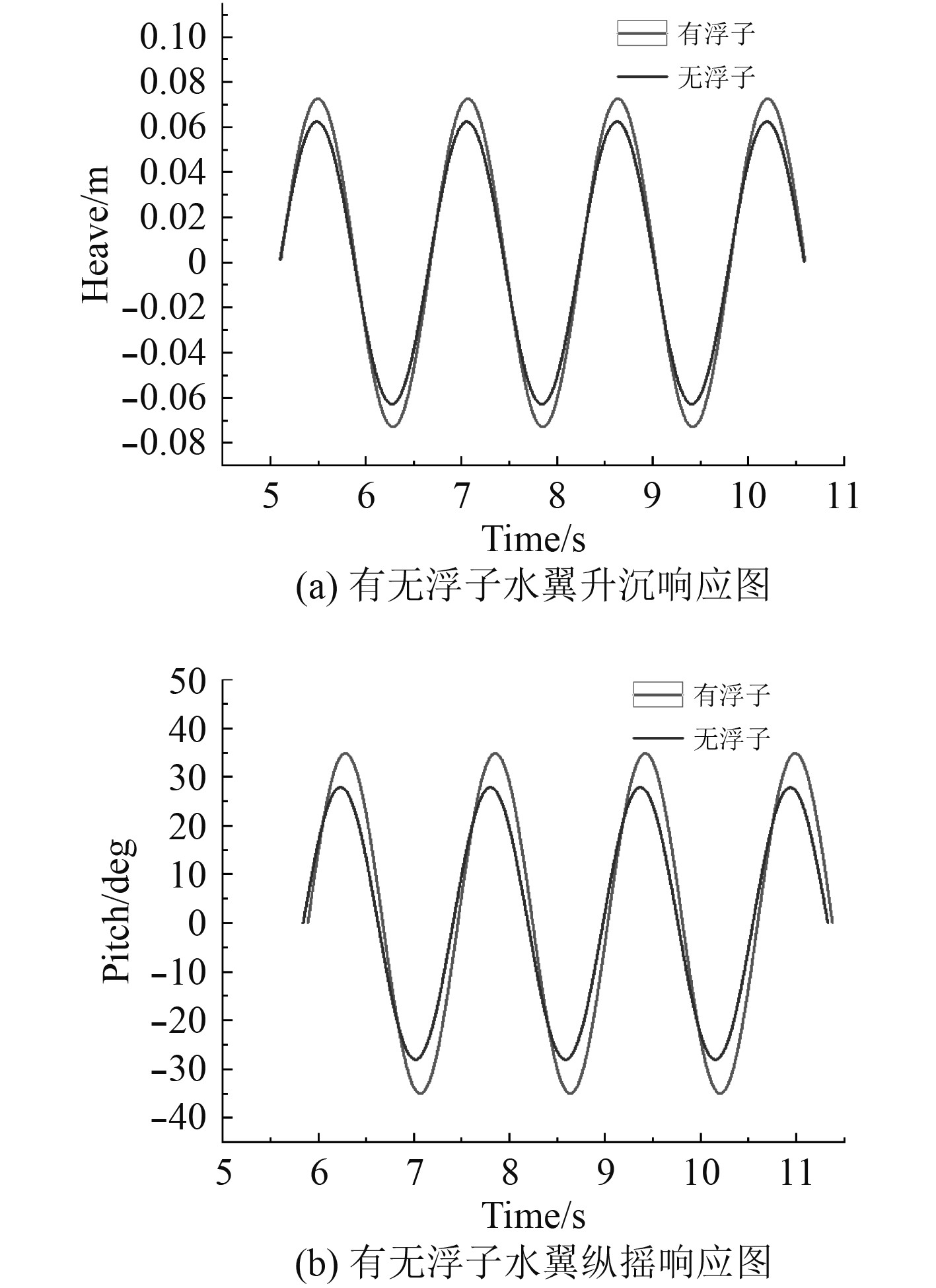
|
图 13 相同工况下有无浮子水翼响应图 Fig. 13 Whether there is a float hydrofoil response diagram under the same working conditions |
由图14可知,在浮子的作用下水翼产生的平均推力变化曲线与无浮子水翼平均推力变化曲线基本一致,在各波弦比下相较于无浮子的水翼均有提高,但随着波弦比的增加两者之间的差距逐渐减小。平均推力提升最大是在波弦比在15~20之间。
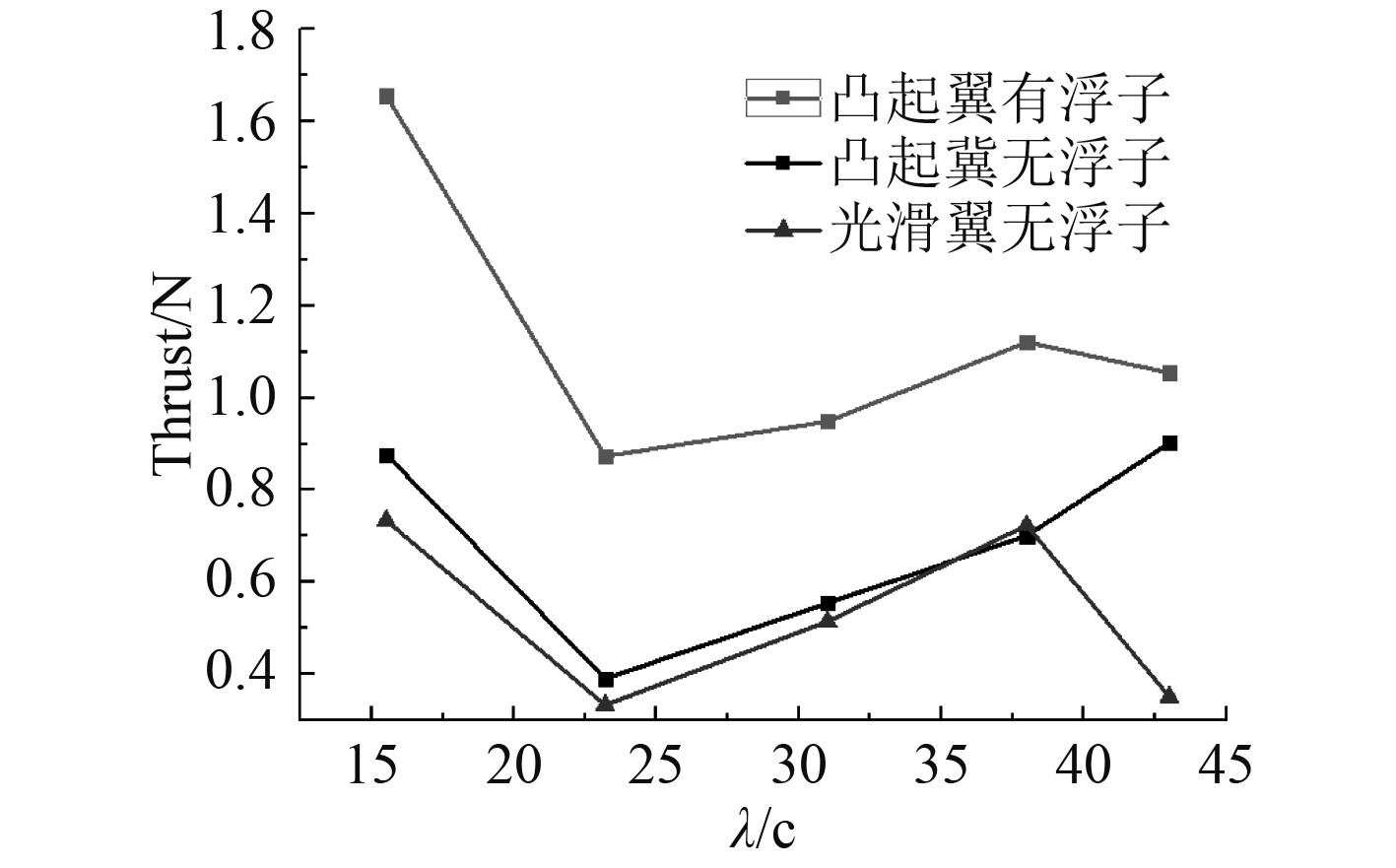
|
图 14 有无浮子水翼不同波弦比平均推力曲线 Fig. 14 The average thrust curve of different chord ratios with or without float fins |
本文基于CFD技术,运用重叠网格技术,建立数值水池,对NACA0015模型及仿真方法进行验证。分步对前缘凸起水翼、与浮子耦合的水翼进行了数值计算,分析计算结果得到以下结论:
1)前缘有凸起翼段由于凸起的作用,改善了水翼表面的压力分布,使得高低压区分布更均匀,分布面积更广,增大了水翼上下表面的压力差,使得水翼更容易产生升力。凸起的存在减少了水翼在大攻角时翼表面涡脱落的现象,减少了水翼能量损失,进而增加了升力沿水平前进方向的分力即水翼推力的产生。
2)浮子的存在改善了波动能量沿水深指数衰减的问题,增加了自由液面下水翼的运动幅值,从而增加了水翼产生的推力。
| [1] |
徐文华, 振动翼能量采集与推进性能研究[D].哈尔滨: 哈尔滨工程大学.
|
| [2] |
王添诚, 振动翼近自由液面水动力特性研究[D].哈尔滨: 哈尔滨工程大学.
|
| [3] |
高昕, 水翼推进性能分析及实验研究[D]. 哈尔滨: 哈尔滨工程大学.
|
| [4] |
TERAO Y. Wave devouring propulsion system-from concept to trans-pacific. [J]. Proceeding of the ASME2009 28th international Conference on Ocean, Offshore and Arctic Engineering.
|
| [5] |
HUANG Sheng-wei, WU Tsung-lin, HSU Yu-ting . Effective energy-saving device of eco-ship by using wave propulsion. [J]. 2/16|2016IEEE.
|
| [6] |
TERAO, Y. SAKAGAMI. N. Design and development of an autonomous wave-prwered boat with a wave devouring propulsion. [J]Vol. 29, No. 1, 89-102
|
| [7] |
王国付.仿鲸鱼鳍凹凸前缘翼型流动分离控制及应用研究[D]. 北京: 中国科学院大学.
|
| [8] |
张佐天, 仿生前缘凹凸鳍性能理论及实验研究[D]. 哈尔滨: 哈尔滨工程大学.
|
| [9] |
Dongmei YANG. Fei SHAO. Chuanglan LI. Overlapping Grid Technique For Numerical Simulation of a Fast-Cruising Catamaran Fitted with Active T-Foils[J]. Joumal of Marine Science and Application, 2019, 18: 176-184. DOI:10.1007/s11804-019-00077-7 |
| [10] |
Alex SKILLEN. The overset grid method, applied to the solution of the incompressible Naver-Stokes equations in two and three spatial dimensions [D].School of Mechanical, Aerospace and Civil Engineering.
|
| [11] |
郝红彬, 一种波浪推进装置的设计和试验研究[D]. 哈尔滨: 哈尔滨工程大学.
|
 2020, Vol. 42
2020, Vol. 42
