2. 浙江工业大学,浙江 杭州 310023
2. Zhejiang University of Technology, Hangzhou 310023, China
为了保证船体结构满足安全要求,船体梁除了需要满足弯曲强度之外,也应满足剪切强度的要求。以油船为例,当其相邻的货舱所装货油的重量相差较大时,尤其是一个货舱为空舱时,那么剪切力就会出现在两舱的横向舱壁及附近的结构上,有可能导致船体结构崩溃[1]。
船体梁极限剪切强度是指船体梁发生剪切屈曲破坏所能承受的最大的剪力,它不同于一般的结构剪切应力和板格理想弹性的剪切屈曲计算,很难获得精确的理论解。目前国内外大量文献都集中于船体梁极限弯曲强度以及残存强度的研究,关于极限剪切强度和受损后残存剪切强度的研究还很少[2]。国际船舶结构大会(ISSC)及众多学者[3-5]推荐采用非线性FEM计算板格加筋板以及船体梁的极限强度。Shama M.A.[6]发现船舶的舷侧板可能产生应力,船体剖面参数会影响最大剪应力值,可以通过剪应力简单估计船体剖面极限剪力。胡勇和崔维成[7]主要分析了散货船受到碰撞损伤后的极限承剪能力,以及影响碰撞破损船体极限剪力的因素,提出了初始屈服剪力计算公式来计算船体梁碰撞损伤后的极限能力。
本文基于有限元数值模拟和理论分析,依次研究了板格、加筋板、船体梁极限剪切强度特性和计算方法,提出了船体梁极限剪力计算公式,并进行了实船的计算和非线性有限元的验证。结果表明,本文所提方法具有较高的精度,能够方便地应用于船舶结构设计和强度校核。
1 板格临界剪应力计算船体结构承受剪力载荷作用时,其绝大部分是由船体板格承受,因此本节将扶强材和主要支撑构件作为板格的简支边界条件,重点研究板格的剪切极限承载力。
设板格的四边受剪力
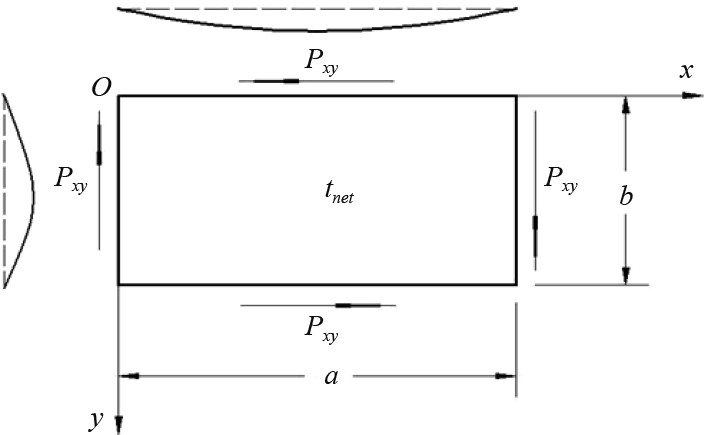
|
图 1 均匀受剪的四边简支板格 Fig. 1 Simplified supported panel with uniform shear force |
板的小挠度理论认为薄板屈曲时板的挠度远小于其厚度,中面在板屈曲时产生的薄膜拉力可忽略不计;板的大挠度理论认为,当板边缘的支承构件具有较大的刚度时,板的中面会产生相当大的薄膜拉力,板中的应力重分布和薄膜拉力可延缓挠度的发展,起着对板的支持作用,从而提高板的承载力,使其远远超过板的分岔屈曲载荷。
目前,板格极限强度计算通常采用大挠度理论,允许载荷重新分布,认为板格的极限剪切强度是板格的边缘纤维达到材料屈服强度时的临界剪应力。《钢质海船入级规范》[8]对于如图1所示,四边简支的板格临界剪应力计算公式具体规定如下:
受剪板格的临界应力
| ${\tau _{cr}} = {C_\tau }\frac{{{R_{eH - P}}}}{{\sqrt 3 }}\text{。}$ | (1) |
式中:
| $\begin{array}{l} {C_\tau } = \left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{c}} 1&\text{,}{}&{\lambda \leqslant 0.84}\text{,} \end{array}} \\ {\dfrac{{0.84}}{\lambda }\begin{array}{*{20}{l}} \text{,}{}&{\lambda > 0.84}\text{。} &{} \end{array}} \end{array}} \right.\end{array} $ | (2) |
| $\lambda = \sqrt {\frac{{{R_{eH - P}}}}{{K{\sigma _E}}}}\text{。} $ | (3) |
| $ K = \left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} {\!\!\!\!\!\!\!\! \sqrt 3 \cdot \left[ {5.34 + 4.0{{(b/a)}^2}} \right]\text{,}}\\ {\!\!\!\!\!\!\!\! \sqrt 3 \cdot \left[ {4.0 + 5.34{{(b/a)}^2}} \right]\text{,}} \end{array}}&{\begin{array}{*{20}{l}} {}\\ {} \end{array}}&{\begin{array}{*{20}{l}} {{\text{当}}a \geqslant b{\text{时}\text{,}}}\\ {{\text{当}}a < b{\text{时}\text{。}}} \end{array}} \end{array}} \right. $ | (4) |
| ${\sigma _E} = 0.9E{(\frac{t}{b})^2}\text{。}$ | (5) |
式中:E为材料的弹性模量,N/mm2;t为板格厚度,mm;a为板格长度,mm;b为板格宽度,mm。
本文选取多艘实船的垂向和斜向板格(共计30块),建立板格剪切屈曲有限元模型,进行极限剪应力有限元计算[9],并与规范板格临界剪应力公式的计算结果做了比较。计算结果如图2所示,图3为典型板格剪切屈曲极限状态的变形图(放大100倍)。
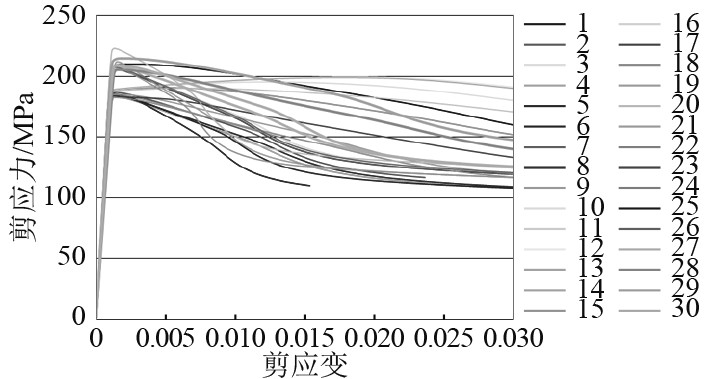
|
图 2 板格应力—剪应变图 Fig. 2 Panel stress-strain curve |

|
图 3 极限状态时的变形图(100倍) Fig. 3 Deformation at ultimate condition(Amplify 100 Times) |
30个板格的剪切屈曲有限元计算结果与现行海船规范板格临界剪应力公式的计算结果的平均偏差为5%之内,表明现行规范公式对于板格的临界剪应力计算具有较高的精度。
2 加筋板的极限剪力计算文献[7]指出当加筋板所有的板格都达到极限剪切强度时,则认为整个加筋板达到剪切极限状态。由此可推出加筋板极限剪力公式:
| ${Q_{u1}} = \frac{1}{{\sqrt 3 }}\sum\limits_{i = 1}^q {{C_{\tau ,i}}} \cdot {b_i} \cdot {t_i} \cdot {R_{eH - P}}_{,i}\text{。}$ | (6) |
式中:
采用板格极限剪力累加建立加筋板的极限剪力式(6)和加筋板剪切屈曲的非线性有限元模型[9],进行实际船舶的10余块加筋板的极限剪力的计算,确定加筋板的极限剪切强度特性,讨论板厚和扶强材类型对式(6)精度的影响。
图4为某一加筋板的3跨(强力构件未建模,用约束替代)5筋模型的剪切极限状态下的变形图(放大10倍)。由图4可以看出,板格发生了明显的剪切变形,扶强材也出现了不同程度的倾斜。

|
图 4 极限状态时的变形图(10倍) Fig. 4 Deformation at ultimate condition(Amplify 10 Times) |
为考察加筋板的极限剪力式(6)对不同板厚和扶强材的适应性,进行14块加筋板的公式法和有限元的计算对比,结果如图5所示。
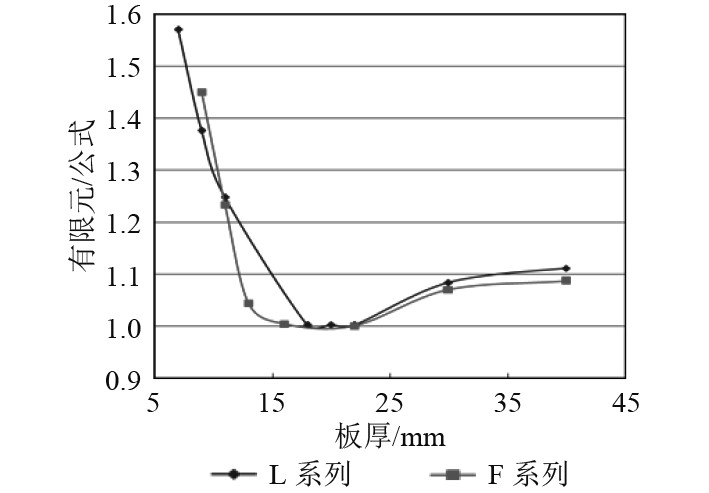
|
图 5 板厚的影响(L为角钢,F为扁钢) Fig. 5 Effect of panel thickness(L is angle bar,F is flat bar) |
可知:
1)板厚小于11 mm时,加筋板有限元剪力与公式剪力的比值随着板厚的增大而减小,差异始终在15%以上;
2)当11 mm<板厚≤30 mm时,加筋板有限元剪力值与公式剪力值吻合最好差异在7%以内。
为了考察加筋板的极限剪力式(6)对不同扶强材的适应性,取L系列(角钢)的10块加筋板,F系列(扁钢)的7块加筋板和T系列(T型材)的3块加筋板进行了公式法和非线性有限元的对比分析,结果如图6所示。
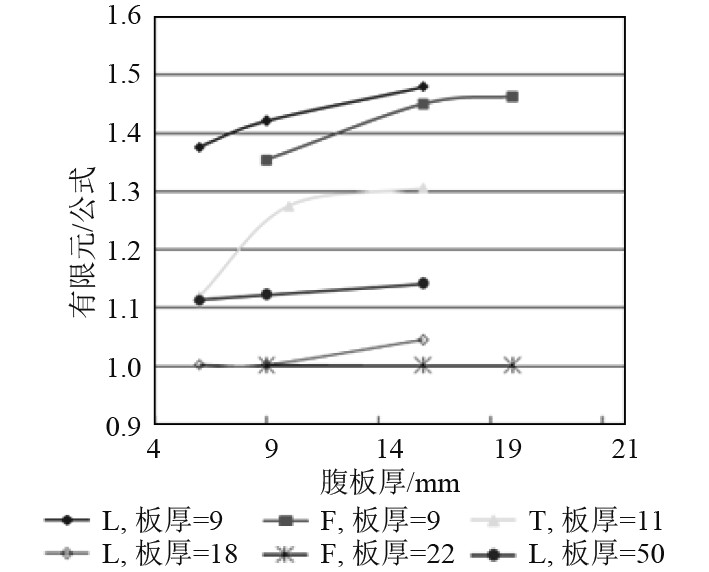
|
图 6 扶强材类型的影响(L为角钢,F为扁钢,T为T型钢) Fig. 6 Effect of stiffeners type(L is angle bar,F is flat bar,T is T bar) |
可知:
1)随扶强材增大,加筋板的有限元剪力值与公式剪力值差异有不同程度增大,意味着扶强材增大,参与剪切的程度越大;
2)同样尺寸,对加筋板抗剪承载力提高的程度依次为T型材、L角钢,F扁钢;
3)对于较薄的加筋板,加强筋对加筋板剪切强度影响较大,加强筋的抗剪作用不容忽视;
4)对于中厚的加筋板,加强筋的影响较小,加强筋的抗剪作用可以忽略。
3 船体梁横剖面的极限剪力计算 3.1 梁剖面极限剪力公式基于加筋板极限抗剪强度的计算方法,认为当船体梁横剖面内所有承剪的加筋板的板格均达到极限剪切强度时,船体梁达到剪切极限状态。基于该假设,可将剖面内所有垂向板格的极限剪力以及斜向板格极限剪力的垂向分量累加,得到船体梁剖面垂向极限抗剪能力的计算公式如下:
| ${Q_U} = \frac{1}{{\sqrt 3 }} \cdot \sum\limits_{i = 1}^n {{{\rm{C}}_{\tau ,i}}} \cdot {b_i} \cdot {t_i} \cdot {R_{eH - P}}_{,i} \cdot {\rm{cos}}{\theta _i}\text{。}$ | (7) |
式中:n为计算剖面上所有垂向和斜向板格的数目;
针对某大型运输船的船中剖面、距首0.25L和距首0.75L最大剪应力作用区域的3个剖面,采用本文方法,以及Abaqus有限元软件,建立一跨舱段模型(长度为主要横框架之间距离),进行考虑几何和材料非线性的有限元计算[9],分别获得3个剖面的剪切极限强度以及多种可能的破损(每个剖面分破损1、破损2、破损3,以及相应的程度,共计7种)后的剖面剩余剪切强度,如表1所示。
|
|
表 1 典型剖面极限剪切强度有限元/规范剪力汇总 Tab.1 FEM/prescriptive ultimate shear stress of typical sections |
由表1可以看出:
1)通过板格极限剪切强度的累加计算船体梁的极限剪切强度,与非线性有限元的结果吻合较好,误差基本上小于15%,个别较大的原因是应用公式计算时,忽略的板格偏多;
2)式(7)即可适用于完整船体梁的极限强度计算,也适用于船体梁破损后的残存强度计算;
3)经分析,船体梁的极限抗剪能力计算时,除了垂向板格之外还应该包括斜板。
4 结 语本文通过板格、加筋板到船体梁的系列研究,获得了船体梁的极限抗剪强度的计算公式,能够快捷、方便地应用于船舶结构设计和强度校核中,具有较强的工程使用价值。主要结论如下:
1)《钢质海船入级规范》[8]等船级社规范中板格的极限剪应力计算公式,与有限元计算结果相比具有较高的精度,可用于板格临界剪应力的快速计算分析;
2)扶强材大小和和形状对加筋板的剪切极限能力有一定的影响:对于较薄的加筋板,加强筋对加筋板剪切强度影响较大,加强筋的抗剪作用不可忽略;对中厚的加筋板,加强筋的影响较小,加强筋的抗剪作用可忽略;
3)经分析,可通过板格极限剪切强度的累加计算船体梁的极限剪切强度和破损后的残存极限剪力;船体梁的极限抗剪能力计算时,为提高计算精度,除了垂向板格之外还应包括斜板;
4)通过板格极限剪切强度的累加计算船体梁的极限剪切强度,与非线性有限元的计算结果吻合较好,能够高效、方便地应用于船舶结构设计和强度校核中。
| [1] |
IACS. Double Hull Oil Tankers -Guide lines for Surveys, Assessment and repair of hull structures[S]. International Association of Cryospheric Sciences (IACS) rec No. 96, 2007.4.
|
| [2] |
PAIK J K, KIM B J, SEO J K. Methods for ultimate limit state assessment of ships and ship-shaped off shore structures: part III hull girders[J]. Ocean Engineering, 2008, 35: 281-286. DOI:10.1016/j.oceaneng.2007.08.008 |
| [3] |
SIMONSEN B C, ESTEFEN S F. Ultimate strength[C]// proc of 15th international ship and off shore structure congress. San Diego, 2003: 265-328.
|
| [4] |
YAO T, BRUNNER E. Ultimate strength[C]// proc of 16th international ship and off shore structure congress. Southamptopm, 2006: 353-438.
|
| [5] |
PAIK J K, BRUNNER E. Ultimate strength[C]// proc of 17th international ship and of shore structure congress. Korea Seoul, 2009: 375-474.
|
| [6] |
SHAMA M A. Shear stress in bulk carriers due to shear loading[J]. Journal of Ship Research, 1975(09): 155-163. |
| [7] |
胡勇, 崔维成. 散货船碰撞损伤后的极限剪切强度[J]. 船舶力学, 2004(04): 68-79. DOI:10.3969/j.issn.1007-7294.2004.04.011 |
| [8] |
中国船级社. 钢质海船入级规范(第9篇散货船和油船结构(CSR))[S]. 北京: 人民交通出版社, 2018.
|
| [9] |
方梦丹. 船体梁极限剪切强度计算方法研究[D]. 杭州: 浙江工业大学, 2016.
|
 2020, Vol. 42
2020, Vol. 42
