2. 中国船舶集团公司第七一三研究所,河南 郑州 450015;
3. 河南省水下智能装备重点实验室,河南 郑州 450015
2. The 713 Research Institute of CSSC, Zhengzhou 450015, China;
3. Henan Key Laboratory of Underwater Intelligent Equipment, Zhengzhou 450015, China
水下非接触爆炸冲击载荷是舰、艇载设备设计时必须要考虑的载荷环境。水下自主航行器、火箭等设备均为细长结构,当其在贮运筒中贮存时,单个减振垫无法对其实现缓冲减振保护作用。一般来说,会沿轴向布置多圈橡胶减振垫,将细长结构与储运筒隔离,达到缓冲减振的目标。但是冲击载荷作用下细长结构容易发生弯曲变形,减振垫不合理的刚度设计与布局将会导致细长结构连接部位弯矩过大,导致结构损伤,降低细长结构的安全可靠性。通过降低减振垫的刚度可以减小传递到细长结构的冲击载荷,但细长结构与储运筒的间隙有限,过小的减振垫刚度会导致冲击过程细长结构位移过大,进而与储运筒内部结构发生碰撞。所以,在设计前期,通过仿真及相应的优化算法对细长结构减振垫刚度及其布置进行优化设计就变的十分关键。
目前,优化算法在设计中的应用已日趋成熟。陈潇凯等[1]结合响应面法和二次序列规划法,对汽车正面抗撞性进行了优化;Marcus等[2]利用神经网络法建立响应面,实现了对吸能盒外形尺寸的优化设计。姜衡等[3]将响应面法与有限元仿真、遗传算法等相结合,对某加工中心整机质量和第1阶固有频率进行多目标优化,在保证加工中心整机动静态性能不降的前提下,减轻了设备质量。
本文以某型水下航行体(复杂细长结构)减振系统为研究对象,研究水下航行体减振系统缩聚梁动力学建模方法、冲击动响应计算方法、减振垫位置参数化建模方法、基于二次序列规划算法的水下航行体减振系统优化设计方法,降低了冲击过程水下航行体危险截面弯矩,提高了水下航行体的抗冲击能力。
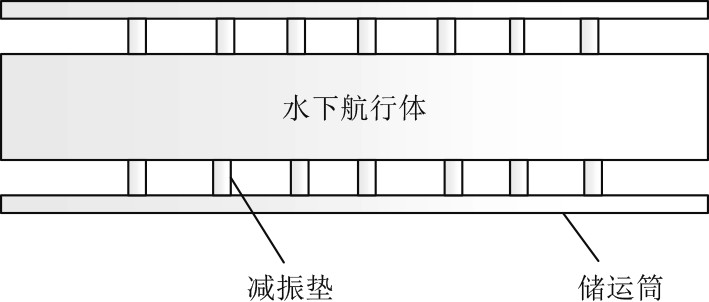
1 水下航行体减振系统动力学建模某水下航行体为细长薄壁壳结构,壳体内部安装大量电子设备,贮存在储运筒中,为减小传递到水下航行体的冲击载荷,在水下航行体与储运筒之间均匀布置7圈减振垫,如图1所示。
|
图 1 水下航行体减振系统示意图 Fig. 1 Schematic diagram of underwater vehicle vibration reduction system |
水下航行体内部安装大量电子、动力设备,在研究其整体动力学特性时,三维精细化建模既没必要也不现实,一般会采用梁模型开展研究,如美国土星5号运载火箭即通过建立梁模型对全箭结构的动力学特性进行了研究计算[4]。
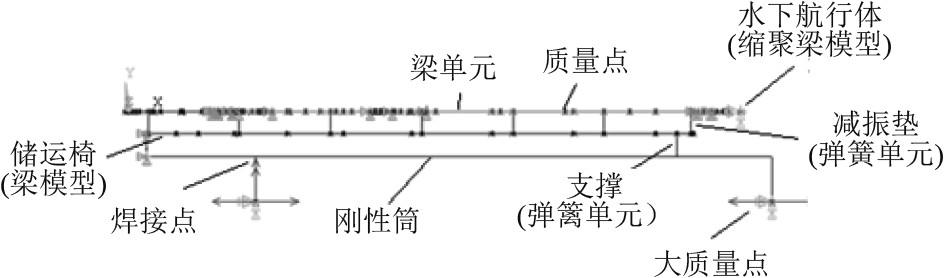
本文使用Ansys三维梁建模功能建立该水下航行体减振系统动力学计算模型。首先根据该水下航行体及其储运筒刚度与质量分布特点,通过刚度的等效与质量的凝聚,建立水下航行体、储运筒三维Beam188梁模型。储运筒外部配有刚性筒,与母体焊接连接,刚性筒上端与储运筒刚性连接,下端与储运筒通过弹性支撑连接。减振垫、弹性支撑均使用三向弹簧combin14单元模拟。建立后的水下航行体减振系统缩聚梁模型如图2所示。
|
图 2 水下航行体减振系统动力学计算模型 Fig. 2 Dynamics calculation model of underwater vehicle vibration reduction system |
减振系统初始设计:每圈减振垫刚度为5E7 N/m,7圈减振垫均匀布置在水下航行体与储运筒之间。
缓冲减振系要求:冲击过程减振垫最大压缩量不大于18 mm,水下航行体部分位置抗弯能力较弱,称为危险截面,许可弯矩不大于300 kNm。
2.2 冲击载荷选取本文以德军标BV043/85规定的冲击输入谱模拟水下爆炸冲击载荷。
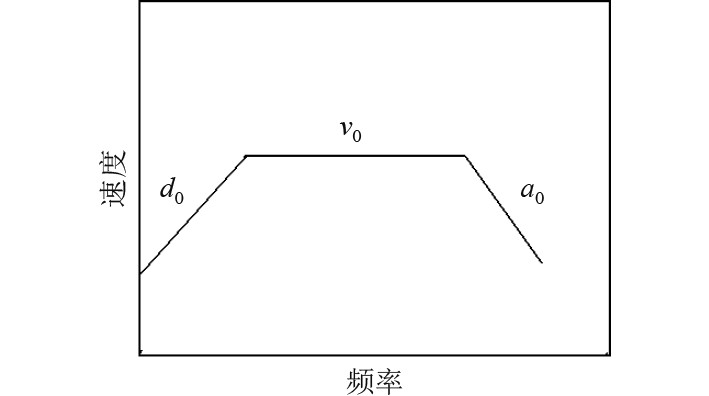
BV043/85规定的冲击输入是三折线谱[5],若采用谱分析计算方法,则可以三折线谱作为输入载荷直接施加到模型上,但更常用的是将三折线谱转换为加速度-时间载荷的正负三角波,这样转换后就可以采用瞬态完全法计算模型冲击动响应,限制更少。
|
图 3 三折线冲击输入谱 Fig. 3 Three-fold line shock input spectrum |
|
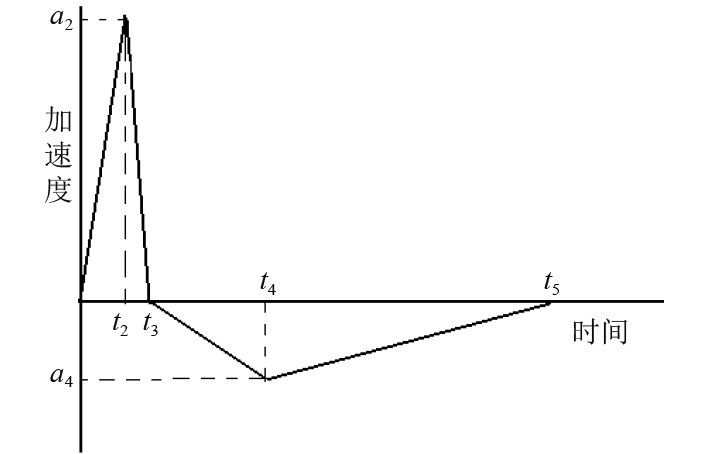
图 4 正负三角波加速度载荷 Fig. 4 Positive and negative triangle wave acceleration load |
三折线谱转换为正负三角波的的公式为:
| ${a_2} = 0.6{a_0}\text{,}$ |
| ${V_1} = 0.75{v_0}\text{,}$ |
| ${t_3} = {{2{V_1}} / {{a_2}}}\text{,}$ |
| ${t_2} = 0.4{t_3}\text{,}$ |
| ${t_5} = {t_3} + \frac{{6{d_0} \times 1.05 - 1.6{a_2}t_3^2}}{{1.6{a_2}{t_3}}}\text{,}$ |
| ${a_3} = {{{a_2}{t_3}} / {\left( {{t_3} - {t_5}} \right)}}\text{,}$ |
| ${t_4} = {t_3} + 0.6\left( {{t_5} - {t_3}} \right)\text{,}$ |
设三折线谱为:低频段(<10 Hz)按位移0.02 m输入,中频段(10~160 Hz)按1.2 m/s输入,高频段(160~600 Hz)按加速度125 g输入,则经转换计算得出的正负三角波参数值为:
| $\begin{split}&{a_2} = 75\;{\rm{g}},\;{a_4} = - 43.58\;{\rm{m}}/{s^2},\;{t_2} = 0.98\;{\rm{ms}},\;\\&{t_3} = 2.4\;{\rm{ms}},\;{t_4} = 27.2\;{\rm{ms}},\;{t_5} = 43.8\;{\rm{ms}}\text{。}\end{split}$ |
本文使用该正负三角波作为系统冲击响应计算的输入载荷。
2.3 阻尼设置由于本文采用瞬态完全法进行系统冲击动响应计算,不能直接使用恒定阻尼比,因而将恒定阻尼比转换为瑞利阻尼。转换时一般可将
基于瞬态动力学方法[6]计算缩聚梁模型系统的冲击动响应,由于Ansys不能直接在模型上施加正负三角波载荷(加速度-时间载荷),本文使用大质量法解决加速度-时间载荷施加问题,即先定义大质量点,并刚性连接大质量点与模型上的冲击载荷输入节点,最后将加速度-时间载荷转换为力-时间载荷,将其施加到大质量点上,通过大质量点将冲击载荷传递到焊接处节点。一般大质量点的质量应不小于系统质量的100倍。
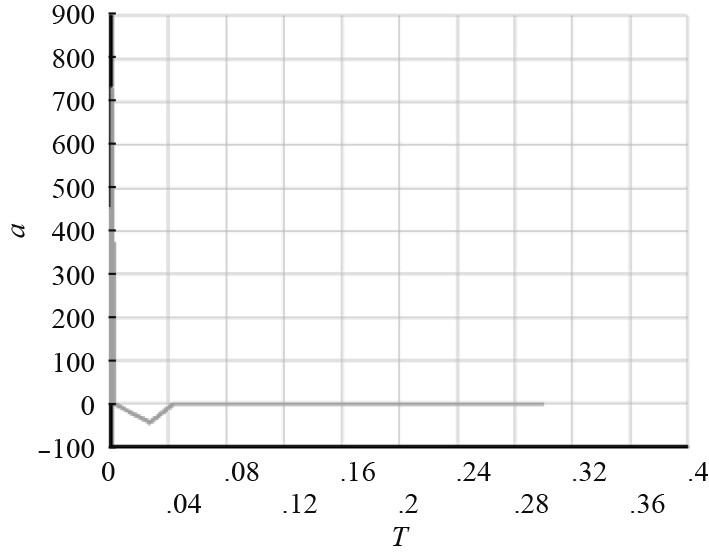
2.5 计算结果分析提取冲击过程焊接点处的加速度响应,如图5所示。焊接点的加速度响应与2.2节要求的冲击输入正负三角波完全相同,说明大质量法可以较好地将加速度-时间载荷施加到刚性筒焊接点处。
|
图 5 焊接点处的加速度响应(正负三角波) Fig. 5 Acceleration response at the welding point (positive and negative triangle wave) |
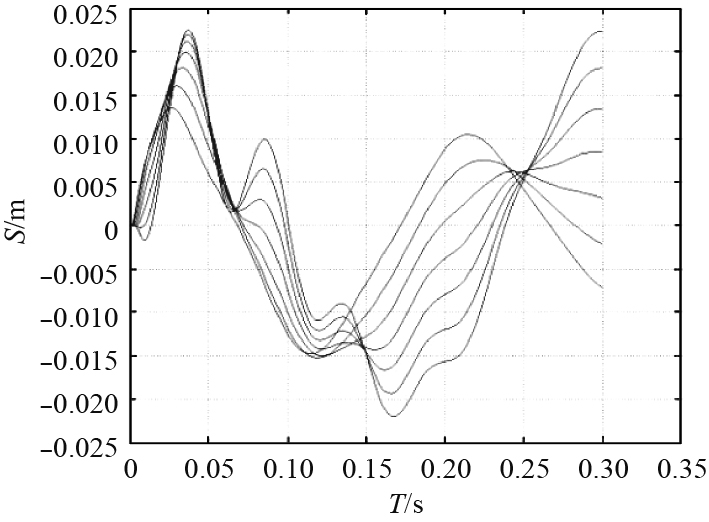
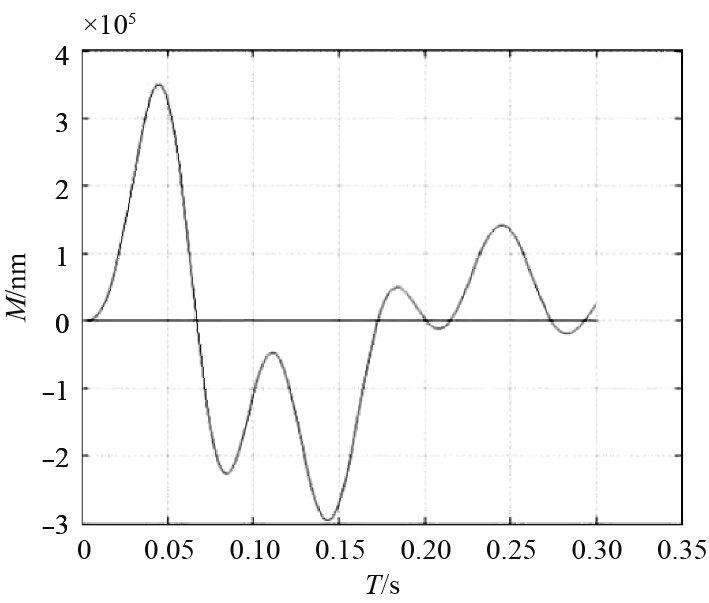
提取冲击载荷下各圈减振垫压缩量变化如图6所示。减振垫最大压缩量为22.5 mm,约出现在0.04 s时刻,大于设计约束值(设计要求减振垫最大压缩量不大于18 mm)。提取冲击过程航行体危险截面的弯矩,如图7所示。冲击过程航行体危险截面最大弯矩为350 kNm,也已超出设计约束(不大于300 kNm)。
|
图 6 冲击过程7圈减振垫的压缩量 Fig. 6 The compression amount of the shock absorber with seven circle during the impact process |
|
图 7 冲击过程航行器危险截面弯矩 Fig. 7 Bending moment of dangerous section of vehicle during impact process |
计算表明,在水下航行体与储运筒间均布7圈整圈刚度为5E7N/m减振垫,不能满足系统缓冲减振设计要求。
3 减振系统优化 3.1 减振垫位置参数建模航行体减振系统优化设计变量为减振垫的刚度及位置,为完成减振系统的优化设计计算,首先必须实现减振垫刚度、位置的参数建模。
模型中减振垫是以弹簧单元来模拟的,弹簧单元有2个节点,一端节点为水下航行体单元节点,另一端节点为储运筒节点,因而改变减振垫位置需要同步改变水下航行体、储运筒单元节点位置。但是水下航行体、储运筒模型是缩聚梁模型,其单元节点位置反映了结构的质量分布、刚度分布,不能更改,也就是不能直接通过改变位置坐标的方法改变减振垫位置,即减振垫位置是非参数化。因而,减振垫位置参数化建模是减振系统优化设计计算首先需要解决的问题。
本文减振垫位置参数化建模方法如下:
1)构建2个数组,依照节点在细长结构缩聚梁模型中的顺序在数组中分别存储节点编号、节点横向坐标值,分别记为节点编号数组、节点位置数组。另构建一个数组,存储细长结构材料、截面特性编号。
2)根据减振垫位置移动需要,改变相应节点位置数组的元素值。
3)使用冒泡法程序对节点位置数组元素值进行从小到大排序,并相应的同步交换节点编号数组元素。
4)使用Beam188单元依次连接重新排好顺序的节点,并根据单元所处区域(根据材料、截面特性数组),赋予相应材料、截面属性。
以上过程均可通过APDL语言编程自动实现。
3.2 优化算法为减小航行体危险截面弯矩,同时控制水下航行体运动幅度,避免冲击过程航行体与储运筒结构发生碰撞,需要对航行体减振系统进行优化设计。根据工程设计需要,设定所有减振垫完全相同以提高减振垫的通用性。
水下航行体减振系统优化的设计变量、约束条件、优化目标归纳如下:
1)设计变量为整圈减振垫刚度K及各圈减振垫位置的横坐标d1,d2,d3,d4,d5,d6,d7;
2)约束条件为减振垫最大压缩量18 mm;
3)优化目标为危险截面弯矩最小。
常用的优化算法有二次连续规划算法、遗传优化算法,本文通过二次连续规划算法实现减振系统的优化。二次连续规划法常用来求解带有约束的非线性数学规划问题,一般会假定目标函数和约束条件是连续可微的。二次连续规划法将目标函数以二阶泰勒级数展开,将原非线性求解问题转化为二次规划问题,通过求解二次规划得到下一个设计点,然后根据优化函数执行一次线性搜索。
优化模型如下:
减振垫位置、刚度
二次序列规划算法[7]一般可以通过一个类牛顿矩阵
最小化
| $\nabla {g_j}{({x_k})^{\rm{T}}}d + {g_j}({x_k}) = 0,j = 1,\cdots,{m_e},$ |
| $\nabla {g_j}{({x_k})^{\rm{T}}}d + {g_j}({x_k}) \geqslant 0,j = 1,\cdots,{m_e},$ |
| ${x_l} - {x_k} \leqslant d \leqslant {x_u} - {x_k}\text{。}$ |
优化后的减振垫布置如图8所示,与初始布局相比(均匀布置,见图2),减振垫需要更靠近水下航行体的底部。优化后的整圈减振垫刚度K为9E6N/m。

|
图 8 优化后的减振垫布置图 Fig. 8 Layout of the optimized vibration damping pad |
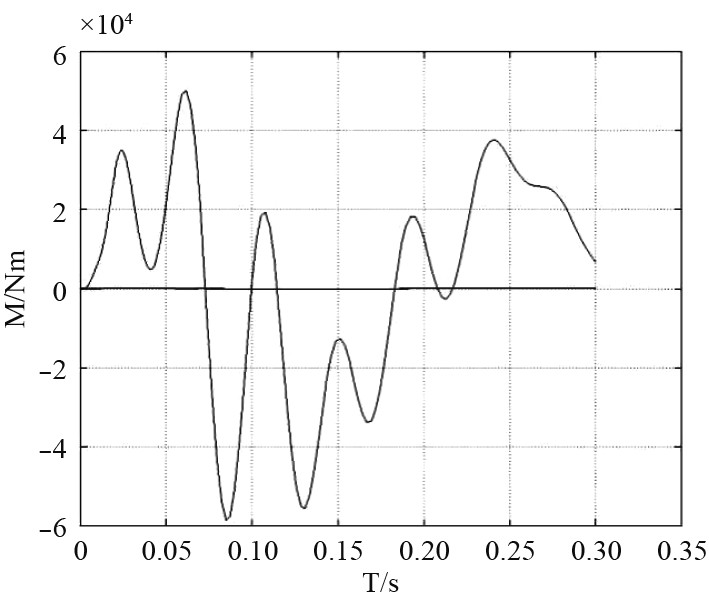
优化后,冲击过程减振垫最大压缩量为17.9 mm,如图9所示。水下航行体危险截面最大弯矩为59 kNm,如图10所示。

|
图 9 优化后冲击过程7圈减振垫的压缩量 Fig. 9 The optimization results of the compression amount of the seven circle vibration damping pad during the impact process |
|
图 10 优化后冲击过程水下航行体危险截面弯矩 Fig. 10 Optimization results of dangerous section bending moment of underwater vehicle during impact process |
优化前后的减振系统缓冲减振能力对比见表1。优化后的各圈减振垫在冲击过程的压缩量变化规律基本相同,即优化后的减振垫方案可以更有效地抑制水下航行体的转动,因而更能有效地利用水下航行体与储运筒的间隙空间,水下航行体危险截面弯矩也更小。
|
|
表 1 减振系统优化前后缓冲减振效果对比 Tab.1 Comparison of buffering and vibration reduction effects before and after optimization of the vibration reduction system |
1)本文采用缩聚梁建模的方法建立了某水下航行体减振系统动力学模型,并计算了水下航行体在冲击载荷下的动态响应;
2)基于APDL语言,通过冒泡法实现缩聚梁模型的节点自动排序,并依据位置判断赋予相应的截面属性,实现了缩聚梁模型减振垫位置参数化建模;
3)将减振垫位置、刚度作为设计变量,将减振垫最大压缩量作为约束条件,将危险截面弯矩最小化作为目标,基于二次序列规划算法,实现了水下航行体减振系统的优化。优化后减振系统可以有效抑制水下航行体在储运筒中转动,即优化后在横向冲击载荷下水下航行体更接近于平动,因而可以提高空间利用率,并降低冲击载荷下水下航行体危险截面弯矩。
| [1] |
陈潇凯, 李邦国, 林逸. 改进响应面法在汽车正面抗撞性优化中的应用[J]. 机械工程学报, 2007, 43(8): 142-145. DOI:10.3321/j.issn:0577-6686.2007.08.025 |
| [2] |
MARCUS R, LARSGUNNAR N, FREDRIK B, etal. Shape optimization of a vehicle crash-box using LS-OPT[C]. 5th European LS-DYNA User conference. Sweden: Engineering Research Nordic, 2005: 27-31.
|
| [3] |
姜衡, 管贻生, 邱志成. 基于响应面法的立式加工中心动静态多目标优化[J]. 机械工程学报, 2011, 47(11): 125-133. |
| [4] |
汪玉, 华宏星. 舰船现代冲击理论及应用[M]. 北京: 科学出版社, 2005.
|
| [5] |
冯麟涵, 汪玉, 杜俭业, 等. 舰船设备冲击响应计算方法等效性研究[J]. 船舶工程, 2011, 33: 210-214. |
| [6] |
张晓阳, 刘建湖, 潘建强, 等. 各主要海军国家设备抗冲击标准之评述[J]. 船舶力学, 2011, 15(11): 1322-1334. DOI:10.3969/j.issn.1007-7294.2011.11.018 |
| [7] |
张庆山. 基于ISIGHT的集成技术的研究及在吊艇架上的应用[D]. 广州: 华南理工大学, 2012.
|
 2020, Vol. 42
2020, Vol. 42
