2. 大连海事大学航海动态仿真和控制实验室,辽宁 大连 116026
2. Laboratory of Marine Simulation and Control, Dalian Maritime University, Dalian 116026, China
随着超大型油船及水下潜航器的出现和研制先进船舶运动控制器的需要,船舶运动数学模型研究工作受到越来越多的关注[1-2],现代控制理论、先进测量技术和系统辨识理论等进一步推动了船舶运动数学模型的发展[3-4]。从模型结构的角度来看,船舶运动数学模型可分为水动力模型和响应型模型,而水动力模型又分为以Norrbin为代表的整体型模型和以MMG(Ship Manoeuvring Mathematical Model Group)为代表的分离型模型。Norrbin模型在分解流体动力的过程中更注重参数演绎的物理含义,给出了一种描述非线性流体动力的简洁形式[5],该成果在瑞典SSPA早期研制的船舶操纵模拟器中广泛应用。
近年来,随着船舶日益大型化、快速化、专业化和现代化,20世纪80年代建立的船舶运动整体型或分离型数学模型对于大型船舶(通常指8万载重吨以上或总长250 m及以上的船舶)来说其精度越来越低,不再适合航海仿真和船舶运动控制器设计的新要求。为了解决大型船舶非线性Norrbin整体型数学模型精度不高的难题,文献[6]针对压载排水量20万吨的矿砂船Vale Brasil旋回试验进行研究,在调节部分流体动力导数与Norrbin辨识的2个非线性力(矩)经验公式的基础上,对原Norrbin船舶运动数学模型进行改进,仿真结果优于改进前,与实船数据较为接近。本文在其基础上针对30万吨级船舶的非线性Norrbin模型精度展开后续研究。文献[7-8]采用MMG模型建模思想为满载30万吨级大型油船KVLCC2号建立了较精确的数学模型,但其建模过程中所需船舶参数繁多,且公式较为复杂。对于一般货轮来说,收集众多船舶参数并不容易,故精度高的MMG模型难以构造,而发展一套新的建模方法有很大难度。本文立足于已有的非线性Norrbin数学模型,挖掘其与船舶大型化密切相关的流体动力导数,对其进行适当放大,并在不改变Norrbin辨识的非线性力(矩)公式的基础上,给出30万吨级船舶的改进Norrbin数学模型。用改进的Norrbin模型对KVLCC2号油船进行仿真实验,对比旋回试验与Z形试验的结果可知改进的Norrbin模型具有较高的精度,且保留了原Norrbin整体型模型所需船舶参数少、物理意义明显的优点。继而将改进的Norrbin模型应用到30万吨级不同船型的船舶旋回预报上,仿真表明具有85.1%的精度,佐证了改进后的Norrbin模型具有较好的泛化性能。
1 Norrbin数学模型改进考虑船舶的平面运动,沿用Abkowitz的研究方案[9],把流体动力X,Y,N展开成Taylor级数时只保留1阶小量,另考虑到船舶左右对称性,相关的导数如
| $ \begin{array}{l} m\Delta \dot u = {X_u}\Delta u + {X_{\dot u}}\Delta \dot u\text{,} \\ m\dot v + m{u_0}r + m{x_c}\dot r = {Y_v}v + {Y_r}r + {Y_{\dot v}}\dot v + {Y_{\dot r}}\dot r + {Y_\delta }\delta\text{,}\\ {I_{zz}}\dot r + m{x_c}\dot v + m{x_c}{u_0}r = {N_v}v + {N_r}r + {N_{\dot v}}\dot v + {N_{\dot r}}\dot r + {N_\delta }\delta \text{。}\\ \end{array} $ | (1) |
由式(1)可知,横漂与转首间存在着强耦合。从航速控制的角度,前进运动与其他2个自由度上的运动相互独立,可单独考虑。船舶运动用状态空间模型描述,便于处理控制作用下船舶的多变量运动问题,对风、浪、流干扰的引入较为直接和准确。将式(1)中的后2项化成矩阵形式,再叠加上Norrbin辨识出的非线性力(矩)公式及风浪干扰,采用“一撇”系统无量纲化,则考虑横漂速度
| $ {{ I}'_{(2)}}{\dot X_{(2)}} = {{ P}'_{(2)}}{X_{(2)}} + {{ Q}'_{(2)}}U + {F'_{{\rm{NON}}}} + {F'_{{\rm{WIND}}}} + {F'_{{\rm{WAVE}}}}\text{,} $ | (2) |
其中:
| $ {F'_{{\rm{NON}}}} = \left[ {\begin{array}{*{20}{c}} {{{Y'}_{{\rm{NON}}}}} \\ {{{N'}_{{\rm{NON}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {C{f_Y}(v,r)} \\ {C{f_N}(v,r)} \end{array}} \right]\text{,} $ | (3) |
| $ {f_Y}(v,r) = \left\{ {\begin{array}{*{20}{c}} {T \cdot r\left| r \right|[ - \displaystyle\frac{1}{{12}} - \frac{1}{{{L^2}}}{{(\dfrac{v}{r})}^2}]\text{,}\quad - \infty < - \frac{1}{L}\frac{v}{r} < - \frac{1}{2}}\text{,} \\ {T \cdot r\left| r \right|[ - \displaystyle\frac{1}{2}\frac{1}{L}\dfrac{v}{r} - \frac{2}{3}\frac{1}{{{L^3}}}{{(\dfrac{v}{r})}^3}]\text{,} - \frac{1}{2} \leqslant - \frac{1}{L}\frac{v}{r} \leqslant \frac{1}{2}} \text{,}\\ {T \cdot r\left| r \right|[\displaystyle\frac{1}{{12}} + \frac{1}{{{L^2}}}{{(\frac{v}{r})}^2}]\text{,}\quad \quad \quad \frac{1}{2} < - \frac{1}{L}\frac{v}{r} < \infty } \text{,} \end{array}} \right. $ | (4) |
| $ {f_N}(v,r) = \left\{ {\begin{array}{*{20}{l}} {T \cdot r\left| r \right|[ - \displaystyle\frac{1}{6}\frac{1}{{{L^{}}}}(\frac{v}{r})]}\text{,} \\ {T \cdot r\left| r \right|[ - \displaystyle\frac{1}{{32}} - \frac{1}{4}\frac{1}{{{L^2}}}{{(\frac{v}{r})}^2} + \frac{1}{6}\frac{1}{{{L^4}}}{{(\frac{v}{r})}^4}]} \text{,}\\ {T \cdot r\left| r \right|[\displaystyle\frac{1}{6}\frac{1}{{{L^{}}}}(\frac{v}{r})]} \text{,} \\ - \infty < - \frac{1}{L}\displaystyle\frac{v}{r} < - \frac{1}{2}\text{,} \\ -\displaystyle \frac{1}{2} \leqslant - \frac{1}{L}\frac{v}{r} \leqslant \frac{1}{2}\text{,} \\ \displaystyle\frac{1}{2} < - \frac{1}{L}\frac{v}{r} < \infty \text{。} \end{array}} \right. $ | (5) |
其中:C为无量纲横流系数,取0.3~0.8;
假定海流干扰为定常流或具有慢时变特性,只影响船舶的平面位置和速度,不影响船舶姿态角,则有速度平衡方程:
| $ \begin{array}{l} {{\dot x}_0} = u\cos \psi - v\sin \psi + {U_c}\cos {\psi _c}\text{,} \\ {{\dot y}_0} = u\sin \psi + v\cos \psi + {U_c}\sin {\psi _c}\text{。} \\ \end{array} $ | (6) |
其中:
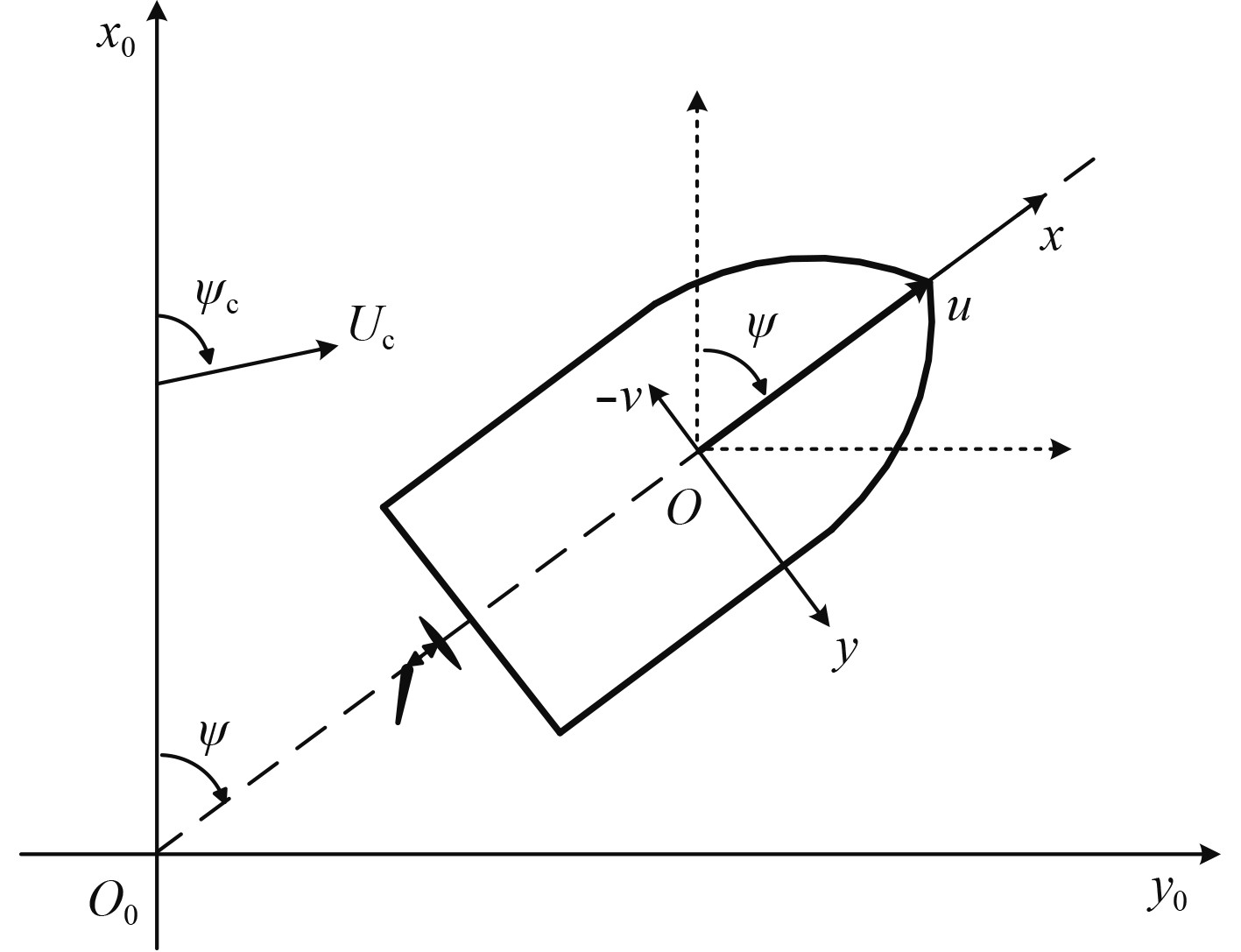
|
图 1 海流干扰示意图 Fig. 1 Diagram of the ocean current disturbance |
从式(4)和式(5)可知,非线性力(矩)的求解只需要知道
根据航海实践,结合理论分析可知船舶大型化后将增大与转首角速度
旋回试验与Z形试验能判定船舶操纵性优劣,被称为“标准操纵试验”,在船舶操纵试验中受到广泛的重视。本节运用原Norrbin模型、改进的Norrbin模型分别进行满载35°右旋回仿真和Z形试验,并与文献[7-8]中的实船试验、MMG模型仿真实验数据进行对比,具体描述见表1。
|
|
表 1 模型仿真实验项目列表 Tab.1 List of the model simulation items |
1979年278 000 t油船ESSO OSAKA号操纵性海试表明,在不改变主机转速、功率的情况下,船舶35°舵角右旋回时,其前进航速由初始动舵时的12 kn下降到定常旋回的3 kn[12],这一显著降速所代表的非线性已不能用
|
|
表 2 KVLCC2号右旋回35°速降系数变化趋势 Tab.2 Change trend of the speed loss coefficient for the tanker KVLCC2 in right 35° turning test |
使用指数下降法拟合速降公式,令响应曲线表达式为:
| $ k(t) = {{\rm{e}}^{ - t/{T_0}}},\begin{array}{*{20}{c}} {}&{t \geqslant 0} \text{,} \end{array} $ | (7) |
由控制理论知识可知,当
| $ \begin{array}{l} {\left. {\displaystyle\frac{{{\rm{d}}k(t)}}{{{\rm{d}}t}}} \right|_{t = 0}} = - \displaystyle\frac{1}{{{T_0}}},{\left. {\displaystyle\frac{{{\rm{d}}k(t)}}{{{\rm{d}}t}}} \right|_{t = {T_0}}} = - 0.368\displaystyle\frac{1}{{{T_0}}},\\ {\left. {{{\left. {\displaystyle\frac{{{\rm{d}}k(t)}}{{{\rm{d}}t}}} \right|}_{t = 2{T_0}}} = - 0.135\displaystyle\frac{1}{{{T_0}}},\displaystyle\frac{{{\rm{d}}k(t)}}{{{\rm{d}}t}}} \right|_{t = 3{T_0}}} = - 0.05\displaystyle\frac{1}{{{T_0}}},\\ {\left. {\displaystyle\frac{{{\rm{d}}k(t)}}{{{\rm{d}}t}}} \right|_{t = 4{T_0}}} = - 0.018\displaystyle\frac{1}{{{T_0}}},{\left. {\displaystyle\frac{{{\rm{d}}k(t)}}{{{\rm{d}}t}}} \right|_{t = \infty }} = 0\text{。} \end{array} $ | (8) |
若定义该响应曲线衰减到初始值2%所需的时间为调节时间,则有
| $\mu = 0.25 + 0.75{{\rm{e}}^{ - t/250}}\text{。} $ | (9) |
图2所示为速降系数的拟合情况,易知式(9)拟合效果良好。
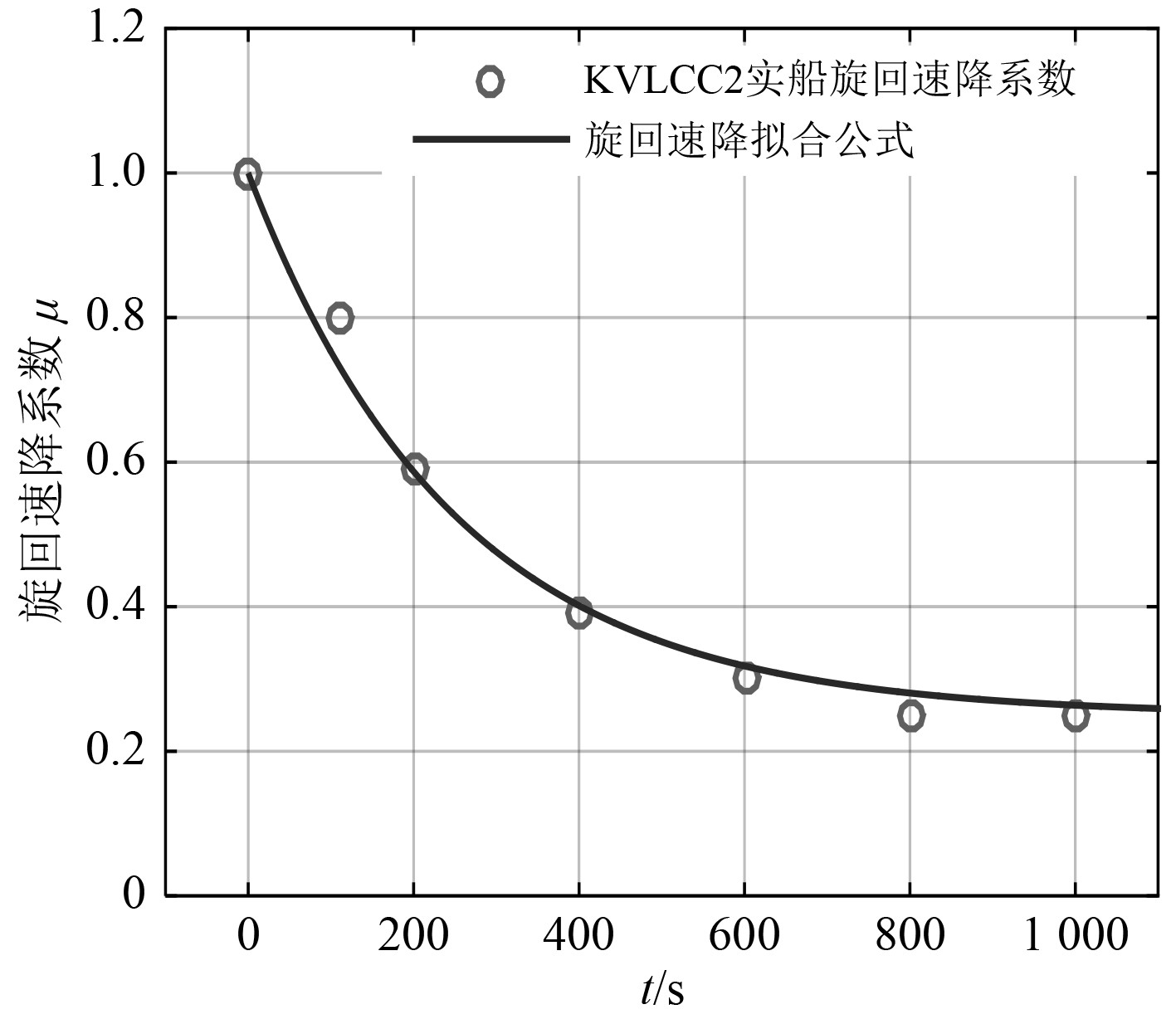
|
图 2 旋回速降拟合 Fig. 2 Curve fitting of the speed loss in ship turning trial |
首先运用原Norrbin模型进行无风流影响下的船舶旋回仿真实验。KVLCC2号油船满载时的主要船型参数[7]如表3所示。考虑到舵机伺服系统的特性,将其等效为一个一阶惯性环节,其时间常数为
| $ \dot \delta = - \frac{1}{{{T_r}}}\delta + \frac{1}{{{T_r}}}{\delta _r}\text{。} $ | (10) |
式中,
|
|
表 3 船舶满载时主要船型参数 Tab.3 Main particulars of ships in full loaded condition |
式(3)中无量纲横流系数C取0.5,图3给出了原Norrbin模型仿真,及按照第1节中Norrbin模型改进策略所做的仿真实验与实船试验的旋回圈对比,易知原Norrbin模型仿真的旋回圈图形符合度较低,对大型船舶来说精度有所欠缺;将与转首角速度
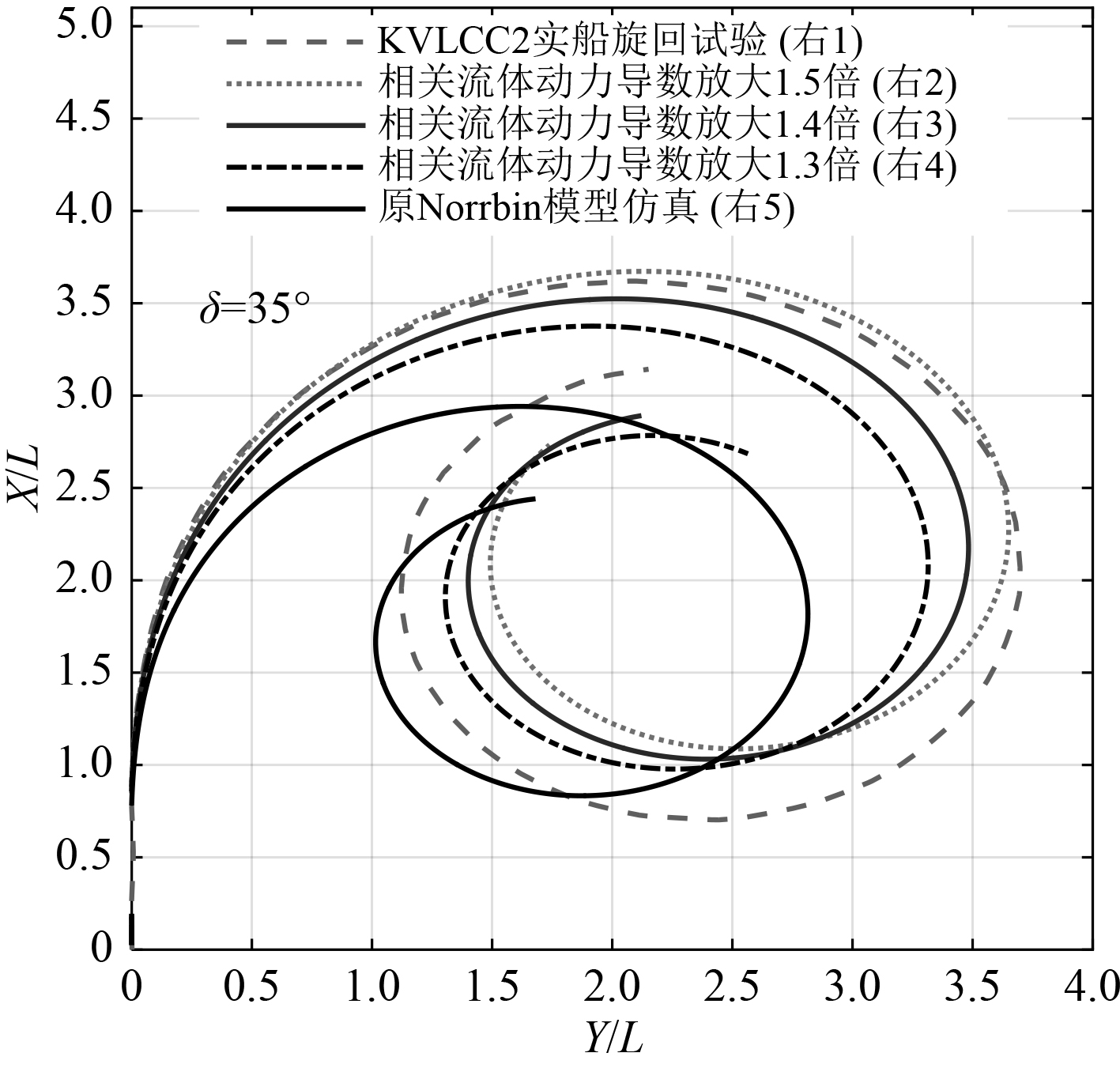
|
图 3 KVLCC2号油船旋回试验对比 Fig. 3 Turning test comparison of the tanker KVLCC2 |
针对改进的Norrbin模型进行仿真实验,具体数据如图4所示。虚线代表KVLCC2号实船旋回数据,点线代表MMG模型旋回仿真数据,实线代表改进的Norrbin模型旋回仿真数据,实船旋回数据与MMG模型仿真数据来源于文献[7-8],图4(b)~图4(d)中横坐标时间
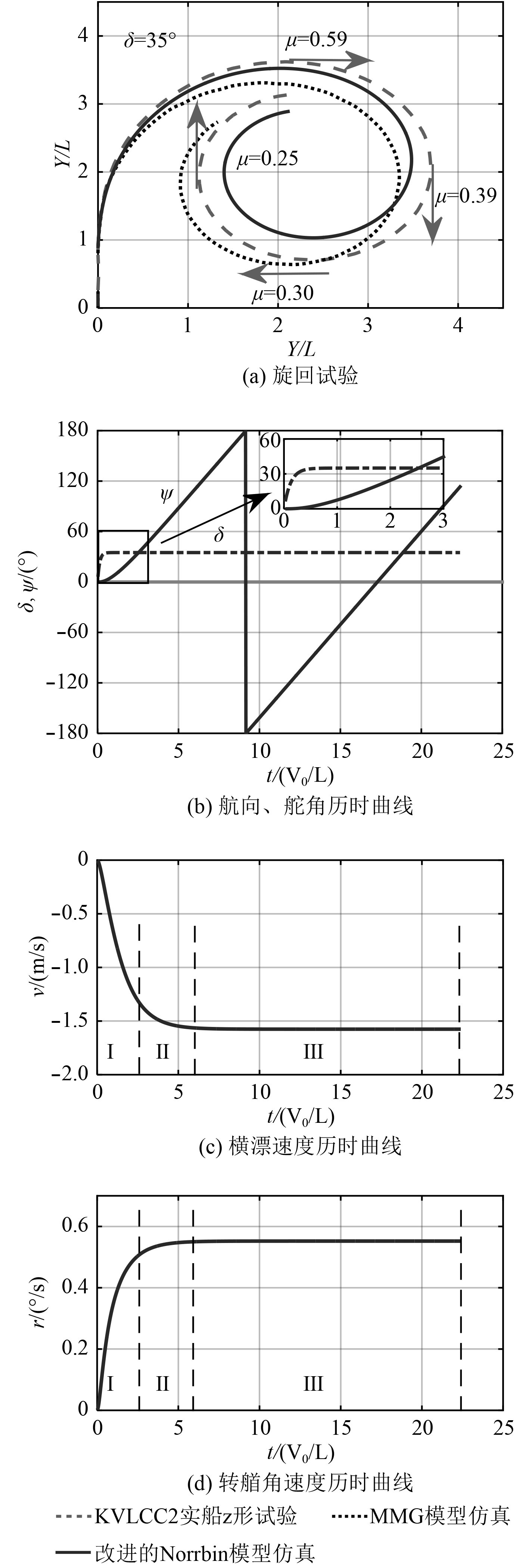
|
图 4 改进的Norrbin模型旋回仿真 Fig. 4 Turning simulation of the improved Norrbin model |
图4(c)和图4(d)说明在旋回的初始阶段Ⅰ,船舶横漂速度
|
|
表 4 KVLCC2号油船满载35°右旋回试验参数 Tab.4 Parameters of the right turning test with 35° for the tanker KVLCC2 in full loaded condition |
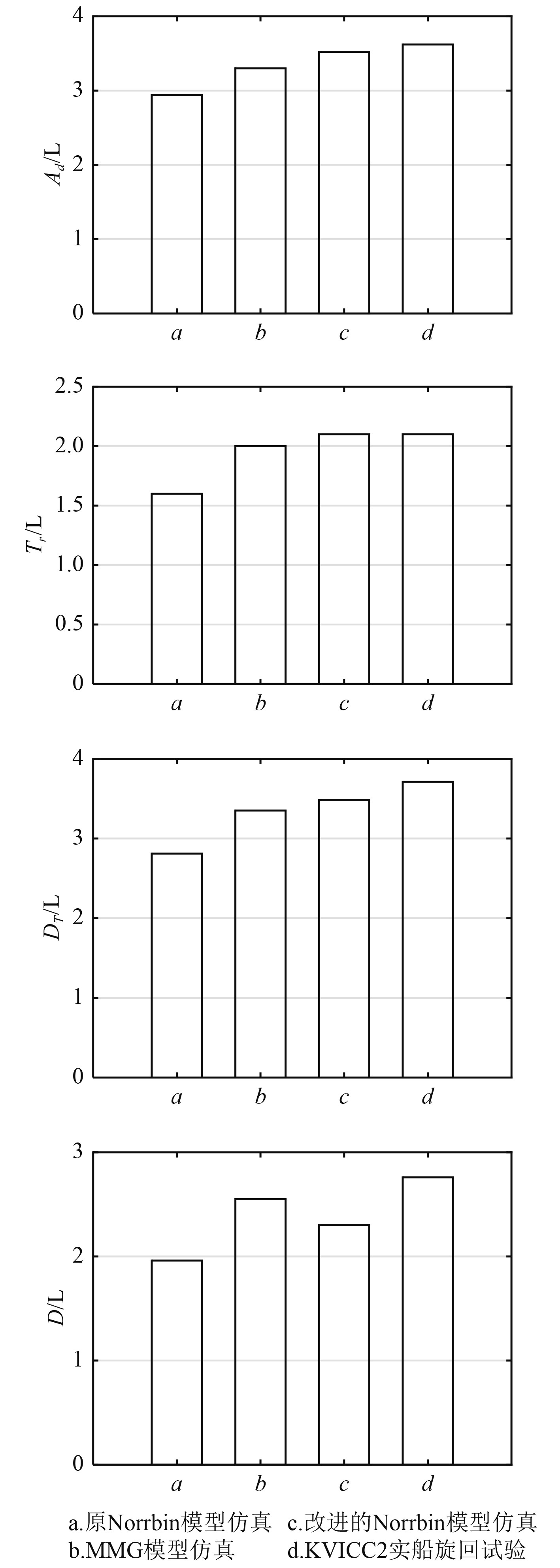
|
图 5 旋回特征参数柱状对比图 Fig. 5 Columnar diagram of the ship turning characteristics |
| $ \begin{array}{l} {{\bar C}_M} = \displaystyle\frac{1}{4}\left( {\frac{{\min \left( {{A_{d{\text{实船}}}},{A_{d{\text{模型}}}}} \right)}}{{\max \left( {{A_{d{\text{实船}}}},{A_{d{\text{模型}}}}} \right)}} + \frac{{\min \left( {{T_{r{\text{实船}}}},{T_{r{\text{模型}}}}} \right)}}{{\max \left( {{T_{r{\text{实船}}}},{T_{r{\text{模型}}}}} \right)}}} \right.{\rm{ + }}\\ \;\;\;\;\;\;\;\left. {\displaystyle\frac{{\min \left( {{D_{T{\text{实船}}}},{D_{T{\text{模型}}}}} \right)}}{{\max \left( {{D_{T{\text{实船}}}},{D_{T{\text{模型}}}}} \right)}} + \frac{{\min \left( {{D_{{\text{实船}}}},{D_{{\text{模型}}}}} \right)}}{{\max \left( {{D_{{\text{实船}}}},{D_{{\text{模型}}}}} \right)}}} \right) \times 100\% \text{。} \end{array} $ | (11) |
其中:
采用第1节中改进的Norrbin模型做10°/10°与20°/20°Z形试验仿真,因Z形试验时船舶降速较少,故此处不考虑船舶速降问题。实船数据与MMG模型仿真数据来源于文献[7-8]。图6和图7为Z形试验的仿真图,同时给出了船舶平面位置、横漂速度和转艏角速度的历时曲线,揭示了Z形试验中一些船舶参量的变化机理。在船舶由一侧舵角最大值转向另一侧的瞬间,
|
|
表 5 Z形试验超越角仿真结果 Tab.5 Simulation results of the zig-zag overshoot angle |
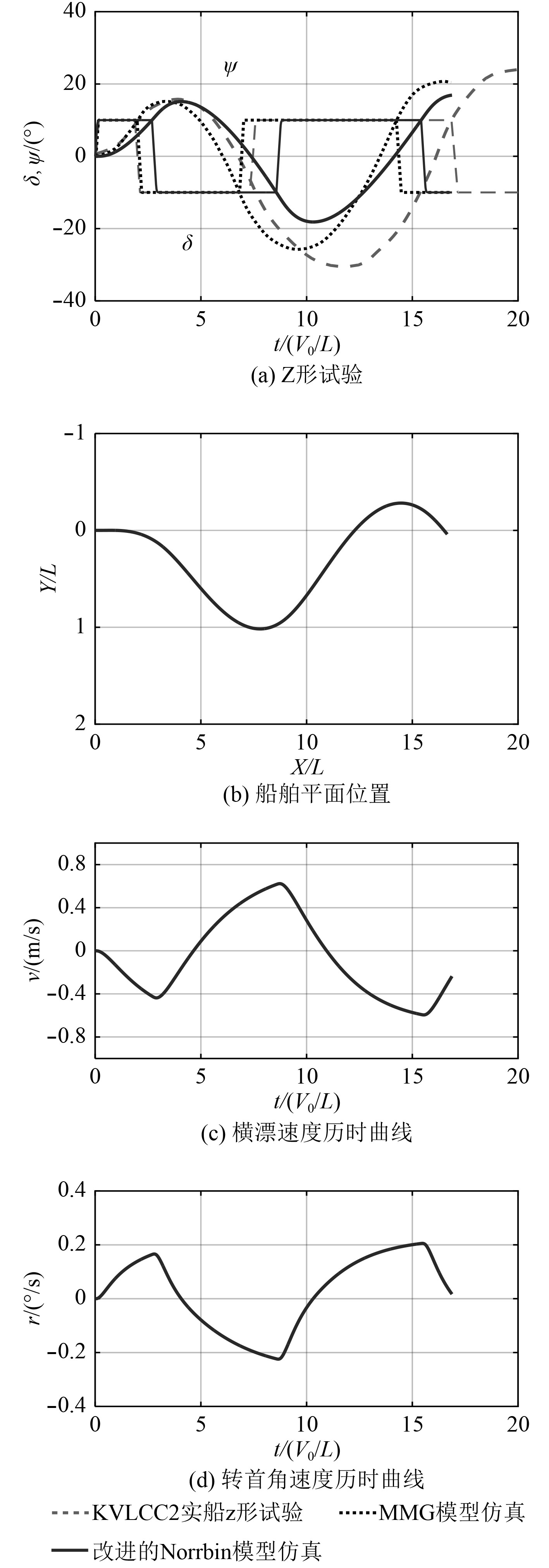
|
图 6 改进的Norrbin模型10°/10°Z形试验 Fig. 6 Zig-zag (10°/10°) test of the improved Norrbin model |
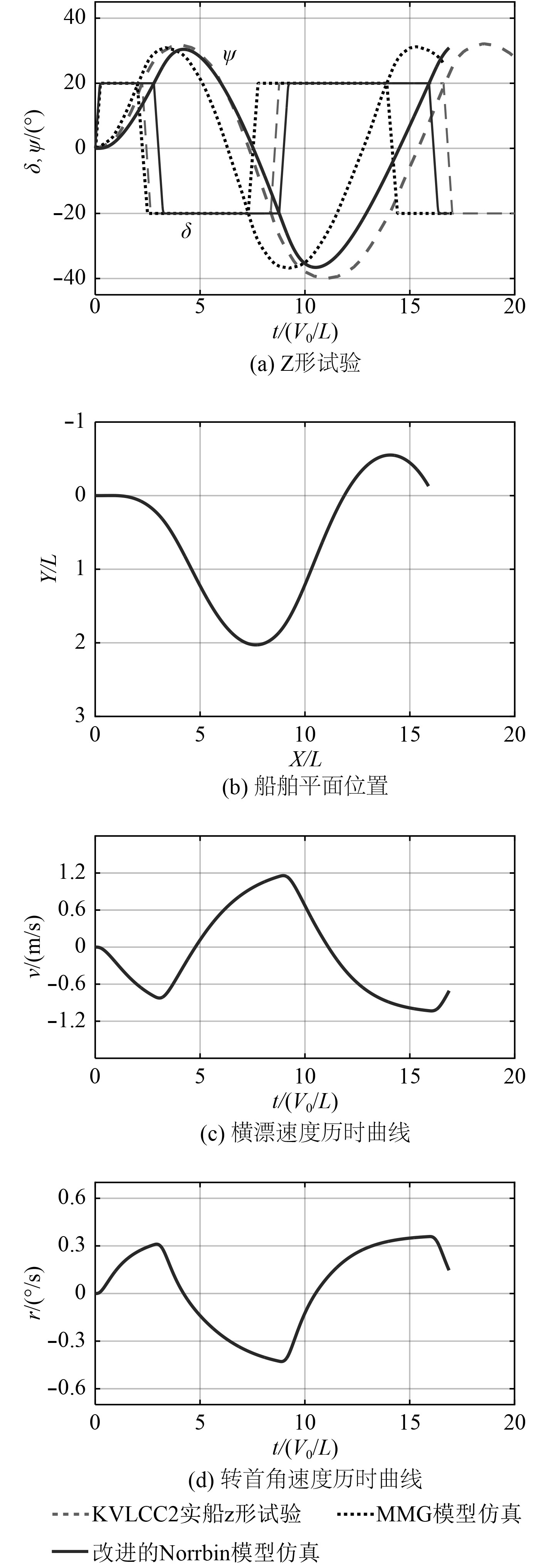
|
图 7 改进的Norrbin模型20°/20°Z形试验 Fig. 7 Zig-zag (20°/20°) test of the improved Norrbin model |
根据MSC.137(76)(《船舶操纵性标准》)规定,因本次试验
由前文讨论可知,改进的Norrbin模型对于30万吨级船舶KVLCC2号具有较好的仿真精度。本节验证改进的Norrbin模型是否适用于排水量等级相差不大的其他船型船舶。
表6给出了大型矿砂船Stellar Topaz号的满载船型参数,图8为改进的Norrbin模型用于矿砂船Stellar topaz号旋回试验的结果对比,对应的海洋环境为风速7.6 m/s,风向040°,3级海况。考虑旋回速降时采用2.1节中的速降模型。图8中虚线为Stellar topaz号实船旋回数据,点线为原Norrbin模型旋回仿真数据,实线为改进的Norrbin模型旋回仿真数据,具体的旋回试验特征参数见表6。经计算可得改进的Norrbin模型用于Stellar topaz号旋回试验仿真平均符合度为85.1%,高于原Norrbin模型73.4%的精度。
|
|
表 6 Stellar Topaz号满载35°右旋回试验参数 Tab.6 Parameters of right turning test with 35° for the ore carrier Stellar Topaz in full loaded condition |
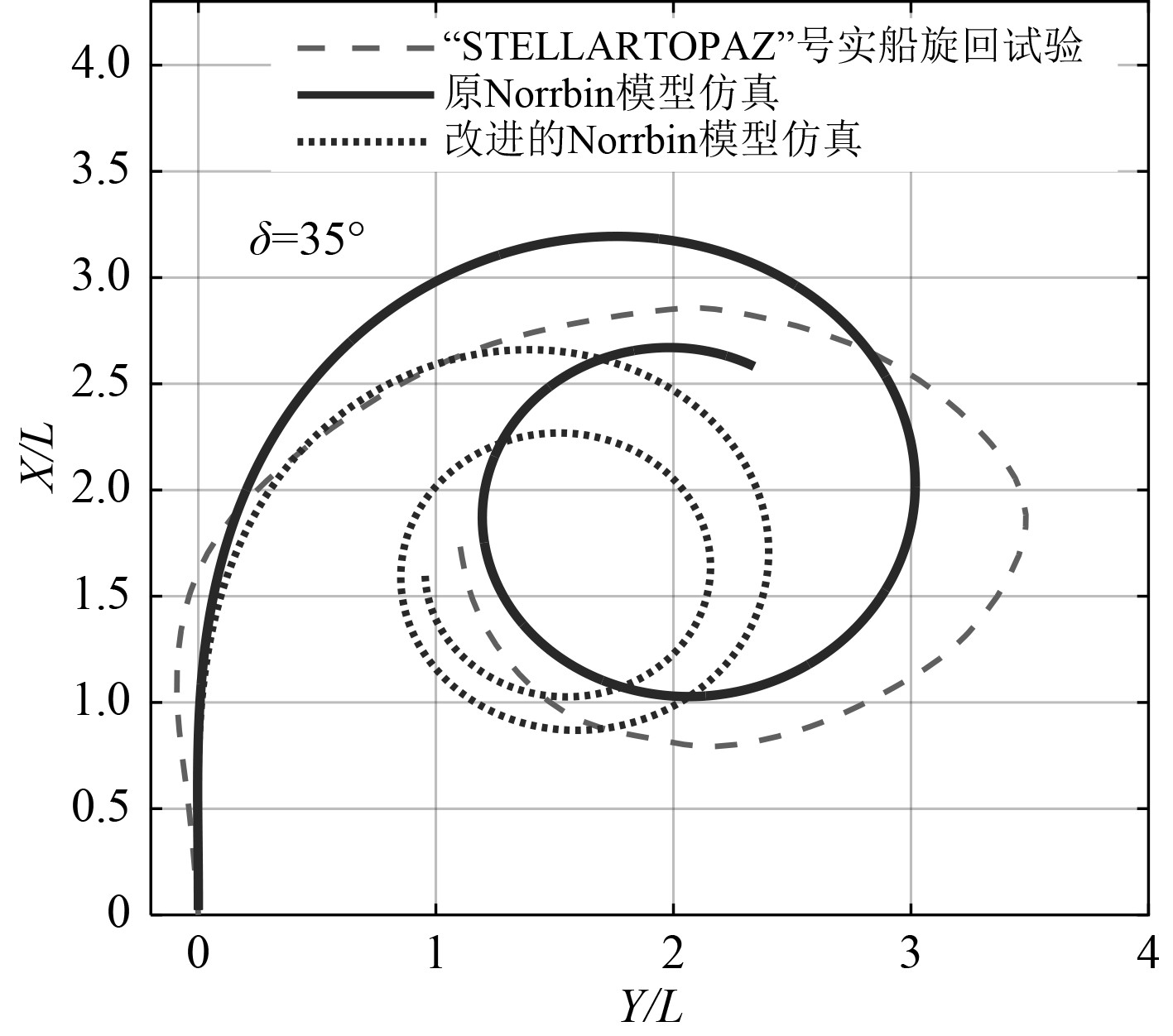
|
图 8 改进的Norrbin模型用于StellarTopaz号旋回试验 Fig. 8 Turning simulation of the improved Norrbin model for the ore carrier Stellar Topaz |
因泛化性验证选取的船舶为不同船型船舶,充分考虑了由于船舶结构不同带来的操纵特性差异化,且仿真实验表明改进的Norrbin模型具有较高的精度,故有较好的泛化性能。
4 结 语本研究立足于原有的非线性Norrbin模型,借鉴已有的研究成果,进一步拓展改进后的非线性Norrbin模型的适用范围。根据大型船舶的特点,挖掘出与其大型化密切相关的流体动力导数。通过在VB与Matlab混合编程的船舶运动模型实验平台反复测试,在不改变Norrbin辨识的非线性力(矩)公式的基础上,将与
| [1] |
吴伟萍. 船舶迎浪航向下的垂荡运动建模与仿真分析[J]. 舰船科学技术, 2018, 40(22): 4-6. WU Weiping. Research on modeling and simulation of heave motion of ships in waves[J]. Ship Science and Technology, 2018, 40(22): 4-6. |
| [2] |
张华军, 谢呈茜, 苏义鑫, 等. 船舶操纵运动仿真中改进变步长龙格库塔算法[J]. 华中科技大学学报(自然科学版), 2017, 45(7): 122-126. |
| [3] |
郭晨, 汪洋, 孙富春, 等. 欠驱动水面船舶运动控制研究综述[J]. 控制与决策, 2009, 24(3): 321-327. DOI:10.3321/j.issn:1001-0920.2009.03.001 |
| [4] |
赵希人, 唐慧妍, 彭秀艳, 等. 船舶横向运动多变量随机控制研究[J]. 船舶力学, 2004, 8(5): 35-41. DOI:10.3969/j.issn.1007-7294.2004.05.005 |
| [5] |
NORRBIN N H. Further studies of parameter identification of linear and nonlinear ship steering dynamics[R]. SSPA, Gothenburg, Sweden, Report 1920-6, 1977.
|
| [6] |
张显库, 杨光平. 大型船舶的非线性Norrbin数学模型改进[J]. 中国航海, 2016, 39(3): 50-53. DOI:10.3969/j.issn.1000-4653.2016.03.012 |
| [7] |
UENO M, TSUKADA Y, KITAGAWA Y. Rudder effectiveness correction for scale model ship testing[J]. Ocean Engineering, 2014, 92: 267-284. DOI:10.1016/j.oceaneng.2014.10.006 |
| [8] |
YASUKAWA H, YOSHIMURA Y. Introduction of MMG standard method for ship maneuvering predictions[J]. Journal of Marine Science and Technology, 2015, 20(1): 37-52. DOI:10.1007/s00773-014-0293-y |
| [9] |
ABKOWITZ M. A. Lectures on ship hydrodynamics steering and manoeuvrability. Hydro and Aerodynamics Laboratory. Report No. Hy-5. Denmark, 1964.
|
| [10] |
张显库, 金一丞. 控制系统建模与数字仿真(第2版)[M]. 大连: 大连海事大学出版社. 2013.
|
| [11] |
CLARKE D, GEDLING P, HINE G. Application of manoeuvring criteria in hull design using linear theory[J]. Naval Architect, 1983, 11(3): 45-68. |
| [12] |
CRANE JR C. L. Manoeuvring trials of the 278000DWT ESSO OSAKA in shallow and deep water[J]. Ocean Currents, 1979, 1: 180. |
| [13] |
SIMMAN 2008: part B benchmark test cases, KVLCC2 description[C]// Proceedings of workshop on verification and validation of ship manoeuvring simulation method, Copenhagen, 2008, 1: B7–B10.
|
| [14] |
张显库, 杨光平, 张强. 一种双极性S函数修饰的非线性船舶航向保持算法[J]. 大连海事大学学报, 2016, 42(3): 15-19. |
| [15] |
IMO. Standards for ship manoeuvrability[S]. RESOLUTION MSC, 2002.
|
 2020, Vol. 42
2020, Vol. 42
