自动舵检测平台为自动舵提供了在陆基条件下运行的环境,对自动舵的检修及研发调试具有重要的意义[1]。船舶运动模型作为预报船舶操纵特性的基础,是检测平台的重要组成部分。目前,描述操纵性的船舶运动数学模型可分为以下三类[2]:1)响应型模型,由20世纪50年代末野本谦作提出,从控制工程的观点将船舶看成一个动态系统,舵角为系统的输入,首向角或首摇角速度为系统的输出;2)整体型模型,由20世纪60年代初Abkowitz提出,把船看作一个整体,不考虑船舶各部分之间的流体动力干扰,研究船舶所受的外力和力矩;3)MMG模型,由20世纪70年代末日本拖曳水池委员会提出,按照物理意义将力和力矩分解为作用于裸体船、敞水螺旋桨和敞水舵,以及三者之间相互干涉的流体动力和力矩。
现有的航向航迹自动舵检测平台使用了航迹自动舵标准(IEC62065)中提出的船舶运动模型,由于该模型对螺旋桨推进力、流体阻力以及船、桨、舵之间相互干涉的流体动力和力矩等物理量采取简化处理,是一种简化的MMG模型,在选用与标准中的典型船型相差较大的船型时,运动仿真误差较大,在实际使用中具有一定局限性[3]。本文利用已具有相当精度的船舶四自由度MMG模型进行仿真试验,提出通过MMG模型仿真结果求取IEC62065模型中相关参数值的方法,将模型转化前后的仿真结果作比较分析,讨论模型间的差异以及对转化方法做出改进。
1 船舶运动模型建立 1.1 IEC62065运动模型的建立国际电工委员会制定的航迹系统性能标准(IEC62065)中[4]提出了包括纵移、横移、转首的船舶三自由度运动模型,其船舶运动方程如下:
| $\left\{ \begin{aligned} & {M_u}\dot u = X + {M_u}vr - {R_u}u \text{,}\\ & {M_v}\dot v = {M_v}ur - {R_v}v \text{,}\\ & {I_z}\dot r = {K_r}\frac{{{u_{\max }}{X^{'}}}}{L}{\delta _a} + \gamma L{R_v}(v - \gamma Lr) - {R_r}r \text{。} \end{aligned} \right.$ | (1) |
式中:3个等式依次描述的是船舶的纵移运动、横移运动以及转首运动。
对纵移运动方程,当船舶以最大速度稳定航行时,有下式成立:
| $\left\{ \begin{aligned} & {\tau _u}\dot u + u = {u_{\max }}{X^{'}} + {\tau _u}vr \text{,}\\ & {\tau _v}\dot v + v = {\tau _v}ur \text{,}\\ & {\tau _r}\dot r + r = {\tau _r}\frac{{K_r^{'}{u_{\max }}{X^{'}}}}{L}\frac{{{\delta _a}}}{{{\delta _{\max }}}} + \frac{{12\gamma (v - \gamma Lr){\tau _r}}}{{L{\tau _v}}} \text{。} \end{aligned} \right.$ | (2) |
式中:
本文对平野数学模型[6]进行改进得到四自由度MMG模型:
| $ \left\{ \begin{aligned} &(m + {m_{11}})\dot u - (m + {m_{22}})vr = {X_{HH}} + {X_{HP}} + {X_{HR}} \text{,}\\ &(m + {m_{22}})\dot v + (m + {m_{11}})u = {Y_H} \text{,}\\ &({I_x} + {m_{44}})\dot p = {K_H} + {K_\phi } + {K_{\dot \phi }} \text{,}\\ &({I_z} + {m_{66}})\dot r = {N_H} \text{。} \end{aligned} \right. $ | (3) |
其中:
对于横向力
本文通过对MMG模型的仿真实验求取IEC62065模型中的相关参数值,实现复杂的四自由度MMG模型向IEC62065模型的转化,使得与IEC62065标准中典型船型相差较大的船型也能够适用于该简化模型。
1)纵移运动方程
对于式(2)中纵移运动方程,当无海流,直航无推力时,
| $u(t) = {u_0}{e^{ - t/{\tau _u}}}\text{。}$ | (4) |
实验设计:应用MMG模型的仿真进行试验,先保持舰船处于匀速直航状态,然后突然使螺旋桨推力为零,同时从0开始计时,让舰船在水的阻力下减速,根据减速过程中纵速与时间的对应关系依照式(4)求解
2)横移运动方程
对于式(2)中横移运动方程,无海流时,操一个舵角,当舰船作稳态旋回时,有
| ${\tau _v} = \frac{v}{{ur}}\text{。}$ | (5) |
实验设计:应用MMG模型的仿真进行旋回试验,分别设置舵角为5°,10°,15°,20°,25°,30°,舰船作不同旋回动作,达到稳态后按照式(5)计算出不同条件下的
3)首向运动模型
对于式(2)中首向运动方程,令
| ${\tau _r}\dot r + r = {K_{}}\delta \text{,}$ | (6) |
无海流时,操一个舵角,当舰船作稳态旋回时,
| $K = \frac{r}{\delta }\text{,}$ | (7) |
对式(6)进行拉普拉斯变换有:
| $r(s) = \frac{{{K_{}}\delta (s) + {\tau _r}r(0)}}{{{\tau _r}s + 1}}\text{。}$ | (8) |
当舵角固定,航向变化率的稳态值显然为:
| $r(t) = K{\delta _{ss}}(1 - {e^{ - t/{\tau _r}}}) + r(0){e^{ - t/{\tau _r}}}\text{,}$ | (9) |
当
| $r(t) = K{\delta _{ss}}(1 - 2{e^{ - t/{\tau _r}}})\text{,}$ | (10) |
因此,当航向变化率
| ${\tau _{\rm{r}}}{\rm{ = }}\frac{{{t}}}{{\ln 2}}\text{。}$ | (11) |
实验设计:应用MMG模型的仿真进行Z形操舵试验,经历周期足够长,使得在每个半周期中航向变化率均能进入稳定状态,记录舵角上跳沿或下跳沿出现到航向变化率为0所经历时间,然后根据式(11)求解
本文利用Matlab对MMG模型进行仿真试验,按照上节模型转化方法得到IEC62065模型中相应参数值:
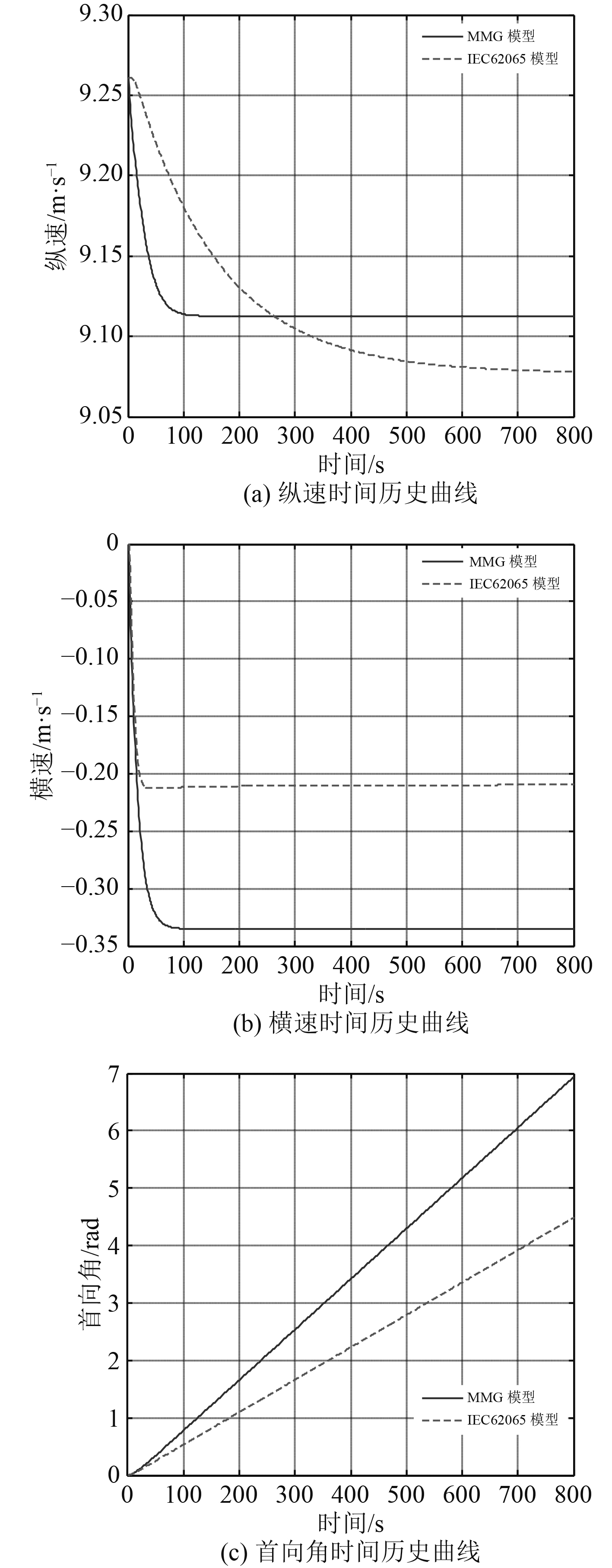
|
图 1 5°舵角下各参数时间历史曲线 Fig. 1 The time curve of each parameter under the rudder angle of 5 degrees |

|
图 2 25°舵角下各参数时间历史曲线 Fig. 2 The time curve of each parameter under the rudder angle of 25 degrees |
在800 s以内,不同舵角下船舶达到稳定旋回后,两模型的纵速、横速以及回转角速度误差如表1所示。
|
|
表 1 两模型在不同舵角下的纵速、横速以及回转角速度误差 Tab.1 The errors of longitudinal velocity,transverse velocity and rotational angular velocity of the two models under different rudder angles |
可以看出,IEC62065模型达到稳定回转所需时间更长,纵速误差随舵角增大而增大,纵、横速误差以及回转角速度误差较大,与原模型拟合度较低。
对比两模型可以发现,对于纵移运动,IEC62065模型中没有考虑y轴方向的附加质量对其的影响,将螺旋桨推进力进行了简单线性归一化处理,将阻力简单定义为阻力系数和纵速的乘积;而MMG模型将x轴和y轴的附加质量都考虑在内,对螺旋桨推力以及阻力的求取都建立在深层次理论分析与广泛的试验研究相结合的基础之上,具有相当的精度[9]。对于横移运动,IEC62065模型同样存在上述问题造成较大误差。对于首向运动,本文在实验设计中直接将IEC62065模型中的公式进行简化处理,忽略不稳定系统
现对模型转化方法做出改进,在以上参数求取实验的基础上,保留求得的
|
|
表 2 IEC62065模型部分参数在不同舵角下的取值 Tab.2 Values of some parameters of IEC62065 model under different rudder angles |
按照表2的参数取值,得到两模型在5°(见图3)和25°(见图4)舵角下的纵速、横速以及首向角时间历史曲线对比图。
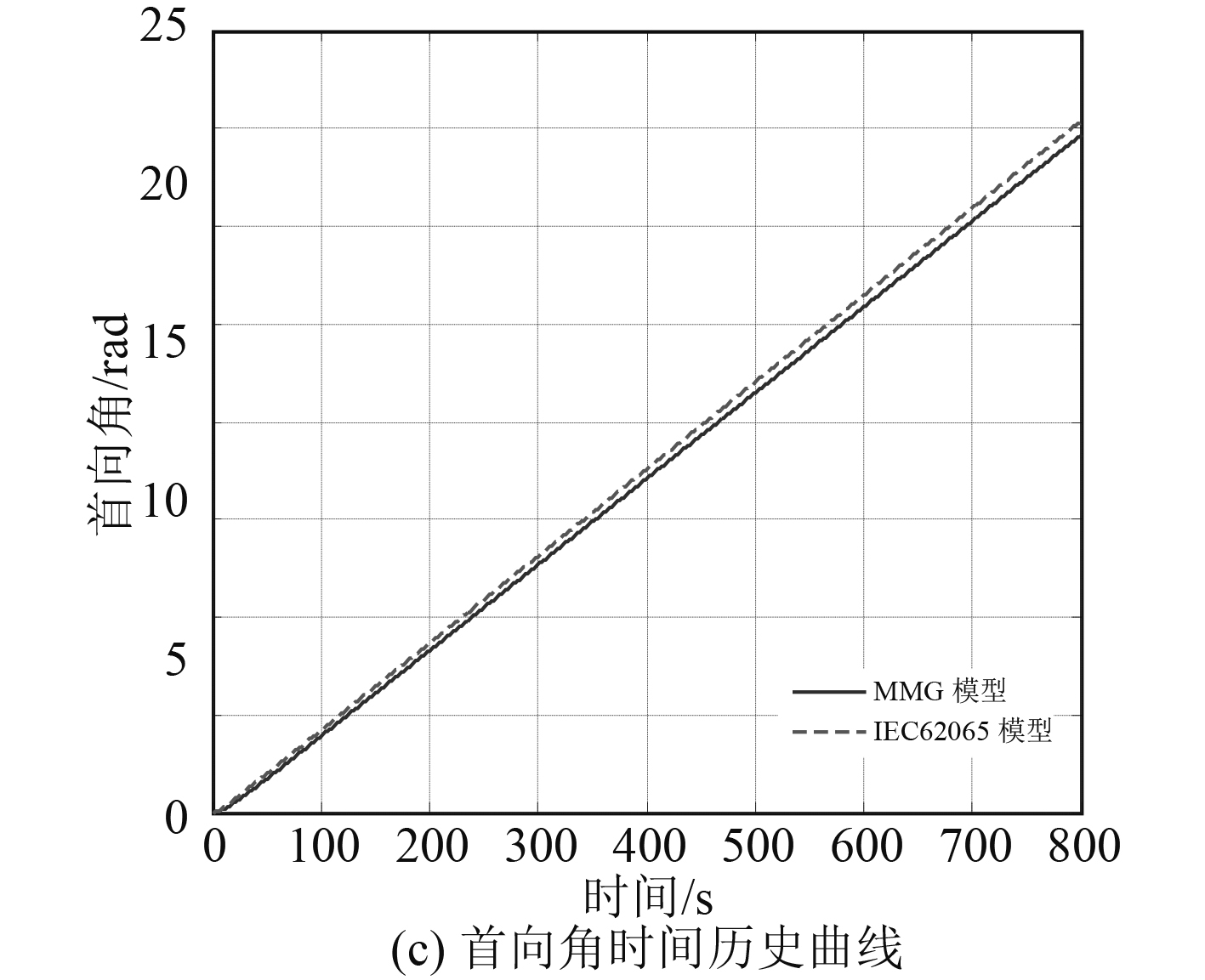
|
图 3 5°舵角下各参数时间历史曲线 Fig. 3 The time curve of each parameter under the rudder angle of 5 degrees |

|
图 4 25°舵角下各参数时间历史曲线 Fig. 4 The time curve of each parameter under the rudder angle of 25 degrees |
在800 s以内,不同舵角下船舶达到稳定旋回后,两模型的纵速、横速以及回转角速度误差如表3所示。
|
|
表 3 两模型在不同舵角下的纵速、横速以及回转角速度误差 Tab.3 The errors of longitudinal velocity,transverse velocity and rotational angular velocity of the two models under different rudder angles |
可以看出,对参数值改进后的IEC62065模型与原模型拟合度较高,纵速最大误差为0.4%,横速最大误差为3.5%,回转角速度最大误差为1.2%,可以认为两模型具有较好的转化效果。
4 结 语本文首次提出了复杂MMG模型转化简单IEC62065模型的方法,设计MMG模型的仿真试验求取IEC62065模型的相关参数值。通过两模型仿真试验结果的对比,将部分参数值随舵角变化做出调整。试验结果表明,采用该方法得到了较好的模型转化效果。
| [1] |
陈永冰, 周岗, 李文魁. 舰船航迹控制系统运行检测平台的设计与实现[J]. 海军工程大学学报, 2011, 23(4): 38-42. CHEN Yong-bing, ZHOU Gang, LI Wen-kui. Design and implement of operation and detection platform for ship track control system[J]. Journal of Naval University of Engineering, 2011, 23(4): 38-42. DOI:10.3969/j.issn.1009-3486.2011.04.008 |
| [2] |
贾欣乐, 杨盐生. 船舶运动数学模型 [M]. 大连: 大连海事大学出版社, 1999: 1-2.
|
| [3] |
许星光, 刘勇, 臧涛, 等. 自动舵性能检测平台中船舶运动模型的建立[J]. 声学与电子工程, 2015(4): 15-18. XU Xing-guang, LIU Yong, ZANG Tao, JIA Yu-zhu. Establishment of ship motion model in automatic rudder performance detection platform[J]. Acoustics and Electronics Engineering, 2015(4): 15-18. |
| [4] |
IEC. Maritime navigation and radiocommunication equipment and systems-track control systems-operational and performance requirements, methods of testing and required test results: IEC62065-2014[S]. [S.I.]: IEC, 2014.
|
| [5] |
孙健, 陈永冰, 周岗, 等. 两种响应型船舶运动模型的对比及适用性分析[J]. 舰船科学技术, 2016, 38(11): 14-19. SUN Jian, CHEN Yong-bing, ZHOU Gang, et al. The comparison and applicability analysis of two kinds of responding ship model[J]. Ship Science and Technology, 2016, 38(11): 14-19. |
| [6] |
孙健, 陈永冰, 周岗, 等. 高速舰船的运动模型适用性分析及海浪中的操纵仿真试验[J]. 舰船科学技术, 2018, 40(1): 41-45+51. SUN Jian, CHEN Yong-bing, ZHOU Gang, et al. The applicability analysis of the model of high-speed and the simulated maneuvering test in waves[J]. Ship Science and Technology, 2018, 40(1): 41-45+51. DOI:10.3404/j.issn.1672-7649.2018.01.007 |
| [7] |
周昭明, 盛子寅, 冯悟时. 多用途货船的操纵性预报计算[J]. 船舶工程, 1983(6): 21-29+36+4. ZHOU Zhao-ming, SHENG Zi-yin, FENG Wu-shi. Prediction and calculation of maneuverability of multi-purpose cargo ships[J]. Ship Engineering, 1983(6): 21-29+36+4. |
| [8] |
李殿璞. 船舶运动与建模 [M]. 北京: 国防工业出版社, 2008.
|
| [9] |
惠子刚. 半潜船操纵运动仿真研究 [D]. 大连: 大连海事大学, 2009. HUI Zi-gang. Simulation study on the semi-submersible ships maneuvering[D]. Dalian: Dalian Maritime University, 2009. |
 2020, Vol. 42
2020, Vol. 42
