与传统单体船相比,小水线面双体船在结构形式、布置特点及动力设备等方面都存在较大的差异,是一个形状极其复杂的空间声源。深刻理解小水线面双体船水下辐射噪声空间分布的规律,获得水下声场的更多信息,对于研究小水线面双体船水下辐射噪声场的产生机理、特性控制、减振降噪具有重要意义。水下辐射声场的指向性是指在距离船体某一参考点等距离处测得的单频或宽带辐射噪声级与舷角之间的关系,反映了船舶水下辐射噪声的空间分布特性,按照空间位置的不同可以分为垂直指向性和水平指向性。影响船舶水下辐射声场指向性的因素有很多,对于小水线面双体船的特殊结构形式,双下潜体之间的声场耦合作用对其水下辐射声场的指向性影响较大。张维[1]运用结构有限元法与声学边界元法,对小水线面双体船振动声学特性数值计算问题进行了研究。薛彦卓[2]较为详细地研究了双体船结构水下中低频辐射噪声特性。杨学猛[3]基于直线阵测量系统获取的拖轮下方辐射噪声数据,获得了拖轮下方的垂直指向性分布曲线。张林根[4]利用虚源方法模拟水面的声学边界条件,分析了圆柱壳之间以及水面影响的耦合声散射效应及规律。刘宁[5]探讨了一种新的测量潜艇水下辐射噪声水平指向性的方法。
1 声固耦合方法声固耦合方法在处理流场与船体之间耦合问题的思路是:将流场看成是一种声学传播介质,对流场进行离散。同时,对结构进行离散,根据流体结构交界面处的连续性条件、流场边界条件,求解声固耦合方程,得到流场离散节点处的声压。
1.1 流场的模拟流场中的声压满足Helmholtz方程:
| ${\nabla ^2}p + {k^2}p = 0\text{。}$ | (1) |
式中:p为声压;k=ω/c为波数,ω为圆频率,c为声波在介质中的传播速度。
声压在无穷远处边界有:
| $\mathop {\lim }\limits_{r \to \infty } r\left( {\frac{{\partial p}}{{\partial r}} + jkp} \right) = 0\text{。}$ | (2) |
式中:r为空间一点处到结构表面点处的距离;j为虚数。
声压在自由液面处有:
| $p{|_{\text{自由液面}}} = 0\text{。}$ | (3) |
根据连续性,结构流场交界面处的流场声压与结构振速满足:
| $\frac{{\partial p}}{{\partial n}} = - j\rho \omega {v_n}\text{。}$ | (4) |
式中:n为结构表面的外法向单位矢量;vn为结构表面的外法向振速;ρ为流体的密度。
对模型进行离散,求解方程,在流体结构交界面处,结构振动会产生流体负载,而声压同时对结构产生一个附加力,同时计算结构动力方程和流场的波动方程:
| $\begin{split} & \left[ {\begin{array}{*{20}{c}} {{M}_{\rm{e}}^{\rm{s}}}&0\\ {\rho {R}_{\rm{e}}^{\rm{s}}}&{{M}_{\rm{e}}^{\rm{f}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{{\ddot u}}_{\rm{e}}}}\\ {{{{\ddot p}}_{\rm{e}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{C}_{\rm{e}}^{\rm{s}}}&0\\ 0&{{C}_{\rm{e}}^{\rm{f}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{{\dot u}}_{\rm{e}}}}\\ {{{{\dot p}}_{\rm{e}}}} \end{array}} \right] + \\ & \left[ {\begin{array}{*{20}{c}} {{K}_{\rm{e}}^{\rm{s}}}&{ - {R}_{\rm{e}}^{\rm{f}}}\\ 0&{{K}_{\rm{e}}^{\rm{f}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{u}_{\rm{e}}}}\\ {{{p}_{\rm{e}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{F}_{\rm{e}}^{\rm{s}}}\\ 0 \end{array}} \right]\text{。} \end{split}$ | (5) |
式中:
求解式(5)即可得到流场的声压。
2 计算模型 2.1 数值模型小水线面双体船不同于规则的板壳组合结构,无法通过解析方法进行计算分析,建立基于声固耦合法的三维数值计算模型,采用在边界上覆盖一层声学无限单元的方法来实现无限流场的模拟,这种无限单元可直接应用于声学有限元流场域的边界上,以提高计算效率[6-8]。选取某型小水线面双体船的试验模型作为分析对象,主要参数见表1,几何模型和水池实物模型如图1所示。
|
|
表 1 小水线面双体船主要参数 Tab.1 Main parameter of SWATH model |

|
图 1 小水线面双体船几何模型与试验模型 Fig. 1 Geometric model and experimental model of SWATH |
声固耦合的数值计算模型如图2所示。其中结构单元尺寸为0.1 m,船体结构的材料密度为7800 kg/m3,杨氏模量为2.16×1011Pa,泊松比为0.3。流场上表面赋予自由液面边界条件,流场下表面赋予无穷远处边界条件,并在船体结构与流场界面处设置流固耦合约束。

|
图 2 小水线面双体船数值计算模型 Fig. 2 Numerical calculation model of SWATH |
定义任意
| $D\left( \theta \right) = \frac{{{{\left( {{p_a}} \right)}_\theta }}}{{{{\left( {{p_a}} \right)}_{\max }}}}\text{。}$ | (6) |
水下辐射声场指向性又分为水平指向性与垂直指向性,对于水平指向性,选取船体吃水深度的一半处的圆形声场进行研究,对于垂直指向性,分为沿船宽方向的垂直指向性和沿船长方向的垂直指向性,沿船宽方向的垂直指向性选取激励力所在的横剖面位置,沿船长方向的垂直指向性选取船体中纵剖面所在的平面。无论水平指向性还是垂直指向性,声压参考值均选取该频率点下声压幅值最大值,水平指向性与垂直指向性示意图如图3~图5所示。
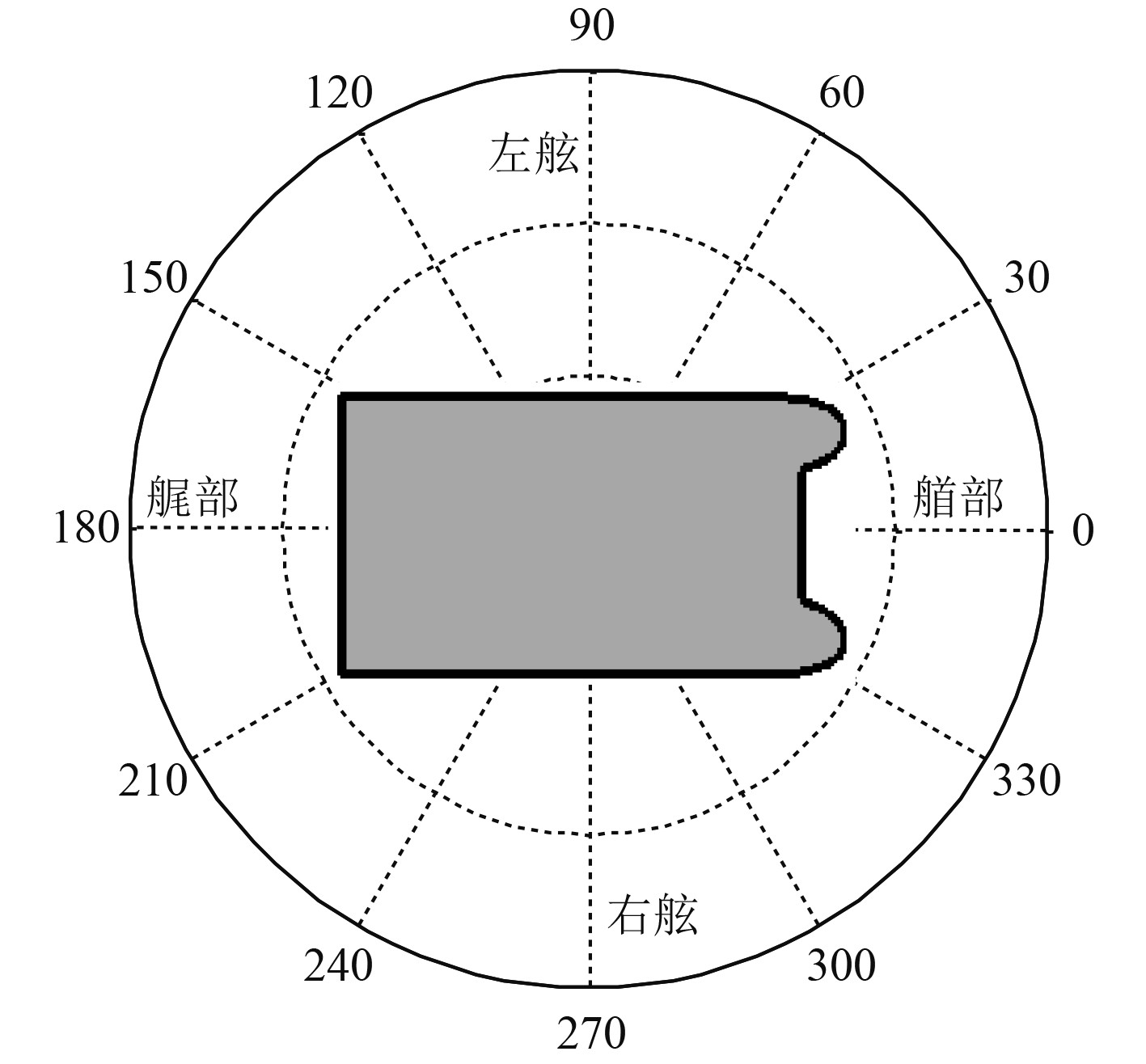
|
图 3 水平指向性示意图 Fig. 3 Horizontal directivity diagram |
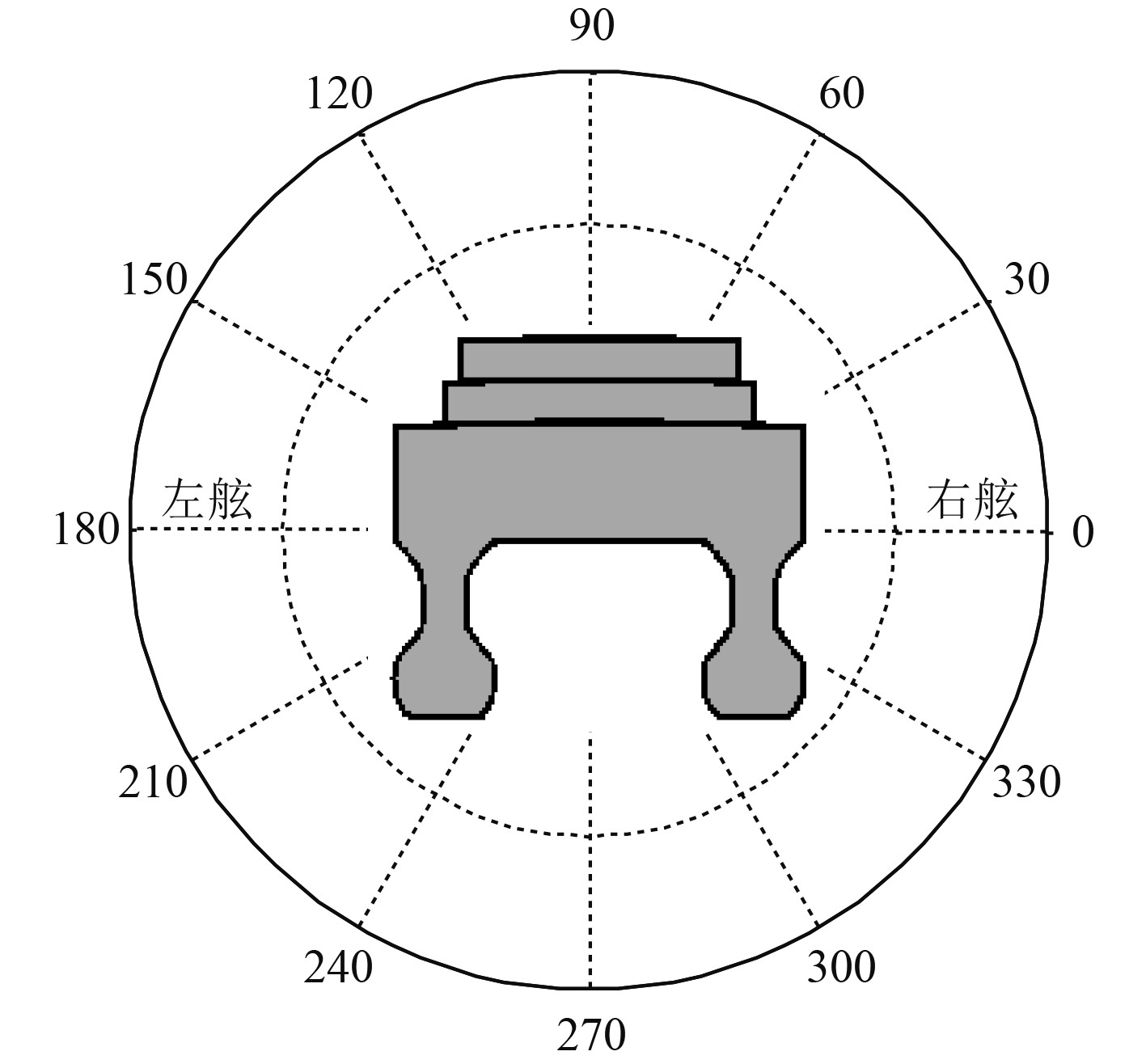
|
图 4 垂直指向性示意图(船宽方向) Fig. 4 Vertical directivity diagram (along the width of ship) |
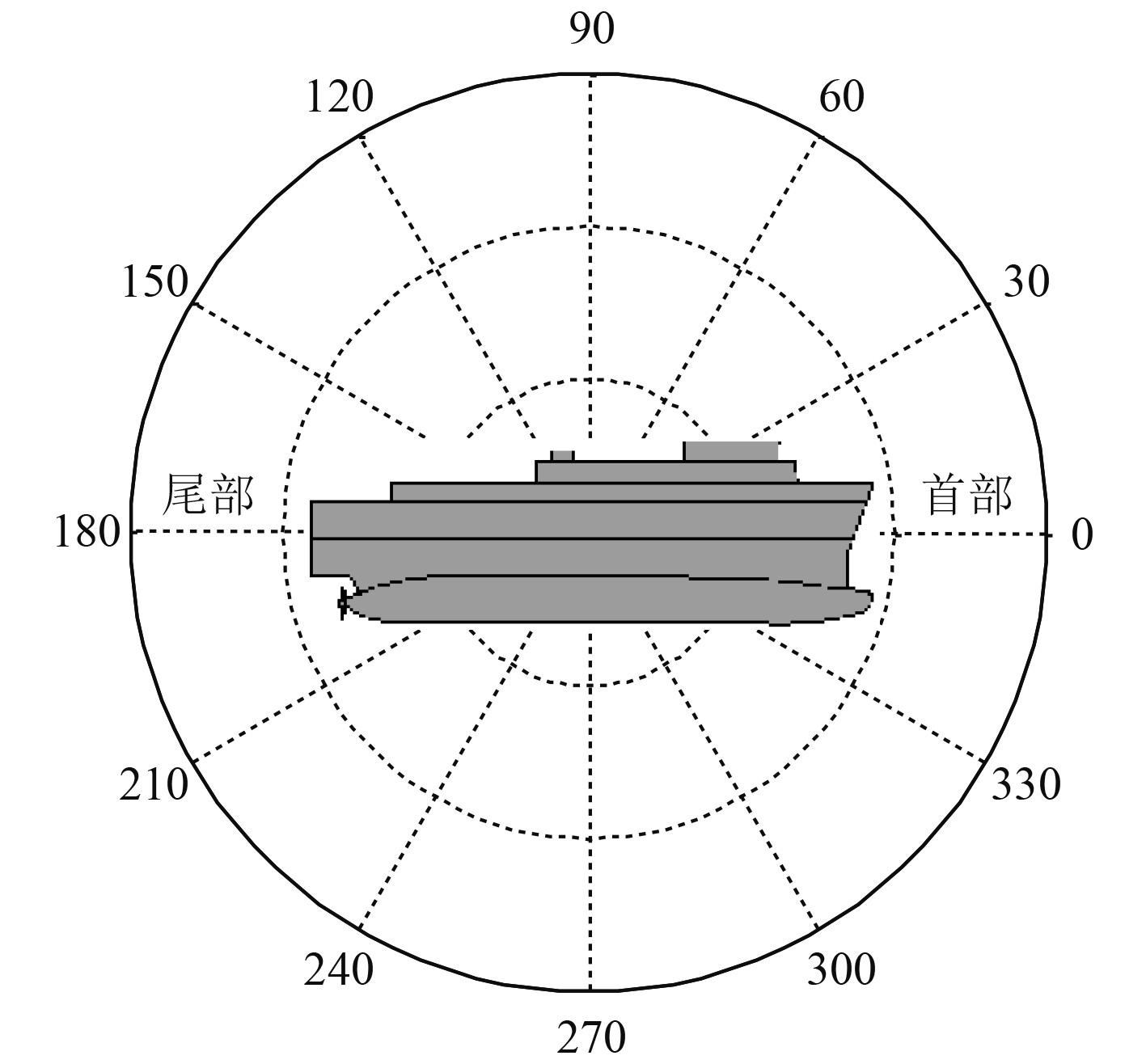
|
图 5 垂直指向性示意图(船长方向) Fig. 5 Vertical directivity diagram (along the length of ship) |
首先计算分析同时激励左右舷主甲板与单独激励左舷主甲板时的水下辐射噪声结果,激励力均垂直于主甲板,2种计算工况均采用单位力激励,计算频段为10~100 Hz,计算结果如图6所示。可以看出,在整个计算的频段范围内,同时激励左右舷主甲板的水下辐射噪声比单独激励左舷主甲板的水下辐射噪声结果大4~4.5 dB。由于双下潜体之间的声场之间存在反射及耦合,且2个激励力导致船体结构振动传递之间的耦合作用,从而使2个结果差异大于3 dB。
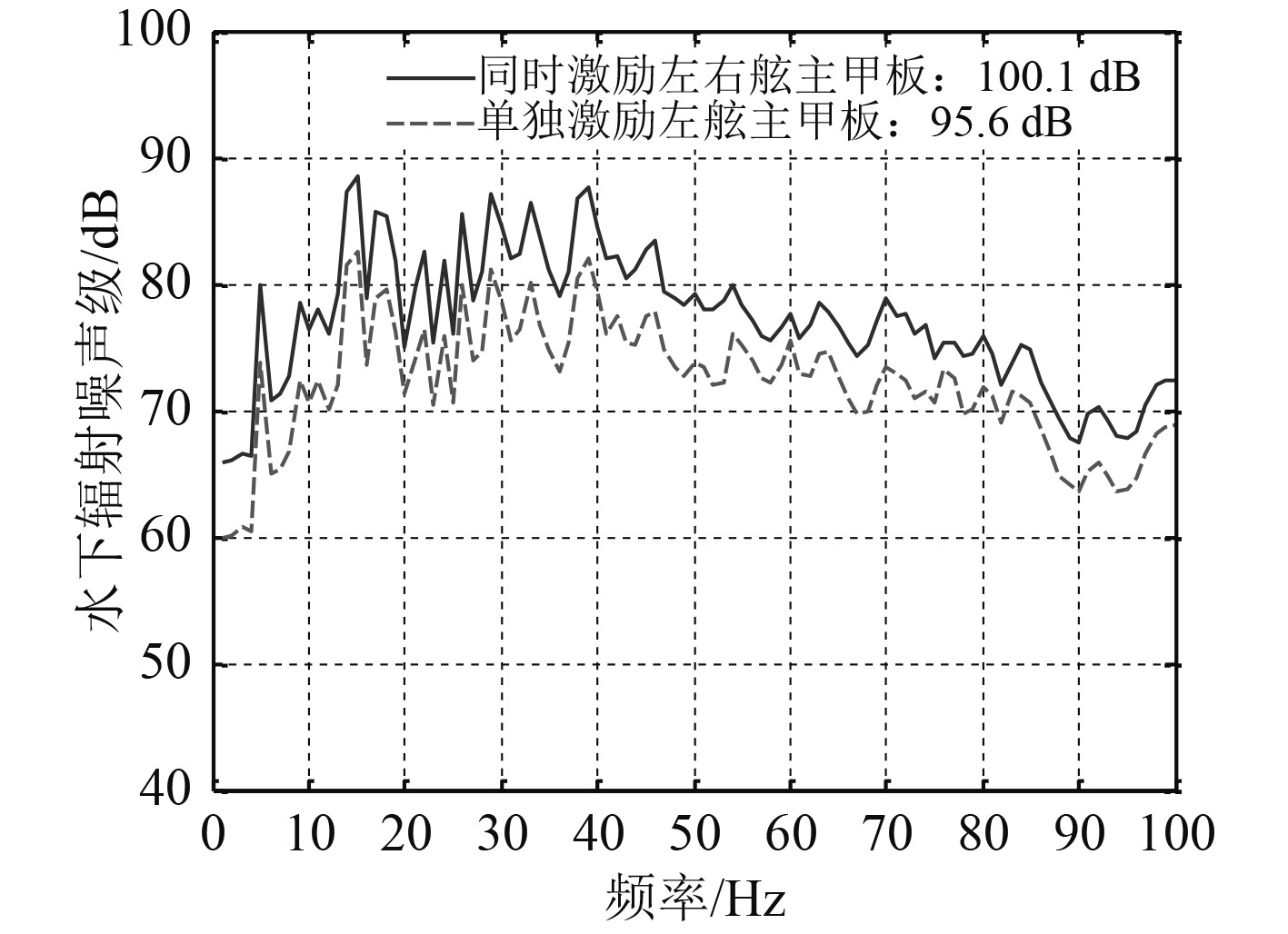
|
图 6 水下辐射噪声对比 Fig. 6 Comparison of underwater radiated noise |
进一步对比同时激励主甲板左右舷与单独激励主甲板左舷的水下辐射声场指向性,从而得到双下潜体的相互耦合作用对水下辐射声场指向性的影响。选取的计算频率为16 Hz,40 Hz。水平指向性、沿船宽方向的垂直指向性以及沿船长方向的垂直指向性计算结果如图7~图12所示。
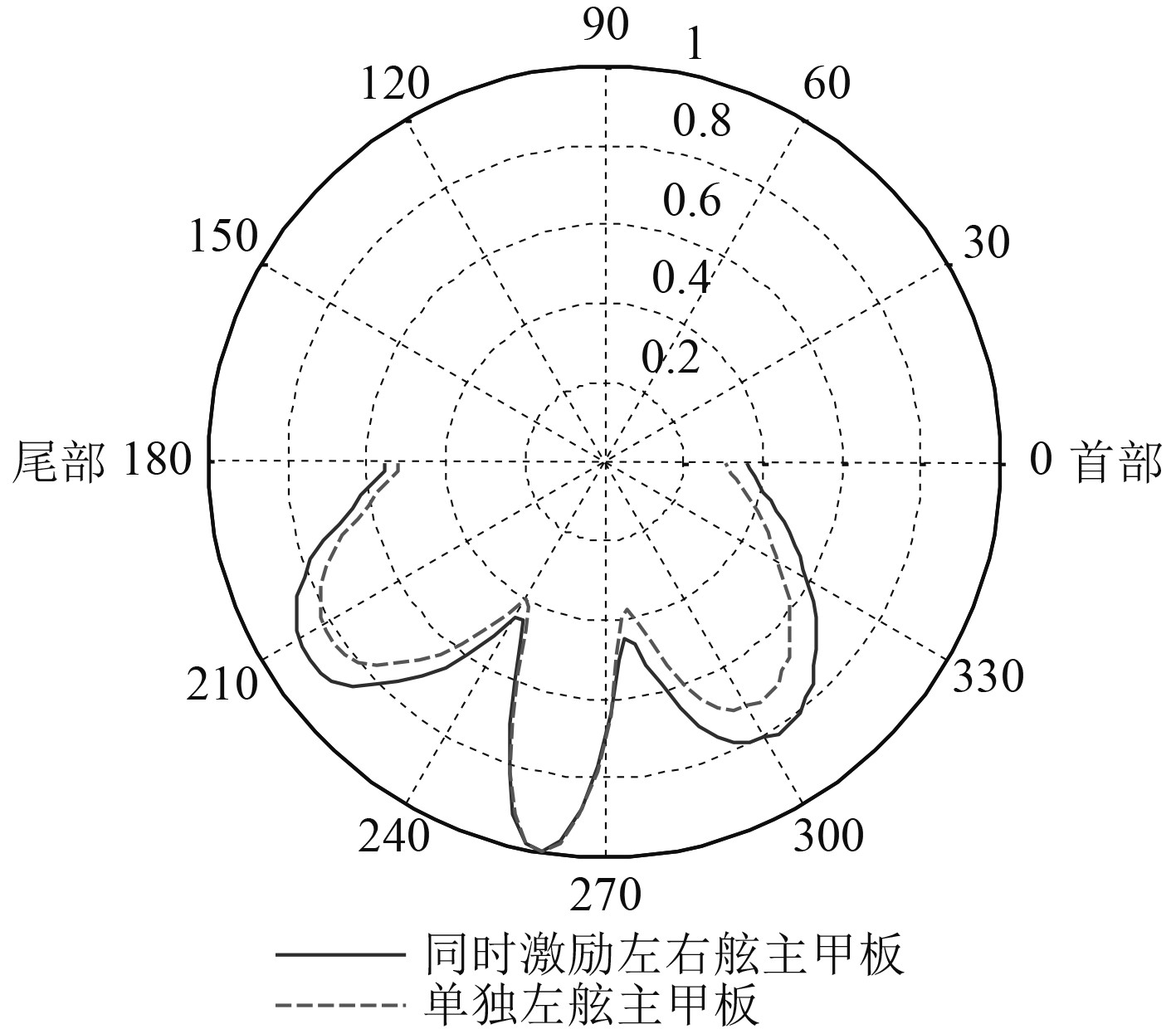
|
图 12 沿船长方向的垂直指向性(40 Hz) Fig. 12 Vertical directivity along the length of ship (40 Hz) |
可以看出:

|
图 7 水平指向性(16 Hz) Fig. 7 Horizontal directivity (16 Hz) |
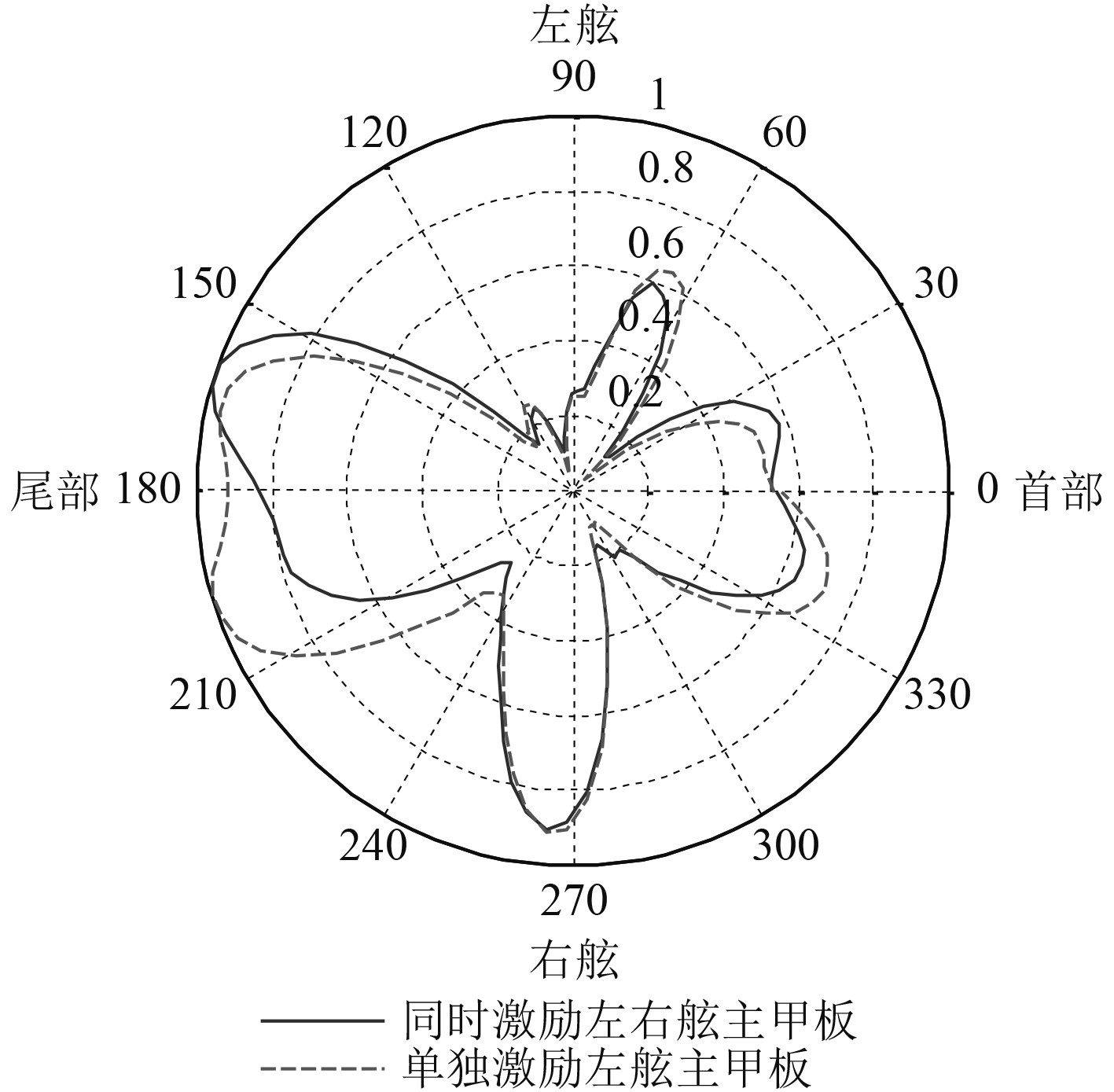
|
图 8 水平指向性(40 Hz) Fig. 8 Horizontal directivity (40 Hz) |
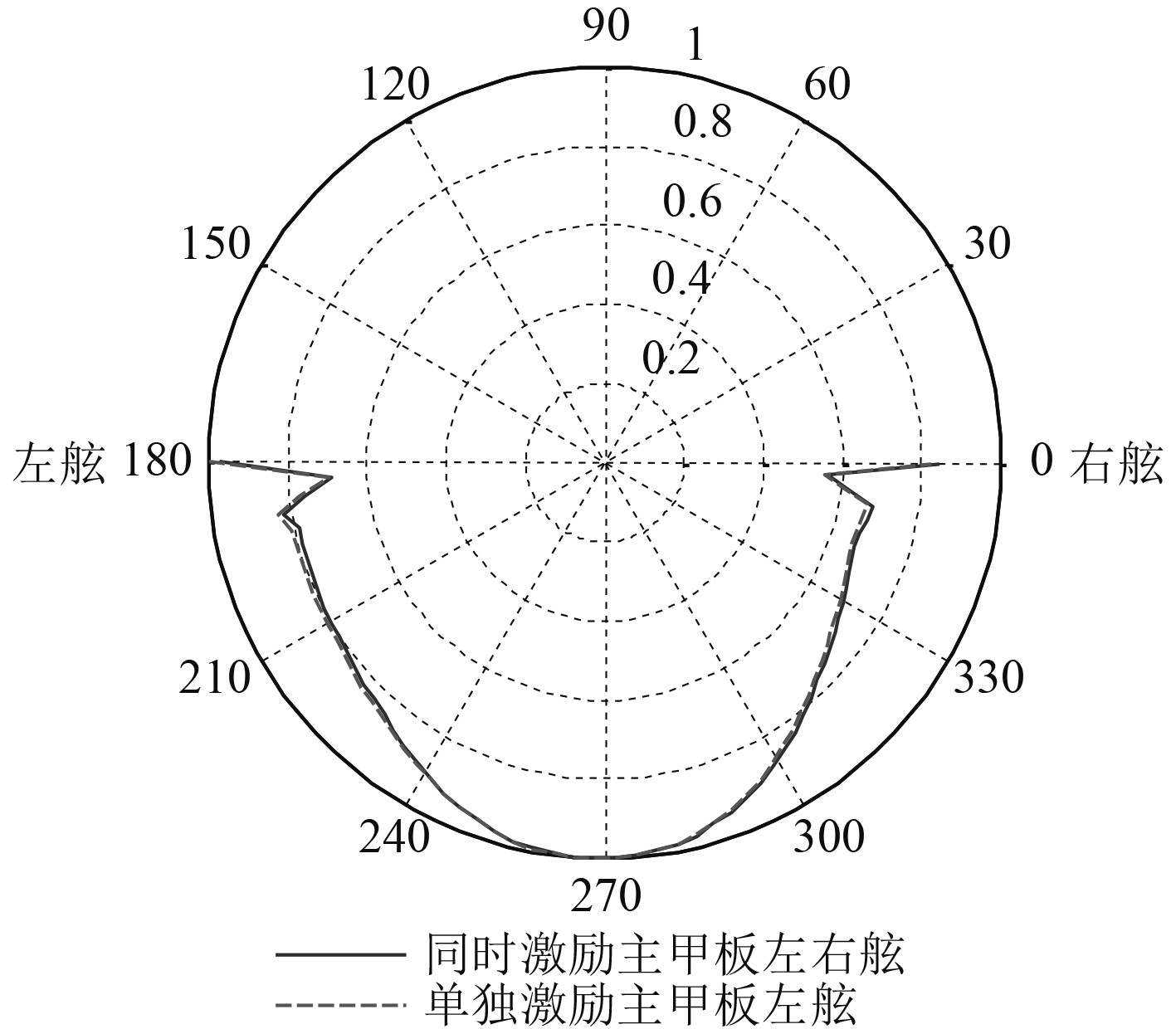
|
图 9 沿船宽方向的垂直指向性(16 Hz) Fig. 9 Vertical directivity along the width of ship (16 Hz) |
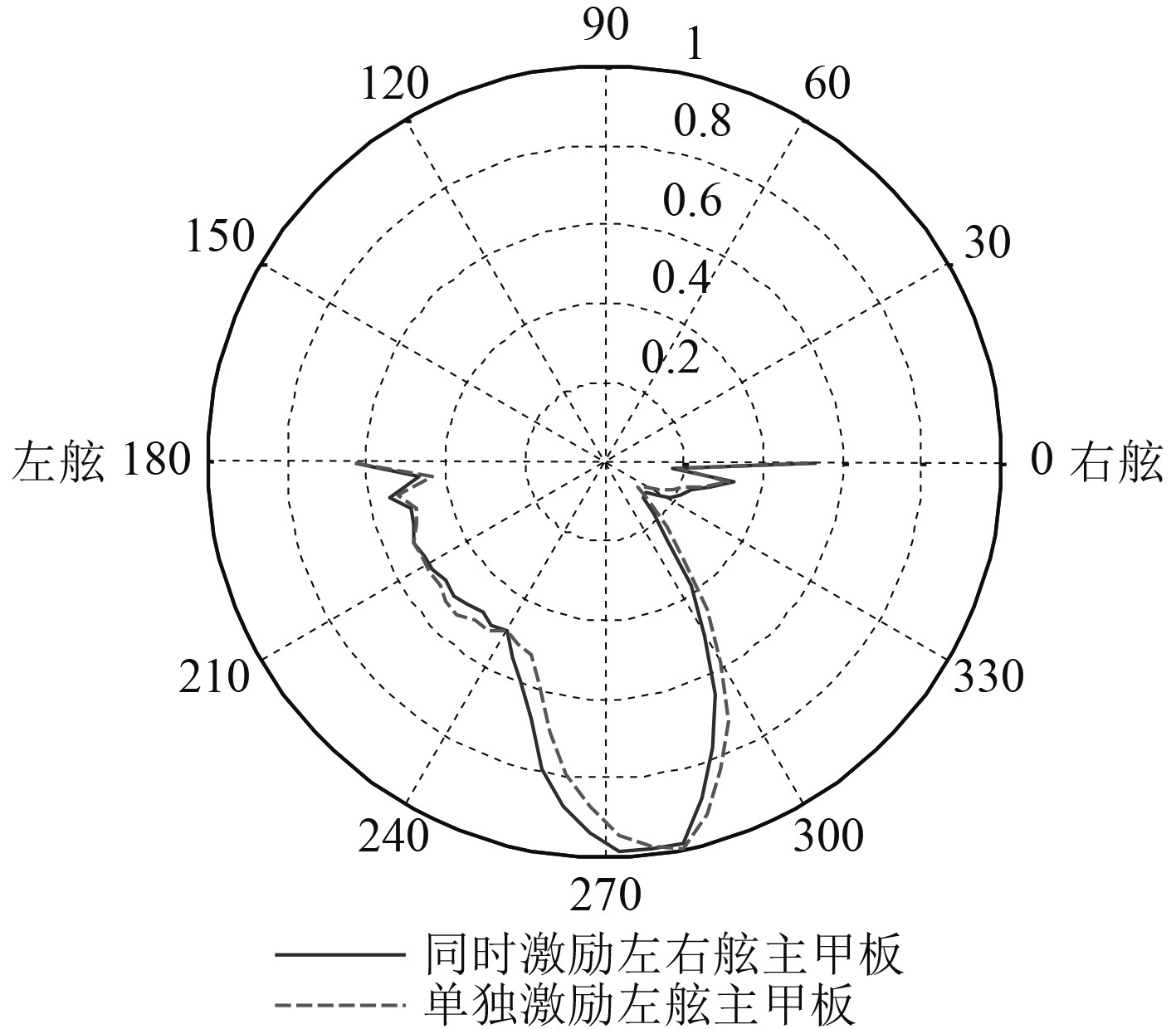
|
图 10 沿船宽方向的垂直指向性(40 Hz) Fig. 10 Vertical directivity along the width of ship (40 Hz) |
1)随着频率的提高,指向性图的波瓣数量逐渐增多;
2)同时激励主甲板左右舷时,尽管激励力、船体结构以及流场相对于中纵剖面基本对称,但由于双下潜体之间的声场耦合作用,指向性图相对于船体结构的中纵剖面并不完全对称分布。
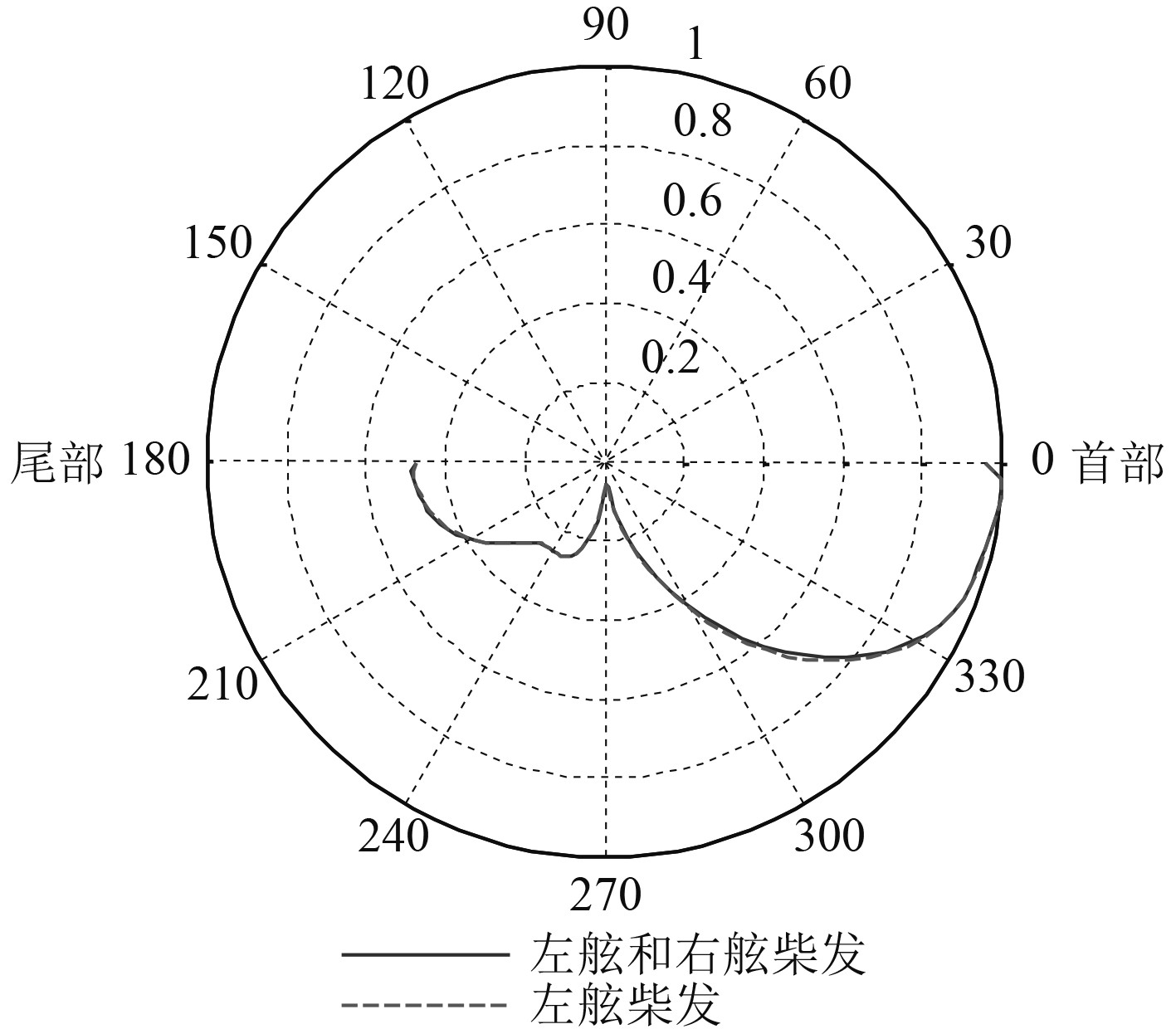
|
图 11 沿船长方向的垂直指向性(16 Hz) Fig. 11 Vertical directivity along the length of ship (16 Hz) |
本文采用声固耦合数值计算方法分析小水线面双体船双下潜体之间的声场耦合作用,对比了同时激励主甲板左右舷和单独激励主甲板左舷的声场指向性规律,得到以下结论:
1)同时激励左右舷主甲板的水下辐射噪声与单独激励左舷主甲板的水下辐射噪声结果差异大于3 dB;
2)随着频率的提高,指向性图的波瓣数量逐渐增多;
3)同时激励主甲板左右舷时,指向性图相对于船体结构的中纵剖面并不完全对称分布;
可见小水线面双体船双下潜体之间的声场耦合对水下辐射噪声与声场指向性均产生了较大影响。
| [1] |
张维, 李明, 陈炉云等. 小水线面双体船声辐射特性研究[J]. 舰船科学技术, 2010, 32(11): 17-20. ZHANG Wei, LI Ming, CHEN Luyun. The structural-acoustic radiation analysis of the small water plane area twin hull ship[J]. Ship science and technology, 2010, 32(11): 17-20. |
| [2] |
薛彦卓, 李硕, 徐利刚, 等. 双体船结构水下中低频辐射噪声特性研究[J]. 中国造船, 2016, 57(1): 94-102. DOI:10.3969/j.issn.1000-4882.2016.01.011 |
| [3] |
杨学猛, 刘彦森, 杜鹏. 船舶水下声辐射垂直指向性的分析与探讨[J]. 噪声与振动控制, 2012(5): 72-75. |
| [4] |
张林根, 吴文伟, 张涛,等. 近水面双圆柱壳耦合声散射研究[J]. 船舶力学, 2014, 18(7): 864-870. DOI:10.3969/j.issn.1007-7294.2014.07.017 |
| [5] |
刘宁, 夏春艳, 刘文帅. 潜艇辐射噪声水平指向性测量方法[J]. 舰船科学技术, 2012, 34(3): 88-90. DOI:10.3404/j.issn.1672-7649.2012.03.019 |
| [6] |
GROTE M, KELLER J. On nonreflecting boundary conditions[J]. Journal of Computational Physics, 1995, 122: 231-243. DOI:10.1006/jcph.1995.1210 |
| [7] |
LU Y C, D'SOUZA K, CHIN C. Sound radiation of engine covers with acoustic infinite element method[J]. SAE Paper, No. 2005-01-2449, 2005.
|
| [8] |
CIPOLLA J L. Acoustic infinite elements with improved robustness[J]. Proceedings of the ISMA2002, Leuven, Belgium, September, 2002, 16-18. |
 2020, Vol. 42
2020, Vol. 42
