0 引　言

内倾船型在航行过程中由于具有良好的隐身性，近年来广泛应用于军事中。其具有的船型特点为折角线以上内倾设计和穿浪型舰首，这种特点使其稳性性能相对于传统的船型来说大大降低。在横风横浪这种极端海况下，船舶在波浪中会发生大幅度的横摇，当复原力矩不足时，会导致船舶倾覆，造成严重的人员财产损失^[1]。

由此，亟需分析横风横浪状态下内倾船型的倾覆概率，以期在舰船航行的过程中，为预防波浪导致船舶发生横摇从而倾覆的情况提供技术理论支撑。传统的分段线性倾覆概率评估方法^[2]对GZ曲线进行等效面积处理时，会使船舶横摇周期发生改变，导致倾覆概率结果偏大。因此本文设计一种内倾船型在横风横浪状态下的倾覆概率评估方法。通过设计内倾船型的运动学方程，确定船舶的倾覆条件，使用蒙特卡罗方法得到倾覆概率的统计估计值，评估内倾船型在横风横浪状态下的倾覆概率。

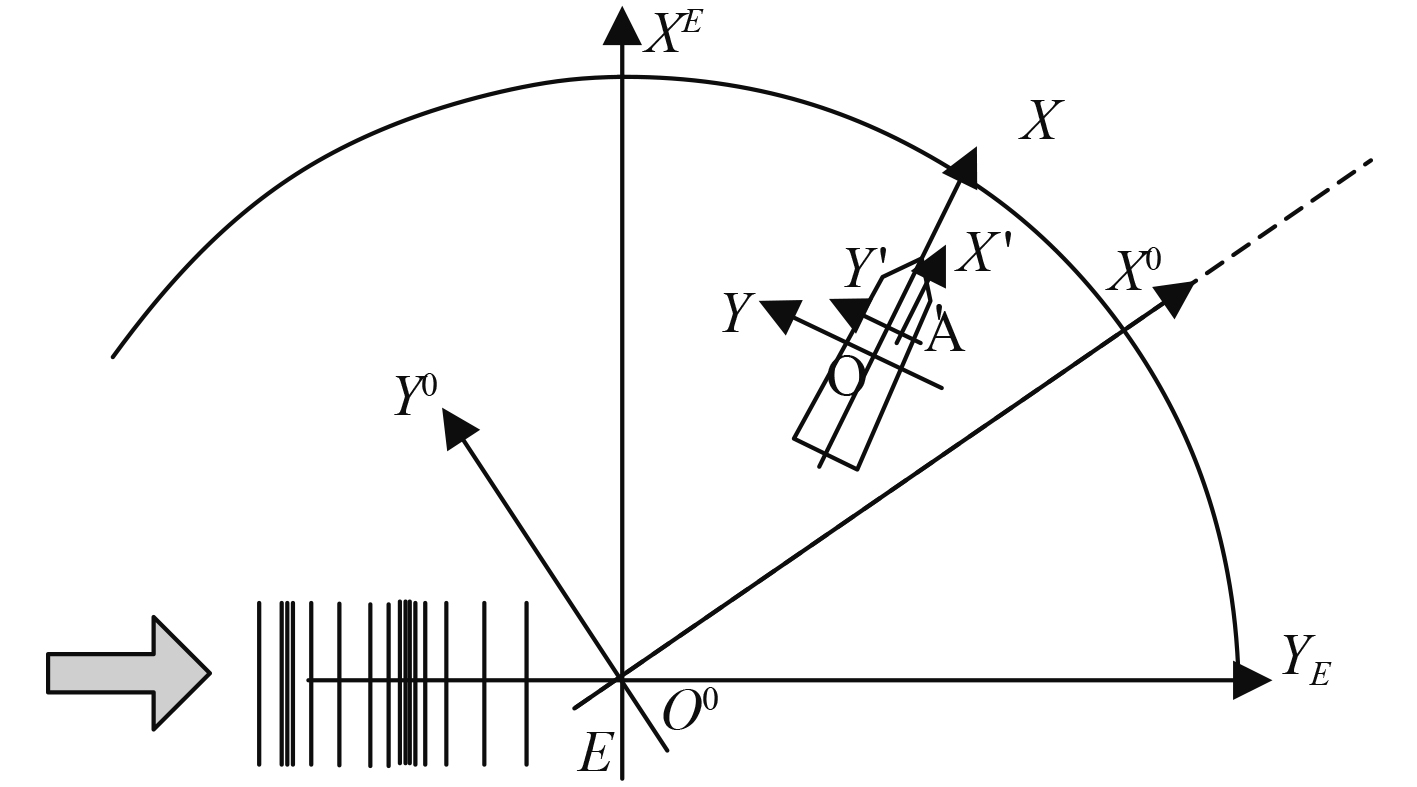
1 内倾船型在横风横浪状态下的倾覆概率评估 1.1 量化分析船舶的横摇运动

为方便研究，需要选取合适的坐标系对内倾船型的运动进行描述，如图1所示。

图中共有4个坐标系，包括空间固定坐标系 $E{X^E}{Y^E}$ ，以船舶运动平均速度直线运动的参考坐标系OXY，船舶初始位置坐标系 ${O^0}{X^0}{Y^0}$ 以及动坐标系 ${O^{'}}{X^{'}}{Y^{'}}$ 。船舶的运动情况比较复杂，船舶基本上将产生六自由度的运动，风倾力矩可以表示为：

${M_{\text{风}}}{\rm{ = }}0.5 \times {\rho _{air}}{C_m}U_w^2{A_L}{H_c}\text{。}$

(1)

式中： ${\rho _{air}}$ 为空气密度； ${C_m}$ 空气阻力系数； $U_w^{}$ 为风速的平均值； ${A_L}$ 为水面以上船舶侧投影面积； ${H_c}$ 为风力作用点距离水动力作用点的高度。波浪力矩可以表示为：

${M_{\text{浪}}}{\rm{ = }}W \cdot h \cdot \gamma \text{。}$

(2)

式中： $W$ 为船舶的排水量； $h$ 为初稳定高度； $\gamma $ 为有效波倾系数。

船舶在横风横浪这种极端海况下航行，可以将横浪看做规则的余弦波，将横风看做平均风和脉动风之和。此时船舶在海面上做线性横摇运动，除此之外，船舶还会受到非线性横风的作用力，因此船舶的运动总体呈现非线性特性^[2]。可以将此时的船舶运动状态描述为：

$\left( {{I_x} + \delta {I_x}} \right) + {B_L} + {B_N} + \Delta C{\rm{ = }}{M_{\text{浪}}} + {M_{\text{风}}}\text{。}$

(3)

式中： ${I_x}$ 为质量惯性力矩； $\delta {I_x}$ 为复加质量惯性力矩；B_L为线性阻尼力矩系数； ${B_N}$ 为非线性阻尼力矩系数； $\Delta C$ 为恢复力矩系数。

1.2 评估倾覆概率

船舶的倾覆与海况和当时的船舶运动状态有关，在对倾覆概率进行评估时，要考虑真实的海洋波浪环境。在船舶真实的航行过程中，当船舶横摇运动超过最大复原力臂所对应的静倾角且持续增大，那么则会发生倾覆^[3-4]。海洋环境条件中，风浪最明显的特点就是具有随机性，因此船舶在海浪中的运动也是随机事件，因此要采用随机理论进行倾覆概率评估，在运动时域模拟的基础上，分析船舶在横风横浪条件下的倾覆情况。将倾覆概率评估过程放在程序当中进行计算时，海面上的大幅度的船舶航行运动是非遍历性的，因此不能只用一个长记录来计算统计值，而是需要一个不同的时历进行多次记录。本文使用蒙特卡罗方法进行计算：

$P_C^*({T_r}) = \frac{{{N_C}}}{{{N_r}}}\text{，}$

(4)

式中： ${N_C}$ 为 ${N_r}$ 个记录中出现倾覆的次数； ${T_r}$ 为相同的记录时长。该方法得到的概率是统计估计值，需要计算置信区间，区间的上限P_t和下限P_u可以表示为：

$\begin{split} & {P_t} = \frac{{{P^*} + \frac{{K_\beta ^2}}{{2{N_r}}} - {K_\beta }\sqrt {\frac{{{P^*}(1 - {P^*})}}{{{N_r}}} + \frac{{K_\beta ^2}}{{4N_r^2}}} }}{{1 + \frac{{K_\beta ^2}}{{{N_r}}}}} \text{，}\\ & {P_u} = \frac{{{P^*} + \frac{{K_\beta ^2}}{{2{N_r}}} + {K_\beta }\sqrt {\frac{{{P^*}(1 - {P^*})}}{{{N_r}}} + \frac{{K_\beta ^2}}{{4N_r^2}}} }}{{1 + \frac{{K_\beta ^2}}{{{N_r}}}}} \text{，} \end{split} $

(5)

式中： ${K_\beta }$ 为宽窄度，对于概率为98%时的可接受的置信度， ${K_\beta }$ =1.9425。在此基础上，结合海洋的波浪谱，能够计算出倾覆概率为：

$P = ({P_t} - {P_u})\frac{{{N_C}}}{{{N_r}}}\text{。}$

(6)

2 实　验 2.1 实验准备

为了验证本文设计的倾覆概率评估方法的准确性，设计模拟实验，分别使用本文的评估方法和传统的评估方法对内倾船型在横风横浪状态下的倾覆概率进行评估，并与模拟实验中的实际倾覆情况进行对比。本文选择1艘内倾船型作为实验船，模型的主要尺度如表1所示。

船模采用玻璃钢材料制成，根据内倾船航行过程中的实际情况，空船重量不应该超过排水量的1/3，且水上、下线性、重心位置、纵向惯量要与实体船一致。模型放在耐波性水池中进行，如图2所示。

该水池长72 m，宽43 m，深4.5 m，且水池相邻的两边设有摇板式造波机，能够模拟出各种波形，对岸分别布置了消波器。本文模型船是在不规则波情况下进行实验，因此需要采用ITTC双参数波谱进行模拟：

${S_{wave}}\left( {{\omega _i}} \right) = \frac{A}{{\omega _i^5}}\exp \left[ { - \frac{B}{{\omega _i^4}}} \right]\text{。}$

(7)

式中： $A = 173.51\dfrac{{H_{\frac{1}{3}}^2}}{{T_0^4}}$ ； $B = \dfrac{{673}}{{T_0^2}}$ ； $H_{\frac{1}{3}}^{}$ 为有义波高； $T_0^{}$ 为波浪特征周期； $\omega $ 为波浪圆频率。在上述实验环境下，分别使用本文设计的方法和传统的分段线性倾覆概率评估方法对该船进行倾覆概率评估，并对评估结果进行比较。

2.2 实验结果比较与分析

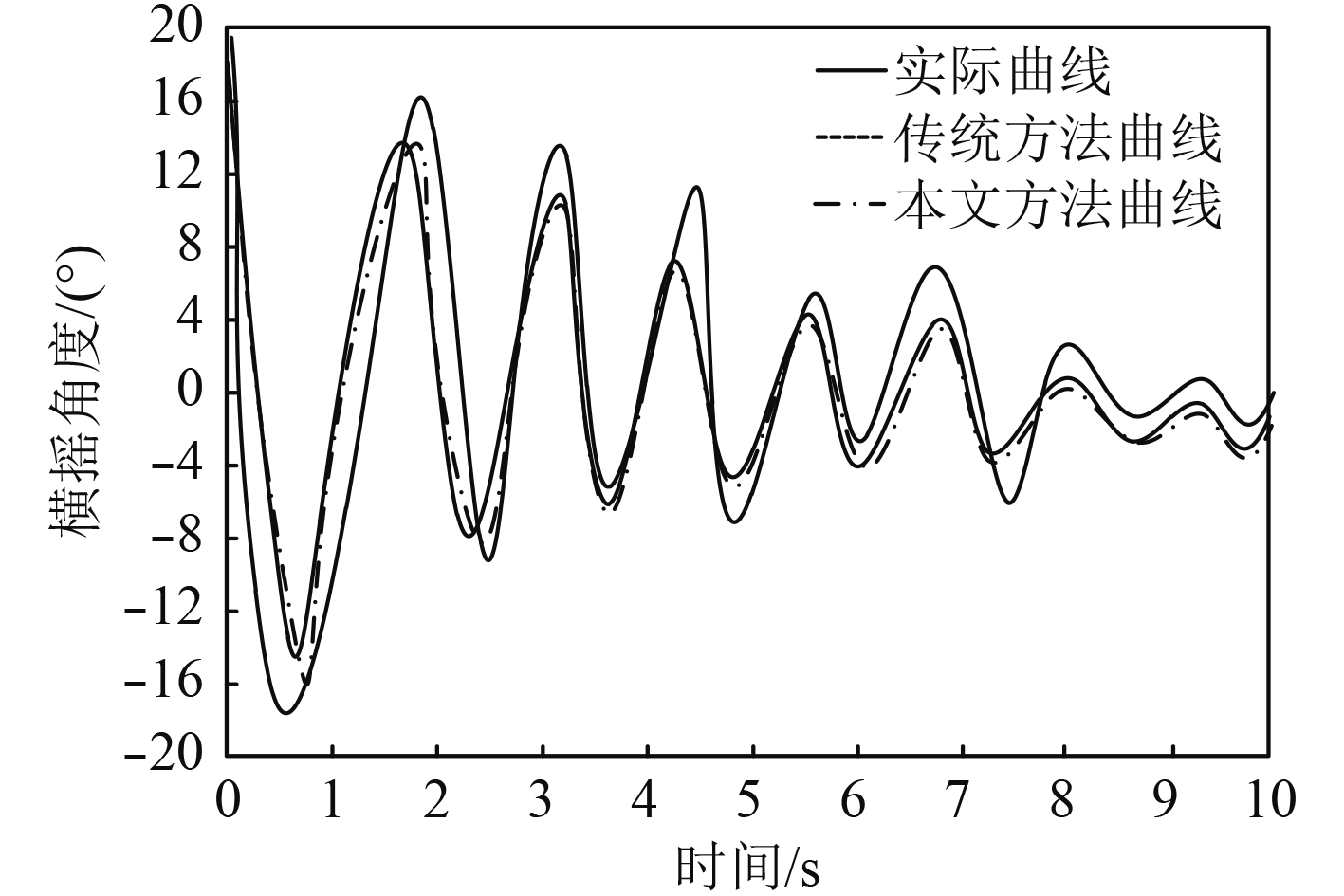
横摇固有周期是船舶横摇运动的重要指标，首先对2种方法进行船舶自由横摇衰减试验。设定船舶航向为0°，起始风向90°，风力30 m/s，浪向90°，波高2 m，周期10个/s。船舶完全适应风浪条件后停止风浪条件，得到其横摇衰减曲线，如图3所示。

船舶横摇固有周期的准确性评估对船的倾覆概率评估起着重要作用。由图3可知，相较于传统方法，本文方法测定的横摇衰减曲线更加贴合实际曲线。说明本文方法测定方法要优于传统方法。

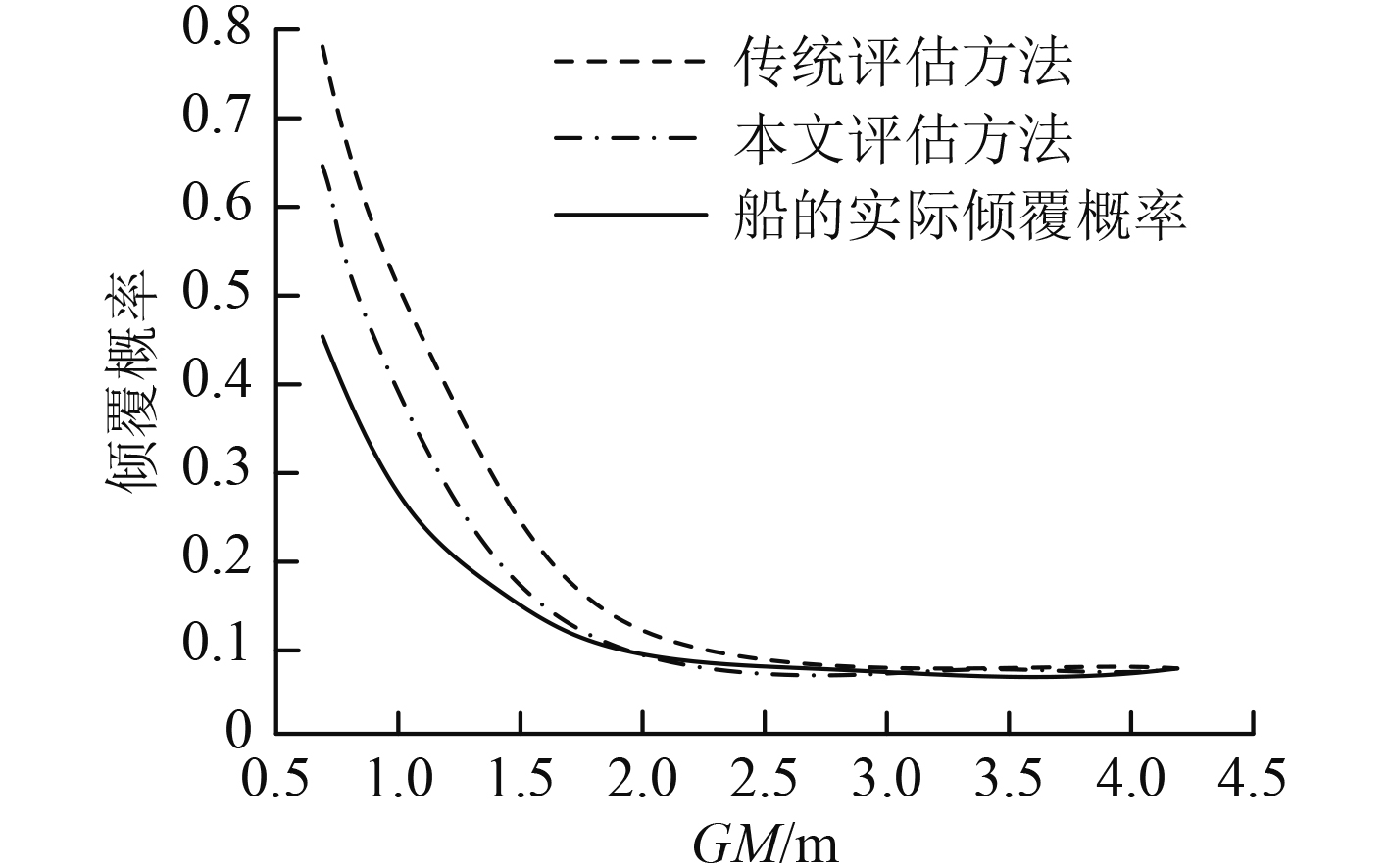
分别对2种方法进行不同GM和不同风速下的倾覆概率评估对比。图4为2种评估方法在不同初稳性高GM下得到的倾覆概率。

在初稳性高为2.0 m的情况下，利用2种评估方法在不同风速下得到的倾覆概率如图5所示。

从图4和图5可以看出，2种方法的评估结果从大体上看，走势基本相似，随着GM的增大，倾覆概率逐渐变小，在相同GM的情况下，风速越大，倾覆的概率越大。但是本文设计的评估方法得到的倾覆概率值更加接近实验中的真实走势，传统的评估方法得到的倾覆概率相对偏大。说明本文设计的概率评估方法得到的评估结果更加准确。

3 结　语

本文针对传统的船舶倾覆概率评估方法所存在的问题，设计一种适用于内倾船型在横风横浪状态下的倾覆概率评估方法，对内倾船型在波浪中的运动状态进行分析和研究，并建立船舶非线性运动方程。通过选择坐标系、求取风倾力矩和波浪力矩，对船舶的运动进行超详细描述，使用蒙特卡罗方法完成倾覆概率的评估。实验发现本文设计的倾覆概率评估方法可以较为准确地评估横风横浪状态下的倾覆概率，可为预防内倾船型运行过程中发生倾覆提供一定的参考。