2. 中国舰船研究院,北京 100101;
3. 哈尔滨工程大学,黑龙江 哈尔滨 150001
2. China Ship Research and Development Academy, Beijing 100101, China;
3. Harbin Engineering University, Harbin 150001, China
船上设备工作产生的宽频激励将不可避免地引起船体结构振动,该宽频振动能量经由基座、甲板等船体结构向响应面传递,将对船舶舒适性和结构安全性产生危害[1]。船体结构是由众多杆、梁和板等弹性构件相互耦合而成的组合结构[2],其中,梁系结构作为船舶结构中的重要部分,是影响船体振动传递的主要因素之一。因此开展船舶梁系结构振动特性影响的研究,对揭示船舶结构复杂多模态振动机制具有重要的指导意义。
李俊[3]从基础理论出发,推导了考虑剪切变形和转动惯量的弯扭耦合薄壁梁自由振动的动态传递矩阵,并给出了其显式表达式。汤华涛[4]利用有限元法推导了空间单元的传递矩阵,研究了悬臂梁结构在含轴向拉压应变时其振动特性变化的问题。Nandakumar 等[5]基于状态矢量法修改阻尼传递矩阵,进行了结构参数识别的分析理论探究。王献忠[6]应用非齐次项的精细积分,提出一种求解加筋圆柱壳动响应的精细传递矩阵方法。
由以上研究可知,一方面现有文献大多聚焦于单跨梁结构和简单组合结构在经典边界条件下的自由振动特性,鲜有学者开展对多跨梁振动机理揭示的研究。同时对于弹性支撑条件下多跨梁结构振动特性研究尚未见公开报道。为此,本文在已有研究成果的基础上,对实际船舶梁系结构进行简化,开展具有弹性支撑的多跨梁其弹性支撑相关参数改变对结构振动特性的影响研究,旨在更好地揭示船体振动特性规律。
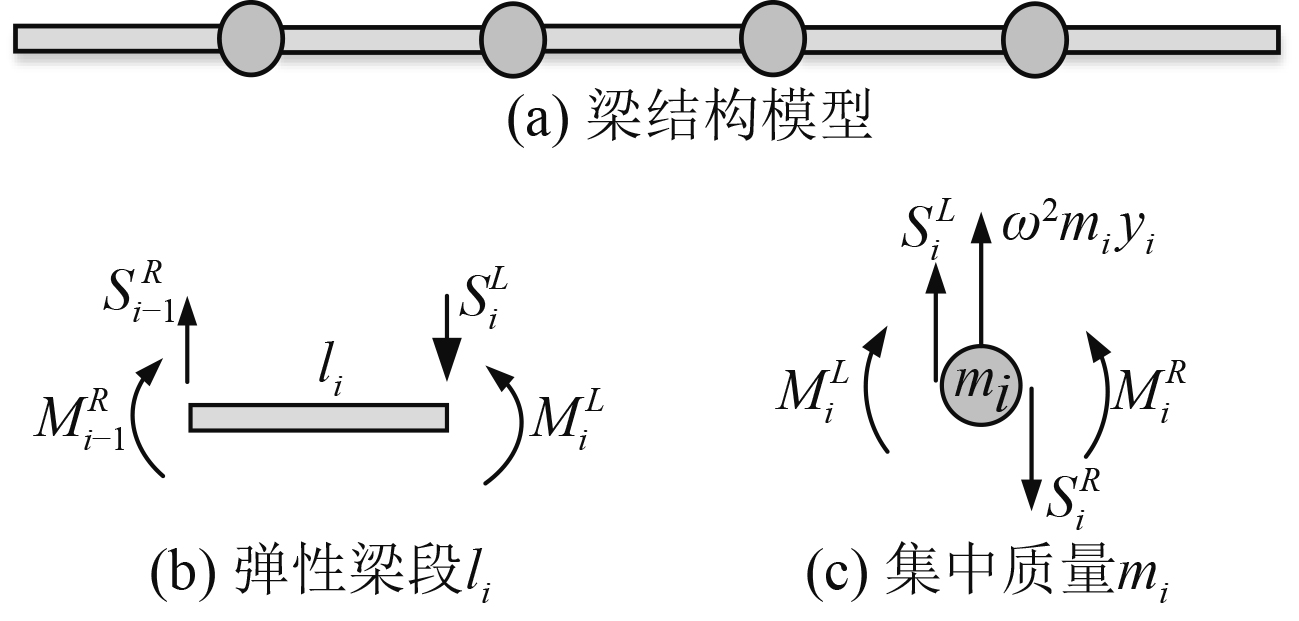
1 多跨梁结构振动特性分析 1.1 梁系结构振动方程将连续梁结构简化为若干个无质量弹性梁段和集中质量,如图1所示。
|
图 1 简单梁结构模型示意图 Fig. 1 Schematic diagram of simple beam model |
此时,将梁上任一点的位移矢量和力矢量作为线性传递矩阵理论[6]分析变量,结构状态矢量:
| ${{Z}} = {\left\{ {y\;\theta \;M\;S} \right\}^{\rm{T}}}\text{。}$ | (1) |
式中:
由传递矩阵法基本方程得:
| $\left\{ \begin{array}{l} \left\{ Z \right\}_i^R = {{{C}}_{ip}}\left\{ Z \right\}_i^L \text{,}\\ \left\{ Z \right\}_{i + 1}^L = {{{C}}_{if}}\left\{ Z \right\}_i^R \text{。}\end{array} \right.$ | (2) |
式中:
取弹性梁段
|
图 2 梁结构计算模型 Fig. 2 Calculation model of beam structure |
对于无质量弹性梁段而言,其右端状态矢量为
| $ \left\{ {\begin{array}{*{20}{c}} {S_{i - 1}^R - S_i^L = 0} \text{,}\\ { - M_{i - 1}^R + M_i^L - S_{i - 1}^R{l_i} = 0} \text{,}\end{array}} \right. $ | (3) |
由弯曲平衡方程可知:
| $ \left\{ {\begin{aligned} & {\theta _i^L = \theta _{i - 1}^R + \frac{{{l_i}M_{i - 1}^R}}{{EI}} + \frac{{l_i^2S_{i - 1}^R}}{{2EI}}} \text{,}\\ & {y_i^L = y_{i - 1}^R + {l_i}\theta _{i - 1}^R + \frac{{l_i^2M_{i - 1}^R}}{{2EI}} + \frac{{l_i^3S_{i - 1}^R}}{{6EI}}} \text{。}\end{aligned}} \right. $ | (4) |
式中:E为材料的弹性模量;
| $ \left\{ \!\!{\begin{array}{*{20}{c}} y \\ \theta \\ M \\ S \end{array}} \!\!\right\}_i^L = \left\{\!\! {\begin{array}{*{20}{c}} 1&{{l_i}}&{\dfrac{{l_i^2}}{{2EI}}}&{\dfrac{{l_i^3}}{{6EI}}} \\ 0&1&{\dfrac{{{l_i}}}{{EI}}}&{\dfrac{{l_i^2}}{{2EI}}} \\ 0&0&1&{{l_i}} \\ 0&0&0&1 \end{array}} \!\!\right\}\left\{\!\! {\begin{array}{*{20}{c}} y \\ \theta \\ M \\ S \end{array}} \!\!\right\}_{i - 1}^R \equiv {C_{if}}Z_{i - 1}^R\text{,} $ | (5) |
取集中质量mi作为分离体,其右端矢量为
| $ \left\{ {\begin{array}{*{20}{c}} y \\ \theta \\ M \\ S \end{array}} \right\}_i^R = \left\{ {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&1&0&0 \\ 0&0&1&0 \\ {{m_i}{\omega ^2}}&0&0&1 \end{array}} \right\}\left\{ {\begin{array}{*{20}{c}} y \\ \theta \\ M \\ S \end{array}} \right\}_i^L \equiv {C_{ip}}Z_i^L \text{,}$ | (6) |
结合式(5)和式(6)可得第i-1个梁段右端至第i个梁段右端的状态矢量传递关系:
| $ Z_i^R = {C_{ip}}{C_{if}}Z_{i - 1}^R \equiv {C_i}Z_{i - 1}^R\text{。} $ | (7) |
式中:
| $ {{{C}}_i} = \left\{ {\begin{array}{*{20}{c}} 1&{{l_i}}&{\dfrac{{l_i^2}}{{2EI}}}&{\dfrac{{l_i^3}}{{6EI}}} \\ 0&1&{\dfrac{{{l_i}}}{{EI}}}&{\dfrac{{l_i^2}}{{2EI}}} \\ 0&0&1&{{l_i}} \\ {{\omega ^2}{m_i}}&{{\omega ^2}{m_i}{l_i}}&{\dfrac{{{\omega ^2}ml_i^2}}{{2EI}}}&{1 + \dfrac{{{\omega ^2}{m_i}l_i^3}}{{6EI}}} \end{array}} \right\}\text{,} $ | (8) |
对于图1所示的连续梁振动系统,有
| $ Z_n^R = {C_n}{C_{n - 1}} \cdots {C_1}{Z_0} \equiv {{C}}{Z_0}\text{。} $ | (9) |
式中,
由两端边界条件,可确定梁首末处的状态矢量
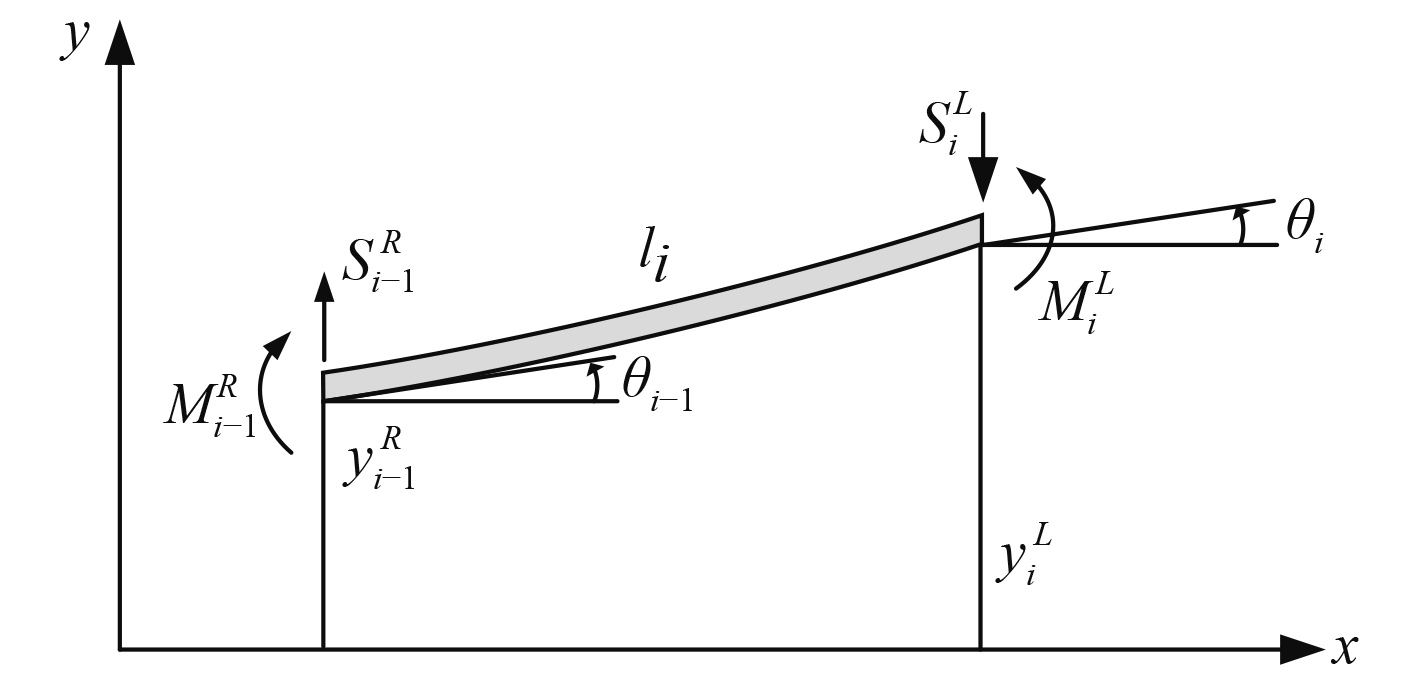
为简化研究,本文以如图2所示的轻质梁段和集中质量组成的多自由度系统为研究对象。各段弹性梁长度

|
图 3 平面横向振动弹性梁段 Fig. 3 Elastic beam section with transverse vibration |
根据边界条件可得,结构两端状态矢量均满足:
| $ {{Z}} = {[0,\;\theta ,\;0,\;S]^{\rm{T}}}\text{。} $ | (10) |
由传递矩阵法解得连续梁的振动模态,经归一处理后前4阶模态振型计算结果如图4所示。
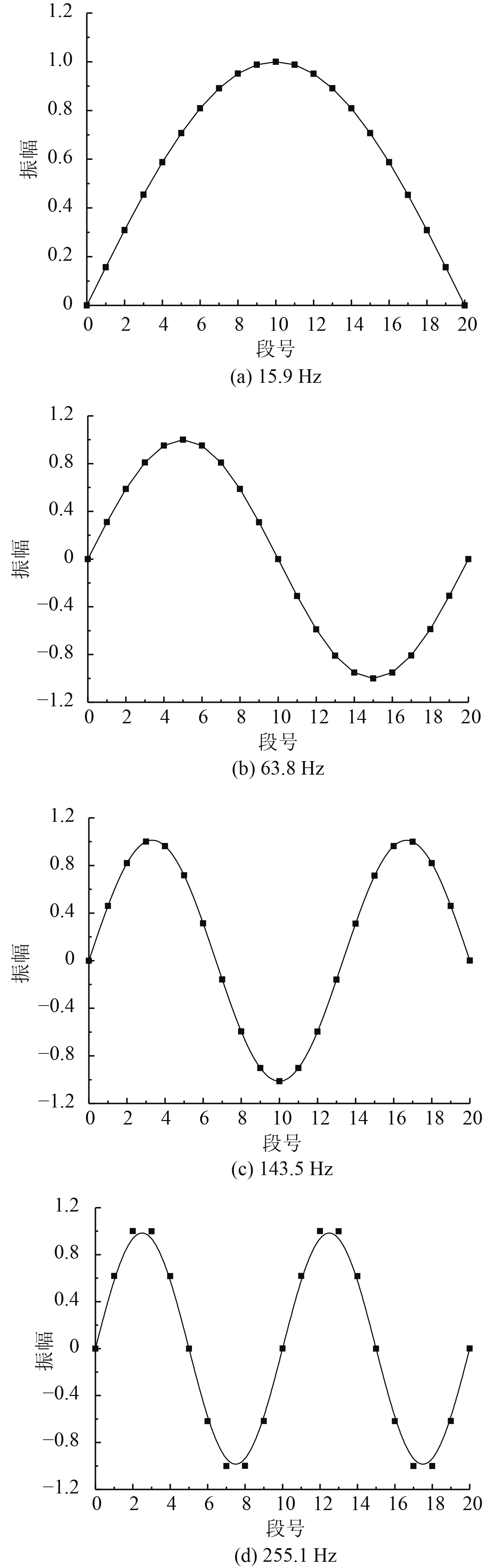
|
图 4 梁结构振动模态振型 Fig. 4 Vibration mode of beam structure |
在连续梁中心位置即第10个集中质量处施加单位力,计算得到第5个集中质量元件5#、第10个集中质量元件10#及第15个集中质量元件15#三点处的强迫振动响应频谱曲线。为保证计算精度,计算频段设为1~200 Hz,计算结果如图5所示。
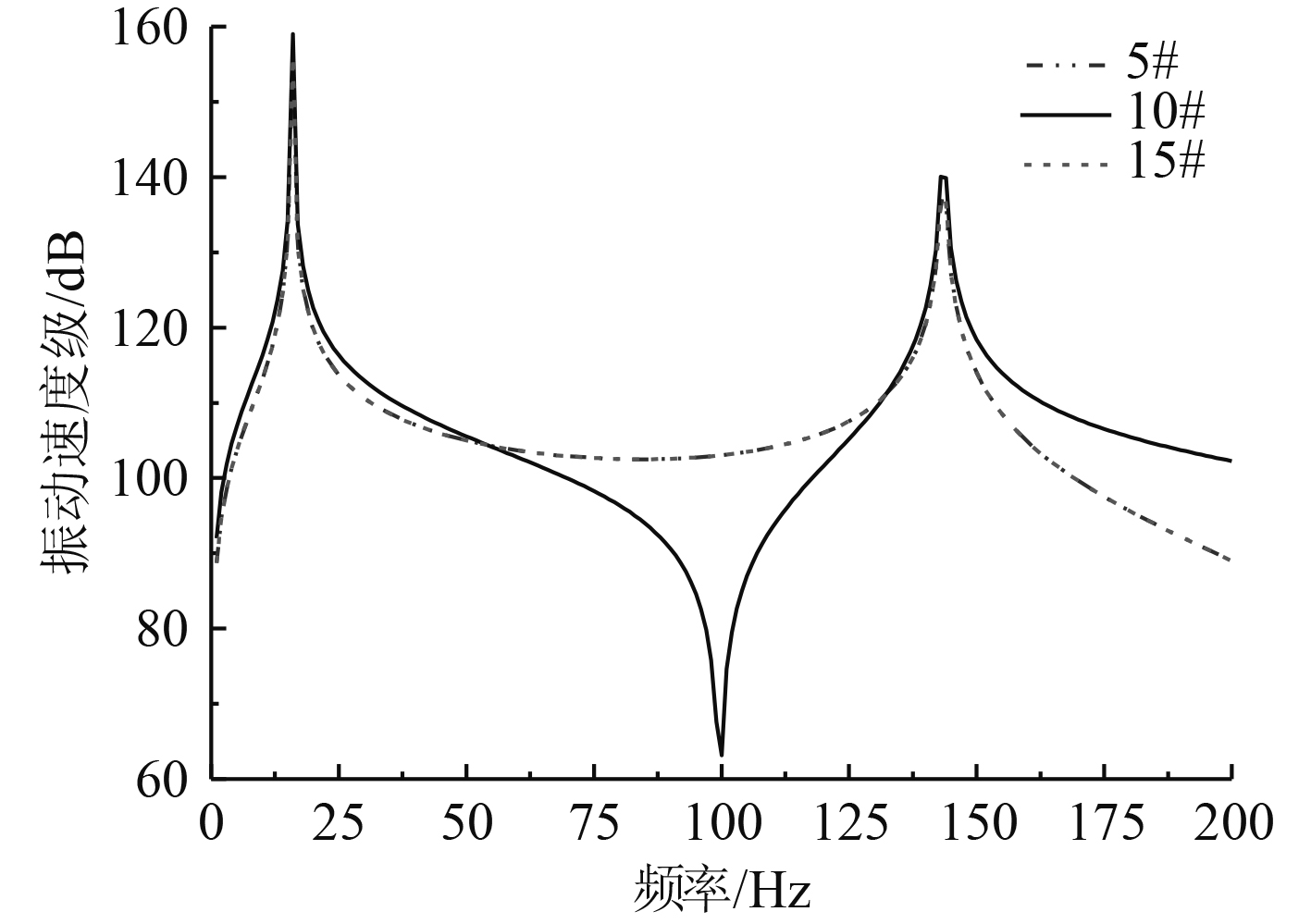
|
图 5 振动响应频谱图 Fig. 5 Vibration response spectrum |
由图5可知,系统振动响应在16 Hz,144 Hz出现峰值,峰值频率与系统第1阶、第3阶固有频率相接近;此外,激励位置处即第10个集中质量元件振动响应存在反共振频率100 Hz;结构振动响应曲线在第2阶固有频率63.8 Hz附近未出现共振峰值,原因是激励位置位于结构第2阶模态振型的节点附近,不能引起结构强振动。除共振峰值频率附近外,结构振动响应均较小。
在16 Hz,64 Hz,100 Hz,144 Hz频率下梁结构各单元的强迫振动响应结果如图6所示。可以看出,共振峰值频率16 Hz,144 Hz下结构响应分布与结构前两阶模态振型相近;系统在64 Hz,100 Hz下各单元振动响应都相对较小。
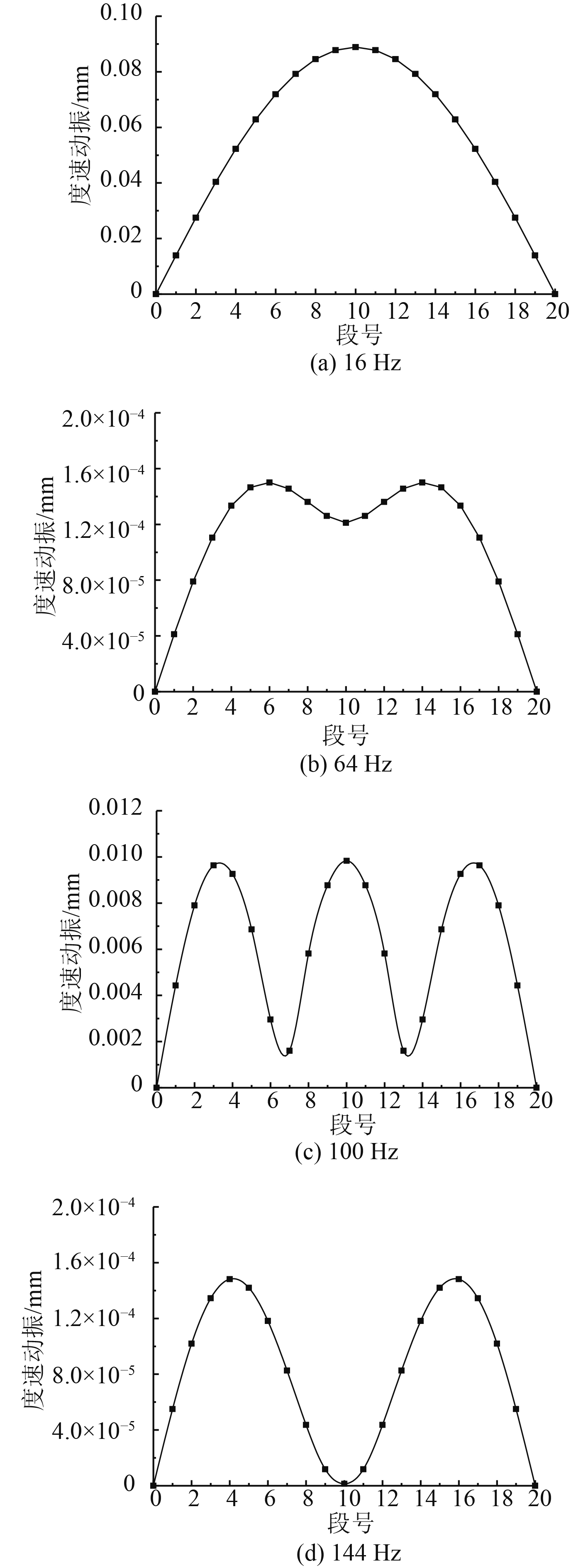
|
图 6 梁结构振动响应分布 Fig. 6 Vibration response of beam structure |
船舶结构存在不同跨度的纵骨、横梁等骨材结构,从而与甲板形成不同尺度的加筋板架结构,本研究仅考虑结构截面方向,以设有弹性支撑的多跨梁近似模拟加筋板或板架结构,其中平板采用弹性梁段和集中质量点模拟;骨材结构采用弹性支撑模拟,为简化研究,这里仅考虑其刚度,计算模型如图7所示。进而研究弹性支撑的跨度和刚度改变对多跨梁结构振动特性的影响。
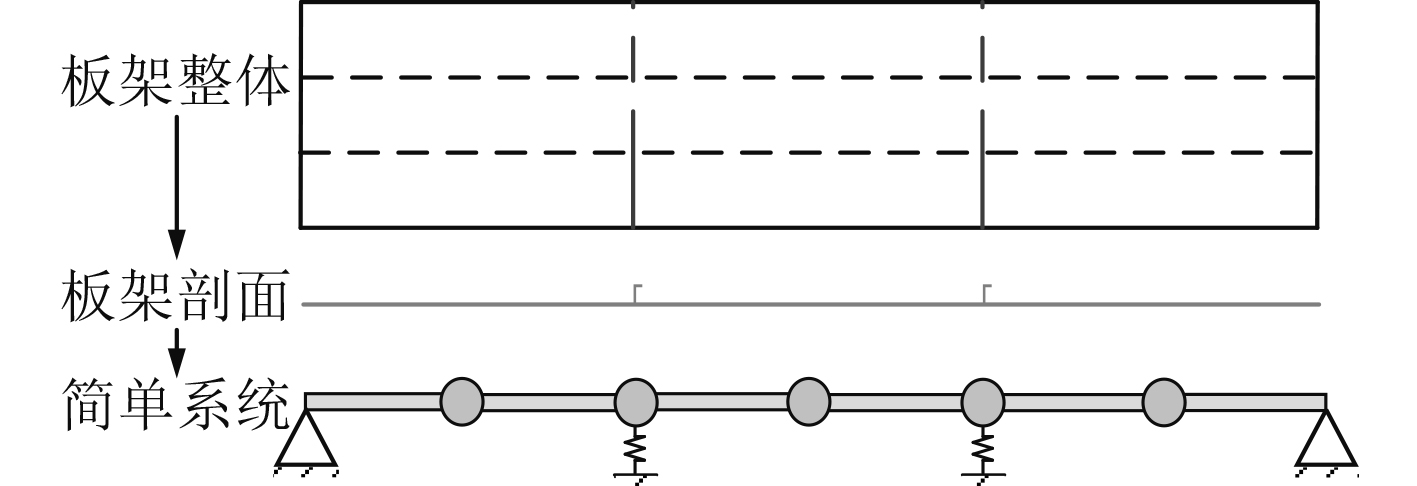
|
图 7 多跨梁计算模型 Fig. 7 Calculation model of multi span beam |
对于设置弹性支撑的集中质量mi,取其作为分离体,支撑刚度为k,其右端矢量为
| $ \left\{\!\! {\begin{array}{*{20}{c}} y \\ \theta \\ M \\ S \end{array}}\!\! \right\}_i^R = \left\{\!\! {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&1&0&0 \\ 0&0&1&0 \\ {{m_i}{\omega ^2} - k}&0&0&1 \end{array}}\!\! \right\}\left\{\!\! {\begin{array}{*{20}{c}} y \\ \theta \\ M \\ S \end{array}}\!\! \right\}_i^L \equiv {C_{ip}}Z_i^L\text{。} $ | (11) |
计算模型采用由60个无质量弹性梁段及59个集中质量构成的多自由度系统模拟多跨连续梁,各段弹性梁弹性模量
本节对于具有弹性支撑的多跨梁结构,两端简支边界下结构跨度分别为6 m,9 m,12 m,15 m,18 m,设支撑刚度均为
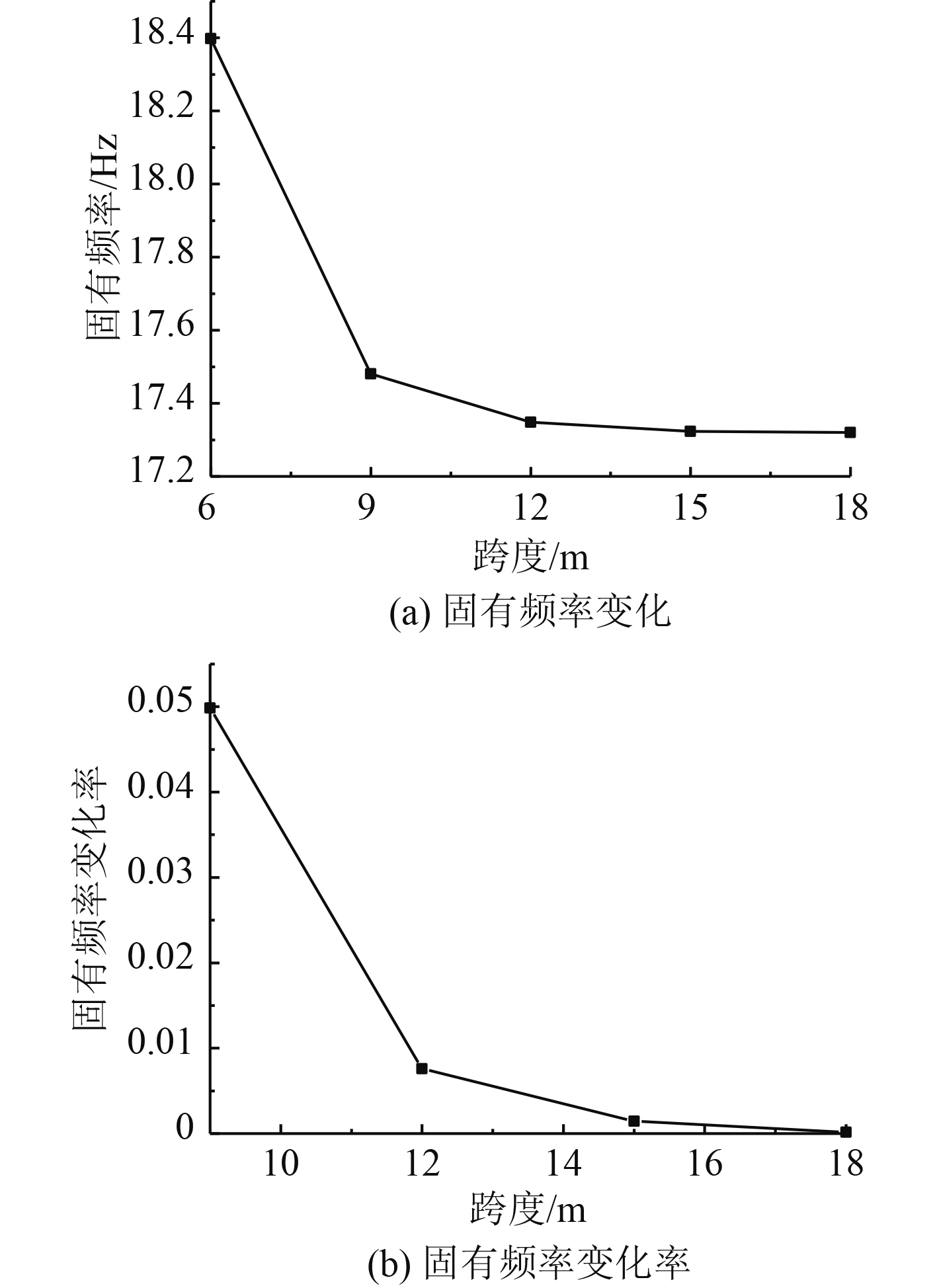
|
图 8 不同跨度系统首阶固有频率变化 Fig. 8 First order natural frequency variation of different span system |
在结构跨度为12 m的多跨梁上,分别均布3~6个弹性支撑,设支撑刚度
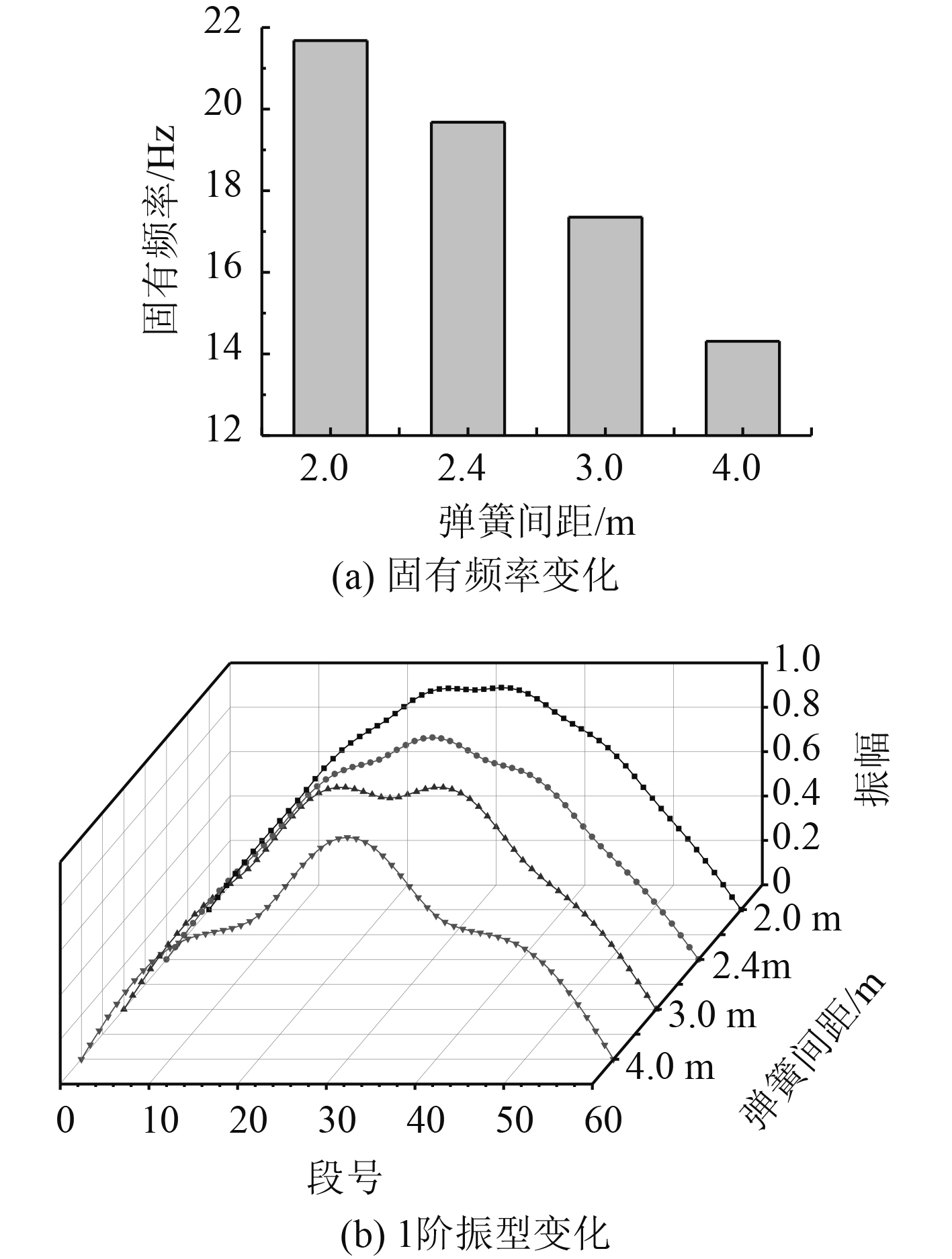
|
图 9 系统自由振动特性变化 Fig. 9 Change of free vibration characteristics of the system |
以结构跨度为12 m、均布5个弹性支撑的多跨梁为研究对象,整体支撑刚度

|
图 10 多跨梁计算模型 Fig. 10 Calculation model of multi span beam |
为了计算不同支撑刚度下的结构模态变化,本文给出了支撑刚度整体依次取1~5 k时结构的固有频率和模态阵型,计算结果如图11所示。可以看出,随支撑刚度的增大,结构固有频率呈上升趋势,且上升幅度越来越小,结构一阶振型也发生变化。
在多跨梁结构左侧1/3即20号点位置施加单位力,计算当支撑刚度改变时,多跨梁系统左侧1/4位置即15号点振动速度响应变化,计算频段定位在1~200 Hz范围,结果如图12所示。可以看出,随支撑刚度的增大,振动响应曲线右移,且右移幅度越来越小,这是因为支撑刚度的增大使得结构固有频率升高所导致的;且随频率升高,振动响应曲线右移幅度越来越小,这是由于支撑刚度的增大对高阶结构固有频率影响小于低阶结构固有频率所造成。
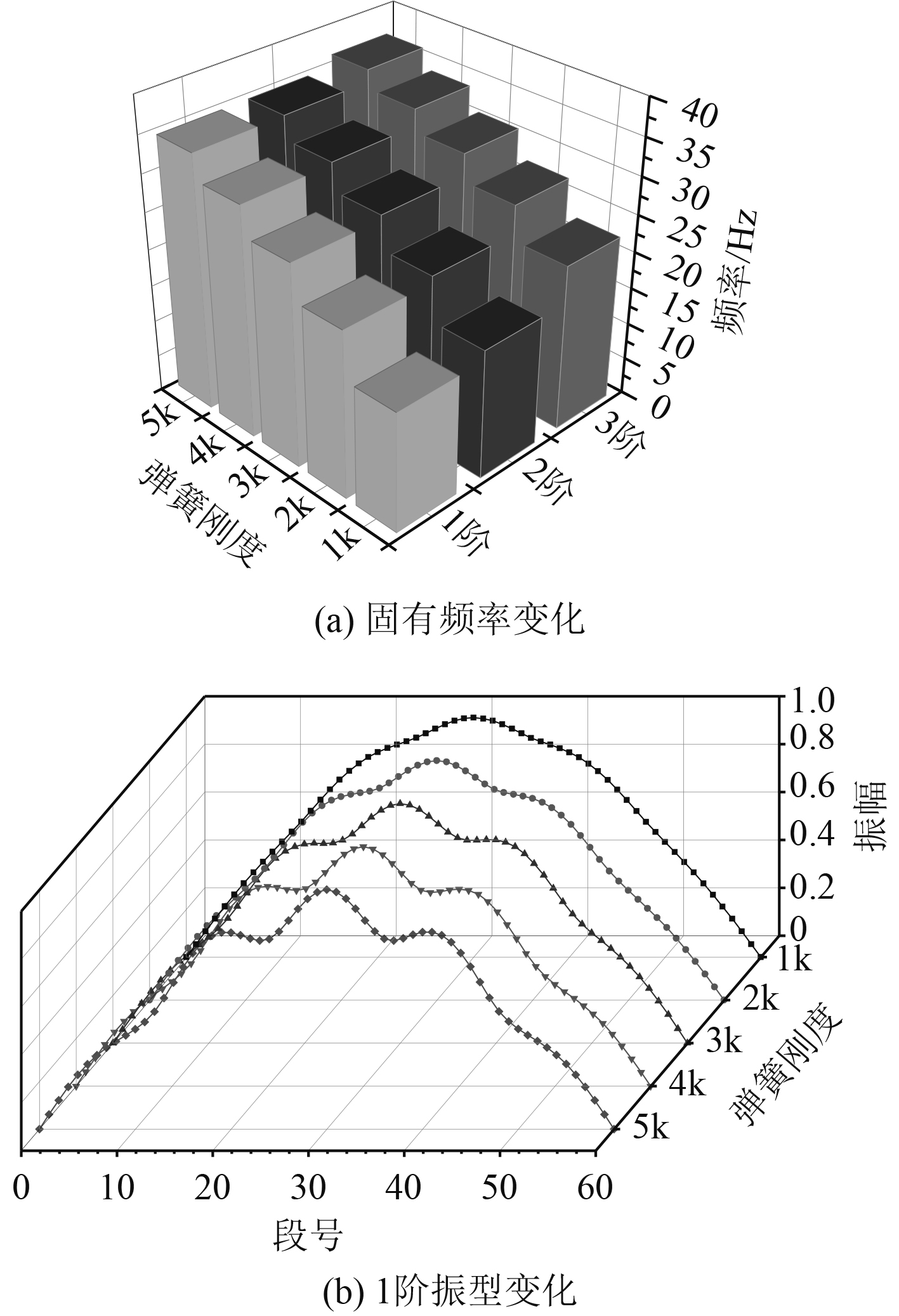
|
图 11 系统自由振动特性变化 Fig. 11 Change of free vibration characteristics of the system |
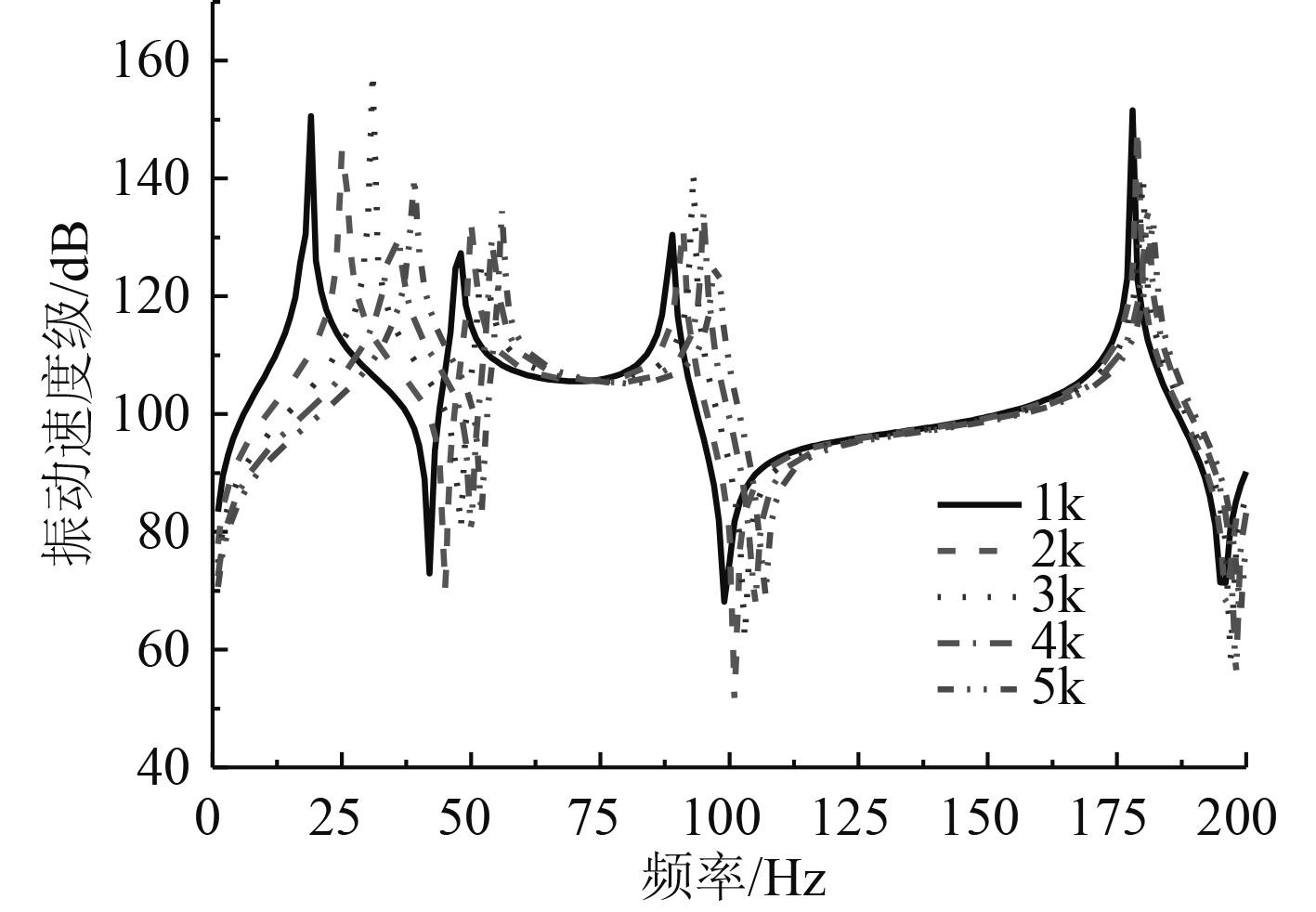
|
图 12 振动速度响应频谱图 Fig. 12 Frequency spectrum of vibration speed response |
对于船舶板架结构,一般由甲板、结构刚度相同且略小的多条纵骨及刚度较大的纵桁结构构成,为此简化后的多跨梁结构中弹性支撑刚度将不完全相同。如图10所示,取两侧支撑刚度
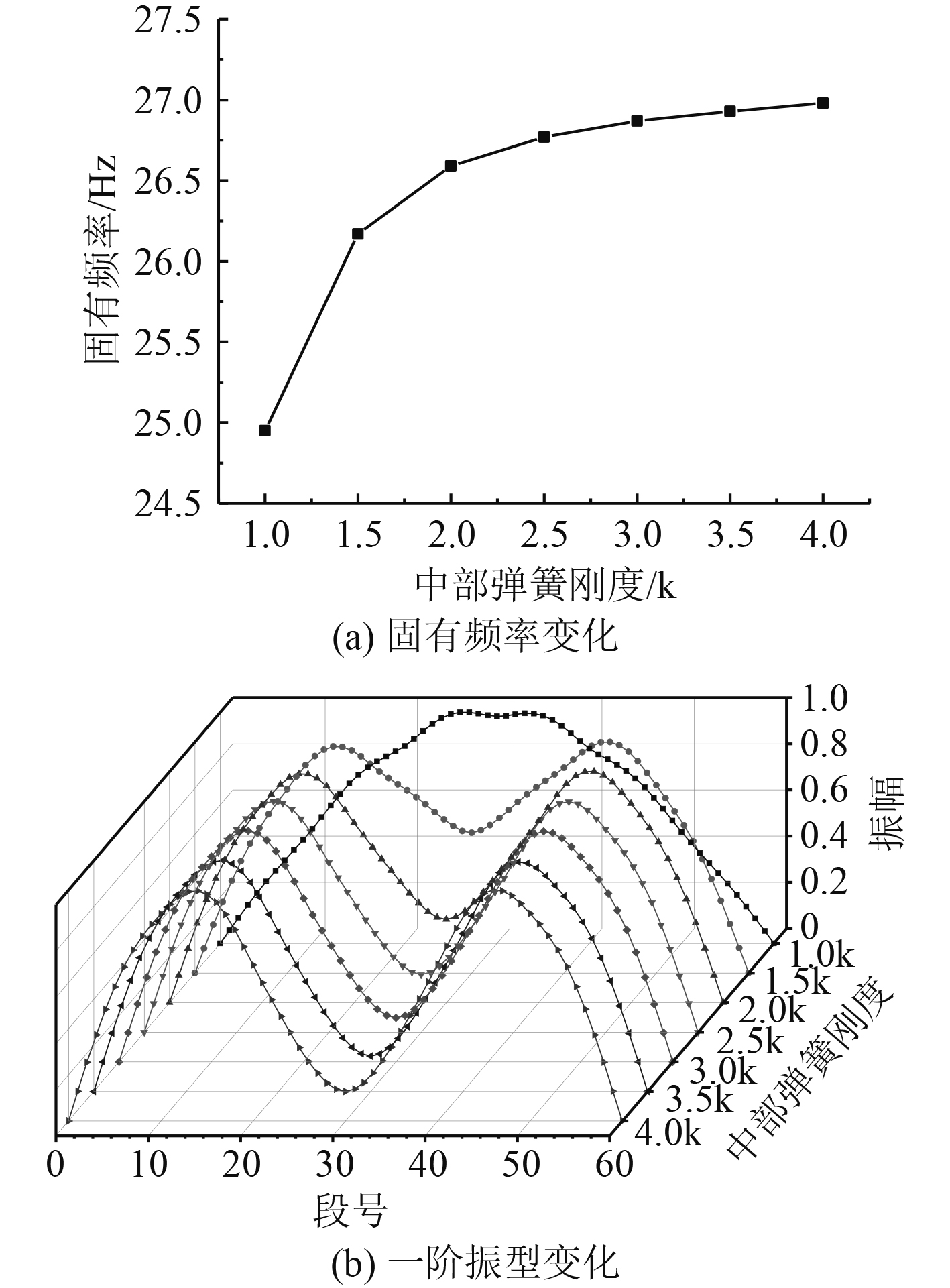
|
图 13 系统自由振动特性变化 Fig. 13 Change of free vibration characteristics of the system |
在多跨梁结构左侧1/3即20号点位置施加单位力,计算得到当中部支撑刚度改变时,多自由度系统左侧1/4位置即15号点在1~200 Hz振动速度响应变化,计算结果如图14所示。可以看出,对于25 Hz,50 Hz,91 Hz附近峰值,随中部支撑刚度的增大,振动响应峰值出现向右偏移现象,这是由于支撑刚度的增大使得结构固有频率升高;对于25 Hz附近峰值,随支撑刚度的增大,峰值右移幅度逐渐减小。

|
图 14 振动速度响应频谱图 Fig. 14 Frequency spectrum of vibration speed response |
本文针对船舶多跨梁结构振动机理揭示不足等问题,基于传递矩阵法开展了弹性支撑对船舶多跨梁结构振动特性的影响规律研究,得出如下结论:
1)对弹性支撑多跨梁结构,系统固有频率随结构跨度增加而下降,随弹性支撑跨度增大而下降,且均逐渐趋于平缓。
2)对弹性支撑多跨梁结构,当支撑刚度整体增加时,结构的固有频率随即增大,增大幅度随刚度的增加趋于平缓。同时结构振动响应曲线右移,右移幅度随频率的升高而减小。
3)选取适当的局部支撑刚度,船体板架结构振动可简化为多跨梁振动。当多跨梁上局部支撑刚度增大时,结构一阶振型最大位移点逐渐由中部向两侧移动,与两端简支的低阶梁结构一阶阵型趋于一致。
| [1] |
金咸定, 夏利娟. 船体振动学[M]. 上海: 上海交通大学出版社, 2011.
|
| [2] |
王杰德, 杨永谦. 船体强度与结构设计[M]. 北京: 国防工业出版社, 1995.
|
| [3] |
李俊, 金咸定. Timoshenko薄壁梁弯扭耦合振动的动态传递矩阵法[J]. 振动与冲击, 2001(4): 59-61. |
| [4] |
汤华涛, 吴新跃. 基于有限元的空间变截面梁传递矩阵[J]. 南京理工大学学报(自然科学版), 2014(1): 78-82. |
| [5] |
NANDAKUMAR P, SHANKAR K. Structural parameter identification using damped transfer matrix and state vectors[J]. International Journal of Structural Stability & Dynamics, 2013, 13(4): 1250076. |
| [6] |
王献忠, 江晨半, 计方, 等. 有限长加筋圆柱壳水下声辐射的精细传递矩阵法[J]. 船舶力学, 2017, 21(4): 503-511. |
| [7] |
 2020, Vol. 42
2020, Vol. 42
