2. 高新船舶与深海开发装备协同创新中心 船海协创中心,上海 200240
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China
复合材料具有比强度高、比模量高、耐腐蚀耐疲劳、结构可塑性好等优点,近年来船舶设计建造开始提倡轻量化、绿色化,因此复合材料逐渐在船舶制造领域得到广泛应用。在船舶和海洋工程领域,复合材料加筋板架结构作为基本承载构件,其强度大小会直接影响结构物整体力学性能。复合材料由增强纤维与基体胶合而成,导致其在服役过程中可能出现不可目视的损伤脱粘与分层,脱粘分层的来源非常广泛,例如制造过程中的残余应力、机械加工(如钻孔)、湿热环境、低速冲击、面外载荷以及设计中产生的材料与结构不连续等[1],所以脱粘分层也成为复合材料层合板结构的一种主要损伤形式,并可能导致复合材料剩余压缩强度显著降低[2]。因此,为了更大限度地发挥复合材料的性能,有必要研究复合材料加筋板的脱粘损伤对结构力学性能影响。
针对复合材料的力学性能及轴压屈曲特性,国内外学者通过理论、试验及数值模拟开展了许多研究。Atevens等[3]进行了工字型筋条复合材料加筋板压缩试验研究,结果表明,加筋板结构的破坏形式主要是筋条的断裂与脱粘、壁板的撕裂。李丽等[4]利用INSTRAON26025电子万能试验机,对高强度、高模量碳纤维复合材料单向板进行了拉伸性能测试,为制定相应拉伸性能测试的试验方法提供了依据。Collombet等[5]针对基体开裂建立了受低速冲击的复合材料层合板数值模型。Dinesh[6]基于1阶剪切变形理论和卡曼假设,考虑几何非线性,采用有限元分析方法将复合材料层合板近似看作准各向同性,基于Tsai-Hill失效准则研究了不同边界条件对层合板屈曲以及后屈曲的影响,数值结果表明层合板在四边简支作用下屈曲载荷最小,在四边固支作用下屈曲荷载较大。目前,针对复合材料在船海领域相关应用的研究仍处于起步阶段,以往研究主要关注复合材料的整体性能,由于大多采用层合板单元进行数值建模很难有效地模拟出目视不可见损伤、层间粘脱及子层屈曲失稳等复合材料特有的力学行为,对于复合材料的损伤演化过程及失效特性的认识也不够透彻。
本文采用渐进损伤分析方法,模拟复合材料从初始损伤至最终完全失效的完整过程。利用Abaqus有限元软件建立复合材料加筋板模型,引入内聚力单元模拟复合材料层间胶层,在层内采用Hashin损伤准则、层间采用二次名义应力强度准则和B-K能量释放率准则。首先对复合材料加筋板模型进行轴压屈曲计算,通过与试验对比分析,验证本文数值模型的合理性。在此基础上考虑贯穿脱粘初始缺陷,模拟筋条-蒙皮间的缺陷演化过程,通过分析对比不同工况计算结果,研究脱粘缺陷对加筋板力学性能及相应压缩失效行为的影响。
1 数值分析模型不同于传统金属材料,复合材料层合板的失效过程复杂,呈现逐渐劣化的特点。起初通过计算复合材料层合板各单向板的实时应力预测结构强度,具体分为首层失效法和末层失效法。首层失效法认为复合材料层合板中任一单层失效即代表整个层合板失效,而末层失效法则认为仅当所有单向层失效后层合板结构才失效。后来发展出的渐进失效分析法考虑层合板的各类局部损伤方式以及材料性能退化,可以准确模拟损伤的破坏机理以及层间耦合作用[7]。因此本文采用渐进失效分析方法进行复合材料加筋板强度分析。
1.1 复合材料层合板的层内损伤复合材料层合板的层内损伤主要指纤维损伤和基体损伤,本文采用Hashin失效准则表征层内损伤材料失效条件及失效模式定义如下:
1)纤维拉伸失效(
| ${\left( {\frac{{{\sigma _{11}}}}{{{X_T}}}} \right)^2} + \alpha {\left( {\frac{{{\tau _{12}}}}{{{S_L}}}} \right)^2} = 1 \text{,}$ | (1) |
2)纤维压缩失效(
| ${\left( {\frac{{{\sigma _{11}}}}{{{X_C}}}} \right)^2}{\rm{ = }}1 \text{,}$ | (2) |
3)基体拉伸失效(
| ${\left( {\frac{{{\sigma _{22}}}}{{{Y_T}}}} \right)^2} + {\left( {\frac{{{\tau _{12}}}}{{{S_L}}}} \right)^2} = 1\text{,}$ | (3) |
4)压缩失效(
| ${\left( {\frac{{{\sigma _{22}}}}{{2{S_T}}}} \right)^2} + \left[ {{{\left( {\frac{{{Y_C}}}{{2{S_T}}}} \right)}^2} - 1} \right]\frac{{{\sigma _{22}}}}{{{Y_C}}} + {\left( {\frac{{{\tau _{12}}}}{{{S_L}}}} \right)^2} = 1\text{。}$ | (4) |
式中:
Hashin失效准则可根据不同损伤类型选取相应的刚度折减系数,当某一铺层内某处出现某种失效类型时,该处相应的材料性能退化参数退化到零,从而能够更为精确地描述复合材料层合板内部的损伤演化过程。
1.2 复合材料层合板的层间损伤对于分层损伤主要采用内聚力单元模拟层与层之间的胶层粘结区域,内聚力单元可以有效地模拟和预测分层损伤产生、扩展和最后分层发生。本文选取插入薄壳内聚力单元的方式模拟层间胶层,在后处理中用分层损伤状态QUADSCRT参数表征材料是否出现分层损伤。采用二次应力失效准则作为分层损伤的初始准则,即
| ${\left( {\frac{{{\sigma _3}}}{N}} \right)^2} + {\left( {\frac{{{\tau _1}}}{S}} \right)^2} + {\left( {\frac{{{\tau _2}}}{T}} \right)^2}{\rm{ = }}1\text{。}$ | (5) |
式中:
损伤起始后,分层损伤扩展采用混合BK能量释放率准则[8]表征,判别式如下:
| ${G_{IC}} + \left( {{G_{IIC}} - {G_{IC}}} \right){\left( {\frac{{{G_{shear}}}}{{{G_T}}}} \right)^\eta } = {G_{TC}} \text{。}$ | (6) |
式中:
复合材料加筋板在轴压过程中,会出现层合板层内的材料失效、刚度退化及层间脱粘扩展,除此之外,加筋板在渐进压溃过程中,还涉及结构大变形、屈曲变形模式变化及界面接触等高度非线性问题。有限元求解时,若采用静力隐式法求解,容易因非线性问题而无法收敛,故本文采用Abaqus动态显式算法进行准静态分析。采用三维连续壳单元对模型进行离散,筋条及蒙皮采用S4R单元,筋条-蒙皮间引入一层内聚力单元模拟胶层,选用COH3D8单元,通过共享节点的方式实现筋条下缘与内聚单元上表面、蒙皮与内聚单元下表面协调。
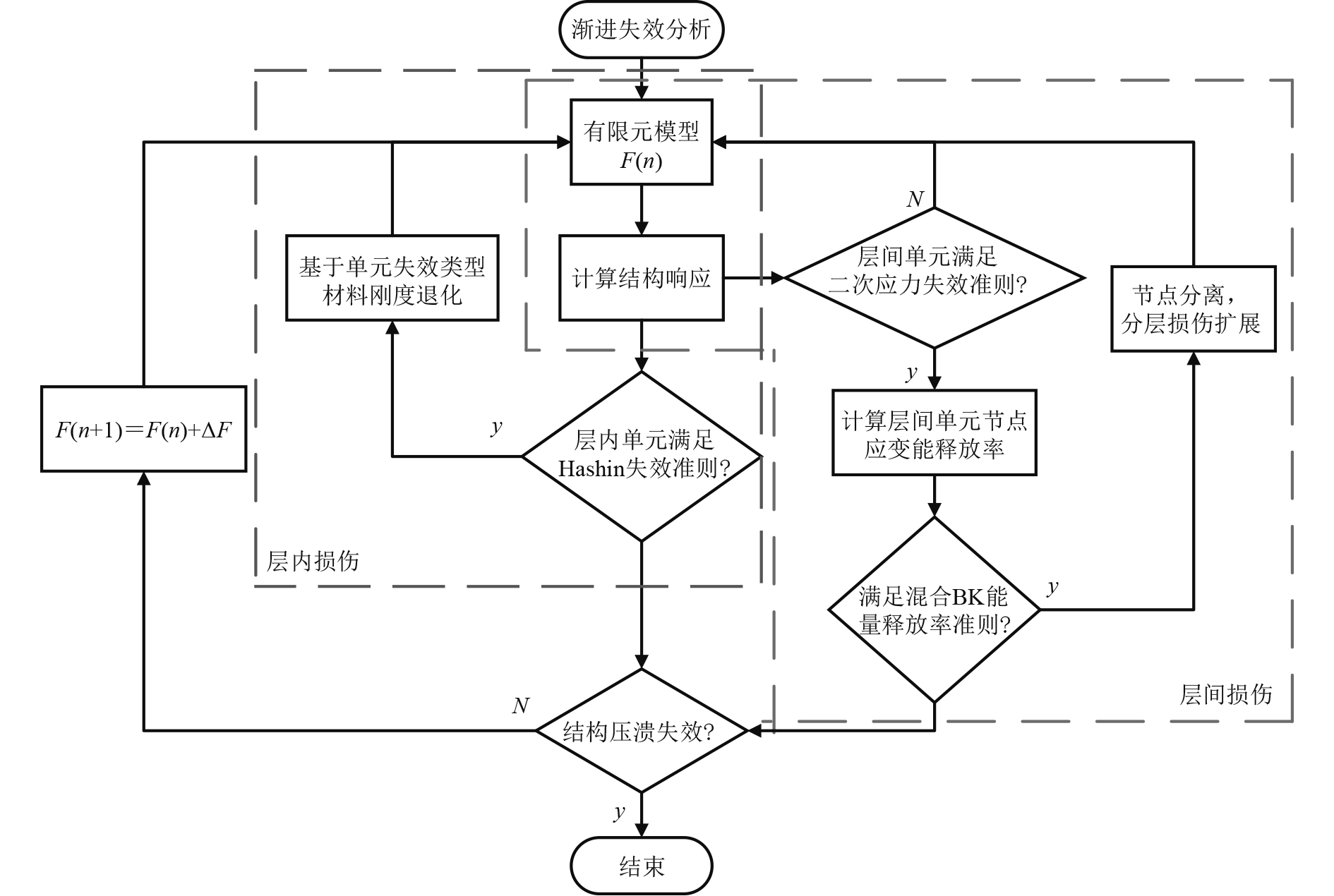
渐进失效分析的具体流程如图1所示。
|
图 1 渐进失效分析流程图 Fig. 1 Flow chart of progressive failure analysis |
选取文献[9]中国产先进复合材料工型加筋板结构进行数值模拟计算,并与试验结果对比分析,验证本文模型的合理性。
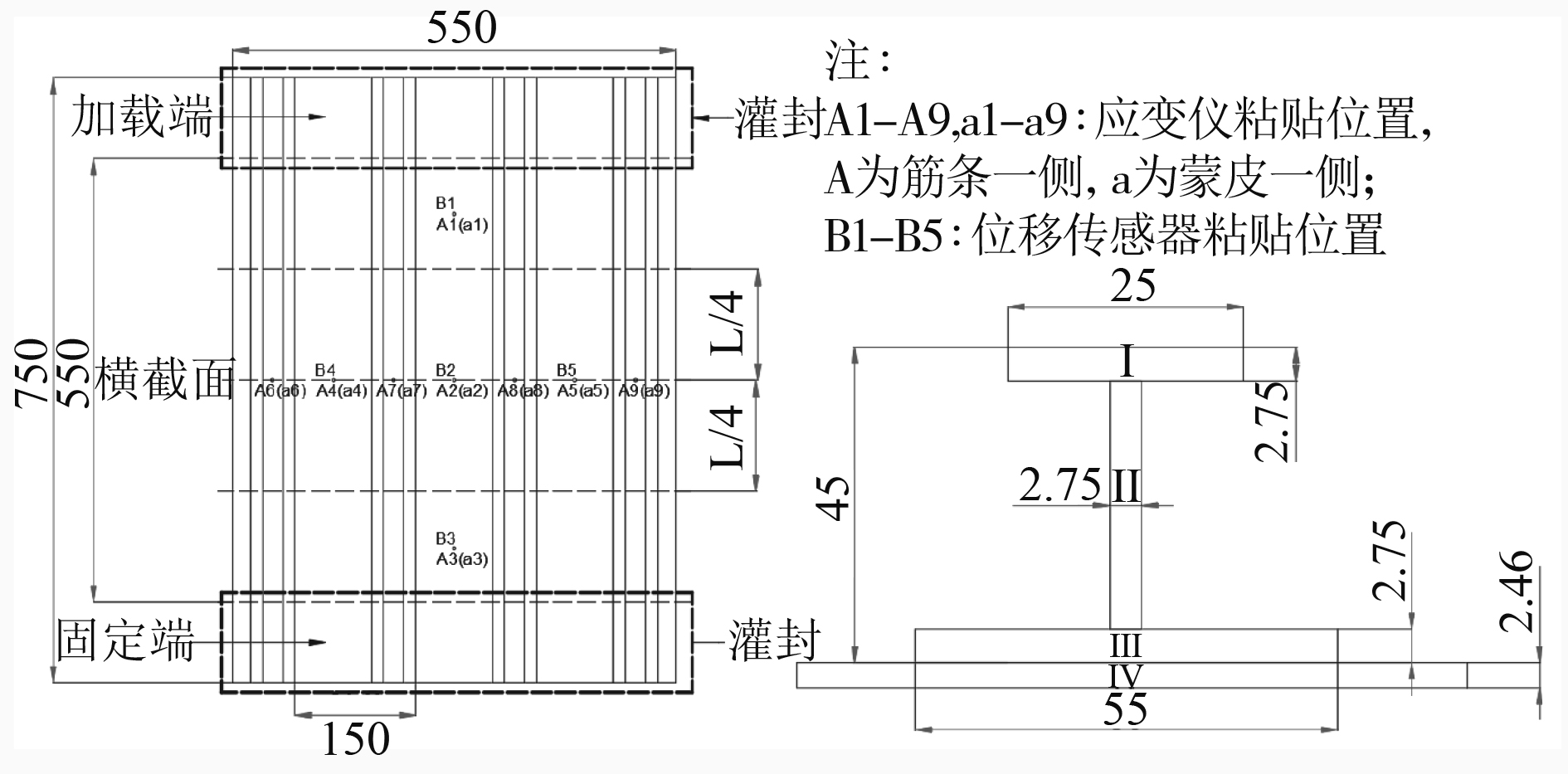
2.1 算例尺寸及材料参数试验所用复合材料加筋板由平面薄壁板与二次粘结的4根工型筋条构成,结构受轴向压缩位移载荷作用,其加载端和夹持端被灌封以保证加载均匀并避免端部压溃,非加载边自由。具体详细信息和几何构型、边界条件等如图2所示。
|
图 2 复合材料加筋板几何构形、边界条件示意图 Fig. 2 Geomotric configuration and boundary conditions of composite stiffened panel |
复合材料加筋板所用材料为高温固化环氧碳纤维单向板BA9916-II/HF10A-3K和碳纤维斜纹织物BA9916-II/HFW220TA,单层厚度分别为0.23 mm和0.125 mm。各区域铺层方式及选用材料如表1所示,复合材料单向板的材料性能参数、层内断裂韧性参数和层间界面参数如表2~表4所示,复合材料密度
|
|
表 1 复合材料加筋板的铺层方式及选用材料 Tab.1 Ply sequences and material of the composite stiffened panel |
|
|
表 2 复合材料加筋板材料性能参数 Tab.2 Material properties of composite stiffened panel |
|
|
表 3 复合材料层内断裂韧性参数(kJ·m−2) Tab.3 Fracture toughness properties of composite materials(unit:kJ·m−2) |
|
|
表 4 复合材料层间界面参数(能量单位:J·m−2,强度单位:MPa) Tab.4 Interlaminar interface properties of composite materials(unit of energy:J·m−2,unit of strength:MPa) |
利用Abaqus有限元软件建立复合材料工型加筋板的有限元模型,模型长度取两端头间有效长度550 mm,内聚层刚度取为基体强度

|
图 3 复合材料加筋板的有限元模型 Fig. 3 Finite element model of composite stiffened panel |
依照试验中应变仪与位移传感器布置方式,输出有限元模型中相同位置应变与位移曲线,图4~图6为本文模型预测与试验结果对比情况。
|
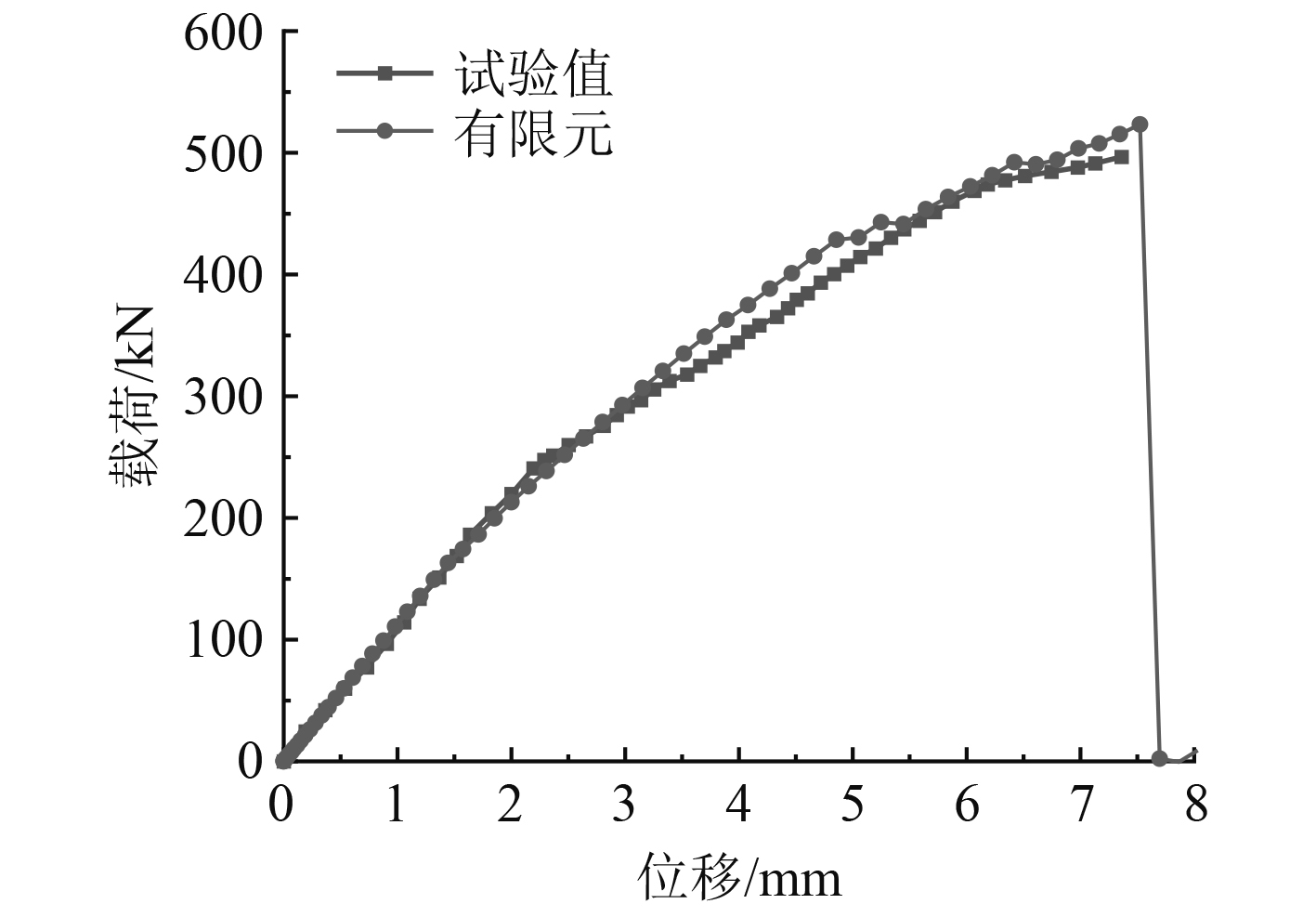
图 4 载荷-位移曲线 Fig. 4 Load-displacement curves |
|
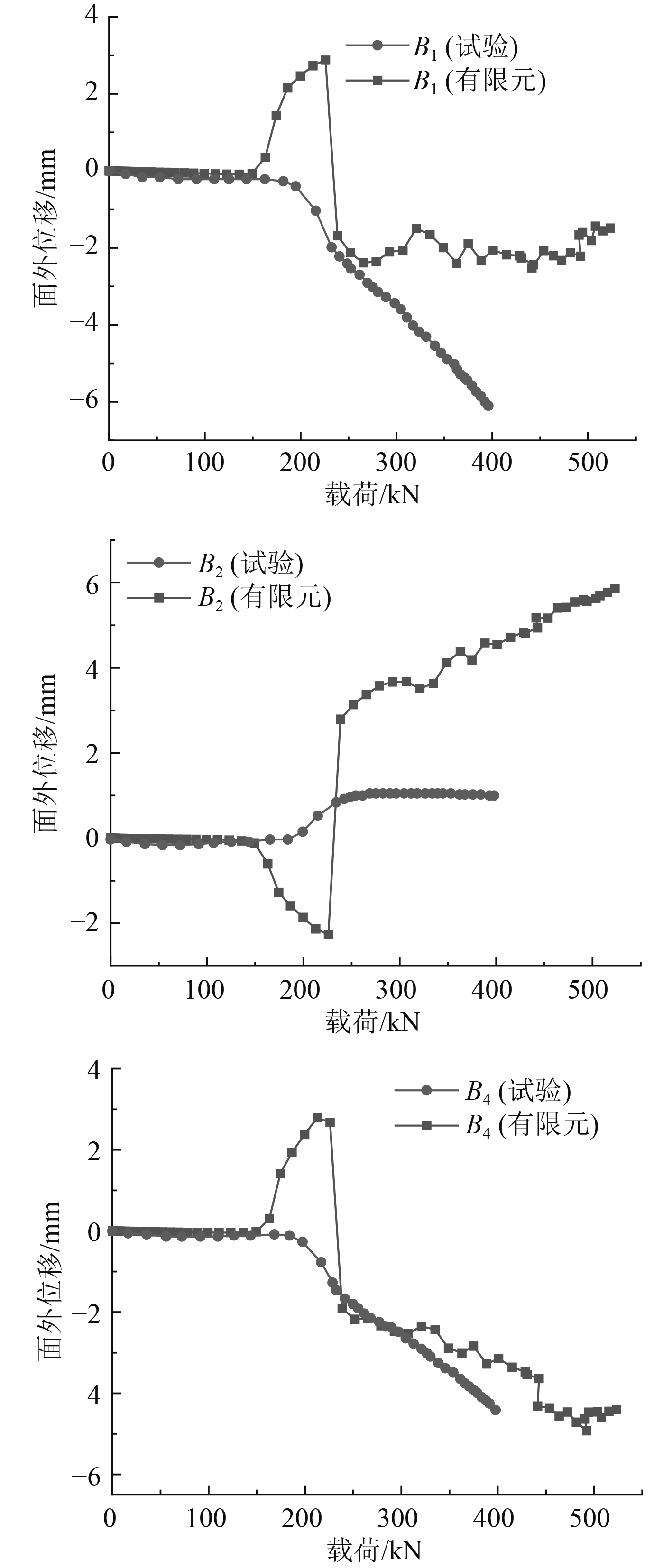
图 6 面外位移-载荷曲线 Fig. 6 Out-of-plane displacement-load curves |
由图4可知,本文模型预测的结构屈曲响应及极限强度值与试验结果吻合良好,误差分别为−3.38%,8.40%。由于有限元模型为理想模型,忽略材料缺陷等因素,故计算所得极限强度偏高。数值预测曲线的趋势及阶段性特征也与试验结果相一致。
图5和图6数值模拟结果中,模型各个位置的应变和面外位移变化趋势与试验结果较为相似。观察到载荷达到200 kN左右时,数值模拟出现与试验结果有所差异的变化,这是因为此时加筋板蒙皮发生了局部屈曲失稳,屈曲后继续加载使加筋板产生了模态突变,即图示短暂波动差异,试验中加筋板试件同样在载荷为200 kN左右产生了较明显的屈曲波数变化[9],因此可认为数值模拟中这个中间过程变化属于合理现象。随着载荷继续增加,数值模拟结果再次与试验结果吻合良好。以上对比结果表明,本文数值模型对于复合材料加筋板在轴压过程的动态响应预报精度较高。

|
图 5 应变-载荷曲线 Fig. 5 Strain-load curves |
本节将详细研究含脱粘缺陷复合材料加筋板屈曲行为以及不同脱粘长度对加筋板整体承载性能的影响。
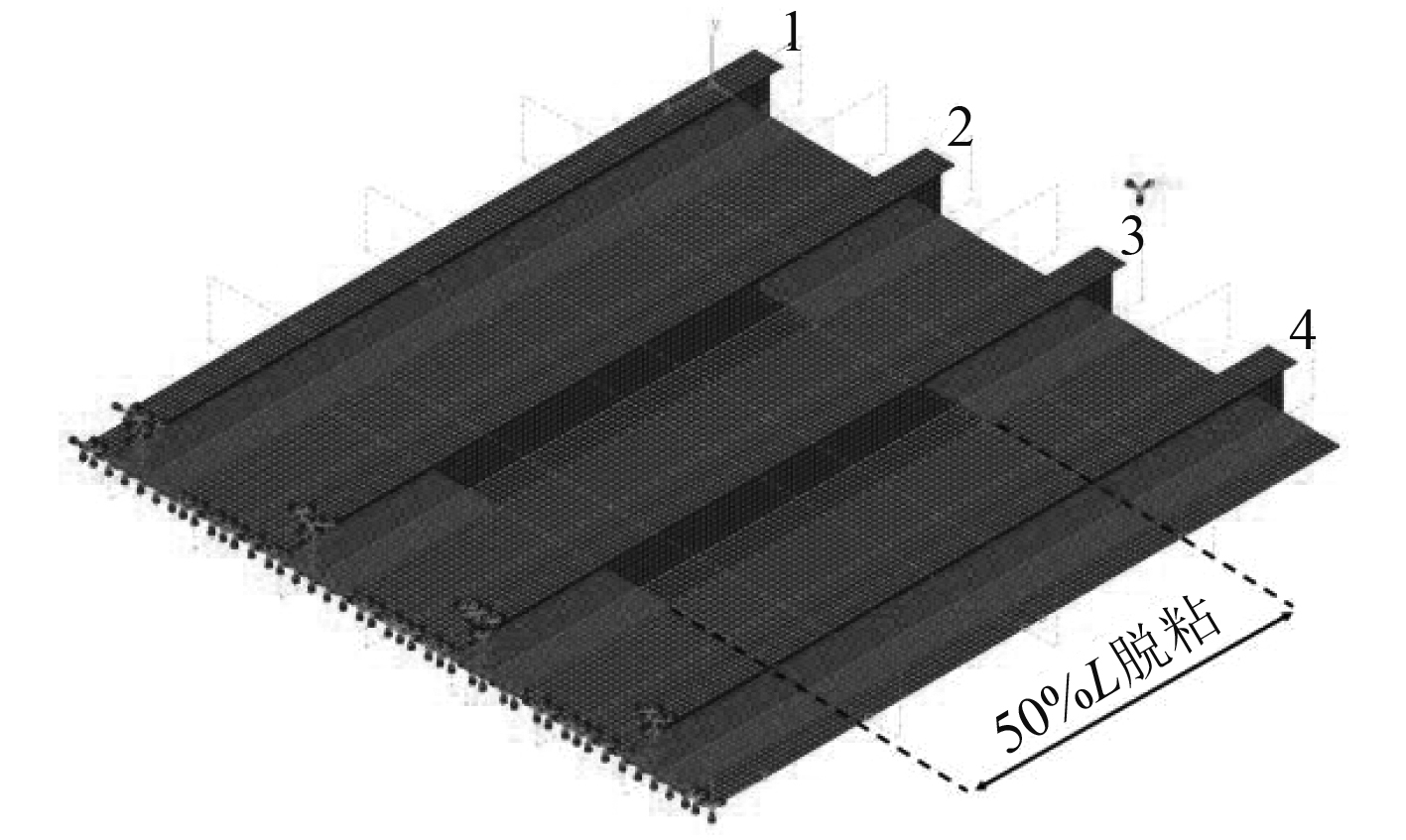
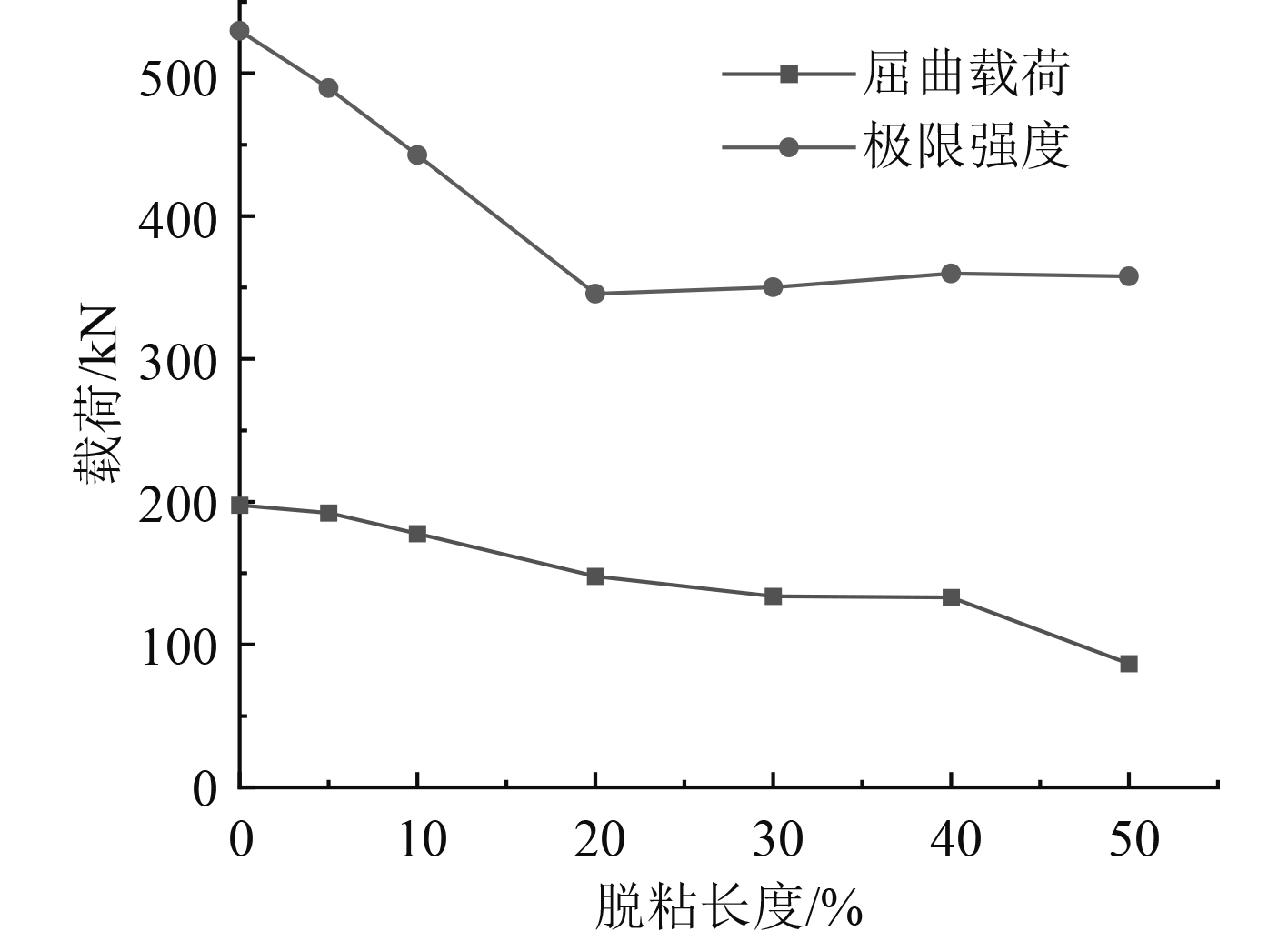
3.1 脱粘缺陷如图7所示,选择2号和3号筋条位置模拟贯穿脱粘,以加筋板中截面为中心,考虑5%~50%L的脱粘长度进行对比研究。通过计算,得到不同脱粘长度下屈曲失效载荷及极限强度变化情况,如图8所示。
|
图 7 脱粘形式(50%L为例) Fig. 7 Debonding form(50%L as an example) |
|
图 8 失效载荷随脱粘长度变化情况 Fig. 8 Failure load varies with debonding length |
极限强度-脱粘长度曲线具有2个明显变化过程,在0~20%的脱粘长度下,加筋板的极限强度有较显著的下降,脱粘长度大于20%L后,加筋板极限强度无明显变化,说明2号和3号筋条已失去对结构极限承载能力的贡献。屈曲载荷呈现出较缓和的下降趋势,脱粘长度大于40%L时才明显减小,曲线出现拐点,这主要是由于较短脱粘对结构刚性无显著影响,而当脱粘较长时,筋条-蒙皮已大部分脱离,结构则更易屈曲。
3.2 损伤演化基于以上失效载荷随脱粘长度的变化情况,选取2段变化过程和拐点处共3个典型工况10%L,20%L和50%L进行研究,分析复合材料加筋板的损伤演化进程,如图9~图11所示。图中QUadscrt>0时,内聚层单元开始失效,而QUadscrt=1时,单元完全失效。

|
图 9 应力云图与内聚力层破坏进程(10%L) Fig. 9 Von mises stress and failure process of cohesive layer(10%L) |

|
图 11 应力云图与内聚力层破坏进程(50%L) Fig. 11 Von mises stress and failure process of cohesive layer(50%L) |
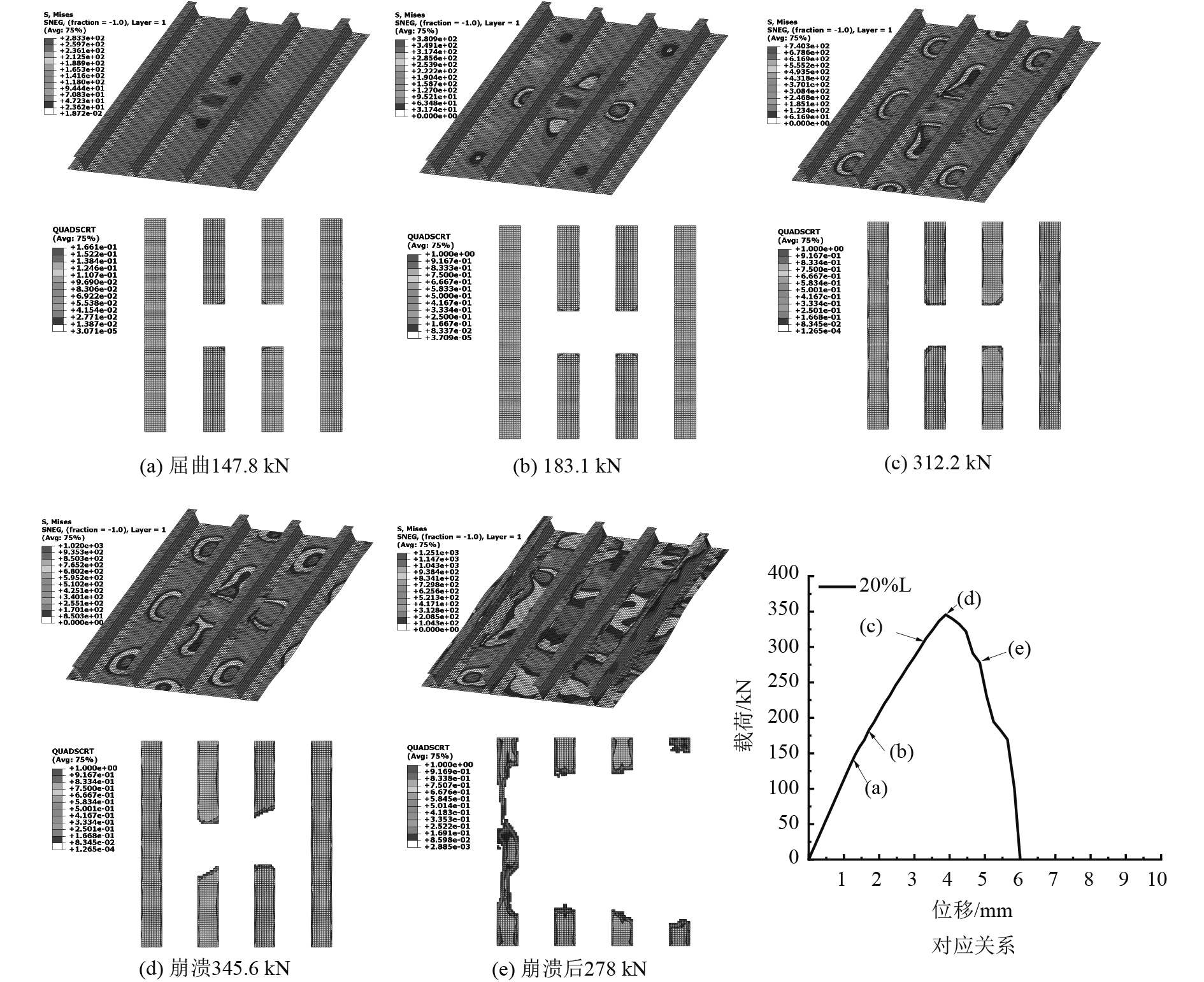
|
图 10 应力云图与内聚力层破坏进程(20%L) Fig. 10 Von mises stress and failure process of cohesive layer(20%L) |
在贯穿脱粘工况下,在脱粘区域,蒙皮与筋条分离,轴压时首先屈曲上拱,此时内聚层胶层前缘单元开始失效,发生裂纹扩展。随着载荷增大,临近结构崩溃的短暂时间内,加筋板应力变化剧烈,内聚层破坏范围由2号和3号筋条位置开始迅速扩大,最终部分筋条发生破断,随后整个结构也失去主要承载能力发生压溃破坏。当脱粘长度较小(10%L)时,加筋板从屈曲到崩溃的过程,应力分布较均匀,临近崩溃时,筋条断裂失效,内聚力层开始较多地失效,裂纹扩展产生较大区域脱粘,因而结构失稳崩溃;当脱粘长度增大至20%L,屈曲到崩溃过程未发生较明显的裂纹扩展,说明直到脱粘区域的筋条断裂失效后内聚力单元才开始大面积失效,导致结构崩溃;而当脱粘长度为50%L时,筋条-蒙皮大部分分离,轴压时蒙皮较早屈曲,随后加筋板整体的应力重分布也较快,因此内聚力层随着蒙皮屈曲与筋条失稳而发生大范围失效。
以上损伤演化分析可知,脱粘长度较小时,加筋板失效模式为筋条断裂或失稳后引发裂纹扩展,结构发生瞬时压溃破坏;脱粘长度较大时,蒙皮首先发生屈曲,并逐渐撕裂胶层引发裂纹扩展,从而导致结构压溃。
4 结 语本文基于渐进损伤分析方法,建立了考虑层内和层间损伤的复合材料工型加筋板轴压屈曲分析模型,并基于该模型研究了脱粘缺陷对加筋板承载性能与失效行为的影响。研究表明:
1)本文模型能较好地模拟出复合材料加筋板的损伤演化过程和压溃行为,所得数值结果与试验观测吻合良好,模型的合理性得以验证。
2)对于含贯穿脱粘缺陷的复合材料加筋板,当脱粘长度较小时,加筋板极限强度会因为脱粘缺陷受到较大削弱;脱粘长度较大时,加筋板极限强度基本稳定,但结构更易轴压屈曲。
3)复合材料加筋板脱粘长度较小时,加筋板失效模式为筋条断裂或失稳后引发裂纹扩展;而脱粘长度较大时,加筋板结构发生整体屈曲和裂纹扩展2种方式叠加的失效模式。
| [1] |
GRAY, B. l.. An Introdution to composite materials[J]. Nanotechnology Magazine, IEEE, 2014, 8(1): 6-16. DOI:10.1109/MNANO.2014.2309495 |
| [2] |
欧阳天, 关志东, 谭日明, 等. 复合材料T型加筋板筋条冲击损伤及冲击后压缩行为试验[J]. 复合材料学报, 2018, 38(10): 95-103. |
| [3] |
ATEVENS K A, RICCI R, Davies GAO. Buckling and post-buckling of composite structures[J]. Composites, 1995, 26(3): 189-199. DOI:10.1016/0010-4361(95)91382-F |
| [4] |
李丽. 高强度、高模量碳纤维复合材料拉伸性能测试方法的研究[J]. 理化检验: 物理分册. 2004, 40(7): 337-340.
|
| [5] |
COLLOMBET F, BONINI J, LATAILLADE J L. A three dimensional modeling of low velocity impact damage incomposite laminates[J]. International Joumal for Numerical Methods in Engineering, 1996, 39: 1491-1516. DOI:10.1002/(SICI)1097-0207(19960515)39:9<1491::AID-NME914>3.0.CO;2-2 |
| [6] |
KUMAR D., SINGH S. B.. Effects of boundary conditions on buckling and postbuckling responses of composite laminate with various shaped cutouts[J]. Composite Structures, 2010, 92: 769-779. DOI:10.1016/j.compstruct.2009.08.049 |
| [7] |
易美琦. 层合板分层损伤等效模拟方法及剩余强度研究[D]. 哈尔滨: 哈尔滨工业大学, 2016.
|
| [8] |
BENZEGGAGH M L, KENANE M. Measurement of mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites with mixed-mode bending apparatus[J]. Composites Science & Technology, 1996, 56(4): 439-449. |
| [9] |
张浩宇, 何宇廷, 冯宇, 等. 先进复合材料薄壁加筋板轴压屈曲特性及后屈曲承载性能[J]. 航空材料学报, 2016, 36(4): 58-66. |
 2020, Vol. 42
2020, Vol. 42
