非线性有限元法是共同规范[1]认可的评估船体极限强度的分析方法,而有限元模型是对实船的模拟,计算成本高。为了简化计算,目前许多学者对船体梁极限强度及剩余强度的研究大多采用简化的箱型梁结构,该结构能否代表实船的有限元模型还需要深入研究。因此,研究简化的船体梁模型对提高有限元计算效率、验证简化模型与完整模型的失效一致性具有重要意义。
船体箱型梁总纵强度模型试验,验证了非线性有限元法计算船体梁极限强度的准确性,文献[2-3]对比分析了试验与数值仿真的结果,发现非有限元法与试验值吻合较好,但试验模型为简化的箱型梁,与实船存在差别。文献[4-8]研究了初始缺陷、屈服应力、强横框跨距、边界条件、加载方式以及网格密度等因素对船体梁极限强度的影响,为合理选择有限元计算参数提供重要指导。文献[10]利用强度稳定综合理论及始屈弯矩法提出了船体梁极限强度的简化计算公式,误差较小。船体梁是典型的加筋板组合结构,加筋板是影响船体梁极限弯矩的关键因素,目前针对船体加筋板极限强度的研究成果十分丰富,Paik等[10-11]采用非线性有限元法研究了边界条件设置、初始缺陷的形状以及侧向载荷大小等对计算结果的影响。Zhang和Kim等[12-13]提出了计算加筋板极限强度的经验公式,该公式与有限元分析结果一致,具有一定的准确性。
本文针对船体梁中垂及中拱弯曲2种失效模式,提出了船体梁舱段完整模型的简化方法。根据该方法对中垂及中拱工况下的散货船舱段完整模型简化,对比分析了完整模型与简化模型的极限弯矩及失效模式,验证该简化方法具有可行性,为研究船体梁极限强度提供了新的分析方法。
1 船体梁总纵强度模型简化方法位于纵桁和强肋板或横梁之间的船体加筋板由于加强筋的存在,使船体梁模型复杂化,加大了船体极限强度的计算成本。因此本文提出了总纵强度舱段模型的简化方法,取船中舱段纵桁和强肋板之间的加筋板,根据中垂及中拱状态时加筋板的拉压状态分析其受压和受拉时的极限强度,根据极限强度相等计算出等效板厚,将加筋板简化为无加强筋的等效板格,加筋板的简化示意如图1所示。根据该方法,可建立中垂及中拱工况下船体梁总纵强度的简化模型。

|
图 1 加筋板简化示意图 Fig. 1 Simplification of stiffened panel |
根据加筋板和等效板的受压极限强度相等,计算受压加筋板的等效板厚。分析加筋板的受压极限强度
| ${\sigma _{u1}} = {\sigma _{u2}}\text{。}$ | (1) |
由于加筋板和板格受压时会有屈曲问题,其受力变形比受拉时的复杂,受压极限强度等于后屈曲的极限强度。目前船体加筋板及板格的受压极限强度分析方法可以选择非线性有限元法、经验公式等。非线性有限元法需要建立有限元模型,虽然计算过程复杂,但其数值分析结果比较准确;而经验公式计算过程简单,但并不是针对所有的船体加筋板及板格都适用,结果可能会有较大误差。因此,在选择极限强度分析方法时需要综合考虑。
1.2 船体受拉加筋板等效板厚计算加筋板的受拉状态与受压状态不同,在轴向拉力作用下加筋板没有屈曲问题,其受拉极限强度等于其屈服极限。因此要将受拉加筋板简化为等效厚度的板格,只需要按照加筋板的横截面积与等效板的横截面积相等,即可算出受拉加筋板的等效板厚,其等效板厚的计算公式如下:
| ${t_{\text{受拉等效}}} = \frac{{bt + n({h_w}{t_w} + {b_f}{t_f})}}{b}\text{。}$ | (2) |
其中:b为加筋板宽度,t为板厚,n为加强筋的数目,
散货船的主尺度如表1所示,船中舱段各加筋板的编号如图2所示,加筋板尺寸如表2所示。材料参数为:钢材牌号HT32,弹性模量
|
|
表 1 散货船主尺度 Tab.1 Principal dimensions of the bulk carrier |
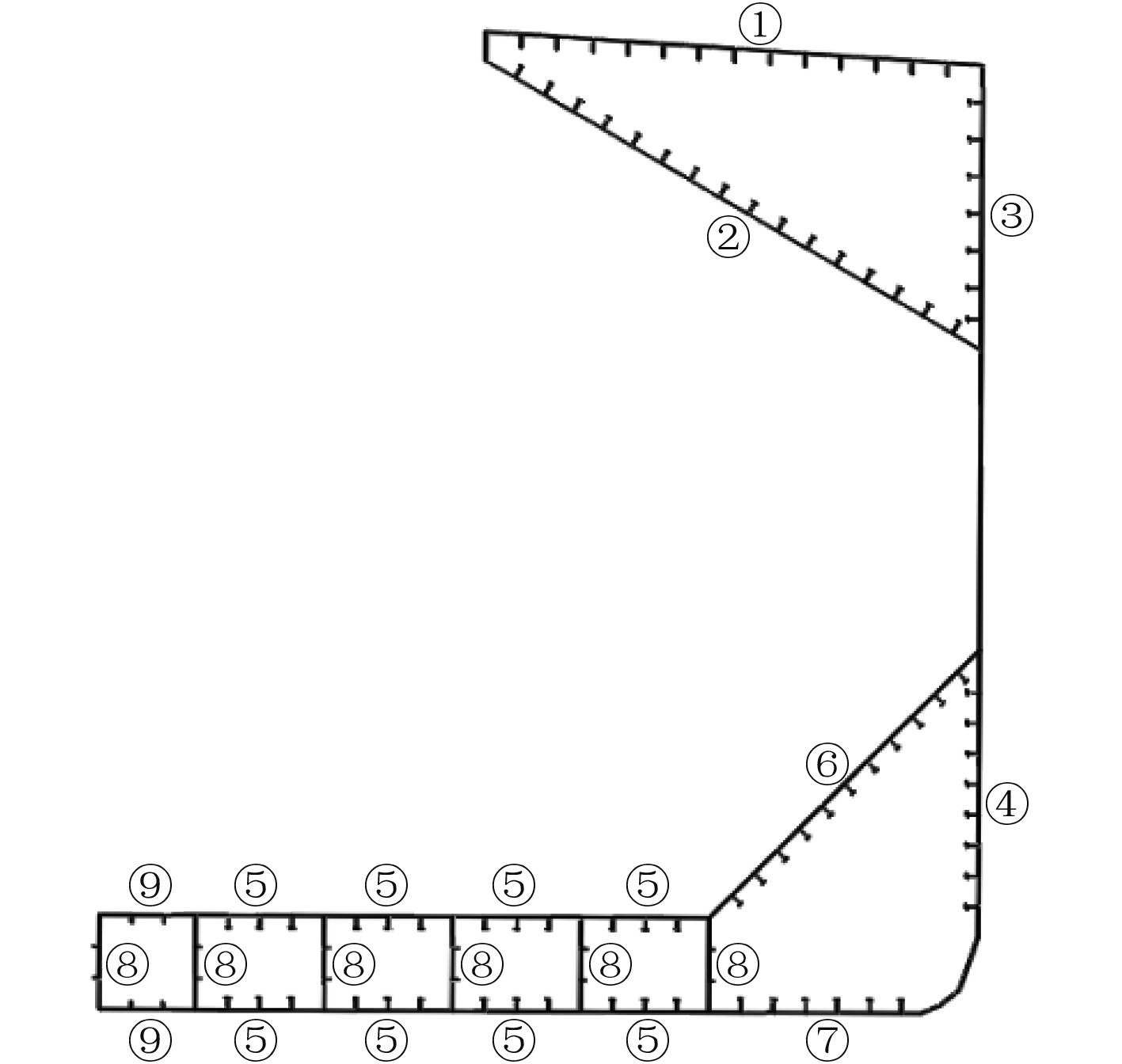
|
图 2 散货船各加筋板编号 Fig. 2 Numbers of bulk carrier’s stiffened panels |
|
|
表 2 各加筋板尺寸(mm)及筋数目 Tab.2 The size (mm) and stiffener amount of each panel |
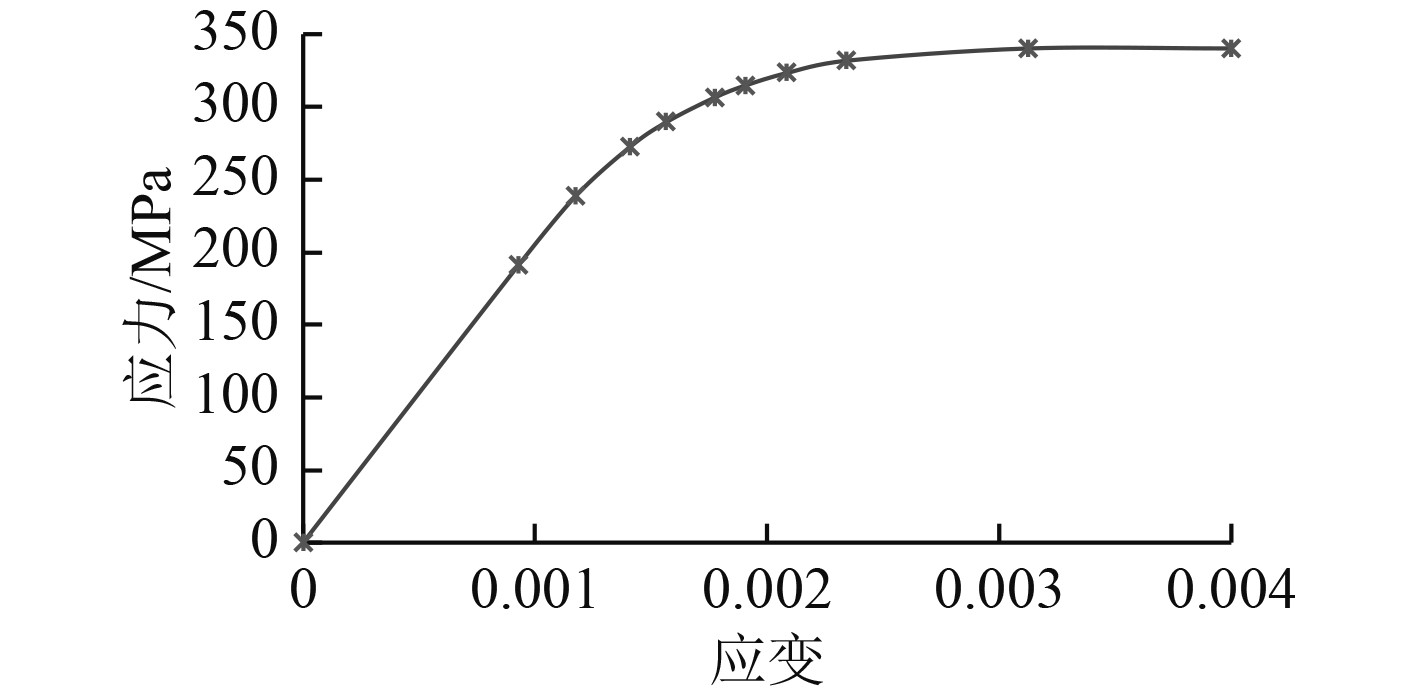
|
图 3 HT32钢材应力应变关系 Fig. 3 HT32 steel’s relationship of stress and strain |
由于经验公式有一定的误差,不一定都适用于计算船体加筋板及板格的受压极限强度,因此本文采用非线性有限元法进行分析。有限元模型按照1/2+1+1/2建立,通过设置约束条件来模拟横梁的影响,而不对横梁建模。定义板长a的方向为Z向,板宽b方向为X向,垂直板面的方向为Y向。在受压边中点外1 cm建立2个RP,RP分别与两端面耦合U3,UR1,UR2,对RP在U3方向上施加1 cm位移,使加筋板压缩,该加筋板的边界条件如表3所示。先分析其1阶屈曲模态,再使用RISK法分析后屈曲的受压极限强度,引入的初始挠度比例因子为板长a的1/1000[15],后屈的极限强度采用RISK法计算。
|
|
表 3 加筋板边界条件 Tab.3 Boundaries of the stiffened panel |
为将加筋板按照受压极限强度相等简化为无筋的板,首先根据以下的板格极限强度的经验公式及板格柔度公式初步估算出等效板厚:
| $\frac{{{\sigma _u}}}{{{\sigma _y}}} = \frac{{2.25}}{\beta } - \frac{{1.25}}{{{\beta ^2}}}\text{,}$ | (3) |
| $\beta = \frac{b}{t}\sqrt {\frac{{{\sigma _y}}}{E}}\text{。} $ | (4) |
其中:
以①号加筋板及其受压等效板为例,给出后屈曲失效云图、应力曲线,分别如图4和图5所示。对比①号加筋板及其等效板的应力曲线:两者在线性段基本一致,达到同样的极限强度后,加筋板的应力迅速减小;而等效板的应力减少较小,可知等效板在达到极限状态后仍有较大的应力储备。各加筋板和等效板的受压极限强度及其误差、受压等效板厚如表4所示,所有的误差绝对值均小于1%。

|
图 4 ①号加筋板后屈曲失效云图 Fig. 4 Post buckling failure of ① stiffened panel |

|
图 5 ①号等效板后屈曲失效云图 Fig. 5 Post buckling failure of ① equivalent panel |
|
|
表 4 受压等效板厚度、极限强度及其误差 Tab.4 The thickness and ultimate strength as well as its error of compressive equivalent panel |
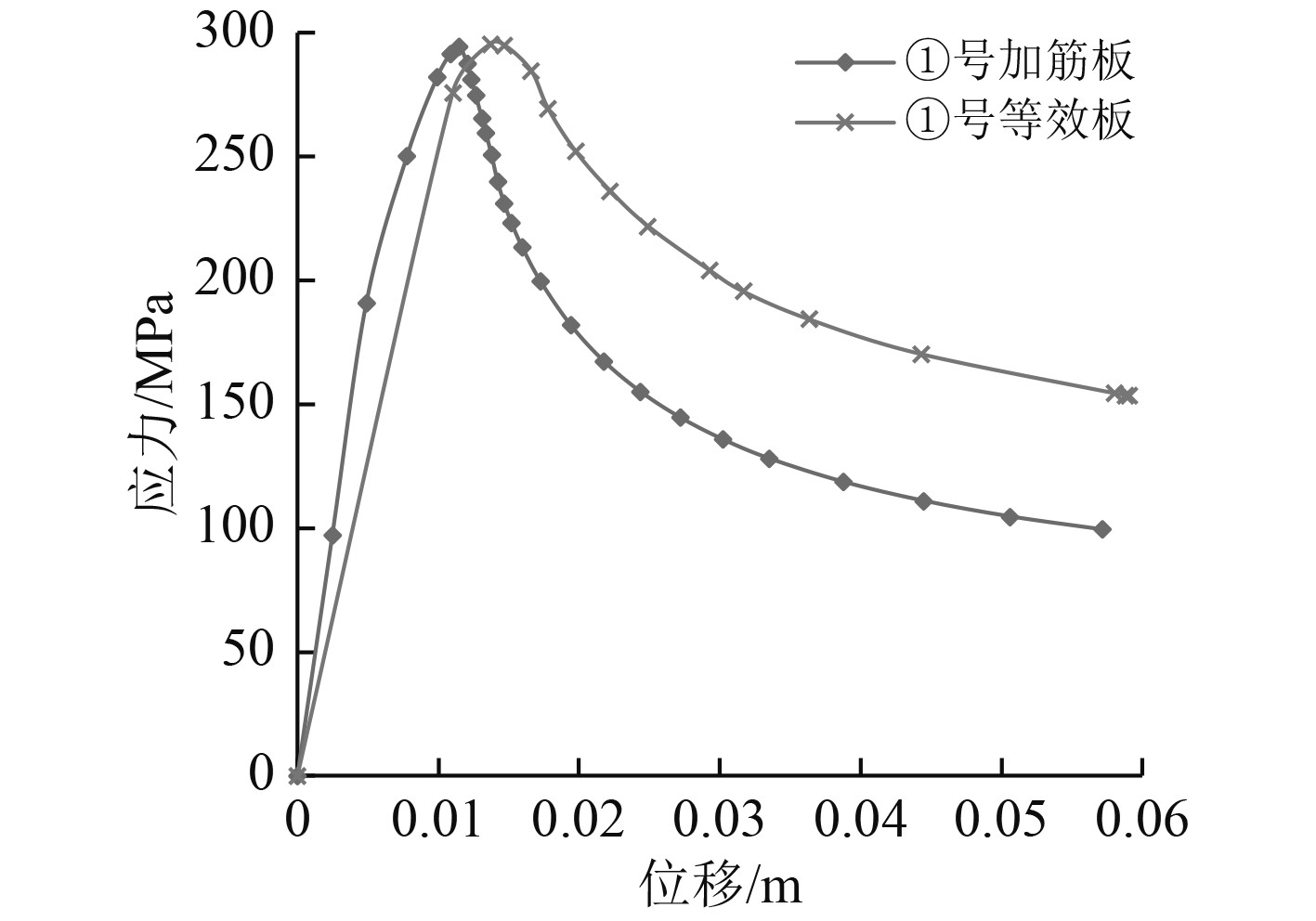
|
图 6 ①号加筋板及等效板应力-位移曲线 Fig. 6 Stress-strain curves of ① stiffened panel and its equivalent panel |
根据1.2的受拉加筋板等效简化方法,利用公式(2)计算出表2各个加筋板的受拉等效厚度,如表5所示。
|
|
表 5 各加筋板的受拉等效厚度(mm) Tab.5 Equivalent thickness (mm) of each tensile panel |
简化模型的主尺度为:舱段长度26390 mm;舱段宽度46000 mm。其三维几何模型如图8所示,按照1/2舱段+1舱段+1/2舱段建立该简化模型。由中拱及中垂各个加筋板的拉压状态,将2.1及2.2计算出的2种厚度,分别赋予该简化模型中间舱段对应的板格,中垂及中拱工况下各个加筋板的等效厚度如表6所示。
|
|
表 6 各加筋板在两种工况下的等效厚度(mm) Tab.6 Equivalent thickness (mm) of each stiffened panel under two conditions |

|
图 7 简化三维几何模型 Fig. 7 Simplified geometric 3D model |

|
图 8 简化模型中垂弯曲失效云图 Fig. 8 Failure mode of simplified model under vertical sagging bend |
在简化模型端面与中和轴的相交处各建立2个RP,将RP与两端面耦合,并将两边的1/2舱段厚度显著加大,使其失效区域发生在中间的舱段;在完整模型横舱壁外与中和轴的交点建立2个RP,RP与横舱壁所在平面耦合,使模型的失效区域也发生在中间的舱段。2个模型RP的边界条件为简支,先分析其一阶屈曲模态,引入初始挠度并利用准静态法分析其极限弯矩。
3.1 中垂工况极限弯矩简化模型与完整模型的失效云图、弯矩-转角曲线如图8~图10所示。比较两者的变形失效云图,简化模型与完整模型均发生了甲板的屈曲变形、船底及舷侧的屈服变形,且完整模型的甲板屈曲变形较大。比较两者的弯矩-转角曲线:完整模型的上升段较陡,比简化模型先达到极限状态。从加筋板与其等效板的应力曲线可知,加筋板首先达到极限状态,比等效板更容易发生屈曲破坏。因而散货船舱段完整模型比其简化模型更容易达到极限状态。

|
图 9 完整模型中垂弯曲失效云图 Fig. 9 Failure mode of intact model under vertical sagging bend |
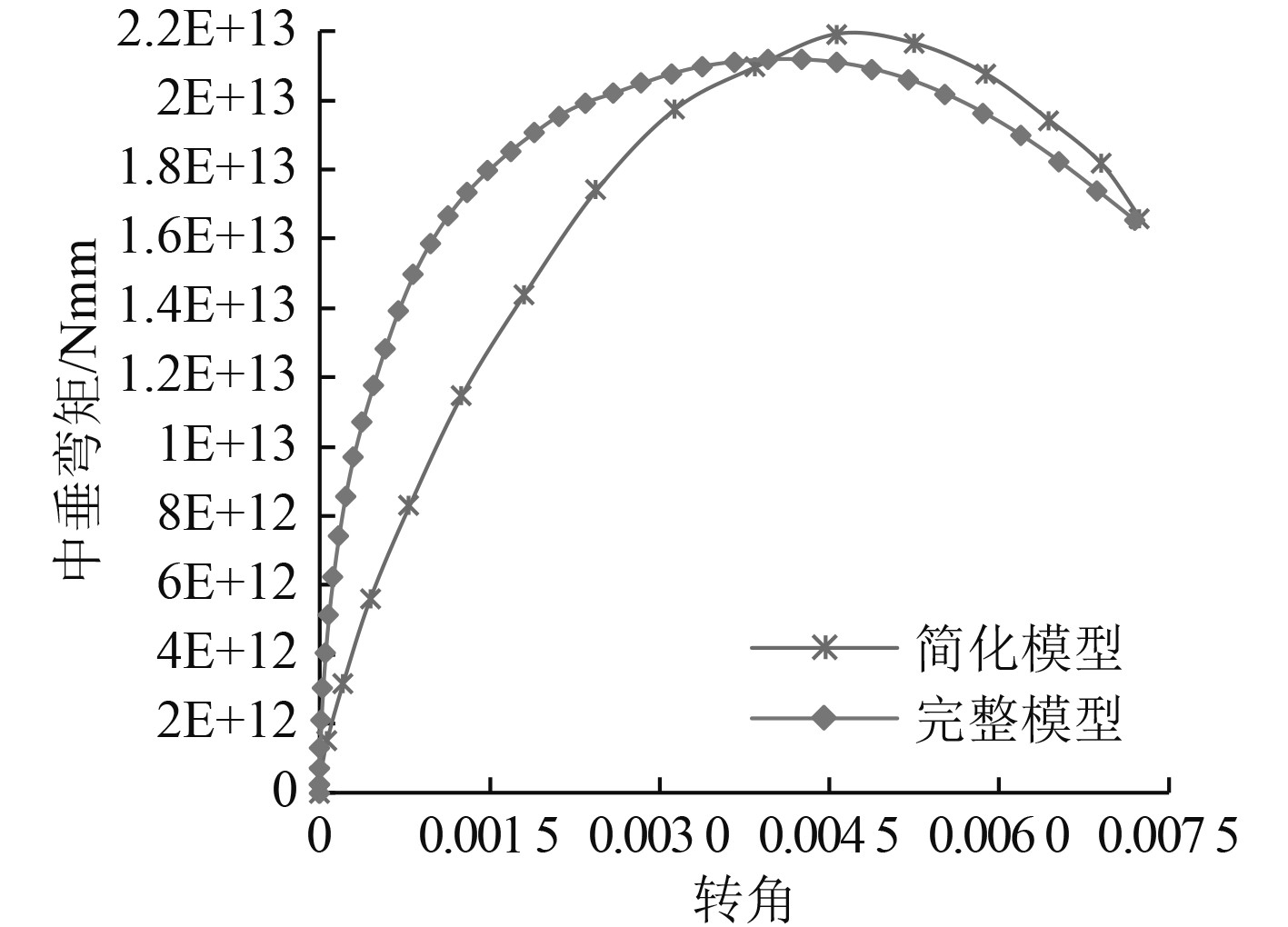
|
图 10 中垂工况弯矩-转角曲线 Fig. 10 Moment-angle curves of sagging bending |
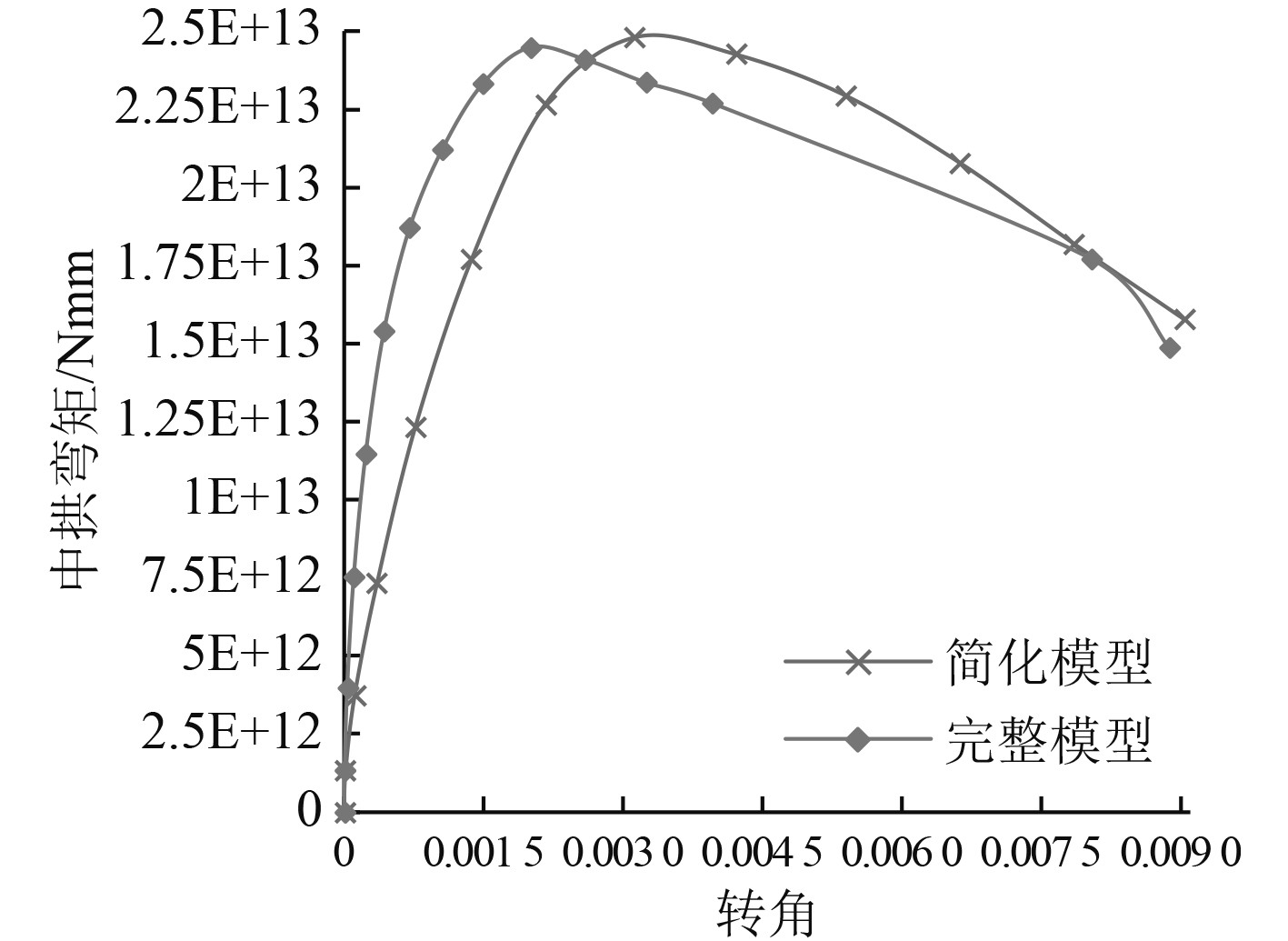
简化模型与完整模型的失效云图、弯矩-转角曲线如图11~图13所示。比较两者的变形失效云图:简化模型与完整模型均发生了船底的屈曲变形、甲板及舷侧的屈服变形,且完整模型的屈曲变形较大。比较两者的弯矩-转角曲线:与中垂弯曲的差别相似,完整模型上升段也较陡,并首先达到极限状态。

|
图 11 简化模型中拱弯曲失效云图 Fig. 11 Failure mode of simplified model under vertical hogging bend |

|
图 12 完整模型中拱弯曲失效云图 Fig. 12 Failure mode of intact model under vertical hogging bend |
|
图 13 中拱工况弯矩-转角曲线 Fig. 13 Moment-angle curves of hogging bending |
中垂及中拱工况下2个模型的极限弯矩如表7所示。极限弯矩误差均在5%以内,且由2种工况的变形云图可知,其失效模式一致,验证了本文提出的简化方法具有可行性,适用于分析散货船的极限强度。
|
|
表 7 两种工况极限弯矩总结(1012 Nmm) Tab.7 Summarized ultimate bending moment under two conditions (1012 Nmm) |
提出船体舱段完整模型的简化方法,建立2种工况的散货船舱段简化模型,对比了2种模型的极限强度和失效模式,得出以下结论:
1)根据本文提出的加筋板简化方法,将受压加筋板简化为等效厚度的板格,考虑了加筋板和等效板的受压极限强度相等,可为计算加筋板的极限强度及剩余强度提供简化的分析模型。
2)船体舱段完整模型及简化模型的极限弯矩误差在5%以内,且考虑了模型的失效一致性,可知本文提出的总纵强度完整模型简化方法具有一定的可行性,对于研究船体极限强度及剩余强度具有参考价值。
3)本文的加筋板及船体梁模型简化方法仅考虑极限强度值和失效模式的一致性,但应力及弯矩曲线没有达到重合,要得到更合理的简化模型需要进一步深入研究。
| [1] |
IACS Common Structural Rules for Bulk Carriers[S], July 2009.
|
| [2] |
吴卫国, 邓卉, 甘进. 船体结构极限强度模型试验技术研究[C]. 纪念《船舶力学》创刊二十周年学术会议论文集, 2017.
|
| [3] |
李政杰, 赵南, 祁恩荣, 等. 典型箱型梁极限强度模型试验分析[J]. 船海工程, 2018, 47(3): 32-35. DOI:10.3963/j.issn.1671-7953.2018.03.007 |
| [4] |
任慧龙, 郎舒妍, 任晨辉, 等. 带有初始缺陷的船体结构极限强度研究[J]. 舰船科学技术, 2015, 37(12): 38-41. DOI:10.3404/j.issn.1672-7649.2015.12.008 |
| [5] |
伍友军, 万琪, 周博. 船体极限强度非线性有限元计算方法[J]. 船舶与海洋工程, 2017, 33(6): 20-25.48. |
| [6] |
万乐天, 吴益辉, 李建强. 基于ABAQUS的船体箱型梁极限强度分析[J]. 水雷战与舰船防护, 2017, 24(4): 62-66. |
| [7] |
GORDO J. M., GUEDES SOARES C.. Experimental analysis of the effect of frame spacing variation on the ultimate bending moment of box girders[J]. Marine Structure, 2014, 37: 111-134. DOI:10.1016/j.marstruc.2014.03.003 |
| [8] |
MING Cai Xua, ZHAO Jun Songa, JIN Pa. Study on influence of nonlinear finite element method models on ultimate bending moment for hull girder[J]. Thin-Walled Structures, 2017, 119: 282-295. DOI:10.1016/j.tws.2017.06.009 |
| [9] |
JEOM Kee Paik, BONG Ju Kim, JUNG Kwan Seo. Methods for ultimate limit state assessment of ships and ship-shaped offshore structures: Part II stiffened panels[J]. Ocean Engineering, 2008, 35: 271-280. DOI:10.1016/j.oceaneng.2007.08.007 |
| [10] |
冯亮, 董胜, 王保森, 等. 箱型梁极限弯矩简化计算方法[J]. 哈尔滨工程大学学报, 2017, 38(3): 1-5. |
| [11] |
JEOM Kee Paik, JUNG Kwan Seo. Nonlinear finite element method models for ultimate strength analysis of steel stiffened-plate structures under combined biaxial compression and lateral pressure actions—Part II: Stiffened panels[J]. Thin-Walled Structures, 2009, 47: 998-1007. DOI:10.1016/j.tws.2008.08.006 |
| [12] |
Shengming ZHANG, Imtaz KHAN. Buckling and ultimate capability of plates and stiffened panels in axial compression[J]. Marine Structures, 2009, 22: 791-808. DOI:10.1016/j.marstruc.2009.09.001 |
| [13] |
KIMA D. K., LIM H. L., KIMB M. S., et al.. An empirical formulation for predicting the ultimate strength of stiffened panels subjected to longitudinal compression[J]. Ocean Engineering, 2017, 140: 270-280. DOI:10.1016/j.oceaneng.2017.05.031 |
| [14] |
雒高龙, 张淑茳, 任慧龙. 船用钢应力-应变关系的数学表达及其在计算加筋板屈曲应力中的应用[J]. 造船技术, 2006, 3: 13-18.42. DOI:10.3969/j.issn.1000-3878.2006.03.004 |
| [15] |
王保森, 董胜, 冯亮, 等. 加筋板极限强度数值计算影响因素及敏感分析[J]. 中国海洋大学学报, 2018, 48(2): 105-112. |
 2020, Vol. 42
2020, Vol. 42
