2. 海军大连舰艇学院 水武与防化系,辽宁 大连 116018
2. Underwater Weapons and Chemical Defense, Dalian Naval Academy, Dalian 116018, China
利用船舶在航行过程中产生的辐射噪声进行特征提取来实现目标识别是水下目标分类识别的一种重要手段,但是由于船舶型号、航速、螺旋桨工况的不同,目标的辐射噪声特征变化较大,特别是在恶劣海况下,识别效果更不令人满意,提取更加具有鲁棒性的特征及研究与特征相匹配的分类识别方法是急需解决的问题。
近年来,随着张量研究的不断深入与发展,张量分解在图像识别,语音信号处理和医学等领域[1]中得到广泛应用。在图像识别领域,周春光等[2]在线性主成分分析的基础上提出了稀疏张量主成分分析算法,有效降低了遮挡对人脸特征提取的影响,并且在不同表情的人脸识别中优于原算法;计雨含利用奇异值分解对人物、表情、向量长度构建的3阶张量进行识别,提高了人脸在光照、角度发生改变时的识别精确度[3]和分类识别时的速度[4];同时在循环次数、特征维数以及训练样本和测试样本数目差别等不同方面对非负张量分解和非负矩阵分解进行的对比也表明了非负张量分解具有的有效性和高效性[5];任卿龙[6]利用不同波段上的遥感图像构建高维张量,对飞机目标和舰船目标进行分级识别也取得了较好的实验结果。在声学领域,王珊[7]在混合矩阵估计中引入张量分解,利用分解后的各个矩阵实现了对多通道混合音乐的盲分离;杨立东[8-9]用语音命令张量经过Tucker分解得到的特征进行识别,平均识别率达到95%,同样对声矢量传感器输出的多维阵列信号进行张量奇异值分解,相比于传统的矢量奇异值分解能够更好地抑制噪声,并对信号子空间的估计更加准确[10]。医学方面,利用张量方法表征脑电信号的时域、频率、空域特征[11],处理肌电信号[12],提取心电信号[13]的操作,均比传统方法具有更高的准确率和相对的优越性。机器学习方面也有关于张量应用的研究[14-15]。
张量分解在图像识别,语音信号处理和医学等领域取得了较好的成果,但在与其具有类似高维结构的船舶辐射噪声信号特征提取和分类识别领域中尚未见到相关报道。本文在船舶辐射噪声特征提取中引入张量,利用张量的空间坐标系具有旋转不变性,以及直接对高维空间进行整体分析和操作的特点进行船舶辐射噪声特征提取和张量构造,并经过张量分解实现对船舶辐射噪声的分类识别。
1 张量分解张量可以直观理解为一个多维数组,是多个矢量的空间乘积,张量的阶是张量不同维上元素个数的数量表达,也被称为way或mode。通常认为向量是张量的1阶表达,矩阵是张量的2阶表达,具有3阶或更高阶数的张量则称为高阶张量。本文提及的张量指的都是高阶张量,用粗体大写字母表示,如
张量分解的思想最早由Hitchcock在1927年提出。1963年,Tucker首次提出了Tucker分解,并在随后进行了完善。1970年,Carroll,Chang和Harshman提出了CANDECOMP/PARAFAC分解,即CP分解[1]。近年来,尹凤等[16]在张量CP分解和Tucker分解的基础上,提出一种利用交替最小二乘法计算高阶张量秩的分解方法。Tucker分解将张量分解为核张量和因子矩阵的形式,类似于矩阵的奇异值分解,因此Tucker分解又被称为高阶奇异值分解(HOSVD)[17],并可以将其看做是奇异值分解(SVD)的高阶形式。本文所采用的张量分解方法就是Tucker分解。
HOSVD将一个
|
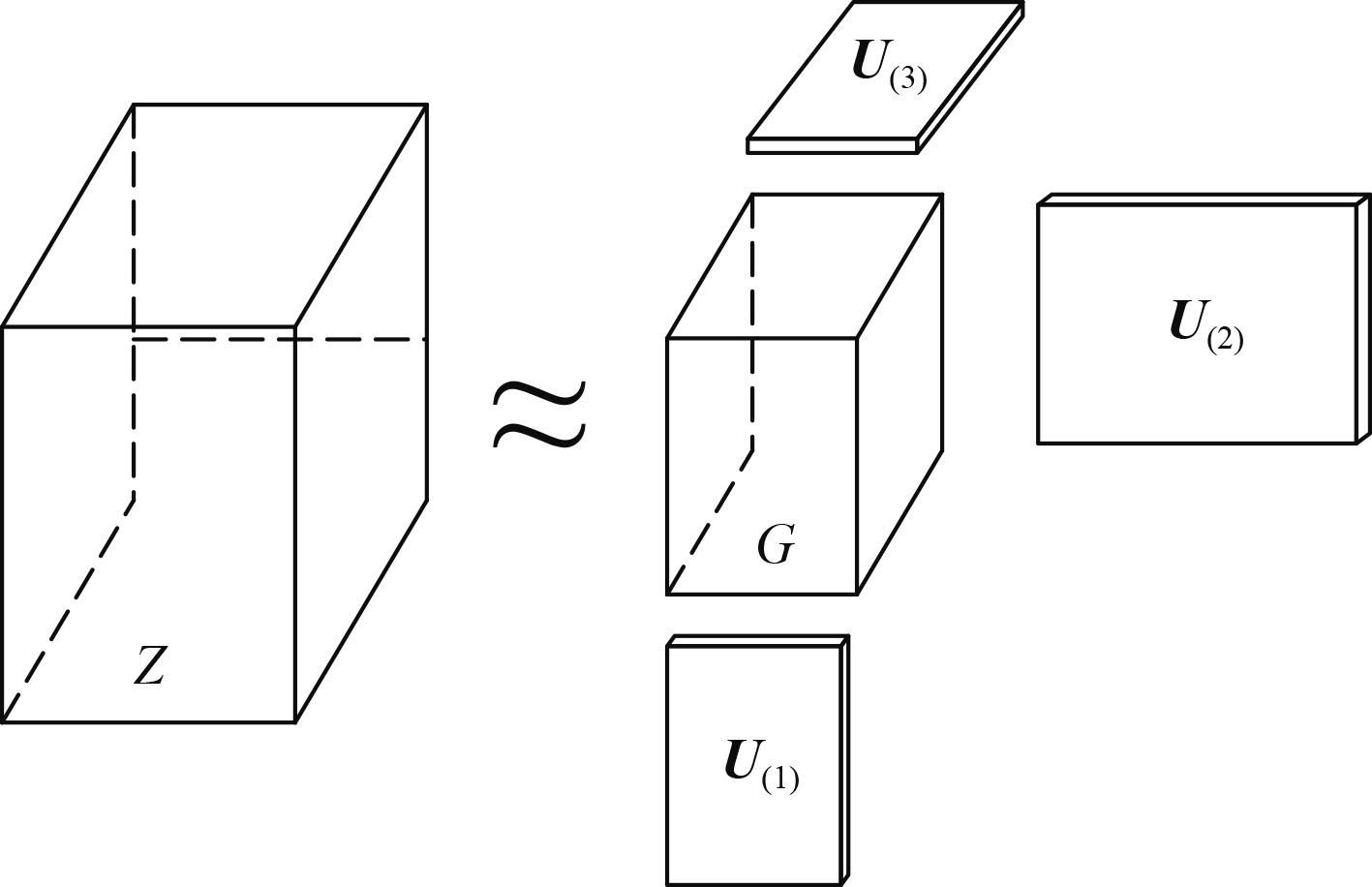
图 1 三阶张量Tucker分解模型 Fig. 1 Tucker decomposition model of a third-order tensor |
对于3阶张量
| ${{Z}} \approx {{G}}{ \times _1}{{{U}}_{\left( 1 \right)}}{ \times _2}{{{U}}_{\left( 2 \right)}}{ \times _3}{{{U}}_{\left( 3 \right)}}{\text{,}}$ | (1) |
其中:
分解后的核张量
| ${{G}} = {{Z}}{ \times _1}{\left( {{{{U}}_{\left( 1 \right)}}} \right)^{\rm{T}}}{ \times _2}{\left( {{{{U}}_{\left( 2 \right)}}} \right)^{\rm{T}}}{ \times _3}{\left( {{{{U}}_{\left( 3 \right)}}} \right)^{\rm{T}}}{\text{。}}$ | (2) |
同奇异值分解一样,高阶奇异值分解中核张量代表原始张量的某些特性,因子矩阵代表着这些特性的重要程度,核张量和因子矩阵也是本文进行舰船辐射噪声分类识别的关键。
2 小波变换张量特征研究表明,船舶信息主要集中在1000 Hz以下的船舶辐射噪声中[18],而1000 Hz以上主要是螺旋桨空化噪声,因此对低频噪声进行分解可以得到更多的船舶信息,更便于船舶特征的提取。离散小波变换可以对信号低频进行分解,因此本文采用的方法是将船舶辐射噪声经过分帧、小波变换、美尔频率倒谱系数(MFCC)提取处理后构建一个帧数×小波分解分量×MFCC特征维数的3阶辐射噪声张量。
2.1 分帧采用交叠分段的方法将船舶辐射噪声分为部分交叠的
| $T = \frac{{{L_s} - {L_z} + {L_{inc}}}}{{{L_{inc}}}}{\text{。}}$ | (3) |
小波变换(WT)是在傅里叶变换(FT)的基础上发展来的,将FT中无限长的三角函数基换成有限长的会衰减的小波基,能够在获得频率信息的同时定位到时间,其与信号
| $\begin{split}F\left( \omega \right) =& \int_{ - \infty }^{ + \infty } {f\left( t \right) * {e^{ - i\omega t}}{\rm{d}}t} \Rightarrow WT\left( {a,b} \right) =\\ &{\left| a \right|^{ - 1/2}}\int_{ - \infty }^{ + \infty } {f\left( t \right) * \varPsi \left( {\frac{{t - b}}{a}} \right){\rm{d}}t}{\text{。}} \end{split}$ | (4) |
其中:
对信号进行小波变换是改变小波的尺度,实现在频域内的伸缩;改变平移量实现在时域内的移动,通过分析
| ${\varPsi _{m,n}}\left( t \right) = a_0^{ - m/2}\varPsi \left( {a_0^{ - m}t - n{b_0}} \right){\text{,}}$ | (5) |
则离散小波变换(DWT)为:
| $DWT\left( {m,n} \right) = a_0^{ - m/2}\int_{ - \infty }^\infty {f\left( t \right) * \varPsi \left( {a_0^{ - m}t - n{b_0}} \right){\rm{d}}t}{\text{。}} $ | (6) |
DWT是一种平分信号带宽的分解算法,它将信号
|
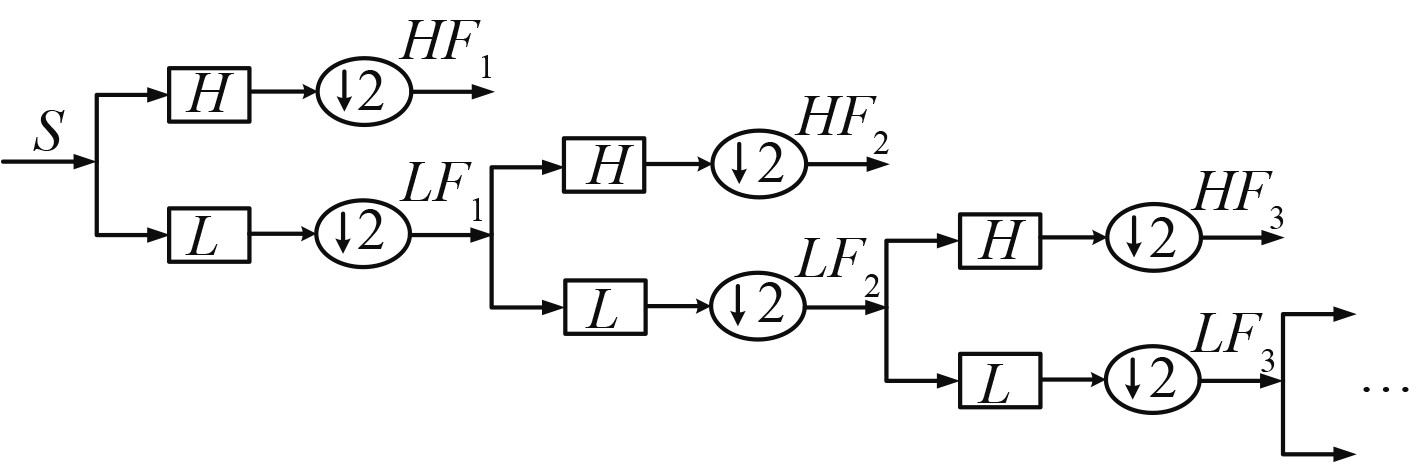
图 2 离散小波变换分解流程 Fig. 2 Decomposition process of discrete wavelet transformation |
图中,L为低通滤波器,H为高通滤波器,↓2为系数为2的降采样滤波器。由于一直在进行降采样,所以虽然滤波器L,H不变,但其滤波带宽一直在减半。如此经过
| $S = H{F_1} + H{F_2} + \cdot \cdot \cdot + H{F_X} + L{F_X}{\text{。}}$ | (7) |
在小波变换中,Morlet小波,Haar小波,Daubechies小波,Meyer小波等是常用的小波,本文进行小波变换时采用的是Daubechies小波,常记为
| $H\left( n \right) = {\left( { - 1} \right)^n}L\left( {2N - n + 1} \right),n = 1,2,...,2N{\text{。}}$ | (8) |
经分类识别实验选取Daubechies小波的阶数
| ${{L(n)}} = \left[ {\begin{array}{*{20}{c}} {0.332670553} \\ {0.806093111} \\ {0.459877502} \\ { - 0.135011020} \\ \begin{gathered} - 0.085441274 \\ 0.035226292 \\ \end{gathered} \end{array}} \right]{\text{。}}$ | (9) |
MFCC特征是一种根据人耳听觉对不同频率的声波灵敏度不同的特性提出的一种听觉感知特性,在信号处理中可以理解为信号的能量在不同频率范围的分布系数占比。计算过程如下[19]:
将分帧后的船舶辐射噪声经上述
| $F\left( k \right) = \sum\limits_{n = 0}^{T - 1} {{S_F}\left( n \right){e^{ - j2\pi nk/T}}} ,0 \leqslant n,k \leqslant T - 1{\text{,}}$ | (10) |
将频谱幅度平方后得到的能量谱通过美尔(Mel)频率滤波器组
| $P\left( m \right) = \ln \left[ {\sum\limits_{k = 1}^T {{{\left| {F\left( k \right)} \right|}^2}} {Q_m}\left( k \right)} \right],m = 1,2...,M{\text{。}}$ | (11) |
式中:
| $C\left( r \right) = \sum\limits_{m = 1}^M {P\left( m \right)\cos \left[ {\left( {2m - 1} \right)r\pi /2M} \right]} ,1 \leqslant r \leqslant R{\text{。}}$ | (12) |
其中:
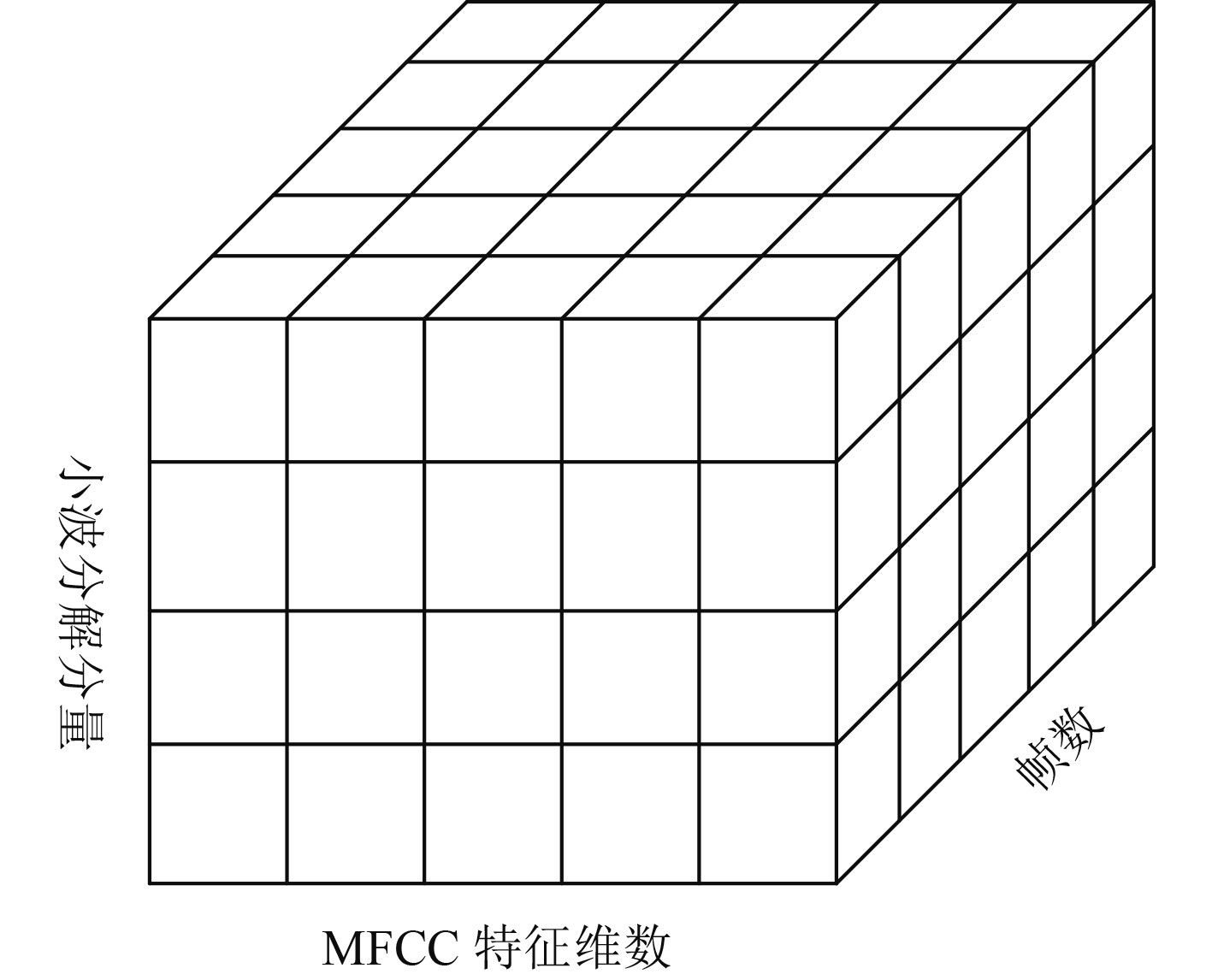
通过上述处理,就可以构建一个帧数×小波分解分量×MFCC特征维数
|
图 3 三阶张量 Fig. 3 A third-order tensor |
对船舶辐射噪声进行分类识别时,设船舶辐射噪声共分为
| ${{\bf{Z}}_{Train}} \approx {{\bf{G}}_{Train}}{ \times _1}{{U}}_{_{\left( 1 \right)}}^{Train}{ \times _2}{{U}}_{_{\left( 2 \right)}}^{Train}{ \times _3}{{U}}_{\left( 3 \right)}^{Train}{\text{,}}$ | (13) |
将测试样本集中每个样本的3阶张量
| ${{\bf{G}}_{Test}} = {{{Y}}_{Test}}{ \times _1}{\left( {{{U}}_{_{\left( 1 \right)}}^{Train}} \right)^{\rm{T}}}{ \times _2}{\left( {{{U}}_{_{\left( 2 \right)}}^{Train}} \right)^{\rm{T}}}{ \times _3}{\left( {{{U}}_{_{\left( 3 \right)}}^{Train}} \right)^{\rm{T}}}{\text{,}}$ | (14) |
通过判别每个测试样本的投影张量
| $\mathop {\arg\min }\limits_{} \sqrt {{{\left\| {{{{G}}_{Test}} - {{{G}}_{Train}}} \right\|}_F}} {\text{。}}$ | (15) |
式中:
分类识别实验中,共有Ⅰ,Ⅱ,Ⅲ类船舶4506个辐射噪声样本,采样频率为25 kHz,每个样本长为6.5536 s。从整个辐射噪声样本中每间隔10个样本取1个作为训练样本集,余下的作为测试样本集,得到451个训练样本,4055个测试样本。对每个样本采用汉明窗进行分帧,每帧长度为8192个采样点,帧移为1024个采样点,分帧后共得到153帧。在小波分解过程中,采用db3小波进行3层小波分解,小波分解后得到4个分量。对每个分量提取12维美尔频率倒谱系数(MFCC)。然后使用上述步骤得到的153帧、4个小波分解分量、12维MFCC特征系数构建一个
|
|
表 1 分类识别概率(%) Tab.1 Probability of classification and recognition (%) |
从实验结果可以看出,本文提出的方法最差识别率为
辐射噪声特征提取是进行目标识别的重要组成部分,提取能够充分表示噪声信息的特征是提高识别率的关键。本文提出的舰船辐射噪声张量特征提取方法,利用小波变换及美尔频率倒谱系数(MFCC)构建具有较高鲁棒性的3阶张量。通过HOSVD张量分解得到训练样本的核张量和各维度上的因子矩阵,将因子矩阵的转置与测试样本构建的张量进行矩阵乘运算得到投影张量,最后通过范数比较核张量和投影张量之间的差异性,确定测试样本所属类别。实验结果表明该方法识别率高,具有一定的优越性。
| [1] |
KOLDA T G, BADER B W. Tensor decompositions and applications[J]. SIAM Re-view, 2009, 51(3): 455-500. DOI:10.1137/07070111X |
| [2] |
周春光, 孙明芳, 王甦菁, 等. 基于稀疏张量的人脸图像特征提取[J]. 吉林大学学报(工学版), 2012, 42(6): 1521-1526. ZHOU Chun-guang, SUN Ming-fang, WANG Su-jing, et al. Face image feature extraction method based on sparse tensor[J]. Journal of Jilin University (Engineering and Technology Edition), 2012, 42(6): 1521-1526. |
| [3] |
计雨含, 王晓东, 姚宇. 基于张量奇异值分解的人脸识别方法[J]. 计算机应用, 2015, 35(S1): 117-121, 126. JI Yuhan*, WANG Xiaodong, YAO Yu. Face identification based on tensor singular value decomposition[J]. Journal of Computer Applications, 2015, 35(S1): 117-121, 126. |
| [4] |
ELIZABETH N, MISHA K, LIOR H. Image classification using local tensor singular value decompositions[J]. 2017 IEEE 7th International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), pp.1-5.
|
| [5] |
梁秋霞, 何光辉, 陈如丽, 等. 基于非负张量分解的人脸识别算法研究[J]. 计算机科学, 2016, 43(10): 312-316. LIANG Qiu-xia, HE Guang-hui, CHEN Ru-li, CHU Jian-pu. Research of face recognition algorithm based on nonnegative tensor factorization[J]. Computrter Science, 2016, 43(10): 312-316. DOI:10.11896/j.issn.1002-137X.2016.10.058 |
| [6] |
任卿龙. 基于支持张量机的遥感图像目标分级识别研究[D]. 哈尔滨: 哈尔滨工业大学. 2017. Ren Qinglong. Research on target hierarchical recognition of remote sensing images based on support tensor machine[D]. Harbin: Harbin Institute of Technology, 2017. |
| [7] |
王珊. 基于非负张量分解的多通道音频信号盲分离研究[D]. 南京: 东南大学, 2015. WANG Shan. Multichannnel audio signals blind sepatation based on nonnegative tensor factorization[D]. Nanjing: Southeast University, 2015. |
| [8] |
XING L, MA Q Zhu M. Tensor semantic model for an audio classification system[J]. Science China Information Sciences, 2013, 56(6): 1-9. |
| [9] |
杨立东.基于张量分析的多因素音频信号建模与应用研究[D]. 北京: 北京理工大学. 2016. YANG Lidong. Study on multifactor audio signal modeling and applications based on tensor analysis[D]. Beijing: Beijing Institute of Technology, 2016. |
| [10] |
樊帆. 基于张量分解的声矢量传感器阵列信号处理方法研究[D]. 吉林: 吉林大学. 2017. FAN Fan. Research on signal processing of acoustic vector sensor array based on tensor decomposition[D]. Jilin: JiLin University, 2016. |
| [11] |
邱静雯, 官金安. 张量时频空模式在脑电信号特征提取中的研究[J]. 计算机与数字工程, 2015(43): 5: 797-804. QIU Jingwen, GUAN Jinan. Fan fan. tensor temporal-frequency-spatial pattern in feature extraction of EEG Signal[J]. Computer & Digital Engineering, 2015(43): 5: 797-804. |
| [12] |
佘青山, 马鹏刚, 马玉良, 等. 基于张量线性拉普拉斯判别的肌电特征提取方法[J]. 东南大学学报, 2017(47): 6:1117-1122. SHE Qingshan, MA Penggang, MA Yuliang, et al. EMG feature extraction based on tensor linear Laplacian discriminant[J]. Journal of Southeast University (Natural Science Edition), 2017(47): 6:1117-1122. |
| [13] |
徐曼. 基于张量分解的胎儿心电信号提取研究[D]. 重庆: 重庆大学. 2017. XU Man. Study on method of fetal electrocar diagram extraction based on tensor decomposition[D]. Chongqing: Chongqing University. |
| [14] |
ND Sidiropoulos, LD Lathauwer, et al. Tensor decomposition for signal processing and machine learning[J]. IEEE Transactions on Signal Processing, 2016, 65(13): 3551-3582. |
| [15] |
STPHAN R, OLEKSANDR S, STEPHAN G. Introduction to tensor decompositions and their applications in machine learning[J]. ArXiv preprint, 1711. 10781, 2017.
|
| [16] |
尹凤, 雷晓军, 黄光鑫. 关于高阶张量的秩 分解方法[J]. 成都理工大学学报(自然科学版), 2019, 42(1): 123-128. YIN Feng, LEI Xiaojun, HUANG Guangxin. On the research of rank decomposition of trnsor with high order[J]. Journal of Chengdu University of Technology (Science & Technology Edition), 2019, 42(1): 123-128. |
| [17] |
LATHAUWER L D, MOOR B D, VANDEWALLE J. A multilinear singular value decomposition[J]. SIAM Journalon Matrix Analysis and Applications, 2000, 21(4): 1253-1278. DOI:10.1137/S0895479896305696 |
| [18] |
王梦璇. 基于小波包分解的舰船辐射噪声特征提取方法研究[J]. 电子设计工程, 2014, 22(4): 81-83. WANG Meng-xuan. Research of ship-radiated noise feature extraction method based on wavelet packet decomposition[J]. Electronic Design Engineering, 2014, 22(4): 81-83. DOI:10.3969/j.issn.1674-6236.2014.04.024 |
| [19] |
程锦盛, 杜选民, 周胜增, 等. 基于目标MFCC特征的监督学习方法在被动声呐目标识别中的应用研究[J]. 舰船科学技术, 2018, 40(9): 116-121. CHENG Jin-sheng, DU Xuan-min, ZHOU Sheng-zeng. Application of the MFCC feature based supervised learning method in passive sonar target recognition[J]. Ship Science and Technology, 2018, 40(9): 116-121. DOI:10.3404/j.issn.1672-7649.2018.09.022 |
 2020, Vol. 42
2020, Vol. 42
