2. 哈尔滨工程大学 水声工程学院,黑龙江 哈尔滨 150001
2. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China
方位估计是声呐目标探测中的重要内容,圆型阵是声呐基阵的常见形式,常用于舰(艇)首声呐、吊放声呐中。然而,在很多实际工程应用领域,圆型阵的孔径大小受到应用条件限制,导致方位分辨力低、阵增益小,严重影响声呐系统的探测性能,难以满足军事应用需要。
目前,圆阵方位估计相关算法的研究主要是通过相位模式空间理论,将一些应用在线阵上很成熟的技术经其转变为符合范德蒙结构的虚拟线阵的阵列形式,这样虽然是从圆阵的阵列上采集到的阵列信号,但是其形式完全符合线阵的形式。基于这个模式空间理论,一大批基于圆阵的相位模式空间理论的波达方向估计算法被提了出来。如Marius Pedavento等[1]提出的UCA–RARE算法,Mathews等[2]提出的UCA–RB–MUSIC和UCA–ESPRIT算法等。这些算法将圆阵转化为线阵形式,虽然能直接采用线阵现有算法,但是孔径却变小了,在圆阵孔径受限情况下,效果并不理想。
圆阵的方位估计性能与阵列孔径相关,阵列孔径越大,方位估计性能越好,因此如果在受应用条件限制阵列孔径较小的条件下,增大阵列孔径,则可提升圆阵的方位估计性能。频率多样性阵列(Frequency diversity array,FDA)技术是近几年新兴的一种阵列信号处理技术,其思想是在方位估计过程中将空间信息和频率信息结合起来,本文结合频率多样性的这一思想,在圆阵上展开研究,通过频率信息扩展其空间孔径。2006年在雷达会议上,Paul和Michael[3]首次提出频率多样性的概念。该算法在发射端引入每个阵列元件之间的频率差,并结合距离和扫描角来提高抗干扰能力[4]。研究者们在关于频率多样性波束形成和接收处理方式[5-6]、目标位置估计[7-8]、与MIMO雷达相结合运用[9-10]以及距离模糊杂波抑制[11-12]等方面进行了研究,目前频率多样性在雷达方面研究技术已经比较成熟,但这种方法需要已知信号的初始相位,因此现有研究主要集中在主动雷达领域,而在被动探测领域的研究鲜有报道。李鹏[13]在被动声呐方位估计中提出了双阵元和三阵元的频率多样性方法,并用实验数据验证了该算法的有效性和优点,解决了被动声呐探测信号初始相位未知的问题,证明频率多样性方法在被动声呐领域具有广阔的研究前景。
对于圆阵,其阵元接收信号相位也包含频率信息和空间信息,因此本文基于频率多样性提出能够扩展圆阵孔径从而提高圆阵方位估计性能的方法,仿真和实验数据验证了该方法能有效提高圆阵分辨率和阵增益。
1 圆阵接收信号模型考虑均匀圆阵,所有阵元均位于同一平面,假设该平面为
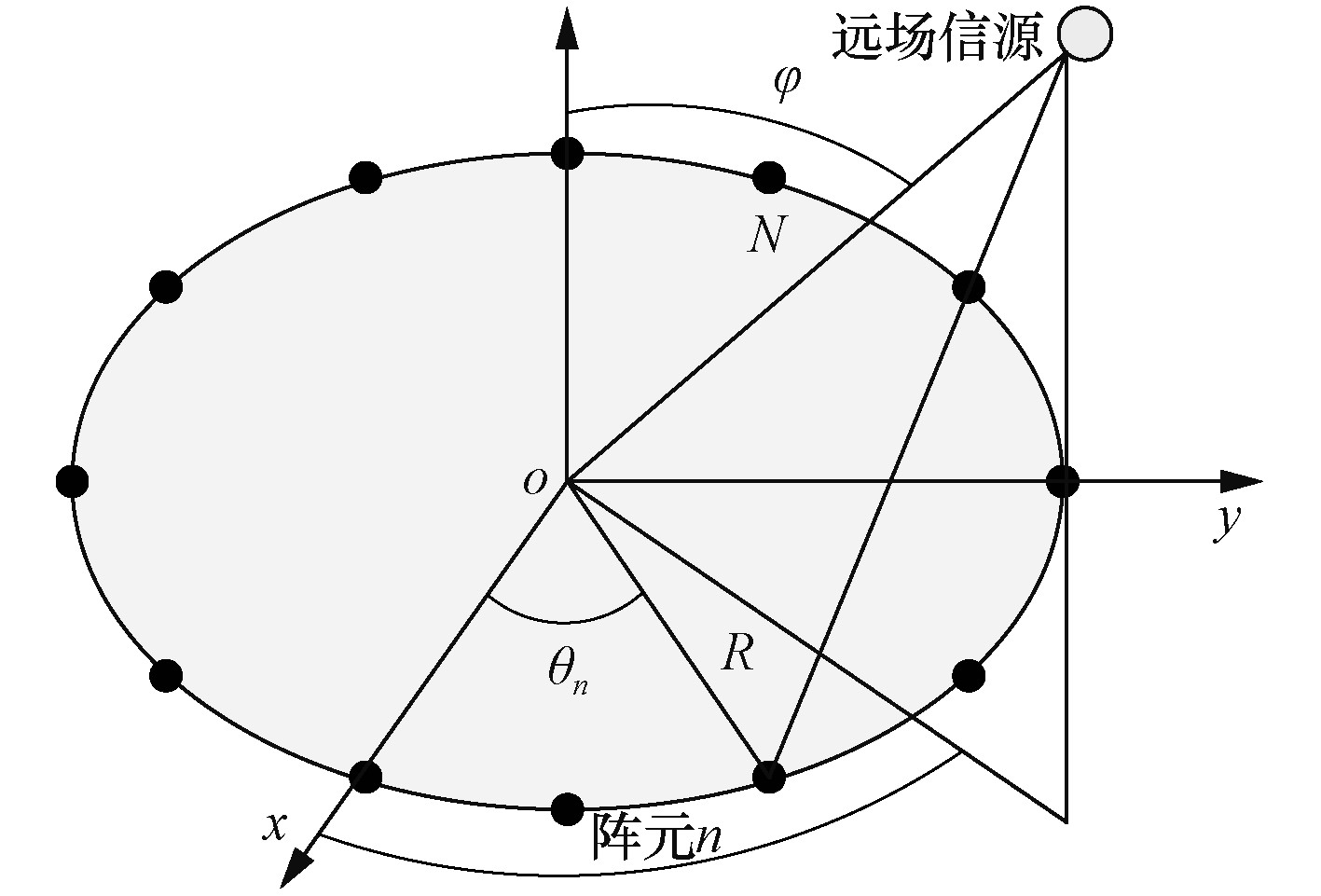
|
图 1 均匀圆阵信号接收模型 Fig. 1 Signal receiving model of uniform circular array |
远场平面波入射到均匀圆阵平面,其水平入射角为
| ${{r}} = [\sin \phi \cos \theta \;\;\sin \phi \sin \theta \;\;cos\phi ]{\text{,}}$ | (1) |
阵元
| ${{{r_n}}} = [R\sin {\phi _n}\cos {\theta _n}\;\;R\sin {\phi _n}\sin {\theta _n}\;\;0]{\text{。}}$ | (2) |
以
| ${\tau _{\rm{n}}} = \frac{R}{c}\cos ({\theta _n} - \theta ){\text{,}}$ | (3) |
假设,阵列输出数据向量为:
| $S(t) = {({s_1}(t),{s_2}(t),...,{s_N}(t))^{\rm{T}}}{\text{,}}$ | (4) |
入射信号矢量为:
| $Y(t) = {({y_1}(t),{y_2}(t),...,{y_K}(t))^{\rm{T}}}{\text{,}}$ | (5) |
| $A(\theta ) = (a({\theta _1}),a({\theta _2}),...,a({\theta _K}){\text{。}}$ | (6) |
其中,
| $a({\theta _n}) = {[{e^{ - j2\pi f{\tau _1}}},{e^{ - j2\pi f{\tau _2}}},...{\rm{ ,}}{e^{ - j2\pi f{\tau _N}}}]^{\rm{T}}}{\text{。}}$ | (7) |
接收阵的噪声表示为:
| $N(t) = [{({n_1}(t),{n_1}(t),...,{n_N}(t)]^{\rm{T}}}{\text{,}}$ | (8) |
则阵列接收信号模型为:
| $S(t) = A(\theta )Y(t) + N(t){\text{。}}$ | (9) |
在雷达领域,频率多样性技术主要是联合距离与角度信息,达到抑制杂波、提高检测性能等目的。借鉴雷达中线列阵频率多样性思想,基于圆阵频率间和阵元间的相位结构角度关系,提出一种圆阵频率多样性方位估计方法,来提升圆阵的方位估计性能。但是雷达中将频率多样性技术用于主动工作方式中,发射的信号为调制信号,初相是可控的,而在被动声呐中,声源各个频点的初相位是未知的、不可控的。因此,想将频率多样性技术应用到被动声呐阵列扩展技术中,首先需要设法消除各个频点的初始相位。
假设信号方向为
| $ {S_n}\left( {{f_1}} \right) = {x_n}\left( {{f_1}} \right) + {n_n}\left( {{f_1}} \right){\text{。}} $ | (10) |
其中:
| $ {Z_n}\left( {{f_1}} \right) = {S_n}\left( {{f_1}} \right)S_1^*\left( {{f_1}} \right) = {x_{n,1}}\left( {{f_1}} \right) + {n_{n,1}}\left( {{f_1}} \right){\text{,}} $ | (11) |
其中,
| ${x_{n,1}}(f1) = {e^{j2\text{π} {f_1}R\cos (\theta - \frac{{2\text{π} n}}{N})/c}}{\text{,}}$ | (12) |
| $\begin{split} {n_{n,1}}\left( {{f_1}} \right) = x_1^*\left( {{f_1}} \right){n_n}\left( {{f_1}} \right) + &{n_n}\left( {{f_1}} \right)n_1^*\left( {{f_1}} \right) +\\ &{x_n}\left( {{f_1}} \right)n_1^*\left( {{f_1}} \right){\text{。}} \end{split} $ | (13) |
假设信号与噪声不相关,噪声
| ${x_{n,1}}({f_1}) = {e^{j2\text{π} {f_2}({{{f_1}}/ {{f_2}}})R\cos (\theta - \frac{{2\text{π} n}}{N})/c}}{\text{,}}$ | (14) |
可知,正常用半径为
经过上述处理后,在对信号相位差的影响上,圆阵半径和频率可以相互转化。因此在阵列空域信息不足时在频率上构建虚拟信号来弥补。
通过频率多样性构造虚拟阵元扩大圆阵孔径的示意图如图2所示。图中,

|
图 2 基于频率多样性的阵列扩展示意图 Fig. 2 Schematic diagram of array expansion based on frequency diversity array |
对
| $Zn(fA) = {x_{{n_{cg}}}}({f_A}) + {n_{{n_{cg}}}}({f_A}){\text{,}}$ | (15) |
| $Zn(fB) = {x_{{n_{cg}}}}({f_B}) + {n_{{n_{cg}}}}({f_B}){\text{,}}$ | (16) |
其中
| $ {x_{{n_{cg}}}}\left( {{f_A}} \right) = {e^{j2\text{π} {f_A}{\rm{Rcos}}\left( {\theta - \frac{{2\text{π} {n_{cg}}}}{N}} \right)/C}},\;{n_{cg}} = 1,2,3, \ldots ,N{\text{;}} $ | (17) |
将式(17)变形为:
| ${x_{{n_{cg}}}}({f_A}) = {e^{j2\text{π} {f_B}({{{f_A}} / {{f_B}}})R\cos (\theta - \frac{{2\text{π} {n_{cg}}}}{N})/c}},\;{n_{cg}} = 1,2,3,...,N{\text{。}}$ | (18) |
此时,可将其视为处理频率为
| $\begin{aligned} & {x_{{n_{cg}}}}({f_B}) = {e^{j2\text{π} {f_B}2R\cos (\theta - \frac{{2\text{π} {n_{cg}} - N}}{N})/c}}, \\ & \quad \quad {n_{cg}} = N{\text{ + }}1,N + 2,N + 3,...,{\text{2}}N {\text{。}} \end{aligned} $ | (19) |
综上,原阵列就转化为一个半径为
由式(17)和式(19)中的相位关系决定的实际阵列和扩展阵列的阵列流形分别为:
| ${A_{{f_{_A}}}} = {e^{ - j2\text{π} {f_{_A}}R\cos (\theta - \frac{{2\text{π} {n_{cg}}}}{N})/c}}{\text{,}}$ | (20) |
| ${A_{{f_{_B}}}} = {e^{ - j2\text{π} {f_{_B}}2R\cos (\theta - \frac{{2\text{π} {n_{cg}} - N}}{N})/c}}{\text{,}}$ | (21) |
| $B(\theta ) = \sum\limits_{{f_{_A}}_{\min }}^{{f_{_A}}_{\max }} {{Z_n}({f_{_A}},\theta )} {A_{{f_{_A}},\theta }} + \sum\limits_{{f_B}_{\min }}^{{f_B}_{\max }} {{Z_n}({f_{_B}},\theta )} {A_{{f_{{_B},\theta }}}}{\text{。}}$ | (22) |
其中:
仿真条件设圆阵的阵元半径为0.8 m,阵元数为32,以高斯白噪声作为声源信号。信号采样频率为100 kHz,声信号入射角度为100°,仿真分析带内信噪比为-3 dB和-20 dB时常规波束形成(CBF)和频率多样性方法的情况。其中,CBF的信号处理频段为1~5 kHz,频率多样性方法的原阵列信号处理频段为2~5 kHz,虚拟扩展阵处理频段为1~2.5 kHz,这样就保证了CBF和频率多样性方法都在同一频段内进行方位估计,仿真结果如图3所示。图中,虚线表示CBF的方位估计的结果,实线表示经过频集扩展后的CBF得到的方位估计结果。通过对比CBF方法和频率多样性方法的仿真结果,可以观察到经过频率多样性方法后分辨力有所提高,阵增益得到明显提升,在右图中观察阵增益提高约3 dB。
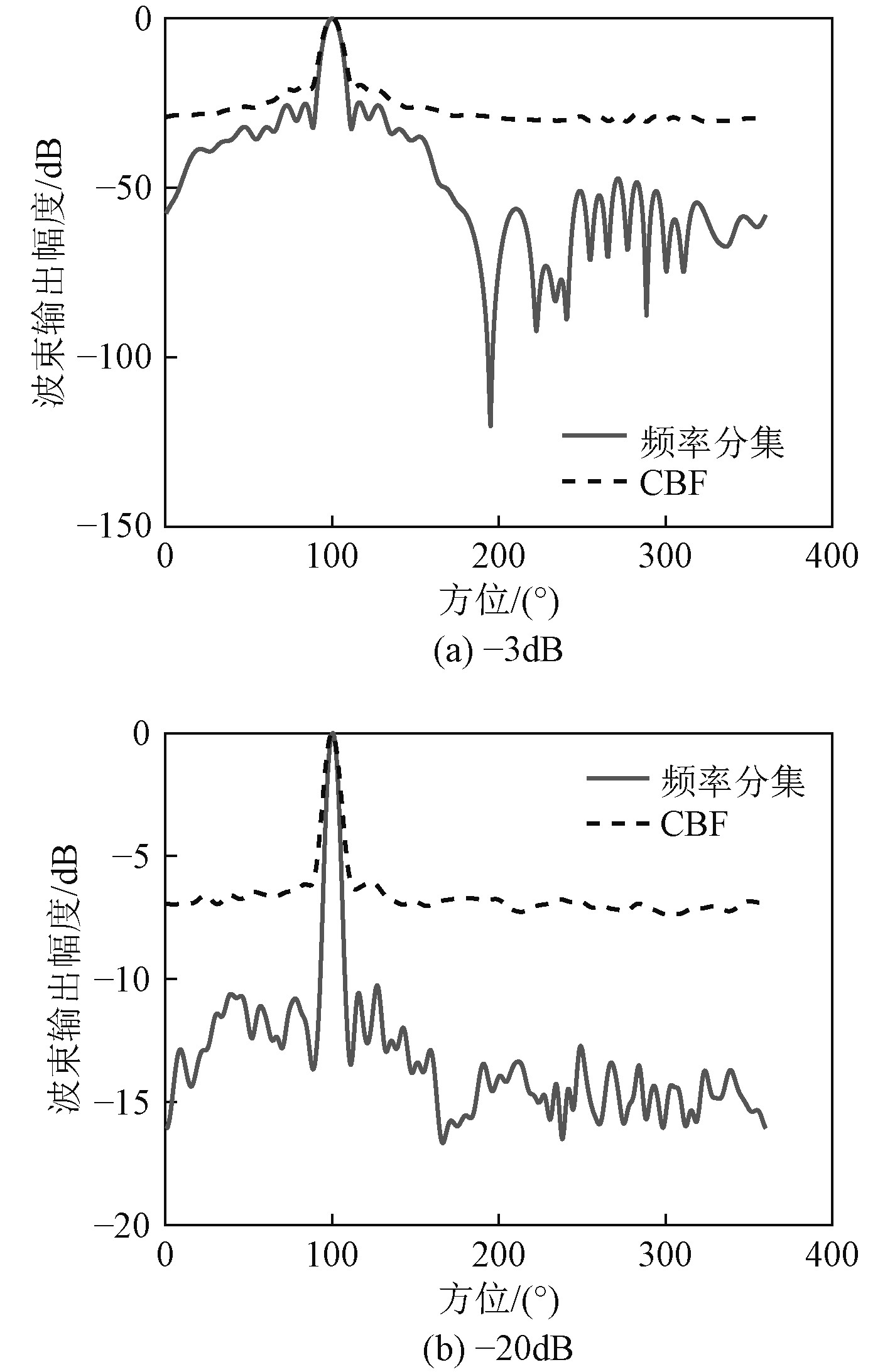
|
图 3 不同信噪比下基于频率多样性算法与常规阵处理仿真对比 Fig. 3 Simulation comparison between frequency diversity array and conventional array processing under different SNR |
为了更直观地观察频率多样性方法对方位分辨力的影响,其他仿真不变,声源信号改为2个,入射角度为100°和115°,依然在-3 dB和-20 dB信噪比条件下进行仿真分析,如图4所示。
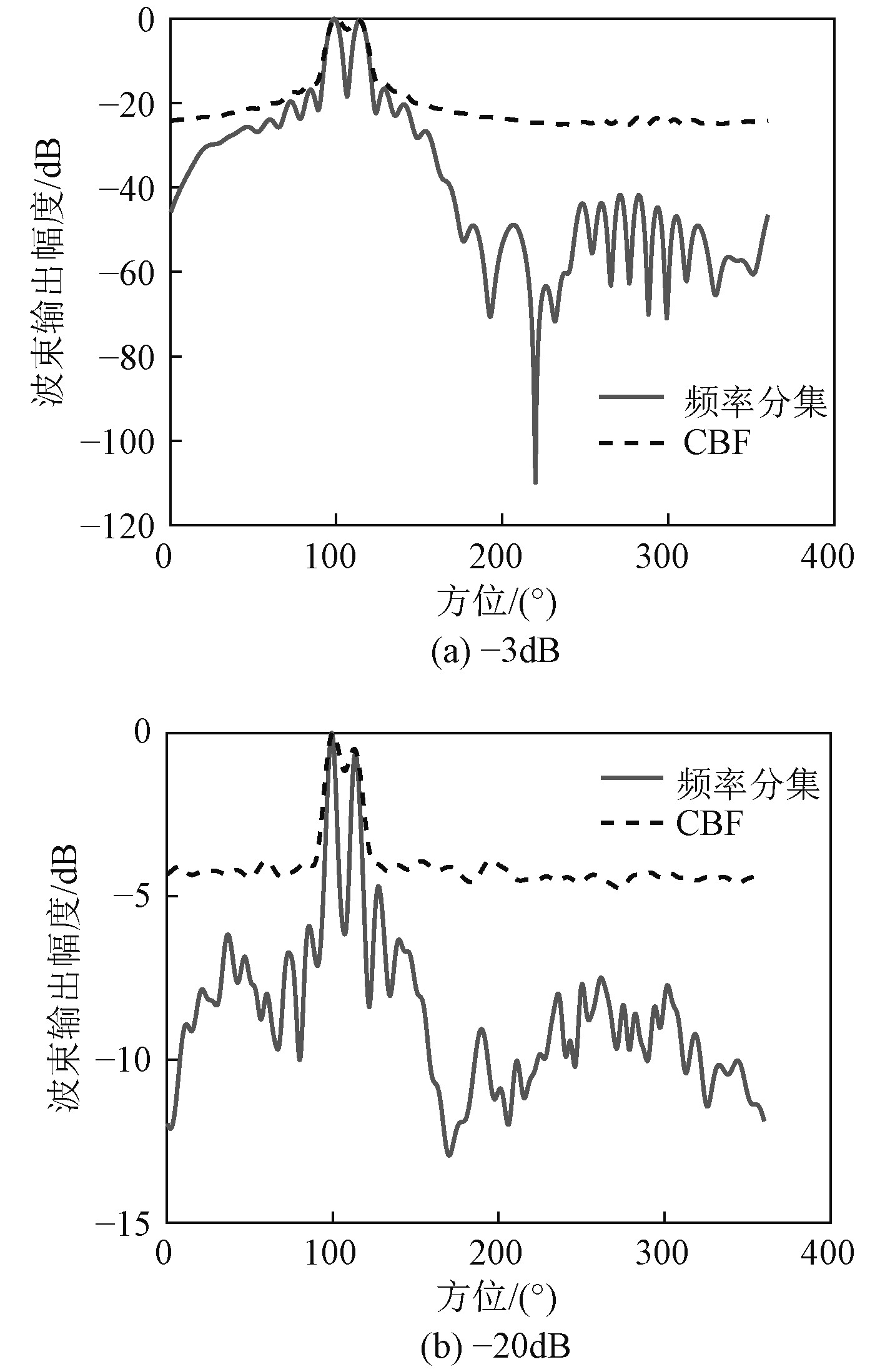
|
图 4 不同信噪比下基于频率多样性与CBF对双目标分辨力对比 Fig. 4 Comparison of dual target resolution based on frequency diversity array and CBF under different SNR |
仿真结果表明,使用CBF算法难以分辨2个方位相近的目标,而经过频率多样性方法处理后再用CBF方法就能很好地将100°和115°的2个目标分辨开,表明圆阵频率多样性方法目标分辨的能力得到有效提升。在2个信噪比下使用频率多样性方法后增益均提升,在-20 dB的情况下,增益为2 dB。因此,以上仿真条件和结果说明频率多样性方法可以有效提高圆阵的方位分辨力和阵增益。
图5为基于半径为0.8 m的32元均匀圆阵的CBF和频率多样性对海上实验数据的处理结果,其中处理频段为2~5 kHz。
由图5可知,常规阵处理方位历程图中噪声干扰较强,目标方位历程不够清晰,经过频率多样性方法处理后,背景噪声干扰明显减少,轨迹更清晰,能更清晰地观察到目标的方位历程。在图5(a)中有若干可能是由于栅瓣引起的假目标,经过频率多样性方法处理后假目标明显得到抑制。在海上实际数据中性能不如仿真数据主要有2种原因:一是可能因为海洋环境噪声不满足假设条件;二是由于目标辐射噪声信号频谱的稀疏性,用于弥补空间信息不足的频率成分缺少或者不存在。但是这种方法对阵增益的提升还是显而易见的。

|
图 5 实验数据方位历程图 Fig. 5 Experimental data orientation progress diagram |
本文提出一种基于圆阵的频率多样性方位估计方法,介绍了频率多样性方法原理,理论推导了频率多样性在被动圆阵声呐上的实现,并用仿真和实验数据对算法的性能进行了验证。仿真结果表明,与CBF相比,所提算法可以有效提高圆阵波束形成的增益,提高分辨力。实验数据处理结果表明,所提算法可以使目标方位历程更加清晰,有效降低背景干扰。结合仿真和实验数据处理结果,本文所提算法有效提升了圆阵的方位估计能力,为圆阵尤其是孔径受限的圆阵在进行被动探测时提供了一种有效可行的方法。
| [1] |
PESAVENTOAND M., BOHME J. F.. Direction of arrival estiamtion in uniform circular arrays composed of directional elements. In Proc. Sensor Array and Multichannel Signal Processing Workshop, Aug. 2002: 503-507.
|
| [2] |
CHERIAN P. M, MICHAEL D. Z.. Eigenstructure techniques for 2D-angle estimation with uniform circular arrays[J]. Ieee Transctions on Signal Prdcessing, 1994, 42(9): 2395-2407. DOI:10.1109/78.317861 |
| [3] |
ANTONIK P, WICKS M C, GRIFFITHS H D. multi-mission multi-mode waveform Diversity[C]// IEEE Conference on Radar, Verona, April 2006: 580-582.
|
| [4] |
胡柏林, 廖桂生, 许京伟. 前视阵频率分集雷达空时杂波特性研究[J]. 电子与信息学报, 2013, 35(11): 2693-2699. |
| [5] |
徐艳红, 史小卫, 文珺. 频率分集阵列稳态波束形成方法[J]. 西安电子科技大学学报: 自然科学版, 2016, 43(5): 41-44. XU Yang-hong, SHI Xiao-wei, WEN Jun. Static beam-forming method of frequency diverse array[J]. Journal of Xidian University: Natural Science ed, 2016, 43(5): 41-44. |
| [6] |
郑昱. 基于频率分集阵列的波束形成研究[J]. 现代雷达, 2015, 37(8): 29-32. ZHENG Yu. A study on the beam forming of frequency diverse array[J]. Modern Radar, 2015, 37(8): 29-32. |
| [7] |
许京伟. 频率分集阵列雷达运动目标检测方法研究[D]. 西安. 西安电子科技大学. 2015. XU Jing-wei. Study on Moving Target Detection with Frequency Diverse Array Radar[D]. XI'an: Xidian University, 2015 |
| [8] |
JONES A M. RIGLING B D. Planar Frequency Diverse Array Receiver Architecture[C]//Radar Conference, Atlanta, USA, MAY 7-11, 2012: 1045-0150.
|
| [9] |
WANG Wen-qin, SHAO Huai-zong. A Flexible Phased-MIMO Array Antenna with Transmit Beamforming[J]. International Hournal of Antennas and Propagation, 2012, 2012: 473-475. |
| [10] |
WANG Wen-qin. Phased-MIMO Radar with Frequency Diversity for Range-Dependent Beamforming[J]. IEEE Sensors Journal, 2013, 13(4): 1320-1328. DOI:10.1109/JSEN.2012.2232909 |
| [11] |
王伟伟, 吴孙勇, 许京伟, 等. 基于频率分集阵列的机载雷达距离模糊杂波抑制方法[J]. 电子与信息学报, 2015, 37(17): 1-7. WANG Wei-wei, WU Sun-yong, XU Jing-wei, et al. Range ambiguilty clutter suppression for airborne radar based on frequency diverse array[J]. Journal of Electronivs & Information Technology, 2015, 37(17): 1-7. |
| [12] |
项喆, 陈伯孝. 频率分集阵列的距离角度解耦的波束形成[J]. 雷达学报, 2018, 7(2): 212219-319. XIANG Zhe, CHEN Bo-xiao. Range-angle decoupled transmit beamforming with frequency diverse array[J]. Journal of Radars, 2018, 7(2): 212219-319. |
| [13] |
LI Peng, ZHANG Xinhua, ZHANG Wenlong. Direction of arrival estimation using two hydrophones: frequency diversity technique for passive sonar[J]. Sensors, 2019, 19(9): 20. |
 2020, Vol. 42
2020, Vol. 42
