0 引　言

纯方位目标跟踪方法是在被动测量的情况下，根据传感器测量到的受到噪声污染的方位数据来估计目标运动特性的跟踪方法，在许多领域有着非常广泛的应用^[1]，例如雷达、水下、航空等领域，特别是在水下环境中，这种跟踪方法备受关注。尤其是本文将要讨论的单站纯方位目标跟踪，它的优点在于可以仅通过单个观测站在隐蔽状态下对目标进行被动的观测，并进行运动参数的估计，从而可以单独秘密地进行行动策划并对目标实施打击。但由于单个观测站所能获得的观测数据有限，系统可观测性差，对目标的定位和跟踪难度更大。因此，单站纯方位目标跟踪是水下目标攻击领域中最受关注的一种方法，它既是目标跟踪算法领域中的基本方法，又是公认的最具挑战性的一大难题。随着水下目标的运动速度不断提高，对水下快速目标的跟踪定位提出了新的挑战。

单站纯方位目标跟踪方法的研究热点集中在批处理和递推类估计两大类方法中。其中递推类估计方法由于模型简单、数据储存量小的特点，更加适合计算机应用，已经成为目标定位跟踪方法的发展方向和研究热点^[2]。由于水下单站纯方位目标跟踪模型是非线性的，线性滤波效果不佳，用于此方面的递推类估计方法有：扩展卡尔曼滤波^[3]、无迹卡尔曼滤波^[4]、粒子滤波^[5]等。

递推类估计方法有一共同难点在于，由于递推的性质，后一时刻的结果依赖于前一时刻，误差易随迭代过程扩大。对于卡尔曼系的算法，还有一大问题在于估计结果对于估计初值的选取十分依赖，起始时刻误差通过迭代始终影响后续时刻的滤波，因此起始时刻初值的准确度对后续的参数估计和目标跟踪的效果有着较大影响。近年来一些文献研究了双向滤波^[6-8]或者是后向平滑^[9-11]的滤波方法，试图通过正反向的滤波，增加对观测数据的利用，以提高估计精度。但这些方法都是针对滤波中上一时刻的优化，没有对滤波初值进行单独优化，对于短时观测的情况，误差降低效果有限。本文的研究是在这种后向滤波思路的基础上，采用一种逆向平滑方法对滤波的初值进行优化，使整个跟踪过程的误差降低，提高短时观测下快速目标跟踪的准确度。

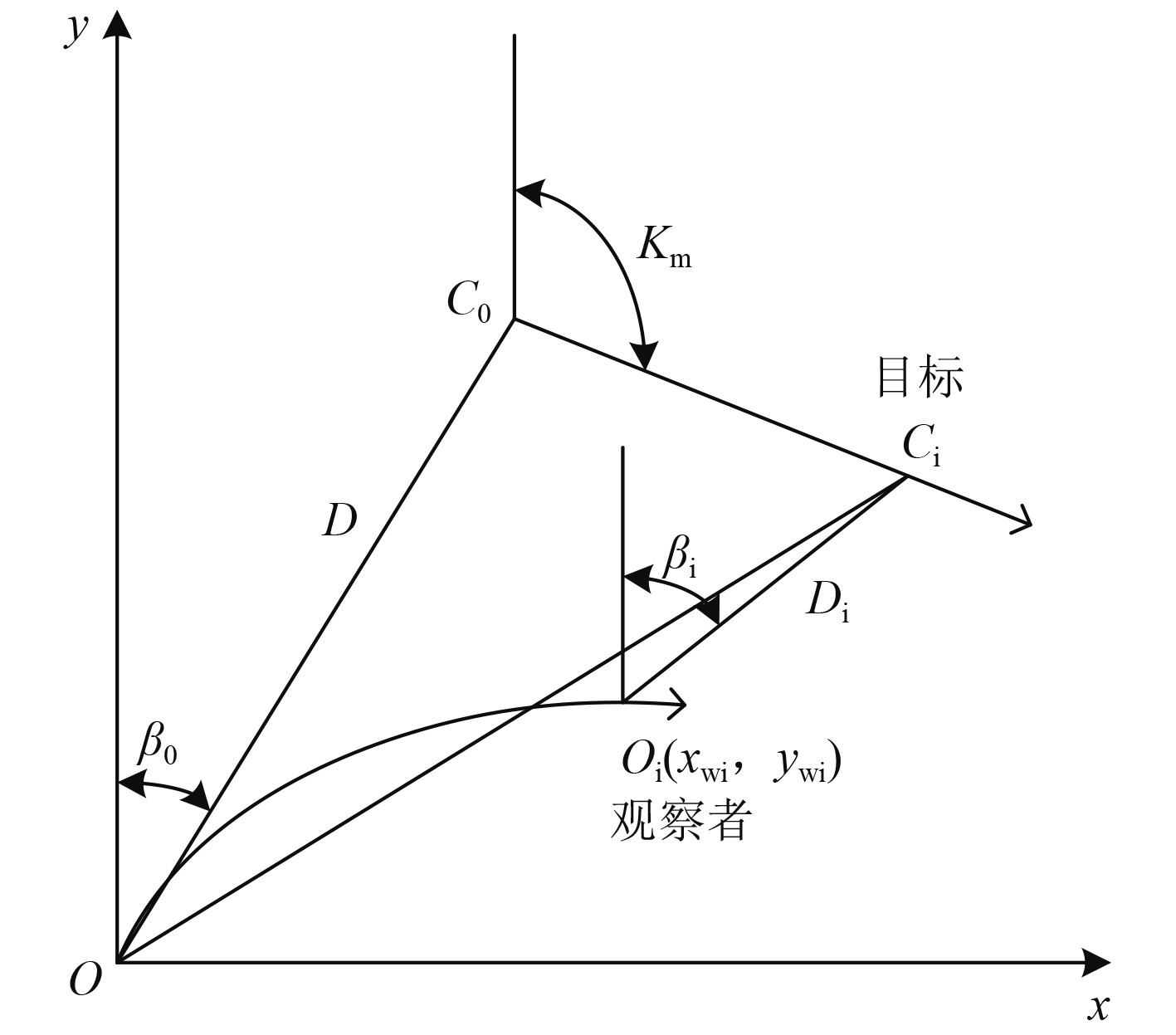
1 单站纯方位目标运动模型

只考虑目标在二维平面运动，假定目标做匀速直线运动，坐标系如图1所示。X轴指向正东，Y轴指向正北，观测站初始位置位于坐标原点，目标在XOY平面运动。 ${D_0}$ 为目标初始距离， ${K_m}$ 为目标运动航向， ${V_m}$ 为目标的运动速度， ${\beta _0},{\beta _1}, \cdots ,{\beta _i}$ 为 ${t_0},{t_1}, \cdots ,{t_i}$ 时刻对应的目标方位， $\left( {{x_{wi}},{y_{wi}}} \right)$ 是 ${t_i}$ 时刻观测平台位置 ${O_i}$ 对应的坐标， ${D_i}$ 是 ${t_i}$ 时刻对应的目标与观测平台之间的距离。显然，对于匀速直线运动的目标， $\left( {{D_0},{K_m},{V_m},{\beta _0}} \right)$ 能够唯一地确定目标的运动轨迹。

定义 ${V_{mx}}$ 为目标运动速度 ${V_m}$ 在x轴的分量， ${V_{my}}$ 为目标运动速度 ${V_m}$ 在y轴的分量， ${x_{m0}}$ 为目标初始位置的x轴坐标， ${y_{m0}}$ 为目标初始位置的y轴坐标，则可得到下式：

$\left\{ {\begin{array}{l} {{V_{mx}} = {V_m}\sin {K_m}} \text{，}\\ {{V_{my}} = {V_m}\cos {K_m}} \text{，}\\ {{x_{m0}} = {D_0}\sin {\beta _0}} \text{，}\\ {{y_{m0}} = {D_0}\cos {\beta _0}} \text{。} \end{array}} \right.{\text{}} $

(1)

显然， $\left( {{V_{mx}},{V_{my}},{x_{m0}},{y_{m0}}} \right)$ 也可以唯一地确定目标的运动轨迹。目标运动分析就是分析求解参量 $\left( {D_0}, {K_m},{V_m},{\beta _0} \right)$ 或 $\left({V_{mx}},{V_{my}},{x_{m0}},{y_{m0}} \right)$ 或其子集的过程。而在目标做匀速直线运动已知 ${\beta _0}$ 时，根据 $\left( {{D_0},{K_m},{V_m}} \right)$ 就可以唯一地确定目标运动轨迹。纯方位目标运动分析就是利用方位观测序列 $\left( {{\beta _0},{\beta _1}, \cdots \cdots ,{\beta _i}} \right)$ ， ${t_i}$ 时刻观测平台位置坐标 $\left( {{x_{wi}},{y_{wi}}} \right)$ 等已知量，求解 $\left( {{D_0},{K_m},{V_m}} \right)$ 或 $\left( {{V_{mx}},{V_{my}},{x_{m0}},{y_{m0}}} \right)$ ，从而估计目标运动轨迹的过程。

首先将目标的状态表示为向量： ${{X}}\left( k \right) = $ ${\left[ {{x_m}\;\;{v_x}\;\;{y_m}\;\;{v_y}} \right]^T}$ ，对于纯方位目标运动分析，目标观测量为目标的方位角，可表示为： ${{Z}}\left( k \right) = {\beta _k}$ 。

对于匀速直线运动的目标，系统的状态空间模型可表示为：

${{X}}\left( {k + 1} \right) = {{\varPhi}} {{X}}\left( k \right) + {{\varGamma w}}\left( k \right){\text{，}} $

(2)

${{Z}}\left( k \right) = {{HX}}\left( k \right) + {{v}}\left( k \right){\text{。}} $

(3)

其中： ${{\varPhi}} = \left[ {\begin{array}{*{20}{c}} 1&{{T_0}}&0&0 \\ 0&1&0&0 \\ 0&0&1&{{T_0}} \\ 0&0&0&1 \end{array}} \right]$ 为状态转移矩阵； ${{\varGamma}} = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{T_0}^2/2} \\ {{T_0}} \\ 0 \\ 0 \end{array}}&{\begin{array}{*{20}{c}} 0 \\ 0 \\ {{T_0}^2/2} \\ {{T_0}} \end{array}} \end{array}} \right]$ 为噪声转移矩阵； ${{H}}$ 为观测矩阵，与观测量的选取有关； ${{w}}\left( k \right)$ 是均值为0方差为 ${{Q}}$ 的系统噪声； ${{v}}\left( k \right)$ 为均值为0方差为 ${{R}}$ 的观测噪声。式（2）称为系统的状态方程，式（3）称为系统的观测方程。

当观测量是方位角时，观测方程可以写为：

${{Z}}\left( k \right) = \arctan \frac{{{y_m}\left( k \right) - {y_w}\left( k \right)}}{{{x_m}\left( k \right) - {x_w}\left( k \right)}} + {{v}}\left( k \right){\text{。}} $

(4)

2 卡尔曼估计算法系

观测方程（4）是非线性的，而卡尔曼滤波算法是线性的，应用于纯方位目标运动分析，通常是将其进行各种方式的处理改进，形成非线性滤波方法。但其实这类算法的核心部分是类似的，以传统的卡尔曼滤波算法为例，说明其原理。

卡尔曼系滤波算法通常首先根据式（2）和式（3）构造递推卡尔曼滤波器，过程如下：

1）状态一步预测

$\hat {{X}}\left( {k + 1|k} \right) = {{\varPhi}} \hat {{X}}\left( {k|k} \right){\text{；}} $

(5)

2）状态更新

$ \hat {{X}}\left( {k + 1|k + 1} \right) = \hat {{X}}\left( {k + 1|k} \right) + {{K}}\left( {k + 1} \right){{\varepsilon}} \left( {k + 1} \right){\text{，}} $

(6)

${{\varepsilon}} \left( {k + 1} \right) = {{Z}}\left( {k + 1} \right) - {{H}}\hat {{X}}\left( {k + 1|k} \right){\text{；}} $

(7)

3）滤波增益矩阵

$ {{K}}\left( {k + 1} \right) = {{P}}\left( {k + 1|k} \right){{{H}}}^{\rm{T}}{\left[ {{{HP}}\left( {k + 1|k} \right){{{H}}}^{\rm{T}} + {{R}}} \right]^{ - 1}}{\text{；}} $

(8)

4）一步预测协方差

${{P}}\left( {k + 1|k} \right) = {{\varPhi P}}\left( {k|k} \right){{{\varPhi}} ^{\rm{T}}} + {{\varGamma Q}}{{{\varGamma}} ^{\rm{T}}}{\text{；}} $

(9)

5）协方差阵更新

$ {{P}}\left( {k + 1|k + 1} \right) = \left[ {{{{I}}_n} - {{K}}\left( {k + 1} \right){{H}}} \right]P\left( {k + 1|k} \right){\text{。}} $

(10)

根据以上步骤，可以进行卡尔曼滤波估计。其中， ${{P}}$ 为目标状态的协方差矩阵，其初值为单位矩阵，后续过程中其取值根据式（9）和式（10）预测更新得出。

这是一个递推的滤波过程，其中 $\hat {{X}}\left( {0|0} \right)$ 的选择成为关键，它对于滤波的结果有非常重要的影响。

3 基于逆向平滑的初值优化

由于卡尔曼滤波算法的递推性质，导致其对滤波初值的选取十分敏感，后段滤波依赖于前段滤波的结果，因此初值误差的影响长时间地存在于滤波过程中。本文提出一种初值的优化方法，通过卡尔曼滤波的逆向递推，对滤波初值进行重新估计，降低初始的估计误差，从而提高整个滤波过程的精度。

3.1 逆向平滑

式（5）~式（10）描述了一般的正向卡尔曼滤波类方法的基本过程，作为递推类的滤波，这一过程是可以进行逆向递推的，其原理如下：

将式（2）展开，有

$\left\{ {\begin{array}{l} {{x_m}\left( {k + 1} \right) = {x_m}\left( k \right) + {T_0}{v_x}\left( k \right) + \frac{{{T_0}^2}}{2} \cdot {w_x}}\text{，} \\ {{v_x}\left( {k + 1} \right) = {v_x}\left( k \right) + {T_0}{w_x}} \text{，}\\ {{y_m}\left( {k + 1} \right) = {y_m}\left( k \right) + {T_0}{v_y}\left( k \right) + \frac{{{T_0}^2}}{2} \cdot {w_y}} \text{，}\\ {{v_y}\left( {k + 1} \right) = {v_y}\left( k \right) + {T_0}{w_y}} \text{，} \end{array}} \right.{\text{}} $

(11)

对于匀速直线运动目标，可以认为目标速度不变，即

${v_x}\left( {k + 1} \right) = {v_x}\left( k \right){\text{，}} $

(12)

将式（11）中等号左右移动，并将式（12）代入整理得：

$ \left\{ {\begin{array}{*{20}{l}} {{x_m}\left( {k + 1} \right) - {T_0}{v_x}\left( {k + 1} \right) - \frac{{{T_0}^2}}{2} \cdot {w_x} = {x_m}\left( k \right)} \text{，}\\ {{v_x}\left( {k + 1} \right) - {T_0}{w_x} = {v_x}\left( k \right)} \text{，}\\ {{y_m}\left( {k + 1} \right) - {T_0}{v_y}\left( {k + 1} \right) - \frac{{{T_0}^2}}{2} \cdot {w_y} = {y_m}\left( k \right)}\text{，} \\ {{v_y}\left( {k + 1} \right) - {T_0}{w_y} = {v_y}\left( k \right)} \text{，} \end{array}} \right.{\text{}} $

(13)

可将方程组（13）用矩阵表示为：

${{\varPsi X}}\left( {k + 1} \right) - {{\varGamma w}}\left( k \right) = {{X}}\left( k \right){\text{。}} $

(14)

其中：

${{\varPsi}} = \left[ {\begin{array}{*{20}{c}}1&{{\rm{ - }}{T_0}}&0&0\\{0}&{1}&{0}&{0}\\{0}&{0}&{1}&{{\rm{ - }}{T_0}}\\{0}&{0}&{0}&{1}\end{array}} \right],{{\varGamma}} = \left[ {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{{T_0}^2/2}\\{{T_0}}\\0\\0\end{array}}&{\begin{array}{*{20}{c}}0\\0\\{{T_0}^2/2}\\{{T_0}}\end{array}}\end{array}} \right]$ 。

将式（14）与式（3）组合，可构造出一组新的状态空间模型。此空间模型同样适用于卡尔曼滤波方法，将这组新的状态空间模型运用到卡尔曼滤波的递推过程中，可以实现从 $k + 1$ 时刻向 $k$ 时刻逆向递推，过程如下：

1）状态一步逆向预测

$\hat {{X}}\left( {k|k + 1} \right) = {{\varPsi}} \hat {{X}}\left( {k + 1|k + 1} \right){\text{；}} $

(15)

2）状态逆向更新

$\hat {{X}}\left( {k|k} \right) = \hat {{X}}\left( {k|k + 1} \right) + {{K}}\left( k \right){{\varepsilon}} \left( k \right){\text{，}} $

(16)

${{\varepsilon}} \left( k \right) = {{Z}}\left( k \right) - {{H}}\hat {{X}}\left( {k|k + 1} \right){\text{；}} $

(17)

3）滤波增益矩阵

$ {{K}}\left( k \right) = {{P}}\left( {k|k + 1} \right){{{H}}}^{\rm{T}}{\left[ {{{HP}}\left( {k|k + 1} \right){{{H}}}^{\rm{T}} + {{R}}} \right]^{ - 1}}{\text{；}} $

(18)

4）一步逆向预测协方差

$ {{P}}\left( {k|k + 1} \right) = {{\varPsi P}}\left( {k + 1|k + 1} \right){{{\varPsi}} }^{\rm{T}} + {{\varGamma Q}}{{{\varGamma}} ^{\rm{T}}}{\text{；}} $

(19)

5）协方差阵逆向更新

${{P}}\left( {k|k} \right) = \left[ {{{{I}}_n} - {{K}}\left( k \right){{H}}} \right]{{P}}\left( {k|k + 1} \right){\text{。}} $

(20)

将通过状态的逆向更新得到的目标状态估计值记为 $\hat {{X}}'\left( k \right)$ 。完成式（15）～式（20）后，重复式（15）～式（20）可以实现一次继续向第 $k– 1$ 时刻的更新，称这种更新为逆向更新或逆向平滑。从 $k$ 时刻的目标状态 $\hat {{X}}\left( k \right)$ 开始，通过 $l$ 次逆向更新，可以得到逆向目标状态估计值 $\left( {\hat {{X}}'\left( {k - 1} \right),\hat {{X}}'\left( {k - 2} \right), \cdots ,\hat {{X}}'\left( {k - l} \right)} \right)$ 。

由于这种逆向平滑的估计值是通过正向的卡尔曼滤波得到的估计值 $\left( {\hat {{X}}\left( 0 \right),\hat {{X}}\left( 1 \right), \cdots ,\hat {{X}}\left( k \right)} \right)$ 再次经过逆向卡尔曼滤波得到的，增加了观测数据的正反向运用，减少了估计的误差。

3.2 初值优化

针对卡尔曼滤波方法对目标状态初始值 $\hat {{X}}\left( 0 \right)$ 的选取十分敏感的问题，将上述逆向平滑滤波运用到对初值的优化中，步骤如下：

1）根据目标状态初始值 $\hat {{X}}\left( 0 \right)$ 和观测值 ${{Z}}\left( 0 \right)$ 进行一次卡尔曼滤波，代入式（5）～式（10）中递推得到 $\hat {{X}}\left( 1 \right)$ ，并更新协方差矩阵为 ${{P}}\left( 1 \right)$ ；

2）根据观测值 ${{Z}}\left( 1 \right)$ ，以及上一步递推得到的 $\hat {{X}}\left( 1 \right)$ 和 ${{P}}\left( 1 \right)$ 代入式（5）～式（10）中，进行新的预测和更新，得到 $\hat {{X}}\left( 2 \right)$ 和 ${{P}}\left( 2 \right)$ 。以此方式继续进行 $m$ 次递推，得到 $\hat {{X}}\left( m \right)$ 和 ${{P}}\left( m \right)$ ；

3）将 $\hat {{X}}\left( m \right)$ 和观测值 ${{Z}}\left( m \right)$ 代入式（15）～式（20）中，进行逆向卡尔曼滤波， $m$ 次递推和更新后得到 $\hat {{X}}'\left( 0 \right)$ ；

4）将逆向更新得到的 $\hat {{X}}'\left( 0 \right)$ 替换 $\hat {{X}}\left( 0 \right)$ ，重新进行卡尔曼滤波，得到新的目标状态估计值 $\left( {\hat {{X}}''\left( 0 \right),\hat {{X}}''\left( 1 \right), \cdots \hat {{X}}''\left( m \right),\hat {{X}}''\left( {m + 1} \right),\hat {{X}}''\left( {m + 2} \right), \cdots } \right)$ 。

对于无迹卡尔曼滤波、扩展卡尔曼滤波及各种改进的卡尔曼滤波方法而言，虽然各方法的具体步骤不同，但由于各种算法的核心部分都是基于卡尔曼滤波的，因此上述初值优化过程也同样适用于其他的卡尔曼系的滤波方法。

新的目标状态估计值是由初值 $\hat {{X}}'\left( 0 \right)$ 替换 $\hat {{X}}\left( 0 \right)$ 后进行滤波得到的，由于 $\hat {{X}}'\left( 0 \right)$ 经过正反向2次滤波，减少了估计误差，提升了初始值的估计精度。由于初值的误差带来的影响在整个滤波过程中均存在，同样初值的优化对于整个滤波过程都会有作用。

4 仿真试验

为了验证所提出的基于逆向平滑的初值优化方法对纯方位目标跟踪轨迹的改善性能，选用无迹卡尔曼滤波和扩展卡尔曼滤波两大经典的卡尔曼系滤波方法进行试验，分别用2种方法进行基于逆向平滑的初值优化，验证使用所提方法优化初值后对整个跟踪结果的改善效果。

4.1 仿真条件

根据快速目标短时跟踪的背景需要，设置目标和观测站运动轨迹如下：目标做匀速直线运动，初始位置坐标为（100 m，–400 m）；目标运动速度为50 kn，航向为–41°，即直角坐标系下目标的初始速度为（−30，40）kn，换算单位后为（–15.42，20.56）m/s，目标真实的状态向量为（100，–15.42，–400，20.56）。观测站的初始位置（0 m，0 m），以45 kn的速度向−36°方向匀速直线运动50 s，而后向–63°方向继续以45 kn速度匀速直线运动100 s。针对目标运动速度快、观测时间较短的问题，设置观测站方位估计频率为10 Hz。设置各项误差条件如下：

1）仿真条件1

观测站方位估计误差的标准差为2°，初始距离估计误差为10%，初始速度矢量估计误差为10%。设置此仿真条件为基础仿真条件，其他仿真条件在此基础上对比。

2）仿真条件2

在条件1的基础上，增加目标方位估计误差的标准差为8°，其他条件不变。

3）仿真条件3

在条件1的基础上，增加初始距离估计误差为20%，其他条件不变。

4）仿真条件4

在条件1的基础上，增加初始速度矢量估计误差为20%，其他条件不变。

4.2 无迹卡尔曼仿真结果对比

在仿真条件1下，分别采用无迹卡尔曼滤波和基于逆向平滑的初值优化的无迹卡尔曼滤波2种方法，进行200次蒙特卡罗试验，并将200次仿真试验中2种方法的误差进行平均，结果如图2所示。

在图2给出的仿真结果中，进行50个采样点的逆向递推，即步数 $m$ 的取值为50。图2（a）为位置坐标的估计值与位置坐标真实值之间误差，2条曲线分别为无迹卡尔曼滤波初值优化前后的误差比较；图2（b）为优化前后速度标量估计值与真实值之间的误差比较；图2（c）展示的是目标航向的估计值与真实目标航向间的误差，在初值优化前后的比较；图2（d）为目标距离估计值与真实值间的误差在初值优化前后的比较。可以看出，对于无迹卡尔曼滤波，经过初值优化后，各项误差均有明显降低，并且这种误差的缩小在整个150 s的观测与估计过程中都存在，尤其对于误差峰值的降低效果明显。在对目标各项参数估计中，经过初值优化的方法比普通的无迹卡尔曼滤波对误差峰值处的降低更为明显，这样可以缩小误差的范围。

为了对比不同仿真条件下初值优化方法的效果，分别在条件1、条件2、条件3、条件4下进行仿真试验，取200次蒙特卡罗试验的误差进行平均，并将优化前后的平均误差统计如表1所示。

对于分别增大方位估计角度误差标准差、增大初始速度估计误差、增大初始距离估计误差后，本文所提方法对无迹卡尔曼滤波的误差降低依然有效，但误差降低率有所下降。

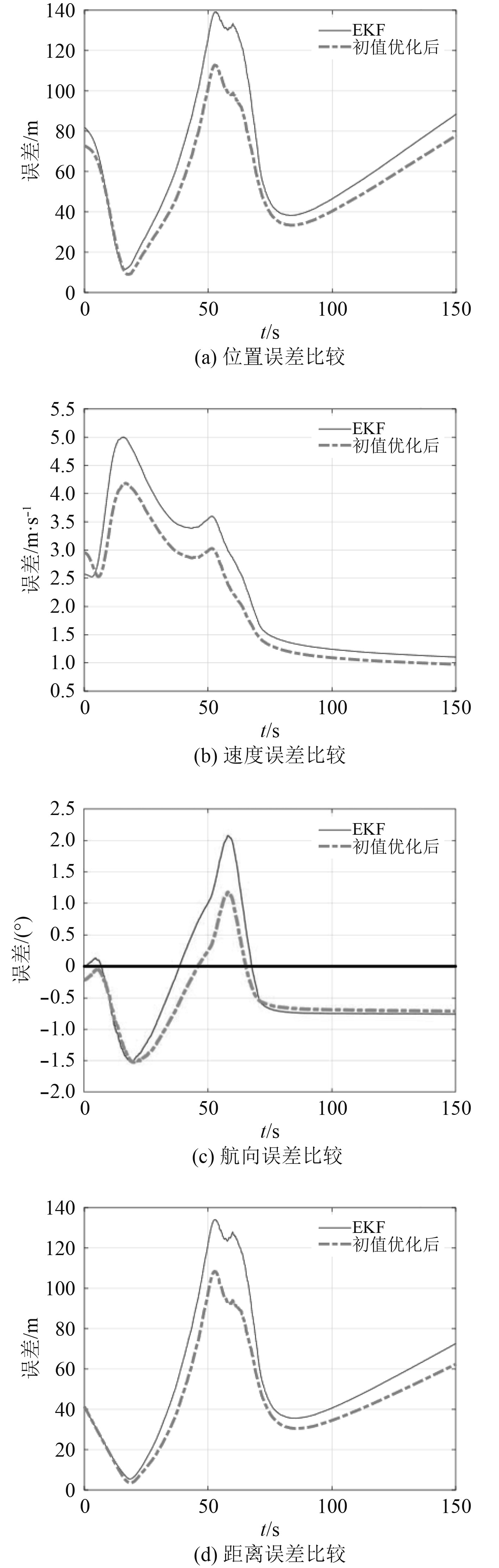
4.3 扩展卡尔曼仿真结果对比

用扩展卡尔曼滤波对比本文所提基于逆向平滑的初值优化的扩展卡尔曼滤波，在给出的仿真条件下分别进行200次蒙特卡罗试验，并将200次仿真结果中2种方法的误差进行平均处理，结果如图3所示。

本次仿真同样进行了50步的逆向递推，即步数 $m$ 的取值为50。图3（a）为2种方法估计的位置坐标与真实位置坐标的误差的比较；图3（b）为2种方法估计速度标量与真实速度标量误差比较；图3（c）为2种方法估计的目标航向与真实目标航向间误差的比较；图3（d）为2种方法估计的目标距离与真实目标距离间误差的比较。对于扩展卡尔曼滤波的各项运动要素估计，经过初值优化后，在几乎整个观测时段内误差均有明显降低，尤其误差峰值的降低更为显著。由于同属卡尔曼系的滤波，扩展卡尔曼滤波与无迹卡尔曼滤波的各项误差基本相似，基于逆向滤波的初值优化方法对于这2种滤波的改善情况也基本相似，都有明显缩小估计误差范围的效果。

分别根据条件1、条件2、条件3、条件4这4组仿真条件进行200次蒙特卡罗试验，统计扩展卡尔曼滤波初值优化前后平均误差，对比结果如表2所示。

由表2可知，在增加方位估计误差标准差、初始速度误差、初始距离误差后，本文所提初值优化方法对扩展卡尔曼滤波的误差降低率下降，但依然有降低误差的效果。

综合表1与表2的结果，本文所提逆向平滑初值优化方法对于无迹卡尔曼滤波和扩展卡尔曼滤波有着相似的效果。对比不同仿真条件下的误差降低率，此优化方法在条件1下有着更高的误差降低率，说明此方法在各项初始误差和方位误差标准差更低、环境条件较好时有更明显的优势。

4.4 逆向滤波步数的影响

对于本文所提的对初值的逆向滤波优化，有一个重要的影响因素即为逆向步数 $m$ 的取值。为了探究所提初值优化方法中逆向滤波步数对误差的影响，在仿真条件1下分别基于无迹卡尔曼滤波和扩展卡尔曼滤波，采用不同步数的逆向滤波对初值进行优化。每种不同的逆向步数优化下，分别进行200次蒙特卡罗试验，每次对目标进行150 s的观测和跟踪，并将150 s内的估计误差求均值。表3为无迹卡尔曼滤波下初值优化前后误差比较，表4为扩展卡尔曼滤波下初值优化前后误差比较。

根据表中数据可以看出，在逆向滤波步数不超过400的时候，经过逆向滤波初值优化的结果具有更低的滤波误差，而逆向滤波步数在450点以上时，未经初值优化的传统滤波方法具有更低的滤波误差。对比不同的运动参数估计，逆向滤波的初值优化对于目标速度和目标距离的估计更加准确，而对于目标航向估计的性能提升相对不明显。对于UKF和EKF，均是在逆向滤波步数为150的时候取得最佳的优化效果，此时对位置坐标估计误差的平均降低率分别达到了65.90%和65.38%。

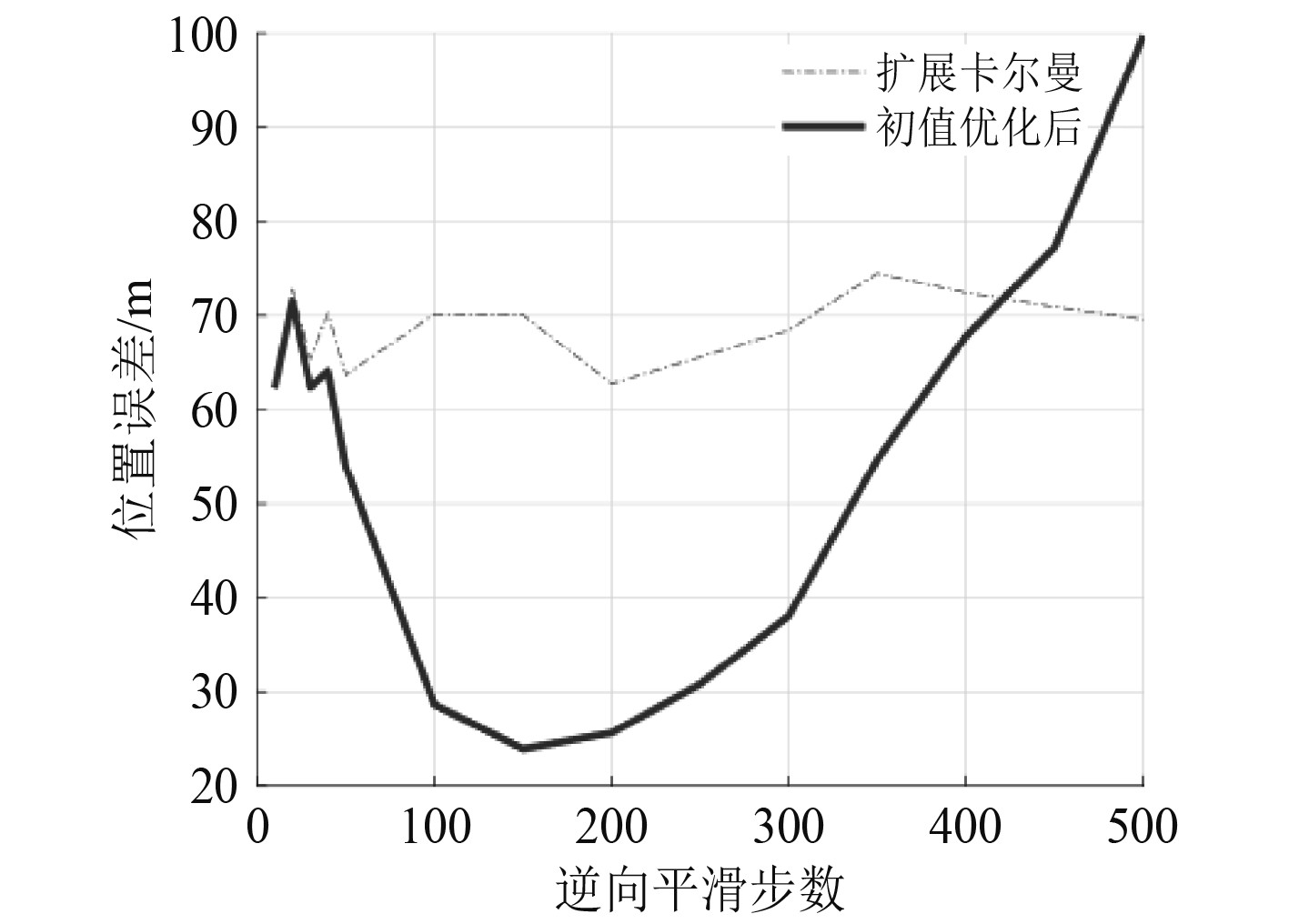
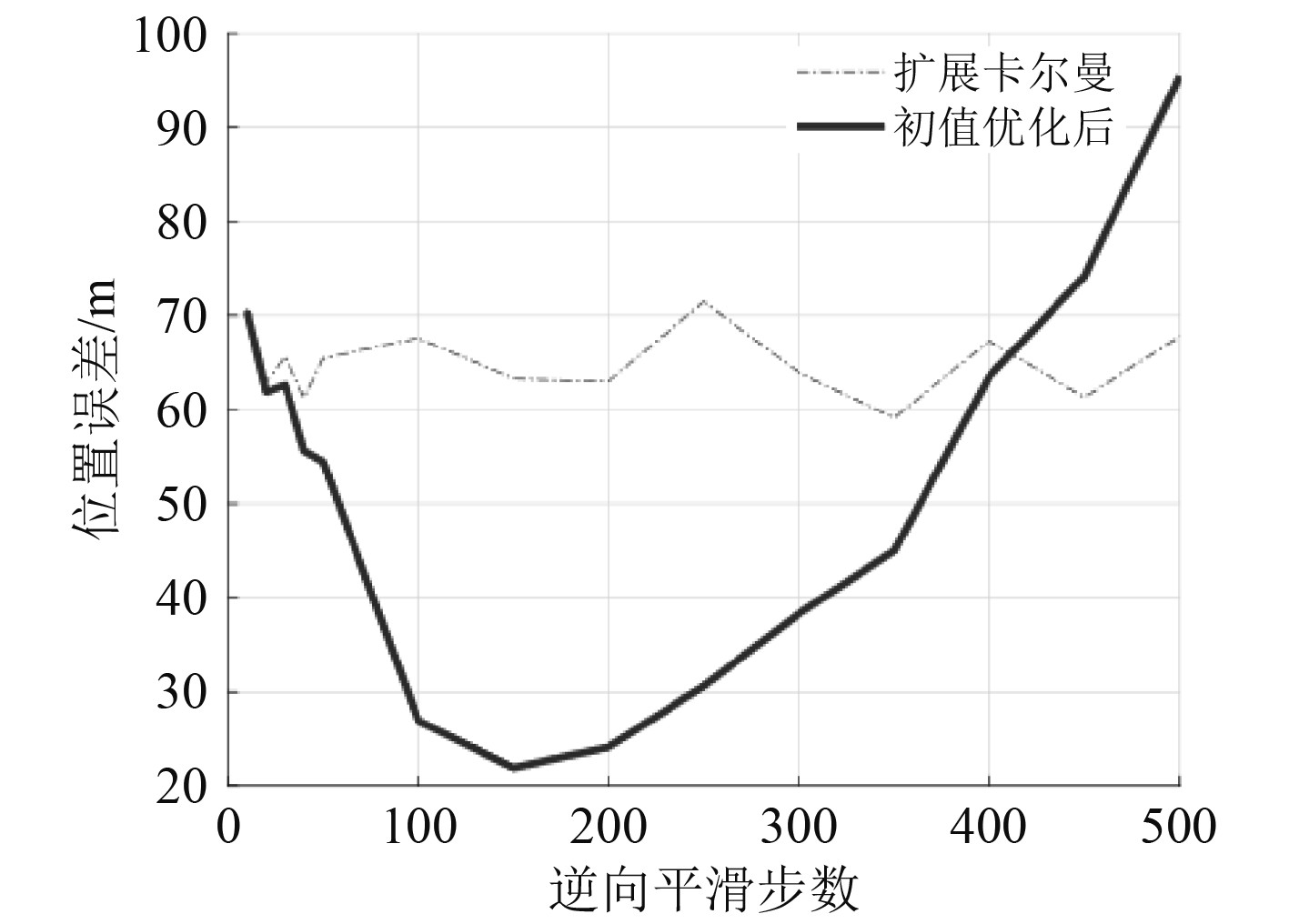
以目标位置坐标的估计为研究对象，比较本文所提的逆向滤波初值优化方法对于UKF和EKF的优化效果，统计不同逆向滤波步数对位置估计误差的影响，结果分别如图4和图5所示。

从图4和图5可以看出，通过改变逆向滤波步数，不论是UKF还是EKF，逆向滤波步数对于优化效果的影响是非线性的。并不是逆向滤波的步数越多优化效果越好，对2种滤波的优化均在逆向滤波步数取值150的时候取得最低的目标位置估计误差，在此之后，随着逆向滤波步数增加估计误差增大，在逆向滤波步数到400点以上，优化后的误差甚至超过原本UKF或EKF的误差，失去了优化的意义。当逆向滤波步数在150点左右时可取得最佳的优化效果，对误差的降低率达到最高。其原因在于在该仿真条件下150点左右正向滤波即观测15 s时估计误差较小，此时估计正向滤波误差取得局部极小值。根据图2（a）和图3（a）所显示的目标位置估计误差，不论对于EKF还是UKF，在观测时刻15 s左右即150点左右时刻，目标位置坐标估计的误差取得极小值，利用此时时段内较小误差的估计值进行逆向滤波，理论上可取得更小的误差，得到初值优化的效果更佳。而滤波误差的极小值点的取得步数或者是滤波收敛的步数是不一定的，它与目标和观测站的运动轨迹有关，因此在不同的场景下的最佳逆向滤波步数是不同的，不具有普适性。

但这并不意味着逆向滤波步数在滤波误差最低时是最佳选择，由于逆向滤波需要取得一定量的观测数据作为先验，更多步数的逆向滤波需要更多的观测数据和观测时长，同时需要更大的计算量。

5 结　语

本文研究背景是基于快速目标短时观测下的目标跟踪，根据仿真结果与比较分析可得，本文所提基于逆向平滑滤波的初值优化方法对于无迹卡尔曼滤波和扩展卡尔曼滤波都有效果，对于目标位置坐标估计误差、目标速度估计误差和目标距离估计误差都有明显的缩小，并且在分别增大方位估计误差标准差、距离初值误差、速度初值误差后，本文所提方法依然有效缩小估计误差。本文所提方法虽然只改变滤波的初值，但在目标跟踪中对于误差的缩小有着长时间的效应。优化的效果和算法的实时性均与逆向平滑的步数有关，在实际应用中，可根据需求选取适合的逆向平滑步数，以满足不同的实际需求。