我国海洋资源非常丰富,各国都在争相发展海洋装备和海洋经济。因此,海洋的开发对于中国的未来发展至关重要[1]。
目标在海洋中受到海洋不均匀性和海底海面反射的影响,这样导致接收到的信号在时域和频域都会产生畸变,使得最终检测能力下降,尤其是对于浅海的目标探测,噪声环境更加复杂、混响也很严重,对探测的影响极其严重。一般的方法是尽可能消除信道的多途效应,但这往往很难办到,而时间反转技术另辟蹊径,其利用声互易性及时反不变性原理,充分利用信道的多途效应,使目标散射回波信号在发射源位置处达到空时聚焦的效果,因此可以达到提高信噪比的目的,进而提高对目标的探测和定位能力。
受光学中相位共扼法的启发,将连续波的相位共扼法拓展到脉冲波的时间反转技术中,并逐渐应用到水声学,用于解决水下探测中遇到的一些问题。1991年,Dowling[2]对时间反转镜(TRM)应用于水声作了定义和基本的理论分析,1996年4月,Kuperman等[3]在美国海军研究机构(Office of Naval Research)的支持下,在地中海进行的时间反转镜浅海试验,证明了海洋中时间反转镜的聚焦效应。
目前国内关于主动时间反转技术探测的文献[4-7]基本都是利用收发合置换能器阵列接收目标散射信号,对其进行时反变换后,再由换能器阵列发射出去,使二次发射信号在目标处形成聚焦,类似于增加对目标照射的强度,因此可以使目标回波增强、进而达到提高探测的效果。这种时间反转技术虽然可以在一定程度上提高回波增益,但是依然不能解决由于多途以及阵元之间时延引起的回波能量扩散、结构复杂的问题,特别是对于探测分辨率要求很高的窄脉冲,这种影响更加严重。另外,通过研究和工程应用实践,时间反转镜的方法也存在缺点,而且应用到工程中也有一定的难度。主要体现在:1)制作收发合置的换能器基阵难度很大,实际操作起来也很复杂;2)驱动时反阵需要采用多通道功放,这使得系统更加复杂,且能耗较大;3)针对时反阵列的信号处理方法很复杂,需要进一步研究和分析。由于时反技术具有反波束形成的特点,本文提出一种改进的时反探测技术,设法让时反后的目标回波信号聚焦在接收阵处。通过这种改进,既可以避开上文中提到的时反技术的缺点,又可以提高增益、改善回波结构。本文对这种主动时反技术进行仿真研究。
1 射线理论模型为了更加深入了解海洋声信道中声波的传播特性,科学家们为此开展了很多研究,并且建立了声波的理论传播模型。一般常用的有射线理论、快速场、多途扩展、抛物线和简正波理论5种声场模型。本文的理论分析基于射线理论展开。
利用射线理论模型,可以十分直观地描述声信号在介质中的传播规律。射线理论模型假设声波由一束声线组成,每一条声线都是垂直于等相位面向外传播。声源发射的声波中不同方向的声线经过不同的传播路径到达接收阵列处,不仅接收信号的幅度会产生不规律的起伏,时延上也会产生拓展,将此现象称为多径效应。
根据射线理论模型,建立声波在水中传播的多径信道模型,水声多径信道的传输响应函数表达式如下:
| $h(t) = \displaystyle\sum\limits_{n = 1}^N {{a_n}\delta (t - {\tau _n})}\text{。} $ |
式中:
声源
| ${f_0}(t) = \displaystyle\sum\limits_j {{a_{0j}}f(t - {t_{0j}})} \text{,}$ |
| ${f_i}(t) = \displaystyle\sum\limits_j {{a_{ij}}{f_0}(t - {t_{ij}})} \text{,}$ |
其中,
将阵元
| ${f_i}(T - t) = \displaystyle\sum\limits_j {{a_{ij}}{f_0}(T - t - {t_{ij}})} \text{。}$ |
阵元
| $\displaystyle\sum\limits_k {\displaystyle\sum\limits_j {{a_{ik}}{a_{ij}}{f_0}(T - {t_{ij}} - (t - {t_{ik}}))} } \text{,}$ |
在目标处的时反信号总和可以表示为:
| $\displaystyle\sum\limits_i {\displaystyle\sum\limits_k {\displaystyle\sum\limits_j {{a_{ik}}{a_{ij}}{f_0}(T - {t_{ij}} - (t - {t_{ik}}))} } }\text{。} $ |
从式(6)可知,当
| $\displaystyle\sum\limits_i {\displaystyle\sum\limits_j {Na_{ij}^2{f_0}} } (T - t)\text{。}$ |
可以看出,经过时反的聚焦后,对目标的照射强度得到了增强,从而可以达到增强目标回波强度的效果。
上述信号经过目标散射后,到达接收阵的信号为:
| ${P_{TR}} = \displaystyle\sum\limits_m {\displaystyle\sum\limits_n {\displaystyle\sum\limits_i {\displaystyle\sum\limits_k {\displaystyle\sum\limits_j {{a_{mn}}{a_{ik}}{a_{ij}} \times } } } } } {f_0}(T\! - \!{t_{ij}}\! -\! (t\! -\! {t_{mn}} - {t_{ik}}))\text{,} $ |
主相干峰的为:
| $\displaystyle\sum\limits_m {\displaystyle\sum\limits_n {\displaystyle\sum\limits_i {\displaystyle\sum\limits_j {N{a_{mn}}a_{ij}^2{f_0}(T - (t - {t_{mn}}))} } } }\text{。} $ |
由式(9)可以知道,因为存在多径信道和阵列时延的影响,导致接收阵列处的回波信号是一个时间展宽的脉冲串,具有复杂的波形结构,且能量不集中,这对目标的检测是很不利的。
1.2 改进主动时反聚焦过程分析对时反聚焦过程进行改进,在散射回波第1次到达接收阵后,将所有阵元的信号相加求和,得到接收阵的回波总信号,然后对其作时反变换,再由各阵元进行发射。
回波信号第一次到达接收阵的信号总和为:
| $\displaystyle\sum\limits_i {\displaystyle\sum\limits_j {\displaystyle\sum\limits_k {{a_{ij}}{a_{0k}}f(t - {t_{ij}} - {t_{0k}})} } } \text{,}$ |
对上述求和后的信号作时反变换后,变换后的信号为:
| $\displaystyle\sum\limits_i {\displaystyle\sum\limits_j {\displaystyle\sum\limits_k {{a_{ij}}{a_{0k}}f(T - t - {t_{ij}} - {t_{0k}})} } }\text{,} $ |
将此信号由各阵元发射,经过信道多径的传播,到达目标处的信号可表示为:
| $\displaystyle\sum\limits_l {\displaystyle\sum\limits_i {\displaystyle\sum\limits_j {\displaystyle\sum\limits_k {{a_{0l}}{a_{ij}}{a_{0k}}f(T - {t_{ij}} - {t_{0k}} - (t - {t_{0l}}))} } } } \text{。}$ |
信号经过目标的二次散射后,第2次到达接收阵时可表示为:
| $ \begin{split} P_{TR}' = &\displaystyle\sum\limits_m {\displaystyle\sum\limits_n {\displaystyle\sum\limits_l {\displaystyle\sum\limits_i {\displaystyle\sum\limits_j {\displaystyle\sum\limits_k {{a_{mn}}{a_{0l}}{a_{ij}}{a_{0k}}} } } } } }\times \\& f(T - {t_{ij}} - {t_{0k}} - (t - {t_{0l}} - {t_{mn}})) \text{。} \end{split} $ |
此信号即为最终的检测信号,当
| $\displaystyle\sum\limits_i {\displaystyle\sum\limits_j {\displaystyle\sum\limits_k {M{N^2}a_{ij}^2a_{0k}^2f(T - t)} } } \text{。}$ |
相反地,如果阵元、路径不同,此时信号在时间上较为分散,不容易相干叠加,信号幅度相对主相干峰小很多,这对检测是很有利的。
1.3 接收信号增益分析传统主动时反聚焦的增益可表示为
| ${P_{TR}} = \displaystyle\sum\limits_m {\displaystyle\sum\limits_n {\displaystyle\sum\limits_i {\displaystyle\sum\limits_k {\displaystyle\sum\limits_j {{f_0}(T - {t_{ij}} - (t - {t_{mn}} - {t_{ik}}))} } } } }\text{,} $ |
在
| $ \begin{split} {P_{TR}} &= \displaystyle\sum\limits_m {\displaystyle\sum\limits_n {\displaystyle\sum\limits_i {\displaystyle\sum\limits_j {N{f_0}(T - (t - {t_{mn}})) } } } } = \\ & \displaystyle\sum\limits_m {\displaystyle\sum\limits_n {M{N^2}{f_0}(T - (t - {t_{mn}}))} }\text{,} \end{split} $ |
| $\begin{array}{l} P_{TR}' = \displaystyle\sum\limits_m {\displaystyle\sum\limits_n {\displaystyle\sum\limits_l {\displaystyle\sum\limits_i {\displaystyle\sum\limits_j {\displaystyle\sum\limits_k {f(T - {t_{ij}} - } } } } } } {t_{0k}} - (t - {t_{0l}} - {t_{mn}})) \text{,} \end{array} $ |
在
| $P_{TR}' = \displaystyle\sum\limits_i {\displaystyle\sum\limits_j {\displaystyle\sum\limits_k {M{N^2}f(T - t) = {M^2}{N^4}f(T - t)} } }\text{。} $ |
对于不同的阵元以及对应的路径,
信号流程:声源第1次发射信号,接收到目标回波后,对其作时反变换后,由发射阵元发射出去,然后接收再次被目标反射的回波。
仿真条件:单阵元,收发合置,阵元和目标距水面和水底的距离都为20 m,阵元和目标的水平距离为50 m,水面反射系数为0.9,水底反射系数为0.8,忽略吸收损失,只考虑直达波和一次反射波,忽略二次以上的声波。发射信号是脉宽为1 ms、频率为10 kHz的CW脉冲波。

|
图 1 发射信号 Fig. 1 Transmitting signal |
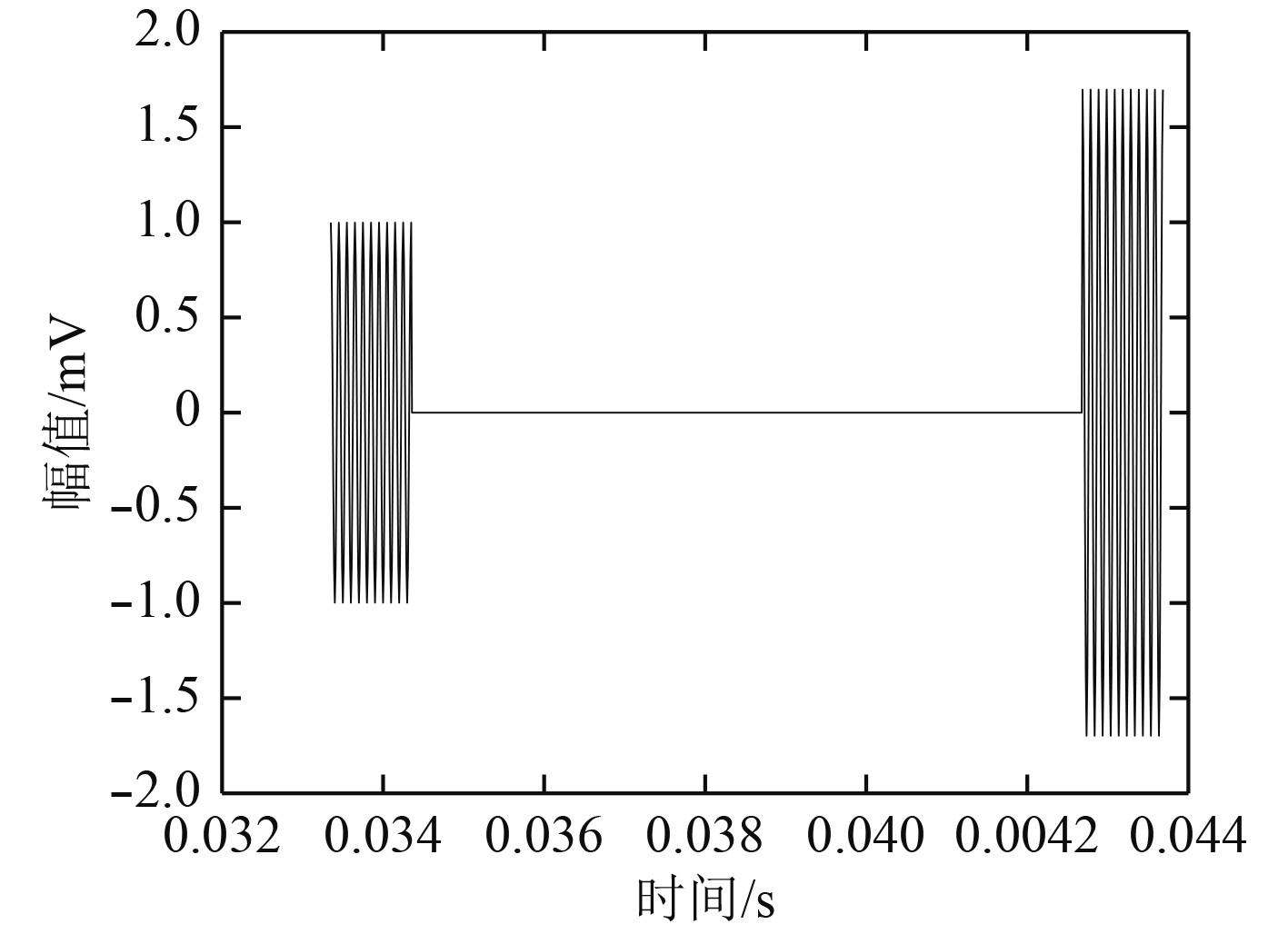
|
图 2 首次到达目标的信号 Fig. 2 First arrival signal |
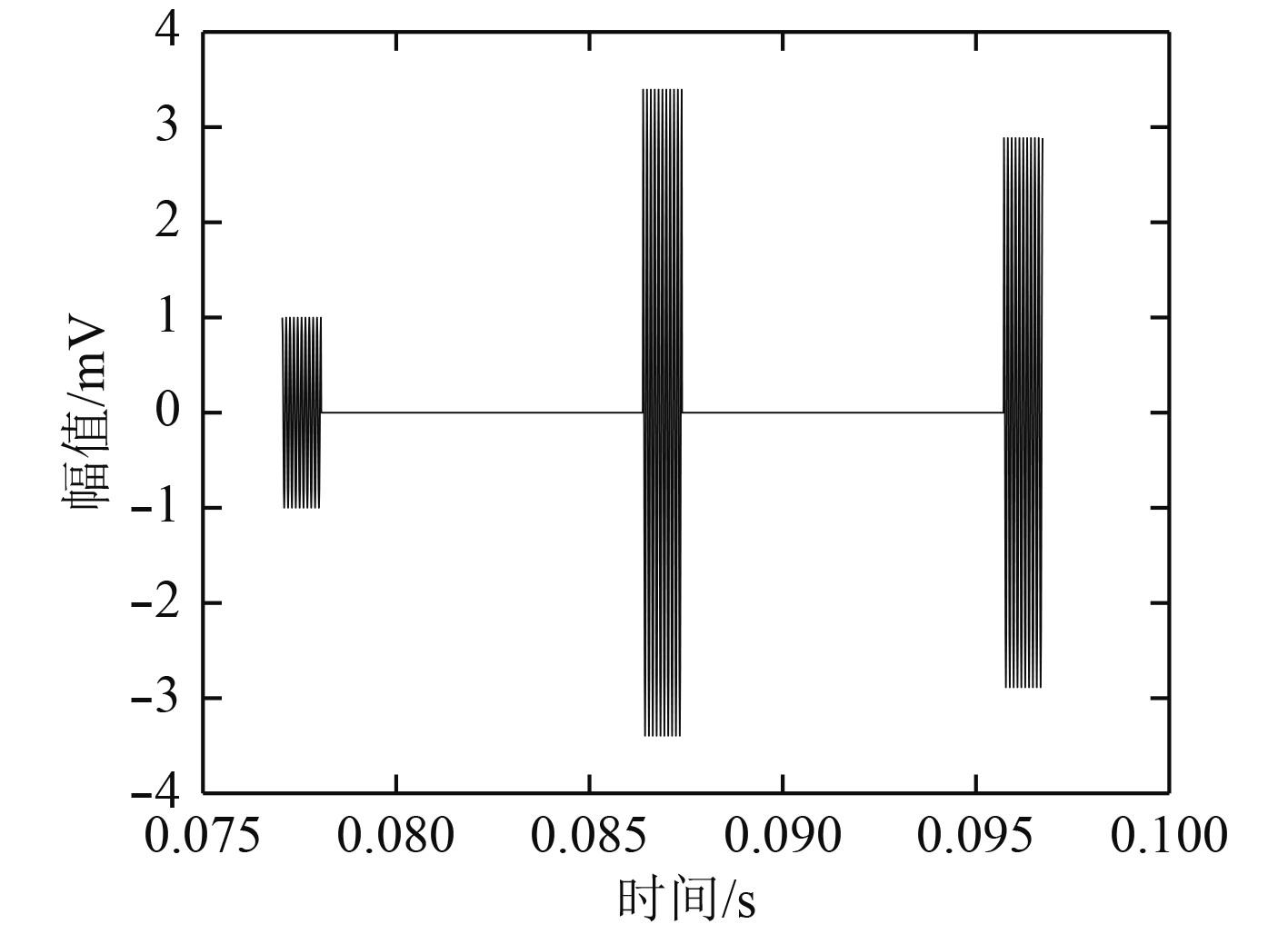
|
图 3 接收阵元首次接收到的回波信号 Fig. 3 The first echo received by the receiving element |
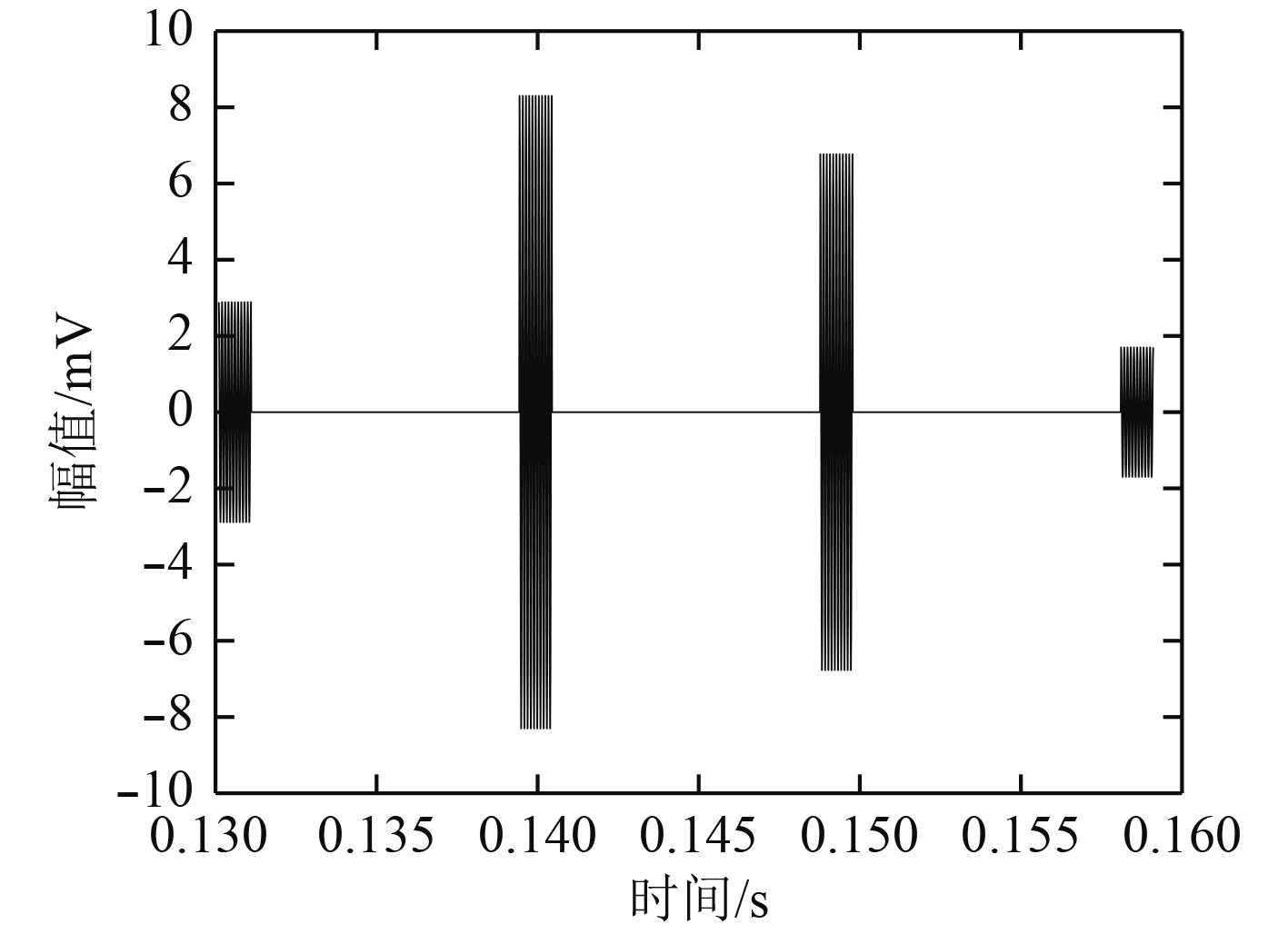
|
图 4 时反发射后到达目标的信号 Fig. 4 The signal that arrives at the target after time reversal |

|
图 5 接收阵元第2次接收到的回波信号 Fig. 5 The second received echo signal of the receiving element |
计算可得,经过时反处理后接收到的回波信号幅度比未经过时反处理的回波信号幅度增加了7.8 dB,说明了时反处理有很好的聚焦效果,但是信号波形结构比原始发射波形要更加复杂,对于信号处理和检测有一定的干扰。
2.2 多阵元主动时反聚焦仿真信号流程:声源第1次发射信号,接收到目标回波后,将各阵元接收到的回波信号同相相加,得到接收阵总回波信号,将其作时反变换后,由发射阵元发射出去,然后接收再次被目标反射的回波。
仿真条件:4阵元等间隔分布,收发合置,阵元间隔为10 m,靠近水面的阵元距离水面10 m,靠近水底的阵元距离水底10 m,目标深度为25 m,接收阵和目标之间的水平距离为50 m,水面和水底的反射系数分别为0.9和0.8,只考虑直达波和一次反射波,忽略2次及以上的反射波。发射信号与单阵元时相同。
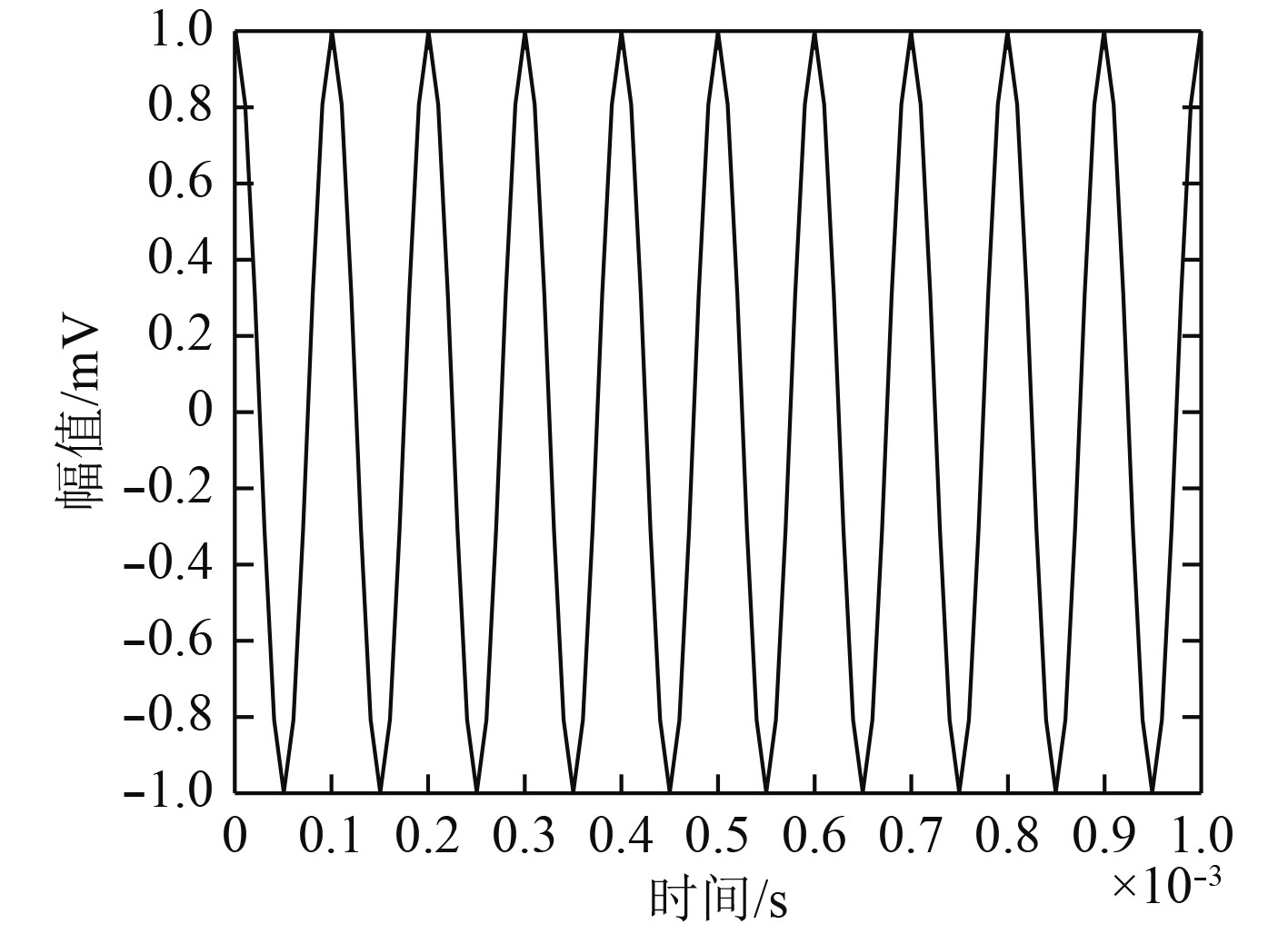
|
图 6 发射信号 Fig. 6 Transmitting signal |
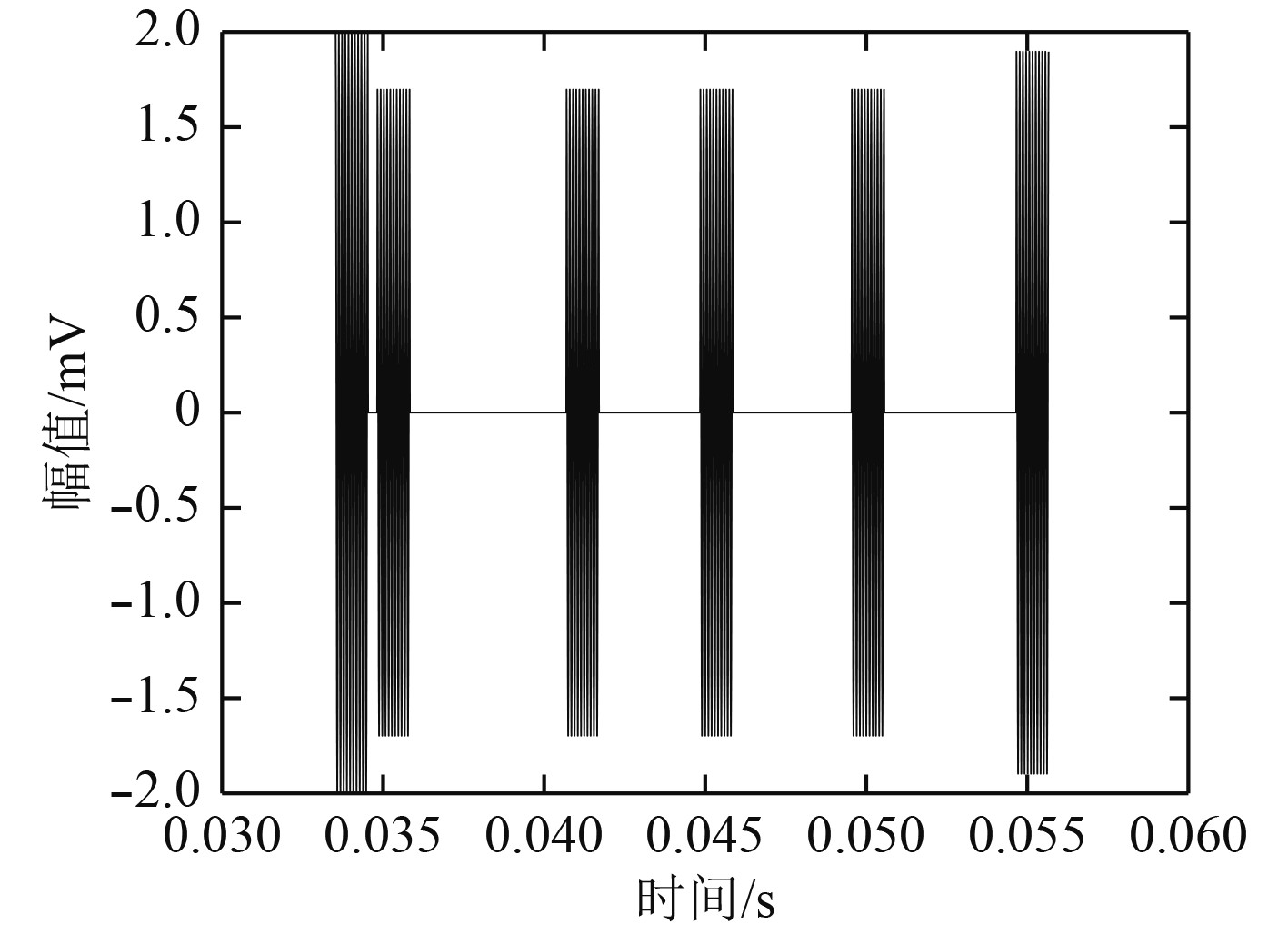
|
图 7 首次到达目标的信号 Fig. 7 First arrival signal |

|
图 8 接收阵各阵元首次接收到的回波信号 Fig. 8 The first echo signal received by the element of receiving array |
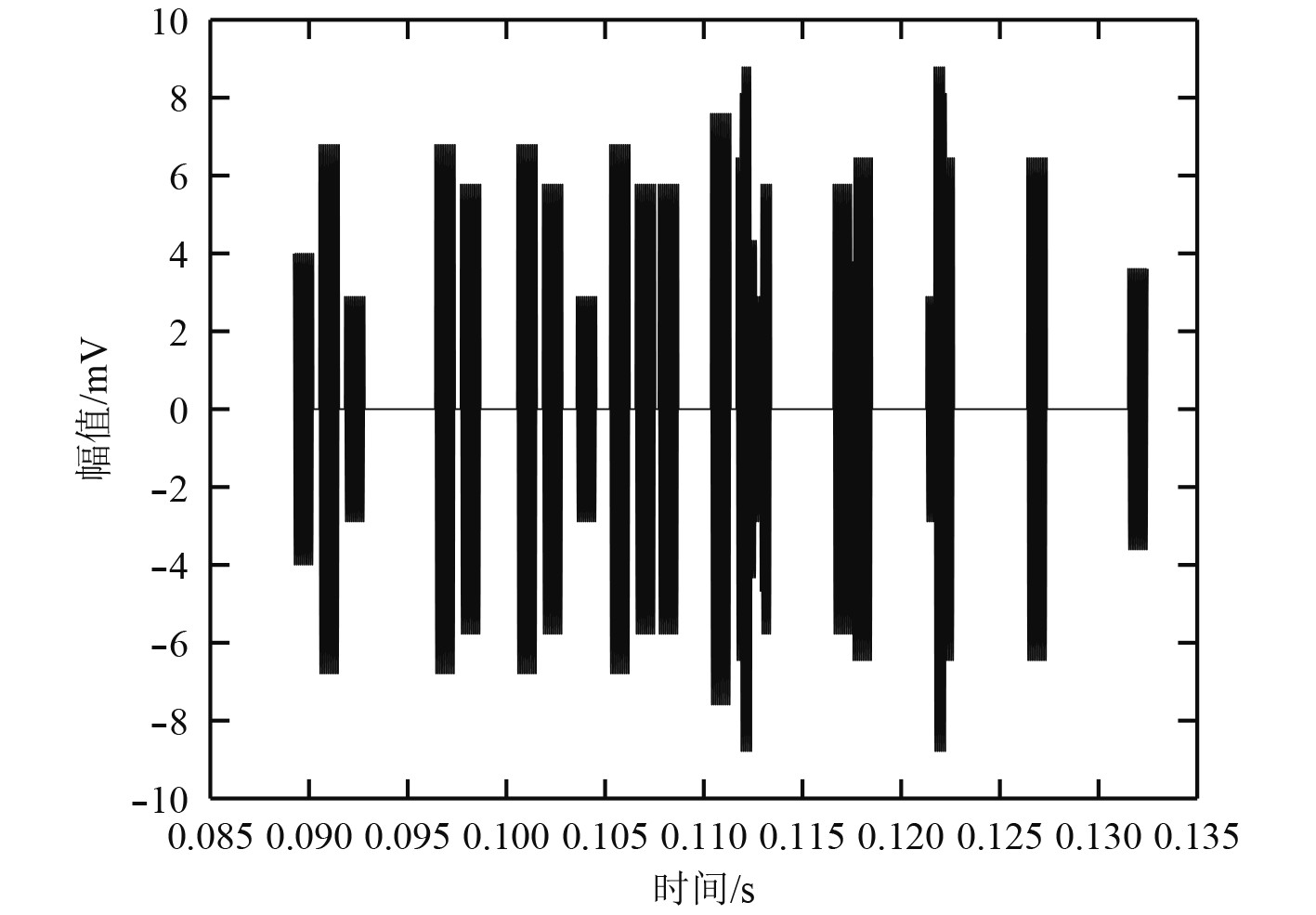
|
图 9 接收阵首次接收到的回波总信号 Fig. 9 The sum of the first echo signals by the receiving array |
在各阵元第1次接收到目标的散射回波后,将其时反再发射(按照先到后发的顺序),这样信号可以在目标处形成聚焦,图10即为信号在目标处聚焦:
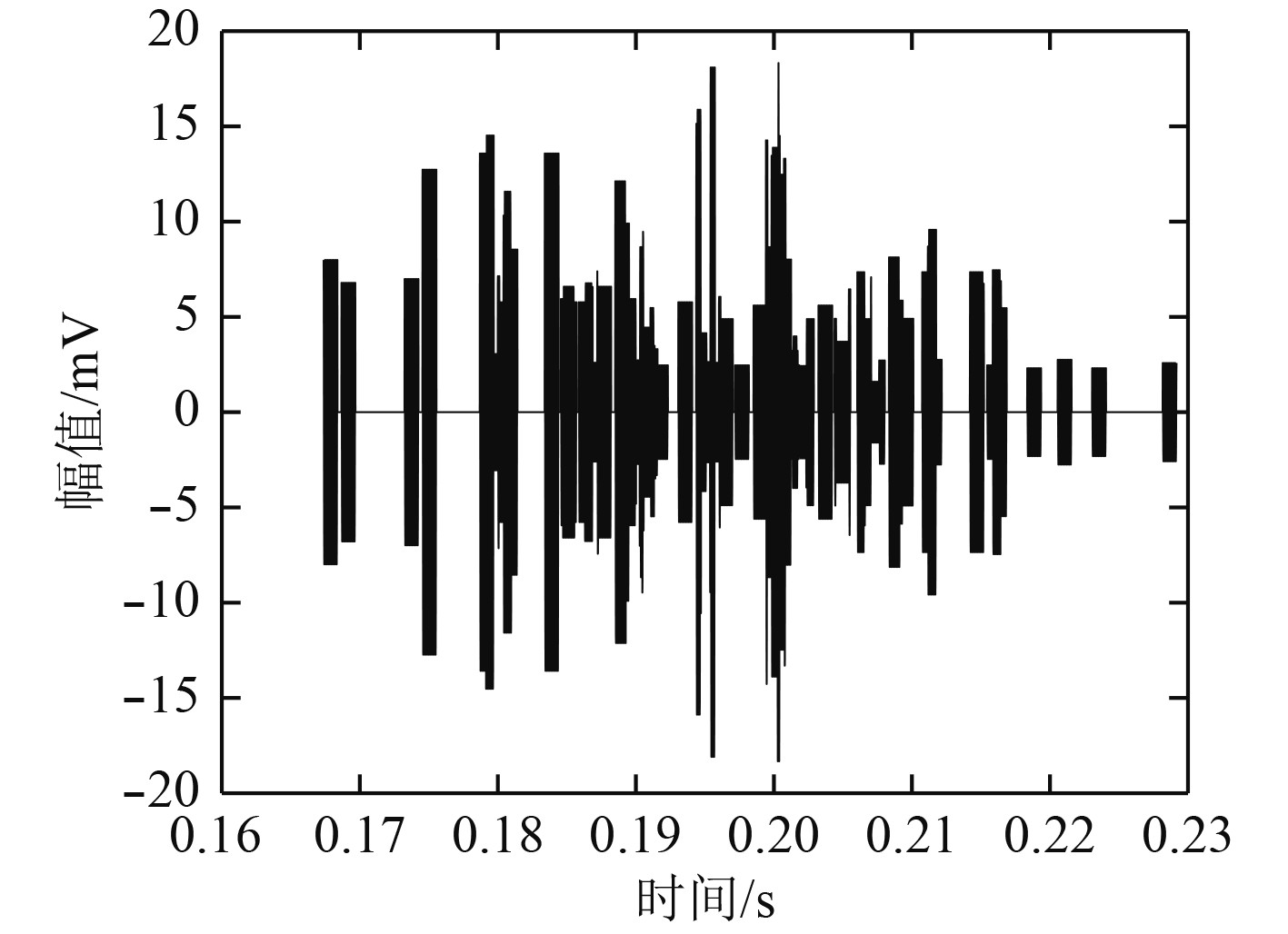
|
图 10 第2次到达目标的信号 Fig. 10 The second signal to target |
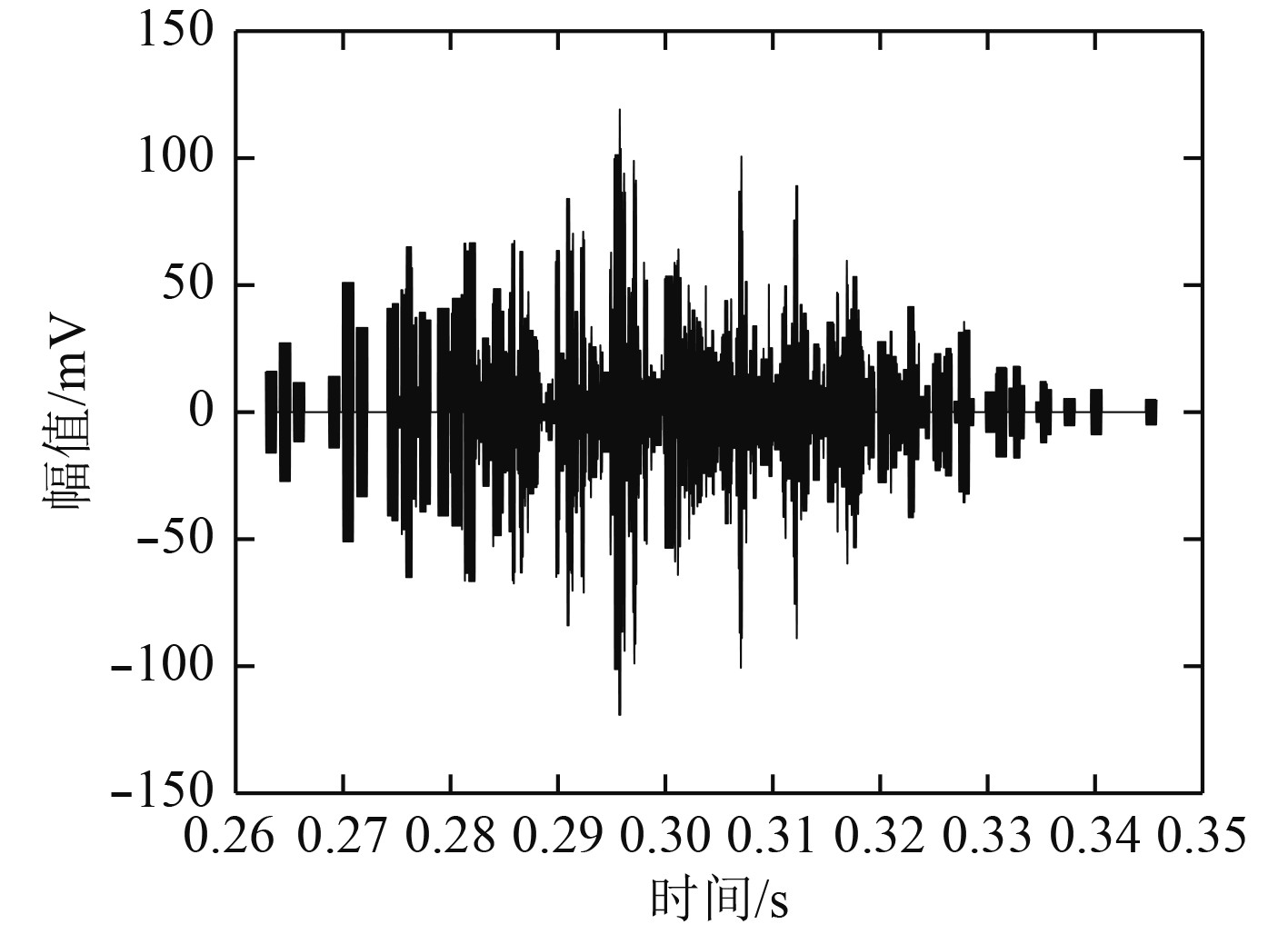
|
图 11 接收阵第2次接收到的回波总信号 Fig. 11 The sum of the second echo signals by the receiving array |
计算可得,处理后得到的检测信号幅度比未经过时反处理的信号幅度增加了12.4 dB,但是信号波形结构相较于原始波形复杂得多,对于信号处理和检测难度也很大。
另一种改进的处理方法,将接收阵各阵元首次接收的回波信号同相相加,得到回波总信号,作时反变换后再将其发射出去,这样第2次发射的信号不会在目标处形成聚焦,而是被目标反射后在接收阵处形成聚焦,进一步提高接收信号幅度。
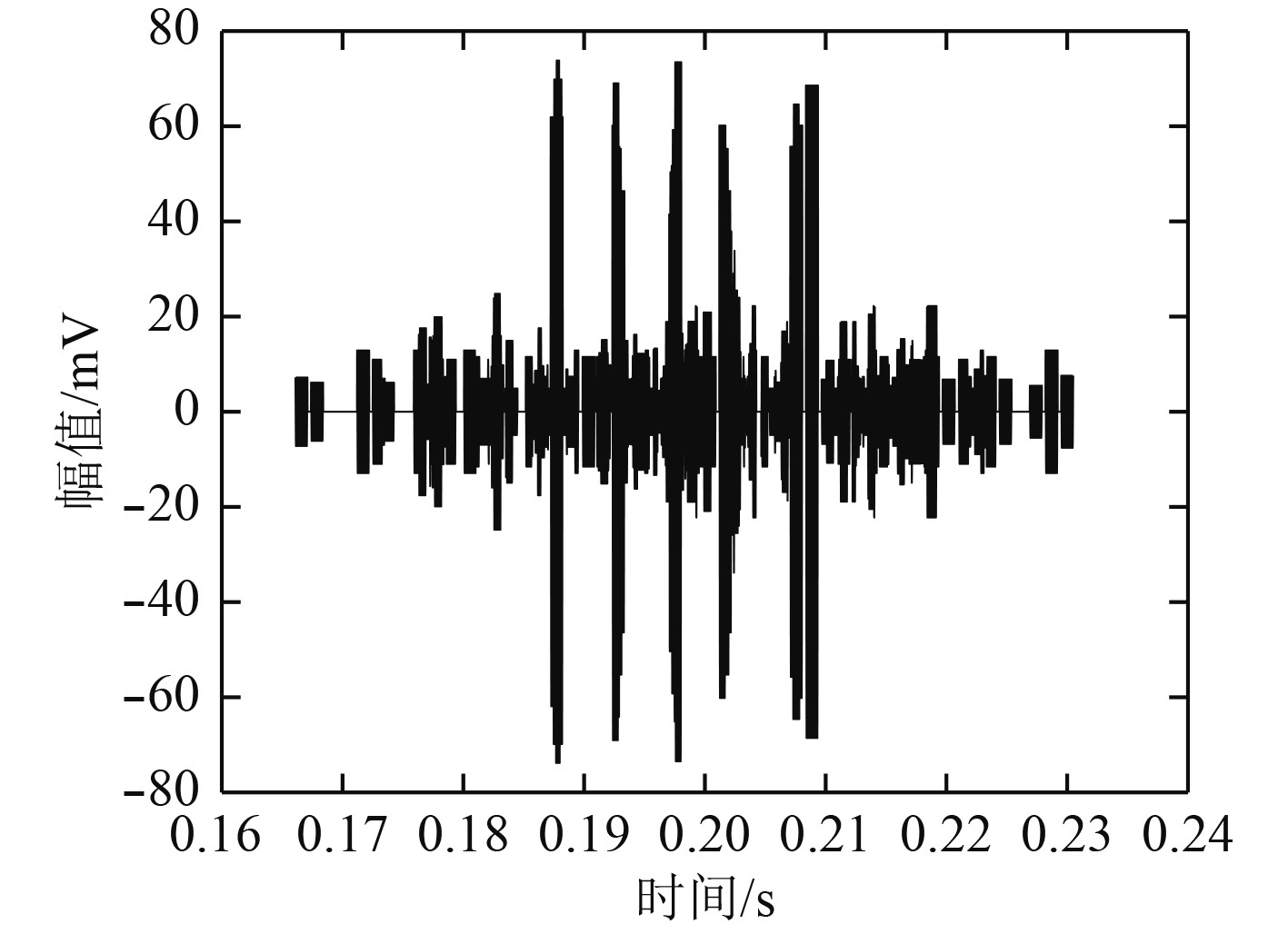
|
图 12 时反处理再发射后到达目标的信号 Fig. 12 Time reverse processing and re-transmitting signals to the target |
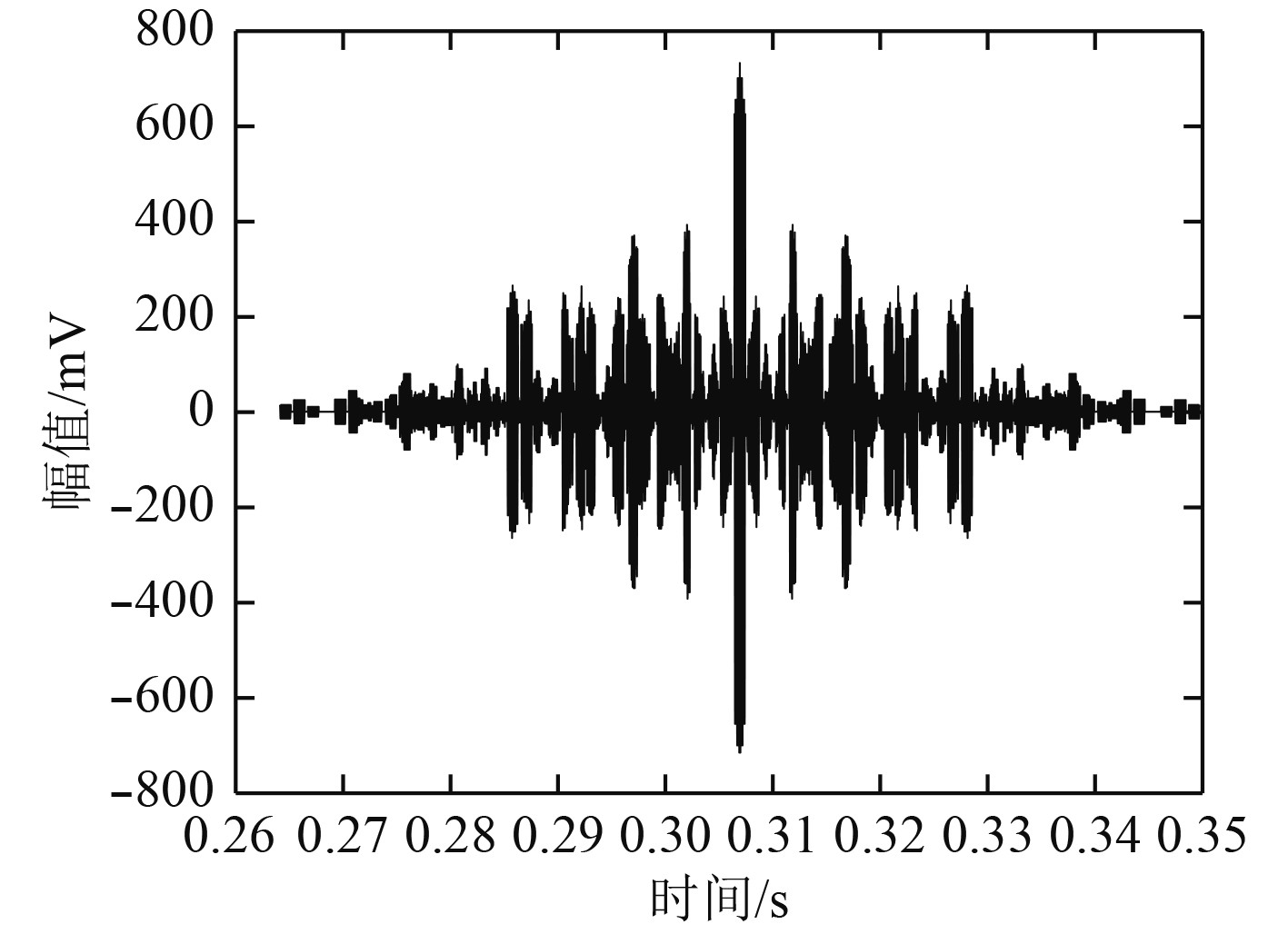
|
图 13 时反处理再发射后接收阵第2次接收到的回波总信号 Fig. 13 The sum of the second echo signals by the receiving array |
从仿真结果计算可得,时反处理再发射后接收到的回波信号幅度比未经时反处理的回波增加了19 dB,而且信号波形结构相比传统时反更加简单明了,能够克服时间反转的不足,说明时反技术对于提高主动声呐的声聚焦有很好的效果。而且接收信号的波形对于后续检测处理有很大的好处。
3 结 语本文对时间反转技术进行理论分析和仿真研究,通过对传统时反技术的改进,可以使目标回波信号在接收处形成聚焦。从仿真结果可以看出,改进后的主动时反探测接收自聚焦技术不仅比传统的时反技术能得到更高的回波增益,而且还能够克服传统时反技术中多径效应和阵列时延造成的信号时间展宽和信号波形结构复杂的缺点,可以降低信号处理和目标检测的难度,一定程度上降低工程应用的难度,具有实际应用价值。
| [1] |
刘小明. 扎实推进海洋强国建设[N]. 人民日报, 2013-08-07: 7.
|
| [2] |
JACKSON D R, DOWLING D R. Phase conjugation in underwater aCOUS—tic[J]. J Acoust Soc Am, 1991, 89(3): 171-181. |
| [3] |
KUPERMAN W A, HODGKISS W S, SONG H C, et a1. Phase co.jugation in the ocean:Experimental demonstration of an acoustic time-levemal mirror[J]. J Acoust Soc Am, 1998, 103(1): 25-40. DOI:10.1121/1.423233 |
| [4] |
阎丽明, 李建龙, 潘翔, 等. 时间反转处理用于掩埋目标探测[J]. 声学学报, 2008, 33(6): 542-547. DOI:10.3321/j.issn:0371-0025.2008.06.009 |
| [5] |
孙琳, 李海森, 陈宝伟, 等. 时反法用于主动的研究与仿真[J]. 系统仿真学报, 2008, 20(1): 2529-2532. |
| [6] |
汪素萍, 宫先仪, 杜栓平. 主动时间反转聚焦技术[J]. 声学与电子工程, 2005, 79(3): 12-14. |
| [7] |
潘翔. 基于时问反转处理的水声信号增强研究[J]. 传感技术学报, 2006, 19(3): 848-850. |
 2020, Vol. 42
2020, Vol. 42

