2. 中国船舶集团公司第七一〇研究所,湖北 宜昌 443000
2. The 710 Research Institute of CSSC, Yichang 443000, China
潜艇管系布局是在有障碍物的潜艇空间里,按照相应管路布管的约束条件,找到一条连接起点与终点并避开障碍物的可行布管路径的过程。管系自动布局的实现主要包括环境建模和路径生成两部分,其中环境建模是将待布管空间映射到抽象模型空间,利用数学语言和方法进行表达以方便计算机规划算法进行处理。因此,环境建模是进行有效管系布局的基础,合理的环境建模对后续布局结果有重要的影响。
管系布局的环境建模方法主要有包括C空间法、自由空间法、Voronoi图法、拓扑图法等在内的图形学方法[1]和以栅格法为代表的单元分解法[2]。图形学方法利用点、线、面等生成具有空间邻接关系和拓扑意义的图,大多适用于障碍物较少、有效布局空间较大的二维空间。以栅格法为代表的单元分解法通用性较强,可以很好地与遗传算法等智能算法相结合,简单且易于实现,是管系布局领域应用最多的一种环境建模方法,但当布管空间较大时,栅格粒度和计算效率的矛盾是尚待解决的一个问题。栅格法作为机器人路径规划和管系布局领域的典型建模方法,受到了很多学者的关注。王伟峰等[3]在传统栅格法中融入单元遍历的思想,提高了栅格法的精确度,但计算量有所增加;韩忠华[4]针对无人机路径规划提出一种高度降维的三维环境建模方法,这种方法兼顾了环境模型的精度要求和规划算法的处理效率;刘晓磊等[5]将栅格法应用于非结构化环境中的机器人路径规划,验证了栅格法对复杂环境的适应性。
为了解决潜艇空间内主干管系的自动布局问题,本文研究一种基于栅格法的潜艇空间管系布局建模方法,该方法综合考虑布管约束以及布局算法的计算效率,有利于路径生成阶段产生好的布管结果。
1 基于栅格法的潜艇空间管系布局建模方法基于栅格法的潜艇空间管系布局建模方法的主要步骤如下:
1)建立布管坐标系,将三维潜艇空间转化为二维潜艇内舱平面;
2)使用基于Sting聚类算法的自适应栅格法处理潜艇内舱平面,生成待布管空间;
3)引入可通行性度量函数表征栅格的可通行性属性,方便利用布管算法生成布管结果。主要思路如图1所示。
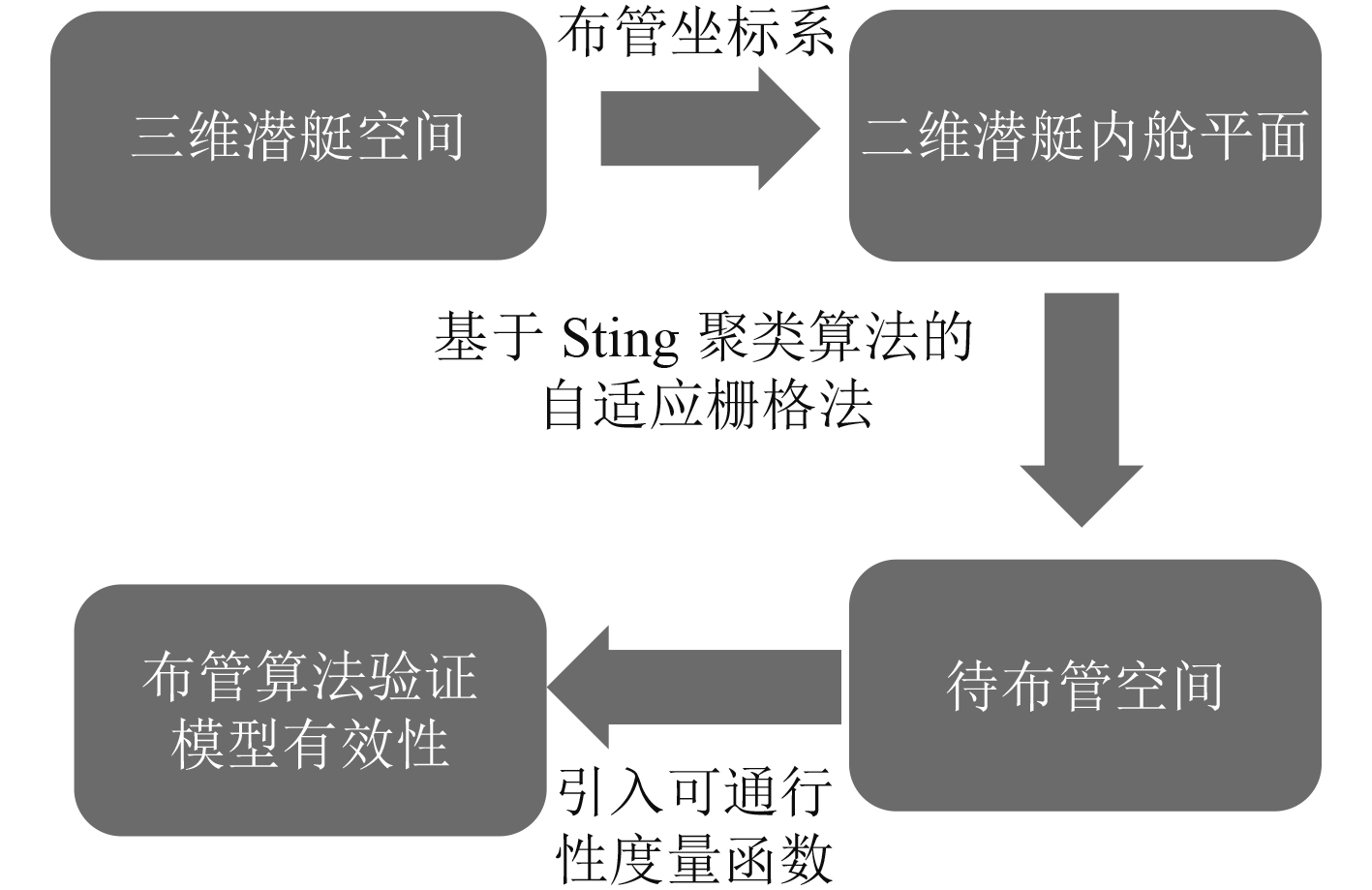
|
图 1 基于栅格法的潜艇空间管系布局建模方法 Fig. 1 A grid-based environment modeling method for piping layout of submarine |
潜艇固壳为由圆柱和圆台拼接而成的不规则体,若在三维空间内做栅格分割(见图2),栅格数量较多,会对管系布局算法的计算效率和准确度产生影响,同时,艇体附近的栅格大多由于圆弧艇体的影响大多不是规则的立方体网格形状,而潜艇管系大多沿舱壁分布。为了减少三维空间内的栅格分割误差,将三维潜艇空间(
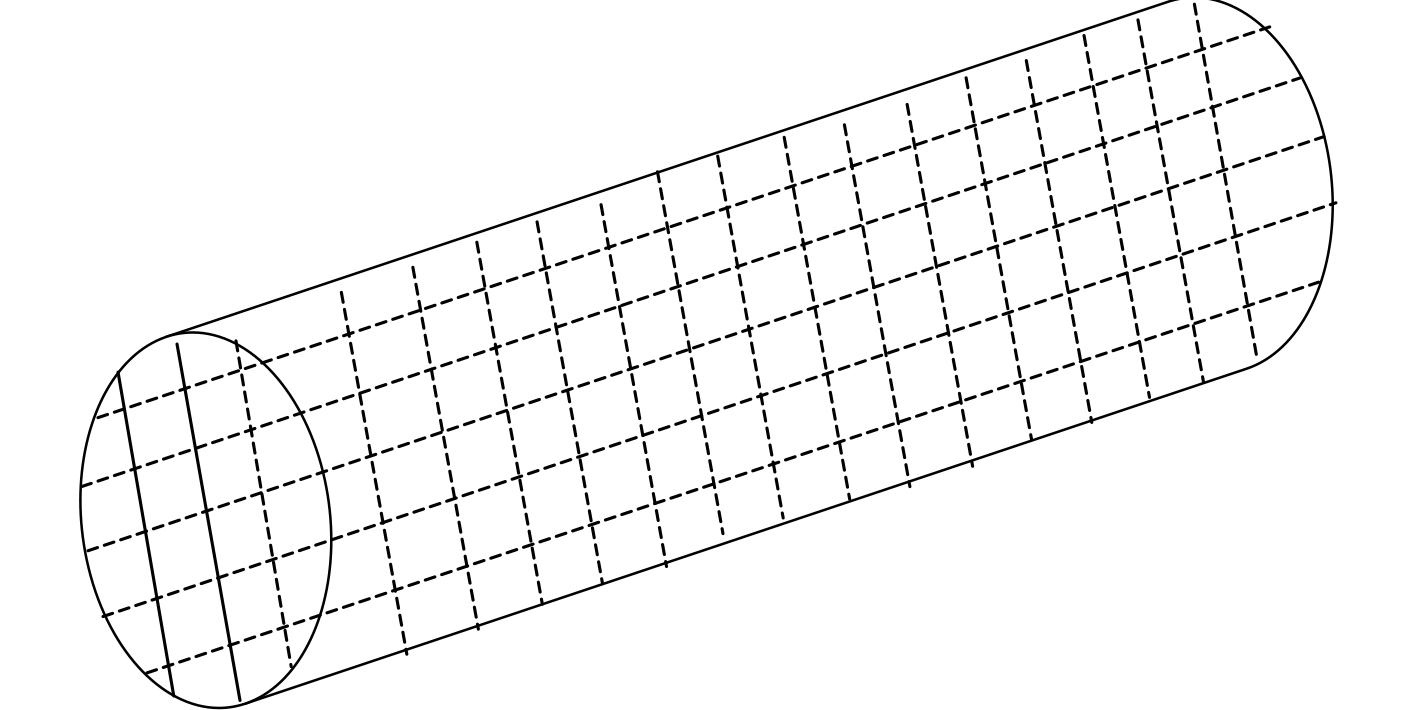
|
图 2 潜艇三维空间栅格分割效果 Fig. 2 Submarine raster segmentation effect in 3D space |
以潜艇最大半径
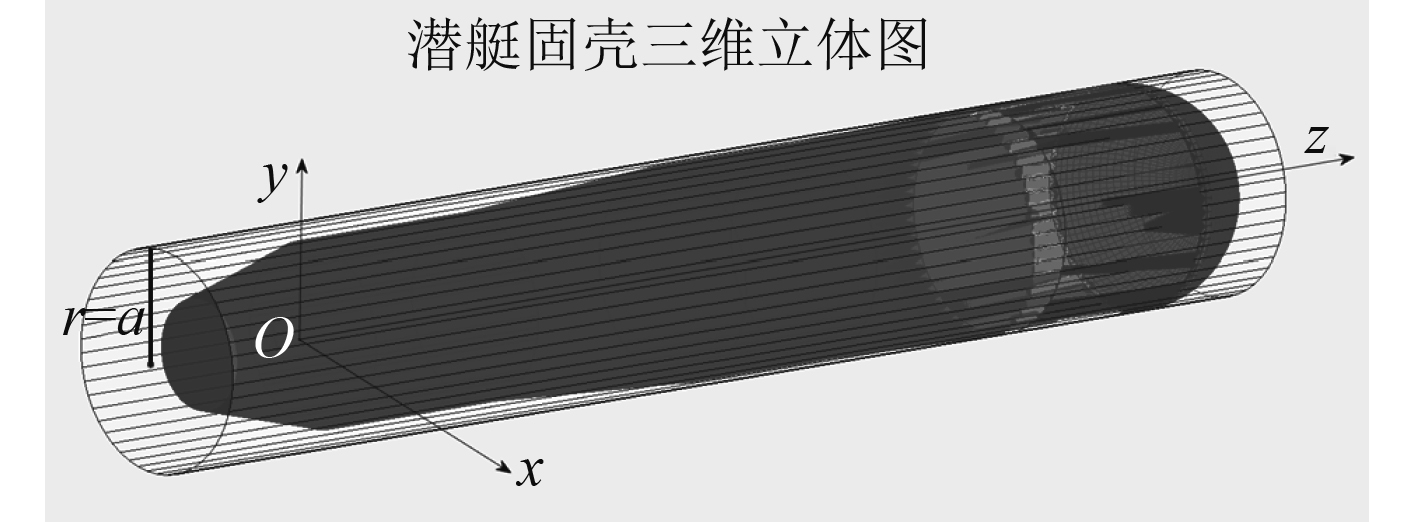
|
图 3 规则圆柱体包围后的潜艇固壳 Fig. 3 Submarine solid shell surrounded by regular cylinder |
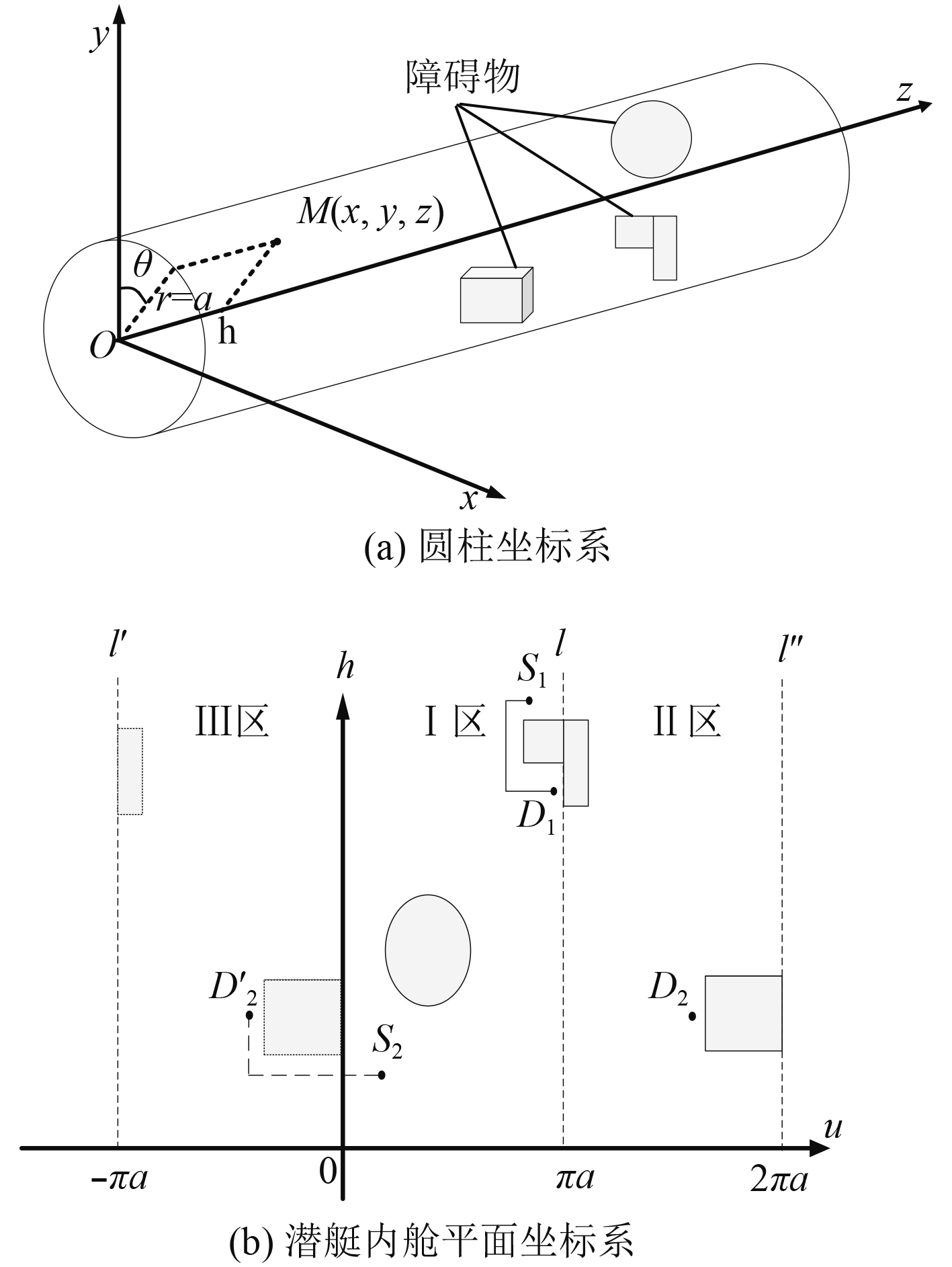
|
图 4 建立布管坐标系 Fig. 4 Setting up the layout coordinate system |
| $\left\{ \begin{array}{l} h = z\text{,}\\ u = \theta r,\theta \in [0,2{\text{π}} ]\text{,}\\ \theta = \arctan \dfrac{x}{y},\theta \in [0,2{\text{π}} ]\text{。} \end{array} \right.$ | (1) |
将圆柱体按照某一条母线展开,图4(b)中
| $\left\{ \begin{array}{l} {u_{{\rm{III}}}}{\rm{ = }}{u_{{\rm{II}}}}{\rm{ - 2}}{\text{π}} a\text{,}\\ {h_{{\rm{III}}}}{\rm{ = }}{h_{{\rm{II}}}}\text{。} \end{array} \right.$ | (2) |
式中,
根据任意指定的管系起点和终点分布的区域,可以将布管策略分为2种情况:一种在Ⅰ区或Ⅱ区就可以完成路径规划,另外一种需在Ⅰ区和Ⅲ区搜索符合条件的路径,如下式:
| $\left\{ \begin{array}{l} {\rm{|}}{u_S}{\rm{ - }}{u_D}{\rm{| > }}{\text π} a,{\text{在Ⅰ区和Ⅲ区搜索路径}}\text{,}\\ {\rm{|}}{u_S}{\rm{ - }}{u_D}{\rm{|}} \leqslant {\text π} a,{\text{在Ⅰ区和Ⅱ区搜索路径}}\text{。} \end{array} \right.$ | (3) |
式中,
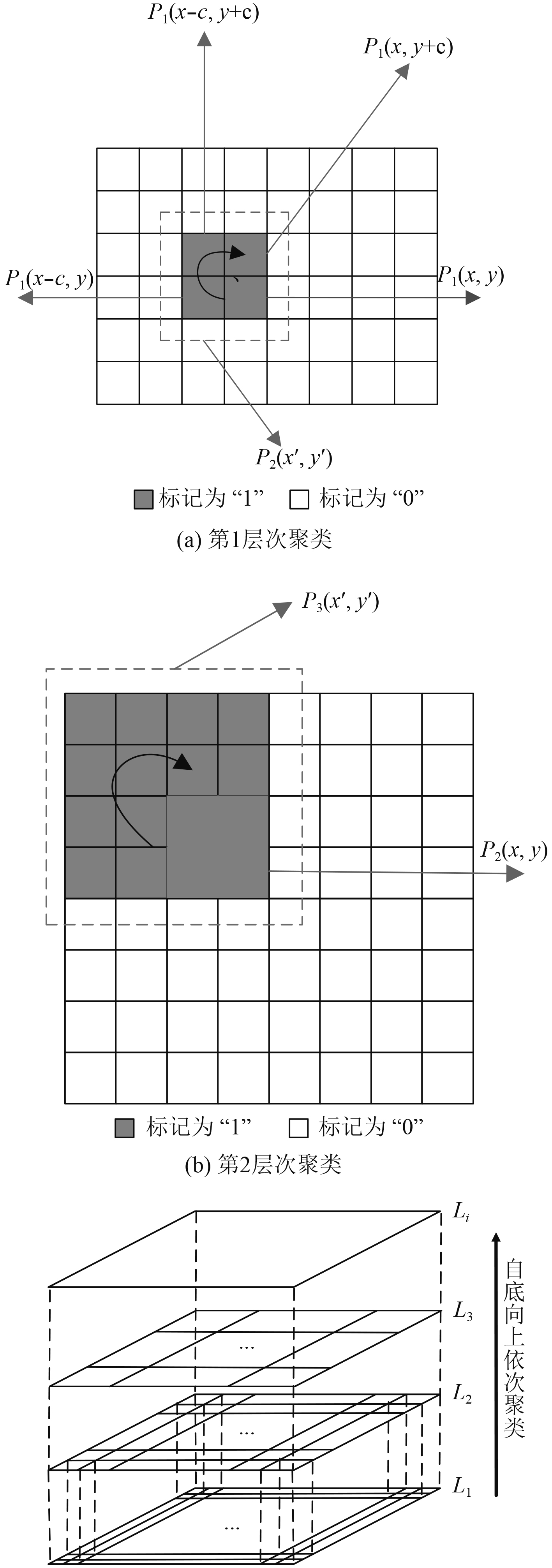
在传统的栅格法中,一般按照管系直径选取均等的栅格粒度对空间进行划分,并对栅格属性进行“0”和“1”的标记以方便计算机程序识别栅格的可布管性,管系布局算法搜索路径时需要遍历空间内每一个栅格以确定可行路径,包括各大小不一的障碍物处大量集聚在一起的不可布管栅格。这意味着均等的栅格粒度不仅缺乏对大小不一障碍物的灵活可适性,同时增加了路径搜索的工作量,影响算法的执行效率。Sting(Statistical Information Grid)算法[8]是一种基于网格的聚类算法,通过自顶向下多层次划分得到的多分辨率网格中的相关统计信息进行聚类。本文提出的基于Sting聚类算法的自适应栅格法[9]在众多栅格基础上对栅格面积进行聚类,可根据不同大小的障碍物生成相应的栅格区域作为栅格粒度,避免了同一栅格粒度过大或过小带来的布管精度损失或搜索效能下降[10]。
基于Sting聚类算法的自适应栅格法的步骤如下:
1)以管系直径为基础栅格粒度对二维潜艇内舱平面图进行划分;
2)用“0”和“1”对每个基础栅格的可布管性进行标记(“0”为完全可布管栅格,“1”为不可布管栅格及未完全被障碍物填充的栅格);
3)根据栅格可布管性的不同,采用自底向上的方式聚类生成不同层级的栅格单元以构建不同粒度的栅格区域。针对某一标记为“1”的栅格
|
图 5 基于sting聚类的自适应栅格法 Fig. 5 Adaptive raster method based on Sting clustering algorithm |
| $\left\{ \begin{array}{l} i = 1{\text{时}}\left\{ \begin{array}{l} x' = x\text{,}\\ y' = y\text{,} \end{array} \right.\\ i \ne 1{\text{时}}\left\{ \begin{array}{l} x' = x - {2^{i - \frac{5}{2}}}c\text{,}\\ y' = y + {2^{i - \frac{5}{2}}}c\text{。} \end{array} \right. \end{array} \right.$ | (4) |
式中,
在管系自动布局过程中,需考虑以下几方面因素:1)除完全避开被障碍物占据的区域以外,在不被障碍物占据的区域(即可通行区域)通行时,不允许紧贴障碍物设置;2)在沿高压、高温等危险性较高的设备布管时需要预留安全距离;3)管路长度尽量短,管路弯头数较少。为此,本文引入可通行性度量函数[11],将栅格与周围障碍物的距离表征为栅格的可通行代价,为管系布局算法中目标函数的建立提供依据。
若定义第
| $f_{{P_i}(x,y)}^{metric} = \sum\limits_{j = 1}^N {{e^{ - d({P_i}(x,y),OB{S_j})}}}\text{,} $ | (5) |
| $ \begin{aligned} & d({P_i}(x,y),OB{S_j}){\text{ = }}\mathop {{\text{min}}}\limits_{{G_j} \in OB{S_j}} d({P_i}(x,y),{G_j}) = \hfill \\ & \quad \quad \mathop {{\text{min}}}\limits_{{G_j} \in OB{S_j}} (\left| {x - {x_{Gn}}} \right| + \left| {y - {y_{Gn}}} \right|),n = 1,2,3 \cdots \text{。}\\ \end{aligned} $ | (6) |
式中:
通过引入可通行性度量函数,每一个栅格的属性可通过一个4元组来描述
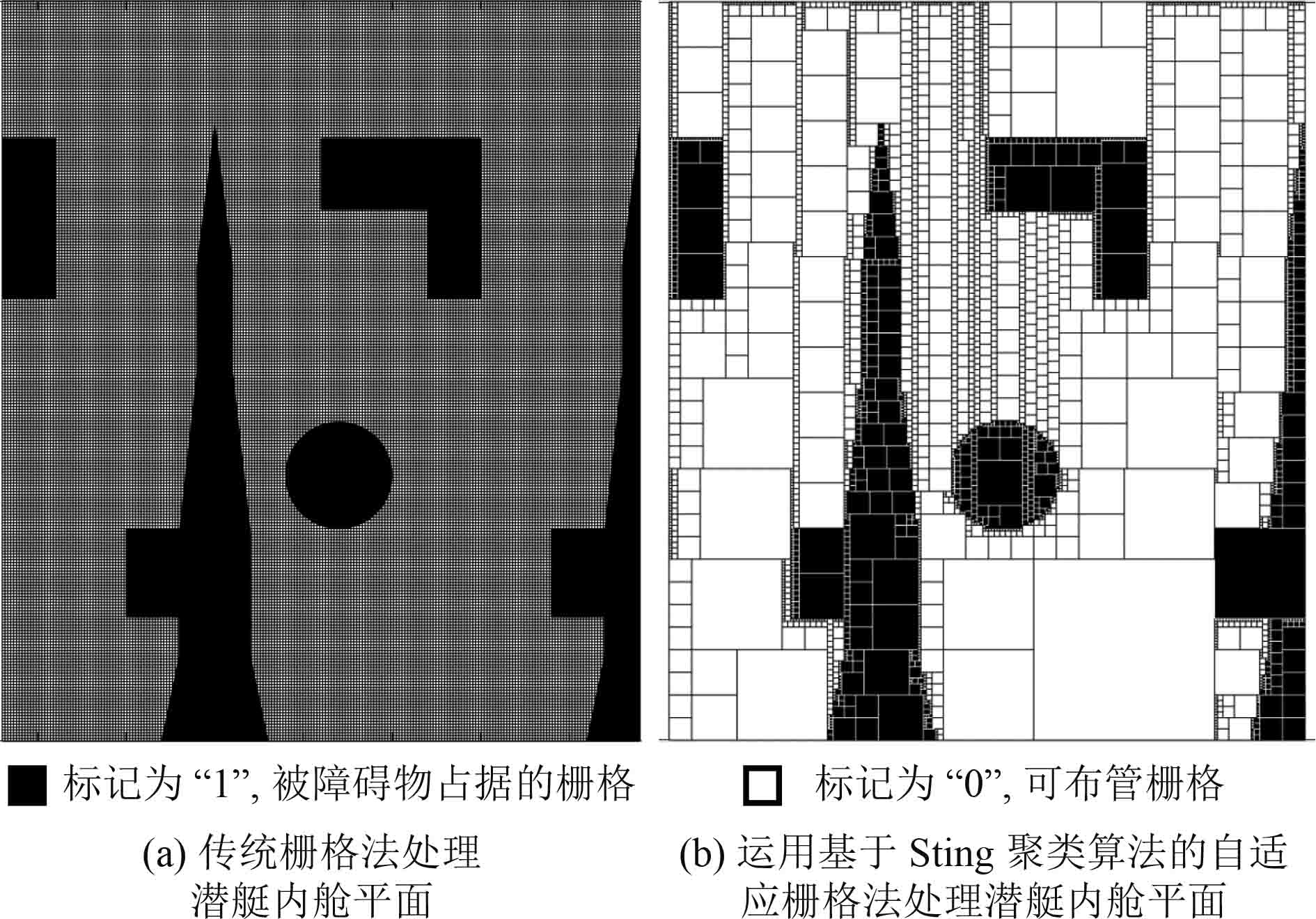
为了验证本文中提出的环境建模方法的合理性和可靠性,利用该方法生成潜艇的二维栅格平面图(见图6(b)),采用A*算法[12]在设置起点和终点的条件下搜索寻求可行管路路径,并对所得到的路径进行分析评估。由于此处采用A*求管路路径只是为了验证本文中的环境建模方法是否有效合理,因此对生成的管路路径的优化性不作探索,此处假设路径搜索沿四邻域进行,管路均为正交分布,栅格
|
图 6 潜艇内舱平面栅格图仿真结果 Fig. 6 Simulation results of plane raster diagram of submarine interior cabin |
| $h(n) = h'(n) + \alpha \cdot {f^{metric}}(n)\text{,}$ | (7) |
| $h'(n) = c \cdot (\left| {{x_n} - {x_D}} \right| + \left| {{y_n} - {y_D}} \right|)\text{。}$ | (8) |
式中:
仿真实验中,使用传统栅格法处理平面图(见图6(a)),考虑布管精度的需要,以管路直径
|
|
表 1 融合sting聚类算法的自适应栅格法仿真结果数据统计 Tab.1 Data statistics of sting clustering algorithm adaptive raster method simulation results |
|
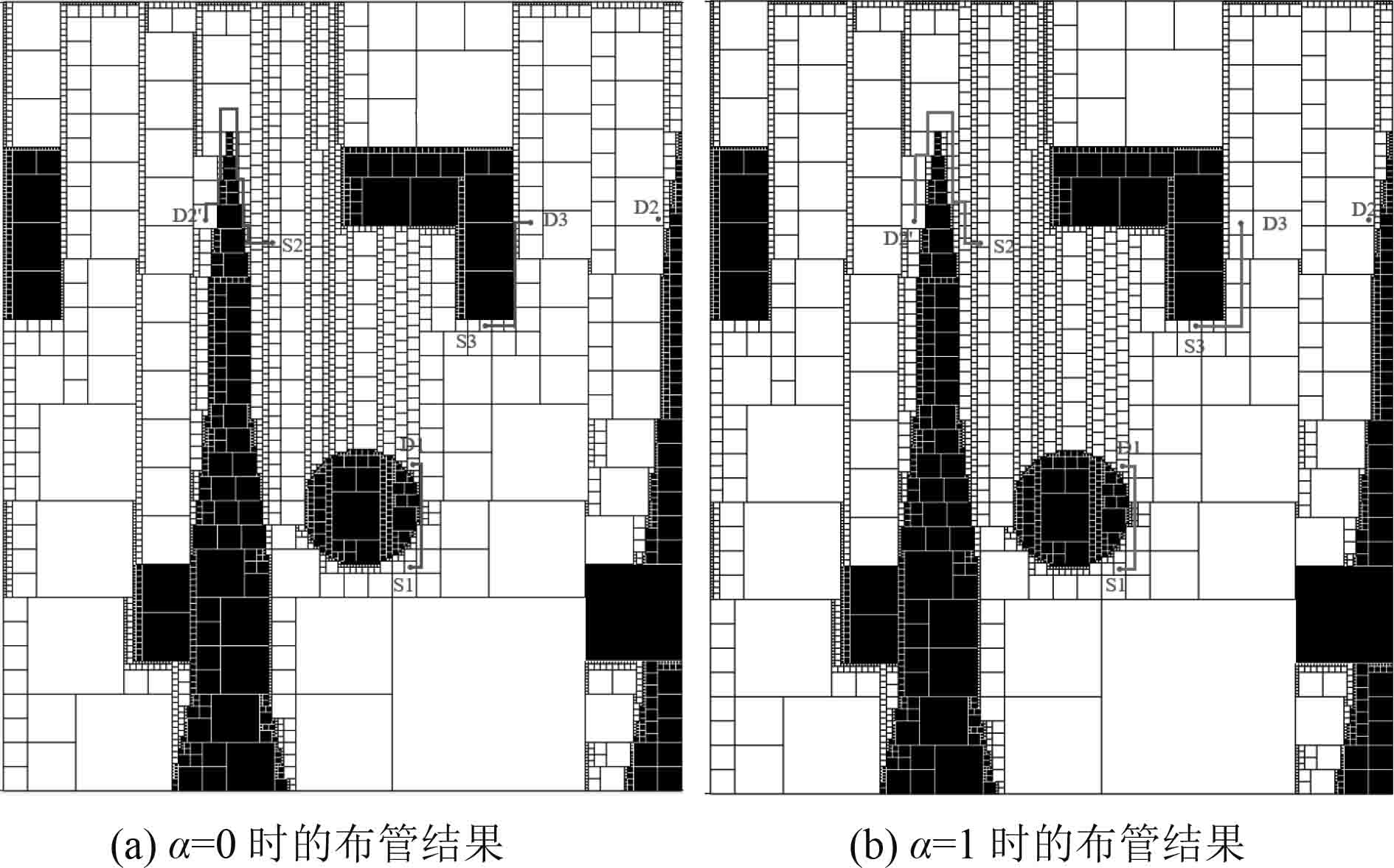
图 7 管路路径布置仿真结果 Fig. 7 Simulation results of pipeline path layout |
|
|
表 2 可通行性度量函数对管路弯头数的影响 Tab.2 The influence of the trafficability metric function on the number of pipe elbows |
面向潜艇管系自动布局需求,针对潜艇形状不规则、潜艇空间管系布局计算量大的难题,提出一种面向潜艇管系自动布局的环境建模方法。通过建立布管坐标系将潜艇三维空间转化为二维内舱平面,利用融合Sting聚类算法的自适应栅格法得到栅格粒度不同的栅格图,大大减少了栅格数量。同时引入了可通行性度量函数衡量栅格与障碍物的距离,为管系布局算法中目标函数的建立提供依据,可以有效提高潜艇管系布局的效率和准确性。
| [1] |
张捍东, 郑睿, 岑豫皖. 移动机器人路径规划技术的现状与展望[J]. 系统仿真学报, 2005, 17(2). ZHANG Han-dong, ZHENG Rui, CEN Yu-wan. Present situation and future development of mobile robot path planning technology[J]. Journal of System Simulation, 2005, 17(2). DOI:10.3969/j.issn.1004-731X.2005.02.068 |
| [2] |
陈智. 基于栅格法多目标路径规划研究[D]. 武汉: 华中科技大学, 2015. CHEN Zhi. Study on the method of multi-objective path panning based on grid[D]. Wuhan: Huazhong University of Science and Technology, 2015. |
| [3] |
WEI-Feng w, W U Yong-Chao, XU Z, et al. Research of the unit decomposing traversal method based on grid method of the mobile robot[J]. Techniques of Automation & Applications, 2013. |
| [4] |
韩忠华, 冯兴浩, 吕哲, 等. 一种改进的无人机路径规划环境建模方法[J]. 信息与控制, 2018, 47(3): 117-124. HAN Zhonghua, FENG Xinghao, LU Zhe, et al. An improved UAV path planning environment modeling method[J]. Information and Control, 2018, 47(3): 117-124. |
| [5] |
L Xiaolei, LIN J, J Zufei, et al. Mobile robot path planning based on environment modeling of grid method in unstructured environment[J]. Machine Tool & Hydraulics, 2016. |
| [6] |
张国栋, 陈金鑫, 吴鹏飞. 基于环境建模的USV轨迹规划技术[J]. 指挥控制与仿真, 2018(5). ZHANG Guo-dong, CHEN Jin-xin, WU Peng-fei. USV trajectory planning based on environmental modeling[J]. Command Control & Simulation, 2018(5). DOI:10.3969/j.issn.1673-3819.2018.05.025 |
| [7] |
白晓兰, 张禹. 航空发动机管路智能布局[J]. 机械设计与制造, 2013(9): 56-59. BAI Xiao-lan, ZHANG Yu. Pipe routing algorithm for aero-engines[J]. Machinery Design&Manufacture,, 2013(9): 56-59. DOI:10.3969/j.issn.1001-3997.2013.09.017 |
| [8] |
WANG W. STING: A statistical information grid approach to spatial data mining[J]. Proc. of the 23rd Very Large Database Conf. 1997, 1997.
|
| [9] |
NAKAHASHI K, DEIWERT G S. Three-dimensional adaptive grid method[J]. AIAA Journal, 1986, 24(6): 948-954. DOI:10.2514/3.9369 |
| [10] |
郭利进, 师五喜, 李颖, 等. 基于四叉树的自适应栅格地图创建算法[J]. 控制与决策, 2011, 26(11). |
| [11] |
史美萍, 吴军, 李焱, 等. 面向月球车路径规划的多约束环境建模方法[J]. 国防科技大学学报, 2006, 28(5): 104-108. SHI Mei-ping, WU Jun, LI Yan, et al. A multi—constrained world modeling method in lunar rover path—planning[J]. Journal Of National University of Defense Technology, 2006, 28(5): 104-108. DOI:10.3969/j.issn.1001-2486.2006.05.021 |
| [12] |
史辉, 曹闻, 朱述龙, 等. A*算法的改进及其在路径规划中的应用[J]. 测绘与空间地理信息, 2009, 32(6). DOI:10.3969/j.issn.1672-5867.2009.06.060 |
 2020, Vol. 42
2020, Vol. 42
