2. 上海大学 机电工程与自动化学院,上海 200444;
3. 中国船舶工业系统工程研究院,北京 100094
2. School of Computer Engineering and Science, Shanghai University, Shanghai 200444, China;
3. CSSC Systems Engineering Research Institute, Beijing 100094, China
在传统的海洋管理和资源开发方面,人力物力成本过高,且存在地形和气候原因限制,需要采取现代化的方法提高工作效率。在这种情况下,无人艇用于海洋安全管理和海洋资源开发的任务中无疑是很合适的。而无人艇在执行海洋安全管理或资源开发时,依赖于轨迹跟踪控制。无人艇由于其结构原因,通常为欠驱动控制系统。国内外已有较多的研究成果。
国外,Do,Jiang和Pan提出将轨迹跟踪问题转换为对跟踪误差的镇定控制问题,综合考虑无人艇动力学及艇体运动数学模型内部结构,结合反步法思想和李雅普诺夫直接法判据,设计出了一种全局一致稳定的无人艇轨迹跟踪控制器,并提出了解放艏向角速度持续激励(PE)条件的方法,使无人艇既能跟踪曲线轨迹,也能跟踪直线轨迹[1 – 2];美国阿拉巴马汉茨维尔大学Fahimi对艇体模型中的存在的不确定项进行分析考虑,使用滑模法设计了适用于欠驱动水面艇的轨迹跟踪跟踪控制器,并进行了实验验证[3];
国内,廖煜雷[4]结合反步法和自适应滑模设计出一种路径跟踪控制器;徐健[5]针对不确定因素,在设计中引入虚拟控制量避免欧拉角奇点,设计出了一种自适应滑模轨迹跟踪控制器;孙志坚[6]在论文[5]的基础上,改进了滑模面和自适应律,设计出一种针对不确定项的自适应滑模跟踪控制器。
在以上研究的基础上,本文综合考虑无人艇的非完全对称性和外界干扰的不确定影响,设计了一种自适应滑模轨迹跟踪控制器。
1 无人艇运动模型 1.1 运动学与动力学模型水面无人艇的轨迹跟踪研究通常只考虑平面三自由度的运动,其运动学模型如下:
| $ {\bf{\eta}}= {{J}}{\rm{(}}{\bf{\eta }}{\rm{)}}{\bf{\upsilon }} $ | (1) |
其中无人艇的位置和姿态向量为
| $ {{J}}({\bf{\eta }}) = \left[ {\begin{array}{*{20}{c}} {\cos \psi }&{ - \sin \psi }&0 \\ {\sin \psi }&{\cos \psi }&0 \\ 0&0&1 \end{array}} \right]\text{,} $ | (2) |
无人艇的动力学模型如下:
| $ {{M}}{\dot{\bf{\upsilon}}} +{{ C}}{\rm{(}}{\bf{\upsilon }}{\rm{)}}{\bf{\upsilon }} +{{ D}}{\rm{(}}{\bf{\upsilon }}{\rm{)}}{\bf{\upsilon }}= {{\tau}} + {{{\tau }}_{\bf{e}}} $ | (3) |
其中:
| $\begin{split} {{M}} = \left[\!\! {\begin{array}{*{20}{c}} {{m_{11}}}\!\!\!&\!\!\!0\!\!\!&\!\!\!0 \\ 0\!\!\!&\!\!\!{{m_{22}}}\!\!\!&\!\!\!{{m_{23}}} \\ 0\!\!\!&\!\!\!{{m_{32}}}\!\!\!&\!\!\!{{m_{33}}} \end{array}} \!\! \!\! \right]{\rm{ = }} \left[\!\! \!\! {\begin{array}{*{20}{c}} {m - {X_{\dot u}}}\!\!\!&\!\!\!0\!\!\!&\!\!\!0 \\ 0\!\!\!&\!\!\!{m - {Y_{\dot v}}}\!\!\!&\!\!\!{m{x_g} - {Y_{\dot r}}} \\ 0\!\!\!&\!\!\!{m{x_g} - {N_{\dot v}}}\!\!\!&\!\!\!{{I_z} - {N_{\dot r}}} \end{array}} \!\! \!\! \right]\text{,}\\[-25pt] \end{split} $ | (4) |
| $ {{C}}({\bf{\upsilon}} ) = \left[ {\begin{array}{*{20}{c}} 0&0&{ - {m_{22}}v - {m_{23}}r} \\ 0&0&{{m_{11}}u} \\ {{m_{22}}v + {m_{23}}r}&{ - {m_{11}}u}&0 \end{array}} \right]\text{,} $ | (5) |
| $ {{D}}({\bf{\upsilon}} ) = \left[ {\begin{array}{*{20}{c}} {{d_{11}}}&0&0 \\ 0&{{d_{22}}}&{{d_{23}}} \\ 0&{{d_{32}}}&{{d_{33}}} \end{array}} \right]\text{,} $ | (6) |
| $ \left\{ \begin{array}{l} {d_{11}} = - {X_u} - {X_{|u|u}}|u| - {X_{uuu}}uu \text{,} \\ {d_{22}} = - {Y_v} - {Y_{|v|v}}|v| - {Y_{|r|v}}|r| - {Y_{vvv}}vv \text{,}\\ {d_{23}} = - {Y_r} - {Y_{|v|r}}|v| - {Y_{|r|r}}|r| \text{,}\\ {d_{32}} = - {N_v} - {N_{|v|v}}|v| - {N_{|r|v}}|r| \text{,}\\ {d_{33}} = - {N_r} - {N_{|v|r}}|v| - {N_{|r|r}}|r| \text{。}\\ \end{array} \right. $ | (7) |
设计如下的全局微分同胚变换量
| $ \left\{ {\begin{array}{*{20}{l}} {{z_1} = x + \dfrac{{{m_{23}}}}{{{m_{22}}}}(\cos (\psi ) - 1)} \text{,}\\ {{z_2} = y + \dfrac{{{m_{23}}}}{{{m_{22}}}}\sin (\psi )} \text{,}\\ {{z_3} = \psi } \text{,}\\ {{z_4} = u} \text{,}\\ {{z_5} = v + \dfrac{{{m_{23}}}}{{{m_{22}}}}r} \text{,}\\ {{z_6} = r} \text{。} \end{array}} \right. $ | (8) |
对控制输入推力与转矩进行如下变换设计:
| $\begin{split} \left\{ {\begin{aligned} & {{f_1}= \frac{1}{{{m_{11}}}}\left({\tau _u} + {m_{22}}vr + \frac{{({m_{23}} + {m_{32}})}}{2}{r^2} - {d_{11}}u\right)} \text{,}\\ & {f_2}=\frac{{{m_{22}}}}{{{m_{22}}{m_{33}} - {m_{32}}{m_{23}}}}\big\{ {\tau _r} + ({m_{11}} - {m_{22}})uv + \\ &\;\;\;\left[\frac{{{m_{11}}{m_{32}}}}{{{m_{22}}}} - \frac{{({m_{23}} + {m_{32}})}}{2}\right]ur + \\ & \;\;\;\left({m_{32}}{d_{22}} - {m_{22}}{d_{32}}\right)v/{m_{22}} - \left({m_{22}}{d_{33}} - {m_{32}}{d_{23}}\right)r/{m_{22}}\big\} \text{。}\\ \end{aligned}} \right.\\[-50pt]\end{split} $ | (9) |
对环境干扰力和力矩进行如下的变换设计:
| $\left\{ {\begin{aligned} & {{f_{e1}} = \frac{1}{{{m_{11}}}}{\tau _1}} \text{,}\\ & {{f_{e2}} = \frac{{{m_{23}}}}{{{m_{22}}{m_{33}} - {m_{32}}{m_{23}}}}\left(\frac{{{m_{33}}}}{{{m_{23}}}}{\tau _2} - \frac{{{m_{32}}}}{{{m_{22}}}}{\tau _3}\right)} \text{,}\\ &{{f_{e3}} = - \frac{{{m_{32}}}}{{{m_{22}}{m_{33}} - {m_{32}}{m_{23}}}}{\tau _3}}\text{,} \end{aligned}} \right. $ | (10) |
根据式(9)与式(10)对式(8)求导可以得到变换后的系统如下式:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot z}_1} = {z_4}\cos ({z_3}) - {z_5}\sin ({z_3})} \text{,}\\ {{{\dot z}_2} = {z_4}\sin ({z_3}) + {z_5}\cos ({z_3})} \text{,}\\ {{{\dot z}_3} = {z_6}}\text{,} \\ {{{\dot z}_4} = {f_1}{\rm{ + }}{f_{e1}}} \text{,}\\ {{{\dot z}_5} = - a{z_4}{z_6} - b{z_5} + \gamma {z_6} + {f_{e2}}} \text{,}\\ {{{\dot z}_6} = {f_2} + {f_{e3}}} \text{。} \end{array}} \right. $ | (11) |
其中
进行控制器设计前,提出3个假设条件。定义进行全局微分同胚变换前的期望速度为
假设1保证了期望轨迹的合理性;假设2类似于弱化的艏向角速度持续激励条件,这种弱化的持续激励条件允许艇前进或是后退,但是艇的纵向速度值不能为0;假设3用于保证所跟踪轨迹的曲率不会过大而使跟踪效果变差。接下来将进行控制器的设计。
当给定期望轨迹矩阵中的位置变量在固地坐标系下的纵向与横向的分量
| $ {z_{3d}} = \arctan \left(\frac{{{{\dot z}_{2d}}}}{{{{\dot z}_{1d}}}}\right)\text{,} $ | (12) |
定义船体坐标系下的位置及姿态跟踪误差
| ${{\bf{\eta }}_e} = \left[\! {\begin{array}{*{20}{c}} {{z_{1e}}} \\ {{z_{2e}}} \\ {{z_{3e}}} \end{array}}\! \right] = \left[ {\begin{array}{*{20}{c}} {\cos ({z_3})}\!\!&\!\!{\sin ({z_3})}\!\!&\!\!0 \\ { - \sin ({z_3})}\!\!&\!\!{\cos ({z_3})}\!\!&\!\!0 \\ 0\!\!&\!\!0\!\!&\!\!1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{z_1} \!-\! {z_{1d}}} \\ {{z_2} \!-\! {z_{2d}}} \\ {{z_3} \!-\! {z_{3d}}} \end{array}} \right]\text{,} $ | (13) |
对式(13)求导,并将式(12)代入计算,得到:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot z}_{1e}} = {z_4} - \sqrt {\dot z_{1d}^2 + \dot z_{2d}^2} \cos ({z_{3e}}) + {z_6}{z_{2e}}}\text{,} \\ {{{\dot z}_{2e}} = {z_5} + \sqrt {\dot z_{1d}^2 + \dot z_{2d}^2} \sin ({z_{3e}}) - {z_6}{z_{1e}}} \text{。} \end{array}} \right. $ | (14) |
引入
| $ {v_p} = \sqrt {\dot z_{1d}^2 + \dot z_{2d}^2} \text{,} $ | (15) |
将式(15)代入到式(14)中,可以得到:
| $\left\{ {\begin{array}{*{20}{l}} {{{\dot z}_{1e}} = {z_4} - {v_p}\cos ({z_{3e}}) + {z_6}{z_{2e}}} \text{,}\\ {{{\dot z}_{2e}} = {z_5} + {v_p}\sin ({z_{3e}}) - {z_6}{z_{1e}}} \text{,} \end{array}} \right. $ | (16) |
为了对位置跟踪误差进行分析,选取李雅普诺夫函数
| $ {V_1} = \frac{1}{2}\left(z_{1e}^2 + z_{2e}^2\right)\text{,} $ | (17) |
对
| $ {\dot V_1} = {z_{1e}}[{z_4} - {v_p}\cos ({z_{3e}})] + {z_{2e}}[{z_5} + {v_p}\sin ({z_{3e}})]\text{。} $ | (18) |
为了使系统稳定,选用
| $ {\varpi _v} = {v_p}\sin ({z_{3e}})\text{,} $ | (19) |
选取虚拟控制量
| $ {z_{4d}} = {v_p}\cos ({z_{3e}}) - {k_1}{z_{1e}}/E\text{,} $ | (20) |
| $ {\varpi _d} = - {z_5} - {k_2}{z_{2e}}/E\text{,} $ | (21) |
其中
定义
| $ {z_{4e}} = {z_4} - {z_{4d}}\text{,} $ | (22) |
| $ {\varpi _{ve}} = {\varpi _v} - {\varpi _{vd}}\text{,} $ | (23) |
将式(22)与式(23)代入到式(16)中,可以得到:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot z}_{1e}} = {z_{4e}} - {k_1}{z_{1e}}/E + {z_6}{z_{2e}}} \text{,}\\ {{{\dot z}_{2e}} = {\varpi _{ve}} - {k_2}{z_{2e}}/E - {z_6}{z_{1e}}} \text{,} \end{array}} \right. $ | (24) |
将式(24)代入到式(18)中,可以得到:
| $ {\dot V_1} = - \;\left({k_1}z_{1e}^2 + {k_2}z_{2e}^2\right)/E + {z_{1e}}{z_{4e}} + {\varpi _{ve}}{z_{2e}}\text{,} $ | (25) |
对
| $ \begin{split} {{\dot z}_{4e}} \!\!=\!& {{\dot z}_4} - {{\dot z}_{4d}} -\\ &{f_1} + {f_{e1}} - {{\dot z}_{4d}} =\\ & \dfrac{1}{{{m_{11}}}}\!\!\left(\!{\tau _u} \!\!+\!\! {\tau _{e1}} \!\!+\!\! {m_{22}}vr \!\!+\!\! \dfrac{{({m_{23}}\! \!+\!\! {m_{32}})}}{2}{r^2} \!\!-\!\! {d_{11}}u \!\!-\!\! {m_{11}}{{\dot z}_{4d}}\!\right)\!\text{,} \\[-18pt] \end{split} $ | (26) |
在式(26)中,取系统的不确定项
| $ {U_1} = {\tau _{e1}} + {m_{22}}vr + \frac{{({m_{23}} + {m_{32}})}}{2}{r^2} - {d_{11}}u - {m_{11}}{\dot z_{4d}}\text{,} $ | (27) |
代入式(27),式(26)可以写为以下形式:
| $ {\dot z_{4e}} = \frac{{({\tau _u} + {U_1})}}{{{m_{11}}}}\text{,} $ | (28) |
定义
| $ {V_2} = {V_1} + \frac{1}{2}{m_{11}}z_{4e}^2 + \frac{1}{2}{\tilde U_1}^2\text{,} $ | (29) |
设计滑模面
| $ {S_1} = {\lambda _1}{z_{4e}} + {\dot z_{4e}} + \frac{{{z_{1e}}}}{{{m_{11}}}} - \frac{{{{\tilde U}_1}}}{{{m_{11}}}}\text{,} $ | (30) |
其中
| $ {S_1} = {\lambda _1}{z_{4e}} + \frac{{{z_{1e}} + {\tau _u} + {{\hat U}_1}}}{{{m_{11}}}}\text{,} $ | (31) |
对
| $ \begin{split} {{{\dot{V}}}_{2}}=&-({{k}_{1}}z_{1e}^{2}+{{k}_{2}}z_{2e}^{2})/E+{{\varpi }_{ve}}{{z}_{2e}}+{{m}_{11}}{{z}_{4e}}{{S}_{1}}-{{\lambda }_{1}}{{m}_{11}}z_{4e}^{2} + \\ &({{z}_{4e}}-{{{\dot{\hat{U}}}}_{1}}){{{\tilde{U}}}_{1}} \text{,} \\[-10pt] \end{split} $ | (32) |
对
| $ {{\dot{S}}_{1}}=\frac{{{\lambda }_{1}}({{U}_{1}}+{{\tau }_{u}})+{{{\dot{\tau }}}_{u}}+{{{\dot{\hat{U}}}}_{1}}+{{{\dot{z}}}_{1e}}}{{{m}_{11}}}\text{,} $ | (33) |
选取李雅普诺夫函数
| $ {V_3} = {V_2} + \frac{1}{2}{m_{11}}S_1^2\text{,} $ | (34) |
对
| $ \begin{split} {{{\dot{V}}}_{3}}=&-\left({{k}_{1}}z_{1e}^{2}+{{k}_{2}}z_{2e}^{2}\right)/E+{{\varpi }_{ve}}{{z}_{2e}}+{{m}_{11}}{{z}_{4e}}{{S}_{1}}-{{\lambda }_{1}}{{m}_{11}}z_{4e}^{2} +\\ & \left({{z}_{4e}}-{{{\dot{\hat{U}}}}_{1}}\right){{{\tilde{U}}}_{1}}+{{S}_{1}}\left[{{\lambda }_{1}}({{U}_{1}}+{{\tau }_{u}})+{{{\dot{\tau }}}_{u}}+{{{\dot{\hat{U}}}}_{1}}+{{{\dot{z}}}_{1e}}\right] \text{,}\\[-10pt] \end{split} $ | (35) |
设计如下的实际控制输入变化率
| $\begin{split} {{\dot{\tau }}_{u}}=&-{{\lambda }_{1}}\left({{\hat{U}}_{1}}+{{\tau }_{u}}\right)-{{\dot{\hat{U}}}_{1}}-{{\dot{z}}_{1e}}-{{m}_{11}}{{z}_{4e}}-\\ &{{k}_{s1}}sat({{S}_{1}})-{{w}_{s1}}{{S}_{1}}\text{,}\end{split} $ | (36) |
其中,
将式(36)代入式(35)中得到:
| $\begin{split} {{{\dot{V}}}_{3}}=&-\left({{k}_{1}}z_{1e}^{2}+{{k}_{2}}z_{2e}^{2}\right)/E+{{\varpi }_{ve}}{{z}_{2e}}-{{\lambda }_{1}}{{m}_{11}}z_{4e}^{2} +\\ &\left({{z}_{4e}}-{{{\dot{\hat{U}}}}_{1}}+{{\lambda }_{1}}{{S}_{1}}\right){{{\tilde{U}}}_{1}}-{{k}_{s1}}sat({{S}_{1}}){{S}_{1}}-{{w}_{s1}}S_{1}^{2}\text{,} \\ \end{split} $ | (37) |
设计如下的自适应律:
| $ {{\dot{\hat{U}}}_{1}}={{z}_{4e}}+{{\lambda }_{1}}{{S}_{1}}\text{,} $ | (38) |
将式(38)代入式(37)可以得到:
| $\begin{split} {\dot V_3} =& - \left({k_1}z_{1e}^2 + {k_2}z_{2e}^2\right)/E + {\varpi _{ve}}{z_{2e}} - \\ &{\lambda _1}{m_{11}}z_{4e}^2 - {k_{s1}}sat({S_1}){S_1} - {w_{s1}}S_1^2\text{。} \end{split} $ | (39) |
接下来将进行对跟踪误差
| ${\dot \varpi _{ve}} = {\dot v_p}\sin ({z_{3e}}) + {v_p}\cos ({z_{3e}})({z_6} - {\dot z_{3d}}) + \frac{{{U_2}}}{{{m_{22}}}} + {Q_1}\text{,} $ | (40) |
其中不确定因素项
| $ \begin{split} {U_2} = & - {m_{11}}{z_4}{z_6} - {d_{22}}{z_5} + \left({d_{22}}{m_{23}}/{m_{22}} - {d_{23}}\right){z_6} + \\ & \frac{{{m_{22}}{m_{33}}{\tau _{e2}} - {m_{23}}{m_{32}}{\tau _{e3}}}}{{{m_{22}}{m_{33}} - {m_{32}}{m_{23}}}} \text{,} \\ \end{split} $ | (41) |
| $ {Q_1} = {k_2}\left({1 / E} - {{z_{2e}^2} / {{E^3}}}\right){\dot z_{2e}} - {{{k_2}{z_{1e}}{z_{2e}}{{\dot z}_{1e}}} / {{E^3}}}\text{,} $ | (42) |
为了使
| $ {z_{6d}} = {\dot z_{3d}} + \frac{{ - {{\dot v}_p}\sin ({z_{3e}}) - {{{{\hat U}_2}} / {{m_{22}}}} - {Q_1} - {k_3}{\varpi _{ve}} - {{{z_{2e}}} /{{m_{22}}}}}}{{{v_p}\cos ({z_{3e}})}}\text{,} $ | (43) |
这里的
得到了
| ${z_{6e}} = {z_6} - {z_{6d}}\text{,} $ | (44) |
将式(44)代入式(40)中,得到:
| $ {\dot \varpi _{ve}} = {z_{6e}}{v_p}\cos ({z_{3e}}) + {\tilde U_2} - {k_3}{\varpi _{ve}} - {{{z_{2e}}} / {{m_{22}}}}\text{,} $ | (45) |
为镇定
| $ {V_4} = {V_3} + \frac{1}{2}{m_{22}}\varpi _{ve}^2 + \frac{1}{2}{\tilde U_2}^2\text{,} $ | (46) |
对
| $ \begin{split} {{{\dot{V}}}_{4}}\!=&-\left({{k}_{1}}z_{1e}^{2}\!+\!{{k}_{2}}z_{2e}^{2}\right)/E\!-\!{{\lambda }_{1}}{{m}_{11}}z_{4e}^{2}\!-\!{{k}_{s1}}sat({{S}_{1}}){{S}_{1}}\!-\!{{w}_{s1}}S_{1}^{2}\!-\\ &{{k}_{3}}{{m}_{22}}\varpi _{ve}^{2} \!+\!\left({{\varpi }_{ve}}\!-\!{{{\dot{\hat{U}}}}_{2}}\right){{{\tilde{U}}}_{2}}\!+\!{{m}_{22}}{{\varpi }_{ve}}{{z}_{6e}}{{v}_{p}}\cos ({{z}_{3e}}) \text{。}\\[-10pt] \end{split} $ | (47) |
设计
| ${{\dot{\hat{U}}}_{2}}={{\varpi }_{ve}}\text{,} $ | (48) |
将式(48)代入到式(47)中,得到:
| $ \begin{split} {{\dot V}_4} \!=\!& - \left({k_1}z_{1e}^2 + {k_2}z_{2e}^2\right)/E - {\lambda _1}{m_{11}}z_{4e}^2 - {k_{s1}}sat({S_1}){S_1} - \\ & {w_{s1}}S_1^2 - {k_3}{m_{22}}\varpi _{ve}^2 + {m_{22}}{\varpi _{ve}}{z_{6e}}{v_p}\cos ({z_{3e}})\text{,} \\ \end{split} $ | (49) |
| $ {\dot z_{6e}} = \frac{1}{\zeta }({\tau _r} + {U_3})\text{,} $ | (50) |
其中
| $ \begin{aligned} {U_3} =& ({m_{11}} - {m_{22}})uv + \left[\frac{{{m_{11}}{m_{32}}}}{{{m_{22}}}} - \frac{{({m_{23}} + {m_{32}})}}{2}\right]ur - \\ & \left({m_{22}}{d_{33}} - {m_{32}}{d_{23}}\right)r/{m_{22}} - \frac{{{m_{32}}}}{{{m_{22}}}}{\tau _{e3}} - \\ &\zeta {{\dot z}_{6d}}\; + ({m_{32}}{d_{22}} - {m_{22}}{d_{32}})v/{m_{22}} \text{,} \\ \end{aligned} $ | (51) |
定义
| $ {V_5} = {V_4} + \frac{1}{2}\zeta z_{6e}^2 + \frac{1}{2}{\tilde U_3}^2\text{,} $ | (52) |
对
| $\begin{split} {{{\dot{V}}}_{5}}\!=\!&-\left({{k}_{1}}z_{1e}^{2}\!+\!{{k}_{2}}z_{2e}^{2}\right)/E\!-\!{{\lambda }_{1}}{{m}_{11}}z_{4e}^{2}\!-\!{{k}_{s1}}sat({{S}_{1}}){{S}_{1}}\!-\!{{w}_{s1}}S_{1}^{2}\!-\\ &{{k}_{3}}{{m}_{22}}\varpi _{ve}^{2} \!+\!{{m}_{22}}{{\varpi }_{ve}}{{z}_{6e}}{{v}_{p}}\cos ({{z}_{3e}})\!+\!\zeta {{{\dot{z}}}_{6e}}{{z}_{6e}}\!-\!{{{\tilde{U}}}_{3}}{{{\dot{\hat{U}}}}_{3}} \text{,}\\[-10pt] \end{split} $ | (53) |
设计滑模面
| $ {S_2} = {\lambda _2}{z_{6e}} + {\dot z_{6e}} + \frac{{{m_{22}}{\varpi _{ve}}{v_p}\cos ({z_{3e}}) - {{\tilde U}_3}}}{\zeta }\text{,} $ | (54) |
将式(50)代入式(54),化简得到:
| $ {S_2} = {\lambda _2}{z_{6e}} + {Q_2} + \frac{{{\tau _r} + {{\hat U}_3}}}{\zeta }\text{,} $ | (55) |
其中
将式(55)代入到式(53)中,得到
| $\begin{split} {{{\dot{V}}}_{5}}\!=\!&-\left({{k}_{1}}z_{1e}^{2}\!+\!{{k}_{2}}z_{2e}^{2}\right)/E\!-\!{{\lambda }_{1}}{{m}_{11}}z_{4e}^{2}\!-\!{{k}_{s1}}sat({{S}_{1}}){{S}_{1}}\!-\!{{w}_{s1}}S_{1}^{2}\!-\\ &{{k}_{3}}{{m}_{22}}\varpi _{ve}^{2} +\zeta {{z}_{6e}}{{S}_{2}}-\zeta {{\lambda }_{2}}z_{6e}^{2}+\left({{z}_{6e}}-{{{\dot{\hat{U}}}}_{3}}\right){{{\tilde{U}}}_{3}}\text{,} \\[-12pt] \end{split} $ | (56) |
对
| ${{\dot{S}}_{2}}={{\dot{Q}}_{2}}+\frac{1}{\zeta }\left[{{\lambda }_{2}}({{\tau }_{r}}+{{U}_{3}}){{\dot{\tau }}_{r}}+{{\dot{\hat{U}}}_{3}}\right]\text{,} $ | (57) |
取李雅普诺夫函数
| $ {V_6} = {V_5} + \frac{1}{2}\zeta S_2^2\text{,} $ | (58) |
对
| $\begin{split} {{{\dot{V}}}_{6}}=&-\left({{k}_{1}}z_{1e}^{2}+{{k}_{2}}z_{2e}^{2}\right)/E-{{\lambda }_{1}}{{m}_{11}}z_{4e}^{2}-{{k}_{s1}}sat({{S}_{1}}){{S}_{1}}-\\ &{{w}_{s1}}S_{1}^{2}-{{k}_{3}}{{m}_{22}}\varpi _{ve}^{2} +\zeta {{z}_{6e}}{{S}_{2}}-\zeta {{\lambda }_{2}}z_{6e}^{2}+\left({{z}_{6e}}-{{{\dot{\hat{U}}}}_{3}}\right){{{\tilde{U}}}_{3}} +\\ &\zeta {{S}_{2}}\left[{{{\dot{Q}}}_{2}}+\frac{{{\lambda }_{2}}({{U}_{3}}+{{\tau }_{r}})+{{{\dot{\tau }}}_{r}}+{{{\dot{\hat{U}}}}_{3}}}{\zeta }\right]\text{,} \\[-15pt] \end{split} $ | (59) |
设计实际控制输入的变化率为:
| $\begin{split}{{\dot{\tau }}_{r}}=&-{{\lambda }_{2}}({{\tau }_{r}}+{{U}_{3}})-{{\dot{\hat{U}}}_{3}}-\zeta {{\dot{Q}}_{2}}-\zeta {{z}_{6e}}-\\ &{{k}_{s2}}sat({{S}_{2}})-{{w}_{s2}}S_{2}^{2}\text{,}\end{split} $ | (60) |
其中,
| $\begin{split} {{{\dot{V}}}_{6}}=&-\left({{k}_{1}}z_{1e}^{2}+{{k}_{2}}z_{2e}^{2}\right)/E-{{\lambda }_{1}}{{m}_{11}}z_{4e}^{2}-{{k}_{s1}}sat({{S}_{1}}){{S}_{1}}-\\ &{{w}_{s1}}S_{1}^{2}-{{k}_{3}}{{m}_{22}}\varpi _{ve}^{2} -{{\lambda }_{2}}\zeta z_{6e}^{2}-{{k}_{s2}}sat({{S}_{2}}){{S}_{2}}-{{w}_{s2}}S_{2}^{2}+\\ &\left({{z}_{6e}}-{{{\dot{\hat{U}}}}_{3}}+{{\lambda }_{2}}{{S}_{2}}\right){{{\tilde{U}}}_{3}}\text{,} \\[-12pt] \end{split} $ | (61) |
设计
| ${{\dot{\hat{U}}}_{3}}={{z}_{6e}}+{{\lambda }_{2}}{{S}_{2}}\text{,} $ | (62) |
将式(62)代入式(61)中,最终得到:
| $ \begin{split} {{\dot V}_6} =& - {{({k_1}z_{1e}^2 + {k_2}z_{2e}^2)} / E} - {k_3}\varpi _{ve}^2 - {\lambda _1}z_{4e}^2 - {\lambda _2}z_{6e}^2 -\\ &{k_{s1}}sat({S_1}){S_1} - {w_{s1}}S_1^2 - {k_{s2}}sat({S_2}){S_2} - \\ &{w_{s2}}S_2^2 \leqslant 0 \text{。} \\ \end{split} $ | (63) |
在本章中进行了欠驱动非对称无人艇轨迹跟踪的自适应滑模控制的设计。在控制器的设计中,使用
定义
| $ \begin{split} {V_6} =& \frac{1}{2}z_{1e}^2 + \frac{1}{2}z_{2e}^2 + \frac{1}{2}{m_{11}}z_{4e}^2 + \frac{1}{2}\tilde U_1^2 + \frac{1}{2}{m_{11}}S_1^2 +\\ & \frac{1}{2}{m_{22}}\varpi _{ve}^2 + \frac{1}{2}\tilde U_2^2 + \frac{1}{2}\zeta z_{6e}^2 + \frac{1}{2}\tilde U_3^2 + \frac{1}{2}\zeta S_2^2 \text{,}\\ \end{split} $ | (64) |
存在一个正常数
| $ l = \min \left\{ \frac{{{k_1}}}{{{E_{\max }}}},\frac{{{k_2}}}{{{E_{\max }}}},{\lambda _1},{k_3},{\lambda _2},,1,1,1,\frac{{{w_{s1}}}}{{{m_{11}}}},\frac{{{w_{s2}}}}{\zeta }\right\}\text{,} $ | (65) |
根据式(63)可以得到
| $ {V_6}(t) \leqslant {V_6}(0){e^{ - 2lt}},\;t \in \left[ {0, + \infty } \right)\text{。} $ | (66) |
对式(66)进行代数替换,可以得到
本章选取了直线与曲线2种跟踪轨迹来证明所设计的控制器的跟踪性能。仿真过程中,艇体模型参数
| $ \left\{ {\begin{array}{*{20}{l}} {{\tau _{e1}} = 0.1{m_{11}} + r(\sin (0.01t) - 1)}\text{,} \\ {{\tau _{e2}} = 0.1{m_{22}} + r(\sin (0.01t) - 1)}\text{,} \\ {{\tau _{e3}} = 0.1\zeta \; + r(\sin (0.01t) - 1)} \text{。} \end{array}} \right. $ | (67) |
控制器参数选取与跟踪结果如下:
1)跟踪直线
艇体的初始位置与姿态为
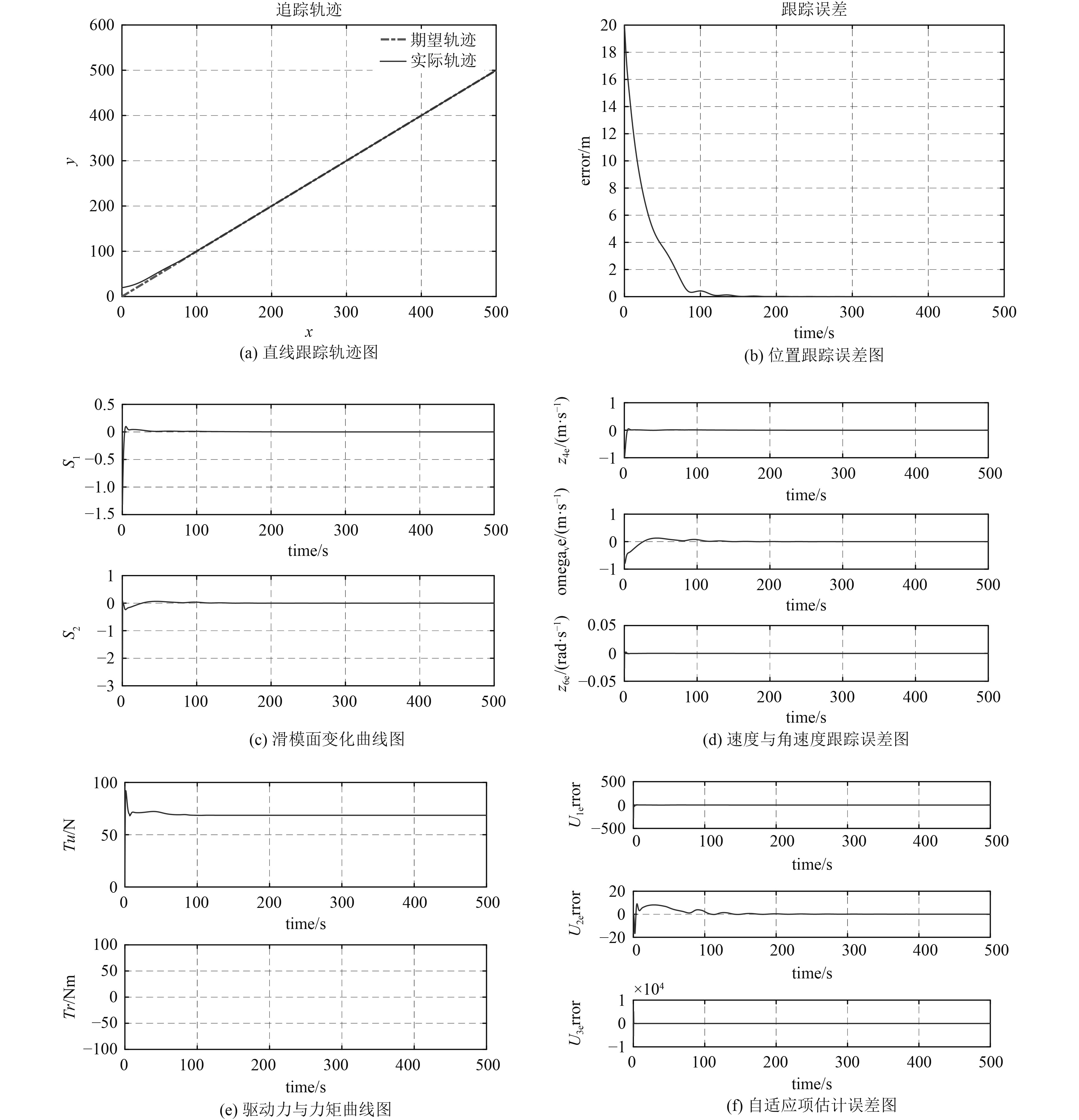
|
图 1 直线轨迹跟踪结果图 Fig. 1 Results of line tracking |
2)跟踪曲线
艇体的初始位置与姿态为

|
图 2 曲线轨迹跟踪结果图 Fig. 2 Results of curve tracking |
本文研究了一类非完全对称欠驱动无人艇的轨迹跟踪控制问题,考虑无人艇系统惯性矩阵与阻尼矩阵的非对称项,通过采用全局微分同胚变换简化模型,在简化后的模型上利用自适应滑模方法和李雅普诺夫直接法设计出轨迹跟踪控制器,该控制器能够实现非完全对称欠驱动无人艇对直线轨迹和曲线轨迹的跟踪,通过仿真实验验证了控制器的有效性。
| [1] |
DO K D, PAN J, JIANG Z P. Global exponential tracking control of underactuated surface ships in the body frame[C]// American Control Conference, 2002. Proceedings of the 2002. IEEE, 2002: 4702–4707.
|
| [2] |
DO K, JIANG Z, PAN J. Underactuated ship global tracking under relaxed conditions[J]. IEEE Transactions on Automatic Control, 2002, 47(9): 1529-1536. DOI:10.1109/TAC.2002.802755 |
| [3] |
FAHIMI F, VAN KLEECK C. Alternative trajectory-tracking control approach for marine surface vessels with experimental verification[J]. Robotica, 2013, 31(1): 25-33. DOI:10.1017/S0263574712000070 |
| [4] |
LIAO Y L, WAN L, ZHUANG J Y. Backstepping dynamical sliding mode control method for the path following of the underactuated surface vessel[J]. Procedia Engineering, 2011, 15(7): 256-263. |
| [5] |
XU J, WANG M, QIAO L. Dynamical sliding mode control for the trajectory tracking of underactuated unmanned underwater vehicles[J]. Ocean Engineering, 2015, 105: 54-63. DOI:10.1016/j.oceaneng.2015.06.022 |
| [6] |
SUN Z, ZHANG G, JIAN Y. Research on the sliding mode control for underactuated surface vessels via parameter estimation[J]. Nonlinear Dynamics, 2018, 91(2): 1163-1175. DOI:10.1007/s11071-017-3937-8 |
| [7] |
VIDYASAGARM. Nonlinear Systems Analysis, 2nd Ed[C]// Society for Industrial & Applied Mathematics, Philadelphia. 2002.
|
 2020, Vol. 42
2020, Vol. 42
