不同于传统开敞式的螺旋桨推进装置,喷水推进装置内藏于船舶,通过将吸入装置内的水加速喷出,利用反向作用力推动船舶航行[1]。近年来,喷水推进装置以其高效率、噪声低和优异的抗汽蚀性能得到广泛应用[2]。进水流道是喷水推进装置进水结构中的关键部位,其性能不仅直接影响到推进泵的进水情况,还会影响到装置的整体性能。已有研究结果表明[3],约7%~9%的轴功率损失于流道内。金平仲[4]基于损失产生的基本原理,用数学推导的方式推导出喷水推进泵装置效率的影响因素,指出进速比、边界层和管道损失系数对管道效率有很大影响,减小管道损失是提高喷水推进效率的关键。Tatsuo Kashiwadani[5]针对表面效应艇MEGURO2,设计了喷水推进系统进水管道。P A Brandner和G J Walker[6-7]采用压力探针和目测的实验方法,对喷水推进泵装置平进口流动进行了定量和定性的实验研究,发现在很大范围的运行工况唇部都有汽蚀发生。魏应三等[8]根据不同的流道倾角建立了6种不同的流道模型,研究了流道倾角对喷水推进泵装置进水流道的影响。彭云龙等[9]以高速摩托艇的喷水推进器为研究对象,对流道几何进行了优化,将喷水推进的效率提高了6%。罗灿等[10]分析了不同流量工况下进水流道各段的水力损失,验证了水力损失与流量的正比关系,发现各段水力损失百分比受流量因素的影响很大。许慧丽[11]对一种平进口式喷水推进器流道建立数值模型,从流道的壁面压力分布、流场均匀性和流动分离3个方面比较和分析了进流方向对流场特征的影响。李臣[12]利用参数化方法设计了4种不同流道倾角的喷水推进泵椭圆形进水流道,并采用三维雷诺平均N–S方程和RNGk–ε湍流模型对其流场和性能进行数值仿真。从流道的出流均匀性、流动分离方面分析在保持进口速比不变,不同流道倾角时流道内流场的变化情况,为喷水推进器进水流道倾角的设计提供依据。本文针对喷水推进装置进水结构能量特性和水力流动特性展开分析,丰富喷水推进装置理论,为进一步优化装置性能提供技术支撑。
1 数值模拟方法 1.1 控制方程自然界的流动需要同时遵循质量守恒、动量守恒和能量守恒三大定律,喷水推进装置的运行忽略传热因素,不考虑能量方程,控制方程包括连续方程和动量方程。将喷水推进装置看做空间固定的有限控制体,水由进口流入,由出口流出,控制体内的流动为常粘度不可压缩的湍流,密度不随时间发生变化。笛卡尔直角坐标系下,本文采用以下偏微分控制方程:
| $\frac{{\partial (\rho {u_i})}}{{\partial {x_i}}} = 0{\text{,}}$ | (1) |
| $\frac{{\partial (\rho {u_i})}}{{\partial t}} + \frac{{\partial (\rho {u_i}{u_j})}}{{\partial {x_j}}} = \frac{{\partial P}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left[ {\mu \left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)} \right] + {F_i}{\text{。}}$ | (2) |
式中:ρ为水的密度;u为速度;P为作用于流体微元体上的压力;μ为水的动力粘度;i,j为坐标轴方向;F为体积力。
1.2 三维几何模型受船底边界层等因素的影响,喷水推进泵装置进口处的水流为不均匀入流,喷水推进泵装置的进口并非进水流道的进口。为保证数值模拟的准确性,不能仅对单独的喷水推进泵装置进行数值模拟,计算域还需包括船底水体部分。为便于网格剖分,将复杂的计算域分为结构相对简单的子域分别绘制,按照水流的前进方向,计算域分为船底水体、进水流道进口收缩段、进水流道弯管段和出口水平段、叶轮进口过渡段、叶轮、导叶和喷嘴共计7个子域,如图1所示。水体的三维尺寸为长30D,宽5D,深8D[13]。
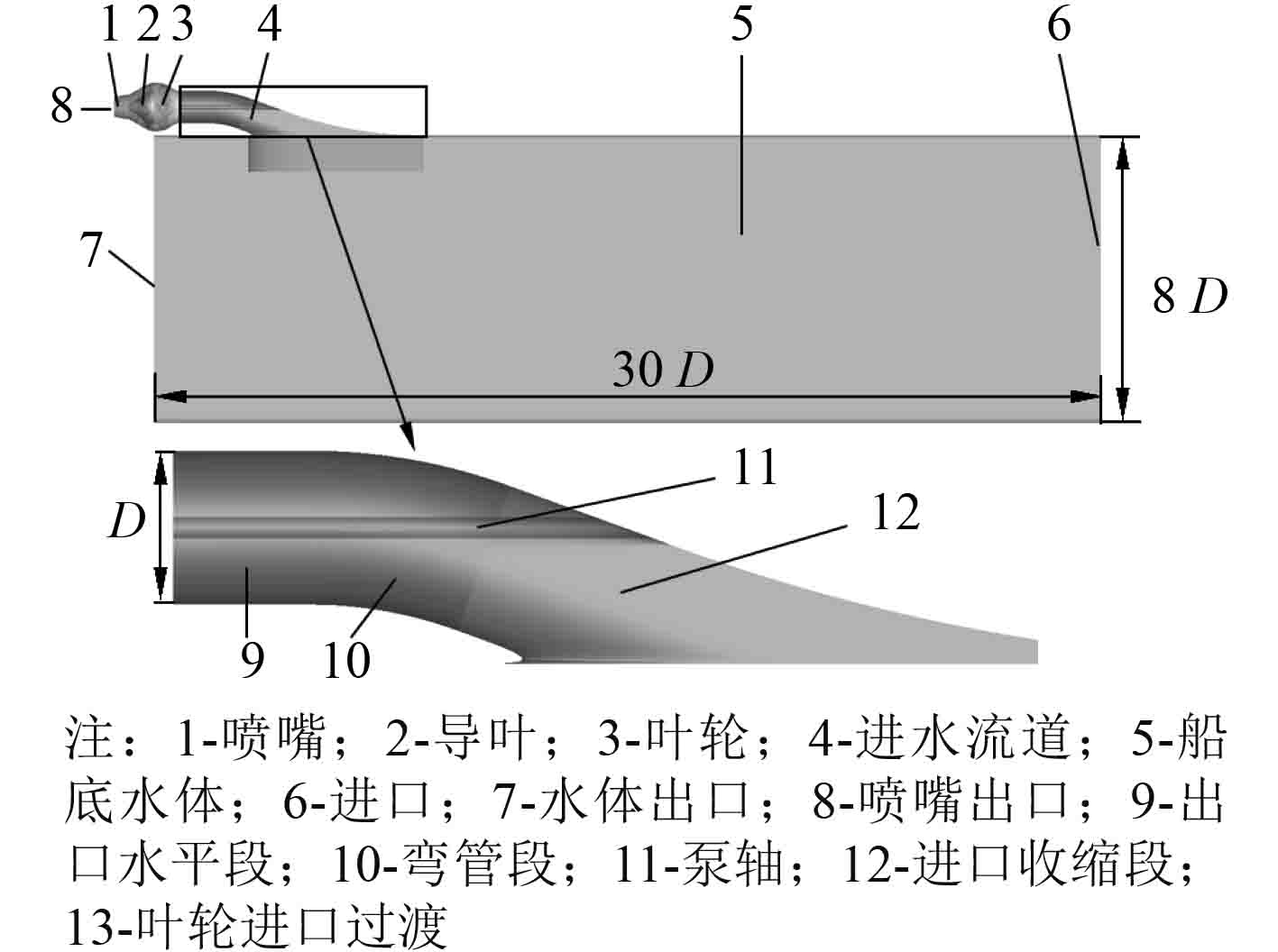
|
图 1 计算域 Fig. 1 Computational domains |
根据作用和几何特征的不同,将进水流道分为进口收缩段、弯管段和出口水平段。为了方便网格的剖分,分别对进口收缩段和弯管段、出口水平段进行建模。研究表明,进水流道的入流倾角、唇角和长度均为影响流道性能的重要因素,这些因素主要集中于进口收缩段,因此主要针对该部分网格展开无关性分析。当进口收缩段的网格数超过103万,进水流道内的水力损失基本不变,计算域网格总数为325万,图2为喷水推进泵及进水流道收缩段的网格。
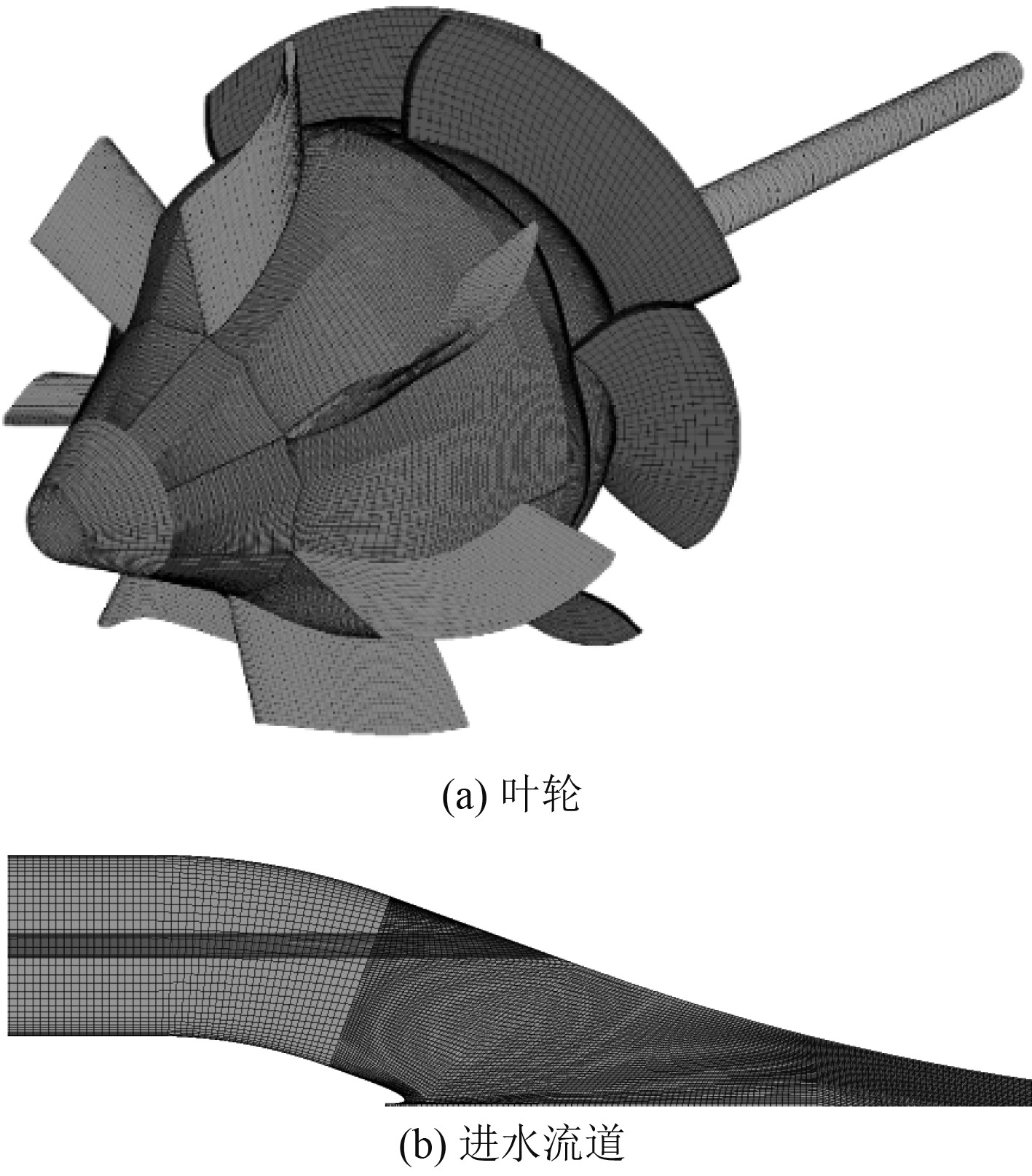
|
图 2 网格剖分 Fig. 2 Mesh generation |
船底水体进口取在离装置进口足够远处,设置为速度进口,大小为8 m/s。出口设置为平均静压出口,参考压力为1 atm。壁面边界为喷水推进装置进水流道、泵轴、叶轮、导叶和喷嘴的固体边界,以及船底矩形水体除进出口外的其他4个面,设置为无滑移条件,并采用scalable壁面函数对壁面进行处理。基于多坐标系法,除与喷水推进泵叶轮进出口断面的交界面设置为动静交界面外,其他均设置为静静交界面,转速设置为700 r/min。
2 计算结果分析 2.1 分析参数为了评价断面上流动的均匀性和平顺性,常选取轴向速度分布均匀度Vau和加权平均角θa展开分析,其计算公式如下式:
| ${V_{au}} = [1 - \sqrt {\sum\limits_{i = 1}^n {{{({v_{ai}}/{v_a} - 1)}^2}/n} } ] \times 100\% {\text{,}}$ | (3) |
| ${\theta _a} = \frac{{\sum\limits_{i = 1}^n {[(90^\circ - \arctan \frac{{{v_{ti}}}}{{{v_{ai}}}}){v_{ai}}]} }}{{\sum\limits_{i = 1}^n {{v_{ai}}} }}{\text{。}}$ | (4) |
式中:va为流道出口断面的平均轴向速度;n为节点数;vai为流量出口断面节点上的轴向速度;vti为流道出口断面节点上的横向速度。
轴向速度分布均匀度Vau值越接近100%,断面上的流速均匀性越好。加权平均角θa值越接近90°,流速方向与断面垂直度越好,水流的平顺性越好。
2.2 水力外特性扬程和效率这2个参数直接反映了泵装置的外特性性能,泵装置的扬程和效率如下式:
| ${H_T} = {{({P_{\rm{int} }} - {P_{outt}})}/ {\rho g}}{\text{,}}$ | (5) |
| $\eta = \frac{{\rho gQ{H_T}}}{P}{\text{。}}$ | (6) |
式中:Q为体积流量,m3/s;ρ为水的密度,取103 kg/m3;g为重力加速度,取9.81 m/s2;HT为推进泵扬程,m;Pint为推进泵进口总压,Pa;Poutt为推进泵出口总压,Pa;η为推进泵效率;P为轴功率,kW。
以最高效率点(BEP)的流量和效率为基准,对其他流量工况的流量和效率作归一化处理。
图3为该装置的外特性曲线,包括装置的Q–H曲线和Q–η曲线。图中工况C的效率最高;在0.5QBEP附近,装置进入水力不稳定区运行;B工况为水力不稳定区的拐点,文献[14]将B工况和A工况分别称为临界失速工况点和深度失速工况点。随着流量的增加,效率逐渐增加,在QBEP处达到最高效率点,流量继续增加时,效率迅速下降。Q–η曲线中,高效区的范围大致在0.76QBEP~1.1QBEP。
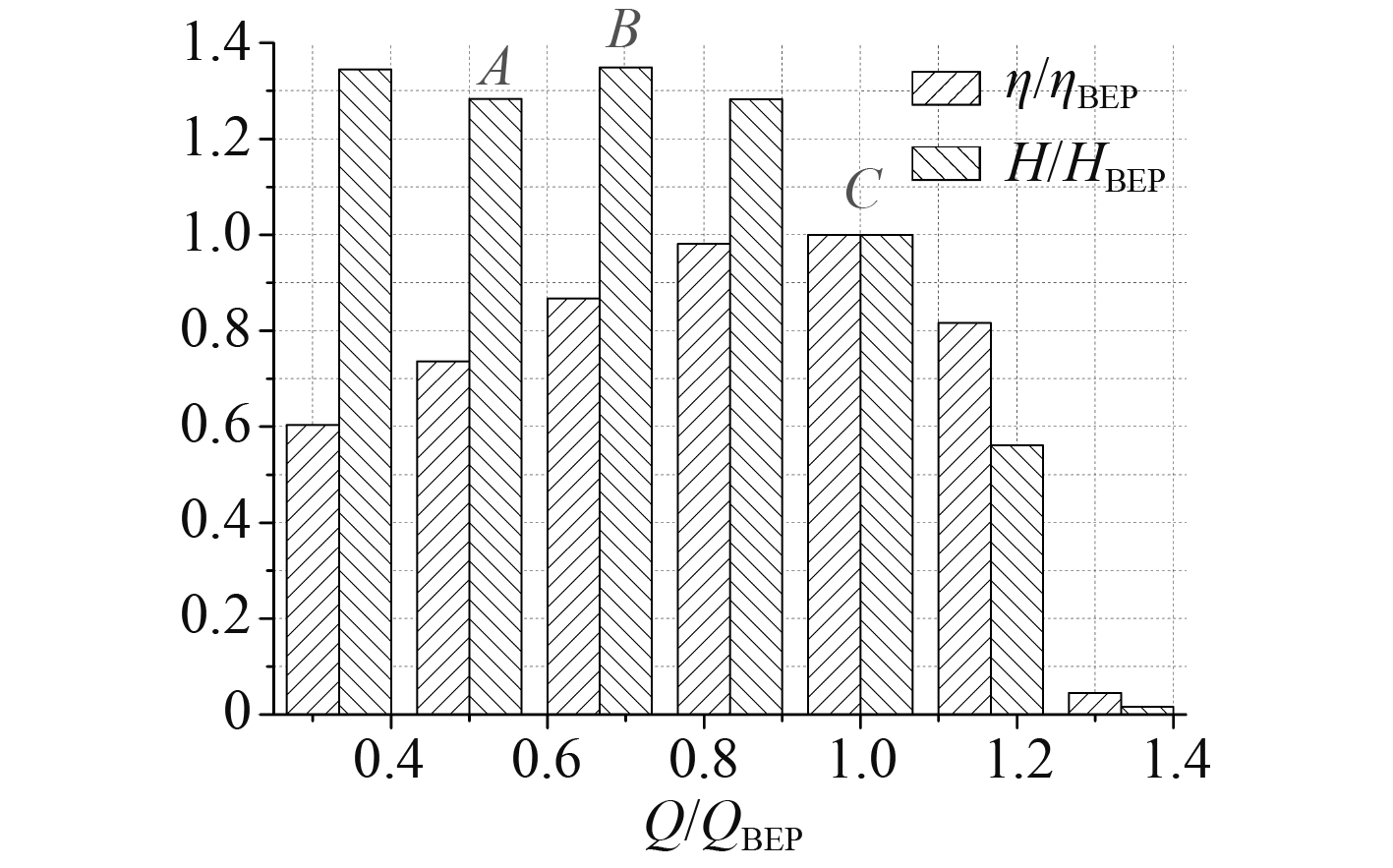
|
图 3 水力性能曲线 Fig. 3 Hydraulic performance curve |
图4为不同流量下流道内的三维流态侧视图和局部细节图。其中,左侧为流道内的三维流态侧视图,右侧显示的是三维流态侧视图黑框范围内的局部加密流线图。通过比较各子图发现:水沿着船底和流道上侧流入装置;唇部附近的流线有凹陷的趋势,流量越小,凹陷趋势越明显,随着流量的增加,流线凹陷趋势逐步减轻;流量为0.33QBEP时,可见在流道背部和弯管段后的流道上部两侧对称分布着十分严重的回流和螺旋流,该回流几乎充斥于唇部上侧的整个进水断面,唇部处的水弯折严重,螺旋流的范围也较大,占据了近一半的流道空间,这样的不良流态将严重影响水泵的入流流态和装置的整体性能;流量超过0.5QBEP后,回流便消失,流量分别为0.5QBEP和0.67QBEP时,仍可见轻微螺旋流的发生,随着流量的进一步增加,螺旋流逐渐消失不见,流道内的水流趋于平顺。

|
图 4 进水流道三维流态侧视图及局部细节图 Fig. 4 Side view and partial detail view of 3-D flow pattern in the passage inlet |
为了详细地捕捉进水流道各段关键断面上的能量特性和流动特征,沿水流的流动方向依次截取了流道进口断面、进口收缩段轴前断面、进口收缩段出口断面、弯管出口断面和流道出口断面等5个特征断面,记为n–n断面(n取1~5),如图5所示。
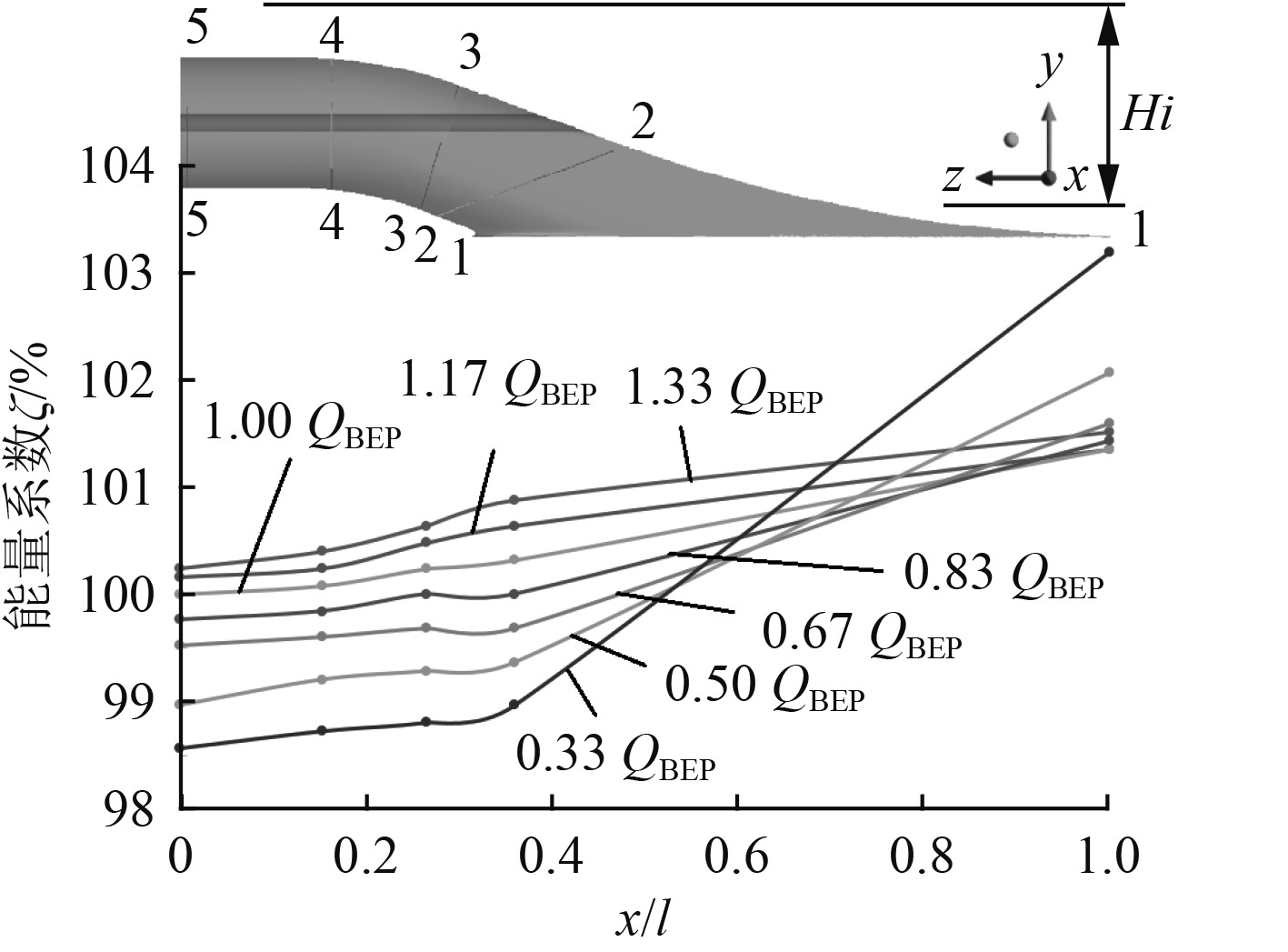
|
图 5 进水流道能量系数曲线 Fig. 5 Energy coefficient curve in the passage inlet |
假定喷水推进装置内的工作介质为不可被压缩的理想流体,因此可以采用伯努利方程计算不同流量工况下各分析断面的能量特性,如下式:
| ${H_i} + \frac{{{P_i}}}{\gamma } + \frac{{v_i^2}}{{2g}} = C{\text{。}}$ | (7) |
式中:γ进水流道进口断面为参考面;Hi为断面高程;Pi为断面压力;vi为断面平均流速。
以最优工况进水流道出口断面能量为基准,计算不同流量工况下各断面能量与其的比值,将该比值定义为能量系数ζ。将不同流量工况下各断面能量系数ζ的计算结果绘制成进水流道能量系数曲线,如图5所示。其中,横坐标为各断面距进水流道出口的相对距离x/l,l为流道长度,纵坐标为断面能量系数ζ。由于不考虑推进泵,流道内的能量损失为水力损失,不存在容积损失和泄漏损失。结果表明,0.33QBEP流量工况下,能量系数ζ变化量最大,随着流量的增加,流道进口到出口断面的能量持续降低,该趋势逐渐下降,水力损失不断增加。流道出口断面能量随着流量的增加而增加,不稳定区流量工况能量增加幅值较大。小流量工况下进水流道背部两侧的回流增加了水力损失,且在流道唇部上侧水流发生偏折流出流道引起了流量损失,由1–1断面过渡到2–2断面、3–3断面时,能量系数ζ曲线斜率较大,随着流量的增加,斜率逐渐减小。由3–3断面过渡到4–4断面时,由于弯管段有螺旋流的存在,小流量工况下的能量系数ζ曲线斜率略高于其他工况。流量超过0.67QBEP后,即高效区附近,4–4断面到5–5断面的水力损失很小,尤其是最高效率点,但随着流量的进一步增加,直管段水力损失增加,能量系数ζ曲线斜率略有增加。
2.5 进水流道断面速度分布情况沿流动方向各断面上的轴向速度分布也反映了流道内的流动特性,故分别将不同流量各断面上的轴向速度分布图如图6所示。比较后发现:1–1断面中心速度较大,2–2和3–3断面上的轴向速度呈现出左右基本对称的趋势;除0.33QBEP流量工况外,断面4–4上的轴向速度也呈左右对称分布;流量在0.33QBEP~0.67QBEP的范围内,2–2断面近唇部处存在负流速,这表明该断面上水流出现反向偏折;除0.33QBEP流量下,5–5断面轴向速度分布左右不对称较严重外,其余各流量下,5–5断面轴向速度分布均较为对称,该断面上的轴向速度分布情况将直接影响到叶轮的进水流态,进一步会影响到装置的性能。
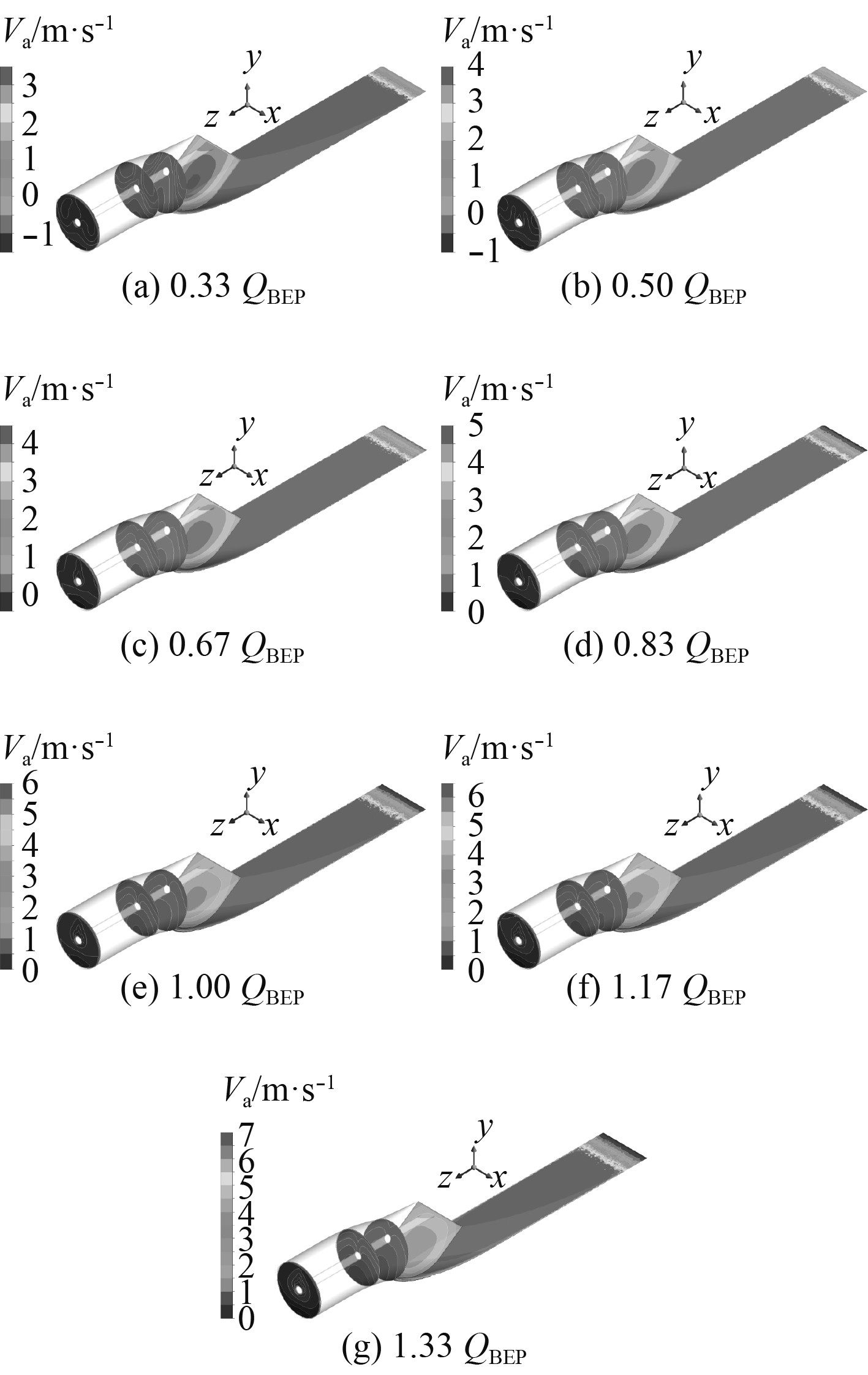
|
图 6 不同流量下各断面轴向速度分布图 Fig. 6 Axial velocity distribution of each section under different flow rates |
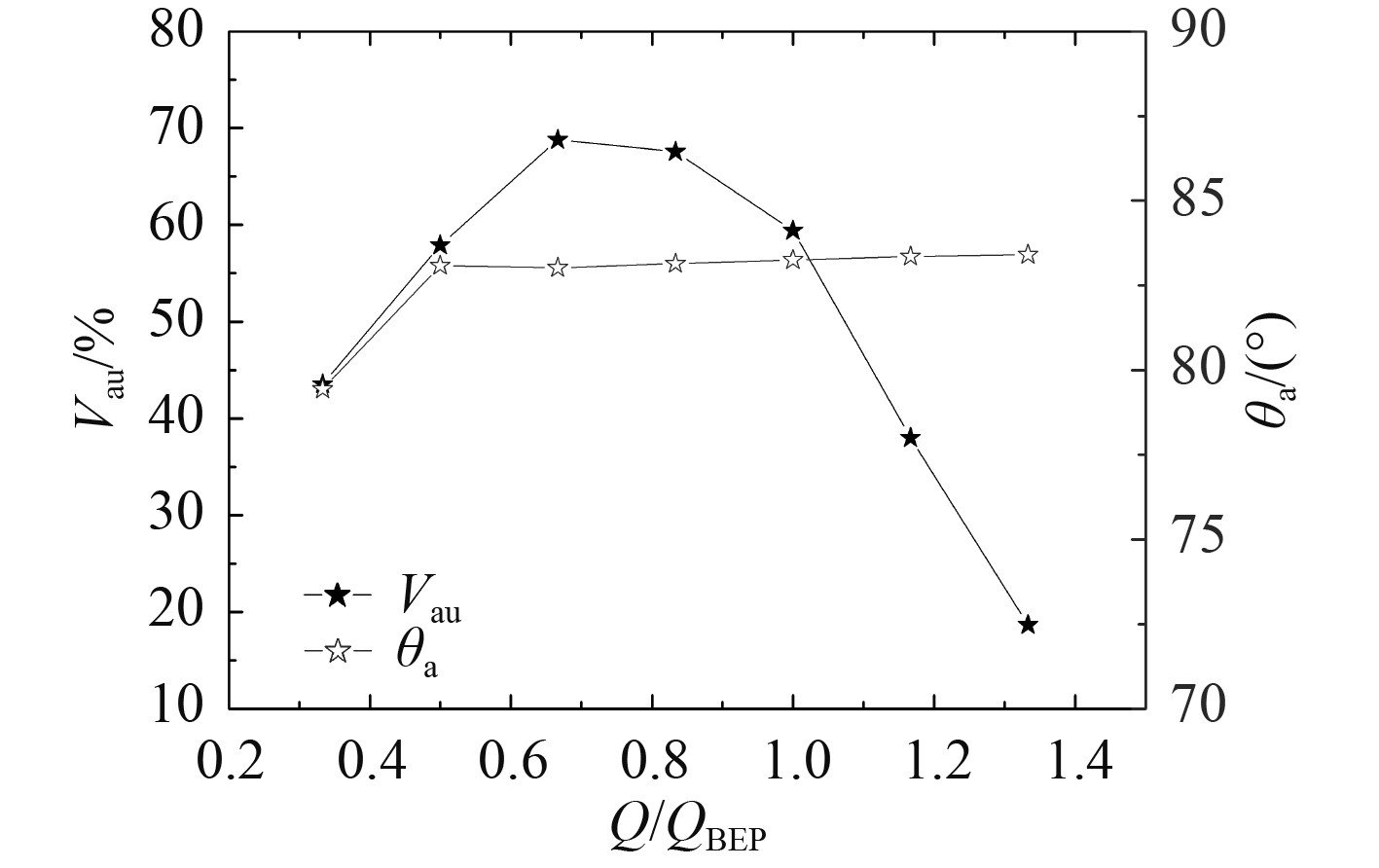
为研究流道出口断面轴向速度分布与装置性能的关系,将5–5断面作为研究对象,分析该断面轴向速度的分布情况,通过式(3)和式(4)计算了各流量下该断面上的轴向速度分布均匀度Vau和加权平均角θa,计算结果如表1所示,变化曲线如图7所示。
|
|
表 1 流道出口断面轴向速度分布均匀度和加权平均角 Tab.1 The uniformity and weighted average angle of the axial velocity distribution on the outlet of passage inlet |
|
图 7 流道出口断面轴向速度分布均匀度和加权平均角变化曲线 Fig. 7 Distribution uniformity and weighted average angle curve of axial velocity on the outlet of the passage inlet |
通过比较发现:1)流量从0.33QBEP增加到0.67QBEP时,Vau分别依次增加了14.36%和10.88%,增幅变小;流量从0.67QBEP增加1.33QBEP时,Vau分别依次减小了1.22%,8.15%,21.43%和19.31%,减幅逐渐增大;0.67QBEP和1.33QBEP的流量工况下,Vau达到最大和最小,分别为68.78%和18.67%,二者之间的差值达50.11%。2)流量从0.33QBEP增加到0.5QBEP时,θa增加了3.63°;流量从0.5QBEP增加到0.67QBEP时,θa减小了0.07°。随着流量的进一步增加,θa单调递增,且增幅越来越小,分别为0.12°,0.11°,0.10°和0.05°;流量分别为0.33QBEP和1.33QBEP时,θa分别取最小值和最大值,分别为79.44°和83.40°。
流道出口断面的Vau与流量之间的关系并非单调变化的,而是先增加后减小,其变化趋势与扬程性能曲线相似,但曲线拐点不一致,这2条曲线的拐点分别发生在0.67QBEP和1.0QBEP。随着流量的增加,出口断面上的θa也非单调变化的,而是先增后减再增的变化趋势,这与装置扬程的整体变化趋势完全相反,二者呈反相关关系,其产生变化的流量拐点亦完全吻合。这表明,装置出口断面上的流态与装置性能有着较为密切的关系,但并非简单的正相关或负相关的关系,最优工况对应的不一定是最优的出口断面流态,这是由于推进泵性能的影响因素较多,流道出口断面流态的好坏只是影响推进泵性能的一个方面。此外,它还反映着流道性能的好坏。
3 结 语基于CFD技术对喷水推进装置进水结构能量特性和水力流动特性展开研究,得出以下结论:
1)喷水推进装置外特性曲线存在明显的水力不稳定区,0.67QBEP流量工况和0.5QBEP流量工况分别为临界失速工况点和深度失速工况点,高效区的范围大致在0.76QBEP~1.1QBEP;
2)小流量工况下,流道背部和弯管段后的流道上部两侧发生严重的回流和螺旋流,随着流量的增加,回流和螺旋流均逐渐消失。
3)0.33QBEP流量工况下,能量系数ζ变化量最大,随着流量的增加,流道进口到出口断面的能量持续降低。由于回流的存在,进口收缩段在小流量工况下能量系数曲线斜率比较陡,该趋势会随着流量增加而趋于平缓。弯管段亦因为螺旋流的缘故,在小流量工况下呈现出较大的斜率。高效区附近的直管段能量系数曲线斜率接近于0,超出高效区,该斜率增加。
4)流道出口断面轴向速度分布均匀度变化曲线与扬程性能曲线趋势相似,但产生变化的流量拐点稍有差异。出口断面速度加权平均角与装置扬程曲线变化趋势完全相反,二者呈反相关关系,产生变化的流量拐点亦完全吻合。
| [1] |
金平仲. 船舶喷水推进[M]. 北京: 国防工业出版社.1986.
|
| [2] |
汤方平. 喷水推进轴流泵设计及紊流数值模拟[D]. 上海: 上海交通大学, 2006.
|
| [3] |
CARLTON J.S.. Marine propellers and propulsion(3rd edition)[M]. Butterworth–Heinemann Ltd. 2012.
|
| [4] |
金平仲. 喷水推进主要参数的确定[J]. 中国造船, 1978, 81-82. |
| [5] |
WADANI T K. On the design method of waterjet inlet of the SES'MEGVRO2[C]. FAST97.
|
| [6] |
P.A.BRANDNER, G.J.WALKER. A waterjet test loop for the tom fink cavitation tunnel[C] //International Conference on Waterjet Propulsion Ⅲ, 2001.
|
| [7] |
BRANDNER P.A., WALKERG.J... An experimental investigation into the performance of a flush water-jet inlet[J]. Journal of ship research, 2007, 51(1): 1-21. |
| [8] |
魏应三, 王永生, 丁江明. 喷水推进器进水流道倾角与流动性能关系研究[J]. 舰船科学技术, 2009, 31(4): 48-53. WEI Yingsan, WANG Yongsheng, DING Jiangming. Research on effect of inclination on characteristics of waterjet duct[J]. Ship Science and Technology, 2009, 31(4): 48-53. DOI:10.3404/j.issn.1672-7649.2009.04.007 |
| [9] |
彭云龙, 王永生, 常书平, 等. 高速摩托艇喷水推进器性能分析及其改进[J]. 大连海事大学学报, 2013, 39(2): 13-17. |
| [10] |
罗灿, 成立, 刘超, 等. 船用喷水推进泵装置水力特性数值模拟[J]. 排灌机械工程学报, 2015, 33(5): 374-379. |
| [11] |
许慧丽, 邹早建. 喷水推进器进流方向对流道内流场的影响数值研究[J]. 水动力学研究与进展(A辑), 2018, 33(02): 181-187. |
| [12] |
李臣, 束晓华, 赵春生. 基于流道倾角对喷水推进泵流道性能的影响研究[J]. 舰船科学技术, 2017, 39(17): 49-53. LI Cheng, SHU Xiaohua, ZHAO Chunsheng. Research on the influence of waterjet duct performance based on inclination of waterjet duct[J]. Ship Science and Technology, 2017, 39(17): 49-53. |
| [13] |
刘承江, 王永生, 张志宏. 喷水推进器数值模拟所需流场控制体的研究[J]. 水动力学研究与进展A辑, 2008, 23(5): 592-595. |
| [14] |
张睿. 轴流泵失速和空化流动特性及其性能改善研究[D]. 上海: 上海大学, 2014. ZHANG Rui. Research on the stall and cavitation flow characteristics and the performance improvement of axial-flow pump[D]. Shanghai: Shanghai University, 2014 |
 2020, Vol. 42
2020, Vol. 42
