2. 海军大连舰艇学院教务处,辽宁 大连 116018
2. Office of Academic Affairs, Dalian Naval Academy, Dalian, 116018, China
波浪水池是船舶与海洋工程问题研究的基础试验设施,在许多复杂水动力学问题研究中发挥着重要的作用。近年来,随着计算机技术的进步,以计算流体动力学方法为基础的数值波浪水池技术得到了蓬勃发展,该技术在计算机上即可仿真物理模型水池的功能,并且可获得丰富的流场细节信息,这使其逐渐在波浪演化[1-6]、船舶性能评估[7-12]等问题的研究中发挥重要作用,已成为当前水动力学技术发展的重要方向之一。
数值波浪水池的造波精度,是衡量其性能的标准。在构建数值波浪水池的过程中,发现波浪在传播过程中非常容易出现衰减,即由数值模拟得到的波浪时历,经谱分析得到的谱密度值明显小于相应的目标谱的谱密度值,而减小的幅度远远超过了由于流体粘性而导致的物理衰减。文献[13]对规则波的数值衰减问题进行了探讨,给出了在数值波浪水池中生成高精度规则波的方法。但不规则波的构成更加复杂,该方法不完全适用于不规则波的模拟。本文从对不规则波模拟精度影响较大的几个因素:网格尺寸、时间步长、欠松弛因子和频率等分数量4个方面,对不规则波数值模拟的精度进行研究,提出不规则波数值模拟的建议。
1 数学模型 1.1 RANS方程波浪的传播属于低速流动,因此波浪的演化可视为粘性不可压缩流体流动,遵循质量守恒方程和动量守恒方程[7]:
| $ {\frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial {x_i}}} = 0,(i = 1,2,3)}{\text{,}} $ | (1) |
| $\begin{split} \rho \frac{{\partial {u_i}}}{{\partial t}} +\rho {u_j}\frac{{\partial {u_i}}}{{\partial {x_j}}} =& \frac{\partial }{{\partial {x_j}}}\left( {\mu \frac{{\partial {u_i}}}{{\partial {x_j}}} -\rho \overline {u_i^\prime u_j^\prime } } \right) - \\ &\frac{{\partial p}}{{\partial {x_i}}} + \rho {f_i}\;\;{\text{,}}(i = 1,2,3){\text{。}} \end{split}$ | (2) |
式中:ρ为流体密度;p为流体压强;ui为流体时均速度分量;fi为流体体积力分量;v为相对于时均流速的湍流脉动速度分量;ν为流体的运动粘性系数;-
上述方程组并不封闭,因此还需要建立与雷诺应力有关的表达式,即建立湍流方程来封闭方程组求解,本文采用的是RNG k-ε湍流模型[14],其表达式为:
| $\frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho k{u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {{\alpha _k}{\mu _{eff}}\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} - \rho \varepsilon {\text{,}}$ | (3) |
| $\begin{split}\frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho \varepsilon {u_i}} \right)}}{{\partial {x_i}}} = &\frac{\partial }{{\partial {x_j}}}\left[ {{\alpha _\varepsilon }{\mu _{eff}}\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \\ &\frac{{C_{1\varepsilon }^*\varepsilon }}{k}{G_k} - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k}{\text{。}}\end{split}$ | (4) |
式中:
采用VOF(Volume of Fluid)方法[15]模拟波面的传播。该方法用体积分数Cq表示网格单元内某项流体体积占总体积的比例,其输运方程为:
| $\left\{ \begin{aligned} & \frac{{\partial {C_q}}}{{\partial t}} + u\frac{{\partial {C_q}}}{{\partial x}} + v\frac{{\partial {C_q}}}{{\partial y}} + w\frac{{\partial {C_q}}}{{\partial z}} = 0 {\text{,}}\\ & \sum\limits_{q = 1}^n {{C_q}} = 1\;\;{\text{,}}\;\;q = 1,2{\text{。}} \\ \end{aligned} \right.$ | (5) |
式中:q1为空气项;q2为水项。
2 数值波浪水池的构建 2.1 数值造波采用边界条件造波法生成波浪,即在造波边界处给出波速和波高的解析解实现数值造波[7]。根据线性叠加原理,长峰不规则波的波高和速度方程为:
| $\eta = \sum\limits_{i = 1}^n {\sqrt {2S({\omega _i})\Delta \omega } \cos ({k_i}x + {\omega _i}t + {\varepsilon _i})} {\text{,}}$ | (6) |
| $\left\{ \begin{split} & {u_1} = \sum\limits_{i = 1}^n {{A_i}{\omega _i}{e^{{k_i}z}}\cos ({k_i}x - {\omega _i}t + {\varepsilon _i})}{\text{,}} \\ & {u_3} = \sum\limits_{i = 1}^n {{A_i}{\omega _i}{e^{{k_i}z}}\sin ({k_i}x - {\omega _i}t + {\varepsilon _i})}{\text{。}} \\ \end{split} \right.$ | (7) |
式中:Ai,ωi,εi,ki,S(ωi)分别为第i个子波的波幅,波浪圆频率,初始相位,波数和波浪频谱密度;U为流速。
2.2 数值消波采用阻尼消波方法消波,该方法在数值水池末端区域加载的动量方程中增加阻尼源项[9],可以有效耗散不同波长和频率波浪的能量。为了增强消波效果,在消波区内沿布设的网格沿波浪传播方向逐渐稀疏,这样可以进一步加快波浪的数值耗散。阻尼消波区的动量方程为:
| $\left\{ \begin{aligned} & \frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial x}} + w\frac{{\partial u}}{{\partial z}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} + \nu \left( {\frac{{{\partial ^2}u}}{{\partial {x^2}}} + \frac{{{\partial ^2}u}}{{\partial {z^2}}}} \right) - \mu (x)u{\text{,}} \\ & \frac{{\partial w}}{{\partial t}} + u\frac{{\partial w}}{{\partial x}} + w\frac{{\partial w}}{{\partial z}} = g - \frac{1}{\rho }\frac{{\partial p}}{{\partial z}} + \nu \left( {\frac{{{\partial ^2}w}}{{\partial {x^2}}} + \frac{{{\partial ^2}w}}{{\partial {z^2}}}} \right) - \mu (x)w {\text{。}}\\ \end{aligned} \right.$ | (8) |
式中:μ(x)为一单调递增函数,消波区内越靠近出口消波功能越强。
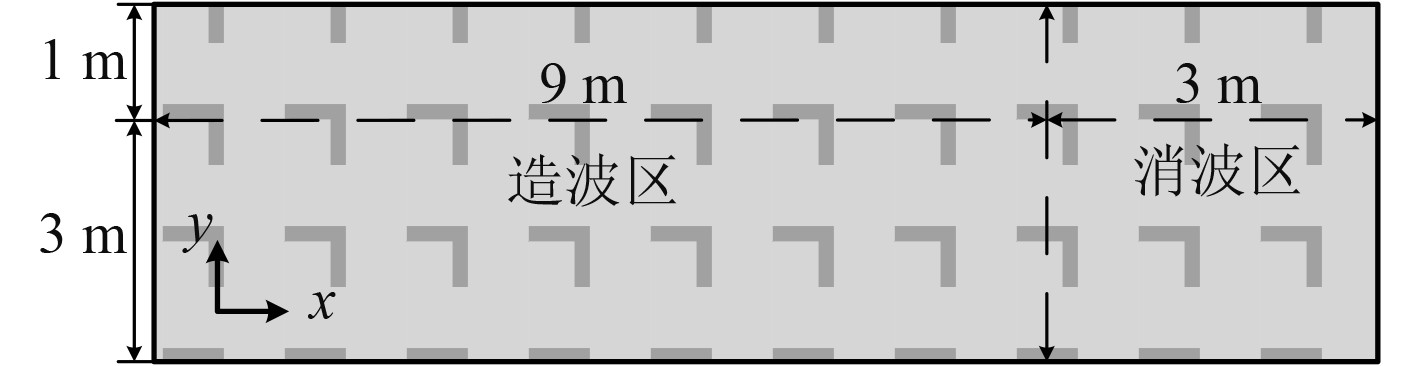
3 不规则波模拟精度影响因素分析为了便于对影响不规则波数值模拟精度的各个因素进行研究,建立一个长12 m,高4 m,深3 m的二维数值波浪水池,如图1所示。选择ITTC双参数谱作为目标谱,不规则波的三一波高为0.1 m,平均周期为1.22 s,平均波长为1.55 m,在数值波浪水池的工作区内距离入口4 m的位置,设置一个波高时历监测点。
|
图 1 数值波浪水池计算域 Fig. 1 Computation domain of numerical wave tank |
网格是影响数值模拟精度的关键因素之一,为了研究网格尺寸对不规则波数值模拟精度的影响,进行两组对比试验,在第1组数值试验中,进行波长方向网格数目对不规则波数值模拟精度的影响研究。在此基础上,在第2组数值试验中保持波长方向的网格数目,进行波高方向不同网格数目的影响研究,最终优选出适合不规则波数值模拟的网格尺寸。
在第1组数值试验中,保持三一波高内的网格数目为12个,在平均波长内分别布设20,30,40个网格。图2(a)为采用3种不同波长方向网格尺寸,所获得的波高时历与理论值的对比,其中线1为模拟值,线2为理论值。采用周期图法对波浪时历进行谱分析,图2(b)为波浪谱的对比图。由对比图可以看出,平均波长内网格数Nx=20时,模拟谱与目标谱误差很大,平均波长内网格数Nx=30时,模拟谱与目标谱吻合较好,平均波长内网格数Nx=40时,模拟谱与目标谱吻合最好。
|
图 2 波长方向网格数的影响 Fig. 2 The influence of grid number along wave length direction |
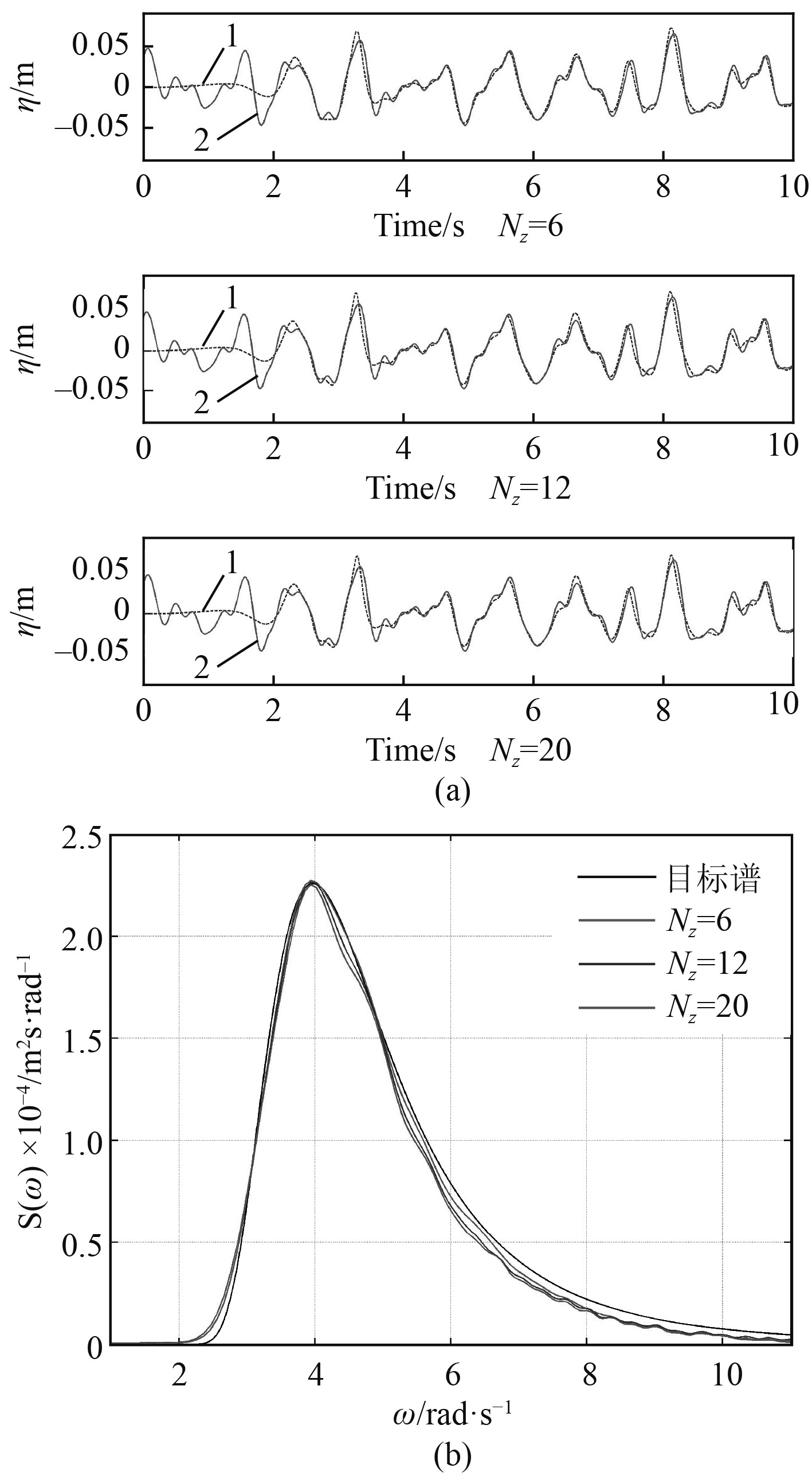
在第2组数值试验中,保持三一波长内的网格数目为40个,在三一波高内分别布设6,12,20个网格。图3(a)为采用3种不同波高方向网格尺寸所获取的波高时历,图3(b)为波浪谱的对比图。由对比图可以看出,当ω<5时,3种情况下的仿真精度相当,当ω>5时,三一波高内布设6个网格时,模拟谱有一定衰减,布设12个网格时,模拟谱与目标谱吻合较好,布设20个网格时,模拟谱与目标谱吻合度最好。
|
图 3 波高方向网格数的影响 Fig. 3 The influence of grid number along wave height direction |
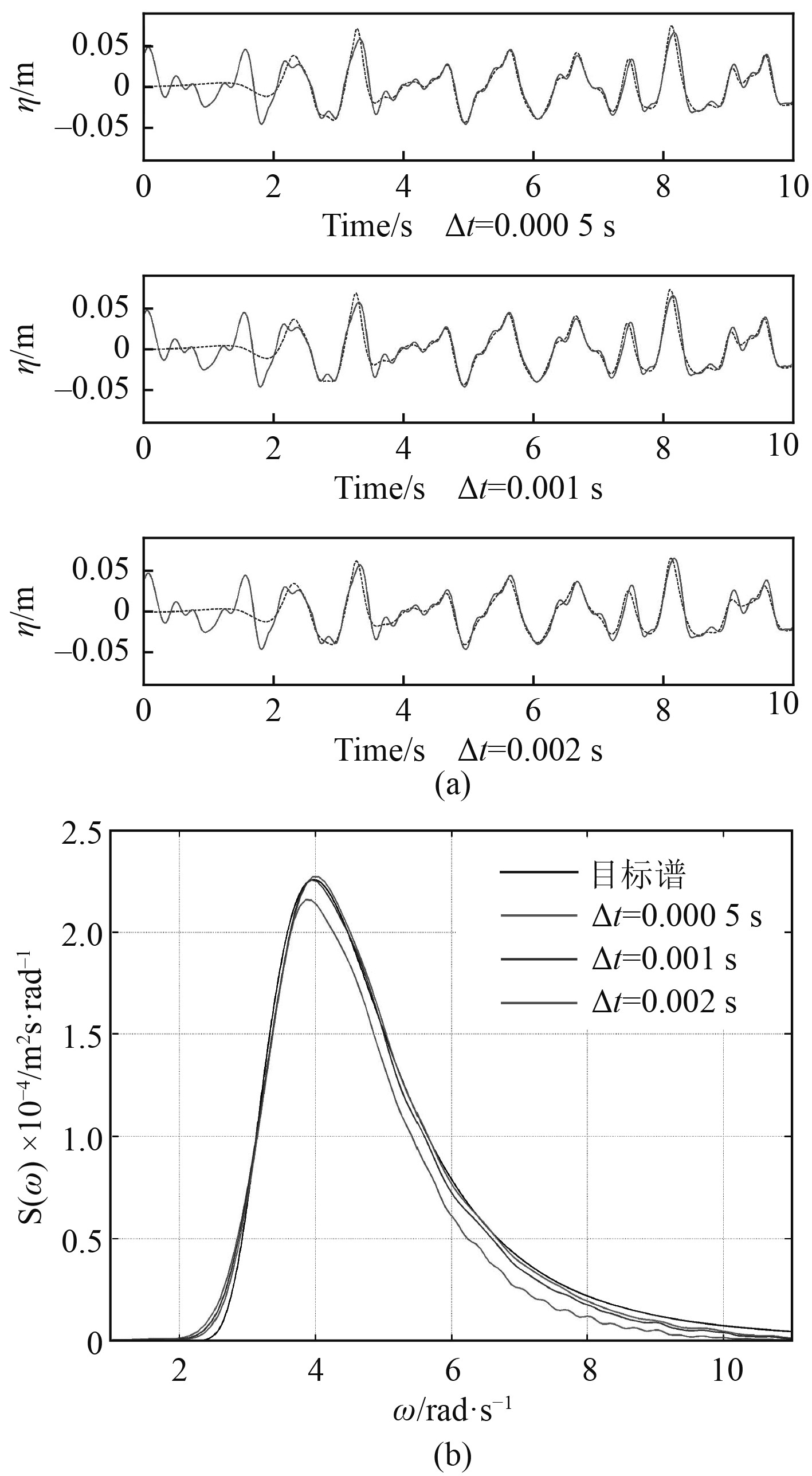
由于数值造波问题需要采用全隐式时间积分方案,该方案在时间域上只具有一阶截差精度,因此需要使用较小的时间步长,以保证获得较高精度的解。为了研究时间步长对不规则波数值模拟精度的影响,进行不同时间步长的对比试验。试验中保持平均波长内的网格数目为40个,三一波高内的网格数目为12个,时间步长分别为0.0005 s,0.001 s,0.002 s。
图4(a)为采用3种不同时间步长所获得的波高时历,图4(b)为波浪谱的对比图。由对比图可以看出,当时间步长为0.002 s时,模拟谱的中高频部分有一定的衰减,时间步长为0.001 s和0.0005 s时,模拟谱与目标谱均吻合较好,其中时间步长为0.001 s时,目标谱高频部分略有衰减,时间步长为0.0005 s时,模拟谱与目标谱吻合最好。
|
图 4 时间步长的影响 Fig. 4 The influence of time step |
欠松弛技术是使数值方程稳定地趋于收敛的一种有效方法。欠松弛因子α的取值范围为0~1。总体来言,增大的α值可以加快收敛速度,但若α取值过大时,可能导致系统很难得到稳定的解,甚至出现发散。减小α值会使计算的稳定性增加,但是若α取得过小,数值计算收敛的速度可能过慢,甚至影响计算的精度。波浪数值模拟属于气液两相流问题,因此,体积分数欠松弛因子对数值造波的精度具有一定影响,为了研究压力和体积分数欠松弛因子对不规则波数值模拟精度的影响,进行2组对比试验,分别选择不同的压力欠松弛因子和体积分数欠松弛因子进行模拟。
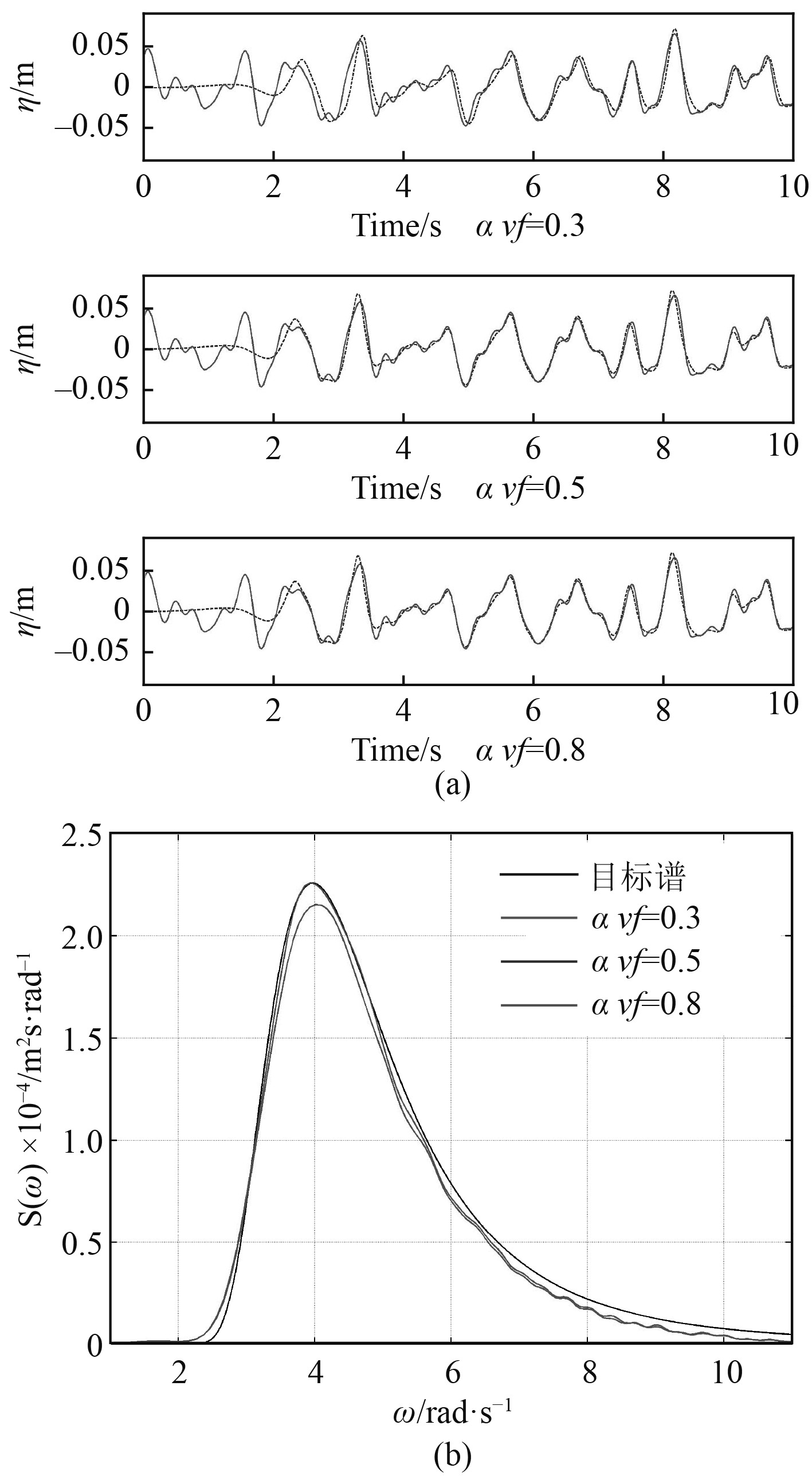
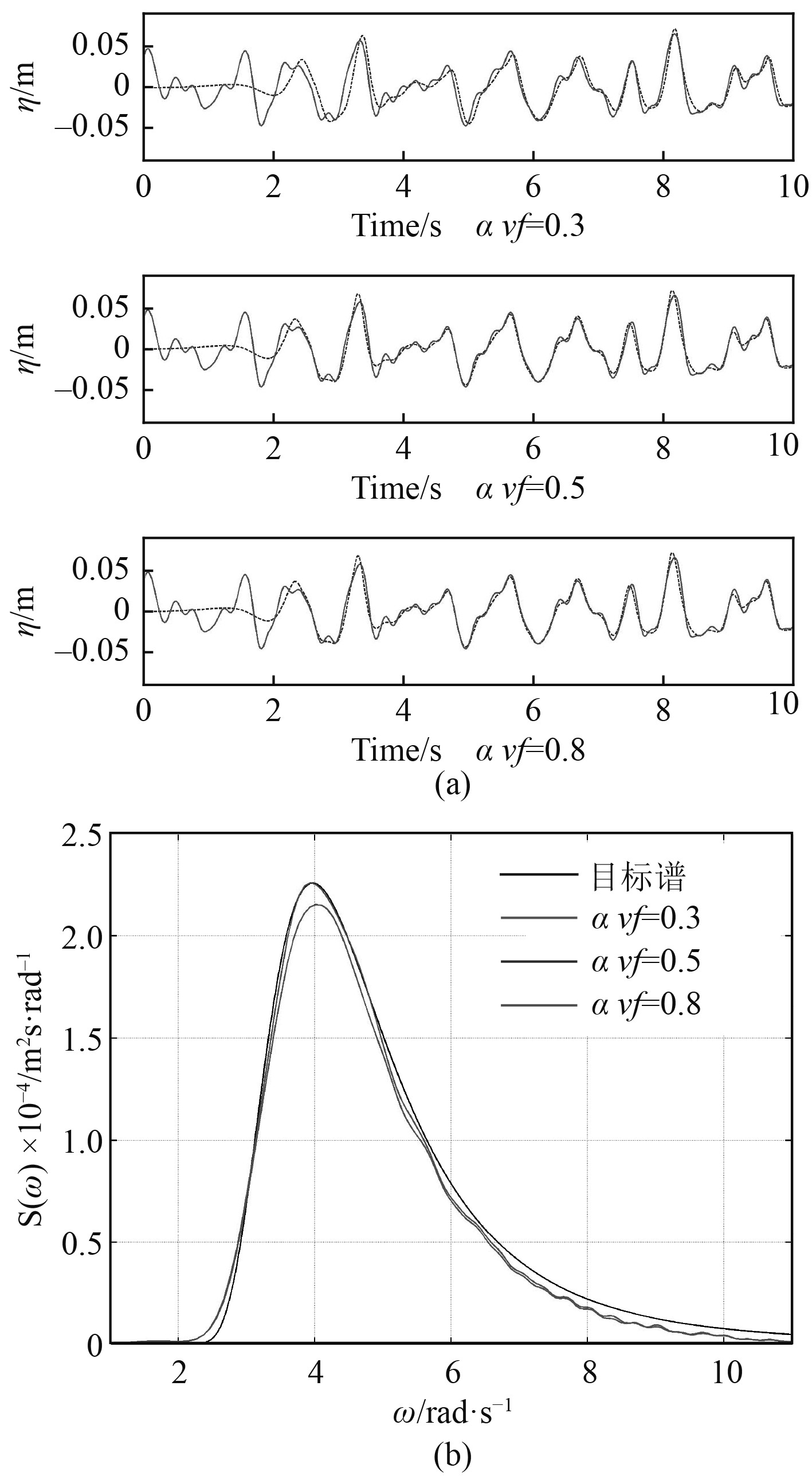
在第1组数值试验中,将压力欠松弛因子设置为0.5,而体积分数欠松弛因子分别取0.3,0.5,0.8。图5(a)为采用3种不同体积分数欠松弛因子所获取的波高时历,图5(b)为波浪谱的对比图。由对比图可以看出,当体积分数欠松弛因子为0.3时,模拟谱中频部分衰减比较明显,当体积分数欠松弛因子为0.5和0.8时,模拟谱与目标谱均吻合良好,且此时得到的2种模拟谱几乎没有差别,这说明体积分数欠松弛因子大于0.5时,即可保证数值仿真的精度。
|
图 5 积分数欠松弛因子的影响 Fig. 5 The influence of relaxation factor of volume fraction |
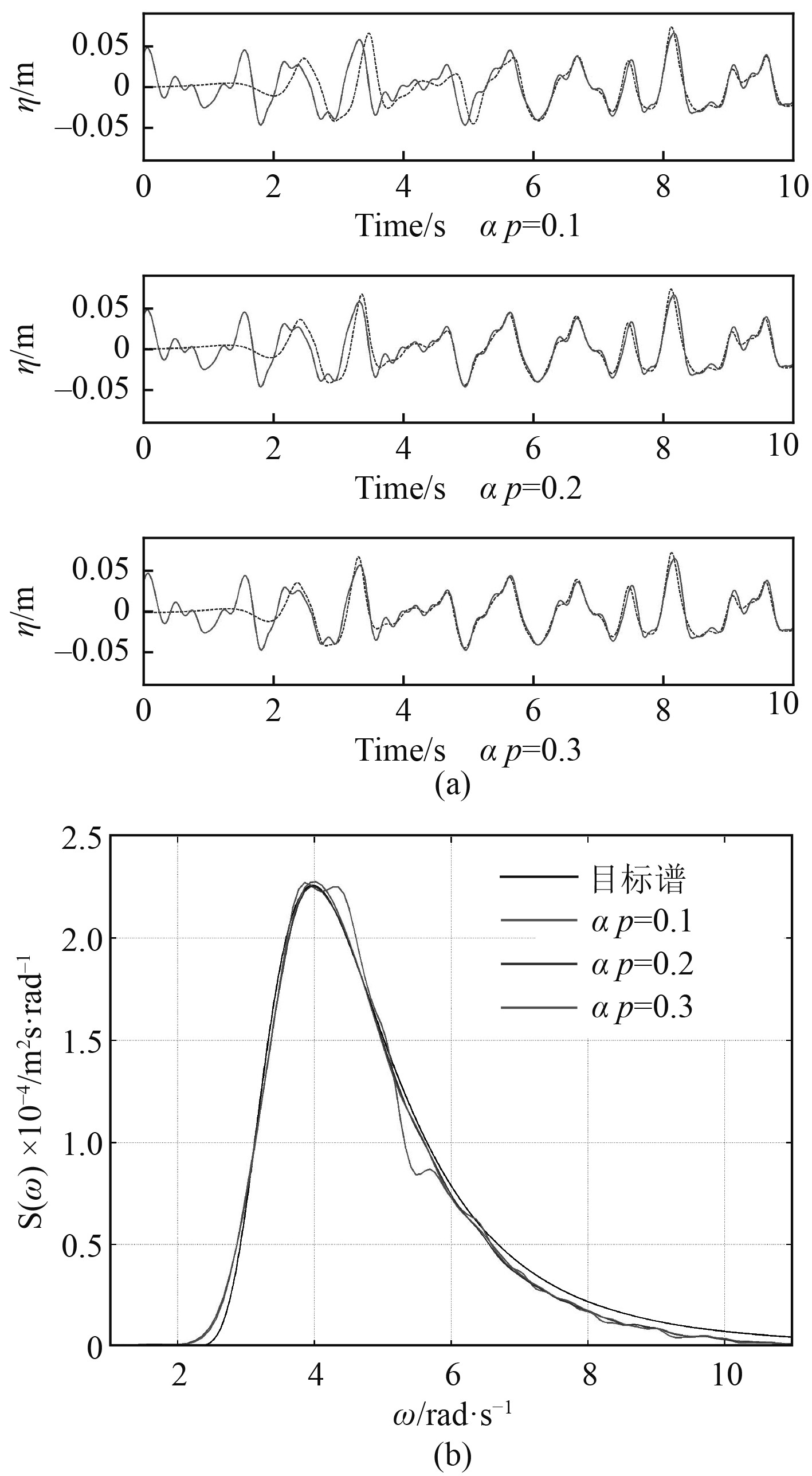
取体积分数欠松弛因子为0.5,而压力欠松弛因子分别取0.1,0.2,0.3。图6(a)为采用3种不同压力欠松弛因子所获得的波高时历。图6(b)为波浪谱的对比图。由对比图可以看出,当压力欠松弛因子为0.1时,模拟谱中频部分产生了一定的误差;当压力欠松弛因子为0.2和0.3时,模拟谱与目标谱均吻合良好,且此时得到的2种模拟谱几乎没有差别,这说明压力欠松弛因子大于0.2时,即可保证数值造波的精度。
|
图 6 压力欠松弛因子的影响 Fig. 6 The influence of relaxation factor of pressure |
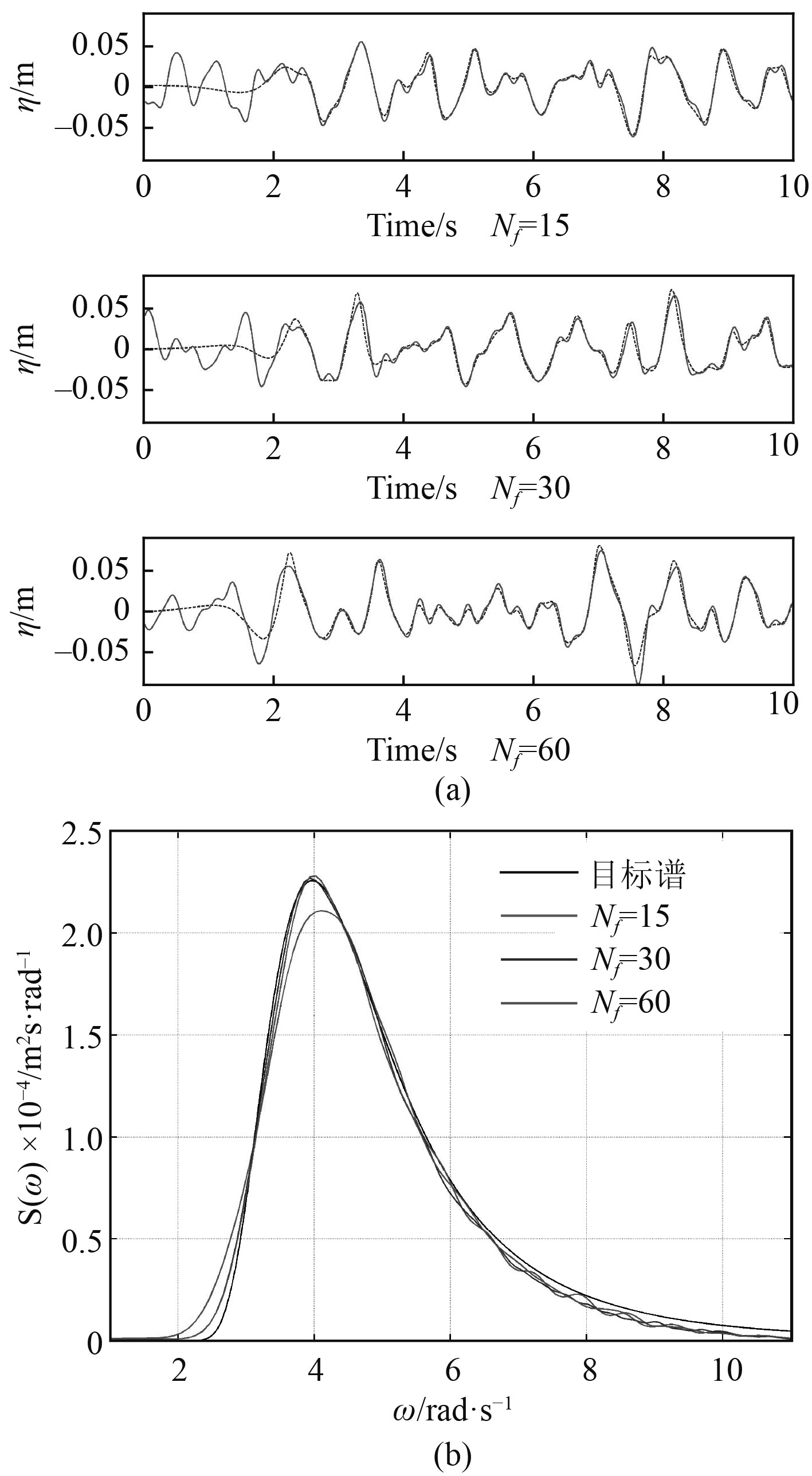
海浪谱的频率范围为0~∞,海浪谱能量大部分集中在某一频率范围,数值模拟时,需要根据线性叠加原理,将该频率范围分割为一定数量的区间,通常采用频率等分法进行分割,频率等分数量过少可能会影响数值造波的精度,过多会增加计算时间,因此需要对频率等分数量开展比较研究。分别将频率等分为:15,30和60份,数值模拟中其他的参数设置为:网格数目在平均波长布设40个,在三一波高内布设20个,时间步长设置为0.001 s,体积分数欠松弛因子和压力欠松弛因子分别设置为0.5和0.3。图7(a)为设置3种不同频率等分数量所获得的波高时历,图7(b)为波浪谱的对比图。从图中可以看出,频率等分为15个时,模拟谱中低频部分有所增大,中频部分有所减小;频率等分为30和60时,模拟谱与目标谱均吻合良好,这说明频率等分数量超过30时,即可保证不规则波数值模拟的精度。
|
图 7 频率等分数量的影响 Fig. 7 The influence of the number of discrete frequencies |
通过上述对比研究可以看出,通过加密网格、缩小时间步长、增大欠松弛因子,增加频率等分数量,可以提高使数值水池生成不规则波的精度,但数值造波的精度并不会随着上述因素的细化和提高而不断提高,即精度的提高是有上限的。与此同时,过度细化网格、缩小时间步长、增加频率等分数量,会使数值计算时间明显增加,且数值模拟中采用过大的欠松弛因子还可能导致数值计算的不稳定。因此,应根据需求平衡计算精度和计算效率关系,选用合适的数值计算参数。根据上述的对比试验结果,提出以下几点不规则波数值模拟的建议:
1)网格数量在平均波长方向为30~40个,三一波高方向为12~20个;
2)时间步长取值为波浪平均周期的1/1000~1/2000;
3)压力和体积分数欠松弛因子分别大于0.2和0.5;
4)频率等分区间数量为30~60个。
4 验 证为了验证本文数值模拟模式的有效性,选择模拟ITTC双参数谱的模型尺度长峰不规则波和实测谱的实尺度长峰不规则波进行数值模拟,与目标谱参数进行比较,验证试验的波浪参数设置如表1所示。
|
|
表 1 波浪谱参数 Tab.1 Wave parameters |
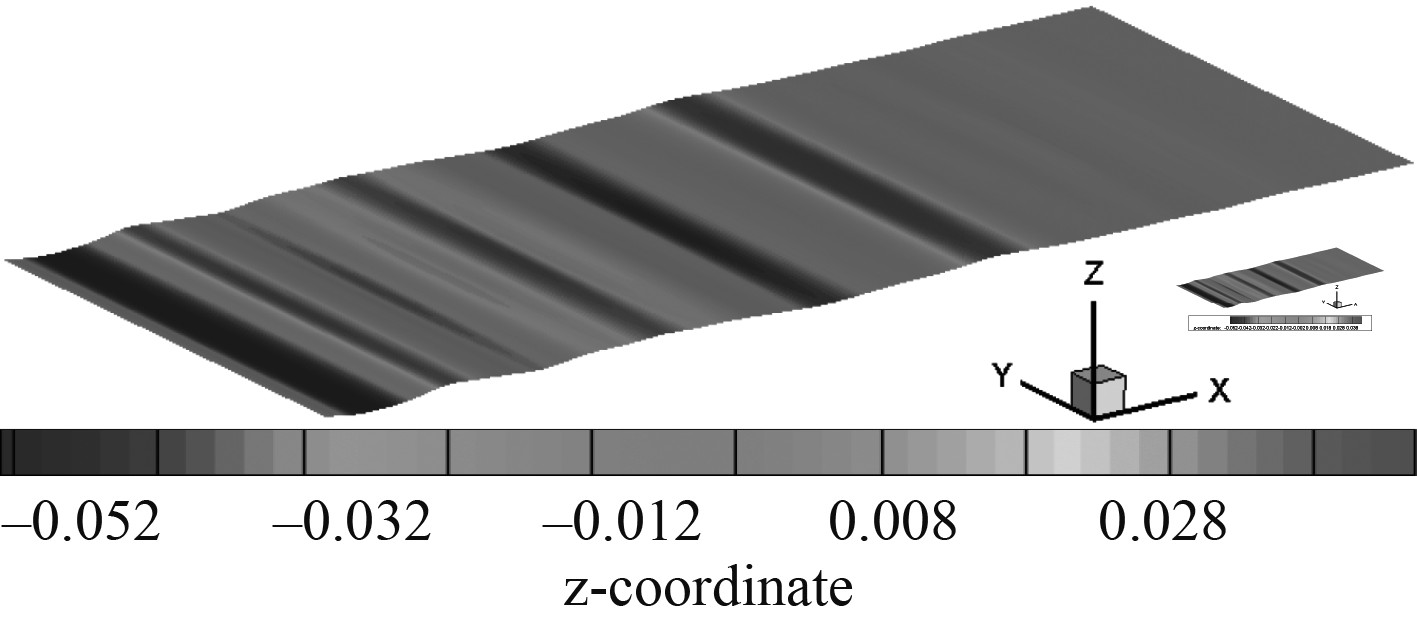
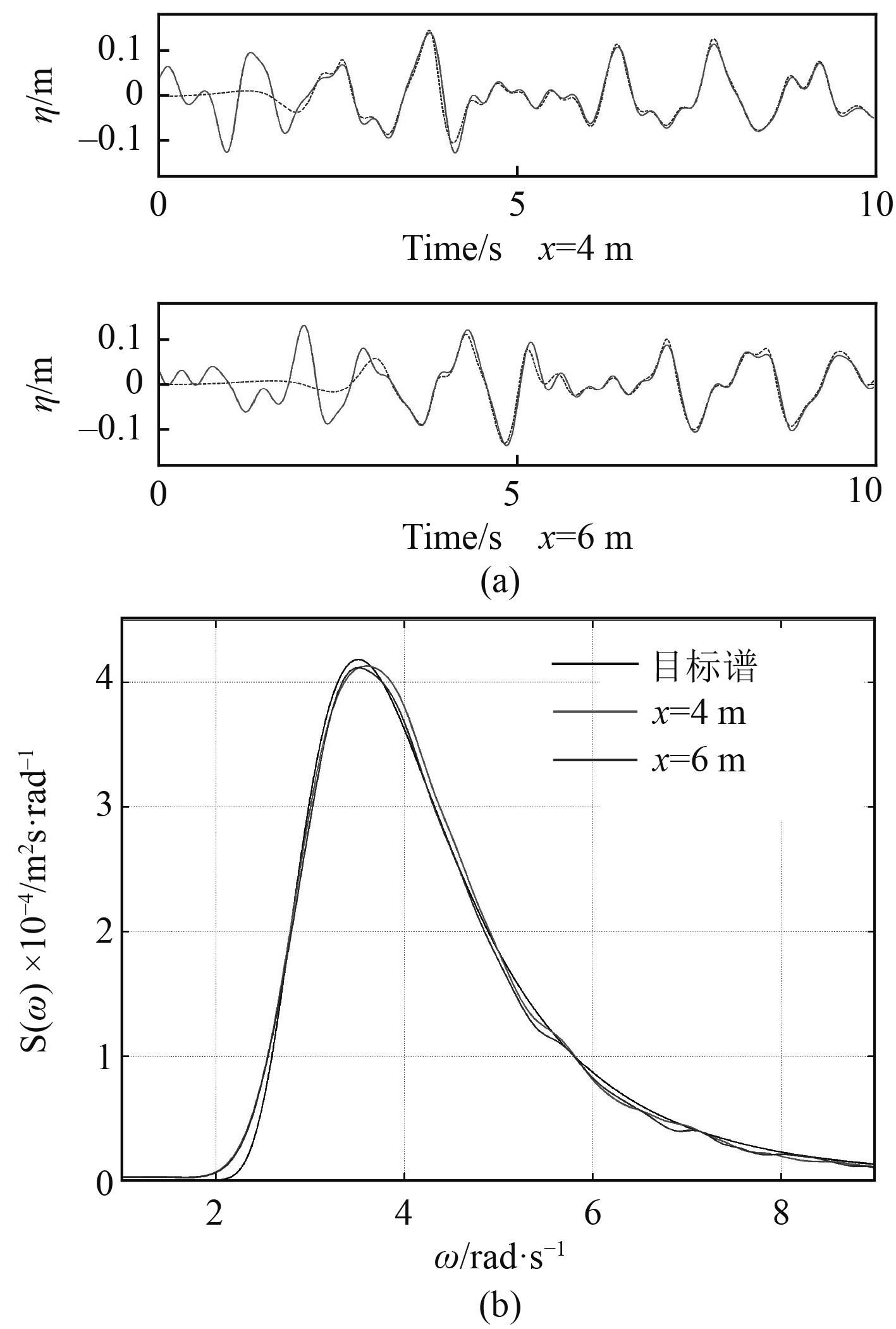
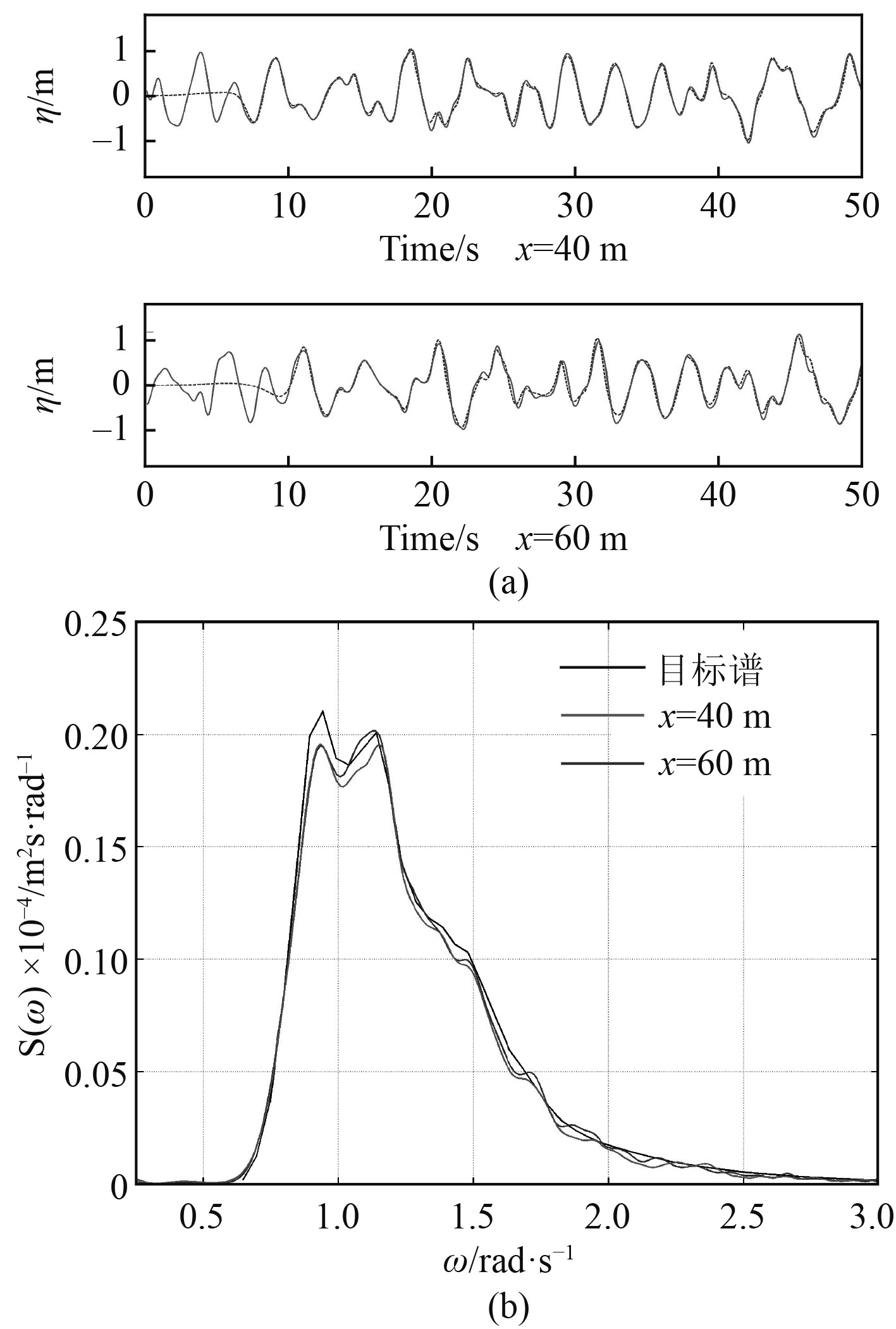
图8为模拟的长峰不规则波的瞬时波面波高分布图。算例1将监测点设置在工作区距入口4 m和6 m处,算例2将监测点设置在工作区距离入口40 m和60 m处,图9(a)和图10(a)为所测得的波高时历,图9(b)和图10(b)为两算例的波浪谱的对比图。通过对比图可以看出,模拟值与目标值吻合较好。
|
图 8 长峰不规则波瞬时波高图 Fig. 8 Instantaneous picture of irregular wave height |
|
图 9 算例1模拟结果 Fig. 9 Sumulation result of case1 |
|
图 10 算例2模拟结果 Fig. 10 Sumulation result of case2 |
中华人民共和国交通部发布JTJ/T 234−2001《波浪模型试验规程》[16]规定了单项不规则波模拟的允许偏差:
1)波谱总能量允许偏差为±10%;
2)谱峰频率模拟值允许偏差为±5%;
3)在谱密度大于或等于0.5倍谱密度峰值的范围内,谱密度分布允许偏差为±15%
4)有效波高、有效周期或谱峰周期允许偏差为±5%。
对监测的波面时历进行谱分析,可以得到本文数值模拟长峰不规则波的各项统计特征值,与目标值的对比如表2所示。表中所列数据为工作区2个监测点数据平均值,其中算例2实测谱有2个谱峰值,因此对比了2处峰值的谱峰频率。从表2可以看出,数值模拟的三一波高略偏小,波浪平均周期及谱峰频率与目标值吻合良好,上述3项特征值的相对误差均在4%以下,谱面积的相对误差低于6%。与规范中的标准相比,本文的模拟相关特征值均低于规范允许偏差。另外,对于实测谱的模拟,本文模拟再现了双峰特征,并且具有较高的精度,说明本文提出的数值模拟方案同样适用于实测海浪的模拟。
|
|
表 2 数值仿真误差 Tab.2 Relative errors of simulation result |
本文采用计算流体动力学方法,在数值水池中生成长峰不规则波。在此基础上,对影响长峰不规则波数值模拟精度的几项因素:网格尺寸、时间步长、欠松弛因子及频率等分数量开展对比试验,研究不规则波数值仿真精度随上述因素的变化规律,给出了不规则波数值模拟的建议。最后,采用本文提出的方法,生成了模型尺度和实尺度的不规则波,符合相关行业标准的要求,验证了本文提出的数值模拟模式的有效性。
| [1] |
PARK J.C., UNO Y., SATO T., et al.. Numerical reproduction of fully nonlinear multi-directional waves by a viscous 3D numerical wave tank[J]. Ocean Engineering, 2004, 31: 1549-1565. DOI:10.1016/j.oceaneng.2003.12.009 |
| [2] |
周勤俊, 王本龙, 兰雅梅, 等. 海堤越浪的数值模拟[J]. 力学季刊, 2005, 26(4): 629-633. ZHOU Qinjun, WANG Benlong, LAN Yamei, et al. Numerical simulation of wave overtopping over seawalls[J]. Chinese Quarterly of Mechanics, 2005, 26(4): 629-633. DOI:10.3969/j.issn.0254-0053.2005.04.019 |
| [3] |
董志, 詹杰民. 基于VOF方法的数值波浪水槽及造波、消波方法演技[J]. 水动力学研究与进展(A辑), 2009, 24(1): 15-21. DONG Zhi, ZHAN Jiemin. Comparison of existing methods for wave generating and absorbing in VOF-based numerical tank[J]. Journal of Hydrodynamics (Ser.A), 2009, 24(1): 15-21. |
| [4] |
冯光, 吴乘胜, 郑文涛, 等. 数值水池短峰不规则波模拟研究[J]. 船舶力学, 2010, 14(4): 347-354. FENG Guang, WU Chengsheng, ZHENG Wentao, et al. Reproduction of short-crested irregular waves by a viscous numerical wave tank[J]. Journal of Ship Mechanics, 2010, 14(4): 347-354. DOI:10.3969/j.issn.1007-7294.2010.04.004 |
| [5] |
CAO Hongjian. Development of viscous numerical wave tank and its application in ocean engineering[D]. Shanghai: Shanghai Jiao Tong University. 2014
|
| [6] |
SHEN Zhi-rong, WAN De-cheng. An irregular wave generating approach based on naoe-FOAM-SJTU solver[J].
|
| [7] |
石博文, 刘正江, 吴明. 船模不规则波中顶浪运动数值模拟研究[J]. 船舶力学, 2014, 18(8): 906-915. SHI Bowen, LIU Zhengjiang, WU Ming. Numerical simulation of ship motions in irregular head waves[J]. Journal of Ship Mechanics, 2014, 18(8): 906-915. DOI:10.3969/j.issn.1007-7294.2014.08.005 |
| [8] |
石博文, 刘正江, 吴明. 基于当前海浪谱的甲板上浪数值模拟[J]. 大连海事大学学报, 2016, 42(3): 31-36. SHI Bowen, LIU Zhengjiang, WU Ming. Numerical simulation of green water based on measured spectrum of ocean wave[J]. Journal of Dalian Maritime University, 2016, 42(3): 31-36. |
| [9] |
吴明, 石爱国, 杨波, 等. 基于CFD的船舶斜浪三自由度运动仿真研究[J]. 计算机应用研究, 2013, 30(7): 2233-2235. WU Ming, SHI Aiguo, YANG Bo, et al. Simulation research of three DOF motions of ship in oblique waves based on CFD[J]. Application Research of Computers, 2013, 30(7): 2233-2235. DOI:10.3969/j.issn.1001-3695.2013.07.079 |
| [10] |
STERN Frederick, WANG Zhaoyuan, YANG Jianming. Recent progress in CFD for naval architecture and ocean engineering[J]. Journal of Hydrodynamics, 2015, 27(1): 1-23. DOI:10.1016/S1001-6058(15)60452-8 |
| [11] |
DIEZ M, BROGLIA R, DURANTE D, et al. Validation of Uncertainty Quantification Methods for High-Fidelity CFD of Ship Response in Irregular Waves[C] // Proc. 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, January 9-13, 2016.
|
| [12] |
SHEN, ZR and WAN, DC. RANS Computations of Added Resistance and Motions of Ship in Head Waves[C] // Proceedings of the Twenty-second International Offshore and Polar Engineering Conference, Rhodes, Greece. 2012, Vol 3, 1096–1103.
|
| [13] |
杨波, 石爱国, 吴明. 基于抗数值衰减的短波数值模拟研究[J]. 水运工程, 2011(12): 30-35. YANG Bo, WU Ming, SHI Aiguo. Research on wave numerical attenuation problem[J]. Port & Waterway Engineering, 2011(12): 30-35. DOI:10.3969/j.issn.1002-4972.2011.12.006 |
| [14] |
YAKHOT, V, ORSZAG, SA, THANGAM, S, GATSKI, TB and SPEZIALE, CG. Development of turbulence models for shear flows by a double expansion technique[J]. Physics of Fluids A, Vol. 4, No. 7, 1510–1520.
|
| [15] |
HIRT, CW and NICHOLS, BD. Volume of fluid method for the dynamics of free boundaries[J]. Comp. Phys. Vol 39, No 1, pp 201–225.
|
| [16] |
中华人民共和国交通部. JTJ/T 234—2001, 波浪模型试验规程[S]. 北京: 人民交通出版社, 2001. Ministry of Transport of the PRC. JTJ/T 234—2001, Wave Model Test Regulation[S]. Beijing: China Communications Press, 2001. |
 2020, Vol. 42
2020, Vol. 42
