自然界中的鱼类具备超凡的运动特性,如快速性、高机动性等。柔性波动方式更是鱼类诸多游动方式中推进特性最优的运动方式之一[1]。鱼类采取柔性波动方式运动时,整个身体采取横向振动变形,其典型代表如幔鱼等。关于鱼形体柔性波动推进的研究最早可以追溯到1970年英国Lighthill[2-3]提出的著名细长体理论,该理论使得行波推进运动方程在势流领域首次拥有了数值解。童秉纲院士、陆夕云院士[4-6]等在此基础上开创了三维行波板理论。随着计算机的发展,邵雪明[7]、王志东[8]等开展了大量的鱼形体粘性行波推进研究工作。
上述研究工作大多针对于鱼形体在低雷诺数下的推进特性,而关于高雷诺数鱼形体的推进特性则少有涉及。不同雷诺数下鱼形体的柔性推进特性势必存在差异,鉴于此,本文在前期研究[9]的基础上开展非定常状态下可变形翼高雷诺数推进特性的数值模拟研究。对不同来流速度、变形位置及不同变形幅值组合形成的翼型进行数值模拟,给出了推力特性以及周围流场情况,为下一步进行连续变形翼流体动力特性试验研究提供初步思路。
1 数值计算方法考虑不可压缩流动湍流问题,其运动控制方程为:
| $\frac{{\partial {u_i}}}{{\partial {x_i}}} = 0\text{,}$ | (1.1) |
| $\frac{{\partial {u_i}}}{{\partial t}} + {u_j}\frac{{\partial {u_i}}}{{\partial {x_j}}} = - \frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{{x_j}}}[(\gamma + {\gamma _t})(\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}})]\text{。}$ | (1.2) |
式中:
本文的柔性翼行波推进运动属于典型的动边界问题,变形翼摆动推进过程中,翼型本身时刻都在做扭曲变形运动,壁面附近计算网格的位置和形状也必须时刻进行相应的调整,因此需要用到Fluent中的动网格技术来捕捉变形翼的运动边界。根据前期工作经验,本文选取动网格技术中的网格重构技术对动边界进行捕捉,具体动网格技术见参考文献[10-11]。
2 计算模型、网格及数值方法验证 2.1 计算模型计算对象为二维的NACA0012翼型,具体如图1所示。
|
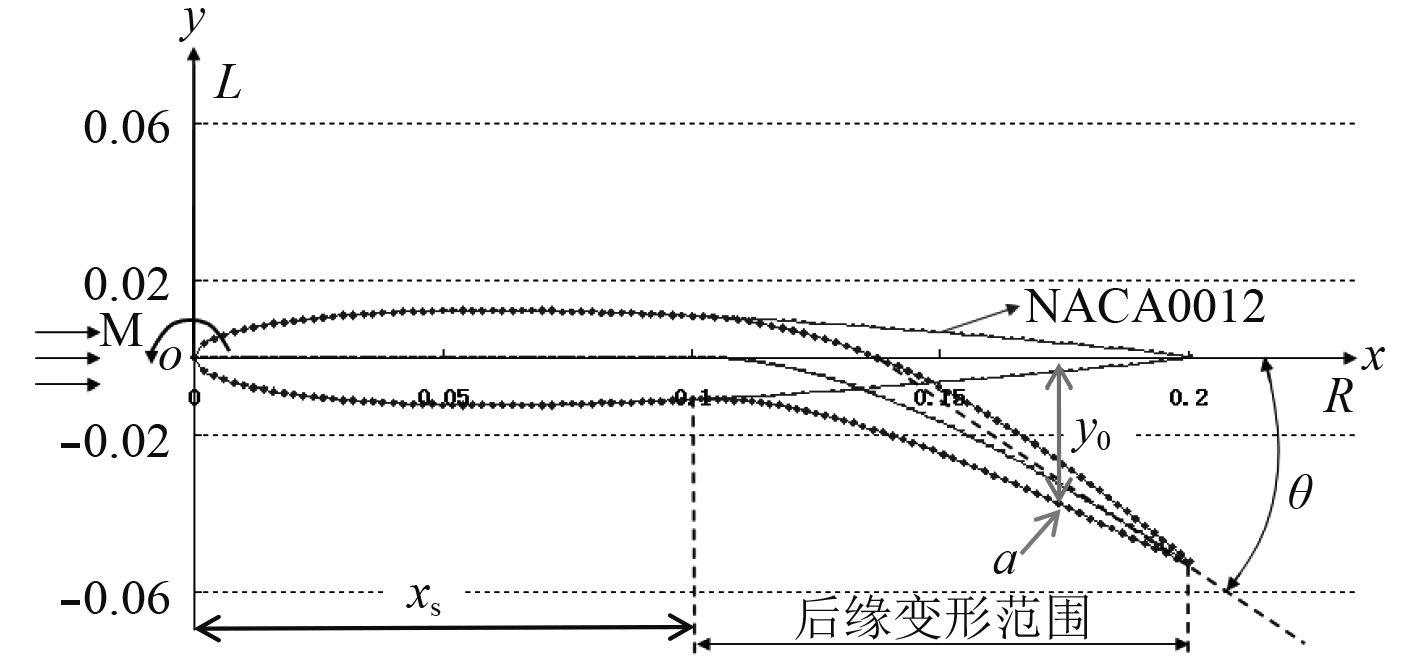
图 1 计算模型示意图 Fig. 1 Diagram of computation model |
可变形翼舵中弧线长c = 0.2 m, 后缘变形起始位置xs,以翼型尾部任意一点a(初始横纵坐标分别为x0和y0,其中x0>xs)为例,翼型变形运动方程如下式:
| $\begin{split}x = & x_0, y = {y_0} + A \cdot \sin (2{\text{π}} ft) = {y_0} +\\ &(c - {x_0}) \cdot \tan (\theta ) \cdot \sin (2{\text{π}} ft)\text{。}\end{split}$ | (1) |
其中f为运动频率,A为运动幅值。
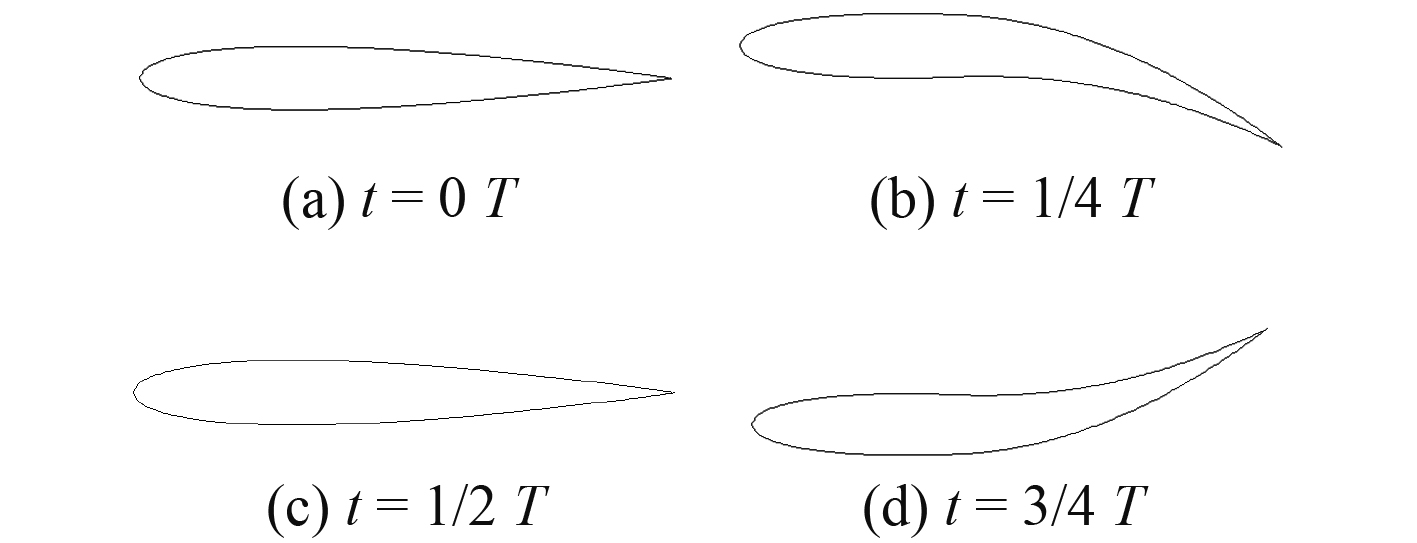
一个运动周期内变形翼的运动过程如图2所示。其中T为运动周期,其与频率f的关系为T = 1/f。
|
图 2 一个周期内可变形翼运动示意图 Fig. 2 Motion diagram of deformable wing in one cycle |
本文选取计算域大小如图3所示。翼型前缘向前3c,设定来流速度的大小与方向;翼型向后6c,设定相对于参考压力点的流体静压值;翼型外表面,设定无滑移条件,同时加载UDF使其按照给定运动方程变形运动;上下边界距离计算模型表面约4c,边界条件亦设为速度入口条件,以模拟无界流场。

|
图 3 计算区域、网格划分以及边界条件 Fig. 3 Computation domain, grid generation and boundary conditions |
本文计算中使用的网格为结构化网格。网格划分基本原则为在模型表面附近网格加密,其中第一层网格间距根据y+确定(y+ 平均值约为1左右)。全局网格大约45万,网格无关性验证工作见参考本文献[10]。
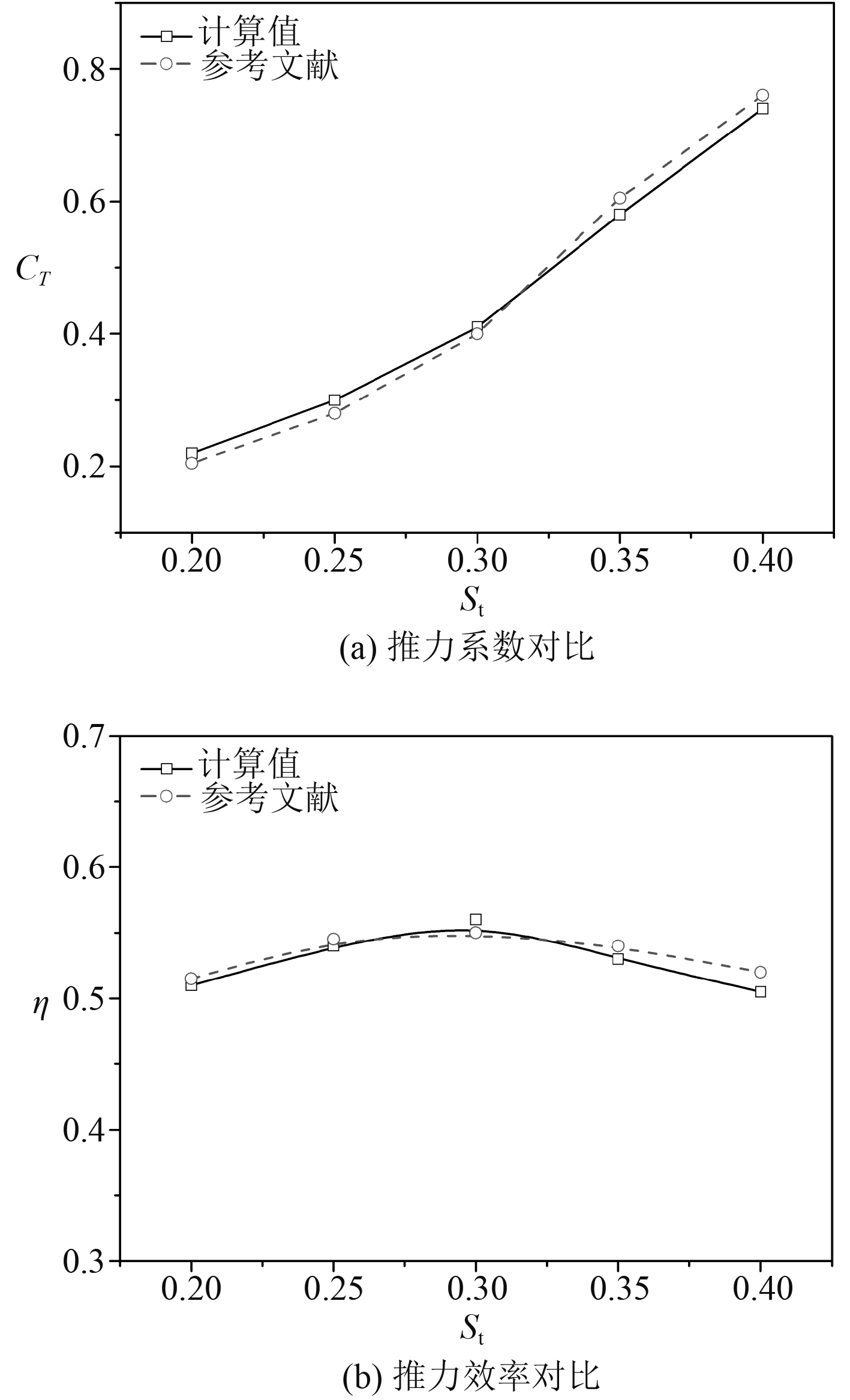
2.3 数值方法验证开展数值方法精度验证工作,计算模型与参考文献[12]一致,即二维NACA0012翼型。该翼型做拍动运动,相关参数设置为:来流速度0.4 m/s,升沉幅值0.75C(C为弦长)。计算翼型在频率为 0.3下的推力系数和推进效率,结果如图4所示。
|
图 4 数值方法验证结果 Fig. 4 Validation results of numerical method |
由图4可知,本文计算得到的拍动翼推力系数和推进效率与参考文献相应的结果近乎一致,最大误差不超过4%,符合数值计算精度的要求。因此本文采用的定网格技术可用于数值求解柔性翼行波推进运动。
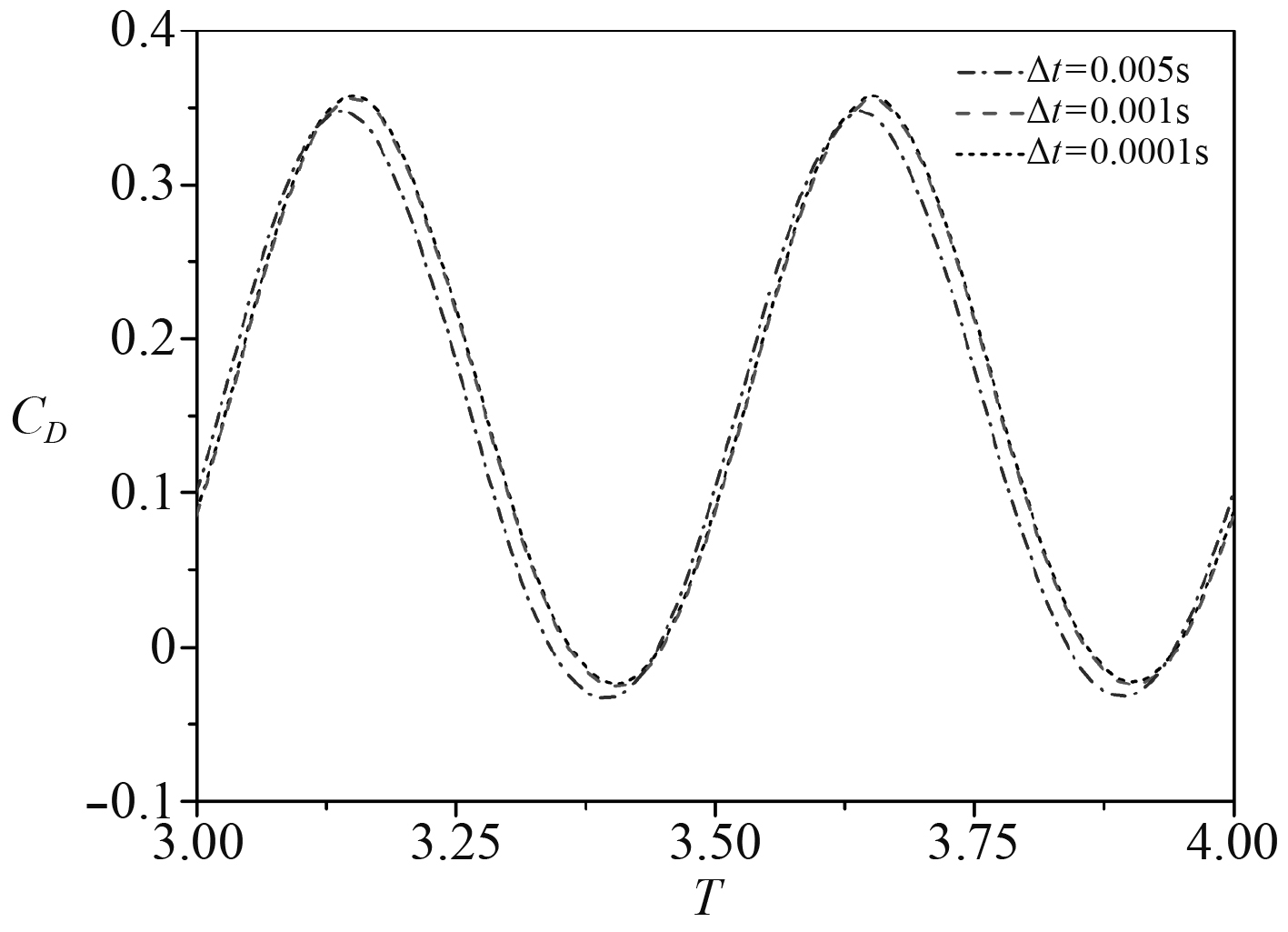
2.4 时间步长选取考虑到时间步长在非定常计算中起到极其重要的作用,本部分开展时间步长选取验证工作。以变形起始位置s = 0.4c, 来流速度V = 1 m/s, 运动周期T = 0.5 s,运动幅值A = 0.021(对应的θ值为10°)为例分别选取时间步长Δt= 0.0001 s, 0.001 s和 0.005 s进行计算验证。计算得到的变形翼阻力系数随时间变化曲线如图5所示。
|
图 5 时间步长验证结果 Fig. 5 Validation results of time step |
其中,CD表示阻力系数,其表达式如下式:
| ${C_D} = \frac{D}{{1/2 \cdot \rho \cdot {V^2} \cdot {c^2}}}\text{。}$ | (2) |
其中:D表示变形翼所受到的阻力值,ρ为水的密度,值为998.2 kg/m3。
从图5可以看出,当时间步长减小至0.001 s后,计算得到的变形翼阻力系数与时间步长为0.0001 s下计算得到的阻力系数变化曲线近乎吻合。因此在后续计算中时间步长Δt设为0.001 s。
3 计算结果及分析 3.1 柔性变形翼推进特性分析对不同来流速度、运动频率和运动幅值下的变形翼推进特性进行数值模拟,共有45个不同组合的工况。具体工况为:来流速度设为V = 0.1 m/s, 0.5 m/s 和1.0 m/s运动幅值设为 A = 0.021 m,0.043 m和0.069 m(对应的θ值分别为10°,20°和30°),运动频率f的变化范围随来流速度不同而相应变化。具体表现为:V = 0.1 m/s时,f取值分别为0.4, 0.5, 0.6, 1.0和2.0 Hz;V = 0.5 m/s时,f取值分别为1.0, 1.5, 2.0, 2.5和3.0 Hz;V = 1.0 m/s时,f取值分别为2.5, 3.0, 3.5, 4.0和4.5 Hz。其原因在于,通过查阅文献[1,4]可知,来流速度越大,克服流体阻力做功所需的运动频率亦越大。因此为了达到研究运动参数对变形翼推进性能的影响同时又兼顾计算效率,本文在低来流速度时,选取较低的运动频率与之匹配,反之亦然。
在进行计算结果分析前,首先对变形翼推力系数和推进效率进行定义。变形翼推进效率实质上为输出功率与输入功率的比值,输出功率可以表征为平均推力与来流速度的乘积,输入功率则可以表示为翼型表面速度压力乘积沿着翼型边界的积分,具体如下式:
| ${C_T} = \frac{T}{{1/2 \cdot \rho \cdot {V^2} \cdot {c^2}}},\;\eta = \frac{{\displaystyle\frac{1}{T}\int_{{t_0}}^{{t_0} + T} {{C_T} \cdot } {\rm d}t \cdot V}}{{\displaystyle\frac{1}{T}\int_{{t_0}}^{{t_0} + T} {\oint_\Gamma {p \cdot \overrightarrow v \cdot {\rm d}l} \cdot {\rm d}t} }}\text{。}$ | (3) |
其中:CT和ƞ分别为推力系数和推进效率;T为变形翼产生的推力;p和v分别为变形翼表面速度和压力分布;Γ为变形翼边界;
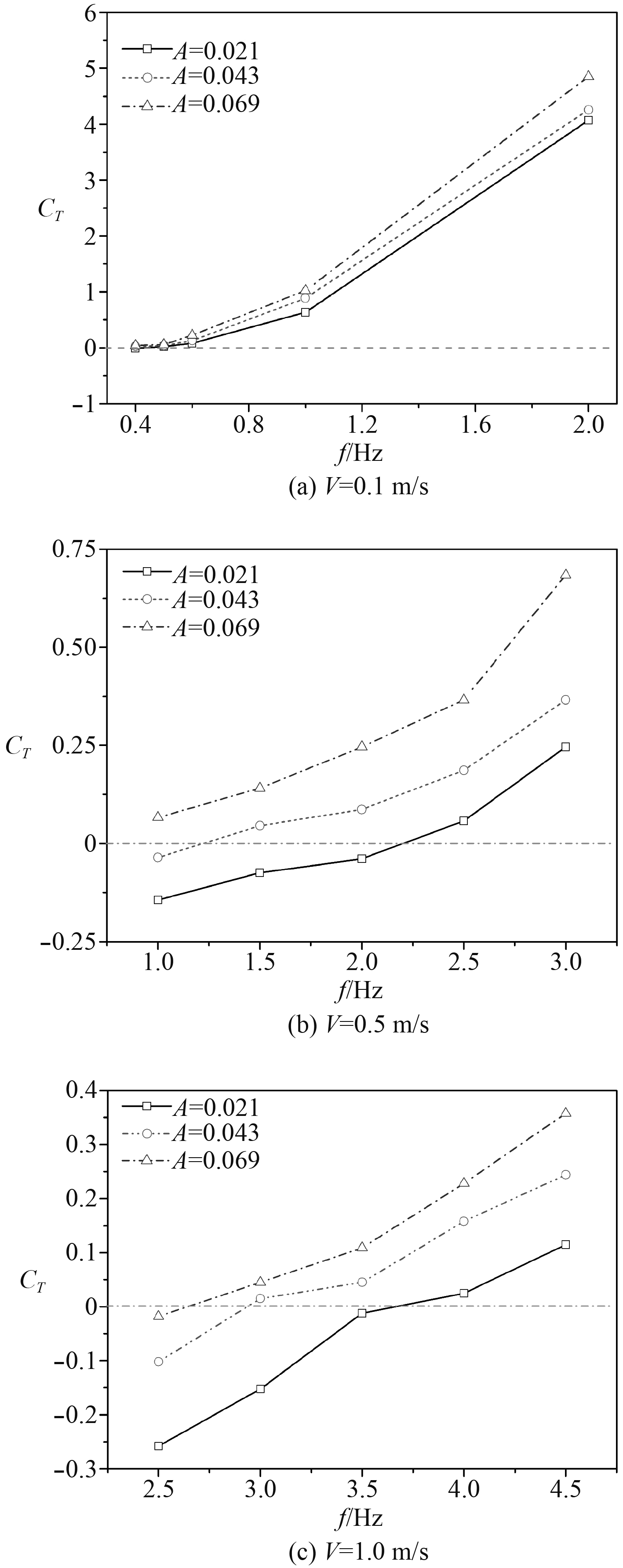
上述计算工况下变形翼推力系数值如图6所示。
|
图 6 不同计算工况下变形翼推力系数值 Fig. 6 Thrust coefficient values of deformed wing under different calculation conditions |
由图6可以看出,变形翼的推力系数值随着运动频率、变形幅值的增大相应增加,此外来流速度越大,系统所需克服流体阻力做的功也越大。具体来说,以运动幅值A = 0.021 m为例,当来流速度从0.1 m/s逐渐增大到0.5 m/s和1.0 m/s时,变形翼可产生正推力对应的运动频率分别为0.5 Hz, 2.5 Hz和4.0 Hz。
为了对不同运动参数组合下变形翼的推进效率进行准确客观的评价,引入一个无量纲参数斯特哈尔数,
| $St = \frac{{2 \cdot A \cdot f}}{V}\text{。}$ | (4) |
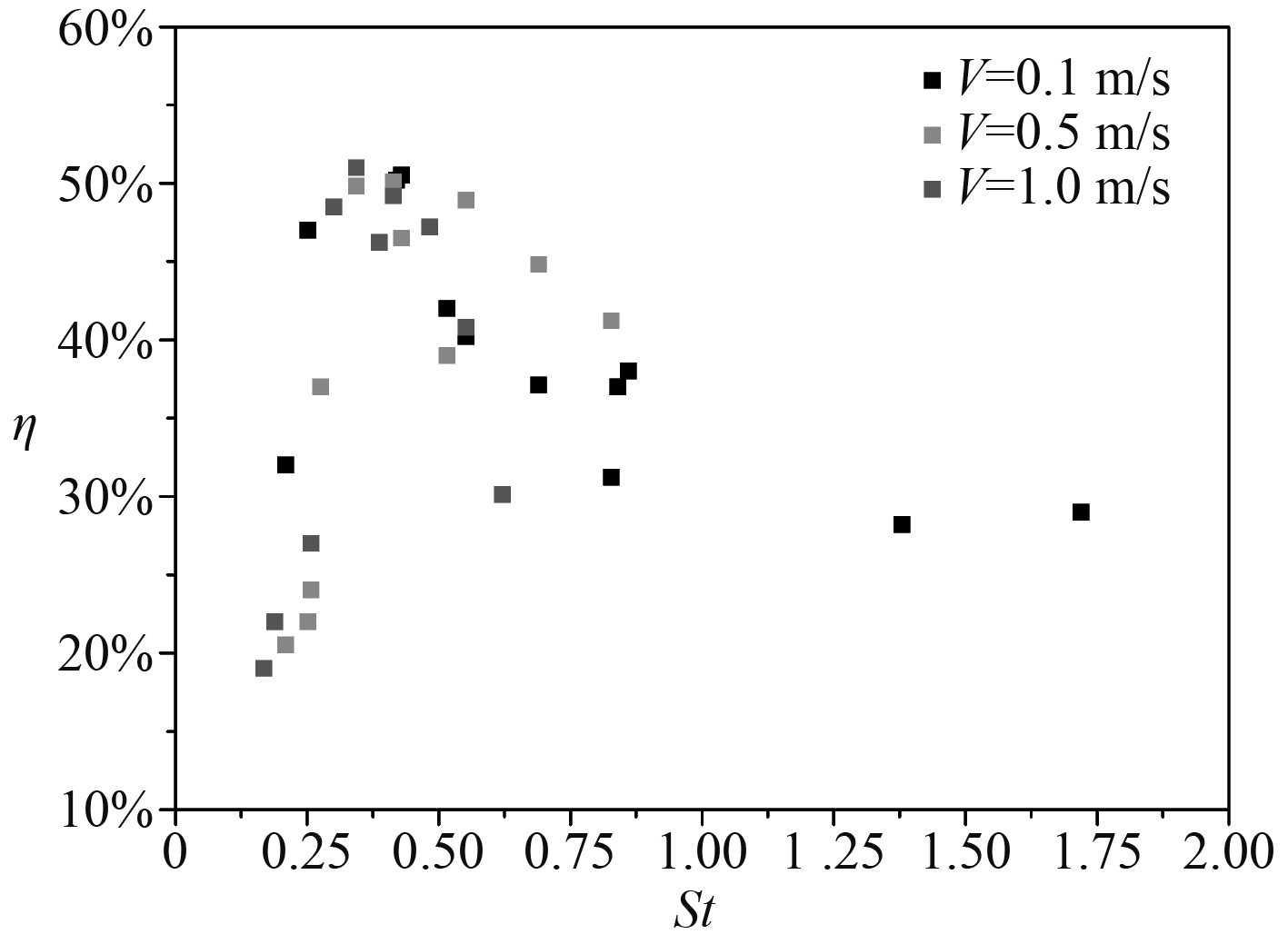
斯特哈尔数将变形翼的主要运动参数结合在一起,可用于准确评价变形翼的推进特性。不同斯特哈尔数下变形翼的推进效率值如图7所示。
|
图 7 不同St数下变形翼推进效率 Fig. 7 Propulsion efficiency of deformable wing at different St numbers |
由图7可以看出,不同来流速度下变形翼的推进效率值随着St数的增加呈现先增大后减小的趋势,存在最佳St数对应最大推进效率。不同来流速度下最大推进效率对应的最佳St值位于0.25~0.40之间。这一结论与参考文献中[12]给出的最佳St=0.30较为吻合。
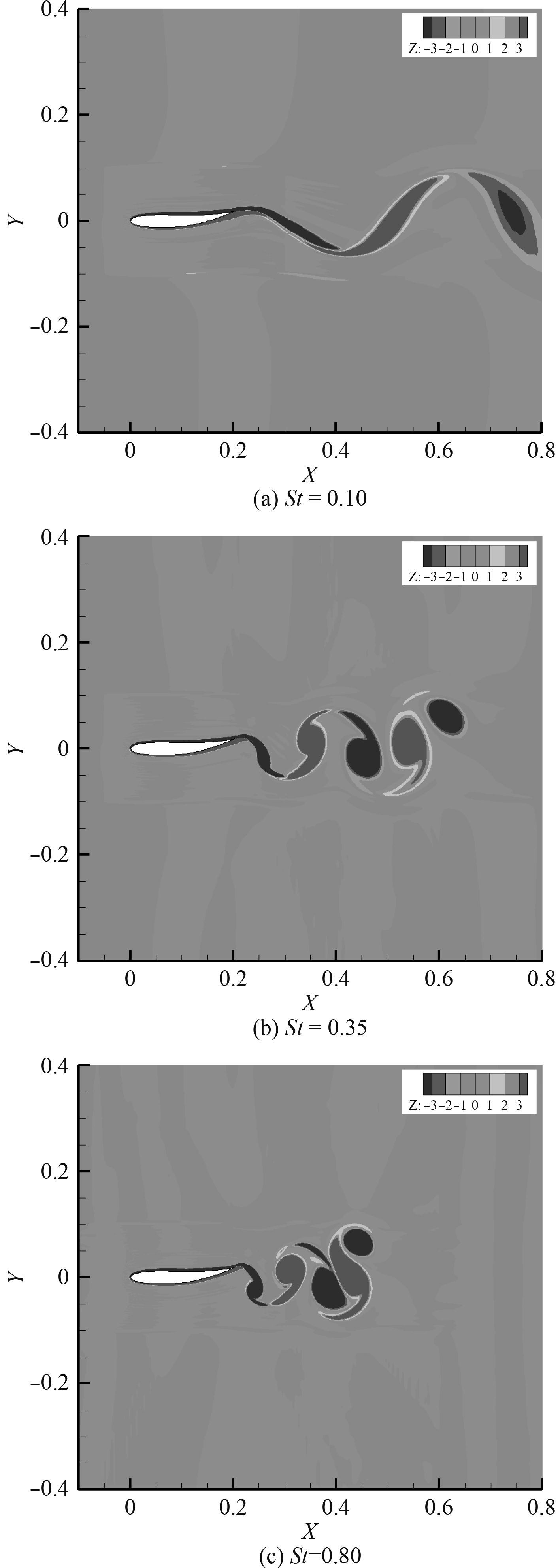
3.2 柔性变形翼流场结构分析上文对不同计算工况下的变形翼运动参数推进特性进行了研究, 本部分将对变形翼的流场结构进行分析,对上述计算结果进行解释。图8为不同St数下变形翼周围的流场结构以及周围压力分布图。其中Z为Z方向的涡量,其表达式如下式:
|
图 8 不同St数下变形翼尾流场涡量图 Fig. 8 Vorticity diagram of the wake flow field of the deformed wing at different St numbers |
| $Z = {\rm{ }}\frac{{\partial {\rm{v}}}}{{\partial {\rm{x}}}} - \frac{{\partial {\rm{u}}}}{{\partial {\rm{y}}}}\text{。}$ | (5) |
其中,u和v分别为水平方向和垂直方向的速度分量。
由图8可以看出,不同St数变形翼尾流场中呈现交错分布的涡环结构。其产生的原因在于,由于变形翼上下边界的运动使得翼型表面的流动分离,并且在来流的作用下向后移动,从而呈现出交错分布的涡环结构。注意到不同St数下变形翼流场涡环结构不同之处在于在低St数下(St=0.10),变形翼尾流场中的涡环结构呈现卡门涡街形式(BvK), 即翼型上缘脱落的涡环在尾流场中呈现顺时针旋转,而下缘脱落的涡环在尾流场中则呈现逆时针旋转;随着St数的增加(St = 0.35, 0.80),变形翼尾流场中则呈现反卡门涡街(rBvK),即即翼型上缘脱落的涡环在尾流场中呈现逆时针旋转,而下缘脱落的涡环在尾流场中则呈现顺时针旋转。如此二者之间相互作用形成一股向后的射流,根据动量定理,向后的射流亦给一个作用于向前的推力,如此变形翼便可以向前运动[17]。
4 结 语本文通过开展不同来流速度、不同运动幅值以及不同运动频率的数值计算,获得变形翼推力系数和推进效率随运动参数的变化规律。此外,通过比较分析不同St数下变形翼周围涡流场结构,定性地从流动机理的角度对上述计算结果进行阐释。本文工作可为后续试验开展提供技术依据和理论指导。
| [1] |
潘定一. 基于沉浸边界法的鱼游运动水动力学机理研究 [D]. 杭州: 浙江大学, 2007.
|
| [2] |
LIGHTHILL. Note on the swimming of slender fish[J]. Journal of Fluid Mechanics, 1960, 9: 305-317. DOI:10.1017/S0022112060001110 |
| [3] |
LIGHTHILL M. Large-amplitude elongated-body theory of fish locomotion[J]. Proceedings of the Royal Society of London. Series B, 1971, 179: 125-132. |
| [4] |
WU T. Swimming of a waving plate[J]. Journal of Fluid Mechanics, 1961, 10: 321-344. DOI:10.1017/S0022112061000949 |
| [5] |
WU T. Hydromechanics of swimming propulsion. Swimming of a two-dimensional flexible plate at variable forward speeds in an inviscid fluid[J]. Journal of Fluid Mechanics, 1971, 46: 337-355. DOI:10.1017/S0022112071000570 |
| [6] |
CHENG J, ZHUANG L, TONG B. Analysis of swimming three-dimensional waving plates[J]. Journal of Fluid Mechanics, 1991, 232: 341-355. DOI:10.1017/S0022112091003713 |
| [7] |
SHAO X M, ZHANG X L. Numerical studies of the hysteresis in locomotion of a passively pitching foil[J]. Journal of Hydrodynamics, 2016, 03: 29-38. |
| [8] |
WANG Z D, et al. Wake vortex characteristics of a flexible oscillating fin[J]. Journal of Bionic Engineering, 2008, 5(1): 49-54. DOI:10.1016/S1672-6529(8)60006-2 |
| [9] |
李永成. 二维可变形翼舵水动力性能数值模拟研究[R]. 中国船舶科学研究中心科技报告.
|
| [10] |
隋洪涛, 李鹏飞, 马世虎, 等. 精通CFD动网格工程仿真与案例实战[M]. 北京: 人民邮电出版社.
|
| [11] |
张晓庆, 王志东, 张振山. 二维摆动水翼仿生推进水动力性能研究[J]. 水动力学研究与进展, 2006, 21(5): 632-639. |
| [12] |
CHAO Li, PAN Guang. Numerical investigation on the force generation ad wake structures of a non-sinusoidal pitching foil[J]. Journal of Fluids and Structures, 2018, 85: 27-39. |
 2020, Vol. 42
2020, Vol. 42
