0 引　言

工程上，某些大型浮筏气囊隔振装置的筏架最大弹性变形量可达3 mm，造成筏架上设备之间产生相对位移，不仅会危及设备的运行安全，还会增大设备振级，降低浮筏的隔振效果。采取一定的控制策略对气囊隔振器进行充、放气，可在一定程度上抑制筏架的弹性变形。

自提出智能气囊隔振装置技术^[1]以来，国内学者在浮筏隔振系统气囊隔振器控制领域开展了大量研究工作，基本解决了气囊缓慢漏气、装置负载变化等工况下筏架姿态不平衡的问题，并且随着研究的深入，控制方法的快速性、稳定性、适应性和收敛性不断提高^[2-8]。然而，上述文献均将筏架视为刚体，未考虑其弹性变形对隔振系统的影响，并且将气囊压力均匀性作为约束条件时筏架弹性变形较大。

为抑制浮筏气囊隔振系统筏架的弹性变形，本文提出一种基于位移传感器参数识别的气囊控制方法。1）在筏架弹性变形较大的位置增设位移传感器，并利用位移参数得到筏架弹性形态的评价指标 $Hs$ ；2）基于气囊压力和高度偏差选取需要调整的气囊编号，并采用模糊控制确定气囊调整时间；3）在试验平台上进行了验证并取得了较好的控制效果。该方法对抑制筏架弹性变形的气囊控制研究有一定指导意义。

1 弹性变形评价指标

将筏架视为柔性体，其实际位移包含刚体姿态位移和弹性变形位移，两者相互耦合，难以完全分离。同时，浮筏上设备重量分布不均、设备启停、气囊缓慢漏气等因素均可造成筏架弹性变形，当筏架产生弹性变形的原因不同时，通过调整气囊压力达到的最大抑制效果也不相同。因此，本文根据筏架变形特性增加位移传感器，并将各个传感器参数的标准差作为筏架弹性变形的评价指标，同时为提高控制算法对不同工况的适应性，在评价指标 $Hs$ 中引入筏架弹性变形的动态权重系数 $k$ ，即

$Hs=\sqrt{\frac{1}{n}\centerdot \left[ \sum\limits_{i=1}^{p}{{{({{x}_{i}}-{{{\bar{x}}}_{n}})}^{2}}+k\centerdot \sum\limits_{j=1}^{q}{{{({{x}_{j}}-{{{\bar{x}}}_{n}})}^{2}}}} \right]}\text{。}$

(1)

其中： ${x_i}$ 为监测筏架刚体姿态的位移传感器参数值，共 $p$ 个； ${x_j}$ 为监测筏架弹性形态的位移传感器参数值，共 $q$ 个； $k$ 为筏架弹性变形的动态权重系数，初始值为1，取值范围为[0，1]； $n = p + q$ ，为浮筏气囊隔振装置垂向位移传感器总数量； ${\bar x_n}$ 为各个位移传感器参数的平均值。

2 控制器设计

由于气囊隔振器的容积较小，属于小流量、小体积的气动控制系统，传统针对大流量、大体积的流量和压力控制方法不再适用。因此，本文采用断续控制方法对气囊进行短时间的充、放气，达到抑制筏架弹性变形的目的。

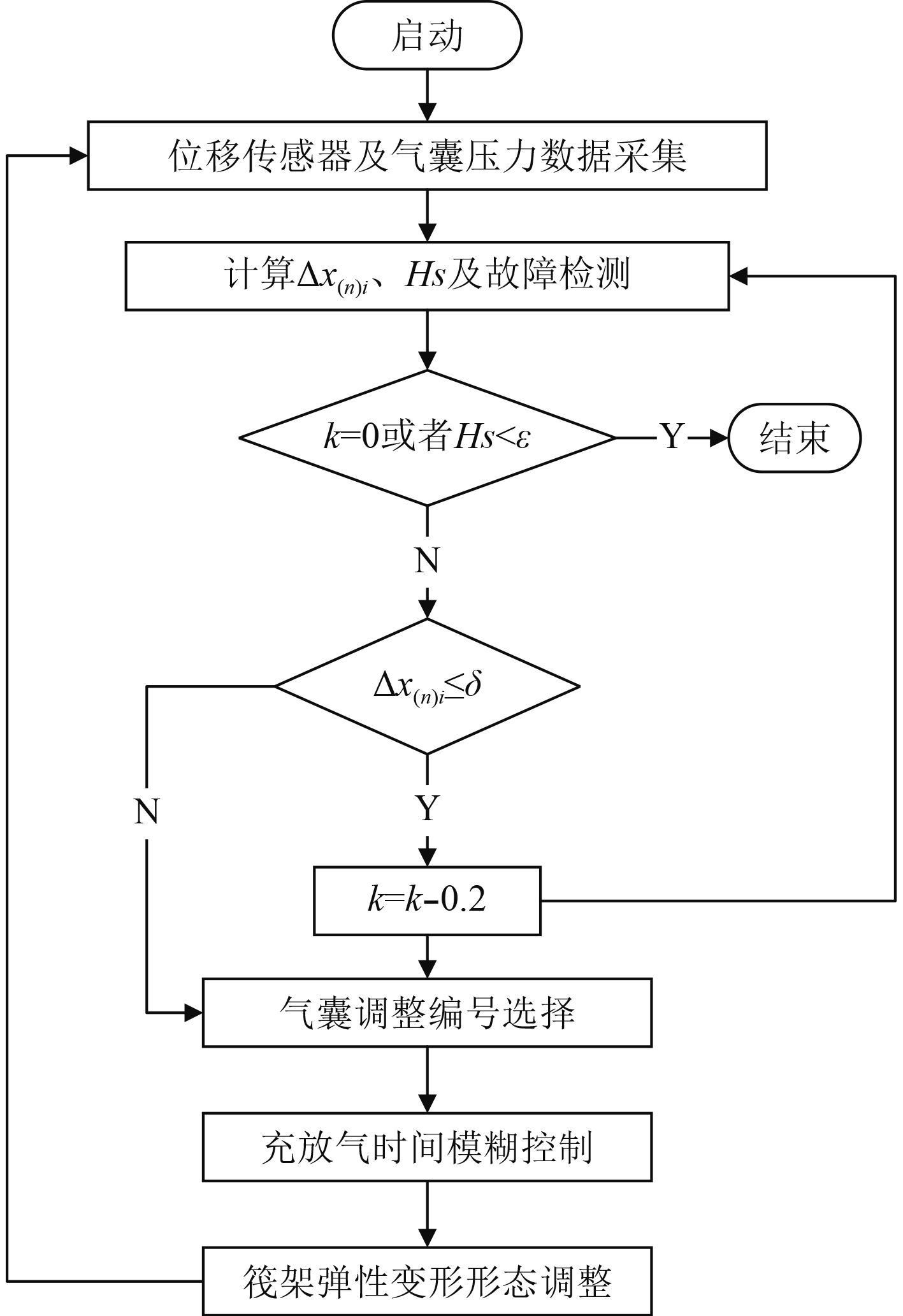
系统的控制原理如图1所示。

1）采集传感器数据并计算 $\Delta {x_{(n)i}}$ 和 $Hs$ ， $k$ 初值取为1，若 $k \ne 0$ 且 $Hs \geqslant \varepsilon $ 则需要对气囊进行调整；

2）判断动态权重系数 $k$ 是否需要调整，其中 $\Delta {x_{(n)i}} = {x_{(n)i}} - {x_{(n - 1)i}}$ 为各位移传感器在最近2次调整过程中的差值，若 $\Delta {x_{(n)i}} \leqslant \delta $ ，则表明最近2次气囊调整对各位移传感器影响不大，此时可认为该 $k$ 值下筏架弹性变形的抑制效果已经达到最大值，为让控制算法快速收敛，需要减小 $k$ 值，若 $\Delta {x_{(n)i}} > \delta $ ，则进行下一步；

3）根据气囊广义高度偏差 ${Q_i}$ 选取需要调整的气囊，并采用模糊控制器确定气囊的充、放气时间，达到抑制筏架弹性变形的控制效果。

为了简化控制器的设计和试验分析，提出以下假设：1）船体处于水平状态，没有横倾和纵倾；2）当浮筏姿态平衡且无弹性变形时，各位移传感器读数为0；3）浮筏系统载荷保持不变。

2.1 气囊选择策略

在筏架调整过程中，各个气囊基本工作在额定高度 $H$ 附近，根据相关文献研究^[9-10]，可认为气囊内部压力与垂向位移满足线性关系，此时可用气囊高度偏差 $\Delta h$ 线性表示气囊压力改变量 $\Delta P$ ，即

$\Delta P=a\centerdot \Delta h\text{，}$

(2)

式中： $a$ 为常数； $\Delta h = h - H$ ， $h$ 为气囊实际工作高度。

由于各个气囊之间存在耦合，依据文献[1]的研究可知，气囊高度偏差 $\Delta h$ 主要由2部分组成：一是由于气囊工作高度耦合造成的偏差 $\Delta {h_c}$ ，另一个是由于气囊气体摩尔数变化或者外界扰动造成的偏差 $\Delta {h_s}$ ，两者相互耦合，难以求解。对气囊实施充、放气主要目的是消除 $\Delta {h_s}$ ，并且相同 $\Delta h$ 下，气囊压力 ${P_i}$ 越大， $\Delta {h_s}$ 所占比例就越小，所需控制量就越小。为准确选择需要调整的气囊，避免气囊频繁的充、放气，必须将气囊压力和气囊高度偏差综合考虑：

${{Q}_{i}}={{\lambda }_{i}}\centerdot \Delta {{h}_{i}}\text{。}$

(3)

式中： ${Q_i}$ 为气囊广义高度偏差，mm； ${\lambda _i}$ 为气囊平均压力与气囊压力的比值， ${\lambda _i} = {{{\bar P} / P}_i}$ ； $\Delta {h_i}$ 为第i个气囊的高度偏差，可通过位移传感器参数插值得到。

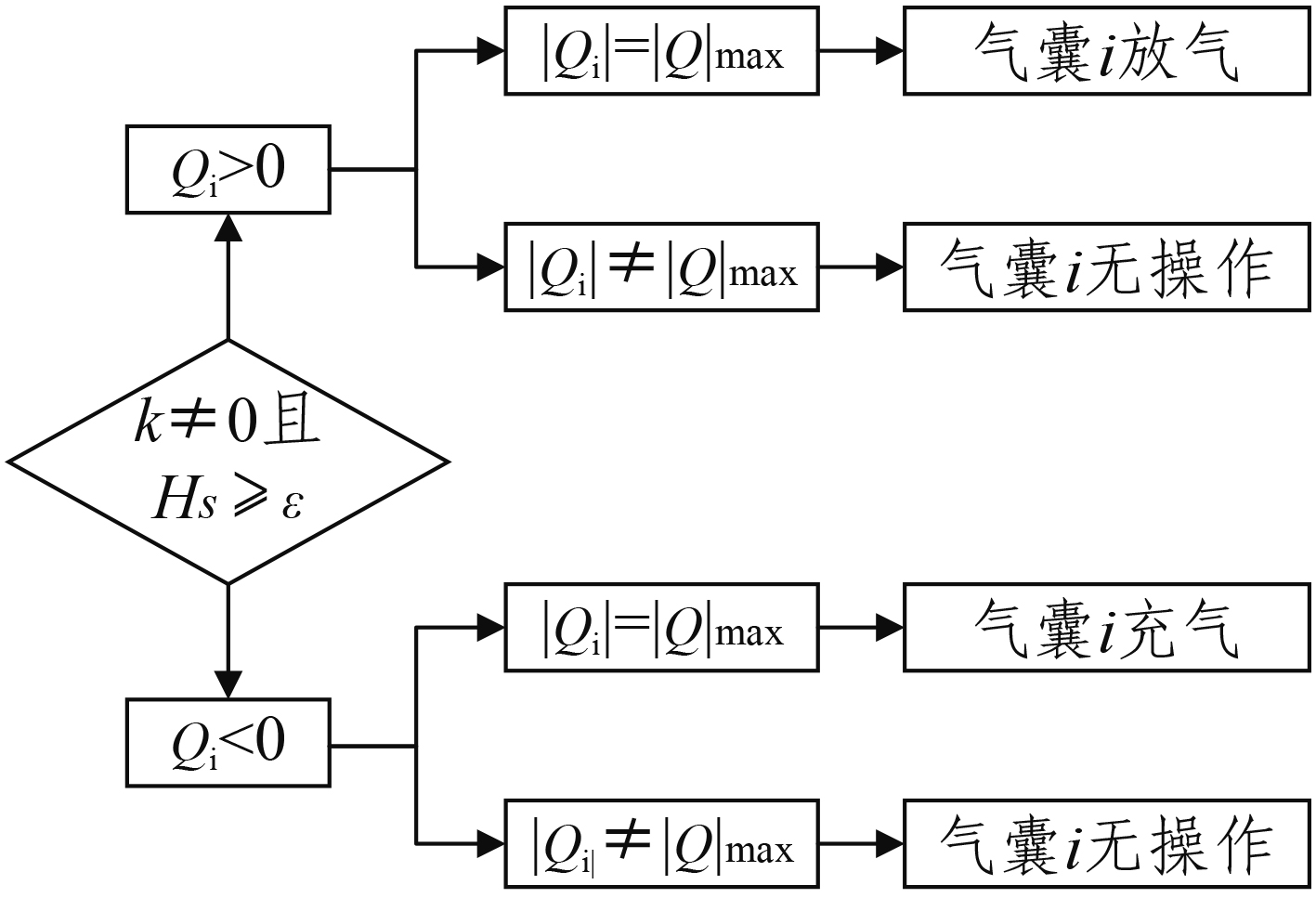
计算得到各个气囊的广义高度偏差 ${Q_i}$ 后，可制定如下气囊选择策略：1）判断气囊是否需要调整（ $k \ne 0$ 且 $Hs \geqslant \varepsilon $ ）；2）计算 ${\left| Q \right|_{\max }}$ ，若 $\left| {{Q_i}} \right| = {\left| Q \right|_{\max }}$ 则对第i个气囊进行调整，否则气囊无操作；3）若 ${Q_i} > 0$ 则对气囊放气，若 ${Q_i} < 0$ 则对气囊充气。气囊选择原理框图如图2所示。

2.2 充放气时间模糊控制

根据气体流动理论，当 ${P_{{\text{气源}}}} \geqslant 1.893{P_{{i}}}$ 时，气体以超音速流向气囊，此时气体流量很大；反之，气体以亚音速流向气囊，此时气体流量相对较小，当两者压力接近时，气体流量几乎为0^[11]。因此，气源压力与气囊压力差取值不同时，相同充气时间内气囊压力变化量差别较大，为保证气囊调整的准确性，在设计气囊充放气控制器时需要考虑气源压力与气囊压力差。

浮筏气囊隔振系统属于多输入、多输出的复杂控制对象，加之系统采取断续充放气，因而传统的控制方法难以取得较好的控制效果^[12]。本文采用模糊控制技术控制气囊的充放气时间，以气囊广义高度偏差 ${Q_i}$ 和气源压力与气囊压力差 $\Delta {P_s}$ 作为输入量，以电磁阀开启时间 $T$ 作为输出量。 $\Delta {P_s}$ 表示为：

$\Delta {P_s} = {P_{{\rm{{\text{气源}}}}}}{\rm{ - }}{P_{{i}}}\text{。}$

(4)

式中，当气囊放气时 $P_{{\rm{{\text{气源}}}}}$ 为0。

${Q_i}$ ， $\Delta {P_s}$ ， $T$ 的模糊论域分别为{−3，3}，{−3，3}，{0，4}。其中 ${Q_i}$ 和 $\Delta {P_s}$ 均采用7个模糊子集：{NB，NM，NS，ZE，PS，PM，PB}，分别表示{负大，负中，负小，零，正小，正中，正大}；电磁阀开启时间 $T$ 采用5个模糊子集：{ZE，PS，PM，PB，PG}，分别表示{零，短开，中开，长开，超长开}，由于排气管路背压为0 MPa，为避免超调，排气时选取短开和中开。模糊输入、输出变量均采用三角形隶属函数，根据Mamdani型模糊推理算法^[13]和实际调试经验设计模糊控制规则表，如表1所示。

3 试验研究

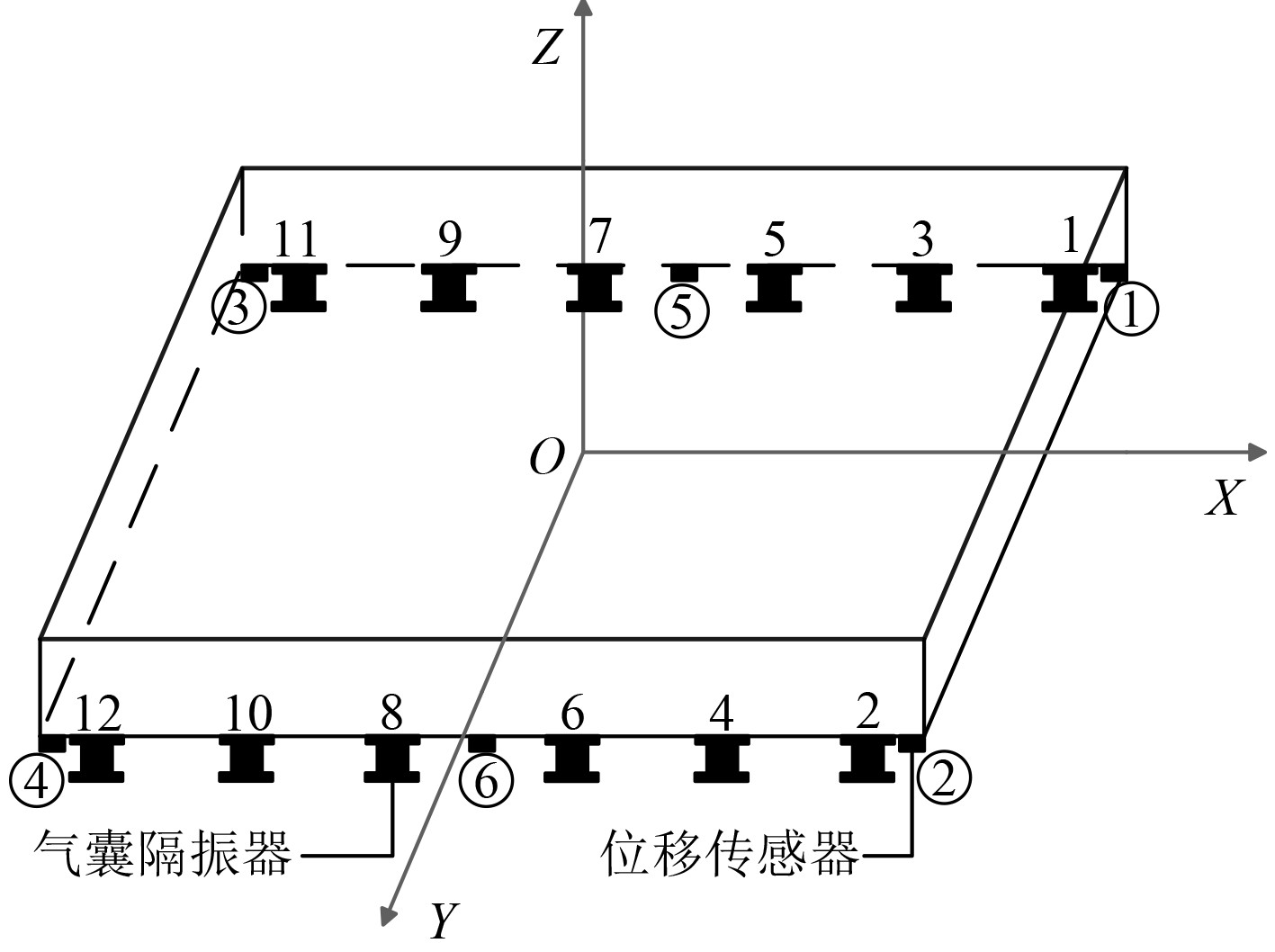
本文试验装置为某型船舶浮筏气囊隔振装置2∶1缩比试验平台，试验装置结构示意图如图3所示。筏架尺寸为5.54 m×3.48 m×0.191 m，沿X轴对称垂向布置12个额定载荷为8 T的气囊隔振器且其内均装有压力传感器，另布置6个垂向位移传感器，1#～4#用于监测筏架刚体姿态，5#，6#用于监测筏架弹性变形，通过1套液压加载装置调整系统载荷，系统额定载荷为96 T。

经过系统调试，确定 ${Q_i}$ ， $\Delta {P_s}$ ， $T$ 的物理论域分别为{−1.2，1.2}，{−3，3}，{0，200}，计算得到量化因子依次为 ${K_{Qi}} = 2.5$ ， ${K_{\Delta Ps}} = 1$ ， ${K_T} = 50$ ；1#，2#，11#，12#气囊的高度偏差 $\Delta h$ 依次用1#～4#位移传感器参数表示，其余气囊高度偏差通过位移传感器参数线性插值得到，如5#气囊的高度偏差 $\Delta {h_5}$ 表示为：

$\Delta {h_5} = {x_1} + \frac{{{l_5}}}{l}({x_5} - {x_1})\text{。}$

(5)

其中， ${x_1}$ ， ${x_5}$ 分别为1#，5#位移传感器位移值； ${l_5}$ 为5#气囊至1#位移传感器的距离； $l$ 为1#，5#位移传感器之间的距离。

为有效验证控制方法的正确性，试验前对各个位移传感器的零点进行校准，消除筏架初始变形的影响；设置相邻2次的充、放气间隔为5 s，以减小浮筏振荡产生的干扰；终止状态为动态综合判据 $Hs < \varepsilon $ ， $\varepsilon $ 取0.2 mm， $\Delta {x_{(n)i}}$ 的收敛指标 $\delta $ 取值为0.1 mm。将系统载荷调整至96 T、气囊充气至额定气压后进行试验，试验结果如图4所示。

可以看出，对气囊隔振器进行控制之前，筏架表现为中部凸起的弹性变形，最大变形量为1.37 mm。采用本文的控制方法对气囊进行16次调整后，各个位移传感器参数值基本在−0.25～0.2 mm之间，筏架弹性变形的抑制效果明显。试验结果表明，本文控制方法可以有效抑制筏架的弹性变形。

4 结　语

本文对抑制浮筏气囊隔振系统筏架弹性变形的气囊控制方法进行研究，提出一种基于位移参数识别的气囊控制方法。考虑到筏架弹性变形的复杂性，提出一种弹性变形的评价指标 $Hs$ ，并引入了动态权重系数以提高控制算法的适应性。根据气囊广义高度差选取需要调整的气囊编号，并采用模糊控制确定气囊调整时间。试验结果表明，该控制方法对筏架弹性变形的抑制效果较好，具有较高的控制精度。