2. 哈尔滨工程大学,黑龙江 哈尔滨 150001
2. Harbin Engineering University, Harbin 150001, China
船舶舱室噪声不仅影响船上设备与仪器的正常使用,同时还影响船舶的安全性、隐蔽性与舒适性[1]。长时间处在较高噪声的环境下,船上人员的正常工作与生活受到干扰,使船员的精神状态与身心健康受到影响,产生诸多隐患。目前世界主要国家以及一些国际权威组织已经制定了一系列船舶舱室噪声控制标准与预报规范,对船舶舱室噪声进行控制。系统建立船舶结构振动与噪声之间的联系,是对船舶舱室噪声进行预报研究的基础。在船舶舱室噪声的研究过程中,统计能量法从能量观点研究和分析振动与噪声,从统计角度对实验对象不同位置的能量关系进行分析。目前,统计能量法已被成功应用于船舶舱室内部的高频噪声预报中[2],基于该方法对不同船型舱室噪声进行的预报分析和优化设计等研究工作也在不断深入。
1 统计能量法基本理论统计能量法在进行舱室噪声预报时具有巨大优势,其所用参数较少、方程简单易解。该方法围绕能量进行研究,主要与振型数和模态密度相似的模态群相关,而对频率、阻尼等与边界条件相关的模态参数关联较小。统计能量法中各子系统能量由共振的振型能量表示。在确定子系统对外界激励源响应的度量方面,振型数与模态密度作为统计能量法的重要参数有着重要的作用[3]。
当复杂结构系统的每个子系统得到确定后,其各子系统与相邻子系统间均有功率流方程:
| ${P_{i{n_i}}} = {P_{dis{s_i}}} + {P_{ij}}\text{。}$ |
式中:
由上述一系列的子系统功率流方程式联立,得到下面的方程组:
| $\begin{array}{l} \omega \left[ {\begin{array}{*{20}{c}} {\!\!\!\!\!\!({\eta _1} \!+\!\!\!\! \sum\limits_{i = 1,i \ne j}^N {{\eta _{1i}}} ){n_1}}\!\!\!\!\!\!\!\!\!\!\!\!&{ - {\eta _{12}}{n_1}}\!\!\!\!& \cdots \!\!\!\!\!\!&{ - {\eta _{1N}}{n_1}} \\ { - {\eta _{21}}{n_2}}\!\!\!\!\!\!\!\!&{({\eta _2} \!\!+\!\!\!\! \sum\limits_{i = 1,i \ne j}^N {{\eta _{2i}}} ){n_2}}\!\!\!\!\!\!\!\!& \cdots \!\!\!\!\!\!&{ - {\eta _{2N}}{n_2}} \\ \vdots \!\!\!\!& \vdots \!\!\!\!& \ddots \!\!\!\!& \vdots \\ { - {\eta _{N1}}{n_N}}\!\!\!\!\!\!\!\!&{ - {\eta _{N2}}{n_N}}\!\!\!\!& \cdots \!\!\!\!\!\!&{({\eta _N} \!\!\!+\!\!\! \sum\limits_{i = 1,i \ne j}^N {{\eta _{Ni}}} ){n_N}} \end{array}}\!\!\!\!\!\! \right]\times \\\;\;\;\; \left[ {\begin{array}{*{20}{c}} { \displaystyle\frac{{{{\bar E}_1}}}{{{n_1}}}} \\ { \displaystyle\frac{{{{\bar E}_2}}}{{{n_2}}}} \\ \vdots \\ { \displaystyle\frac{{{{\bar E}_N}}}{{{n_N}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\bar P}_{i{n_1}}}} \\ {{{\bar P}_{i{n_2}}}} \\ \vdots \\ {{{\bar P}_{i{n_N}}}} \end{array}} \right]\text{。}\\[-50pt]\end{array}$ |
式中:
每一个结构或声学子系统都具有一个与时间和空间平均声压或振速成比率的稳态能量水平。
对于质量为
| $\left\langle {{v^2}} \right\rangle = \frac{E}{M}\text{,}$ |
对于体积为
| $\left\langle {{p^2}} \right\rangle = \frac{{E\rho {c^2}}}{V}\text{。}$ |
式中:
至此能量与响应间的关系得到了确立,能量与响应量之间可由相互转换得到[4]。
统计能量法进行系统建模的依据是能量平衡原则,即在外载荷作用下结构系统在能量输入、传输和损耗等方面达到能量平衡。首先理解子系统的概念及其划分原则,才能从子系统的划分开始对复杂系统进行高频响应预报。子系统作为储存能量的载体,是一组有着相似动力特性的模态群。复杂系统由各种子系统组成,并在激励源的作用下耦合。统计能量法针对的是高模态密度,因而选取得子系统一定满足在响应频段内模态数不小于5[5]。
2 模型建立本文选取激励载荷施加形式、船体板结构形式以及声腔子系统形式3种变量作为文中的基本研究参数。依据是本文围绕统计能量模型的研究分为输入、系统与输出3部分。在模型输入环节,激励载荷施加形式是主要影响参数;在模型的系统环节,船体板结构形式、声腔子系统形式与舾装敷设是主要影响参数;而在模型的输出环节,数据处理的方式方法则是考虑的重点。
2.1 研究对象模型简介本文的研究对象为1艘大型水面船舶,首先建立该船的有限元模型[6]如图1所示。该船体模型的主尺度及主要性能参数如表1所示。

|
图 1 全船有限元模型示意图 Fig. 1 FEM model of ship |
|
|
表 1 船体模型的主尺度及主要性能参数 Tab.1 Principal dimension and main performance parameters of the ship model |
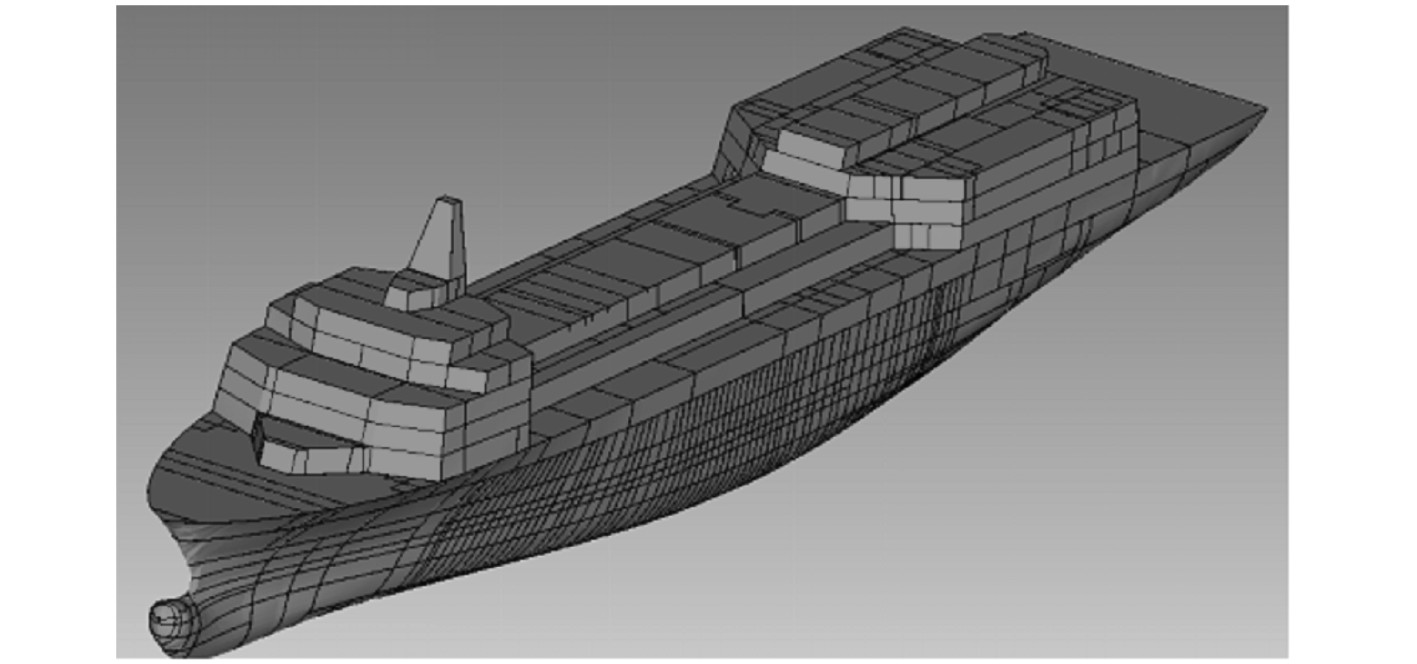
将该船的有限元模型导入振动声学分析软件Vaone,由点连成面的方式生成板,选择板的类型,损耗因子默认;定义板的厚度;选择船体板结构的材料,确定其惯性矩、截面积与周长;选择船体板结构形式的材料,确定横纵2个方向的加筋的间距与类型。最后形成一个完整的船体板结构子系统,如图2所示。
|
图 2 船体板结构子系统模型 Fig. 2 Subsystem model of plate structure |
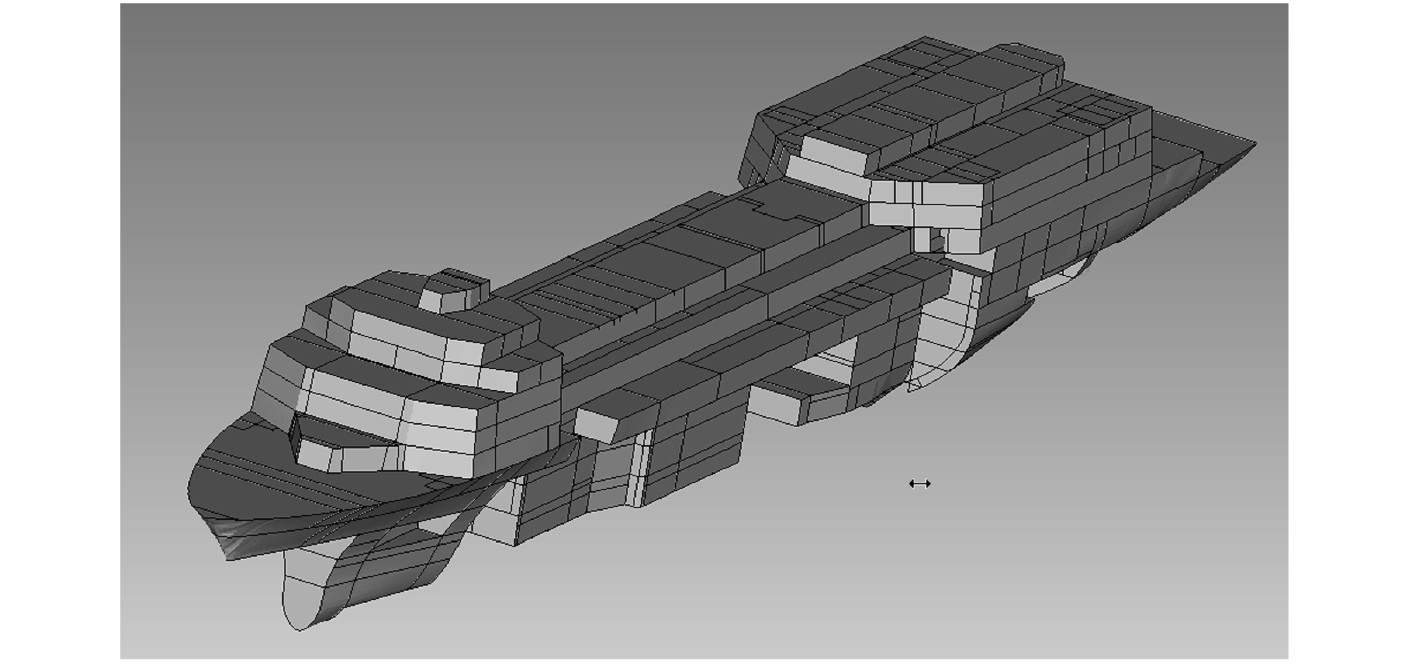
建立声腔子系统,选择流体属性为空气,损耗因子默认,其他参数不变。各独立声腔建立完成后,通过连接形成一个完整统一的声腔子系统,如图3所示。
|
图 3 声腔子系统模型 Fig. 3 Subsystem model of acoustic cavity |
本文采用整体拆分的角度,将全船模型分为3部分进行研究讨论,针对性地解决不同参数分别对船舶舱室噪声预报产生怎样的影响,以及多参数对船舶舱室噪声产生怎样的影响这2个主要问题。将全船分为3段分别进行不同参数的计算与分析,不同位置舱室的噪声预报将更有针对性,使预报结果更为直观与准确,本文中将三段式舱室噪声预报与统计能量法相结合的方案在应用上十分新颖、行之有效且有利于解决实际问题。三段式分配原则如下:
1)全船不同位置存在结构上的不同;
2)全船船首、船中与船尾的设备载荷也不同;
3)全船整体分析体量过大,分为3部分进行研究效率更高。
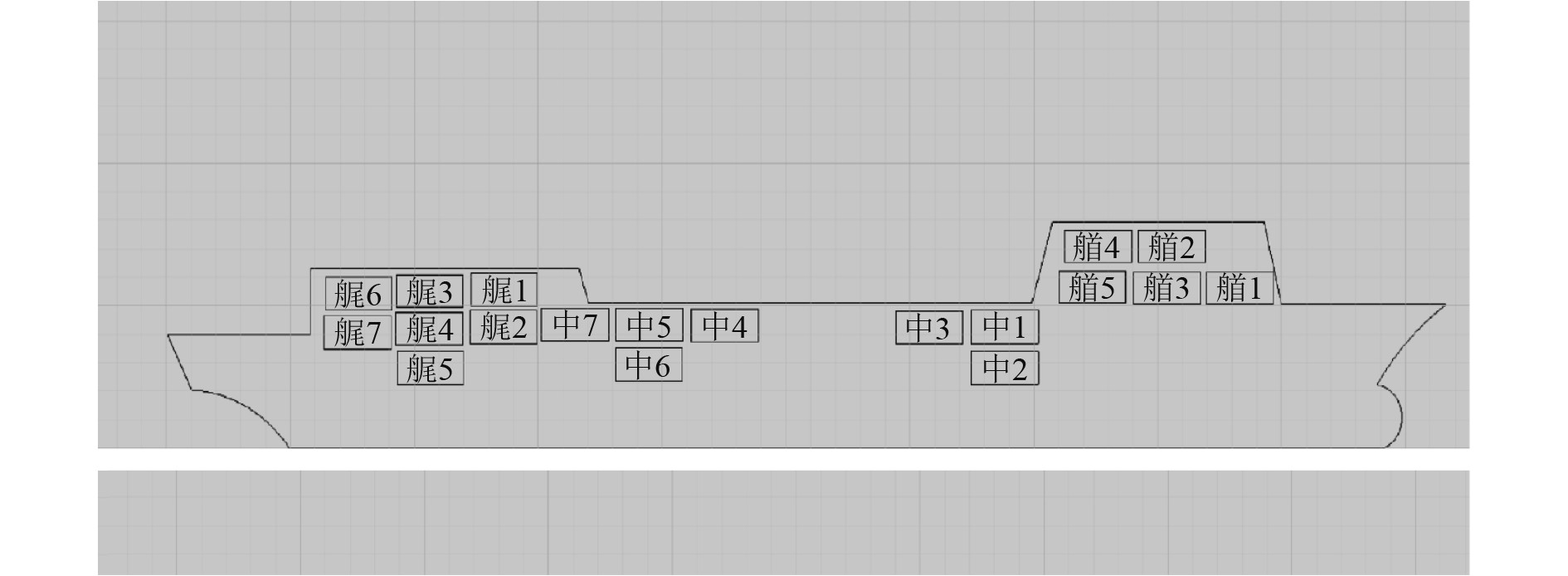
依照三段式方法分配后的样本舱室位置分布示意图如图4所示。其中船首选取5个舱室,船中与船尾各选取7个舱室,一共选取19个样本舱室进行研究。
|
图 4 三段式分配下的样本舱室位置分布示意图 Fig. 4 Diagram of cabins' position |
首先给模型施加激励载荷,激励载荷主要来自螺旋桨、主机、柴油机、舵机、空调器以及各种泵,载荷类型分为船舶空气噪声激励载荷及设备振动载荷2种,可由不同频率下对应的声功率级与振动加速度级大小来反映载荷大小。
1)螺旋桨产生的设备载荷
螺旋桨振动加速度级如表2所示。
|
|
表 2 螺旋桨振动加速度级 Tab.2 Vibration acceleration level of propeller |
2)主机、柴油机产生的设备载荷
|
|
表 3 主机振动加速度级 Tab.3 Vibration acceleration level of main engine |
|
|
表 4 主机声功率级 Tab.4 Acoustic power level of main engine |
3)空调器载荷
|
|
表 5 柴油机振动加速度级 Tab.5 Vibration acceleration level of diesel engine |
|
|
表 6 柴油机声功率级 Tab.6 Acoustic power level of diesel engine |
空调设备振动加速度级如表7所示。
|
|
表 7 空调设备振动加速度级 Tab.7 Vibration acceleration level of air conditioning equipments |
4)舵机产生的设备载荷
|
|
表 8 舵机振动加速度级 Tab.8 Vibration acceleration level of steering engine |
|
图 8 多参数方案影响下的舱室噪声预报结果 Fig. 8 Prediction result of ship cabin noise under the multiparameter control |
|
|
表 9 舵机声功率级 Tab.9 Acoustic power level of steering engine |
5)泵载荷
|
|
表 10 泵振动加速度级 Tab.10 Vibration acceleration level of pumps |
|
|
表 11 泵声功率级 Tab.11 Acoustic power level of pumps |
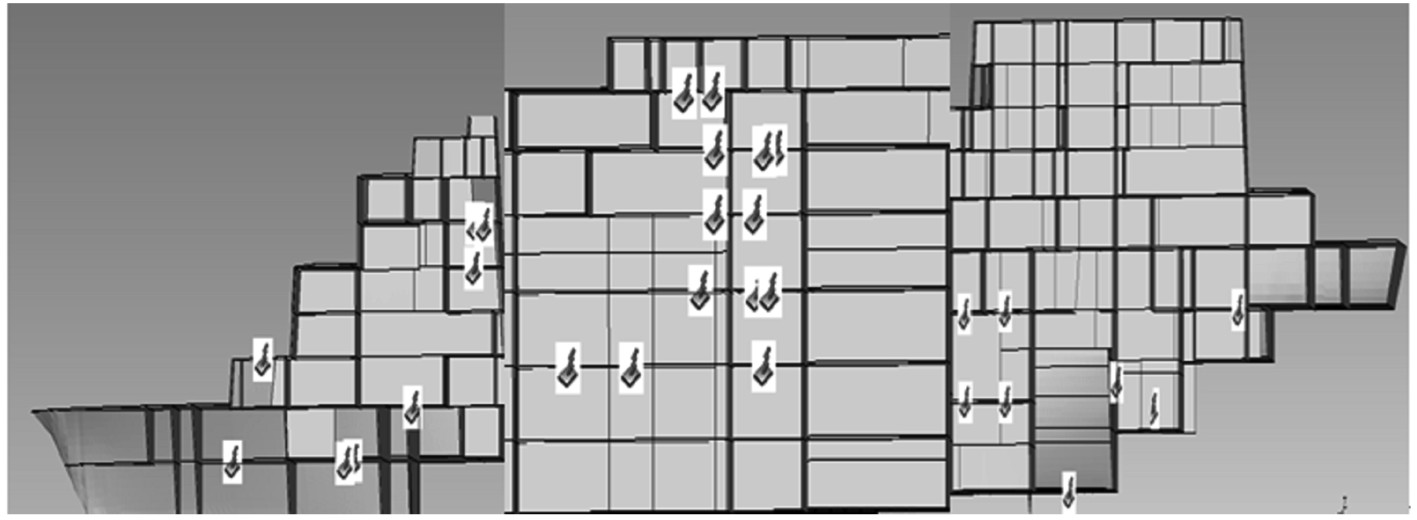
以上给出了各主要设备的激励载荷,根据各设备载荷的具体位置,将载荷施加在船体结构中。图5与图6给出了船舶空气噪声激励载荷及设备振动载荷的施加情况。
|
图 5 船舶舱室噪声设备空气噪声载荷施加示意图(从左至右依次为首、中、尾) Fig. 5 Diagram of airborne noise's loading position(From left to right:bow,midship,stern) |
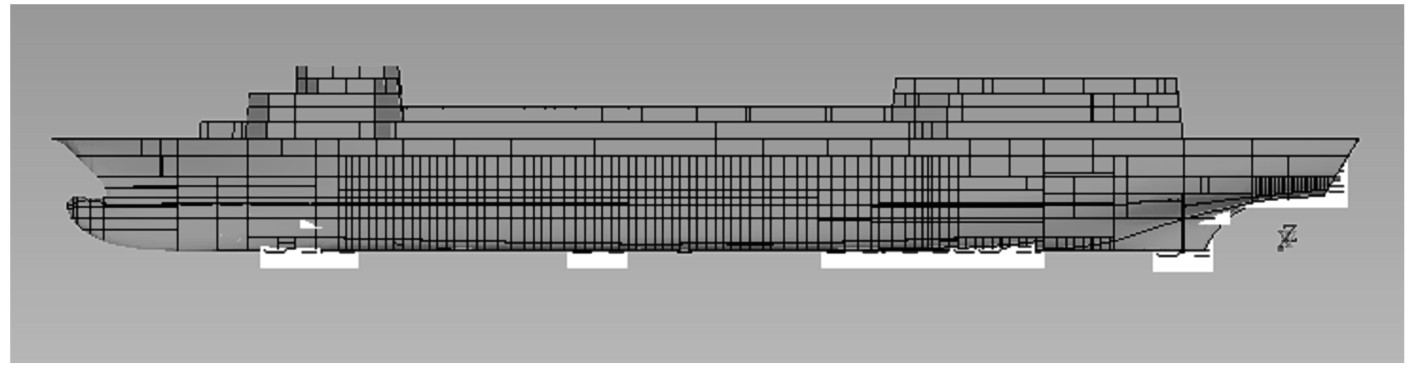
|
图 6 船舶舱室噪声设备振动激励载荷施加示意图 Fig. 6 Diagram of vibration noise's loading position |
在确定了激励载荷后,确定船体板的属性与船体板结构形式属性。根据实船CAD图纸要求确定所有涉及到板的基本属性,船体板的基本数据如表12所示。其中船体板材料的选取如表13所示。
|
|
表 12 船体板基本属性 Tab.12 Basic properties of plates |
|
|
表 13 船体板材料属性 Tab.13 Material properties of plates |
在确定全船各位置船体板的基本属性后,根据实船CAD图纸要求确定所有船体板结构形式的属性,其中部分船体板结构形式属性示意如表14所示。
|
|
表 14 部分船体板结构形式属性 Tab.14 Structural properties of plates |
确定船体板属性与船体板结构形式属性后,再确定船体各部分舱室的划分形式与舾装的敷设方式(舾装按照对象船原始输入状态要求进行敷设),如表15所示。
|
|
表 15 各部分舱室的声腔子系统形式与舾装敷设 Tab.15 The forms of acoustic cavity's subsystem and laying outfitting |
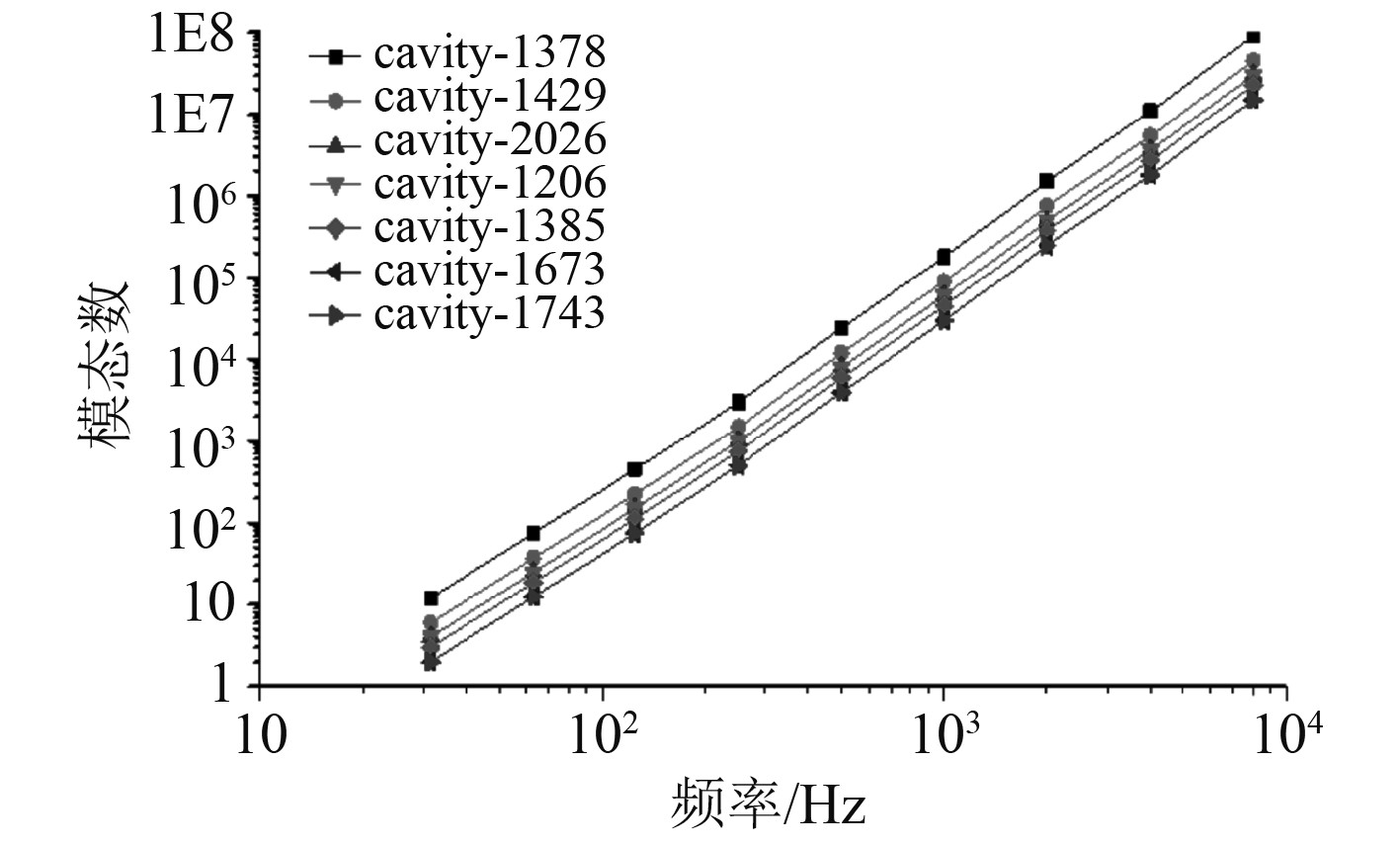
在多参数的影响下,部分船舶舱室模态数如图7所示。
|
图 7 模态数 Fig. 7 Modal number |
由于模态数在计算频率(100~8000 Hz)下都大于5,因此满足统计能量法的基本要求[5]。将所选研究对象舱室沿船首至船尾依次排开,对已确定的多参数方案影响下的船舶舱室噪声数据进行整理,得到表16。
|
|
表 16 多参数方案下的全船舱室噪声数据 Tab.16 Data of ship cabin noise under the multiparameter control |
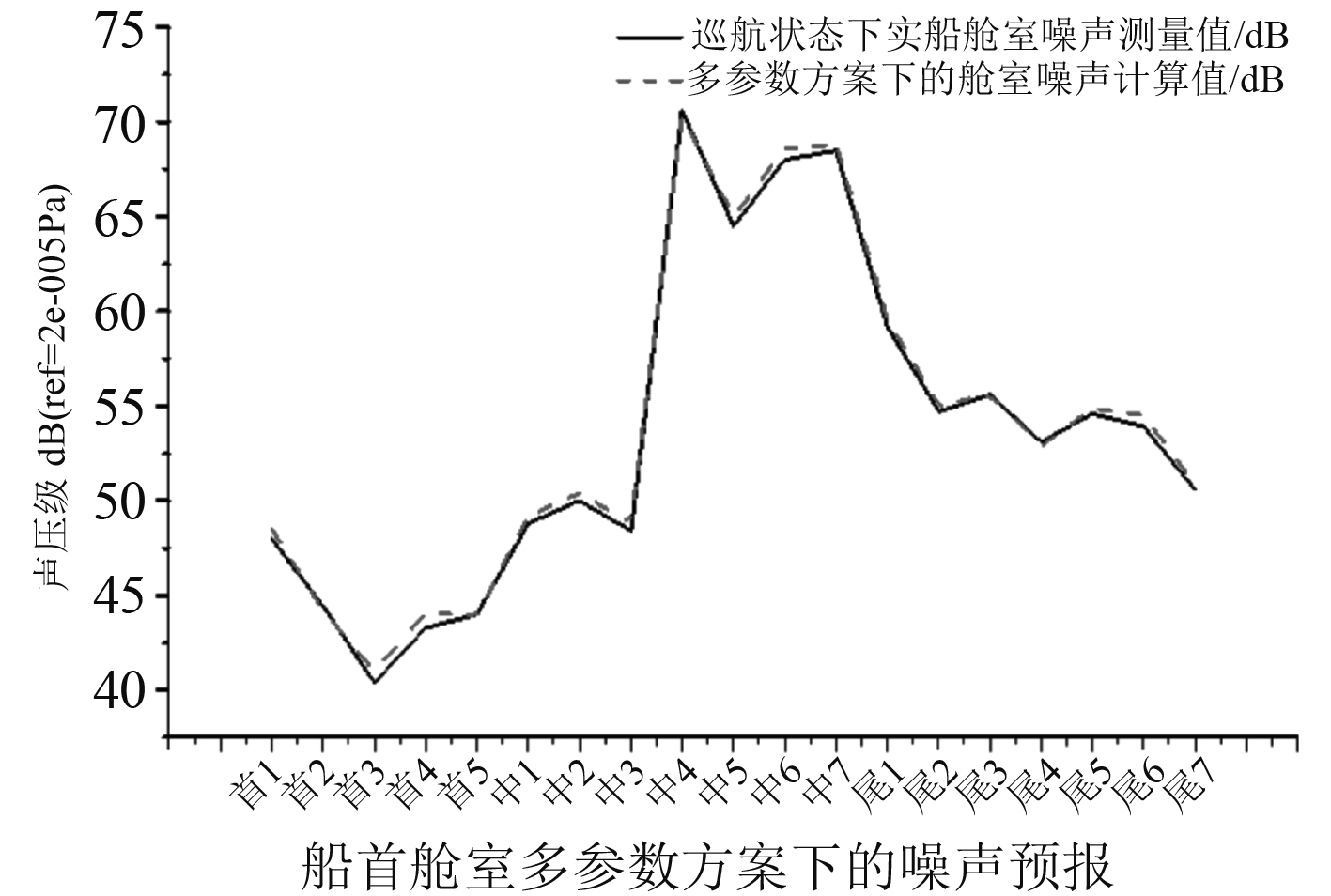
根据表16数据绘制多参数方案影响下的船舶舱室噪声预报结果,如图8所示,从左到右表示从船首至船尾依次分布的舱室。
图8中2条线分别为巡航状态下实船舱室噪声测量值(实线)和多参数方案下的舱室噪声计算值(虚线)。从图中2种线的对比看出,船首舱室(5个)巡航状态下实船舱室噪声测量值的范围为40.4~48.0 dB,船首舱室的平均噪声测量值为44.0 dB;船首舱室多参数方案下的舱室噪声计算值的范围为41.0~48.5 dB,船首舱室的平均噪声计算值为44.3 dB;船首舱室的平均测量值与平均计算值之间相差约0.3 dB。船中舱室(7个)巡航状态下实船舱室噪声测量值的范围为48.4~70.6 dB,平均噪声测量值为59.8 dB;船中舱室多参数方案下的舱室噪声计算值的范围为48.8~70.3 dB,平均噪声计算值为60.2 dB;船中舱室的平均测量值与平均计算值之间相差约0.4 dB。船尾舱室(7个)巡航状态下实船舱室噪声测量值的范围为50.6~59.2 dB,船尾舱室的平均噪声计算值为54.5 dB;船尾舱室多参数方案下的舱室噪声计算值的范围为50.9~59.6 dB,平均噪声计算值为54.8 dB;船尾舱室的平均测量值与平均计算值之间相差约0.3 dB。
因此,在考虑了激励载荷、船体板结构形式与声腔子系统形式3种参数以及敷设舾装后形成的船舶舱室噪声预报方案,模型噪声计算值与实船噪声测量值之间的差异较小。分析图8中2条线中的数据,计算多参数方案下舱室的平均噪声值与巡航状态下实船平均舱室噪声测量值,得到表17。
|
|
表 17 与实船巡航状态下的结果进行对比 Tab.17 Conduct a comparison with the cabin noise results of actual cruising condition |
从表17可看出,多参数方案下全船各部分舱室的平均舱室噪声值与巡航状态下实船舱室噪声测量值的平均值十分接近。多参数方案与巡航状态下实船相比,船首舱室、船中舱室、船尾舱室的平均噪声计算值比平均噪声测量值分别大0.3 dB,0.4 dB和0.3 dB。
因此全船巡航状态下实船舱室平均测量值为53.7 dB,多参数方案船尾舱室的平均舱室噪声值为54.0 dB,比实船平均舱室测量值仅大0.3 dB,符合利用统计能量法进行舱室噪声预报时,计算值与实测值两者之间最大相对误差不超过3 dB的可接受范围[5],验证了本文舱室噪声预报方案的可行性,该结果符合实验要求。由此可见本文多参数各项数据的选取总体上是准确的,形成的全流程预报方案合理且可行。
5 结 语本文研究激励载荷施加、船体板结构形式、声腔子系统形式以及敷设舾装4种参数下船体各部分舱室噪声的影响,并与巡航状态下船首部分、船中部分以及船尾部分的舱室噪声进行对比,验证了所选多参数方案的合理性与可行性。多参数方案具体选取与结论如下:
1)本文采用的激励载荷分为船舶空气噪声激励载荷及设备振动载荷2种,船体板结构形式在定义时注意加筋间距与加筋方向。
2)根据舱室所在位置进行声腔子系统形式与舾装敷设。船首舱室采用纵向排列2倍声腔(长10 m,宽5 m,高5 m)的声腔子系统形式,并以采用D方案(舱壁首先敷设20+20 mm厚多晶丝防火板其次外贴DFR-2阻燃棉白布)进行舾装敷设为主;船中舱室采用4倍声腔大小(长10 m,宽10 m,高5 m)的声腔子系统形式,并以采用B方案(舱壁首先敷设100 mm厚浦森2号其次外贴DFR-2阻燃棉白布)进行舾装敷设为主;船尾舱室采用横向排列2倍声腔大小(长5 m,宽10 m,高5 m)的声腔子系统形式,并以采用B方案(舱壁首先敷设100 mm厚浦森2号其次外贴DFR-2阻燃棉白布)进行舾装敷设为主。
3)多参数方案下全船各部分舱室的平均舱室噪声值与巡航状态下实船舱室噪声测量值的平均值十分接近,全船巡航状态下实船舱室平均测量值为53.7 dB,多参数方案船尾舱室的平均舱室噪声值为54.0 dB,比实船平均舱室测量值大0.3 dB;两者之间最大相对误差不超过3 dB,在可接受范围之内[5],验证了基于统计能量法的本文噪声预报方案的可行性。
| [1] |
朱瑞仪. 船舶结构振动传递规律的工程预报及抑制[D]. 上海: 上海交通大学, 2014.
|
| [2] |
李丹. 船舶舱室噪声预示的统计能量分析研究[D]. 大连: 大连理工大学, 2003.
|
| [3] |
MAXIT. L, GUYADER. J. L. Extension of SEA model to subsystems with non-uniform modal energy distribution[J]. Journal of Sound and Vibration 2003, 265: 337-358.
|
| [4] |
CREMER L, HECKEL L, UNGAR E E. structural vibrations and sound radiation at audio frequencies[M]. Structure-bourn sound (second edition). Berlin: Springer-Verlag, 1988.
|
| [5] |
姚德源, 王其政. 统计能量分析原理及其应用[M]. 北京: 北京理工大学出版社, 1995.
|
| [6] |
邵亮. 统计能量法在船舶舱室噪声预报中的应用[J]. 舰船科学技术, 2012, 34(5): 98-100+107. SHAO Liang. Prediction and research of ship cabin noise with statistical energy analysis[J]. Ship Science and Technology, 2012, 34(5): 98-100+107. DOI:10.3404/j.issn.1672-7649.2012.05.023 |
| [7] |
HYNNA P, KLINGE P, VUOKSINEN J. Prediction of structure-borne sound transmission in large welded ship structures using statistical energy analysis[J]. Journal of Sound and Vibration, 1995, 180(4): 583-607. DOI:10.1006/jsvi.1995.0101 |
| [8] |
LI T Y, ZHANG X M, ZUO Y T. Structural power flow analysis for a floating raft isolation system consisting of constrained damped beams[J]. Journal of Sound and Vibration, 1997, 202(1): 47-54. DOI:10.1006/jsvi.1996.0788 |
 2020, Vol. 42
2020, Vol. 42
