2. 上海交通大学海洋工程国家重点实验室,上海 200240
2. State Key Laboratory of Ocean Engineering, Shanghai Jiaotong University, Shanghai 200240, China
为提高舰船结构声隐身性,应用复合材料是一项行之有效的措施。复合材料具有比强度和比刚度高、阻尼损耗因子大等优势,体现力学设计和结构设计的统一[1-2]。通过添加特定阻尼材料或采用阻尼夹芯结构设计,复合材料层合板可较好地满足减振降噪需求。石勇等[3]从材料类型、铺层形式、减振效果等方面论述层合板在潜艇中应用技术趋势。李海涛等[4]基于声传递矩阵法推导层合板结构反射、透射系数公式,对比材料参数、背衬形式、声入射角度对低频段声辐射的影响。胡泊[5]建立复合材料围壳结构散射目标强度预报模型,以降低声反射为目标对比反声材料优化对围壳目标强度的影响。
连接形式是复合材料层合板结构设计、建造的重要环节。层合板与金属框架结构的连接方式包括胶接连接和螺栓连接:胶接连接认为层合板与框架连接为完全连接,即认为连接是完整的、不存在缺陷,力学性能连续;螺栓连接是将螺栓和螺母将层合板连接在框架面板上。对于层合板与金属框架的连接问题,Le等[6]研究层合板与钢质主船体间的连接形式,对比螺栓及胶接工艺在非承载构件中的力学特性。Wright等[7]研究护卫舰钢质横舱壁与FRP结构间的连接形式,提出用于蒙皮材料与钢板间的“Tuningfork”连接形式。Cao等[8]针对钢框架与FRP结构间的混合连接形式,提出大型船体结构的轻质连接形式。邢立峰等[9]对比不同螺栓连接形式的连接强度及破坏形式,表明3倍孔边距可实现复合材料层合板螺栓连接最大承载力。张大伟等[10]对胶接连接、螺栓连接、焊接、金属插入连接等连接类型进行概述,对比各种连接工艺的优缺点。李立业等[11]对夹芯复合材料/钢板连接接头进行试验和数值研究,研究接头各设计参数对接头弯曲刚度的影响。杨筵东[12]分析孔径大小、布置位置对碳纤维复合材料凸头螺栓/单螺栓连接结构强度的影响,用实验对数值计算进行验证。为提高板架结构声振水平,吴锦武等[13]定义铺设角为设计变量、辐射声功率为优化目标,对4层和8层层合板结构声功率实施最小化。李想等[14]以钉载均匀分配时螺栓载荷为已知量,以钉孔间隙为未知量,优化各钉近似均匀分配时钉孔间隙。邵祝涛[15]等针对层合板多排多列机械连接问题,提出连接效率判别指标,利用枚举法对排列布局实施优化。Peng等[16]采用自动化建模技术建立多钉连接的有限元模型,结合遗传算法对连接板厚度和铺层顺序实施优化,有效地降低钉载分布的不均匀性。
当前,大多数研究关注于层合板连接中结构强度、疲劳、破损等问题,而对声振特性影响的研究较少。本文针对该问题开展层合板螺栓连接方式对结构振动-声辐射特性影响的研究,建立基于声振控制的层合板连螺栓布置优化模型并实施优化,为实现舰船结构减振降噪提供技术参考。
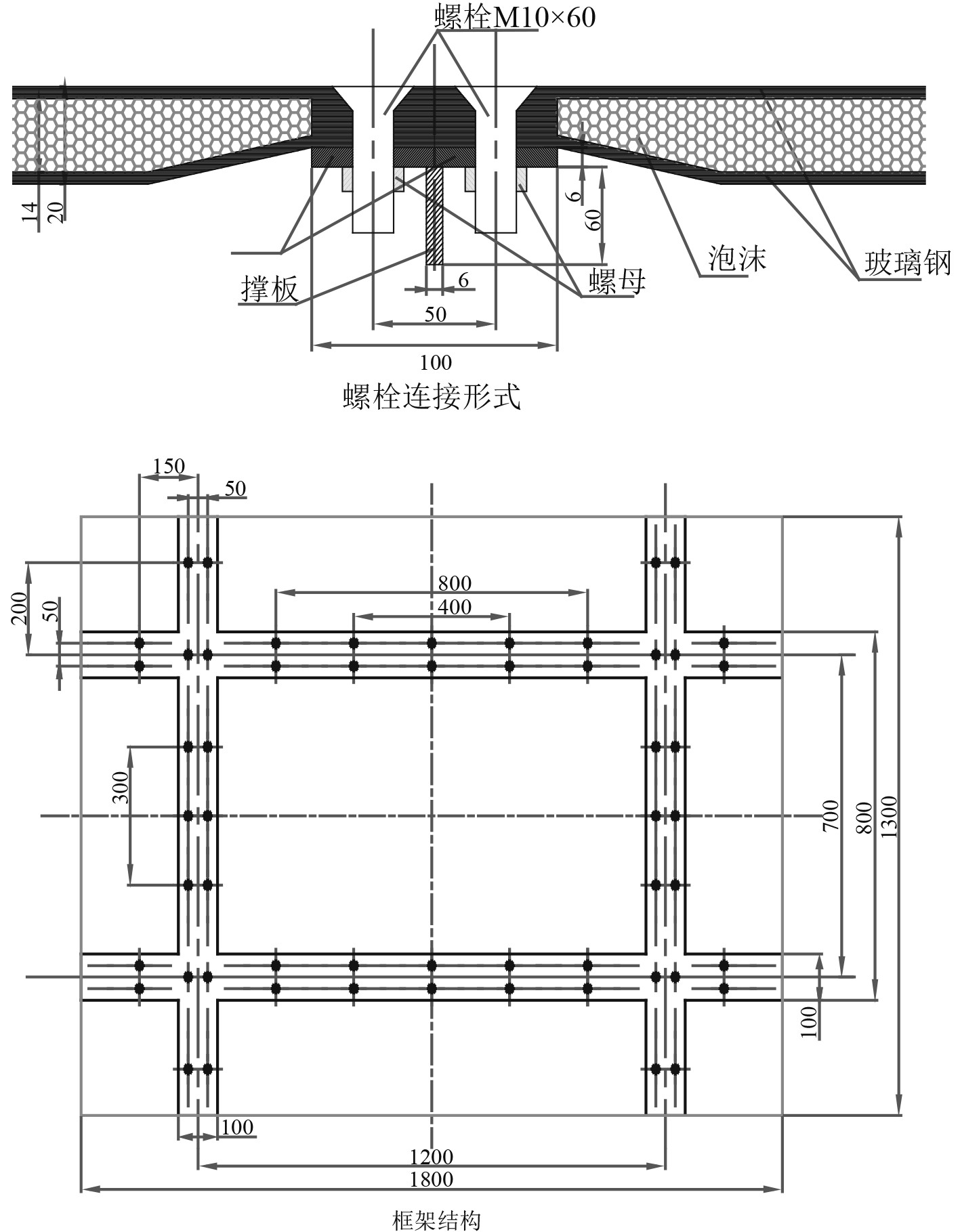
1 层合板连接形式概述复合材料层合板结构广泛应用于舰船结构中,以达到减振降噪目标。板架结构通常由复合材料层合板和金属框架结构组成。框架结构由底部竖支撑板和顶部面板组成,如图1所示。
|
图 1 复合材料层合板结构连接图 Fig. 1 Connection diagram of composite laminated structure |
框架面板宽0.10 m、板厚0.006 m;竖支撑板高度0.06 m、板厚0.006 m;黑点为双排布置的连接螺栓为,螺栓间距0.05 m,螺栓型号M10×60。层合板厚度0.02 m,内部芯厚度0.014 m。
2 典型板架结构声振分析对比典型工艺下胶接连接和螺栓连接板架结构声振特性的差异。
2.1 连接模型分别建立板架结构胶接连接和螺栓连接的计算模型。2个模型的差异在于对面板连接的处理,胶接连接模型中节点为共点,螺栓连接模型中螺栓用弹簧单元模拟。在弹簧单元模型中,螺栓刚度与螺栓直径、螺栓材料、层合板厚度、预紧力等相关。
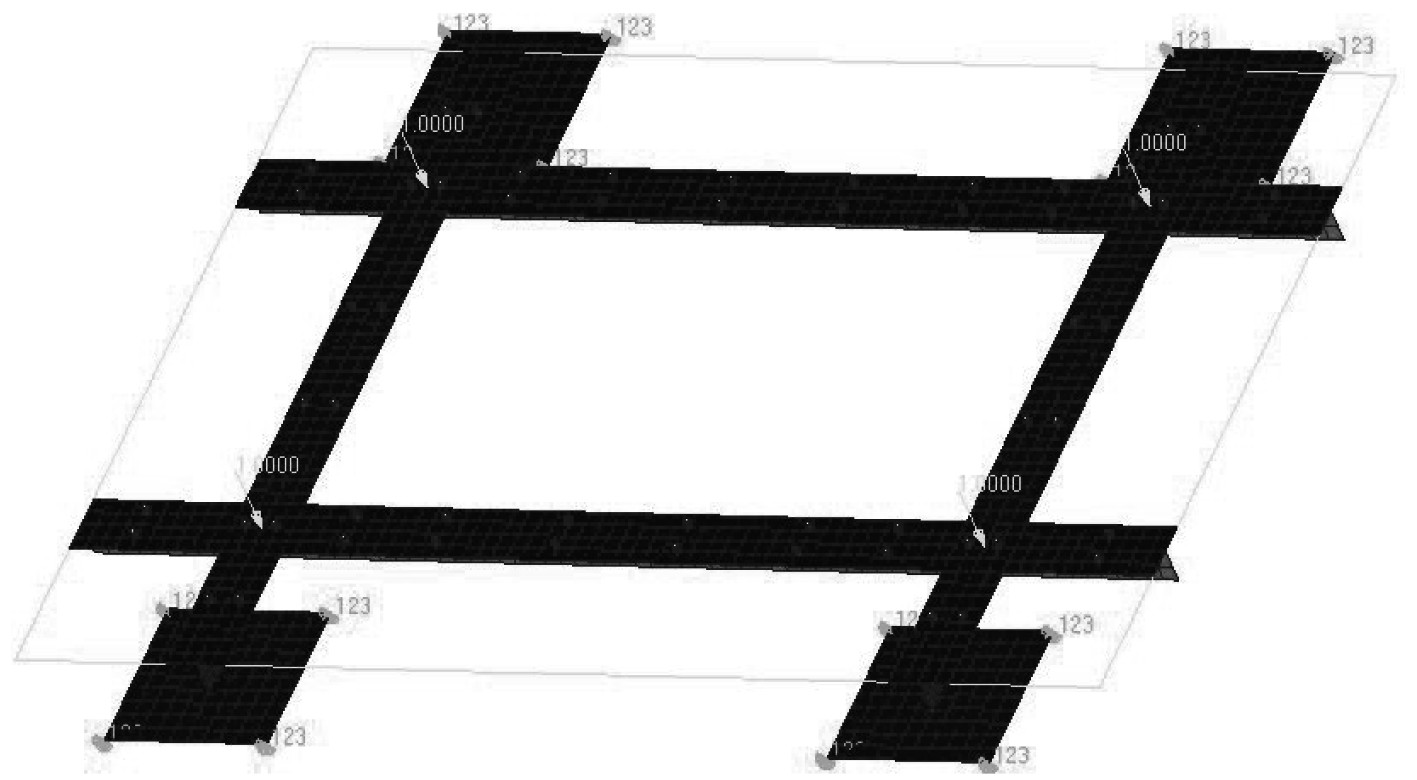
图2中,板架结构的4个角点为固支约束。
|
图 2 框架结构边界约束与受力 Fig. 2 Boundary constraints and loading |
金属框架由铝合金焊接,复合材料层合板有3层,中间层是芯层材料层,外面两层包裹着玻纤材料层,各材料力学特性如表1所示。
|
|
表 1 板架结构材料力学特性 Tab.1 The mechanical properties of structure frame |
开展胶接连接和螺栓连接板架结构的模态分析。板架结构前6阶振型如图3所示,左图为胶接连接模型振型、右图为螺栓连接模型振型。

|
图 3 结构振型对比 Fig. 3 Mode shapes |
对比图3可知,螺栓连接模型在第5阶中出现内卷,而在其他阶振型差异不是太大。
表2所示为胶接连接模型和螺栓连接模型板架结构的前10阶固有频率对比。
|
|
表 2 固有频率对比 Tab.2 Natural frequency |
对比表1可知,胶接连接和螺栓连接的板架结构固有频率在第3阶后差异非常明显。表明如直接采用胶接连接模型来模拟螺栓连接结构,将出现一定差异。为更精确地预报层合板板架结构的声振特性,需采用螺栓连接模型进行模拟。
2.4 声辐射分析在板架结构横竖面板连接处受外谐激励力的作用,共4个作用点。分别对胶接连接和螺栓连接的板架结构开展动力响应分析。以结构表面振动速度为边界,以层合板结构为声辐射面建立声边界元模型,应用边界元法进行结构声辐射计算。
在声辐射分析中,声介质为空气,其参数如下:密度ρ=1.225 kg/m3;声速c=340 m/s;声功率W0=1×10–12W。
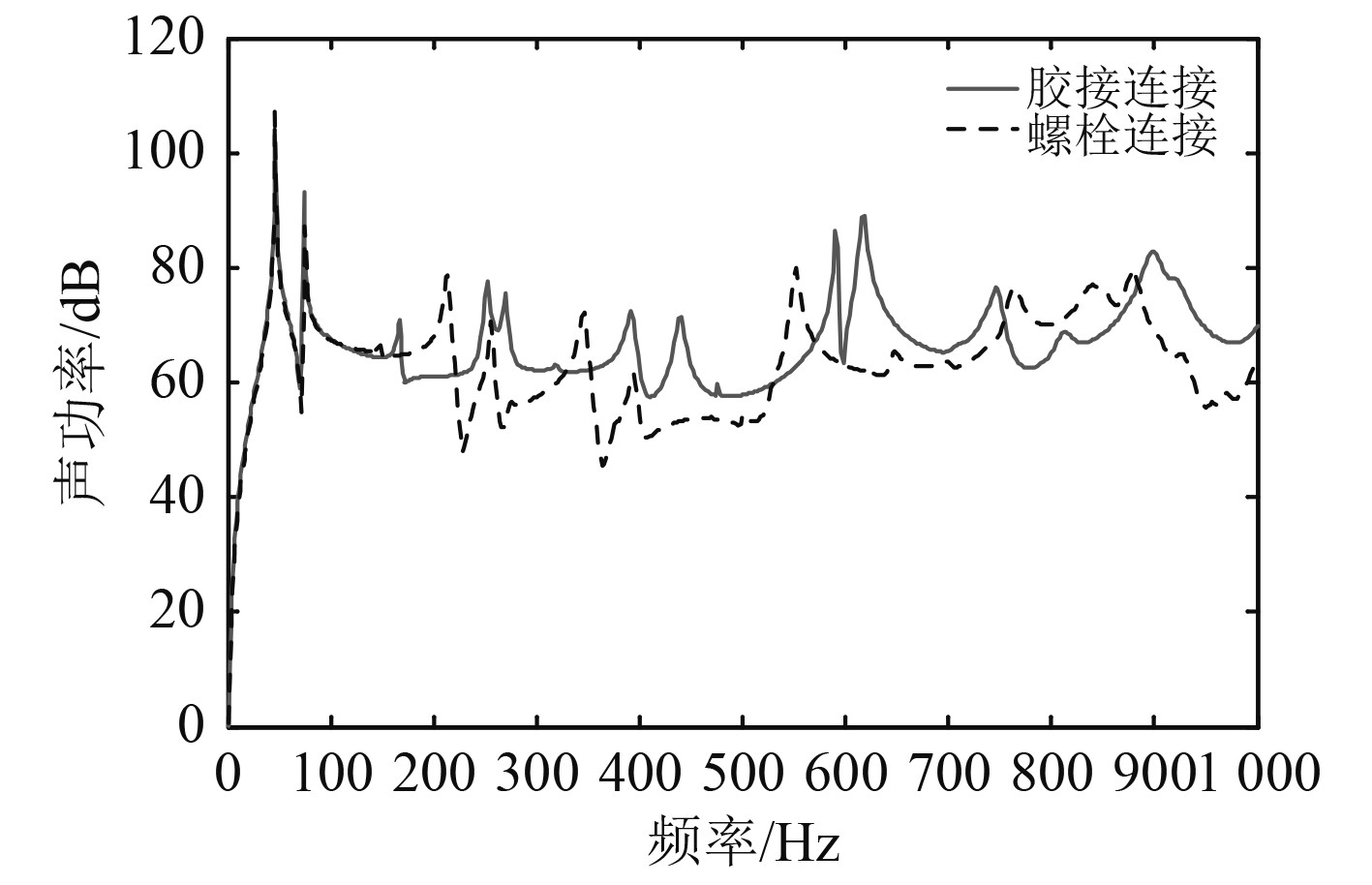
图4为胶接连接和螺栓连接的板架结构的声辐射功率对比。计算频率范围在10~1000 Hz之间,在10~200 Hz频带内步长为1 Hz,在200~1000 Hz频带步长为2 Hz。
|
图 4 声辐射功率对比 Fig. 4 Comparison of acoustic radiation power |
对比图4可知,胶接连接和螺栓连接的板架结构声功率差异非常大,除峰值(46 Hz)处外,在高频段差异明显,这与固有频率差异相对应。
3 层合板连接优化模型由图4可知,螺栓连接影响板架结构声振特性。基于弹簧模型的连接螺栓参数将影响板架结构总体刚度。通过改进连接螺栓参数(刚度)及其布置位置可改善板架结构声振特性。
3.1 螺栓连接模型优化概述为提高板架结构声振特性,开展螺栓布置位置及设计参数的优化。以声辐射功率(或总级)最小为优化目标,以螺栓参数(刚度)K及布置位置X为设计变量的层合板结构声振优化模型为:
| $\begin{split} &{\rm{Find}}\;K = {[{K_1},{K_2}, \cdot \cdot \cdot ,{K_{\rm{i}}}]^{\rm{T}}}\text{,}\\ &X = {[{x_1},{x_2}, \cdot \cdot \cdot ,{x_{\rm{i}}}]^{\rm{T}}},{\rm{i}} = 1,2, \cdot \cdot \cdot ,k\text{,} \\ &{{\rm{Min}}\;\frac{1}{2}{{Re}}\int_\varOmega ^{} {{{{p}}_{\rm{f}}}} {\bf{v}}_{\rm{n}}^*{\rm{d}}\varOmega }\text{,}\\ &{{\rm{s}}.{\rm{t}}.\;{w_j}\sum\limits_{j = 1}^m {{f_{\rm{j}}}} \geqslant {w_j}\sum\limits_{j = 1}^m {{f_{j0}}} }\text{,}\\ &{\sum\limits_{i = 1}^k {{m_i}} \leqslant \sum\limits_{i = 1}^k {{m_{i0}}} }\text{,}\\ &{K_{}^{\rm{l}} \leqslant {K_{\rm{i}}} \leqslant K_{}^{\rm{u}},x_{}^{\rm{l}} \leqslant {x_{\rm{i}}} \leqslant x_{}^{\rm{u}}}\text{,}\\ &{g({K_{\rm{i}}},{x_{\rm{i}}}) \leqslant 0}\text{。} \end{split}$ | (1) |
式中:
考虑到第1阶频率最直接地反映结构固有特性,因而1阶频率权重系数最大,其他阶次的权重系数依次减少,权重系数值如表2所示。
根据工程实际需求,分别实施板架结构的螺栓连接刚度优化或螺栓布置位置优化。
3.2 考虑螺栓刚度的约束优化在该优化模型中,仅考虑螺栓刚度变量因素。考虑螺栓直径为通用尺寸,定义3个螺栓尺寸,即
图1中,共布置28对螺栓。将不同阶次权重系数代入式(1)中,获得仅考虑螺栓刚度的优化模型:
| $\begin{split} &{{\rm{Find}}\;K = {{[{K_1},{K_2}, \cdot \cdot \cdot ,{K_{\rm{i}}}]}^{\rm{T}}},{{i}} = 1,2, \cdot \cdot \cdot ,28}\text{,}\\ &{{\rm{Min}}\;\frac{1}{2}{{Re}}\int_\varOmega ^{} {{{{p}}_{{f}}}} {{v}}_{{n}}^*{\rm{d}}\varOmega }\text{,}\\ &{{\rm{s}}.{\rm{t}}.\;{w_j}\sum\limits_{j = 1}^{10} {{f_j}} \geqslant 73.69}\text{,}\\ &{\sum\limits_{i = 1}^{28} {{m_i}} \leqslant \sum\limits_{i = 1}^{28} {{m_{i0}}} }\text{,}\\ &{K \in [{K^8},{K^{10}},{K^{12}}]}\text{,}\\ &{g({K_{\rm{i}}},{x_{\rm{i}}}) \leqslant 0}\text{。} \end{split}$ | (2) |
式中,各符号的含义与式(1)相同。
3.3 考虑螺栓位置的约束优化在该优化模型中,仅考虑螺栓位置变量因素,设板架结构横竖面板连接处的4对螺栓位置是固定的。结合不同阶次权重系数,获得仅考虑螺栓位置的优化模型:
| $\begin{split} &{{\rm{Find}}\;X = {{[{x_1},{x_2}, \cdot \cdot \cdot ,{x_{\rm{i}}}]}^{\rm{T}}}\text{,}\;\;{{i}} = 1,2, \cdot \cdot \cdot ,24}\text{,}\\ &{{\rm{Min}}\;\frac{1}{2}{Re}\int_\varOmega ^{} {{{{p}}_{{f}}}} {{v}}_{{n}}^*{\rm{d}}\varOmega }\text{,}\\ &{{\rm{s}}.{\rm{t}}.\;{w_j}\sum\limits_{j = 1}^{10} {{f_{\rm{j}}}} \geqslant 73.69}\text{,}\\ &{x_{}^{\rm{l}} \leqslant {x_{\rm{i}}} \leqslant x_{}^{\rm{u}}}\text{,}\\ &{g({K_{\rm{i}}},{x_{\rm{i}}}) \leqslant 0}\text{。} \end{split}$ | (3) |
式中,各符号的含义与式(1)相同。
3.4 考虑螺栓刚度、螺栓位置的综合优化为进一步改善板架结构声振特性,获得更好的声学优化效果。将连接螺栓刚度和螺栓位置的优化综合起来,实施同时考虑螺栓刚度、螺栓位置的综合优化。结合式(1)~式(3),获得板架结构综合优化模型:
| $\begin{split} &{{\rm{Find}}\;K = {{[{K_1},{K_2}, \cdot \cdot \cdot ,{K_{\rm{i}}}]}^{\rm{T}}},{{i}} = 1,2, \cdot \cdot \cdot ,28}\text{,}\\ &{X = {{[{x_1},{x_2}, \cdot \cdot \cdot ,{x_{\rm{i}}}]}^{\rm{T}}}{i} = 1,2, \cdot \cdot \cdot ,24,}\\ &{{\rm{Min}}\;\frac{1}{2}{{Re}}\int_\varOmega ^{} {{{{p}}_{{f}}}} {{v}}_{{n}}^*{\rm{d}}\varOmega ,}\\ &{{\rm{s}}.{\rm{t}}.\;{w_j}\sum\limits_{j = 1}^{10} {{f_{\rm{j}}}} \geqslant 73.69,}\\ &{\sum\limits_{i = 1}^{28} {{m_i}} \leqslant \sum\limits_{i = 1}^{28} {{m_{i0}}} ,}\\ &{K \in [{K^8},{K^{10}},{K^{12}}],}\\ &{x_{}^{\rm{l}} \leqslant {x_{\rm{i}}} \leqslant x_{}^{\rm{u}},}\\ &{g({K_{\rm{i}}},{x_{\rm{i}}}) \leqslant 0}\text{。} \end{split}$ | (4) |
式中,各符号的含义与式(1)相同。
式(2)~式(4)描述了考虑不同优化目标的层合板板架结构螺栓连接方式的优化模型。在实际工程中,考虑到螺栓布置的对称性,描述螺栓布置位置参数的设计变量数量将减少。
4 复合材料层合板连接方式优化通过定义设计变量、约束条件和优化目标,建立基于噪声控制的层合板连接方式优化模型。通过在iSIGHT集成优化平台上进行二次开发,进行连接螺栓刚度、螺栓位置的优化,实现板架结构的减振降噪目标。
4.1 考虑螺栓刚度的优化通过开展螺栓刚度优化,在板架结构横竖面板连接处的4对螺栓直径由10增加到12;在四周8对螺栓直径由10减少到8,螺栓质量有稍微减少。
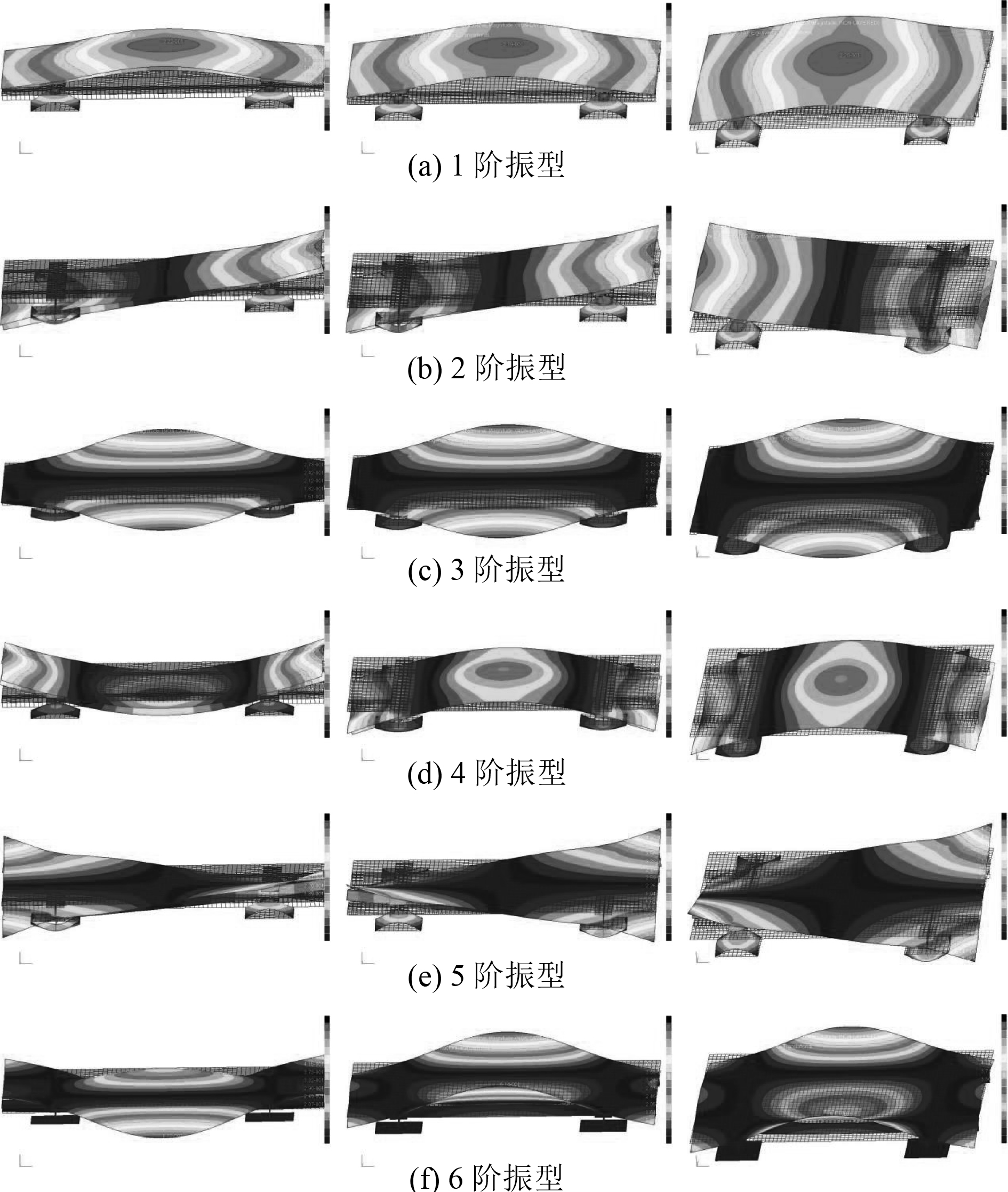
图5左图为板架结构在实施螺栓刚度优化后的前6阶振型,刚度优化前后前10阶固有频率对比如表3所示。
|
|
表 3 固有频率对比 Tab.3 Natural frequency |
|
图 5 结构振型 Fig. 5 Mode shapes |
对比图1、图5和表3可知,通过实施螺栓刚度优化,结构振型差异不太明显。结构固有频率有一定的差异,在高频率段更为明显。
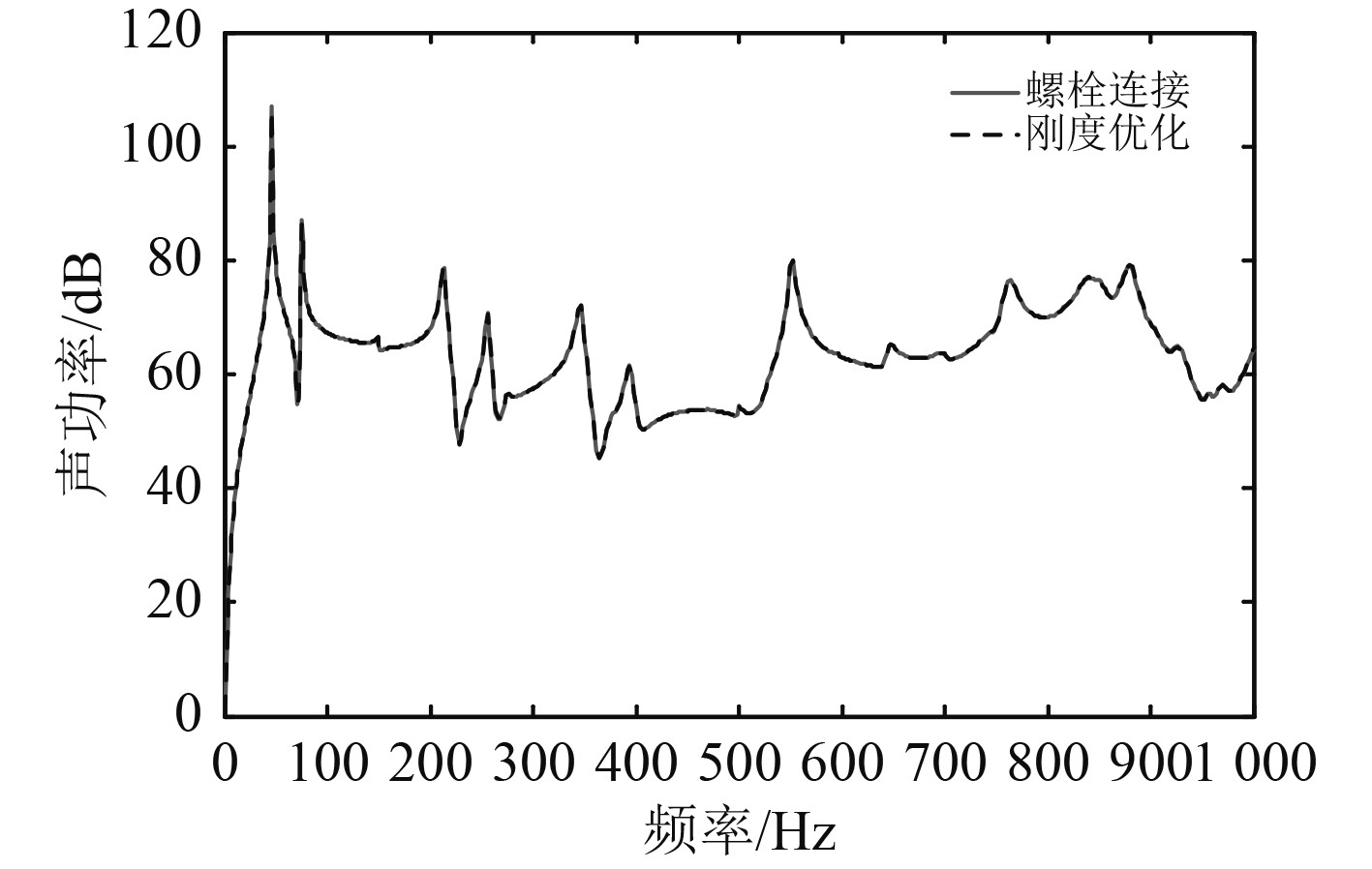
图6为刚度优化前后声辐射功率对比。
|
图 6 声辐射功率对比 Fig. 6 Comparison of acoustic radiation power |
对比图6可知,在开展螺栓刚度优化后,框架结构的声辐射特性有一定改善,从结构减振降噪来看开展结构优化是有成效的。
4.2 考虑螺栓位置的约束优化开展螺栓连接位置优化,在中部区域连接螺栓的间距改变、间距增加,靠近交叉点处螺栓间距变小,各连接螺栓不再均匀分布,如图7所示。
板架结构位置优化后前6阶振型见图5,连接位置优化后的前10阶固有频率见表3。
对比图1、图5和表3可知,通过实施螺栓位置优化,结构振型差异不太明显。结构固有频率有一定的差异,在高频率段更为明显。
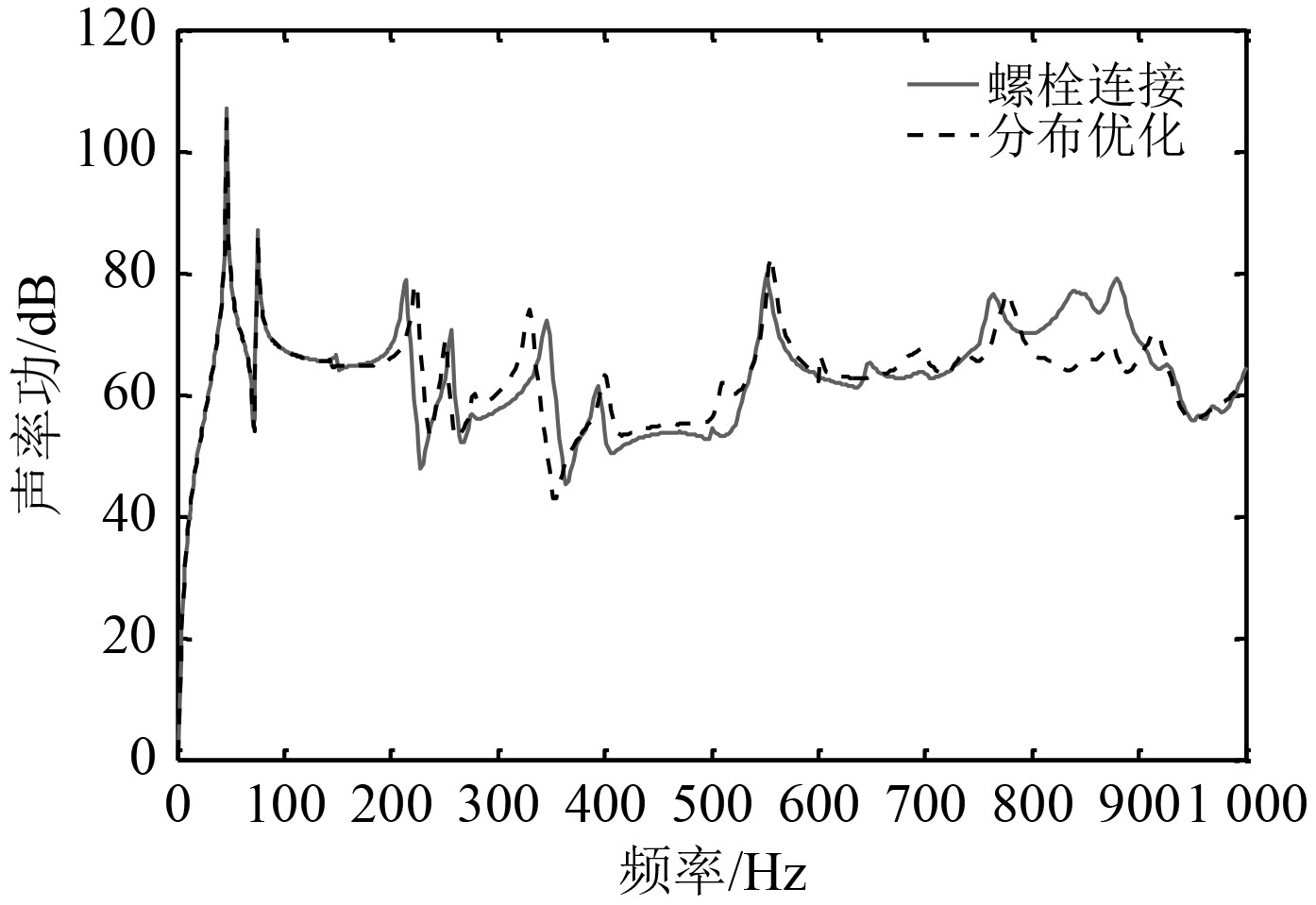
图7为位置优化前后的声辐射功率对比。
对比图8可知,在开展螺栓位置优化后,板架结构的声辐射特性有一定改善,从结构减振降噪来看开展结构优化有成效。

|
图 7 复合材料围壳结构连接图 Fig. 7 Connection diagram of composite materials structure |
|
图 8 声辐射功率对比 Fig. 8 Comparison of acoustic radiation power |
开展考虑螺栓刚度、螺栓位置的综合优化。在实施结构优化后,在板架结构横竖面板连接处的4对螺栓直径由10增加到12;在四周8对螺栓直径由10减少到8,螺栓质量有稍微减少。
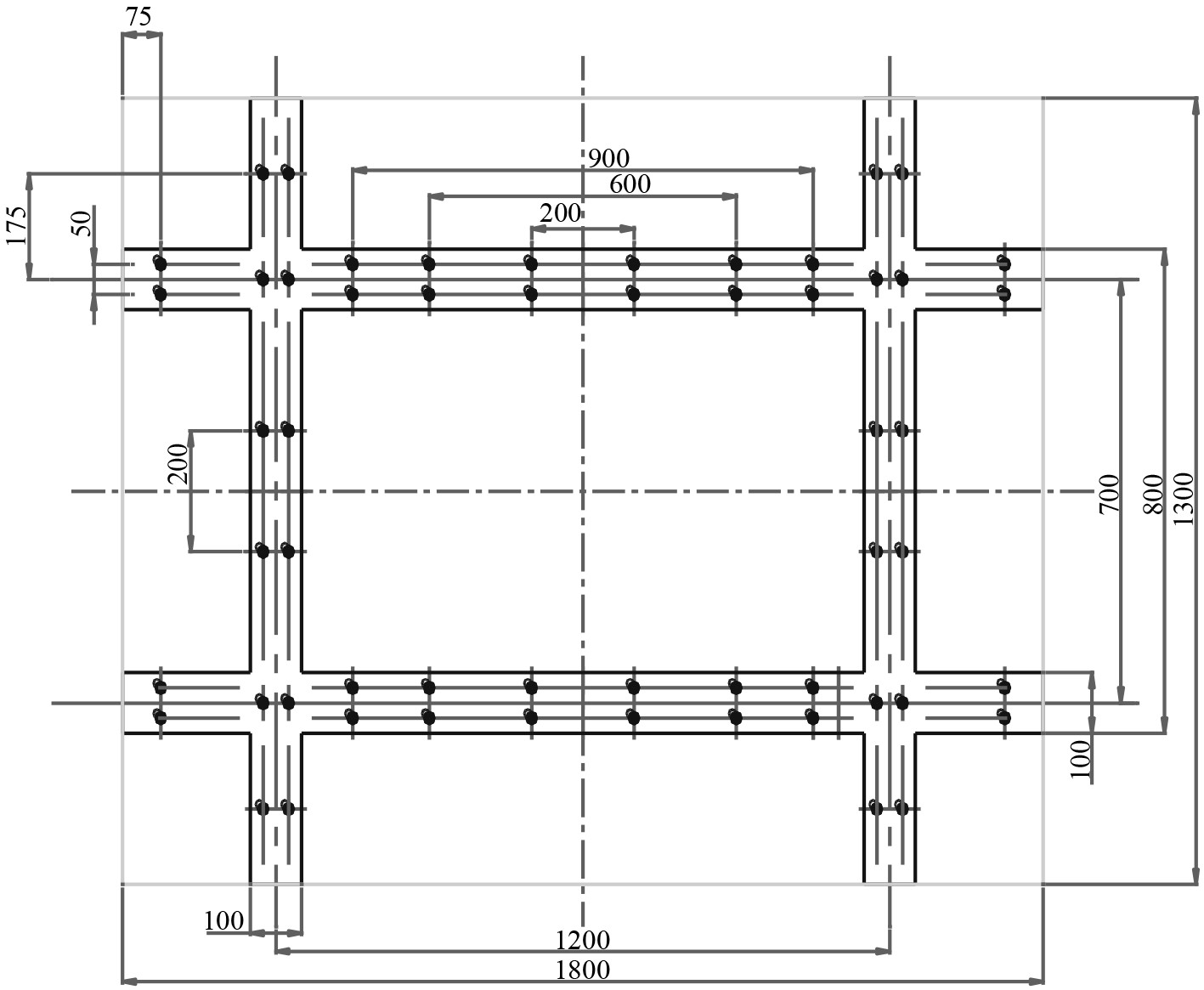
同时,在中部区域部分连接螺栓的间距改变、间距增加,靠近交叉点处螺栓间距变小,各连接螺栓不再是均匀分布,如图9所示。
|
图 9 复合材料围壳结构连接图 Fig. 9 Connection diagram of composite materials structure |
图5右图为板架结构螺栓刚度、螺栓位置的综合优化后的前6阶振型。螺栓连接位置优化后前10阶固有频率见表3。
对比图1、图5和表3可知,通过实施螺栓刚度、螺栓位置的综合优化,结构振型差异不太明显。结构固有频率有一定差异,高频段更为明显。
图10为螺栓刚度、螺栓位置的综合优化前后的声辐射功率对比。

|
图 10 声辐射功率对比 Fig. 10 Comparison of acoustic radiation power |
对比图10可知,实施综合优化后,复合材料板架结构的声辐射特性有明显改善,综合优化取得更好地优化效果。
4.4 声功率总级分别计算胶接模型、螺栓连接模型、刚度优化、位置优化和综合优化的板架结构声辐射功率总级。计算包括10~200 Hz、200~1000 Hz和10~1000 Hz三个频段声功率总级,如表4所示。
|
|
表 4 声功率总级(dB) Tab.4 Total level of acoustic power(dB) |
由表4可知,在声辐射功率声功率总级方面,在开展结构优化后其声辐射功率的总级明显降低,采用综合优化效果最为显著。
5 结 语以复合材料层合板框架结构的螺栓连接工艺为基础,分析复合材料层合板螺栓连接方式对结构声振特性的影响,建立以声学控制为目标的层合板结构螺栓连接优化模型并实施优化计算。计算表明实施优化后结构声学性得到明显改善,达到结构优化之目的。研究成果为复合材料结构的设计、建造及质量评估提供参考。
| [1] |
PLANTEMA F J. Sandwich construction: the bending and bulking of sandwich beams, plates and shells[M]. New York: Wiley, 1966.
|
| [2] |
VINSON J R. The behaviour of sandwich structures of isotropic and composite materials[M]. USA: Technomic Publishing Company, 1999.
|
| [3] |
石勇, 刘宇, 刘鑫, 等. 夹层复合材料在潜艇声隐身结构中的应用及其相关技术研究[J]. 材料开发与应用, 2008, 23(6): 22-25. SHI Yong, LIU Yu, LIU Xin, et al. Application of sandwich composite in submarine sound stealth structure[J]. Development and Application of Materials, 2008, 23(6): 22-25. |
| [4] |
李海涛, 朱锡, 王林, 等. 水下均匀复合层结构的声特性研究[J]. 武汉理工大学学报, 2008, 30(6): 105-109. LI Hai-tao, ZHU Xi, WANG Lin, et al. Investigation of sound field in homogeneous multiple-layer structures in water[J]. Journal of Wuhan University of Technology, 2008, 30(6): 105-109. |
| [5] |
胡泊. 反声复合材料指挥室围壳声目标强度研究[D]. 北京: 中国舰船研究院, 2017年3月. HU Po. Research on target strength of submarine sails made by sound-reflecting composites[D]. Beijing: China Ship Scientific Research & Development Academy, March, 2017. |
| [6] |
LE LAN J Y, PARNEIX P. Composite material superstructures[C]// International Conference on Nautical Construction with Composite Materials, Paris, France, 1992.
|
| [7] |
WRIGHT P N H, WU Y, GIBSON A G. Fiber reinforced composite-steel connections for transverse ship bulkheads[J]. Plastics, Rubber and Composites, 2000, 29(10): 549-557. DOI:10.1179/146580100101540761 |
| [8] |
CAO J, GRENESTEDT J L. Test of a redesigned glass-fiber reinforced vinyl ester to steel joint for use between a naval GRP superstructure and a steel hull[J]. Composite Structures, 2003, 60(6): 439-445. |
| [9] |
邢立峰, 曹安港, 毕凤阳, 等. 纤维增强复合材料螺栓连接性能试验研究[J]. 舰船科学技术, 2018, 40(2): 102-105. XING Li-feng, CAO An-gang, BI Feng-yang, et al. An experimental study on bolt joint performance of fiber reinforced composite materials[J]. Ship Science and Technology, 2018, 40(2): 102-105. DOI:10.3404/j.issn.1672-7649.2018.02.019 |
| [10] |
ZHANG D W, ZHANG Q, FAN X G, et al. Review on joining process of carbon fiber-reinforced polymer and metal: Methods and joining process[J]. Rare Metal Materials and Engineering, 2018, 47(12): 3686-3696. DOI:10.1016/S1875-5372(19)30018-9 |
| [11] |
李立业, 陈赵, 祁恩荣. 夹芯复合材料/钢板胶接接头力学特性[J]. 舰船科学技术, 2013, 35(9): 110-114. LI Li-ye, CHEN Zhao, QI En-rong. Mechanical behaviors of adhesively-bonded composite-to-steel joints[J]. Ship Science and Technology, 2013, 35(9): 110-114. DOI:10.3404/j.issn.1672-7649.2013.09.022 |
| [12] |
杨筵东. 碳纤维复合材料典型连接结构力学性能分析[D]. 哈尔滨: 哈尔滨工业大学, 2016年6月. YANG Yan-dong. Mechanical performance analysis of carbon fiber composites typical bolted joints[D]. Harbin: Harbin Institute of Technology, June, 2016. |
| [13] |
吴锦武, 彭文辉, 赵飞. 分层有限元模型下层合板声功率优化设计[J]. 振动与冲击, 2015, 34(16): 85-146. WU Jin-wu, PENG Wen-hui, ZHAO Fei. Optimal design of acoustic power of laminated composite plate based on layer-wise FEM[J]. Journal of Vibration and Shock, 2015, 34(16): 85-146. |
| [14] |
李想, 谢宗蕻. 复合材料多钉连接钉载分配均匀化的泰勒展开方法[J]. 哈尔滨工业大学学报, 2019, 51(11): 108-115. LI Xiang, XIE Zong-hong. A Taylor expansion algorithm for the load distribution homogenization ofmulti-bolt composite joints[J]. Journal of Harbin Institute of Technology, 2019, 51(11): 108-115. DOI:10.11918/j.issn.0367-6234.201811201 |
| [15] |
邵祝涛. 层合板机械连接强度分析与优化及软件开发[D]. 大连: 大连理工大学, 2012. SHAO Zhu-tao. Trength analysis and optimization of mechanical joints in composite laminates and development of software[D]. Dalian: Dalian University of Technology, 2012. |
| [16] |
PENG X B, CHI H, WAN X P. Research on the automodeling technology and load distribution optimization for multi-bolt composite joints[J]. Advanced Materials Research, 2013, 721: 556-562. DOI:10.4028/www.scientific.net/AMR.721.556 |
 2020, Vol. 42
2020, Vol. 42
