2. 南通理工学院 电气与能源工程学院,江苏 南通 226000
2. Electrical and Energy Engineering College, Nantong Institute of Technology, Nantong 226000, China
由于破冰过程的特殊性及层冰物理力学性质的复杂性,准确预测破冰船在层冰中的冰阻力十分困难。早期,Spencer[1],Lindqvist[2]和Riska[3]等根据层冰与船舶相互作用的几个阶段,将总阻力划分成不同的部分,结合大规模的模型试验和实船数据,提出相应算法对层冰破冰阻力进行了研究。为了模拟船-冰相互作用,Wang[4]通过考虑破碎,弯曲及碎冰形成3个连续过程,基于力学冰破坏模型,采用几何网格法对冰锥相互作用进行了数值模拟。Nguyen[5]将这一推导出的冰破坏模型应用于船-冰相互作用,模拟动态定位(DP)船在层冰下的运动。Su[6]进一步考虑了冰阻力与船舶运动的耦合问题,优化船-冰接触模型,对连续破冰模式进行数值模拟。
本文根据简化后的连续破冰过程,运用编程语言,模拟理想状态下破冰船在层冰条件下的运动过程,计算破碎力,建立完整的破碎力算法流程图。由于简化后的连续破冰过程假设层冰脱落后马上消失,并不考虑层冰破碎后碎冰在船首的运动,因此计算出的阻力值较实际值偏低。本文在理想假设的基础上,考虑船首部分碎冰运动引起的浸没阻力,对破碎力进行修正,计算修正后破冰阻力,得到破冰船在破冰过程中的冰阻力变化曲线。同时对不同工况下的船-冰运动进行数值模拟,分析船速、冰厚等因素对破冰阻力的影响。
1 破冰船连续破冰过程的数值模拟根据Valanto[7]对连续破冰过程中船-冰相互作用的分析,当船首与层冰发生接触时,接触区域的层冰自由边缘发生局部挤压破碎,此时层冰破坏模式主要是挤压破坏和剪切破坏。随着船的前进,船首与层冰接触面积增大,破碎力增加,层冰发生弯曲倾斜,当层冰内部的应力超过其应力极限,层冰发生弯曲破坏。发生弯曲破坏的层冰从冰层上断裂下来,在船体的作用下进一步加速并旋转,直至失去与船舶的接触。船首与新的层冰边缘接触,开始新一轮循环,如图1所示。

|
图 1 连续破冰过程的4个阶段 Fig. 1 Four stages of continuous ice-breaking process |
在数值模拟过程中,假设:
1)船-冰相互作用是一个连续的过程,包括层冰的破碎,弯曲,断裂的循环;
2)船-冰相互作用仅发生在船体水线面处,且忽略船在破冰运动过程中的垂直运动;
3)在挤压断裂过程中,接触区域平面保持平整;
4)在发生弯曲断裂时,冰面弯曲断裂的形状认为是圆形的。
1.1 层冰破坏模式分析 1.1.1 确定接触面积在数值模拟过程中,船体与层冰的接触情况是判断破冰过程破碎力大小的关键。层冰在发生弯曲破坏后,会产生环向裂缝和径向裂缝。其中环向裂缝与层冰边缘的交点是判断弯曲破坏过程中冰层破损形状的关键位置,在数值模拟中,环向裂缝被理想化为破碎半径R的函数[1]:
| $R = {C_l} \cdot l\left( {1.0 + {C_V} \cdot v_n^{rel}} \right)\text{。}$ | (1) |
式中:Cl和Cv为经验参数;Cl为破冰半径与特征长度的比例;Cv为浮冰的大小随碰撞速度的变化而变化。这里,Cl为正值,Cv为负值。在程序中,Cl、Cv的值是可调控的,取值情况可根据实验进行调整。vnrel为船体相对于层冰离散点的垂直破冰速度,l为层冰特征长度:
| $l = {\left( {\frac{{Eh_i^3}}{{12\left( {1 - {\nu ^2}} \right){\rho _w}g}}} \right)^{\frac{1}{4}}}\text{。}$ | (2) |
式中:E为弹性模量;hi为冰厚;ν为泊松比;ρw为海水密度;g为重力加速度。
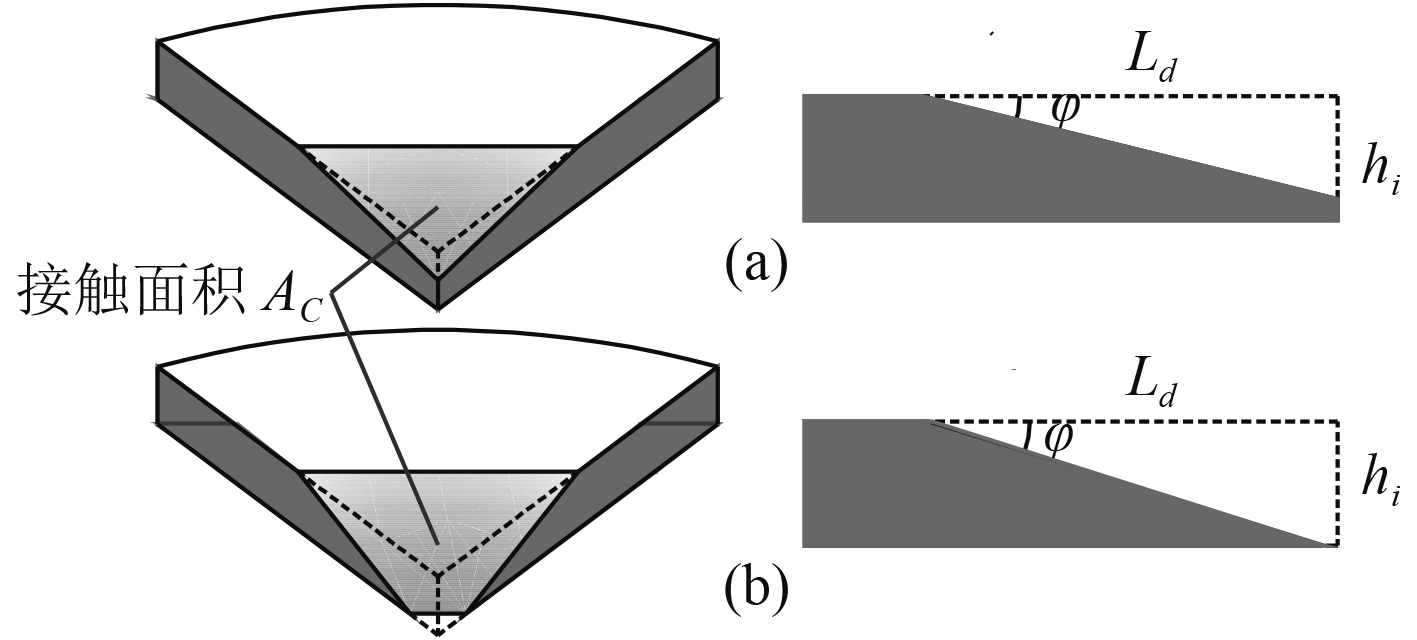
基于上述理想化破冰过程,根据冰厚与破冰半径的大小关系,接触面积可以分为三角形接触和四边形接触2种情况,如图2所示。
|
图 2 船冰接触面积的2种计算模式 Fig. 2 Two cases for the calculation of contact area |
2种接触模式下的接触面积计算公式如下:
情况1 当
| $ {A_C} = \frac{1}{2}{L_h}\frac{{{L_d}}}{{\cos \left( \varphi \right)}}{\text{,}} $ | (3) |
情况2 当
| $ {A_C} = \frac{1}{2}\left( {{L_h} + {L_h}\frac{{{L_d} - {h_i}/\tan \left( \varphi \right)}}{{{L_{\rm{d}}}}}} \right)\frac{{{h_i}}}{{\sin \left( \varphi \right)}}{\text{。}} $ | (4) |
式中:AC为接触面积;Lh为冰层上表面的挤压宽度;Ld为冰层上表面的挤压深度。
1.1.2 计算破碎力Fcr及垂直分量力FV破碎力Fcr与接触面积AC的关系式如下:
| ${F_{cr}} = {\sigma _c} \cdot {A_C}{\text{。}}$ | (5) |
式中:σC为层冰抗压强度;AC为接触面积。
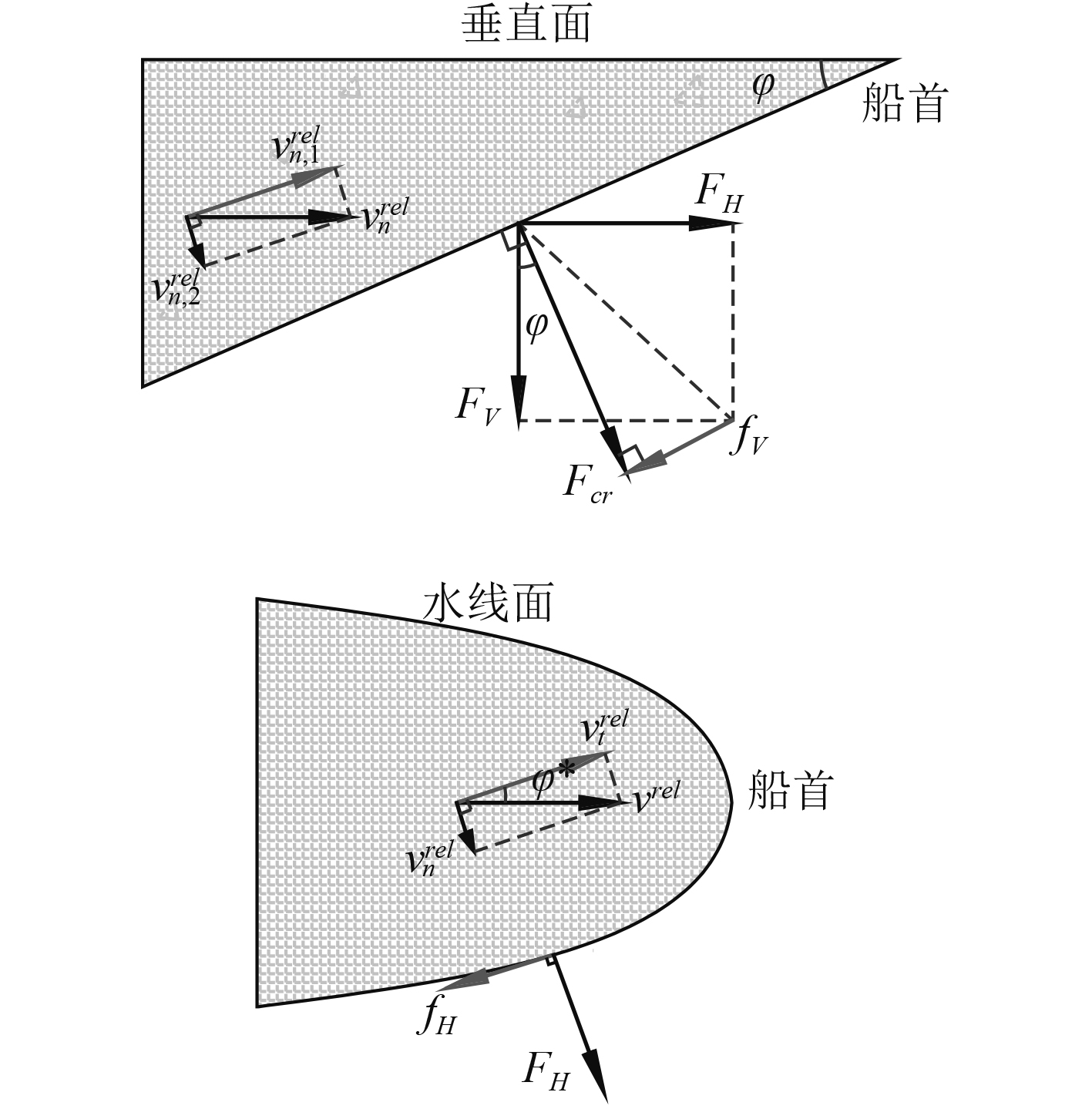
破碎力Fcr分为水平方向分力FH和垂直方向分力FV。若考虑摩擦阻力[6],则摩擦阻力也分为水平方向分力fH和垂直方向分力fV,fH与相对速度分量vtrel成正比,fV与相对速度分量
|
图 3 力和速度分量 Fig. 3 Force and velocity components. |
由于在模拟过程中忽略船体的垂直运动,船体的摩擦力可根据船-冰相对速度来确定。其中,摩擦力分力与破碎力分力如下:
| ${f_H} = \frac{{{\mu _{\rm{i}}}{F_{cr}}v_t^{rel}}}{{\sqrt {{{\left( {v_t^{rel}} \right)}^2} + {{\left( {v_{n,1}^{rel}} \right)}^2}} }}{\text{,}}$ | (6) |
| ${f_V} = \frac{{{\mu _{\rm{i}}}{F_{cr}}v_{n,1}^{rel}}}{{\sqrt {{{\left( {v_t^{rel}} \right)}^2} + {{\left( {v_{n,1}^{rel}} \right)}^2}} }}{\text{,}}$ | (7) |
| ${F_H} = {F_{cr}}\sin \left( \varphi \right) + {f_V}\cos \left( \varphi \right){\text{,}}$ | (8) |
| ${F_V} = {F_{cr}}\cos \left( \varphi \right) - {f_V}\sin \left( \varphi \right){\text{。}}$ | (9) |
式中:μi为层冰摩擦系数;vtrel和
| $v_t^{rel} = V \cdot \cos \left( {\varphi *} \right){\text{,}}$ | (10) |
| $v_{n,1}^{rel} = V\sin \left( {\varphi *} \right)\cos \left( \varphi \right){\text{。}}$ | (11) |
为了判断层冰的弯曲情况,Kerr[8]引出失效载荷Pf的概念,即冰层的承载能力。
| ${P_f} = {C_f}{\left( {\frac{\theta }{\text π}} \right)^2}{\sigma _f}h_i^2{\text{。}}$ | (12) |
式中:θ为冰楔的开角,σf为层冰的弯曲强度,hi为层冰厚度,Cf为经验系数,其变化会影响船速与阻力之间的关系,取值情况可根据实验进行调整。在数值模拟过程中,通过比较破碎力在垂直方向上的分力与失效载荷的大小,判断层冰是否发生弯曲失效。当垂直分量力FV<Pf时,层冰仅在冰缘处发生挤压破坏;当垂直分量力FV≥Pf时,层冰发生弯曲破坏.
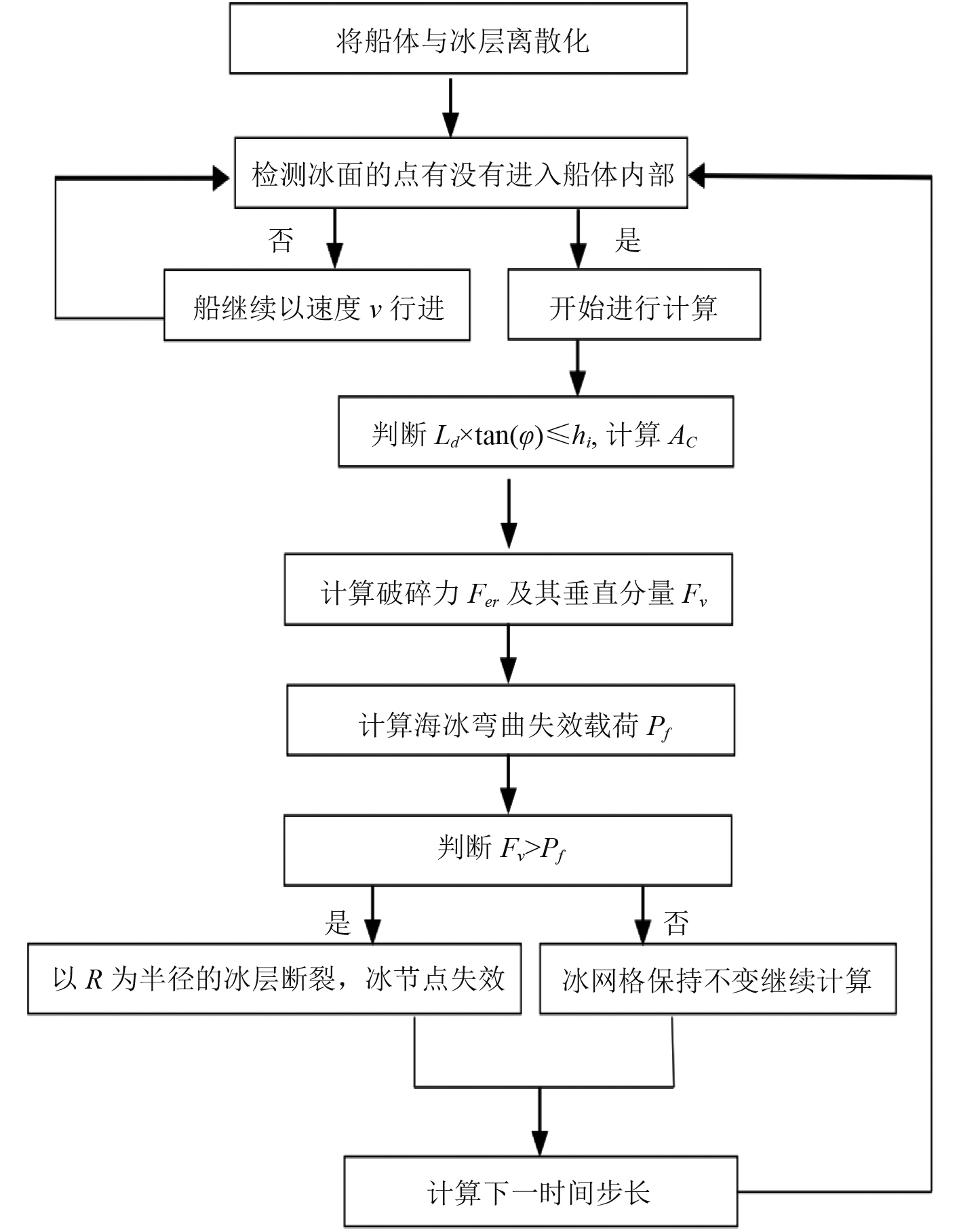
破碎力在数值模拟中的计算流程图如图4所示。
|
图 4 破碎力计算流程图 Fig. 4 Flow chart of ice breaking force calculation |
浸没力是指冰层发生弯曲失效后,断裂的碎冰在船首处翻转滑移所产生的阻力。在数值模拟中,假定船首发生弯曲破坏的滑冰脱落后消失,但在实际情况中,船首的碎冰会被淹没并随着船体滑行。根据Zhou[9]的模型试验观测,船舶模型底部几乎没有浮冰滑动,大部分浮冰以较低的漂移速度在冰缘附近横向移动。根据Lindqvist算法对破冰阻力的划分,考虑浮冰势能的损失和船体与浮冰之间的摩擦之后可得浸没阻力为[10]:
| ${R_S} = \left( {{\rho _w} - {\rho _i}} \right)g{h_i}\left( {BT\frac{{B + T}}{{B + 2T}}} \right) + \mu {A_f}{\text{。}}$ | (13) |
式中:ρw为海水密度;ρi为层冰密度;g为重力加速度;hi为冰厚;B为船宽;T为船长;μ为摩擦系数;Af为船首面积。
当船速增加时,碎冰与船体接触碰撞更加频繁,与船体产生的摩擦力增大,浸没阻力增加。考虑浸没阻力与船速之间的关系,修正后的浸没阻力为:
| ${R_S}\left( {{v_{\rm rel}}} \right) = {R_S}\left( {1 + \frac{{9.4{v_{\rm rel}}}}{{\sqrt {gL} }}} \right){\text{。}}$ | (14) |
式中:vrel为船体与层冰之间的相对速度,L为船长。
理想状态下的数值模型不考虑碎冰在船首处的运动,在原有数值模型上增加对浸没力计算,对破碎力进行修正,得到破冰力。修正后的计算模型的模拟结果在理论上比原有的数值模型更加精确。
2 经验公式计算方法 2.1 Spencer算法Spencer算法将总阻力RT分为敞水阻力ROW,冰浮阻力RB,冰清阻力RC和破冰阻力RBR,即RT=ROW+RB+RC+RBR。RB,RC,RBR即公式中系数为CB,CC,CBR的部分,2010年,Jeong[11]对公式中的无量纲系数进行了修正。修正后的公式:
| $ \begin{aligned} {R_I} = &{R_{OW}} + {R_B} + {R_C} + {R_{BR}}= \\ & 13.14{V^2} + {C_B}\Delta \rho g{h_i}BT + {C_C}{\left( {\frac{V}{{\sqrt {g{h_i}} }}} \right)^{ - \alpha }}{\rho _i}B{h_i}{V^2} + \\ & {C_{BR}}{\left( {\frac{V}{{{\sigma _f}{h_i}/{\rho _i}B}}} \right)^{ - \beta }}{\rho _i}B{h_i}{V^2}{\text{。}} \\[-12pt] \end{aligned} $ | (15) |
式中:CB为冰浮阻力系数;CC为冰清阻力系数;CBR为破冰阻力系数;α为作用力指数,β为傅汝德数指数,取值如表1所示。V为破冰船航行速度;B为船宽;T为吃水;ρi为海冰密度;∆ρ为水冰密度之差;hi为冰厚;σf为冰的弯曲强度;g为重力加速度。
|
|
表 1 Spencer算法中无量纲系数取值 Tab.1 Constants in Spencer formulation for ice resistance. |
Lindqvist[2]算法将总阻力分为3个部分:破碎阻力RC,弯曲阻力RB和浸没阻力RS。各分力及总阻力表达式如下:
| $ {R_C} = 0.5{\sigma _f}h_i^2\frac{{\tan \varphi + \mu \displaystyle\frac{{\cos \varphi }}{{\cos \psi }}}}{{1 - \mu \displaystyle\frac{{\sin \varphi }}{{\sin \psi }}}}{\text{,}} $ | (16) |
| $ \begin{split} {R_B} = & \frac{{27}}{{64}}{\sigma _f}B\frac{{h_i^{1.5}}}{{\sqrt {\displaystyle\frac{E}{{12\left( {1 - {\nu ^2}} \right){\rho _w}g}}} }}\left( {\tan \psi + \mu \frac{{\cos \varphi }}{{\cos \psi \sin \alpha }}} \right) \times \hfill \\ & \left( {1 + \frac{1}{{\cos \psi }}} \right) \hfill {\text{,}}\\[-15pt] \end{split} $ | (17) |
| $ \begin{split} {R_S} = & \left( {{\rho _w} - {\rho _i}} \right)g{h_i}B\left( {T\frac{{B + T}}{{B + 2T}} + \mu \left( {0.7L - \frac{T}{{\tan \varphi }} - } \right.} \right. \\ & \left. {\left. {\frac{B}{{4\sin \alpha }} + T\cos \varphi \cos \psi \sqrt {\frac{1}{{\sin {\varphi ^2}}} + \frac{1}{{\tan {\alpha ^2}}}} } \right)} \right){\text{,}} \end{split} $ | (18) |
| ${R_I} = \left( {{R_B} + {R_C}} \right)\left( {1 + \frac{{1.4V}}{{\sqrt {g{h_i}} }}} \right) + {R_S}\left( {1 + \frac{{9.4V}}{{\sqrt {gL} }}} \right){\text{。}}$ | (19) |
式中:
Riska算法[3]是根据波罗的海的一些全尺度试验数据得出的,主要公式如下:
| ${R_I} = {C_1} + {C_2}V{\text{,}}$ | (20) |
| $ \begin{split} {C_1} = & {f_1}\frac{1}{{\frac{{2T}}{B} + 1}}B{L_{par}}{h_i} + \left( {1 + 0.021\phi } \right) \times\\ & \left( {{f_2}Bh_i^2 + {f_3}{L_{bow}}h_i^2 + {f_4}B{L_{bow}}{h_i}} \right) {\text{,}} \end{split} $ | (21) |
| ${C_2} = \left( {1 + 0.063\phi } \right)\left( {{g_1}h_i^{1.5} + {g_2}B{h_i}} \right) + {g_3}{h_i}\left( {1 + 1.2\frac{T}{B}} \right)\frac{{{B^2}}}{{\sqrt L }}{\text{。}}$ | (22) |
式中:L为垂线间长;B为船宽;T为吃水;hi为冰厚;Lpar为平行中体的长度;Lbow为水线处的船首长度;V为航行速度;ϕ为艏倾角;f1,f2,f3,f4,g1,g2,g3为经验系数,取值如表2所示。
|
|
表 2 Riska算法中经验系数取值 Tab.2 Constants in Riska formulation for ice resistance. |
根据破冰船Icebreaker Research Vessel的船体型值,对船体水线进行离散化。由于破冰时船体与层冰的作用位置主要为船首部位,所以编程时对船体首部的离散点进行3次样条插值,降低离散点之间的间隔,保证计算的精度。层冰理想化为无限大的平面,将平面离散化为无数个间隔相同的离散点,层冰离散点间隔为0.5 m。
图5为船体水线与冰缘的接触示意图,定义向量xv∈RNv×2为船体节点的x,y位置,定义向量xi∈RNi×2为冰边节点的x,y位置,当海冰受到垂直方向力FV大于海冰弯曲失效载荷Pf时,破碎半径为R的层冰部分冰节点失效,图5(b)中虚线部分即失效的冰网格节点,冰缘节点随之更新。在任意时刻步长ti,检测第j个冰节点与第k个船节点Djk之间的距离,检测冰节点是否进入船体内部,判定船体与层冰边缘是否有接触,当冰节点与船体发生接触,计算冰网格与船体型线2个交叉点之间的距离Lh及冰节点尖端到船-冰接触点连线的垂直距离Ld,根据式(3)和式(4)得到接触面积AC。

|
图 5 船体水线与冰缘的离散化 Fig. 5 Discretization of ship waterline and ice edges |
在数值模型中,冰区长为220 m,宽为60 m,时间步长为0.05 s,Cf取值为3.1。破冰船主尺度及层冰物理力学性质参数如表3和表4所示。
|
|
表 3 破冰船主尺度 Tab.3 Primary dimensions of Icebreaker Research Vessel |
|
|
表 4 层冰力学特性 Tab.4 Ice mechanical properties |
本文以破冰船Icebreaker Research Vessel为实例,计算3~5 kn船速、0.8~1.5 m冰厚下的冰阻力。以破冰阻力曲线对破冰时间t的平均值表示破冰阻力,并与3种经验算法进行对比验证。
|
|
表 5 12种不同船速和冰厚下的算例 Tab.5 Case of different velocity and ice thickness |
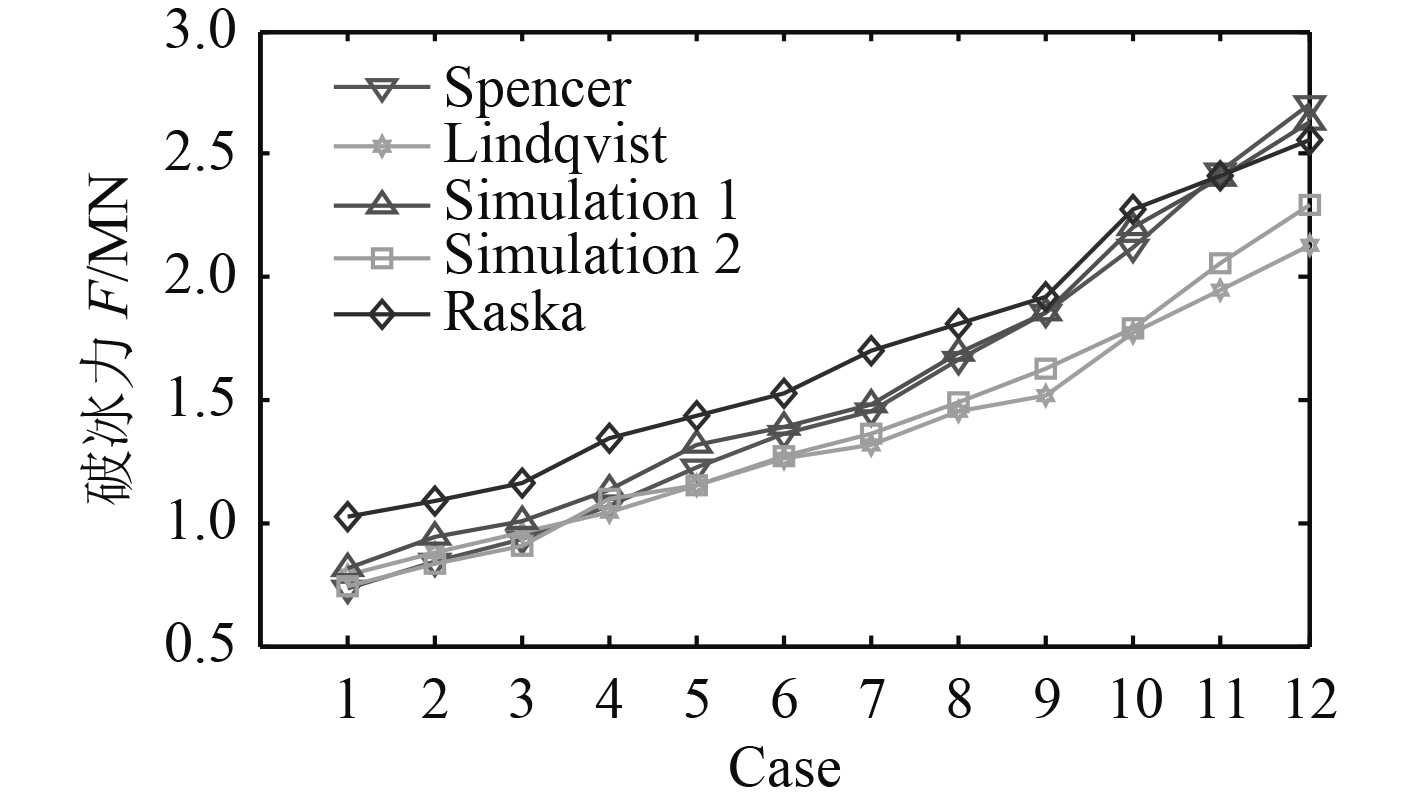
12种算例下冰阻力变化曲线图如图6所示。
|
图 6 冰阻力经验公式值与数值模拟结果的比较 Fig. 6 Comparison of ice resistance obtained by empirical formulas and numerical simulation. |
其中,simulation1为修正后的数值模拟结果,simulation2为修正前的数值模拟结果。Lindqvist算法出现较早,虽然考虑了船体形状及层冰力学性质对冰阻力的影响,但是由于理论依据不足,且试验时采用的船型较小,所以对冰阻力的预估一般偏低。
由图6数据及曲线走势可以看出,修正前的数值模拟结果simulation2与经验公式结果趋势相同,但结果总体偏低。当船速为3 kn、冰厚为0.8 m时,修正后的模拟结果比修正前高10%左右;当船速为5 kn、冰厚为1.5 m时,修正后的模拟结果比修正前高出18%左右;当船速为5 kn、冰厚达到2 m时,修正后的模拟结果比修正前高出31%左右。考虑浸没阻力后,数值模拟结果与经验公式结果更为吻合,说明修正后的数值模型更加精确,模拟结果更加可靠。
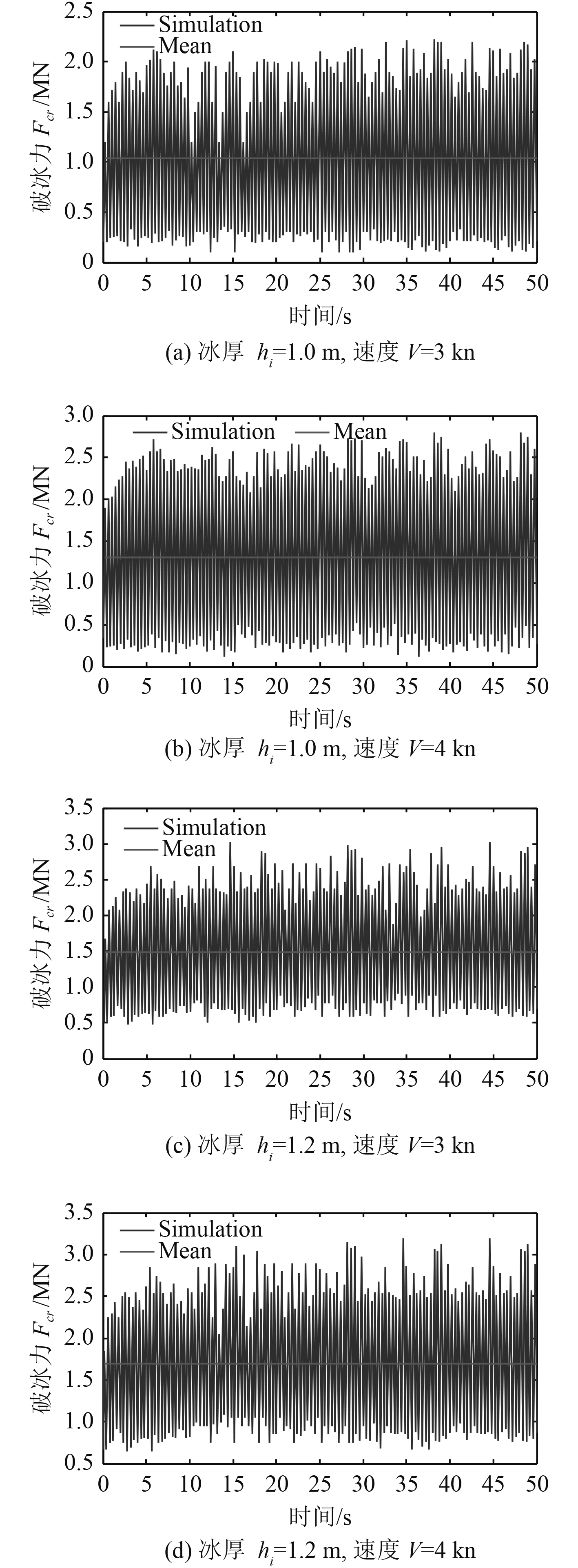
3.4 冰厚和船速对冰阻力的影响分析在数值模拟中,本文以1.0 m,1.2 m冰厚,3 kn,4 kn航速为例,比较分析破冰船在破冰时的冰阻力曲线图,如图7所示。
|
图 7 破冰阻力时历曲线及平均值 Fig. 7 Time history of ice resistance and mean values |
由图7可知,船冰接触力随时间变化并没有周期变化的规律,阻力值的不规则性是由于破冰模式性质的变化造成的。有时是破碎为主,有时是弯曲。当部分冰层被船体首部连续压碎而不发生弯曲破坏时,破碎力会急剧增大。
当船刚开始进入冰层时,阻力是逐渐增加的,当船体首部完全进入冰层之后,虽然阻力值依然变化剧烈,但是总体均值趋于稳定。船体和层冰接触时会产生很大的碰撞力,当层冰弯曲失效时,船舶会经历一个短暂的“卸载”过程,在数值模型中,船首处只受浮碎冰产生的浸没阻力,所以破冰阻力的曲线变化较为剧烈。
随着船速和冰厚的增加,冰阻力总体均值呈增加趋势。在船速增加时,冰阻力的总体均值增加,但曲线变化趋势较为平缓;在冰厚增加时,冰阻力曲线的振荡幅度增加,峰值的变化幅度也较大,说明在数值模拟结果中,冰阻力对冰厚变化的敏感度较高。
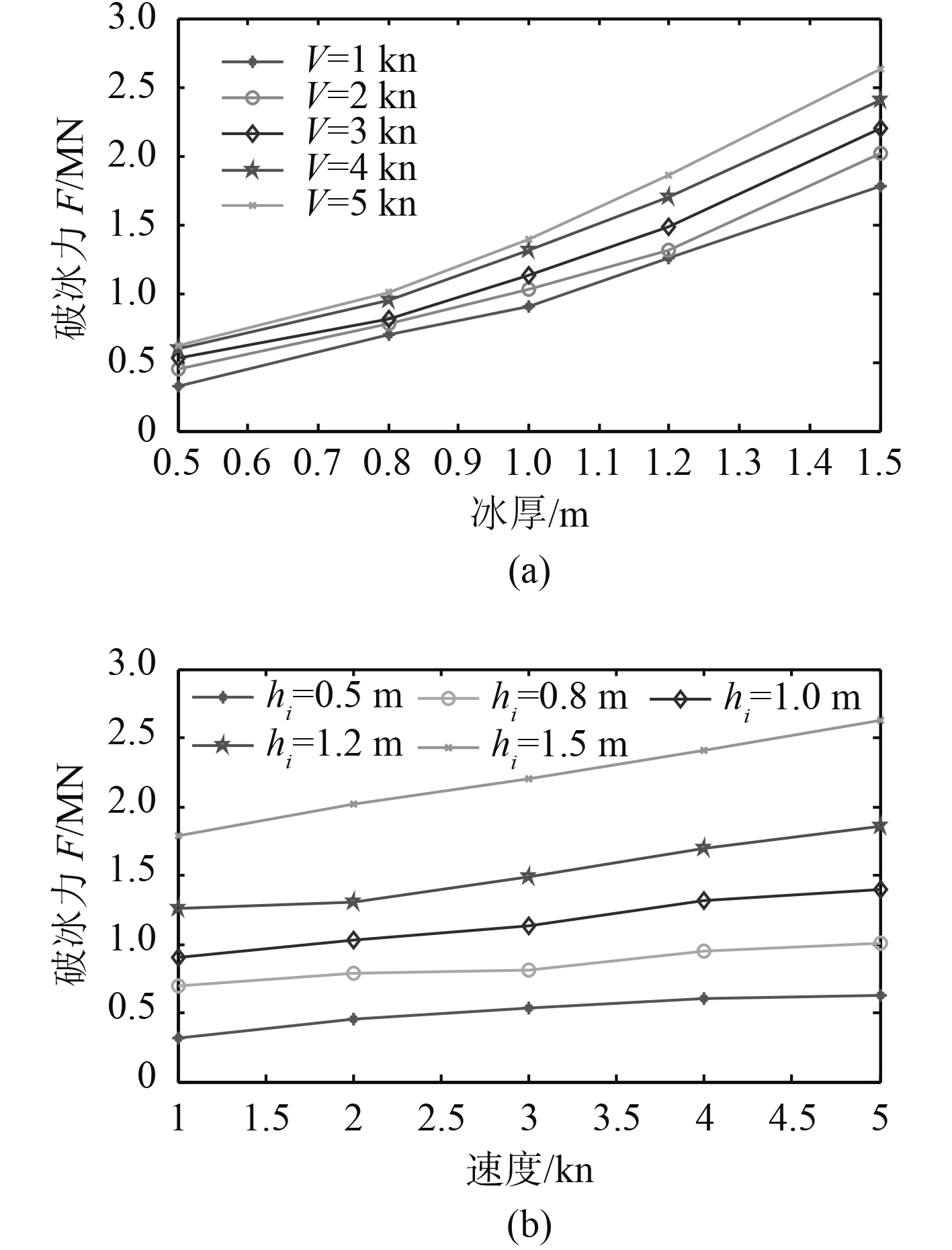
图8为不同船速及冰厚下,冰阻力的变化曲线,其中破冰阻力取破冰阻力曲线对破冰时间t的平均值。对图中曲线进行多项式拟合,可得到对应的拟合方程式。
|
图 8 不同船速及冰厚下破冰阻力变化曲线图 Fig. 8 Ice resistance at different Ice thickness and speeds |
| $ \left\{ \begin{array}{l} {y_{_1}} = 0.6229{x^2} + 0.1463x + 0.165{\text{,}}\\ {y_{_2}} = 0.8612{x^2} - 0.1974x + 0.3525{\text{,}}\\ {y_{_3}} = 0.9886{x^2} - 0.3051x + 0.4347{\text{,}}\\ {y_{_4}} = 0.8198{x^2} + 0.1743x + 0.3028{\text{,}}\\ {y_{_5}} = 0.9401{x^2} + 0.1447x + 0.3057{\text{,}} \end{array} \right. $ | (23) |
| $ \left\{ \begin{array}{l} {{y'}_{_1}} = 0.0609x' + 0.337{\text{,}}\\ {{y'}_2} = 0.0768x' + 0.6183{\text{,}}\\ {{y'}_3} = 0.1269x' + 0.7721{\text{,}}\\ {{y'}_4} = 0.1576x' + 1.0469{\text{,}}\\ {{y'}_5} = 0.2089x + 1.5798{\text{。}} \end{array} \right. $ | (24) |
其中:x为冰厚hi,y1-5为破冰阻力F在速度1~5 kn时的破冰阻力;x’为航速V,y’1-5为破冰阻力F在冰厚在0.5 m,0.8 m,1.0 m,1.2 m和1.5 m时的破冰阻力。
从图8(a)可以看出,在冰厚超过0.8 m时,曲线斜率减小,平均变化率增加,冰厚从0.5 m增加至0.8 m时,冰阻力增加9.83%,冰厚从1.2 m增加至1.5 m时,冰阻力增加23.88%,当冰厚大于1.5 m时,冰阻力增加可达到50%。对式(24)来说,随着冰厚的增加,曲线斜率增大,所以,随着冰厚的增加,冰阻力变化速率增大。对图8(b)来说,船速的增加虽然也会引起冰阻力的增加,但影响效果较小,随着船速增加,冰阻力的增加约为6%~9%。由式(23)可以看出,
本文根据连续破冰过程,运用编程语言建立理想状态下的船-冰运动模型,对层冰冰况下破冰船的破冰运动进行数值模拟,并建立完整的算法流程图。同时,考虑理想状态下运动模型忽略船首碎冰这一现象,增加对浸没阻力的计算,对数值模拟的破冰阻力进行修正,并简单探讨了航速和冰厚对破冰阻力的影响,可以得出结论:
1)增加浸没阻力修正后的数值模型模拟结果与经验公式计算结果更加吻合,对冰阻力的预报更加准确、可靠。
2)在冰厚、层冰弯曲强度及层冰摩擦系数等参数不变的情况下,航速的增加会引起冰阻力的增大,但增加趋势较小,船速增加1 kn,冰阻力的增加约为6%-9%。当船速变化量Δv< 1 kn时,冰阻力的变化量Δy不会发生明显变化。
3)相比于船速,冰厚变化所引起的冰阻力的变化跨度较大。随着冰厚增加,冰阻力时历曲线振荡幅度增加,变化速率增大。当冰厚大于1.2 m时,冰阻力增加速率达到23%以上。
由于在模型中没有考虑冰厚对层冰抗弯强度等性质的影响,模拟结果可能略有偏差,在接下来的研究计算中会进一步进行修正。
| [1] |
SPENCER D. A standard method for the conduct and analysis of ice resistance model tests[M]. NRCC, Institute for Marine Dynamics, 1992.
|
| [2] |
LINDQVIST, GUSTAV. A straight forward method for calculation of ice resistance of ships[C]. Luleaa, Sweden, Port and Ocean Engineering under Arctic Conditions. 1989: 722.
|
| [3] |
RISKA K, WILHELMSON M, ENGLUND K, et al. Performance of merchant vessels in ice in the Baltic, winter navigation research board NO.52[R]. Helsinki: Finnish Maritime Administration, 1997.
|
| [4] |
WANG S., 2001. A dynamic model for breaking pattern of level ice by conical structures[D]. Helsinki : Department of Mechanical Engineering, Helsinki University of Technology, 2001.
|
| [5] |
NGUYEN D T, SØRBØ A H, SØRENSEN A J. Modelling and control for dynamic positioned vessels in level ice[J]. IFAC Proceedings Volumes, 2009, 42(18): 229-236. DOI:10.3182/20090916-3-BR-3001.0006 |
| [6] |
Biao SU, Kaj RISKA, Torgeir MOAN. A numerical method for the prediction of ship performance in level ice[J]. Cold Regions Science and Technology, 2010, 60: 177-188. DOI:10.1016/j.coldregions.2009.11.006 |
| [7] |
VALANTO, P.. The resistance of ships in level ice[J]. SNAME Transactions, 2001, 109: 53-83. |
| [8] |
KERR A. The bearing capacity of floating ice plates subjected to static or quasi- static loads[J]. Journal of Glaciology, 1976, 17(76): 229-28. |
| [9] |
ZHOU Quan, PENG Heather. Numerical investigations of ship-ice interaction and maneuvering performance in level ice[J]. Cold Regions Science and Technology, 2016, 122: 36-49. DOI:10.1016/j.coldregions.2015.10.015 |
| [10] |
ZHOU Li, CHUANG Zhenju, BAI Xu. Ice forces acting on towed ship in level ice with straight drift. Part Ⅱ: Numerical simulation[J]. International Journal of Naval Architecture and Ocean Engineering, 2017, 1-10. |
| [11] |
JEONG Seong-Yeob, CHOI Kyungsik, et al. Prediction of ship resistance in level ice based on empirical approach[J]. International Journal of Naval Architecture and Ocean Engineering, 2017, 9: 613-623. DOI:10.1016/j.ijnaoe.2017.03.007 |
| [12] |
HU Jian, ZHOU Li. Further study on level ice resistance and channel resistance for an icebreaking vessel[J]. International Journal of Naval Architecture and Ocean Engineering, 2019, 8: 169-176. |
| [13] |
CHO Seong-Rak, LEE Sungsu. A prediction method of ice breaking resistance using a multiple regression analysis[J]. Int. J. Nav. Archit. Ocean Eng, 2015, 7: 708-719. DOI:10.1515/ijnaoe-2015-0050 |
| [14] |
王钰涵. 连续破冰模式下破冰船的冰力研究[J]. 海洋工程, 2013, 31(4): 68-73. WANG Yu-han. Study of ice force about icebreaker based on continuous breaking pattern[J]. The Ocean Engineering, 2013, 31(4): 68-73. |
| [15] |
LUBBAD R, LØSET S. A numerical model for real-time simulation of ship-ice interaction[J]. Cold Regions Science and Technology, 2011, 65: 111-12. DOI:10.1016/j.coldregions.2010.09.004 |
| [16] |
NGUYEN D T, SØRBØ A H, SØRENSEN A J. Modelling and control for dynamic positioned vessels in level Ice[C]//Proceedings of 8th Conference on Manoeuvring and Control of Marine Craft (MCMC’ 2009). 2009: 229-236.
|
| [17] |
LAU, Michael, et al. Preliminary results of ship maneuvering in ice experiments using a planar motion mechanism[J]. In: Proceedings of the 17th International IAHR Symposium on Ice. 2004. p. 479-487.
|
 2020, Vol. 42
2020, Vol. 42
