2. 江苏科技大学 船舶与海洋工程学院,江苏 镇江 212000
2. School of Naval Architecture and Ocean Engineering, Jiangsu University of Science and Technology, Zhenjiang 212000, China
出于减噪的目的,一些船舶设置有自循环系统,利用船舶航行时迎流面所产生的动压头抽吸海水,降低冷凝器的用水量减少水泵的运行次数[1-2]。然而在系统与海水连通处,为防止各种杂物进入系统管道,通常在入口处设置格栅,当自循环系统工作时,海水流经格栅会产生剪切层分离等现象,从而在格栅表面及附近流场产生强大的压力脉动场,分析格栅的压力脉动特性,对船舶降噪具有重大意义。
本文基于计算流体力学(CFD)分析方法,在不同雷诺数Re、不同长宽比L/B下进行数值模拟,分析单方柱[3-4]的主要绕流参数和压力脉动的变化规律。在此基础上,取定截面长宽比,分析雷诺数以及间距比对多方柱[5-6]绕流参数以及压力脉动的影响。
1 数学模型计算流体力学(CFD)是流体力学的重要分支,在计算机科学发展下产生的介于数学、流体力学和计算机之间的交叉学科,主要研究内容是通过计算机和数值方法来求解流体力学的控制方程,对流体力学问题进行模拟和分析,主要遵循质量守恒、动量守恒和能量守恒三大定律,使用三大基础方程对其进行描述,文章中未考虑温度变化,因此不考虑能量守恒方程,剩余两项的表述如下:
1)连续性方程
连续性方程是质量守恒定律在流体力学中具体表达,对流体采用连续介质模型,密度和速度在时间以及空间上都是连续、可微函数,数学表达式如下:
| $\frac{{\partial \rho }}{{\partial t}} + \frac{{\partial (\rho {u_x})}}{{\partial x}} + \frac{{\partial (\rho {u_y})}}{{\partial y}} + \frac{{\partial (\rho {u_z})}}{{\partial z}} = 0\text{,}$ |
2)运动方程
运动方程是牛顿第二定律即动量守恒定律在流体力学中的具体表达,假设流体不可压缩时,数学表达式如下:
| $ \rho \dfrac{{{\rm D}{u_x}}}{{{\rm D}t}} = \rho {f_x} - \dfrac{{\partial p}}{{\partial x}} + \mu \Bigg(\dfrac{{{\partial ^2}{u_x}}}{{\partial {x^2}}} + \dfrac{{{\partial ^2}{u_x}}}{{\partial {y^2}}} + \dfrac{{{\partial ^2}{u_x}}}{{\partial {z^2}}}\Bigg) \text{,} $ |
| $ \rho \dfrac{{{\rm D}{u_y}}}{{{\rm D}t}} = \rho {f_y} - \dfrac{{\partial p}}{{\partial y}} + \mu \Bigg(\dfrac{{{\partial ^2}{u_y}}}{{\partial {x^2}}} + \dfrac{{{\partial ^2}{u_y}}}{{\partial {y^2}}} + \dfrac{{{\partial ^2}{u_y}}}{{\partial {z^2}}}\Bigg) \text{,} $ |
| $ \rho \dfrac{{{\rm D}{u_z}}}{{{\rm D}t}} = \rho {f_z} - \dfrac{{\partial p}}{{\partial z}} + \mu \Bigg(\dfrac{{{\partial ^2}{u_z}}}{{\partial {x^2}}} + \dfrac{{{\partial ^2}{u_z}}}{{\partial {y^2}}} + \dfrac{{{\partial ^2}{u_z}}}{{\partial {z^2}}}\Bigg) \text{,} $ |
本文计算主要采用SST k-ω,集成k-ε与k-ω两种模型的优势,近壁面处使用k-ω模型,边界层使用k-ε模型,考虑湍流剪应力的输运效应,对有压力梯度引起的分离现象模拟更加精确,数学表达式如下:
| $ \dfrac{\partial }{{\partial t}}\left( {\rho k} \right) + \dfrac{\partial }{{\partial {x_i}}}\left( {\rho k{u_i}} \right) = \dfrac{\partial }{{\partial {x_j}}}\left( {{\varGamma _k}\dfrac{{\partial k}}{{\partial {x_j}}}} \right) + {G_k} - {Y_k} + {S_k} \text{,} $ |
| $ \dfrac{\partial }{{\partial t}}\left( {\rho \omega } \right) \!+\! \dfrac{\partial }{{\partial {x_i}}}\left( {\rho \omega {u_i}} \right) \!=\! \dfrac{\partial }{{\partial {x_j}}}\left( {{\varGamma _\omega }\dfrac{{\partial \omega }}{{\partial {x_j}}}} \right) \!+\! {G_\omega } - {Y_\omega } \!+\! {D_\omega } \!+\! {S_\omega } \text{。} $ |
式中:Gk为层流速度梯度产生的湍流动能;Gω由ω方程产生;Γk和Γω是k和ω的扩散率;Yk和Yω由扩散产生的湍流;Dω为正交发散项。
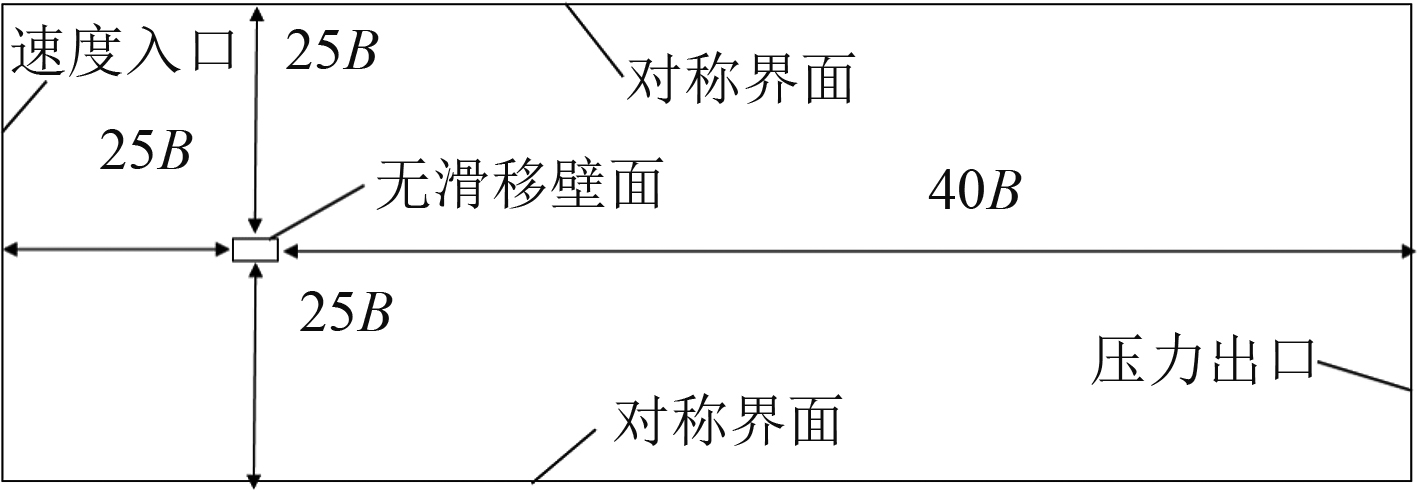
2 计算模型 2.1 计算域及边界条件选择计算域大小的选择至关重要,从理论上来说计算域越接近真实流场其计算结果越真实,但是对于CFD计算来说,计算资源也是需要考虑的因素,受限于电脑的运行速度,计算域越小计算越快,因此需要在保证计算结果的前提下选择较小的计算域。参考时忠民等[7]对绕流边界影响的研究,取数值模拟计算域的进口距方柱取25B,上下两侧边界距方柱取25B,出口距方柱取40B,其中方柱长为L,宽为B。计算域边界左侧为速度入口,右侧为压力出口,上下两侧为对称边界,方柱表面取为无滑移壁面,如图1所示。
|
图 1 方柱绕流几何模型示意图 Fig. 1 Geometric model diagram of flow around rectangular cylinder |
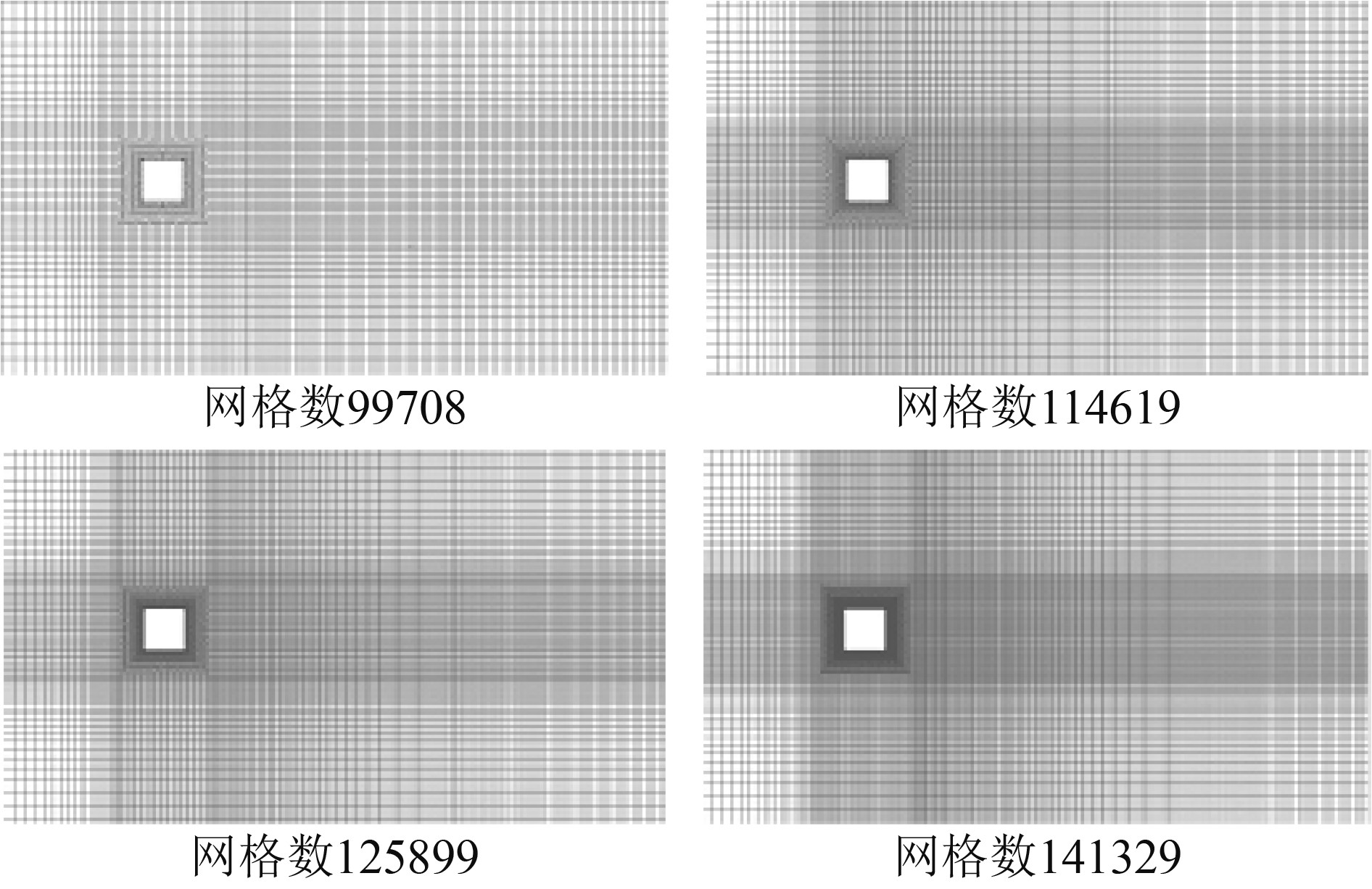
在数值模拟计算中,首先要验证网格独立性。网格划分是前期最重要的工作且耗费时间长,网格的疏密及质量直接影响着计算规模的大小和计算结果的精确程度。通常认为当网格密度达到一定程度后,继续增加网格量对于计算结果的影响非常小,此时可以认为网格疏密对于计算结果的影响可以忽略。网格划分方式时均采用结构化网格,质量均可保证在0.8以上,可忽略质量差异对结果的影响。图2给出了本文验证网格独立性所采用4套网格。
|
图 2 不同密度网格示意图 Fig. 2 Different density grid diagram |
对于非稳态计算,时间步长的选取也将影响数值模拟结果的准确性。采用库朗数(CFL)来调节计算的稳定性与收敛性。CFL越大,收敛速度加快但稳定性逐渐降低。表1给出雷诺数Re=5000时,不同网格和时间步长下方柱绕流的升力系数的均方根值Cl.rms,阻力系数的平均值Cd.mean,斯特劳哈尔数St及各结果间的相对误差。
|
|
表 1 不同网格和时间步长下方柱绕流计算结果 Tab.1 Calculation results of flow around square column with different grid and time step |
从表1可以看出,网格密度和CFL的变化对平均阻力系数Cd.mean和斯特劳哈尔数St的影响较小,最大相对误差仅为3.87%。升力系数的均方根Cl.rms在网格数量较低时计算结果偏小,当网格数量到达11万以上后计算结果也趋于稳定。因此考虑到计算消耗,本文划分网格时采用114 619网格数量的划分方式,时间步长上CFL值设置为5。
针对所选用的网格以及时间步长,并与文献进行对比,验证数值方法的正确性,结果如表2所示。
|
|
表 2 数值文献结果对比 Tab.2 Comparison of numerical and literature results |
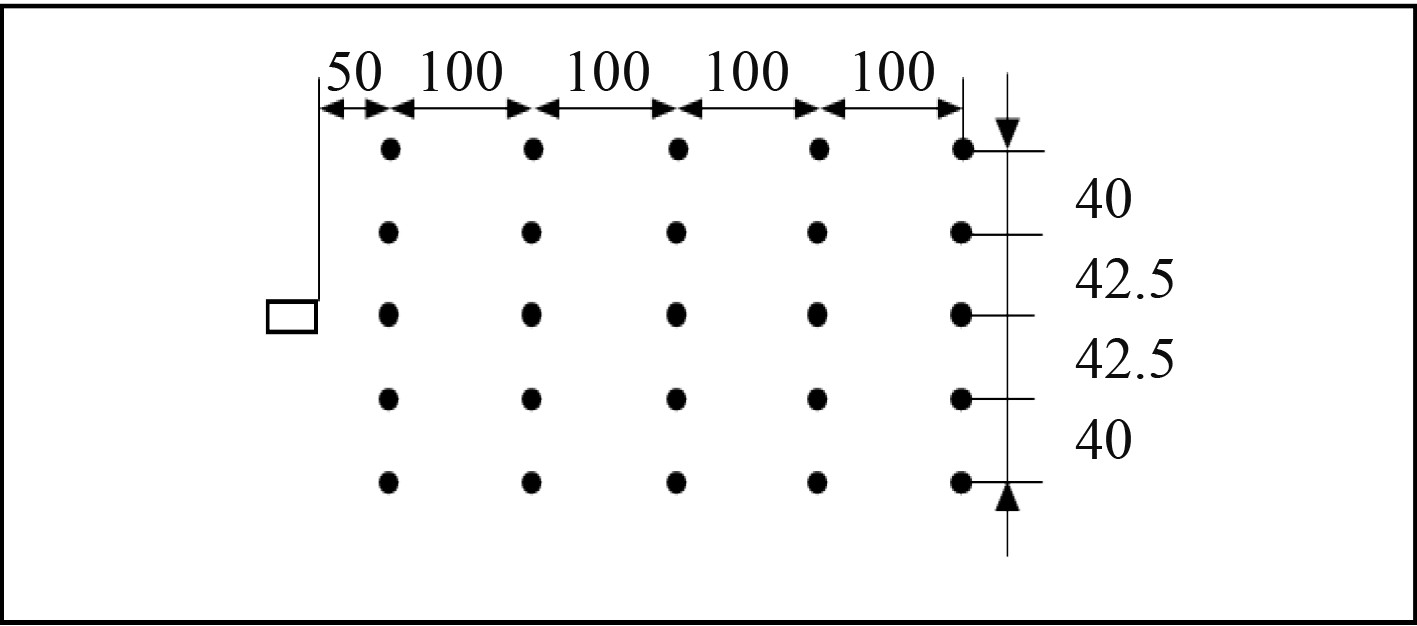
探究方柱后流场压力脉动分布规律,在后方均布25个监测点,左上角为1号监测点,从左向右依次编号,具体情况如图3所示。多方柱绕流时,模拟实船格栅布置情况,以5个单方柱并列,在保持截面长宽比L/B=2不变的情况下,改变两方柱中心距离D的尺寸从而改变方柱间距比D/B,本文取D/B=(5,4,3,2),多方柱时监测点与单方柱相同,具体尺寸布置及网格情况如图4和图5所示。
|
图 3 监测点分布示意图 Fig. 3 Distribution diagram of monitoring points |

|
图 4 方柱位置布置示意图 Fig. 4 Schematic diagram of the position layout of the rectangular cylinder |

|
图 5 网格示意图 Fig. 5 Grid diagram |
给定截面长宽比L/B为2,不同的雷诺数Re下绕流参数(升力系数的均方根值Cl.rms、阻力系数的平均值Cd、涡脱频率F、斯特劳哈尔数St)如图6所示,脉动压力变化如图7所示。

|
图 6 绕流系数变化曲线 Fig. 6 Curve of variation of flow coefficient |

|
图 7 脉动均方根值曲线 Fig. 7 Pulsating root-mean-square curve |
如图中所示,升力系数、阻力系数,斯特劳哈尔数变化很小,可以忽略不计,涡脱频率随雷诺数线性增加。各个监测点的脉动均方根值随着雷诺数的增加而增加,总体来看,不同雷诺数下,压力脉动均方根值变化趋势趋于吻合。从监测点的位置来看,上面2行监测点均方根值远离方柱呈现下降的趋势,但变化幅度较小。位于流场中间的监测点压力脉动均方根值远离方柱也呈现下降趋势,但变化剧烈。下方2行监测点压力脉动均方根值随距离增加而逐渐增大。
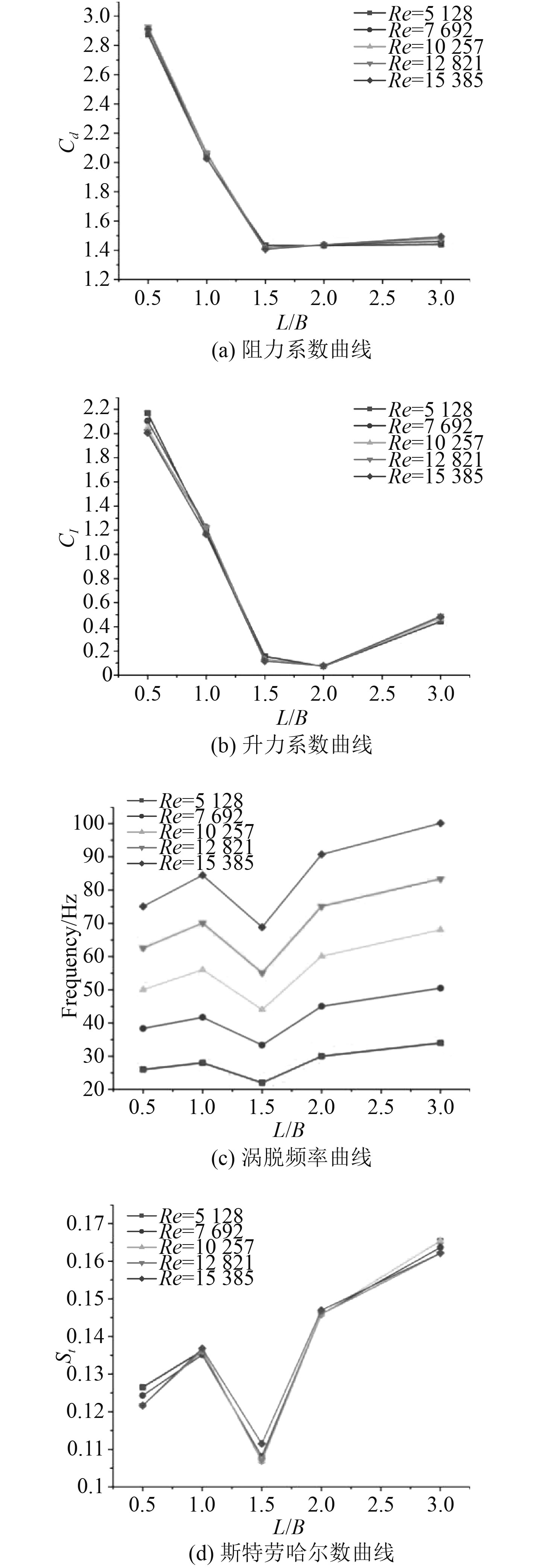
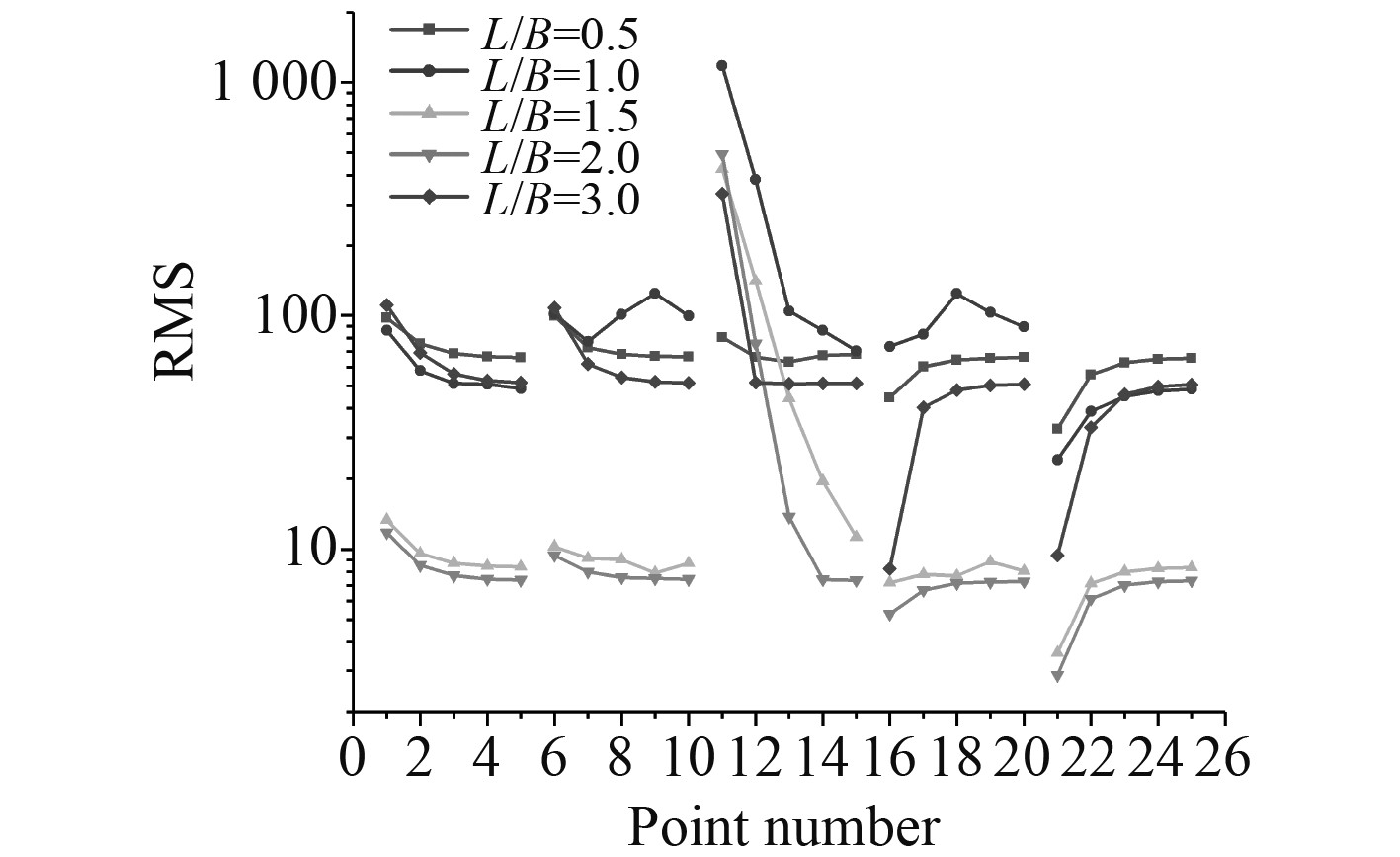
3.1.2 方柱截面长宽比影响分析方柱截面的长宽比会对方柱后的流动产生显著影响,本文分别取长宽比L/B为0.5,1,1.5,2,3的方柱进行数值模拟。各雷诺数下,不同长宽比时绕流参数如图8所示。选取Re=15385时,针对不同截面长宽比,各个监测点压力脉动均方根值曲线如图9所示。
|
图 8 绕流系数变化曲线 Fig. 8 Curve of variation of flow coefficient |
|
图 9 脉动均方根值曲线 Fig. 9 Pulsating root-mean-square curve |
由图可知,不同雷诺数下,各绕流参数随截面长宽比变化趋势相同。当L/B=1,2时,阻力系数、升力系数以及斯特劳哈尔数重合较好;L/B=0.5,1.5,3时,阻力系数、升力系数以及斯特劳哈尔数在各自雷诺数下存在差异。阻力系数曲线与升力系数曲线先下降再上升,阻力系数曲线在L/B=1.5取得最小值,升力系数曲线在L/B=2.0时取得最小值。涡脱频率曲线的变化规律与斯特劳哈尔数曲线相同,在监测范围内先增大再减小,在L/B=1.5取得最小值时,逐渐增大。长宽比L/B=1.5,2时,压力脉动均方根值明显小于其他长宽比下结果,其中L/B=2时结果最小。长宽比L/B=0.5,1,3时,压力脉动的均方根值较接近,交替出现最大值。
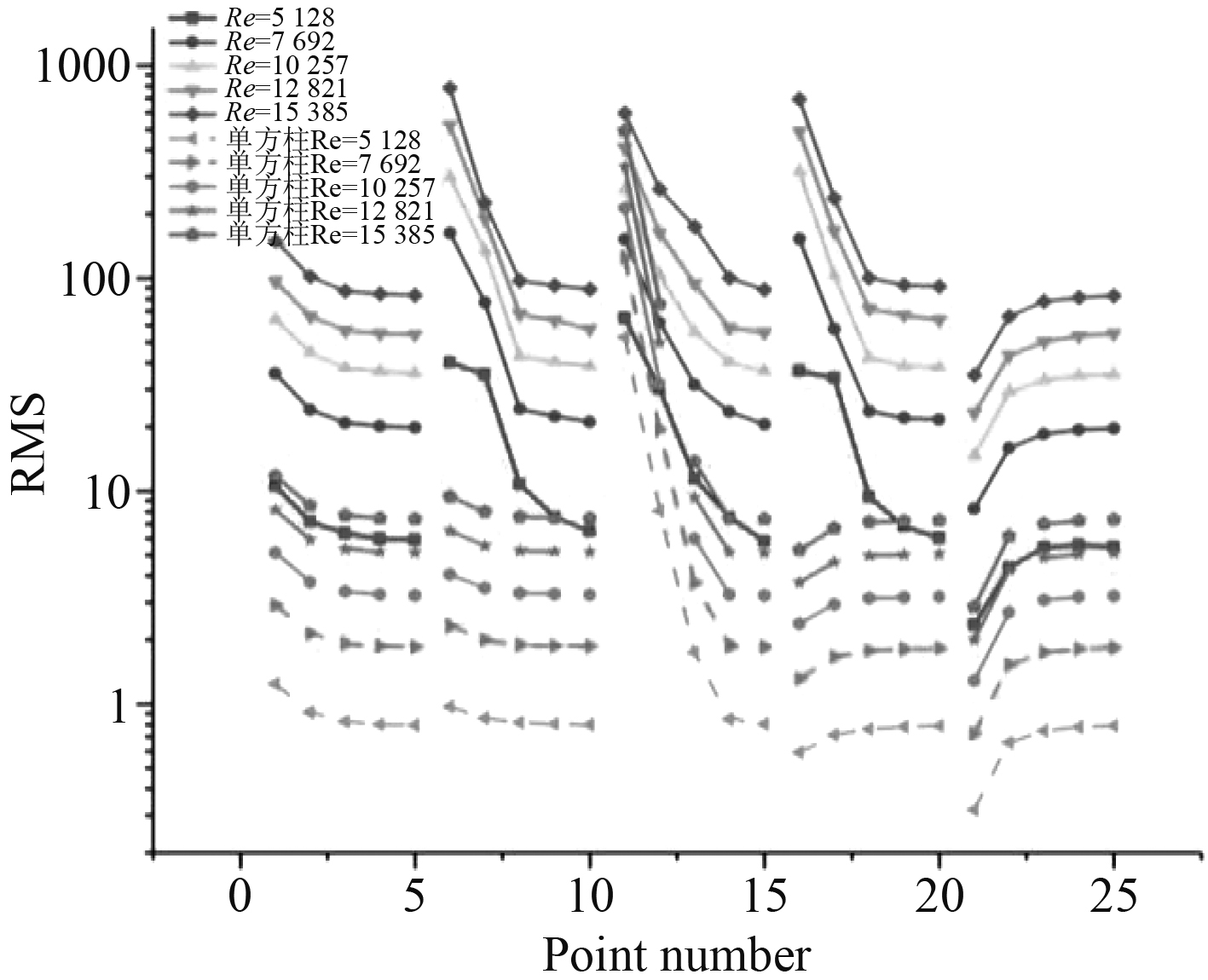
3.2 二维方柱群分析 3.2.1 雷诺数影响分析方柱的间距比D/B=5,不同雷诺数下,方柱群绕流参数如图10所示,方柱群后压力脉动压力如图11所示。

|
图 10 绕流系数变化曲线 Fig. 10 Curve of variation of flow coefficient |
|
图 11 脉动均方根值曲线 Fig. 11 Pulsating root-mean-square curve |
从图中可以看出,与单方柱相比,柱群的升力系数与阻力系数都有明显的增加,其中位于中间位置的方柱3改变最小,中间两侧的方柱2与方柱4改变最大。方柱3的涡脱频率与斯特劳哈尔数较单方柱有所下降,其余方柱明显增加。从总体结果来看,对称布置的方柱1与方柱5,方柱2与方柱4绕流参数变化趋势与幅度接近一致。与单方柱相比,方柱群的压力脉动均方根值均显著变大,从均方根值变化趋势看,除了中间一行监测点外,其余监测点变化趋势与单方柱相同。
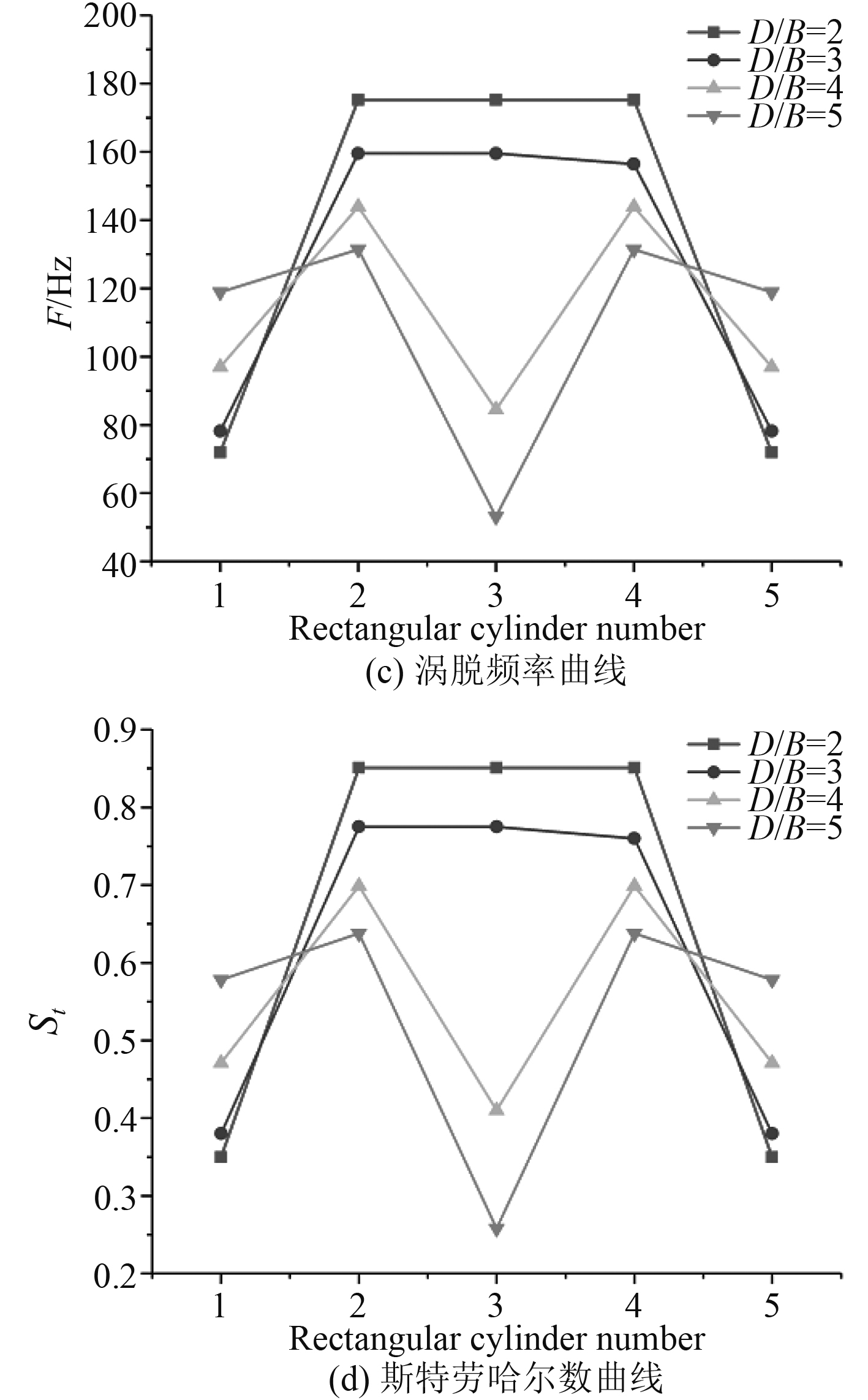
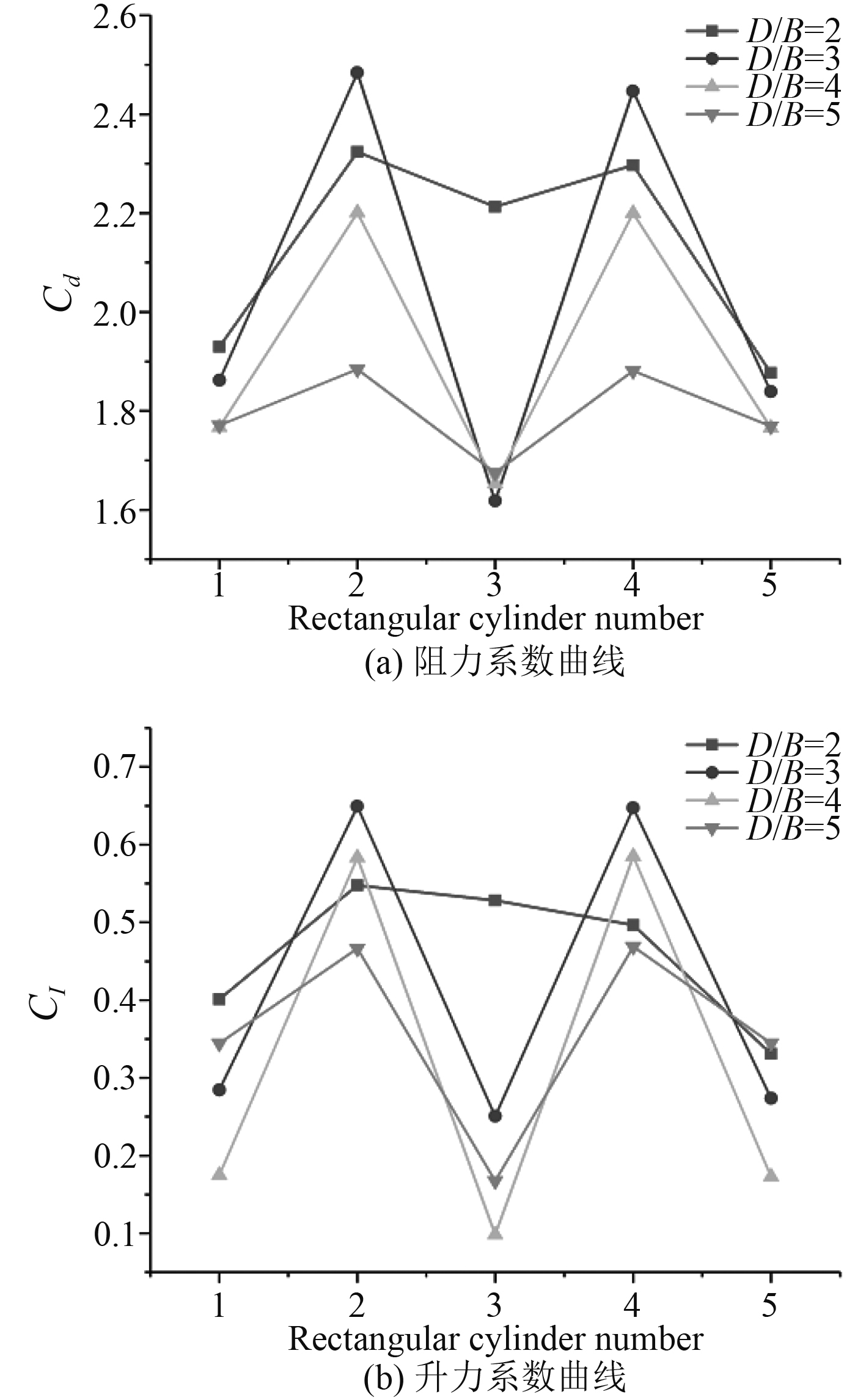
3.2.2 方柱间距影响分析雷诺数为15385时,不同间距比时方柱群绕流参数如图12所示,不同方柱间距比下各监测点压力脉动脉动压力如图13所示。
|
图 12 绕流系数变化曲线 Fig. 12 Curve of variation of flow coefficient |
|
|
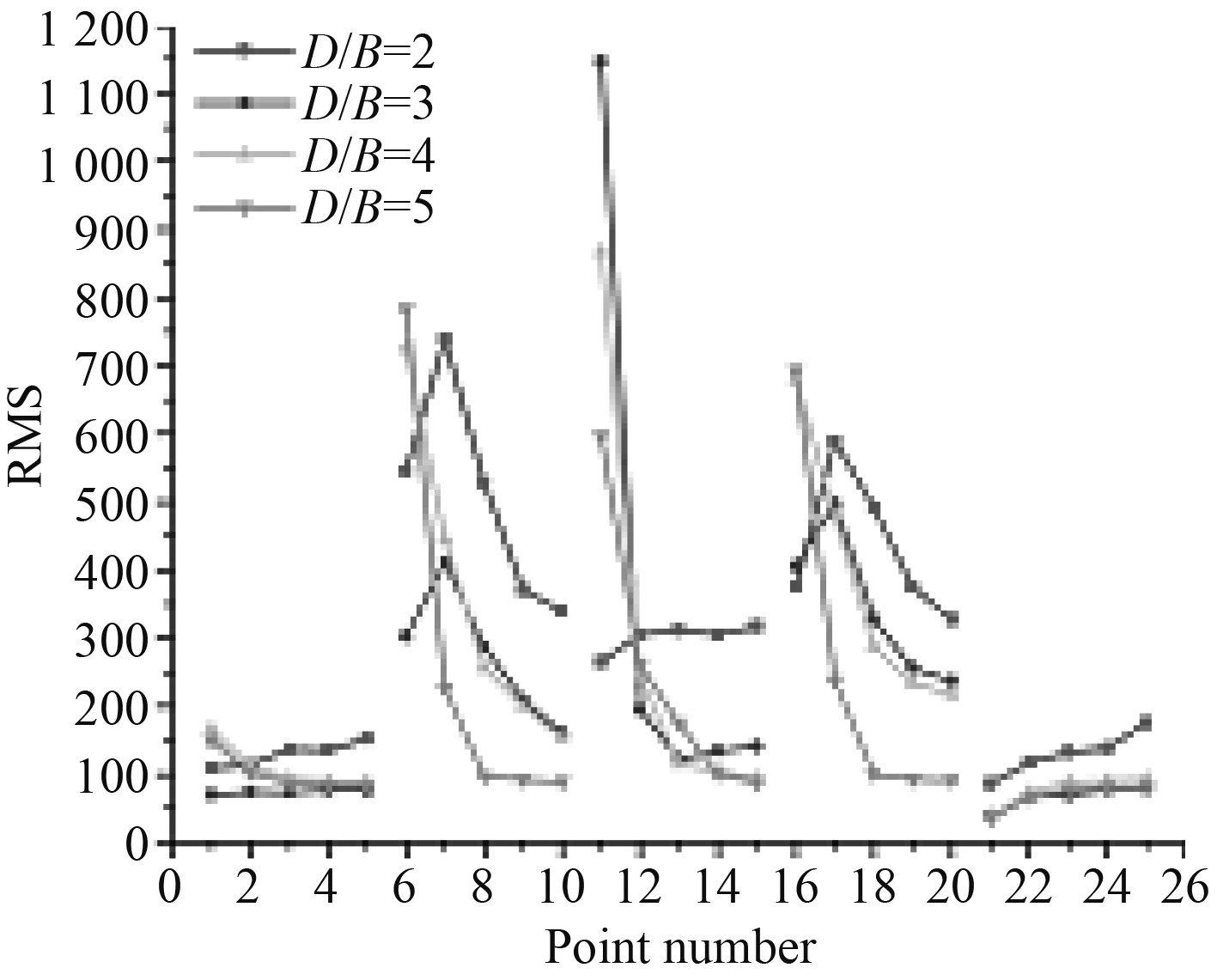
图 13 脉动均方根值曲线 Fig. 13 Pulsating root-mean-square curve |
从图中可以看出,绕流参数曲线(升力系数的均方根值Cl.rms,阻力系数的平均值Cd,涡脱频率F、斯特劳哈尔数St)均具有很好的对称性,方柱1和方柱5,方柱2和方柱4主要参数基本吻合。随着间距比的增大,升力系数与阻力系数呈现减小的趋势,方柱3变化最为剧烈。内部三方柱涡脱频率随间距比的增大而减小,但最外侧两方柱涡脱频率随间距比的增大而增大,当D/B=2,3时,中间方柱与其周围方柱涡脱频率差幅较小,随着间距增大,呈明显下降趋势。斯特劳哈尔数曲线变化规律说涡脱频率变化曲线大致相同。方柱间距比对流场压力脉动的影响很明显,位于流场前方的监测点压力脉动随间距比变化混乱,无规律可循。流场后方的监测点可以明显发现,间距比D/B=2时压力脉动的均方根值大于其它间距比结果。
4 结 语本文分析了方柱的主要绕流参数和压力脉动随雷诺数以及方柱截面长宽比L/B的变化规律。在此基础上,取定L/B=2,分析了雷诺数以及间距比对绕流参数以及压力脉动的影响,现得出以下结论:
单个二维方柱下,雷诺数主要影响脉动压力,各监测参数均随截面长宽比发生较大改变;多方柱并列时,监测点参数较单方柱均有所提高,方柱间距比对脉动压力影响较大。
| [1] |
王磊, 常书刚. 潜艇噪声与综合降噪技术的应用[J]. 航海技术, 2007(2): 44-48. DOI:10.3969/j.issn.1006-1738.2007.02.023 |
| [2] |
陈小剑. 舰船噪声控制技术[J]. 海洋工程装备与技术, 2015(3). DOI:10.3969/j.issn.2095-7297.2015.03.002 |
| [3] |
OKAJIMA A, UENO H, SAKAI H. Numerical simulation of laminar and turbulent flows around rectangular cylinders[J]. International Journal for Numerical Methods in Fluids, 1992, 15(9): 999-1012. DOI:10.1002/fld.1650150906 |
| [4] |
秦浩, 肖姚, 宋文武, 等. 大雷诺数下方柱绕流PIV试验及数值模拟[J]. 工程热物理学报, 2018, 39(8): 91-97. QIN Hao, XIAO Yao, SONG Wen-wu, et al. PIV experiment and simulation of flow around a square cylinder at high reynolds numbers[J]. Journal and Engineering Thermophysics, 2018, 39(8): 91-97. |
| [5] |
沈立龙, 刘明维, 吕启兵, 等. 双排并列三方柱绕流数值模拟[J]. 科学技术与工程, 2014, 14(23). SHEN Li-long, LIU Ming-wei, LU Qi-bing, et al. Numerical simulation of the flow around double-row tied for three square cylinders[J]. Science Technology and Engineering, 2014, 14(23). DOI:10.3969/j.issn.1671-1815.2014.23.011 |
| [6] |
李聪洲, 张新曙, 胡晓峰, 等. 高雷诺数下多柱绕流特性研究[J]. 力学学报, 2018, 50(2): 233-242. LI Chong-zhou, ZHANG Xin-shu, HU Xiao-feng, et al. The study of flow past multiple cylinders at high reynolds numbers[J]. Chinese Journal of Theoretical and Applied Mechanics, 2018, 50(2): 233-242. |
| [7] |
时忠民, 刘名名, 郭晓玲. 计算域对圆柱绕流数值模拟结果的影响[J]. 中国水运(下半月), 2013, 13(7): 83-86. |
 2020, Vol. 42
2020, Vol. 42
