2. 上海交大海洋水下工程科学研究院有限公司,上海 200231
2. Shanghai Jiaotong University Underwater Engineering Institute Co., Ltd., Shanghai 200231, China
随着海洋工程的多样化发展,海洋工程船舶日趋大型化,且配合施工作业的船体开槽多。双体船具有大甲板面积、稳定性好、阻力性能优良、操纵性能好等诸多优点,因此在海工船舶新船型中得到了广泛应用,如HLV-Svanen号、Pioneering Spirit号等。荷兰的HLV-Svanen号是1艘自航式风电安装双体船,船长103 m,最大可安装风叶直径达140 m,最大起吊高度达75 m,最大起重能力达8 700 t,连接桥长度约为船长的1/5。足够的起吊高度和起吊能力,以及占船长4/5的片体间作业空间,为风机的整体运输与安装提供了条件。瑞典Pioneering Spirit号船长382 m,宽124 m,起重能力达48 000 t,是目前世界上唯一一艘能够实现海洋平台整体拆除或安装起吊的船舶。Pioneering Spirit号首部采用双体船型,首部片体间距59 m,其余船体部分采用单体船型。首尾配备2套不同的起重设备,船首片体内侧对称配有8个起重臂,用于上部平台模块的拆除与安装;尾部配有一个摆动梁架式起重机,用于导管架的拆除与安装。本文的研究对象为1艘船长为170 m的超大型多功能洋工程双体船,双体间距达65 m,间距片体宽度比达到了2.6,远大于其他海洋工程双体船,独特的船型同时对船体的水动力性能提出了更高的要求,研究其在开敞海海况下的运动响应和波浪载荷,是此类超大型双体船研发的前提。
在船体运动响应和波浪载荷研究的进展中,其理论研究主要集中在切片理论和势流理论。早期,AL Dinsenbacher[1]提出了一种估算双体船所受波浪载荷的方法,该方法是将船放置在正弦波中计算静水压力和惯性载荷;Fang C.C.等[2]根据对线性频域理论,研究了一种常规波浪中双体船水动力运动响应的非线性时域方法,并与试验的数据结果进行对比,发现用非线性时域方法比线性频域方法更准确地预报双体船的大幅度运动响应;严锋[3]对漂浮式潮流电站双体船载体的水动力性能进行了分析,并在水动力性能研究的基础上对片体及连接桥结构强度进行了分析与校核;耿彦超等[4]用二维半理论和程序对某高速穿浪双体船在斜浪中的运动响应及连接桥结构的波浪诱导载荷进行了预报,验证了程序的适用性;邓磊等[5]基于RANS方程和VOF模型,对船体粘性兴波波场求解,研究了SWATH在迎浪规则波中纵向运动和波浪载荷的非线性特性。本文基于三维势流理论,对超大型双体船满载工况下的六自由度运动响应及波浪载荷短期预报进行研究,包括波浪载荷各分量沿船长分布规律,以及波浪载荷沿船宽分布规律,得到了双体船各横截面和连接桥各纵截面载荷最大统计值,为后续的双体船结构详细设计提供参考依据。
1 计算理论 1.1 三维势流理论势流理论假定速度势存在,并且满足拉普拉斯方程和四类边界条件:自由面条件、海底条件、物面湿表面条件和辐射条件(无穷远处边界条件)[6]。速度势可由拉普拉斯方程和边界条件唯一确定,得到速度分布,再结合伯努利方程计算得到湿表面的压力分布,最后沿物体湿表面积分得到压力合力。
当入射波波长远远大于波高时,可把总的速度势ϕ线性分解为辐射势和绕射势:
| $\varphi = {\varphi _{_R}} + {\varphi _{_D}}\;{\text{,}}$ | (1) |
| ${\varphi _{_R}} = i\omega \mathop \sum \limits_{j = 1}^6 {\xi _j}{\varphi _{_j}}\;{\text{,}}$ | (2) |
| ${\varphi _{_D}} = {\varphi _{_1}} + {\varphi _{_2}}\;{\text{。}}$ | (3) |
式中:ξj指刚体假定下物体六自由度振荡运动的幅值;φj为单位辐射势;φ2表示物体固定在原位置时引起的对入射波的扰动;φ1为入射波速度势。
| ${\varphi _1} = \frac{{igA\cos h\left[ {\nu (z + H)} \right]}}{{\omega \cos h\nu H}}{e^{ - i\nu x\cos \beta - i\nu y\sin \beta }}\;{\text{。}}$ | (4) |
式中:g为重力加速度;β为入射波方向角;H为水深;v是色散关系的实根。
| $\frac{{{\omega ^2}}}{g} = \nu \tan h\nu H\;{\text{。}}$ | (5) |
通过求解在确定的边界条件下的Laplace方程,从而求得流场中的辐射速度势和绕射速度势。
1.2 运动方程根据牛顿定律,考虑附加质量、阻尼力和激励力,建立刚体系统的简谐运动方程如下式:
| $[ - {\omega ^2}(M + a(\omega )) + i\omega (b(\omega )) + C]X(\omega ,\beta ) = F(\omega ,\beta )\;{\text{。}}$ | (6) |
式中:M为船体质量;a(ω)为附加质量;b(ω)为阻尼系数;C为回复力系数;X(ω, β)
短期海况可视为均值为0的平稳正态随机过程[6]。此时船体在波浪下的运动响应可以看成线性时不变系统。由随机过程理论可得,以海浪的作用作为输入,其输出的波浪载荷也是均值为0的平稳正态随机过程。输入与输出的关系如下式:
| ${S_W}\left( {\omega ,{H_{1/3}},{T_z},V,\theta } \right) = {H^2}(\omega ,V,\theta ){S_\xi }\left( {\omega ,{H_{1/3}},T} \right)\;{\text{。}}$ | (7) |
式中:ω为波浪圆频率;V为航速;θ为浪向角;H1/3为有义波高;Tz为波浪的特征周期;Sξ(ω, H1/3, T)为海浪谱密度;SW(ω, H1/3, T, V, θ)为波浪载荷;H(ω, V, θ)为频率响应函数的模。
2 计算模型 2.1 水动力模型以超大型多功能海洋工程双体船为研究对象,具体主尺度参数如表1所示。船体主甲板配有可行走门式起吊系统,水动力模型如图1所示。计算中坐标原点取为重心在水线面上的投影点,以船首方向为X轴正方向,左侧片体方向为Y轴正方向,竖直向上方向为Z轴正方向。
|
|
表 1 超大型多功能海洋工程双体船主尺度 Tab.1 The main scales of super large multi-purpose marine engineering catamaran |

|
图 1 三维计算模型 Fig. 1 Three-dimensional model |
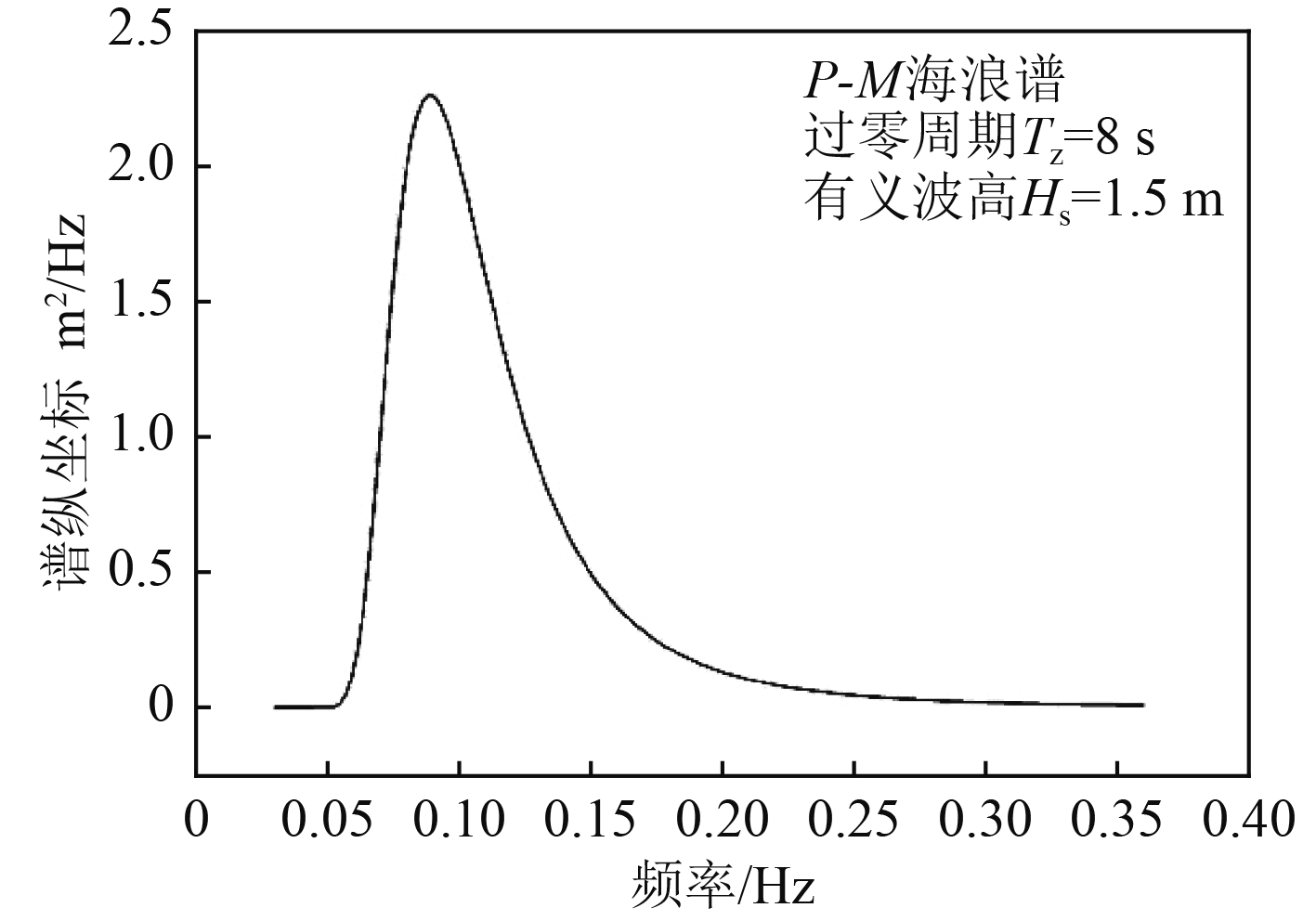
计算海浪选用不规则波,波浪谱采用ITTC推荐的双参数P-M波谱,考虑到船舶的具体航行海区与实际航行情况,有义波高为1.5 m,平均过零周期为8 s,海浪谱密度曲线如图2所示,具体计算环境条件如表2所示。
|
图 2 P-M海浪谱密度 Fig. 2 P-M wave spectral density |
|
|
表 2 环境条件 Tab.2 Environmental conditions |
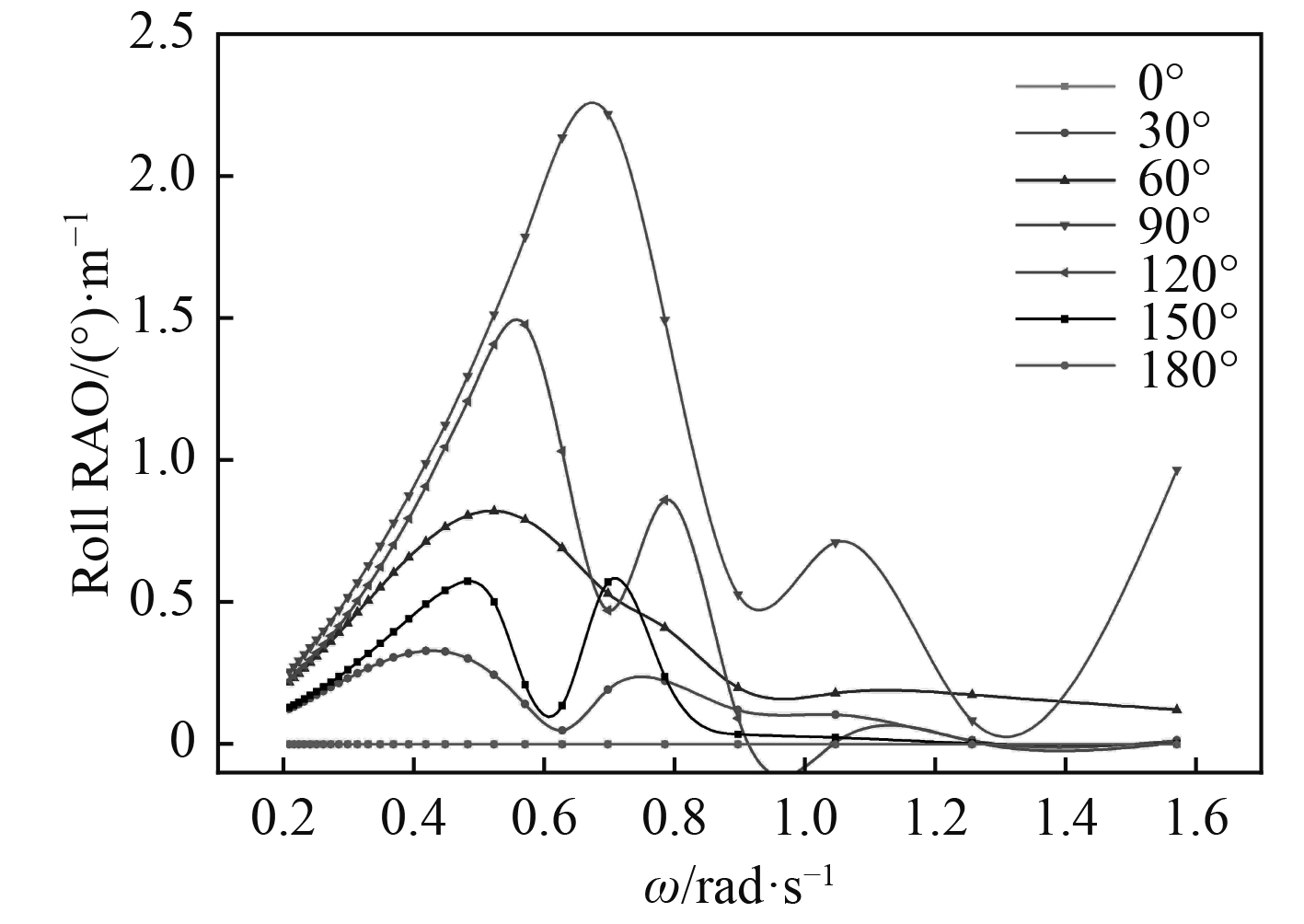
超大型海洋工程双体船主甲板配备有大型起吊系统,起吊过程中双体船的横摇响应和纵摇响应是关注的重点,也是保证船舶安全作业的重要参考。图3和图4分别为各个浪向下双体船横摇、纵摇幅值响应算子。运动幅值响应算子是单位波幅下船体运动响应值。浪向90°时横摇响应最大,在圆频率0.7 rad/s时出现峰值;浪向180°时纵摇响应最大,在圆频率0.57 rad/s时出现峰值。
|
图 3 横摇RAO Fig. 3 Roll RAO |

|
图 4 纵摇RAO Fig. 4 Pitch RAO |
重点对满载迁移工况下的双体船横摇、纵摇以及垂荡运动响应进行分析。运动响应谱反映了在规定海况下响应幅值与波浪频率之间的关系,图5为双体船在不同浪向下的横摇、纵摇、垂荡响应谱变化曲线。运动响应有义值和极值预报反映了超大型双体船在不同海况下运动的剧烈程度,表3和表4为运动响应有义值和极值预报结果。
|
|
表 3 运动响应有义值预报 Tab.3 The prediction of significant motion response |
|
|
表 4 运动响应极值预报 Tab.4 The prediction of maximum motion response |

|
图 5 运动响应谱 Fig. 5 The spectrum of Motion response |
由图5和表3、表4可知,双体船的横摇运动在波浪周期8~10 s时比较剧烈,变化幅度较大,最大值出现在横浪时,周期为9.6 s,此时角速度、角加速度也最大;纵摇运动在波浪周期为10 s时幅值迅速增大,达到极值后迅速减小,在随浪状态下达到最大,此时角速度、角加速度也达到极值,在横浪时纵摇运动幅度最小;垂荡运动在波浪周期8~13 s时较剧烈,变化较大,最大值出现在横浪状态下,波浪周期为13 s。在迁移过程中船舶应尽量避免在波浪周期为8~13 s区域内航行。
4 波浪载荷短期预报分析 4.1 波浪载荷沿船长分布规律所预报的船体横截面上波浪载荷各分量包括横向剪切力、垂向剪切力、水平弯矩、水平压力、横向和纵向弯矩,各分量方向如图6所示,不同浪向下波浪载荷沿船长分布曲线如图7所示。横坐标表示横截面位置,纵坐标表示波浪载荷在该横截面上的最大统计值。波浪载荷极值情况如表5所示。

|
图 6 横截面波浪载荷分量示意图 Fig. 6 Schematic diagram of wave loads component in cross sections |

|
图 7 波浪载荷沿船长方向分布规律 Fig. 7 Distribution of wave loads along ship length |
分析可知:水平压力沿船长分布规律在各浪向下基本一致,在距船首约20 m,即1/6船长处出现极值,最大值出现在迎浪状态下;横向剪切力及横向扭矩是导致双体船扭转变形的重要成分,横向剪切力和横向扭矩在首斜浪状态下达到最大,最大值出现在船舯附近;垂向剪切力与纵向弯矩是引起双体船中拱中垂弯曲的主要影响,垂向剪切力分布呈双峰曲线,在1/4和3/4船长处达到峰值,纵向弯矩分布呈单峰曲线,在船中处达到峰值。
|
|
表 5 横截面波浪载荷极值分布 Tab.5 Distribution of wave loads extreme values in cross sections |
超大型双体船两片体由连接桥连接,连接桥结构承担着片体之间传递的各种弯矩及应力,连接桥的横向强度是连接桥结构强度研究的重点,而波浪载荷沿船宽方向的分布规律更直观地反映连接桥各纵截面所受波浪诱导载荷极/值情况。连接桥所受载荷包括左右片体相对横摇产生的横向弯矩;左右片体纵摇不同步产生的纵向弯矩;左右片体艏摇不同步产生的水平弯矩;左右片体横荡不同步产生的横向分离力;左右片体垂荡不同步产生的垂向剪切力;左右片体纵荡不同步产生的纵向剪切力[5]。不同浪向下连接桥所受载荷沿船宽分布曲线如图8所示,横坐标表示纵截面位置,纵坐标表示波浪载荷在该纵截面上的最大统计值。

|
图 8 波浪载荷沿船宽方向分布曲线 Fig. 8 Distribution of wave loads along ship width |
横坐标[−45, −20]、[20,45]表示左右片体宽度范围,[−20, 20]表示连接桥宽度范围。从图8和表6可看出:横向分离力和水平扭矩在连接桥与片体连接处急剧增加,且在连接桥宽度范围内基本稳定在某一值附近;纵向剪切力、纵向弯矩、垂向剪切力在片体宽度范围内逐渐增大,在连接桥处最大且保持稳定;横向弯矩曲线在连接桥范围内先降后升,中部偏右出现最小值,在靠近左片体处出现峰值;计算海况中有义波高为1.5 m,根据不规则波的最大有义波长为有义波高的60倍,即最大有义波长为90 m,与船宽相等,而纵向剪切力、纵向弯矩及水平扭矩在首斜浪时最大,两片体处于斜浪波谷位置,连接桥处于波峰位置;横向分离力、垂向剪切力在横浪时最大,横向弯矩在横浪时于左片体连接处取得最大值,此时两片体处于波峰位置,连接桥处于波谷位置。
|
|
表 6 纵截面波浪载荷极值分布 Tab.6 The distribution of wave loads extreme values in longitudinal section |
超大型海洋工程双体船片体间距大,且船体尾部有大开口,主甲板配备一套可行走门式起重系统,是目前国际上少有的新型多功能海洋工程双体船。运用三维势流理论,考虑了超大型海洋工程双体船片体之间的相互干扰,对船体满载迁移工况下的运动响应以及波浪载荷进行预报分析,主要得到以下结论:
1)超大型双体船横浪时横摇和垂荡响应最大,纵摇角在随浪和迎浪时响应最大,各浪向下的运动响应在波浪周期8~13 s时最剧烈。
2)在波浪载荷沿船长分布规律中分析得到,各浪向下水平压力在距船首约1/6船长处出现极值,且最大值出现在迎浪状态;横向剪切力和横向扭矩在首斜浪状态下达到最大,最大值出现在船舯附近;垂向剪切力呈双峰曲线,在1/4和3/4船长处达到峰值;纵向弯矩分布呈单峰曲线,在船中处达到峰值。
3)在波浪载荷沿船宽分布规律中分析得到,连接桥处波浪载荷数值最大,横向分离力、纵向剪切力、纵向弯矩以及水平扭矩均在连接桥处增长明显,且在连接桥宽度范围内基本稳定在某一值附近;横向弯矩在连接桥与片体连接处剧增,在连接桥宽度范围内先降后升。
4)波浪方向影响船体运动响应剧烈程度,也影响波浪载荷沿船长和船宽的具体分布。
| [1] |
AL DINSENBACHER. Method for estimating loads on catamaran cross-structure[J]. Marine Technology , 1970, 7(4): 477-489.
|
| [2] |
FANG C. C., CHAN H. S., INCECIK A. Investigation of motions of catamarans in regular waves[J]. Ocean Engineering. 1997, 24(10): 946-966.
|
| [3] |
严锋. 300 kW潮流电站双体船载体设计[D]. 哈尔滨: 哈尔滨工程大学, 2010.
|
| [4] |
耿彦超, 顾学康, 汪雪良. 高速双体船斜浪中运动响应及连接桥波浪载荷预报[J]. 船舶力学, 2010, 14(4): 385-392. |
| [5] |
邓磊, 董文才, 姚朝帮. 迎浪规则波中小水线面双体船纵向运动及波浪载荷非线性特性数值分析(英文)[J]. 船舶力学, 2017, 21(3): 249-262. DOI:10.3969/j.issn.1007-7294.2017.03.001 |
| [6] |
戴仰山, 沈进威, 宋竞正. 船舶波浪载荷[M]. 北京: 国防工业出版社, 2007: 104-105.
|
| [7] |
毛筱菲. 双体船连接桥波浪载荷的试验研究[J]. 船海工程, 2003(6): 10-12. DOI:10.3963/j.issn.1671-7953.2003.06.005 |
| [8] |
LEE C. M. et al. Prediction of motion and hydrodynamic loads of catamaran [J]. Marine Technology, 1973, 10(4): 392-405.
|
| [9] |
陈攀. 双体客船波浪载荷及强度计算分析[J]. 船舶工程, 2015, 37(11): 1-5+13. |
| [10] |
徐伟. 三体船波浪诱导运动及载荷的数值预报研究[D]. 上海: 上海交通大学, 2008.
|
 2020, Vol. 42
2020, Vol. 42
