2. 海军研究院,北京 100161
2. Naval Research Academy, Beijing 100161, China
随着现代反舰武器的发展,各类大型舰船面对的威胁形式由船体外远距离爆炸向精确制导式的穿入船体内爆,由于船体内部空间的限制,爆炸载荷在船体内部不断反射汇聚,因此其对结构和人员的毁伤作用将比在船体外爆炸要更加显著。为了更好地抵御战斗部舱内爆炸载荷,研究舱内爆炸载荷的特性和规律就成为了防护领域的热点问题。M.kurki[1]对舰船结构在舱内爆炸载荷作用的变形破坏模式进行了数值仿真研究。侯海量等[2-3]开展了典型舱室模型的舱内爆炸试验,研究了舱内爆炸载荷的作用过程及舱室板架在内爆载荷下的失效模式。孔祥韶等[4]研究了3种不同的角隅连接结构型式对冲击波在角隅汇聚情况的影响,并基于图象法解释了冲击波在角隅的汇聚现象。C.Geretto等[5]进行了一系列实验研究固方支板在不同空间约束程度(自由空间、半约束和完全约束)的内爆加载作用下的变形,分析了不同载荷下的变形规律和空间约束程度对变形的影响。姚术健等[6]进行了钢箱结构在内部爆炸下的变形规律试验研究,并拟合了箱体壁板挠厚比与爆炸当量之间的经验公式。陈攀等[7]采用数值方法研究了舱室内爆冲击波壁面反射特性及爆点位置对舱室内爆载荷的影响。杨亚东[8]等采用镜像法和非线性叠加处理获得了长方体密闭空间内爆炸冲击波传播和叠加分析模型。但对于内爆载荷作用的另一个重要参数,目标壁面受到的载荷总冲量尚没有估算方法。本文采用时间及空间区域划分的方法,建立舱内爆炸下目标壁面所受载荷的简化模型,提出目标壁面受到的总冲量简化工程计算方法,可为舰船舱室结构变形计算及抗内爆载荷设计提供参考。
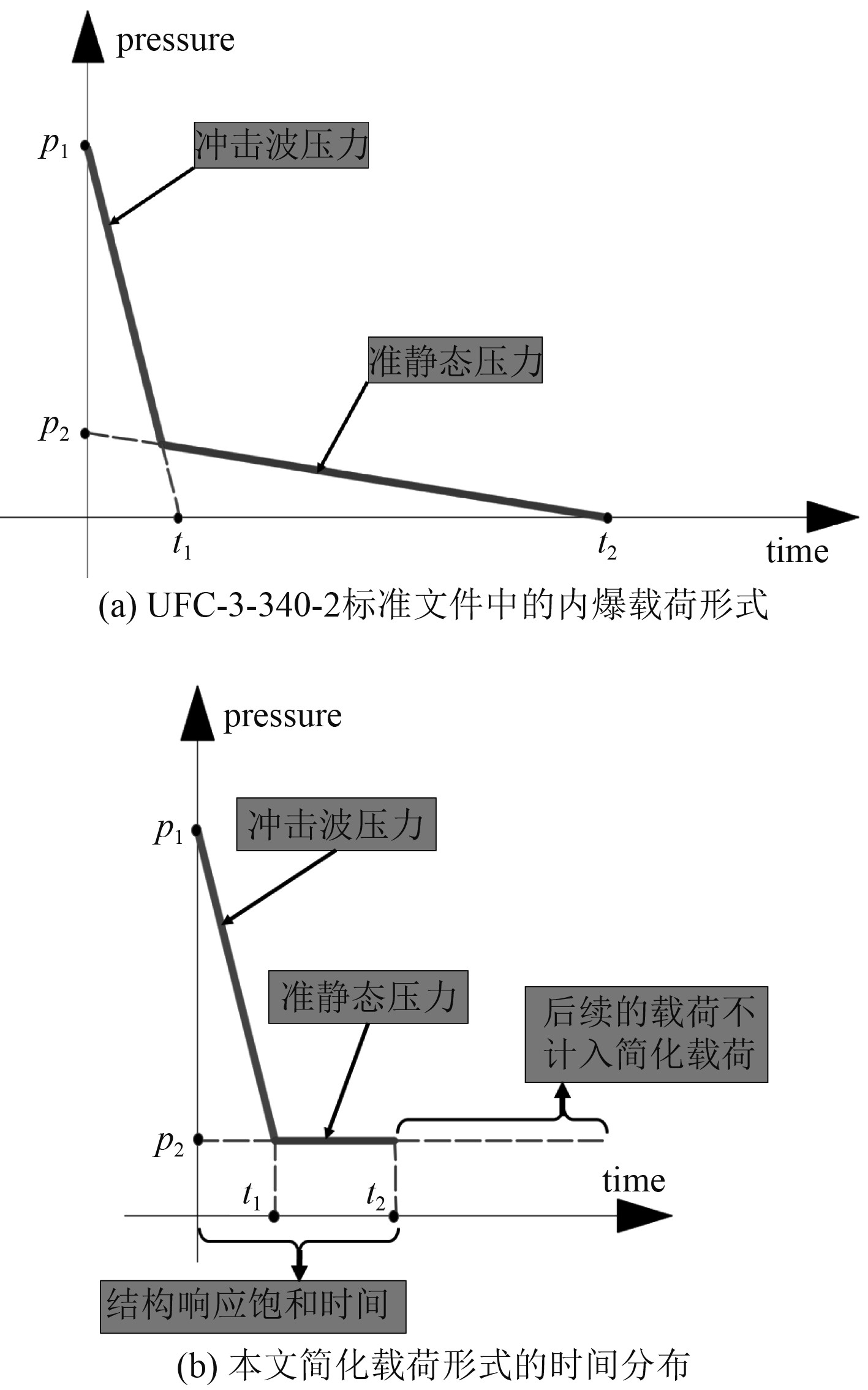
1 舱内爆炸载荷简化模型时间分布对舱内爆炸载荷进行简化处理,可以将其载荷先按作用时间顺序分为爆炸冲击波阶段和准静态压力阶段,第1阶段爆炸冲击波阶段,冲击波的多次反射作用由于都属于作用时间短的脉冲载荷,基于冲量等效的原则,认为多次反射的波峰可以合并为一个大的尖三角脉冲载荷,且忽略其反射冲击波强度上升的时间;第2阶段准静态压力阶段则主要受到后续准静态压力的作用,其特点为载荷峰值较小,但作用时间长,载荷强度的衰减速度相对较慢,故可以在简化的瞬态尖脉冲载荷基础上,将后续的准静态压力简化为紧接着的一个衰减相对平缓、持续时间更长的长三角载荷。因此通过以上对试验结果和有限元仿真计算结果的定性研究和分析,假设爆炸冲击波的正压作用时间结束时,舱内爆炸载荷再立即转入准静态压力作用阶段,在时间分布上将典型壁面上的内爆冲击波载荷和准静态压力载荷简化为瞬态尖脉冲载荷和长三角载荷的叠加作用,其载荷形式如图1(b)所示,这种按时间顺序的阶段划分方法与美国标准文件UFC-3-340-2[9]的中单点载荷替代整个壁面载荷的形式基本一致。其差别主要有两点:一是冲击波载荷和准静态压力是否有重叠作用的时间,UFC-3-340-2中冲击波载荷与准静态压力载荷有一段同时作用的区域,而本文所用的载荷形式假设爆炸冲击波的正压作用时间结束时,再转入准静态压力作用阶段,即2种压力载荷没有重叠区;二是准静态压力载荷持续时间的不同。在UFC-3-340-2规范文件中将准静态压力从形成到衰减值大气压力的时间段内的载荷全部计入内爆载荷形式,而本文的准静态压力载荷只选取了准静态压力的前一段时间作为载荷的持续时间,因为有关研究结果表明[10],在持续较长时间的爆炸冲击波及后续准静态压力载荷作用下,金属薄板架结构的动态响应存在一个饱和阈值。板架结构在冲击波载荷作用下先产生大挠度变形,而后由于四周边界条件的约束,板的中面会产生较大的拉伸膜力效应,进而使得板架结构承载能力随其变形的增加而得到一定程度的增强,相比之下后续的载荷强度却在逐渐衰减,这就导致结构的变形在到达一定值后不再继续增加,其动态响应达到饱和阈值,后续的压力载荷将不影响结构的最终变形。从结构响应动态响应饱和阈值的研究工作可见,舱内爆炸载荷的载荷形式需要考虑结构动态响应饱和阈值的影响,结构响应达到饱和阈值之后的持续作用的载荷为无效载荷,所以将结构变形达到饱和阈值的时间称为饱和响应时间[11],只将这段饱和响应时间内的持续载荷计入舱内爆炸作用的有效载荷且忽略该时段内准静态压力的衰减。因此本文最终给出的舱内爆炸载荷如图1(b)所示。
|
图 1 舱内爆炸冲击波载荷及准静态压力简化模型(时间分布) Fig. 1 Simplified model of explosion shock wave load and quasi-static pressure in the cabin(time distribution) |
图1(b)中的舱内爆炸简化载荷时间分布,为一个梯形脉冲载荷(冲击波)与矩形脉冲载荷的联合载荷,其载荷模型的关键参数有4个,分别是反射冲击波超压峰值p1、冲击波超压正压作用时间t1、准静态压力值p2和准静态压力载荷有效作用时间t2。由于舱内爆炸的载荷特性不仅由时间分布决定,还受舱内室内爆炸载荷的空间位置的影响。因此为了得到这4个参数的简化计算方法,需要对舱内爆炸载荷按空间进行区域划分。
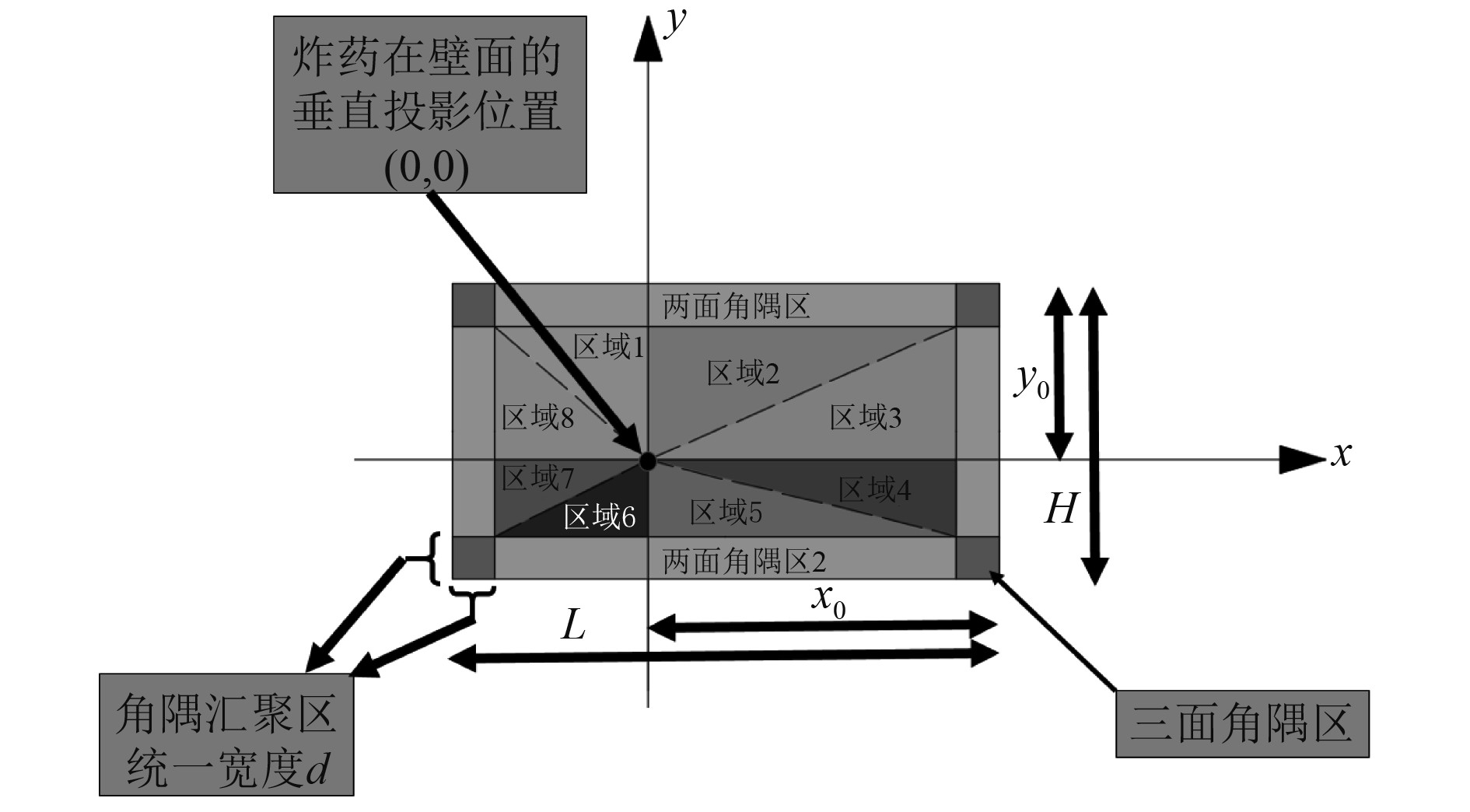
2 舱内爆炸载荷简化模型空间分布如图2所示,以炸药在壁面的垂直投影位置为原点建立壁面坐标系,壁面长边长度为L,壁面短边长度为H,舱室宽度为B,将舱内爆炸下壁面各点受到的爆炸冲击波超压峰值p1按空间分布划分为三大类区域,第1类区域为非角隅中间区域,第2类为两面边界交汇的两面角隅区,第3类为三面边界交汇的三面角隅区。依据其各自的载荷特性,分别对三类区域的反射冲击波超压峰值p1建立其简化计算方法。其中舱内爆炸载荷受角隅汇聚效应影响的区域范围较为固定,为便于简化计算,将边界角隅汇聚区的统一宽度d取为壁面短边长度H的1/10,即d=0.1H。

|
图 2 舱内爆炸下壁面峰值压力空间分布模型 Fig. 2 Spatial distribution model of peak pressure under the explosion in the cabin |
对于第1类的非角隅中间区域,将其分为8个相类似的三角区域。以图2中区域3为例,对该区域的内爆载荷峰值p1进行简化计算。将中间区域3内各点的爆炸冲击波超压峰值p1假设为一个连续的平面函数,该平面函数由三角区域的3个点p1(0,0),p1(0,x0-d)和p1(x0-d,y0-d)确定,即三点确定一个平面函数p1=f(x,y),再由所得平面函数计算出区域内各点(x,y)的超压峰值p1(x,y),如图3所示。为了求得该平面函数,就要先确定3个角点A点、B点和C点的超压峰值计算方法。根据Henrych提出的经验公式(1)可计算这3个点的爆炸冲击波入射超压峰值

|
图 3 中间区域3的内爆冲击波反射超压峰值分布 Fig. 3 Peak distribution of shock wave reflection overpressure in the center area 3 |
| $ \scriptsize\Delta {p_{\text{m}}} = \left\{ {\begin{aligned} & {\frac{{1.40717}}{Z} + \frac{{0.55397}}{{{Z^2}}} - \frac{{0.03572}}{{{Z^3}}} + \frac{{0.000625}}{{{Z^4}}},}&{0.05 \leqslant Z \leqslant 0.3}{\text{,}} \\ & {\frac{{0.61938}}{Z} - \frac{{0.03262}}{{{Z^2}}} + \frac{{0.21324}}{{{Z^3}}},}&{0.3 \leqslant Z \leqslant 1}{\text{,}} \\ & {\frac{{0.0662}}{Z} + \frac{{0.405}}{{{Z^2}}} + \frac{{0.3288}}{{{Z^3}}},}&{1 \leqslant Z \leqslant 10}{\text{。}} \end{aligned}} \right. $ | (1) |
其中:
为便于解释说明,将这3个点的反射超压峰值p1(0,0),p1(0,x0-d)和p1(x0-d,y0-d)分别记为pA,pB和pC。由于pA为炸药正对壁面的投影位置处(0,0)的峰值超压,因此(0,0)点处的爆炸冲击波入射角φ为0°,冲击波在壁面的反射为正反射,对于正反射,其峰值超压的计算公式[12]为:
| ${p_1} = 2\Delta {p_{m}} + \frac{{6\Delta p_{m}^2}}{{\Delta {p_{m}} + 7{p_0}}}{\text{,}}$ | (2) |
其中
对于点(0,x0-d)和(x0-d,y0-d),要确定其反射冲击波超压峰值pB和pC则需要先确定其入射角φ的大小。以点(0,x0-d)为例,其入射角
| $\varphi = \arctan \frac{{{{y}_0} - d}}{D}{\text{。}}$ | (3) |
当φ小于规则反射极限角φ0时,爆炸冲击波在该点发生规则斜反射,其反射冲击波超压峰值仍然近似按式(2)计算,空气的规则反射极限角近似取为40°;当φ大于等于规则反射极限角φ0时,爆炸冲击波在该点处发生马赫反射,其反射冲击波峰值压力pB按式(4)计算[12]:
| ${p_1} = \Delta {p_{{\rm m}G}}(1 + \cos \varphi ){\text{,}}$ | (4) |
其中ΔpmG为相同药量在刚性壁面爆炸时空气入射冲击波超压峰值。由于刚性壁面的限制和阻挡,爆炸冲击波可看成是只向一半的无限空间传播,进行镜像对称,则
| $ \scriptsize\Delta {p_{{\text{mG}}}} = \left\{ {\begin{aligned} & {\frac{{1.77292}}{Z} + \frac{{0.87937}}{{{Z^2}}} - \frac{{0.07144}}{{{Z^3}}} + \frac{{0.001575}}{{{Z^4}}},}&{0.05 \leqslant Z \leqslant 0.3}{\text{,}} \\ & {\frac{{0.78037}}{Z} - \frac{{0.05178}}{{{Z^2}}} + \frac{{0.42648}}{{{Z^3}}},\;}&{0.3 \leqslant Z \leqslant 1}{\text{,}} \\ & {\frac{{0.0834}}{Z} + \frac{{0.643}}{{{Z^2}}} + \frac{{0.6576}}{{{Z^3}}},\;}&{1 \leqslant Z \leqslant 10}{\text{。}} \end{aligned}} \right. $ | (5) |
将式(5)代入式(4)即可求得当该点发生马赫反射时,其爆炸冲击波反射超压峰值p1。采用式(1)~式(5)的判定及计算方法,分别求出点(0,x0-d)和(x0-d,y0-d)处的反射冲击波超压峰值pB和pC。如此则分别求出了区域3的3个角点(0,0),(0,x0-d)和(x0-d,y0-d)的反射冲击波超压峰值pA,pB和pC。再由以上这3个点的坐标(0,0,pA),(0,x0-d,pB)和(x0-d,y0-d,pC)计算求得整个区域3内各个点的反射冲击波超压峰值所满足的平面函数的表达式p1=f(x,y),其一般形式为:
| $ {p_1}\left( {x,y} \right) = {k_1}x + {k_2}y + {C_1}{\text{。}} $ | (6) |
其中:k1,k2,C1为根据(0,0,pA),(0,x0-d,pB)和(x0-d,y0-d,pC)三点坐标确定的常数,且对于区域3来说,C1=pA。
通过以上简化计算方法,对于中间区域划分成的8个小三角区域内任意一点,均可采用式(1)~式(6)的计算方法,求得其爆炸冲击波反射超压峰值p1。
2.1.2 两面角隅区对于图2中第2类的两面角隅区,根据其位置,也将其分成上下左右4个区域,以两面角隅区1为例,依据仿真计算结果的角隅压力载荷特性,建立该区域内各点的爆炸冲击波反射超压峰值p1的简化分布及计算方法,如图4所示。

|
图 4 两面角隅区1的内爆冲击波反射超压峰值分布 Fig. 4 Peak distribution of shock wave reflection overpressure in the dihedral corner region 1 |
对两面角隅区的峰值及比冲量进行简化计算时,可以认为对于两面角隅区1,在其区域统一宽度(d)的方向上,反射冲击波的峰值压力和比冲量无变化,即p1(x1,y0)=p1(x1,y1)=p1(x1,y2),其中(x1,y0),(x1,y1),(x1,y2)为两面角隅区1内x坐标相同,y坐标不同的3点。
因此在图4中的两面角隅区1中任意一点(x,y)的反射冲击波超压峰值只是与x坐标有关的函数,即p1(x,y)=f(x,y0)=f(x);将两面角隅区1的爆炸冲击波反射超压峰值假设为线性分段函数p1=f(x),该分段函数由图4中D点、E点和F点这3点处的反射冲击波超压峰值确定,而这3个点在壁面坐标系下的坐标分别为(x0-L+d,y0),(0,y0)和(x0-d,y0)。在求出了线性分段函数后,即可采用该函数计算求得两面角隅区1内任意点处的爆炸冲击波反射超压峰值。因此,需要先求解这3个点处的反射冲击波超压峰值。为便于解释说明,将这3个点的反射超压峰值p1(x0-L+d,y0)、p1(0,y0)和p1(x0-d,y0)分别记为pD、pE和pF。
以点D处反射峰值压力pD求解为例,先根据式(1)计算D点处的爆炸冲击波入射超压峰值Δpm,再代入式(2)~式(5)求出点D处不考虑角隅汇聚增强效应的反射冲击波峰值压力pDO。点D属于两面角隅汇聚边界,相邻的另一壁面角隅点的反射冲击波会在D点与其反射冲击波发生叠加效应,近似相当于D点有2倍反射冲击波超压的作用,因此可以认为点D处反射峰值压力pD的最终计算式为:
| ${p_{{D}}} = {\rm{2}}{p_{{{DO}}}}{\text{,}}$ | (7) |
同样计算步骤及方法对于点E和F有:
| ${p_{{E}}} = {\rm{2}}{p_{{{EO}}}}{\text{,}}$ | (8) |
| ${p_{{F}}} = {\rm{2}}{p_{{{FO}}}}{\text{。}}$ | (9) |
由获得的D,E,F三个点的坐标(x0-L+d,y0,pD),(0,y0,pE)和(x0-d,y0,pF)确定线性分段函数p1=f(x),如下式:
| $ {p_1} = \left\{ {\begin{array}{*{20}{c}} {{k_3}x + {C_2}{\text{,}}\;\;\;\;\;\;\;{x_0} - {\rm{L}} + d \leqslant x \leqslant 0}{\text{,}}\\ {{k_4}x + {C_2}{\text{,}}\;\;\;\;\;\;\;\;\;\;0 \leqslant x \leqslant {{\rm{x}}_0} - d}{\text{。}} \end{array}} \right. $ | (10) |
其中:k3为图4中DE直线段的斜率;k4为图4中EF直线段的斜率;C2为(0,y0)处反射冲击波超压峰值
通过式(10)可以计算出两面角隅区1内任意一点(x,y)的反射冲击波超压峰值压力p1。对于其他的两面角隅区的任意一点,均可采用式(1)~式(5)、式(7)~式(10)的计算方法,求得其爆炸冲击波反射超压峰值p1。
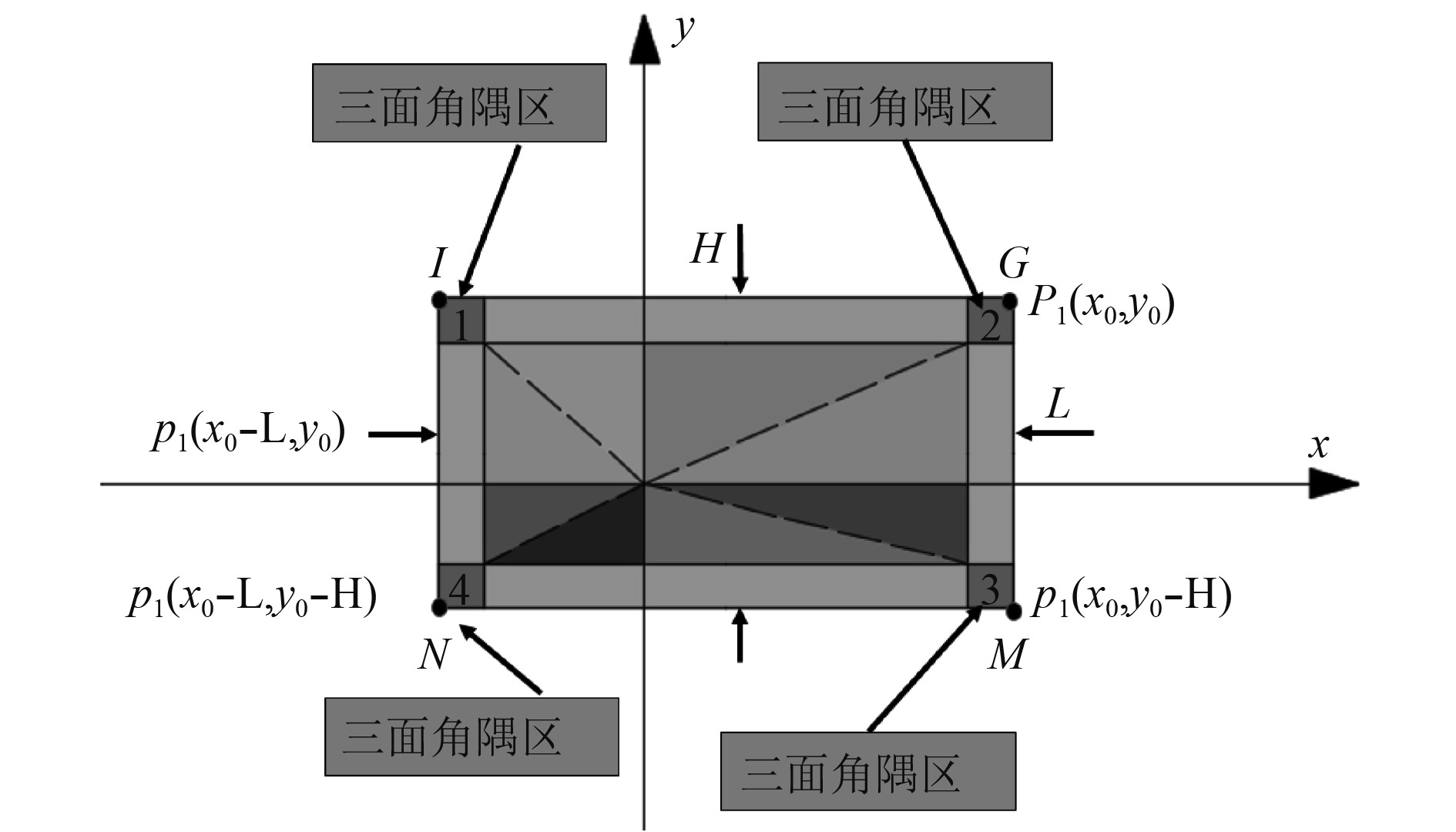
2.1.3 三面角隅区对三面角隅区反射超压峰值进行简化计算时,忽略这部分反射冲击波压力和比冲量差值,近似地认为区域内各点的反射冲击波压力和比冲量相同,然后根据冲量等效原则将三面角隅区的载荷等效成均布载荷,各个三面角隅区内均布压力载荷的初始峰值分别由角隅位置4点(G点,M点,N点,I点)的反射超压峰值确定,即三面角隅区内各点处的反射冲击波峰值均与其相应的角隅点的峰值压力相同。
以图5所示三面角隅区2为研究对象,建立其反射冲击波超压峰值简化计算方法。首先根据式(1)可计算G点处的爆炸冲击波入射超压峰值Δpm,再代入式(2)~式(5)求出点G处不考虑角隅汇聚增强效应的反射冲击波峰值压力pGO。点G属于三面角隅汇聚边界,相邻的另2个壁面角隅点的反射冲击波会在G点与其反射冲击波发生叠加效应,近似相当于G点有3倍的反射冲击波超压的作用,因此可以将点G处反射峰值压力pG的最终计算式为:
|
图 5 三面角隅区位置分布 Fig. 5 Location distribution of the trihedral corner area |
| ${p_{\rm{G}}} = 3{p_{{\rm{GO}}}}{\text{。}}$ | (11) |
再根据之前的均布载荷近似简化处理,则对三面角隅区2内任意一点(x,y)的反射冲击波超压峰值压力p1(x,y)均与G点处相同,即p1(x,y)为常函数,所以有:
| $ {p_{\rm{1}}}(x,y) = {C_3}{\text{,}} $ | (12) |
其中对于三面角隅区2,C3=pG。对于其他的两面角隅区的任意一点,均可采用式(1)~式(5)、式(11)~式(12)的计算方法,求得其爆炸冲击波反射超压峰值p1。
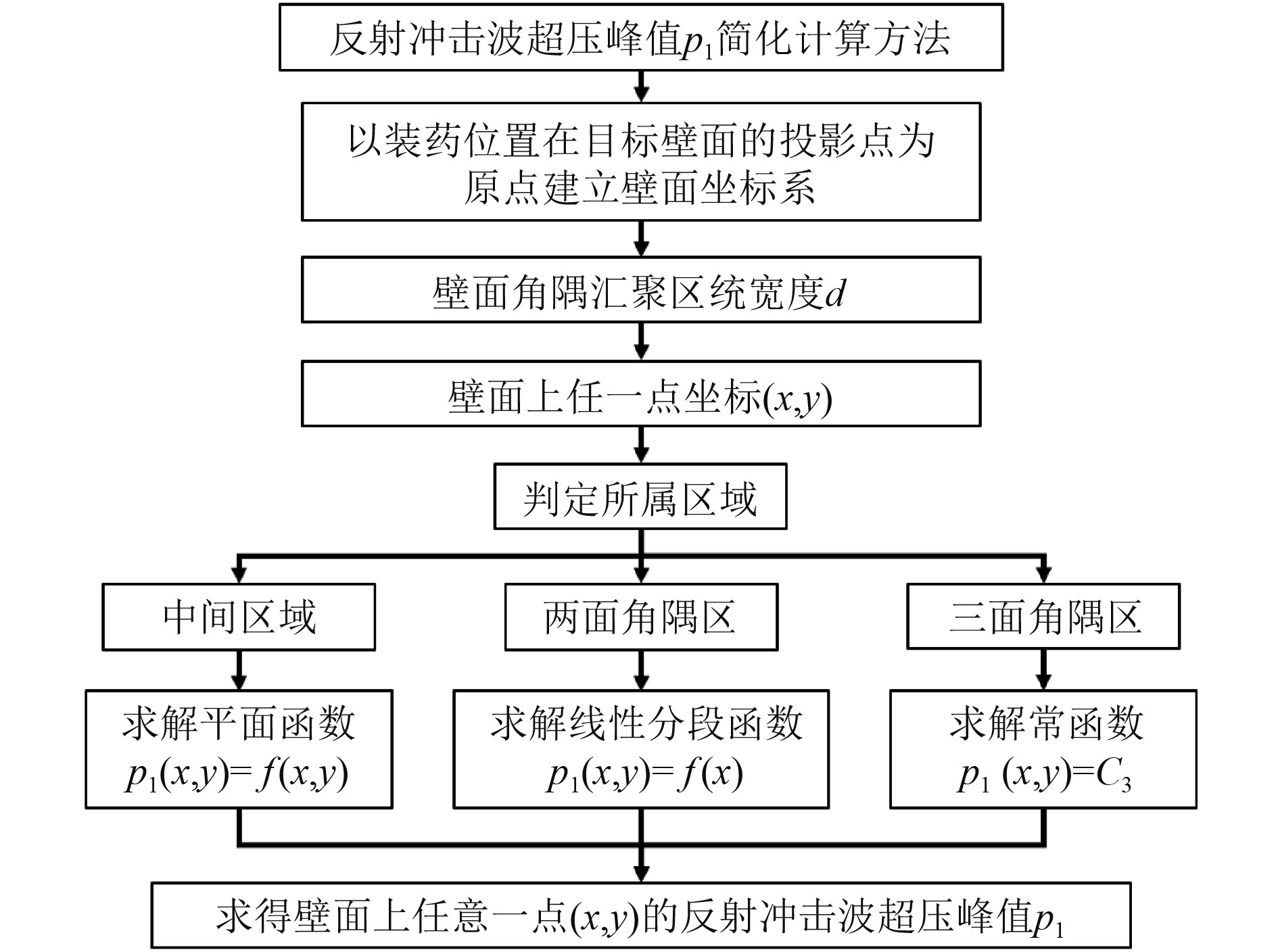
综上所述,舱内爆炸载荷下目标壁面上任意一点的反射冲击波超压峰值p1的求解过程如图6所示。
|
图 6 反射冲击波超压峰值p1求解流程图 Fig. 6 Flow chart of reflection shock wave overpressure peak p1 |
由于反射冲击波超压峰值p1在计算时被划分成了3个不同的区域,冲击波超压正压作用时间也需要按各自的区域分别计算。
2.2.1 非角隅中间区域由于简化模型的时间分布忽略了冲击波的到达时间而假设各点的冲击波同时到达,因此对于同一个区域内的各点,也假设其冲击波超压的持续时间相同。同样以中间区域3为研究对象,计算其冲击波超压的正压作用时间t1。
空气中爆炸冲击波正压作用时间的计算公式为:
| ${t_ + } = 1.35 \times {10^{ - 3}}{Z^{{1 / 2}}}{W^{{1/ 3}}}{\text{,}}$ | (13) |
根据式(13)计算图3中A点、B点和C点的冲击波正压作用时间tA+,tB+和tC+,由于之前假设同于区域内的各个点的正压作用时间相同,因此取这3点正压作用时间的平均值为区域内的正压作用持续时间,即有:
| ${t_1} = \frac{1}{3}({t_{{{A + }}}} + {t_{{{B + }}}} + {t_{{{C + }}}}){\text{。}}$ | (14) |
由式(14)计算可得中间区域3内各点冲击波正压作用时间。对于中间区域的8个小区域都可采用相同的方法和式(14)计算其区域内的正压作用时间。
2.2.2 两面角隅区对于两面角隅区的冲击波超压正压作用时间t1,采用和中间区域相同的简化处理方法求得两面角隅区域内平均化的冲击波正压作用时间。以两面角隅区1为例,计算其的区域内的冲击波超压正压作用时间。首先采用式(13)分别计算图4两面角隅区1中3点D点、E点和F点的爆炸冲击波正压作用时间tD+,tE+和tF+,同样取这3点的正压作用时间的平均值为两面角隅区1内的平均正压作用持续时间,即有:
| ${t_1} = \frac{1}{3}({t_{{{D + }}}} + {t_{{{E + }}}} + {t_{{{F + }}}}){\text{。}}$ | (15) |
由式(13)和式(15)计算可得两面角隅区内各点冲击波正压作用时间。对于其余的两面角隅区都可采用相同的方法计算其区域内的正压作用时间t1。
2.2.3 三面角隅区由于三面角隅区的范围较小,在该范围内各点的正压作用时间随位置的变化可近似忽略,因此对于三面角隅区内各点的冲击波超压正压作用时间t1,可用角隅一点的正压作用时间代替。以三面角隅区2为例,计算其区域内的冲击波超压正压作用时间。采用式(13)计算图5(三面角隅区2)中G点的正压作用时间tG+,由于以G点的正压作用时间代替整个三面角隅区2内各点的冲击波正压作用时间,因此该区域内各点的正压作用时间为:
| ${t_1} = {t_{{{G + }}}}{\text{。}}$ | (16) |
其他三面角隅区的冲击波超压正压作用时间t1同样可由式(13)和式(16)的方法计算得到。
2.3 准静态压力值和准静态压力载荷有效作用时间对于舱内爆炸下的准静态压力值p2和准静态压力载荷有效作用时间t2,不需要采用区域划分的方法进行简化,而是假设壁面上任何一点的的准静态压力值和有效作用时间都相同。
2.3.1 准静态压力值对于舱内爆炸下舱内爆炸下的准静态压力值p2的计算,其核心问题之一是有限密闭空间内爆炸产物形成的准静态压力值的求解,而研究表明有限空间内爆炸形成的准静态压力值是装药质量与有限空间容积之比(W/V)的函数,并有一系列的基于该比值的拟合经验公式,本文则采用Carlson经验公式计算舱内爆炸形成的准静态压力值:
| ${p_2} = 1.3\left( {W/V} \right){\text{。}}$ | (17) |
其中:W为装药质量,V为舱室内部的空间体积。对于壁面上任意一点(x,y),其准静态压力值p2可用式(17)计算。
2.3.2 准静态压力载荷有效作用时间根据第1节的时间分布载荷的简化过程分析,准静态压力载荷的另一个重要参数是有效作用时间,因为结构在持续较长时间的爆炸冲击波及后续准静态压力的作用下其变形存在一个饱和阈值,在变形达到饱和阈值之后,后续载荷的作用将不再引起更多的变形。因此准静态压力载荷的有效作用时间t2即是结构变形到达饱和阈值的响应饱和时间ts。孔祥韶等[8]针对密闭空间内爆炸载荷计算方法及结构的饱和响应时间进一步开展了系列仿真计算研究,并提出了内爆载荷下板结构的无量纲的饱和响应时间的经验公式:
| ${t_s} = \lambda \cdot {L_0}\sqrt {\frac{\rho }{\sigma }} {\text{。}}$ | (18) |
其中:ts为板结构的饱和响应时间,ms;λ为无量纲系数,取值范围为16.0~17.5;L0为正方形板边长,m;ρ为板材料密度,g/cm3;σ为屈服强度,MPa。从式(18)可见,板结构的饱和响应时间与结构板厚无关。但该经验公式是基于正方形的平板结构建立的,而实际情况下舱室的壁面往往是长度和高度不相同的矩形,因此在式(18)基础上稍作修改。取矩形壁面长边和短边的平均值作为长度参数,以尽量同时考虑壁面长边和短边对其饱和响应时间的因素,因此有:
| ${t_s} = \frac{1}{2}\lambda \cdot (L + H)\sqrt {\frac{\rho }{\sigma }}{\text{。}} $ | (19) |
由之前的分析和图1(b)的时间分布模型可知,结构变形到达饱和阈值的响应饱和时间ts即是准静态压力载荷有效作用的时间t2。因此由式(19)即可求得内爆载荷下目标壁面上任意一点(x,y)处准静态压力载荷的有效作用时间t2。
2.3.3 目标壁面受到的舱内爆炸载荷的总冲量前文建立了舱内爆炸载荷简化时空分布模型,对于内爆载荷下目标壁面上任意一点的舱内爆炸载荷,基于经验公式基础上,给出了相应的求解其模型关键参数的简化计算方法。通过图1(b)的载荷时间分布形式可见,由这4个关键载荷参数(p1,t1,p2,t2)可计算出任意一点(x,y)处受到的内爆载荷有效比冲量I(x,y),其计算式为:
| $I(x,y) = \frac{1}{2}({p_1} + {p_2}){t_1} + {p_2}({t_2} - {t_1}){\text{。}}$ | (20) |
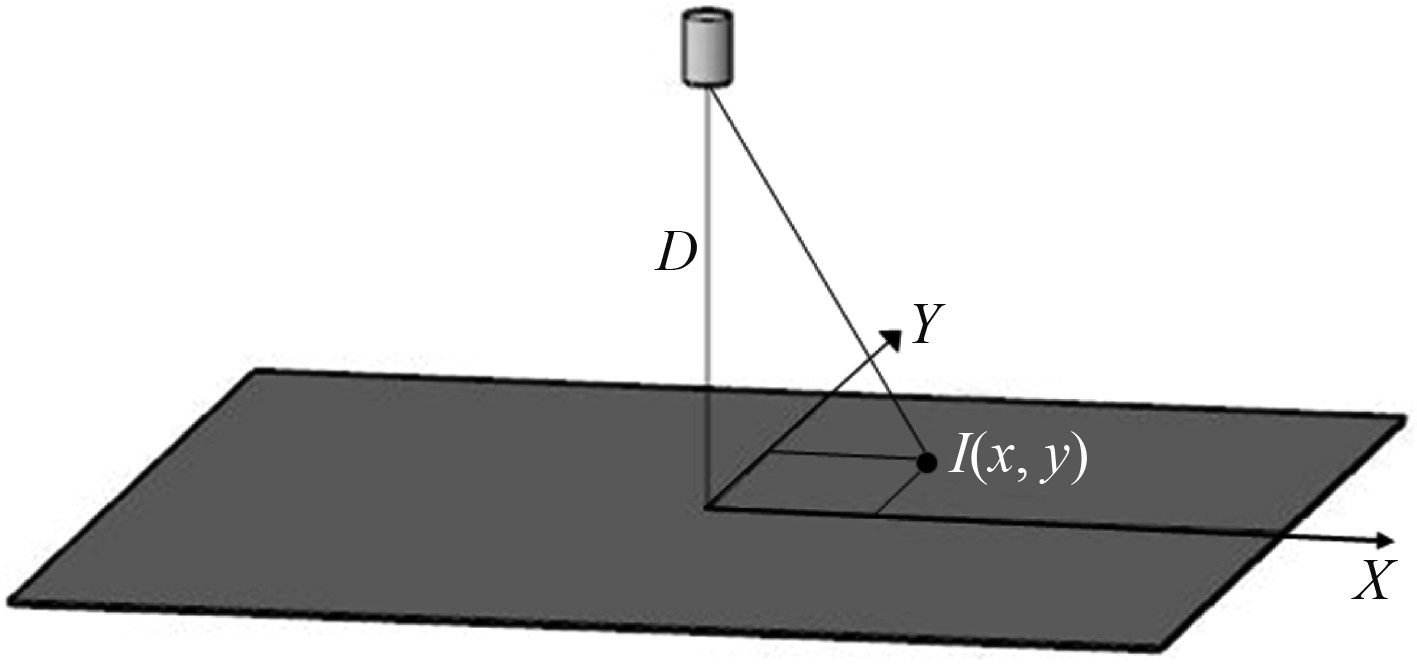
其中p1,t1,p2,t2都是与坐标位置(x,y)有关的函数。由于p1和t1的简化计算方法都与目标壁面的区域划分有关,因此在计算壁面受到的总冲量时,也需要先分别按各自区域求解其冲量,在进行求和得到壁面的总冲量。
|
图 7 舱内爆炸作用下目标壁面比冲量计算示意图 Fig. 7 Schematic diagram of calculation of target wall specific impulse under the action of explosion in cabin |
对于第一类中间非角隅区内的8个区域,记中间区域i的受到的冲量为:
| ${I_{1i}} = \iint {I\left( {x,y} \right)}{\rm{d}}x{\rm{d}}y{\text{。}}$ | (21) |
以图8中间区域3为例,舱内爆炸简化载荷对整个中间区域3的面积进行二重积分,得到该区域的总冲量为:
|
图 8 目标壁面总冲量计算区域划分 Fig. 8 Division of total impulse calculation area on target wall |
| $ \begin{split} & {I_{13}} = \iint\limits_{{D_{13}}} {I\left( {x,y} \right)} {\rm{d}}x{\rm{d}}y{\text{,}}\\ & {D_{13}} = \left\{ {(x,y)\left| {0 \leqslant y \leqslant {k_{13}}x,0 \leqslant x \leqslant {x_0} - d} \right.} \right\}{\text{。}} \end{split} $ | (22) |
其中
同理可求得第1类的中间区域内4个分区域i各自的冲量I1i,则第1类中间区域受到的总冲量为:
| ${I_1} = \sum\limits_1^8 {{I_{1i}}} {\text{。}}$ | (23) |
对于第2类两面角隅区的4个区域,记两面角隅区域j受到的冲量为I2j,以图8两面角隅区1为例,舱内爆炸简化载荷对整个两面角隅区1的面积进行二重积分,得到该区域的总冲量为:
| $ \begin{split} &{I_{21}} = \iint\limits_{{D_{21}}} {I\left( {x,y} \right)} {\rm{d}}x{\rm{d}}y {\text{,}} \\ &{D_{21}} = \left\{ {(x,y)\left| {{y_0} - d \leqslant y \leqslant {y_0},{x_0} - L + d \leqslant x \leqslant {x_0} - d} \right.} \right\}{\text{。}} \end{split} $ | (24) |
同理可求得第2类的两面角隅区内4个分区域j各自的冲量I2j,则第2类两面角隅区受到的总冲量为:
| ${I_2} = \sum\limits_1^4 {{I_{2j}}}{\text{。}} $ | (25) |
对于第3类三面角隅区的4个区域,记三面角隅区域k受到的冲量为I3k,以图8中三面角隅区2为例,舱内爆炸简化载荷对整个三面角隅区2的面积进行二重积分,得到该区域的总冲量为:
| $ \begin{split} &{I_{32}} = \iint\limits_{{D_{32}}} {I\left( {x,y} \right)} {\rm{d}}x{\rm{d}}y {\text{,}}\\ &{D_{32}} = \left\{ {(x,y)\left| {{y_0} - d \leqslant y \leqslant {y_0},{x_0} - d \leqslant x \leqslant {x_0}} \right.} \right\}{\text{。}} \end{split} $ | (26) |
同理可求得第3类的三面角隅区内4个分区域k各自的冲量I3k,则第3类两面角隅区受到的总冲量为:
| ${I_3} = \sum\limits_1^4 {{I_{3j}}}{\text{。}} $ | (27) |
采用简化计算模型得到目标壁面受到的舱内爆炸载荷总冲量为:
| ${I_{NZ}} = {I_1} + {I_2} + {I_3}{\text{。}}$ | (28) |
将所述舱内爆炸载荷简化模型通过Matlab程序化实现,并采用文献[13]中相同的工况和舱内爆炸数值仿真方法,建立有限元模型并计算分析,验证所提出简化计算模型的有效性,其计算结果对比如表1所示。从计算结果可见,对于文献中所提供2个舱内爆炸工况的仿真计算结果,本文提出的简化计算模型计算结果与仿真结果的误差都在10%以内,吻合情况较好。
|
|
表 1 仿真及简化模型计算结果 Tab.1 Results of simulation and simplification |
本文对舱内爆炸载荷相关参数计算进行了一定的简化处理,将舱内爆炸下目标壁面受到的内爆载荷在时间分布上分为爆炸冲击波作用和准静态压力作用2个阶段,在空间分布上分为中间非角隅区两面角隅区和三面角隅区,并基于此分布建立了舱内爆炸下目标壁面所受载荷的简化计算模型,提出了目标壁面所受总冲量的简化计算方法,其计算结果与有限元仿真结果吻合较好,对舱室结构的抗内爆载荷设计具有一定的实用价值,可以为舱内爆炸载荷强度及结构变形的快速工程估算提供参考。
| [1] |
KURKIT M. Contained explosion inside a naval ves-sel: Evaluation of the structural response [M]. Espoo: Helsinki University of Technology, 2007.
|
| [2] |
侯海量, 朱锡, 梅志远. 舱内爆炸载荷及舱室板架结构的失效模式分析[J]. 爆炸与冲击, 2007(2): 151-158. HOU Hai-liang, ZHU Xi, MEI Zhi-yuan. Study on the blast load and failure mode of ship structure subject to internal explosion[J]. Explosion and Shock Waves, 2007(2): 151-158. DOI:10.3321/j.issn:1001-1455.2007.02.010 |
| [3] |
侯海量, 朱锡, 李伟, 等. 舱内爆炸冲击载荷特性实验研究[J]. 船舶力学, 2010, 14(8): 901-907. HOU Hai-liang, ZHU Xi, LI Wei, et al. Experimental studies on characteristics of blast loading when exploded inside ship cabin[J]. Journal of Ship Mechanics, 2010, 14(8): 901-907. DOI:10.3969/j.issn.1007-7294.2010.08.011 |
| [4] |
孔祥韶, 吴卫国, 李俊, 等. 角隅结构对舱内爆炸载荷影响的实验研究[J]. 中国造船, 2012(3): 40-50. KONG Xiang-shao, WU Wei-guo, LI Jun, et al. Experimental research of influence of corner structure on blast loading under inner explosion[J]. Shipbuilding of China, 2012(3): 40-50. |
| [5] |
GERETTO C, CHUNG KIM YUEN S, NURICK G N. An experi-mental study of the effects of degrees of confinement on the response of square mild steel plates subjected to blast loading[J]. International Journal of Impact Engineering, 2015, 79: 32-44. DOI:10.1016/j.ijimpeng.2014.08.002 |
| [6] |
姚术健, 张舵, 郑监, 等. 内部爆炸作用下钢箱结构变形规律性实验[J]. 爆炸与冲击, 2017(5): 964-968. YAO Shu-jian, ZHANG Duo, ZHENG Jian, et al. Experimental study of deformation of steel box subjectrd to interal blast loading[J]. Explosion and Shock Waves, 2017(5): 964-968. |
| [7] |
陈攀, 刘志忠. 舱室内爆冲击波载荷特性及影响因素分析[J]. 舰船科学技术, 2016, 38(2): 43-48. CHEN Pan, LIU Zhi-zhong. Research on loading of explosive and influencing factors inside closed cabin[J]. Ship Science and Technology, 2016, 38(2): 43-48. DOI:10.3404/j.issn.1672-7649.2016.2.009 |
| [8] |
杨亚东, 李向东, 王晓鸣. 长方体密闭结构内爆炸冲击波传播与叠加分析模型[J]. 兵工学报, 2016, 37(8): 1449-1455. YANG YA-dong, LI Xaing-dong, WANG Xiao-ming. An analytical model for propagation and superposition of internal explosion shockwaves in closed cuboid structure[J]. Acta Armamentarii, 2016, 37(8): 1449-1455. DOI:10.3969/j.issn.1000-1093.2016.08.016 |
| [9] |
UFC 3-340-02(Unified Facilities Criteria): Structures to Resist the Effects of Accidental Explosions [R]. Department. of the Army, the NAVY and the Air Force, Washington, DC, USA, 2008.
|
| [10] |
ZHU L, YU T X. Saturated impulse for pulse-loaded elastic-plastic square plates[J]. International Journal of Solids & Structures, 1997, 34(14): 1709-1718. |
| [11] |
孔祥韶, 周沪, 郑成, 等. 基于饱和响应时间的封闭空间内爆炸载荷等效方法研究[J]. 爆炸与冲击. 2019(2). KONG Xiang-shao, ZHOU Hu, ZHENG Cheng, et al. An equivalent calculation method for confined-blast load based on saturated response time [J]. Explosion and Shock Waves, 2019(2). |
| [12] |
孙业斌. 爆炸作用与装药设计[M]. 北京: 国防工业出版社, 1987.
|
| [13] |
陈鹏宇, 侯海量, 刘贵兵, 等. 水雾对舱内装药爆炸载荷的耗散效能试验研究[J]. 兵工学报, 2018, 39(5): 927-933. CHEN Peng-yu, HOU Hai-liang, LIU Gui-bing, et al. Experimental investigation on mitigating effect of water mist on the explosive shock wave inside cabin[J]. Acta Armamentarii, 2018, 39(5): 927-933. DOI:10.3969/j.issn.1000-1093.2018.05.012 |
 2020, Vol. 42
2020, Vol. 42
