2. 中交上海航道装备工业有限公司,上海 200000;
3. 华润燃气(上海)有限公司,上海 210000
2. China Jiaotong Shanghai Waterway Equipment Industry Co., Ltd., Shanghai 200000,China;
3. China Resources Gas (Shanghai) Co., Ltd., Shanghai 210000,China
从1829年起人们就开始对金属疲劳机理进行探索,之后很多学者对横幅载荷中加入多个过载波形进行研究。McEvily,Kalnaus,Makabe等对不同种类材料进行了单峰过载试验。试验结果表明,在横幅载荷中加入一个或多个过载波形之后,疲劳裂纹扩展速率会相应的降低,试件的疲劳寿命会增加。随后一些学者对块状形式的载荷波形进行研究,根据研究结果得到了不同载荷形式下过载对疲劳裂纹扩展速率的影响规律,并提出单峰过载情况下的疲劳裂纹扩展速率预报模型[1]。
2008年,Tianwen对铝合金材料7075-T651高低载荷疲劳裂纹扩展行为进行了试验研究,并在Wheeler模型的基础上,提出一个用来预报材料过载迟滞效应的修正模型。2014年,王珂等在保载-疲劳裂纹扩展速率模型的基础上,提出一个考虑保载与过载共同影响的疲劳裂纹扩展速率预报模型。之后利用崔维成、Kalnaus等所进行的试验对模型进行验证,证明了该模型的可靠性[1]。
经过对过载保载-裂纹扩展的研究可以发现,许多学者对钛合金材料的疲劳寿命进行过试验与预报方法的研究,但主要集中在单峰过载疲劳与多峰过载疲劳,对考虑过载与保载共同影响的研究较少,考虑到海洋环境的复杂性及舰船工作状态的不确定性,开展钛合金材料过载保载-疲劳裂纹扩展速率的研究很有必要。因此,开展钛合金材料过载保载-疲劳裂纹扩展速率的试验研究对寿命预报方法的完善有重要的科学价值,对解决其他工程应用有重要的意义。
1 试验设计与开展 1.1 材料选择钛合金材料Ti-6Al-4V是第一个被研制成功的实用型钛合金,而且大量应用于舰船的关键节点和潜艇的耐压壳结构,本试验所用试件根据国家标准GB/T 3620.1-2007制备。
|
|
表 1 Ti–6Al–4V化学性质 Tab.1 Chemical composition of Ti–6Al–4V(wt%). |
|
|
表 2 Ti–6Al–4V材料性能 Tab.2 Mechanical properties of Ti–6Al–4V |
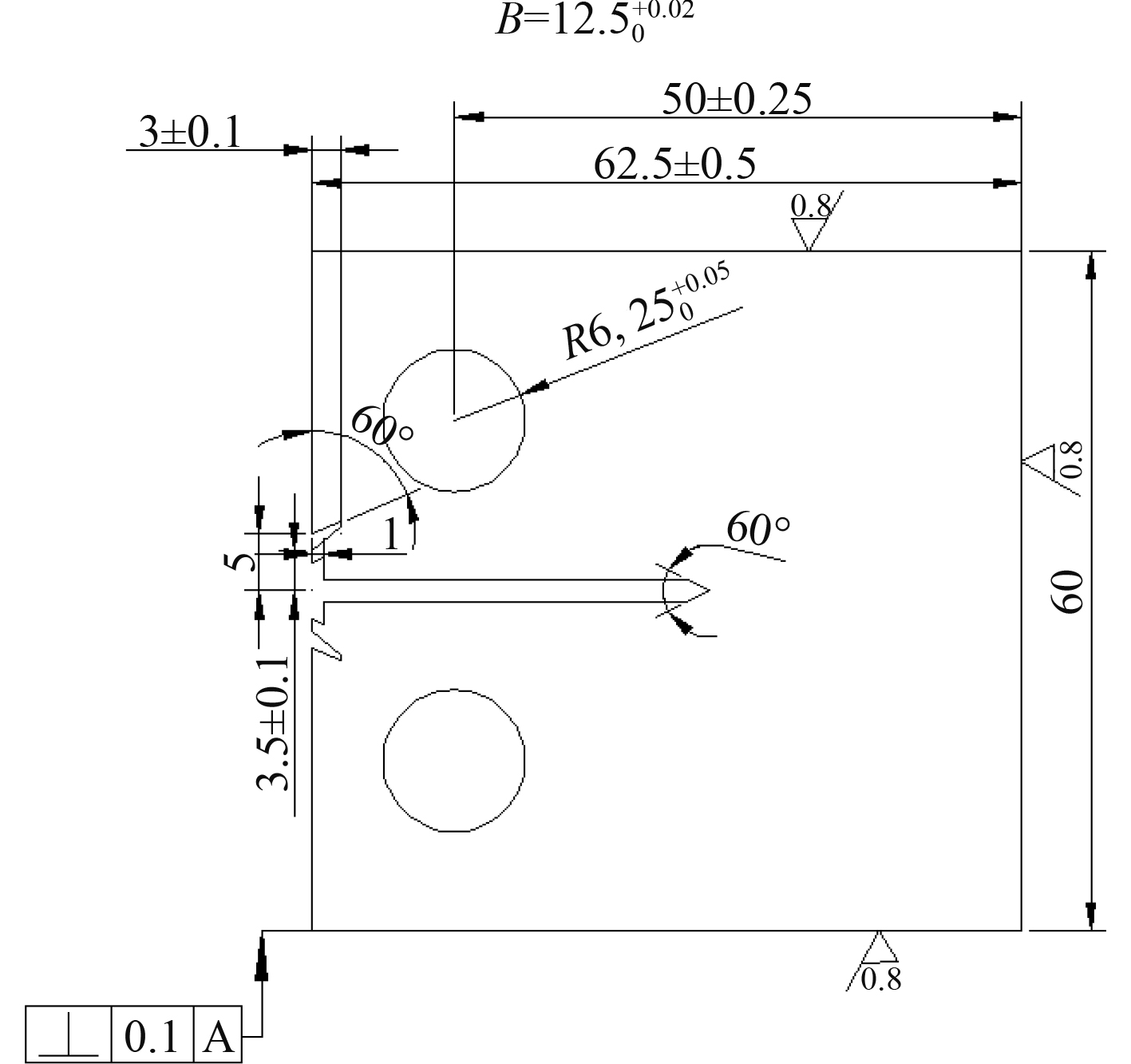
本次过载保载-疲劳裂纹扩展速率试验是在室温环境下进行,试验设备采用100 kN电子蠕变持久疲劳试验平台,试验机和引伸计的精度均满足国标GB/T6398-2000和美国标准ASTME647《Standard Test Method for Measurement of Fatigue Crack Growth Rates》的要求。本试验采用根据GB/T 6398-2000加工制备的CT试样,且在CT试样顶部开夹持槽以满足不同引伸计的量程,尺寸标准如图1所示。
根据国标GB /T 21143−2007规定,
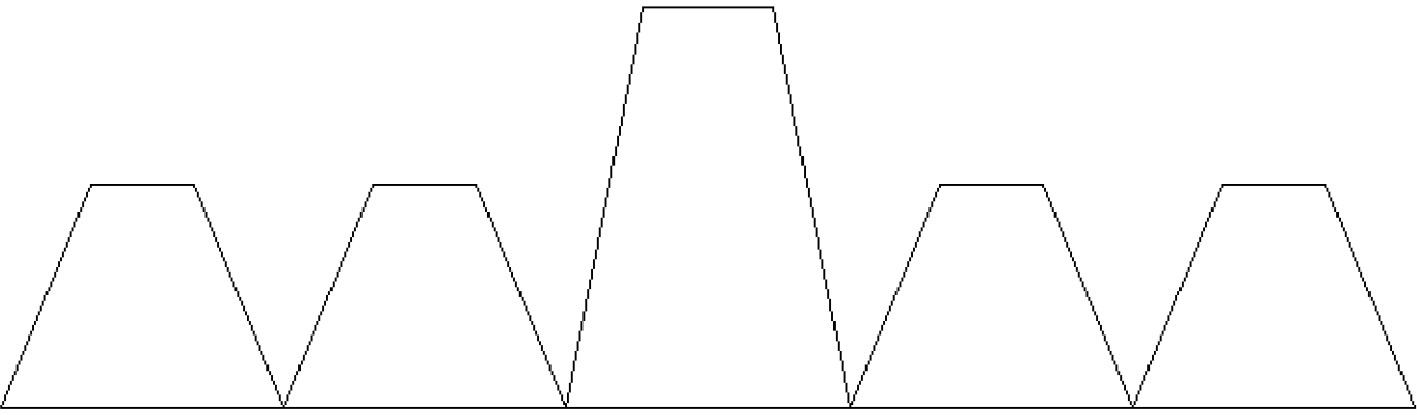
本文进行的是弹性范围内的过载保载-疲劳裂纹扩展速率试验,最大载荷为8 kN,过载比OLR=1.2,1.5,载荷比R=0.03,保载时间为30 s,过载-疲劳裂纹扩展速率可视作保载时间为0的过载保载-裂纹扩展速率试验,试验载荷谱如图2所示。当试样在应力循环
|
图 1 CT试样标准尺寸(mm) Fig. 1 Schematic showing the size of samples of CT(mm). |
|
图 2 载荷谱 Fig. 2 Schematic representation of dwell fatigue load |
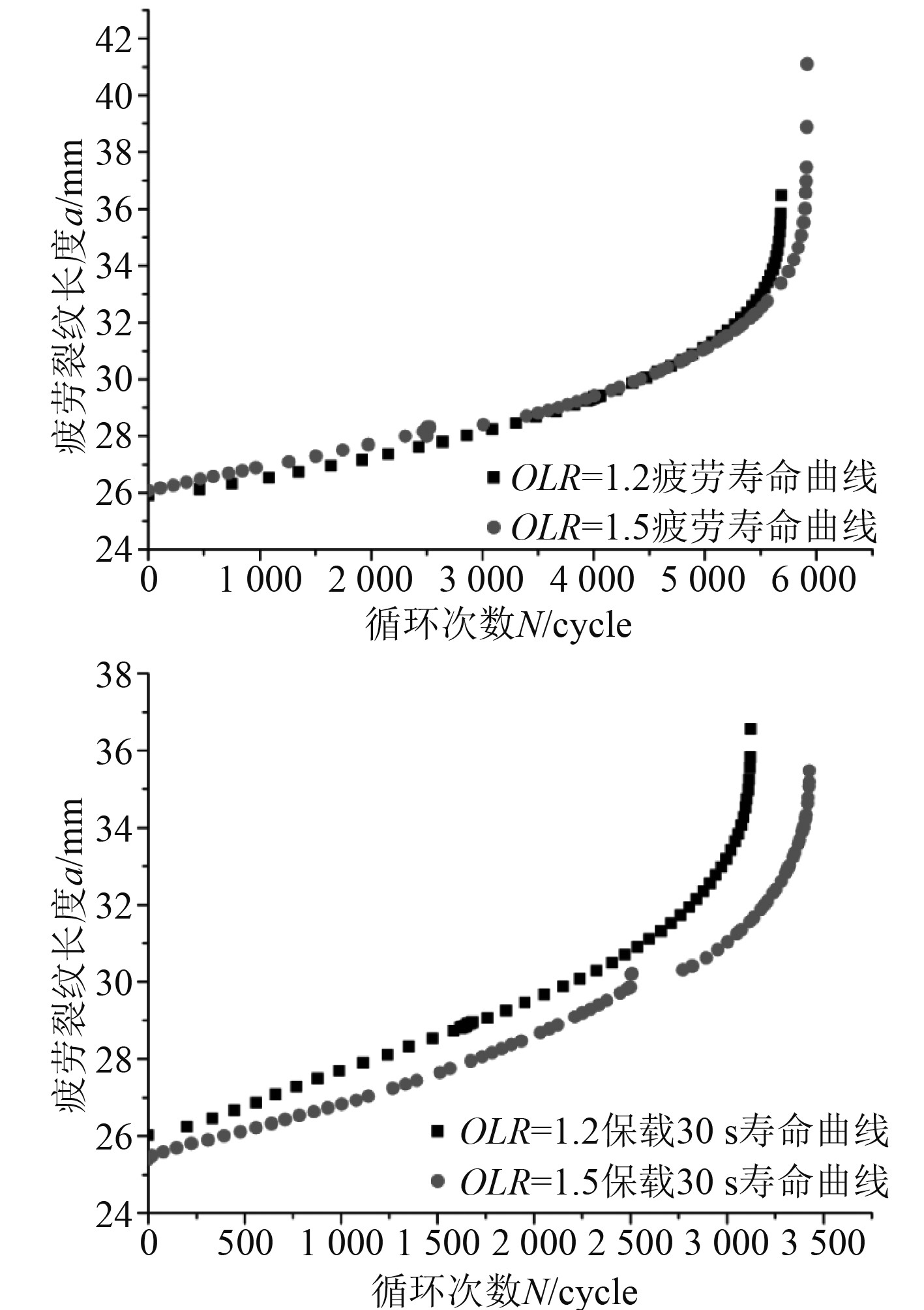
每一组试验做3组作为对照试验,保留试验效果最明显的一组试验数据,同时对试验结果进行分析,得到裂纹长度a与循环次数N的关系曲线,即为Ti–6Al–4V疲劳寿命曲线,如图3所示。
|
图 3 a-N曲线 Fig. 3 a-Ncurves |
可以看出,
利用割线法对
|
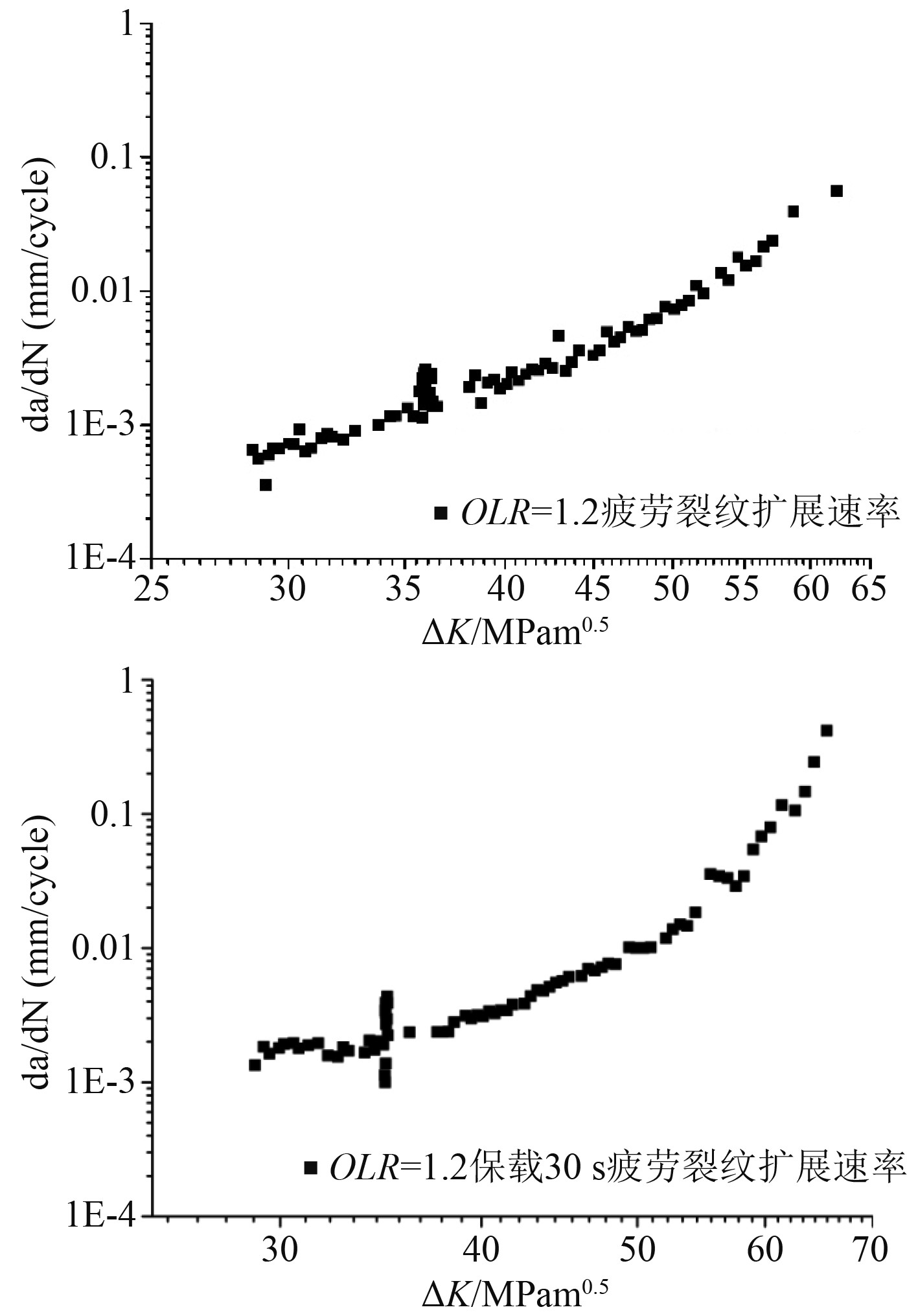
图 4 过载比OLR=1.2保载-疲劳裂纹扩展速率曲线 Fig. 4 OLR=1.2 dwell-fatigue crack growth rate curve |
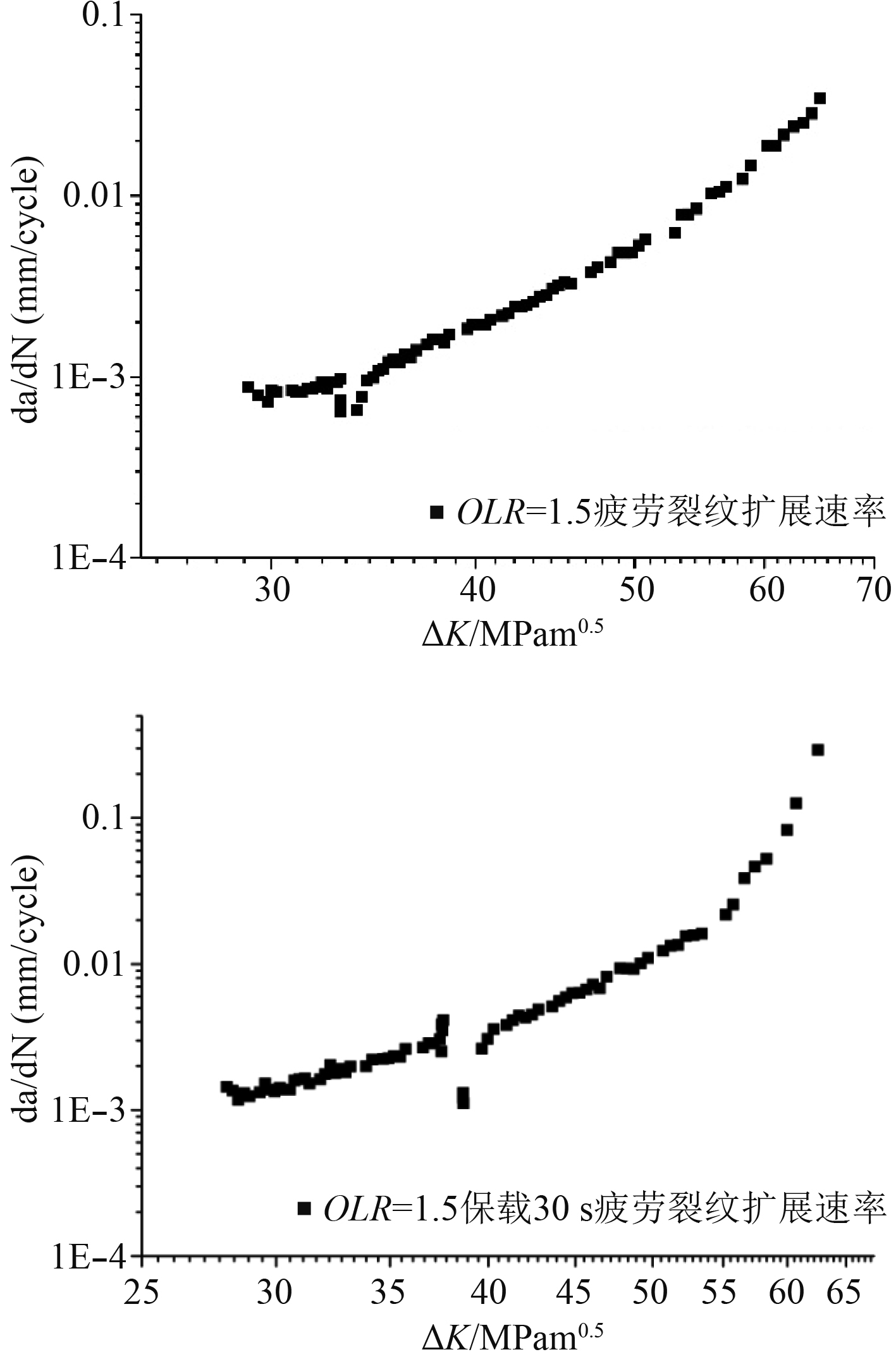
|
图 5 过载比OLR=1.5保载-疲劳裂纹扩展速率曲线 Fig. 5 OLR=1.5 dwell-fatigue crack growth rate curve |
| $\begin{split} &K = \left( {2 + \dfrac{a}{W}} \right) \times \\ &\dfrac{{0.866 \!+\! 4.64\left( {\dfrac{a}{W}} \right) \!-\! 13.32{{\left( {\dfrac{a}{W}} \right)}^2} \!+\! 14.72{{\left( {\dfrac{a}{W}} \right)}^3} - 5.6{{\left( {\dfrac{a}{W}} \right)}^4}}}{{{{\left( {1 - \dfrac{a}{W}} \right)}^{1.5}}}} \times \\ &\dfrac{F}{{B{W^{0.5}}}}\text{。} \end{split}$ | (1) |
由图4和图5的
过载载荷的引入,会使试件的裂纹扩展速率有明显的增加,之后会产生一定的迟滞区域,即过载迟滞效应。随着过载比OLR的增加,试件裂纹扩展速率回复到常幅载荷裂纹扩展速率的时间增加,也就是说迟滞区域会随着过载比的增加而增加。
3 预报结果分析 3.1 预报模型选择与修正本文所应用的模型为王珂等提出的考虑过载载荷次序因子
| $\begin{array}{l} \dfrac{{\rm{d}}a}{{\rm{d}}N} = {\varPhi _{RC}} \times \\ \left\{\!\!\begin{array}{l} {A_1}\dfrac{{{{\left[ {\Delta K \!-\! \left( {\Delta {K_{thR}}\! -\! \Delta {K_{th - s}}} \right)\left( {1 \!- \!{e^{ - k(a - d)}}} \right)\! - \!\Delta {K_{th - s}}} \right]}^{{m_1}}}}}{{1 - {{\left( {{K_{\max }}/{K_C}} \right)}^{{n_1}}}}} \!+\! \\ {A_2}{t_{hold}}{\left[ {\dfrac{{\left( {{\sigma _{\max }} - {\sigma _R}} \right)}}{{\left( {{\sigma _Y} - {\sigma _R}} \right)}}} \right]^\kappa }{\left( {\dfrac{{\Delta K}}{{1 - {{\left( {\dfrac{{{K_{\max }}}}{{{K_C}}}} \right)}^{{n_2}}}}}} \right)^{{m_2}}} \end{array}\!\!\right\} \end{array}\text{,}$ | (2) |
该公式在保载-疲劳裂纹扩展速率预报公式的基础上增加了考虑过载和保载时间的在载荷次序影响因子
| ${\varPhi _{RC}} = {\left( {\frac{{{r_{pi}}}}{{{r_{pOLC}}}}} \right)^m}\text{,}$ | (3) |
式中,考虑过载载荷作用与过载保载时间共同作用的塑性区域大小可以表示为:
| ${r_{pOLC}} = {r_{pi}} + \left( {{r_{OLC}} - {r_{pi}}} \right)\left[ {\exp \left( { - \frac{{{a_i} - {a_{OLC}}}}{{{a_R} - {a_i}}}} \right)} \right]\text{,}$ | (4) |
其中,
| ${r_{pi}} = \frac{1}{{\text{π}} }{\left( {\frac{{{K_{IC}}}}{{{\sigma _{{\rm{ys}}}}}}} \right)^2} + \frac{1}{{\beta {\text{π}} }}\left(\frac{{\Delta K}}{{2{\sigma _{ys}}}}\right)\text{,}$ | (5) |
| ${r_{OLC}} = \frac{1}{{\beta {\text{π}} }}\left( {\frac{{{K_{OLC}}}}{{{\sigma _{{\rm{ys}}}}}}} \right)\text{,}$ | (6) |
式中,
| ${r_{pR}} = \frac{1}{{\text{π}} }{\left( {\frac{{{K_{IC}}}}{{{\sigma _{{\rm{ys}}}}}}} \right)^2} + \frac{1}{{\beta {\text{π}} }}\left(\frac{{\Delta K}}{{2{\sigma _{ys}}}}\right)\text{。}$ | (7) |
通过叠代法,求出裂纹扩展速率恢复到常幅循环载荷作用时的裂纹长度
| ${a_R} = {a_{OLC}} + {r_{OLC}} - {r_{pR}}\text{。}$ | (8) |
通过以上公式的叠代,可以得到考虑过载载荷的载荷次序因子公式,将载荷次序因子代入保载-疲劳裂纹扩展公式,得到考虑过载载荷次序效应的疲劳裂纹扩展速率模型。
3.2 预报结果与试验结果对比按照就叠代得到的公式对试验结果进行预报,模型参数如表3所示,预报结果与试验结果对比如图6和图7所示。
|
|
表 3 模型参数 Tab.3 Model parameter |
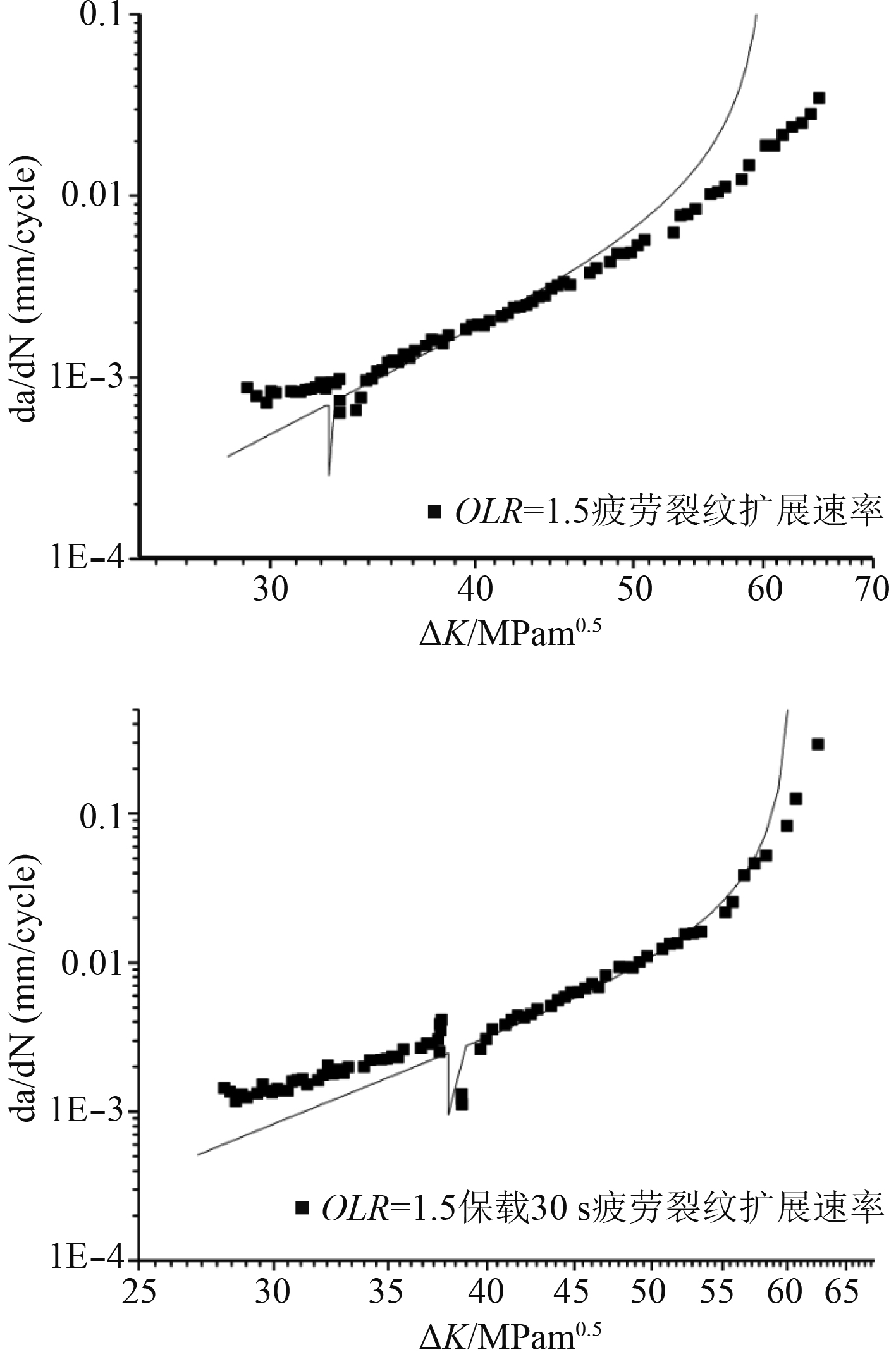
|
图 7 过载比OLR=1.5保载-疲劳裂纹扩展速率预报与试验对比曲线 Fig. 7 OLR=1.5 dwell-fatigue crack growth rate prediction and experimental comparison curve |
由图6和图7可以看出,该模型对单峰过载保载-疲劳裂纹扩展速率有较好的预报结果,特别是当过载载荷引入之后,模型预报结果与试验结果能够很好地拟合,体现过载载荷引起的迟滞效应。由于裂纹扩展速率试验过程中,过载载荷处保留所有数据点,导致迟滞区域曲线拟合效果不如应力强度因子较小处,但能够明显看出随着过载比的增加,迟滞区域逐渐增大。从总体来看,该公式能够较好地预报过载保载共同作用下的裂纹扩展速率。
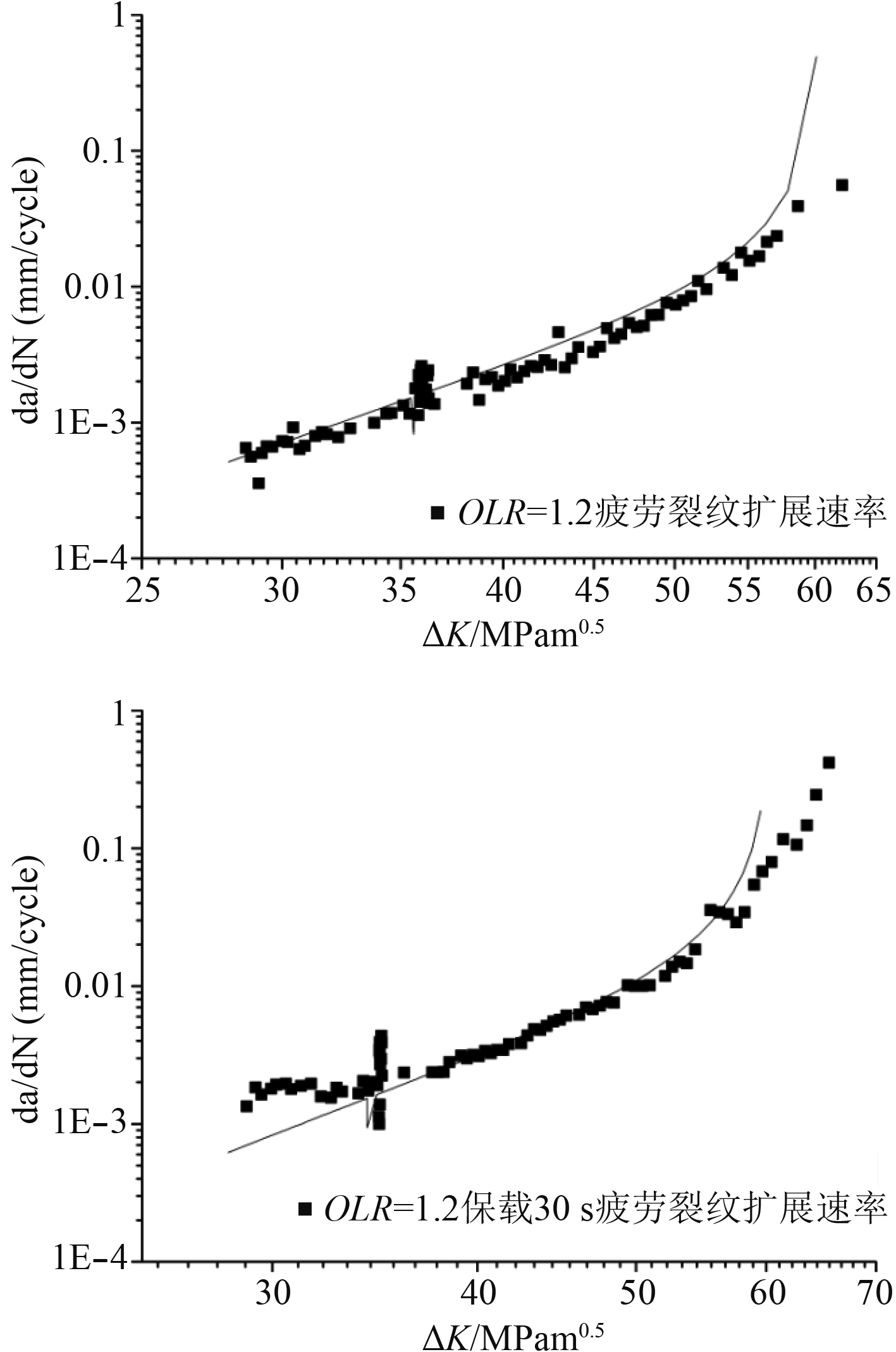
|
图 6 过载比OLR=1.2保载-疲劳裂纹扩展速率预报与试验对比曲线 Fig. 6 OLR=1.2 dwell-fatigue crack growth rate prediction and experimental comparison curve |
由于舰船工作环境的特殊性,在服役过程中某些关键节点会承受不同载荷次序的作用,从而导致材料的疲劳失效。为了研究载荷次序对裂纹扩展速率的影响,本文重点研究了引入过载载荷的过载疲劳及过载-保载疲劳裂纹扩展速率,设计开展了不同过载比下的一系列试验并进行数据分析。在此基础上,对试验结果进行预报,并验证预报模型的准确性。
1)随着保载时间的增加,过载保载-疲劳寿命逐渐降低,并且随着过载比OLR的增加,试件的寿命也有一定程度的增加。也就是说,在过载保载-疲劳裂纹扩展速率试验中,适当引入过载载荷会使试件的疲劳寿命有相应的延长;
2)保载时间t对TC4长裂纹保载-疲劳裂纹扩展速率具有明显的影响,随着应力强度因子范围
3)过载载荷的引入,会使试件的裂纹扩展速率有明显的增加,之后会产生一定的迟滞区域,即过载迟滞效应。随着过载比OLR的增加,试件裂纹扩展速率回复到常幅载荷裂纹扩展速率的时间增加,也就是说迟滞区域会随着过载比的增加而增加;
4)该预报模型对过载保载-疲劳裂纹扩展速率有较好的预报结果,特别是当过载载荷引入之后,模型预报结果与试验结果能够很好拟合,体现过载载荷引起的迟滞效应,明显看出随着过载比的增加,迟滞区域逐渐增大,因此,可以认为该公式能够较好地预报过载保载共同作用下的裂纹扩展速率。
| [1] |
王珂, 王哲. 过载保载对金属材料疲劳裂纹扩展速率影响研究[J]. 船舶力学, 2017(7): 895-906. DOI:10.3969/j.issn.1007-7294.2017.z1.075 |
| [2] |
沙宇. 铝合金疲劳裂纹扩展的压载荷效应与过载效应研究[D]. 哈尔滨: 哈尔滨理工大学, 2011.
|
| [3] |
张丽娜, 吴学仁, 刘建平. 疲劳裂纹扩展中单峰过载引起的残余应力强度因子计算[J]. 机械强度, 2011(3): 432-437. |
| [4] |
赵荣国, 罗希延, 任璐璐, 等. 航空发动机涡轮盘用GH4133B合金疲劳裂纹扩展行为研究[J]. 机械工程学报, 2011(18): 55-65. |
| [5] |
钟安, 方劲, 沈先莱, 等. 高载比和高载出现频率对随机加载疲劳裂纹扩展行为的影响[J]. 重庆建筑大学学报, 1995(3): 8-20. |
| [6] |
耿越, 陈吉. 单峰过载对2205双相不锈钢疲劳裂纹扩展速率的影响[J]. 机械工程材料, 2018(1): 59-63. DOI:10.11973/jxgccl201801001 |
| [7] |
孟维迎, 谢里阳, 刘建中, 等. 玻璃纤维增强铝锂合金层板单峰过载疲劳寿命性能对比研究[J]. 航空学报, 2016(5): 1536-1543. DOI:10.7527/S1000-6893.2016.0108 |
| [8] |
杨广里, 张常青. 40车轴钢短裂纹单峰过载迟滞效应的研究[J]. 铁道学报, 1994(1): 108-112. DOI:10.3321/j.issn:1001-8360.1994.01.001 |
| [9] |
JONES R E. Fatigue crack growth retardation after single-cycle peak overload in TC4 titanium alloy[J]. Engineering Fracture Mechanics, 1973. |
| [10] |
KALNAUS S, FAN F, JIANG Y, et al. An experimental investigation of fatigue crack growth of stainless steel 304L[J]. International Journal of Fatigue, 2009. |
| [11] |
LEFRANC P, SARRAZIN-BAUDOUX C, DOQUET V, et al. Investigation of the dwell period’s influence on the fatigue crack growth of a titanium alloy[J]. Scripta Materialia, 2009. |
| [12] |
EVANS W J, GOSTELOW C R. The effect of hold time on the fatigue properties of a β-processed titanium alloy[J]. Metallurgical Transactions A, 1979. |
 2020, Vol. 42
2020, Vol. 42
