2. 海军装备部上海局,上海 201206
2. Shanghai Bureau of the Naval Equipment Department, Shanghai 201206, China
2020年初,美国国防部高级研究计划局(DPRPA)发起了“海上列车”项目[1],要求通过物理连接或海上编队等方式实现4艘百吨级无人艇编队航行,研究目标之一是减小航行阻力以提高航程。多船编队航行时,编队内各船因相互作用的影响,有望获得一定减阻效果[2]。实现减阻的原因可能有2个:一是多个船体在不同相对位置和不同航速下,多艘船的兴波可能产生有利干涉而形成减阻,这与多体船“消波减阻”的原理类似[3];二是前方船对来流形成一定的遮挡效应,可一定程度减小后船面临的来流速度。通过数值分析和阻力预报,能够对编队航行船舶的相互位置布局提供一定的指导,从而实现合理的船间布局,达成节能阻力的目的。本文采用基于Dawson法的2阶面源法对4艘Wigley船的不同布局形式进行兴波阻力计算与分析,归纳兴波阻力与各船相互位置的变化规律,分析有利干涉情况,探索多船编组航行减阻的机理。
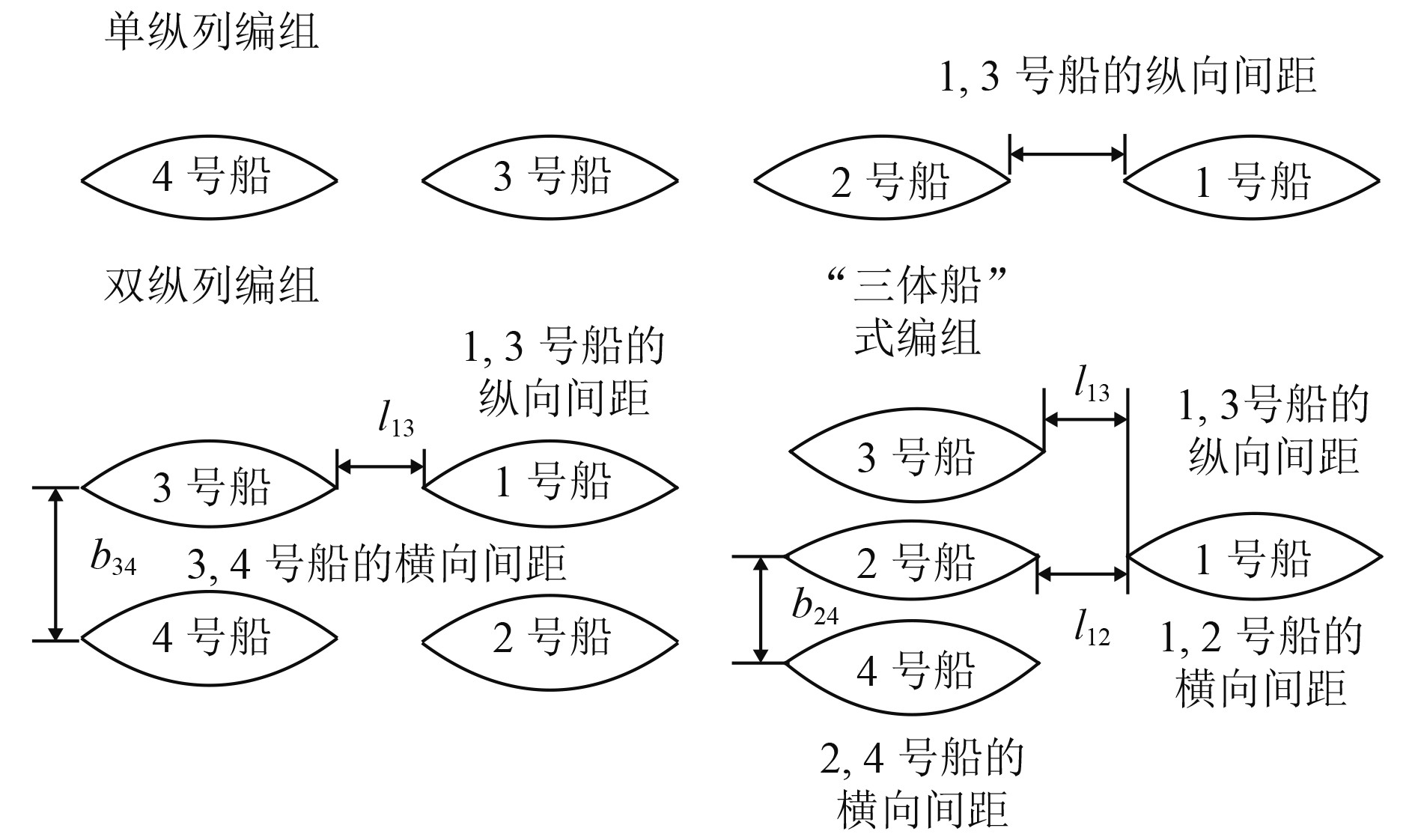
1 计算模型与理论方法 1.1 计算模型为减小船型特征对编组航行阻力特性的影响,更好突出多船编队队形对阻力的影响效果,选用Wigley船作为计算对象,主要参数如表1所示,船型如图1所示。Wigley船作为阻力计算的标准模型之一,广泛用于阻力特性分析和计算方法验证。参考“海上列车”设想,取4艘Wigley船组成编队单元,采取单纵列、双纵列和“三体船”式编组等3类典型编队方式,编队方式及主要队形参数的定义如图2所示。其中,单纵列航行编组方式的参数主要为各船间的纵向间距
|
|
表 1 Wigley主要船型参数 Tab.1 Parameters of the Wigley ship |

|
图 1 Wigley船型示意图 Fig. 1 Ship from of the Wigley ship |
|
图 2 编组航行方式与主要队形参数 Fig. 2 Formations of the ships and its parameters. |
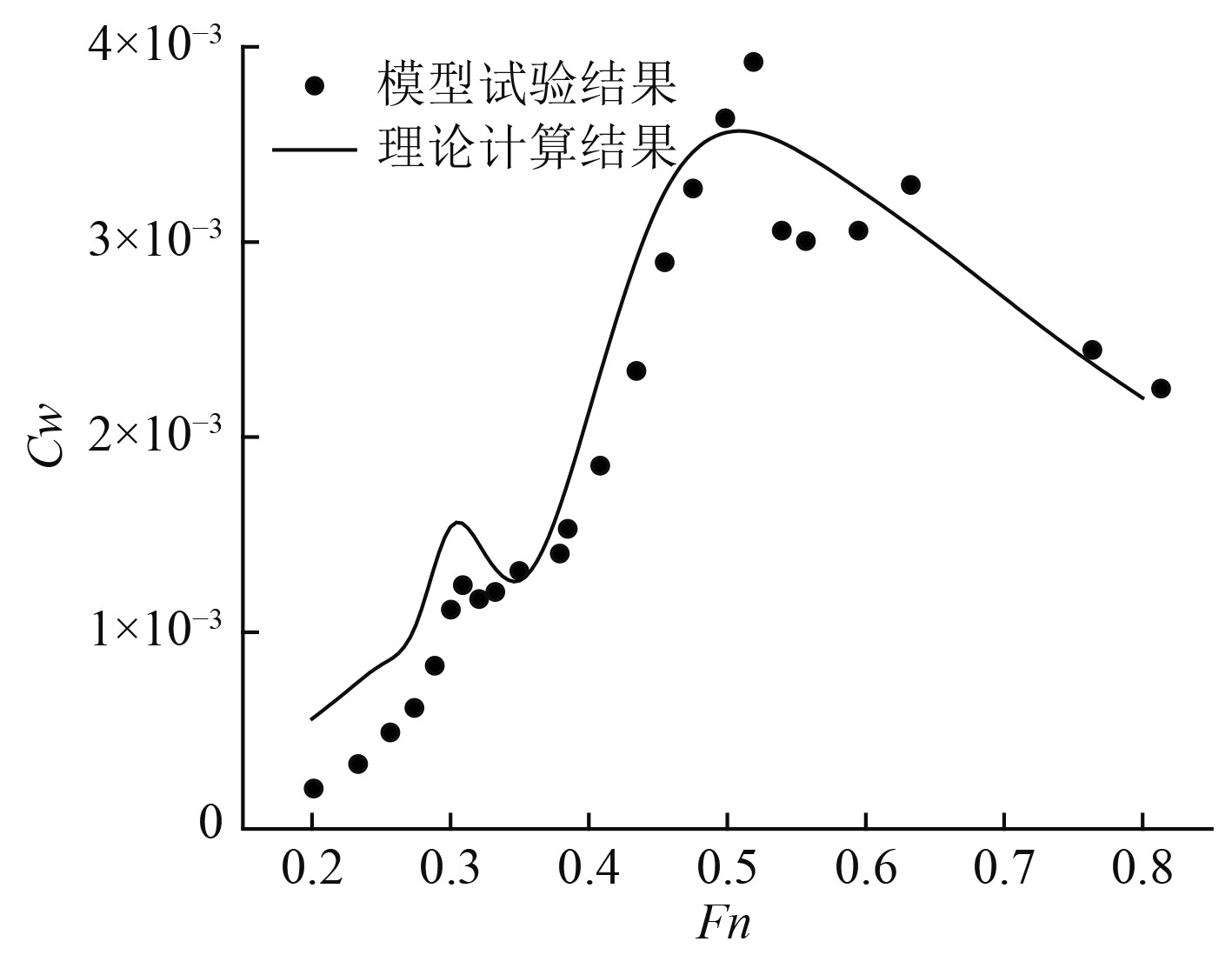
考虑兴波阻力是中高航速下船舶阻力的主要成分,本文主要对兴波阻力系数进行分析。采用基于Dawson法的2阶面源法[4],取线性自由面条件,船体保持浮态固定,船体保持固定的初始纵倾和升沉,不随速度的增大和船体压力分布变化而变化。计算程序以多体船兴波阻力预报程序为基础进行微调,适应更多种不同航行编组队形的要求。采用上述计算程序,对Wigley单船计算结果与模型试验结果[5]进行对比,如图3所示。计算结果与模型试验结果相比,趋势基本吻合,精度可接受。
|
图 3 单船计算结果与模型试验结果对比 Fig. 3 Comparison of the calculation results vs. the model test data |
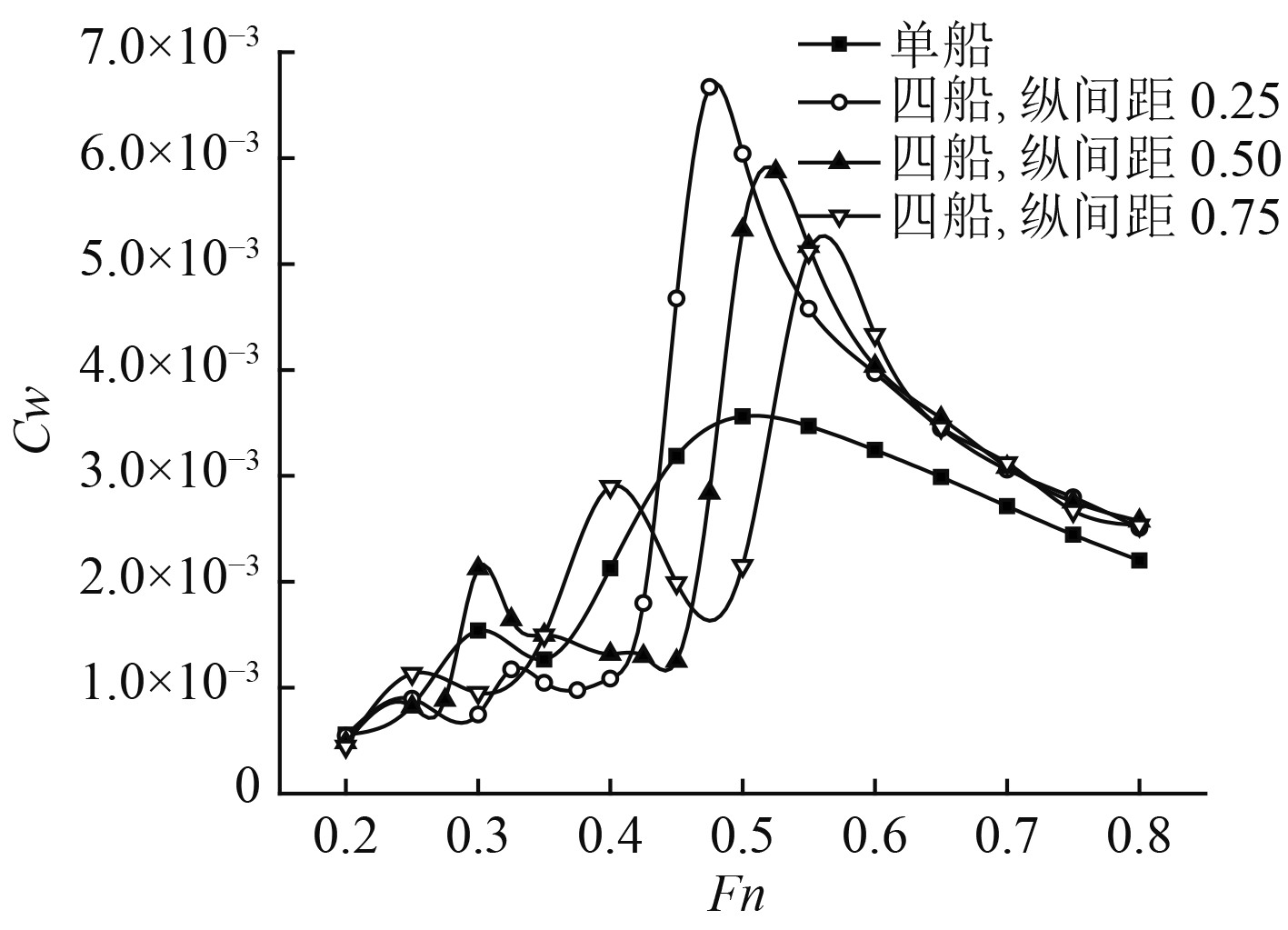
4艘Wigley船排成一列纵队航行,考虑各船纵向间距
|
图 4 四船成单列航行的纵队兴波阻力系数 Fig. 4 Wave-making resistance coefficient of the four Wigley ships in a single column |
由计算结果可知:随着纵向间距增大,

|
图 5 四船成一列纵队航行时的波形图(l12=0.25,Fn=0.475) Fig. 5 Free surface wave height of the single column formation(l12=0.25,Fn=0.475) |

|
图 6 四船成一列纵队航行时的波形图(l12=0.5,Fn=0.45) Fig. 6 Free surface wave height of the single column formation(l12=0.25,Fn=0.475) |
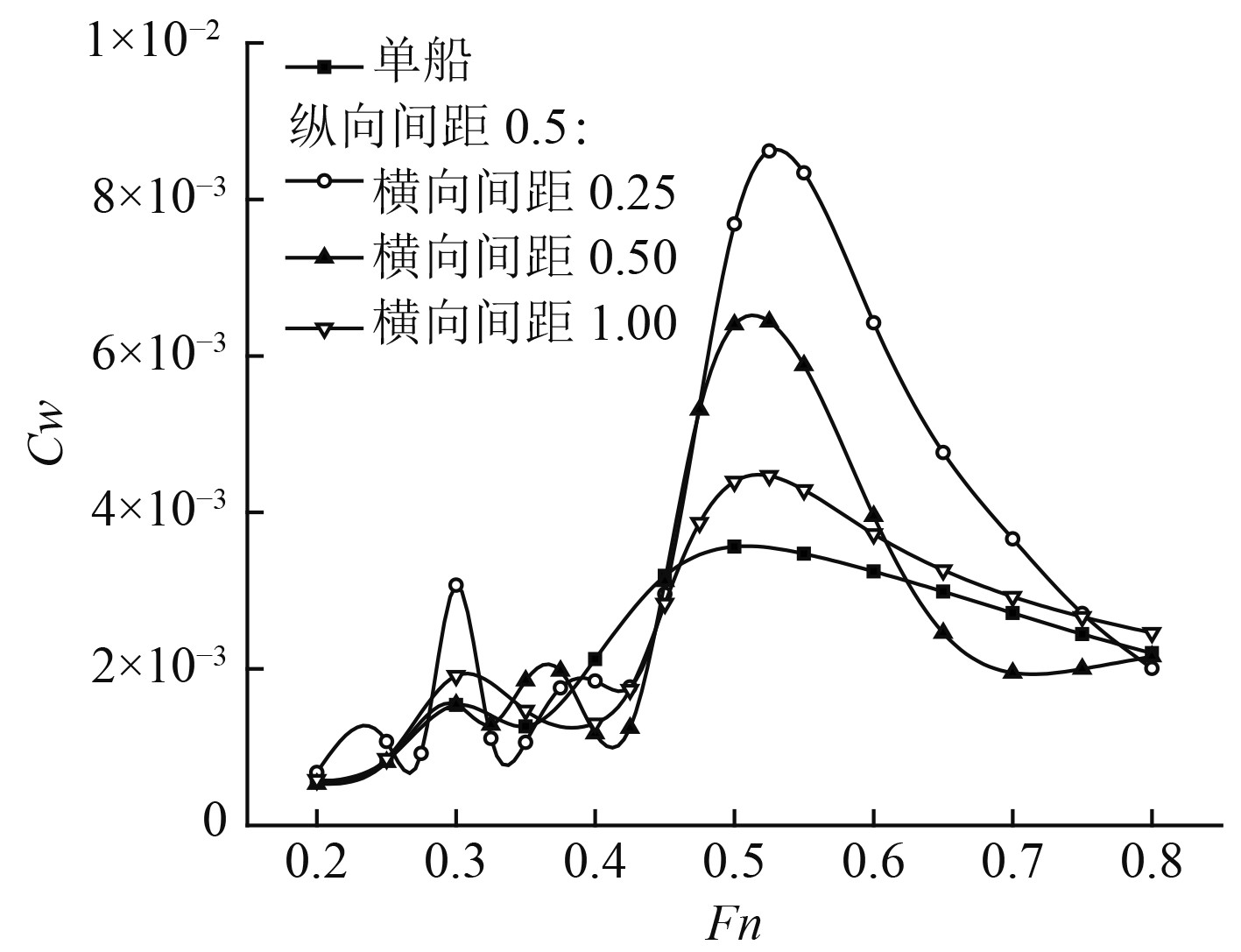
4艘Wigley船排成两列纵队航行,每列为2船,每行2船的船首横向齐平,整体队形呈规则的矩形,
|
图 7 四船成双纵列航行的兴波阻力系数(变横间距) Fig. 7 Wave-making resistance coefficient of the four Wigley ships in double columns (In various transverse gaps) |
|
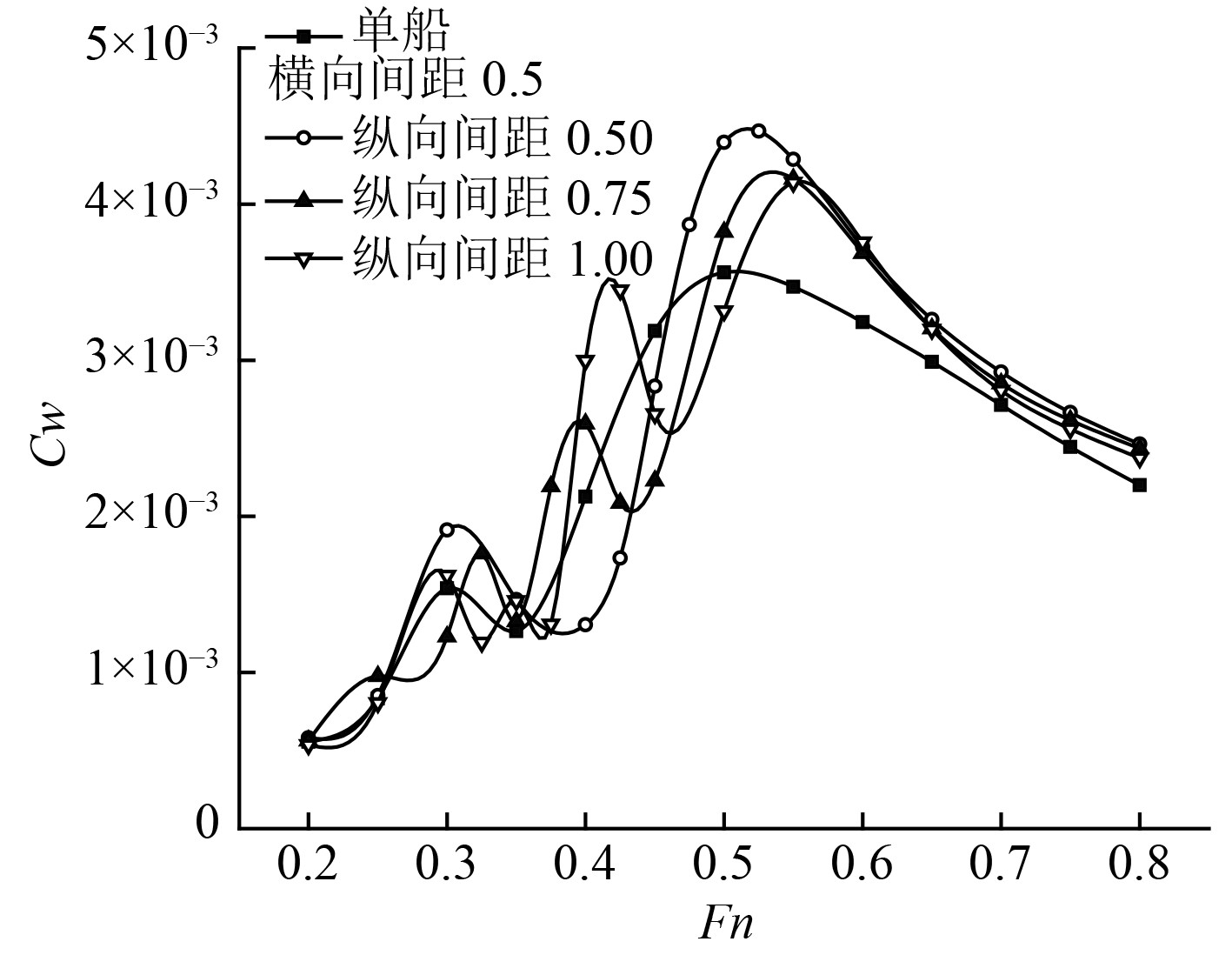
图 8 四船成双纵列航行的兴波阻力系数(变纵间距) Fig. 8 Wave-making resistance coefficient of the four Wigley ships in double columns (In various longitudinal gaps) |
由计算结果可知:对变横间距情况,

|
图 9 四船成两列纵队航行时的波形图(b13=0.25,l34=0.5,Fn=0.5) Fig. 9 Free surface wave height of the double columns formation(b13=0.25,l34=0.5,Fn=0.5). |
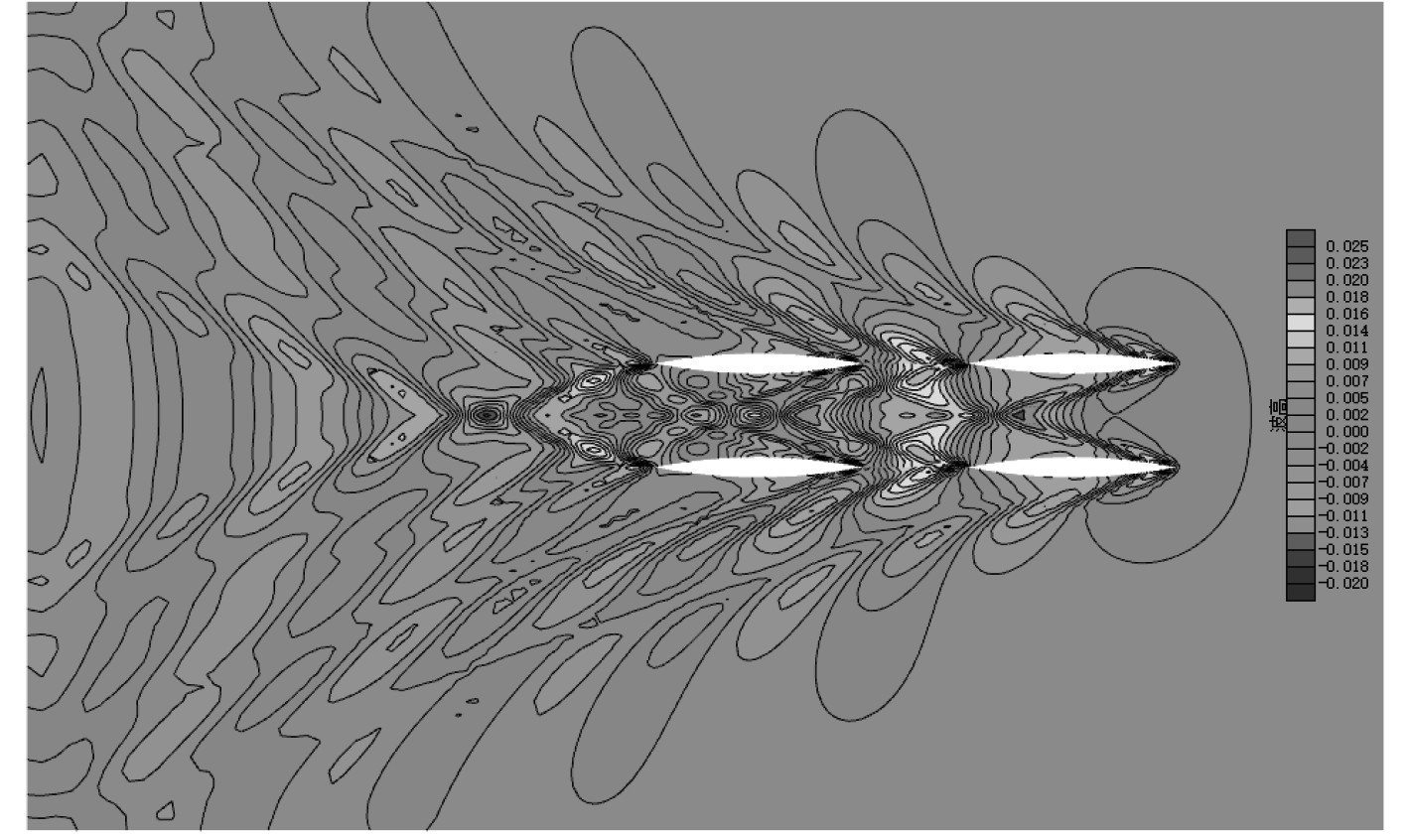
|
图 10 四船成两列纵队航行时的波形图(b13=0.5,l34=0.5,Fn=0.4) Fig. 10 Free surface wave height of the double columns formation(b13=0.5,l34=0.5,Fn=0.4). |
4艘Wigley船排成“三体船”式编队航行,中间2船成一个纵列,前后纵向距离为
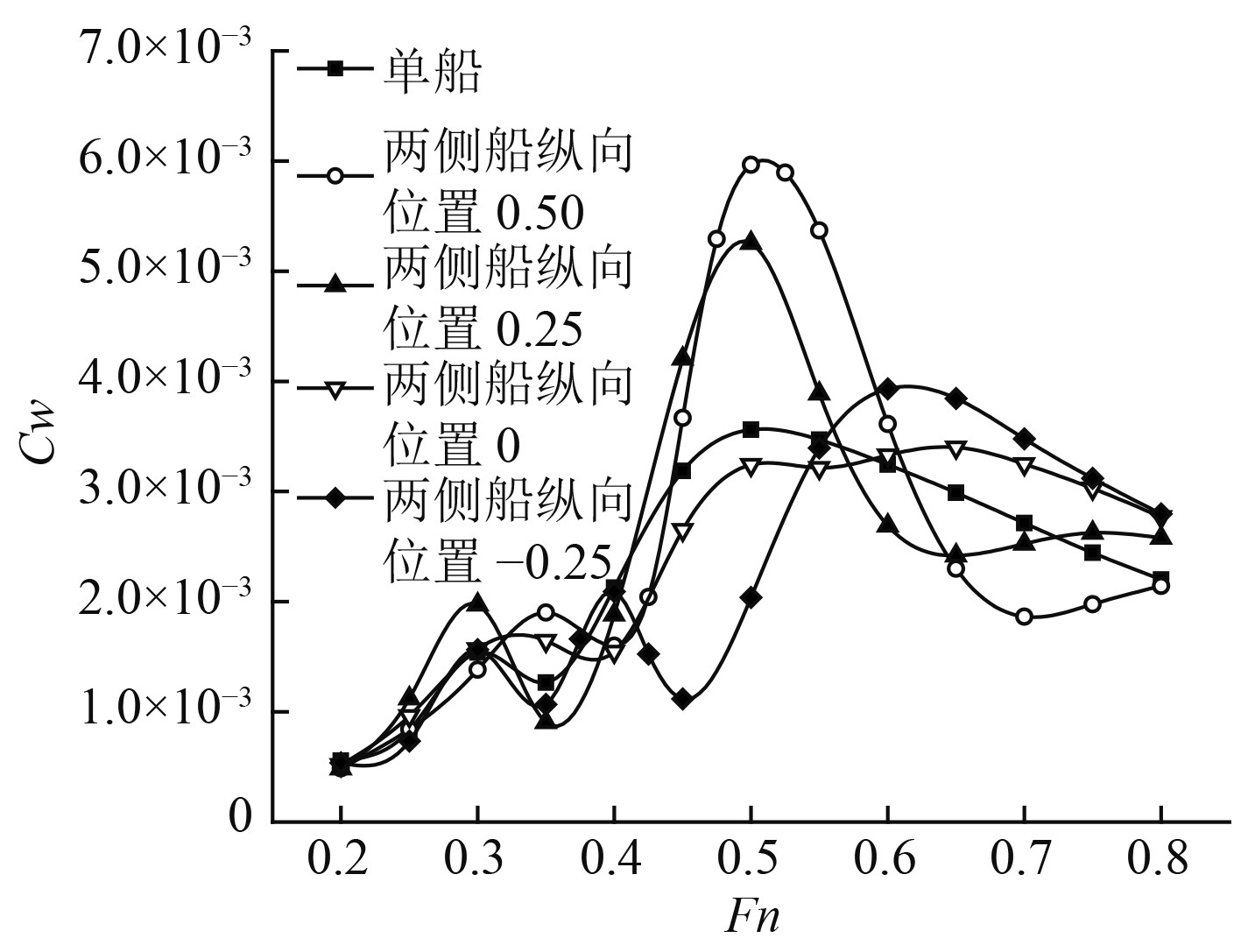
|
图 11 四船成“三体船”队形的兴波阻力系数(中间两船间距不变,变外侧两船纵向位置) Fig. 11 Wave-making resistance coefficient of the four Wigley ships in trimaran type formation (In various transverse gaps) |
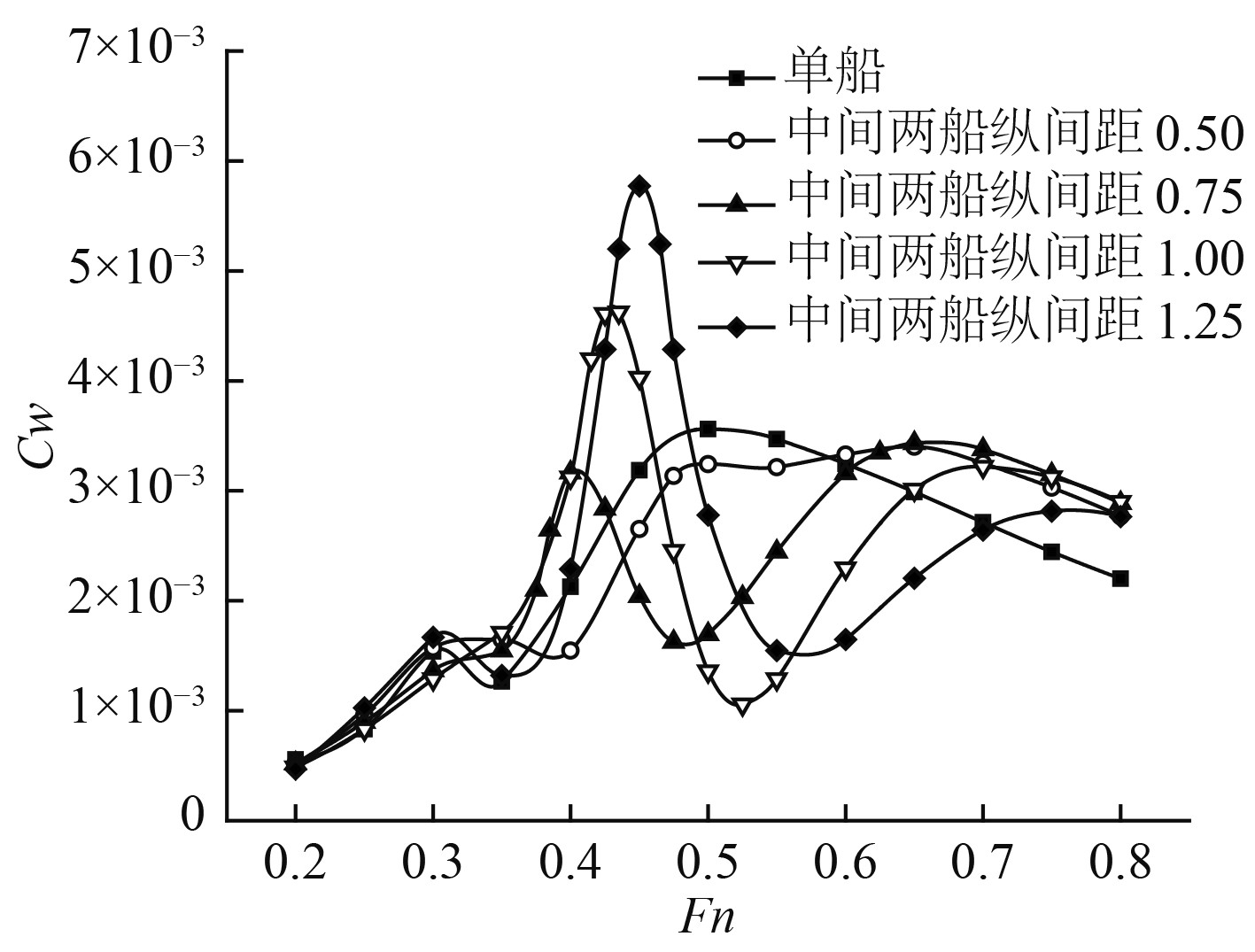
|
图 12 四船成“三体船”队形的兴波阻力系数(外侧两船间距不变,变中间两船纵向距离) Fig. 12 Wave-making resistance coefficient of the four Wigley ships in trimaran type formation (In various longitudinal gaps) |
由计算结果可知:对变外侧两船纵向位置情况,

|
图 13 四船成“三体船”式编队航行时的波形图(b23=0.5,l13=−0.25,Fn=0.45) Fig. 13 Free surface wave height of the trimaran type formation(b23=0.5,l13=−0.25,Fn=0.45) |
|
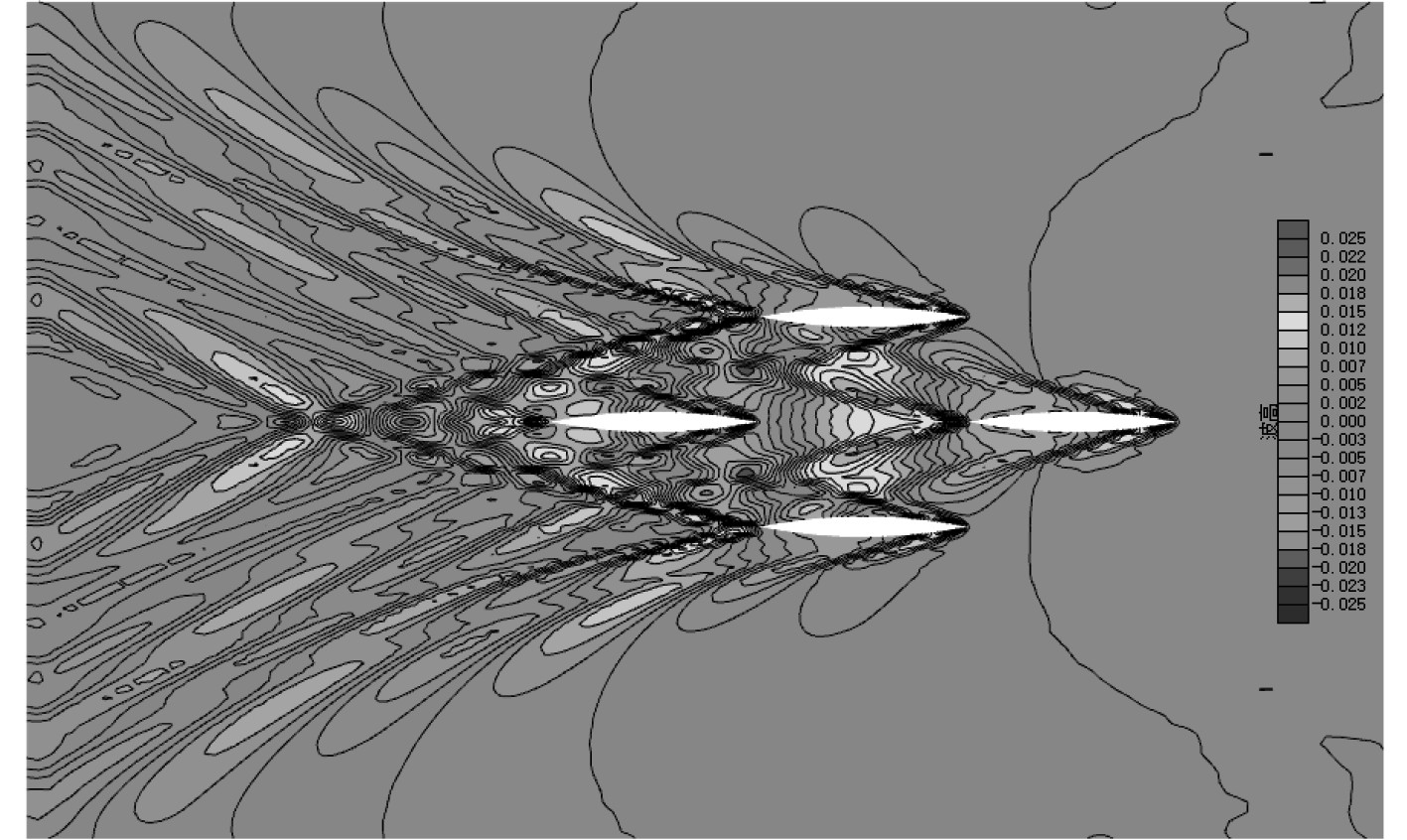
图 14 四船成“三体船”式编队航行时的波形图(b23=0.5,l13=1.00,Fn=0.525) Fig. 14 Free surface wave height of the trimaran type formation(b23=0.5,l13=1.00,Fn=0.525) |
对比4艘Wigley船分别成单列纵队、双列纵队和“三体船”式编队下的兴波阻力系数可知:
1)对单列纵队编队方式,当船与船之间的纵向间距
2)对双列纵队编队方式,当
3)对“三体船”式编队方式,当外侧两船船首纵向位置与1号船船尾平齐或略超前,中纵剖面横向距中间两船中纵剖面距离为0.5倍水线长时,在
综合对3种典型队形的计算分析可知:在
1)本文重点对兴波阻力系数进行了计算分析,未计算形状阻力和摩擦阻力,未计入推进器、附体等影响,也未分析编队4船中各船分别受到的阻力情况,主要结论仍属原理性探讨。为获取更为全面的结论,后续还需对各种阻力成分进行充分的计算研究和试验验证。
2)本文计算中保持船体固定,未计及不同航速下的船体浮态变化,可能影响计算结果的准确性[6]。初步试算表明,不同于多体船阻力计算,多船编组航行计算时,若对各个船体均考虑浮态自由度条件,迭代计算过程可能较为复杂[7],甚至可能难以收敛,后续也需深入研究。
3)本文提出的不同编队形式,对常规船舶来说,编队内各船的横向和纵向间距均相对较小,存在明显碰撞风险,不利于安全航行。而对无人船来说,可通过多船间的协同控制[8]保持编队间距和减阻效果,具有较好应用前景,但后续对风浪条件下的编队控制技术也需开展深入研究。
| [1] |
Tactical Technology Office, DARPA. Sea Train. Broad Agency Announcement. HR001120S0010. 2020.01.
|
| [2] |
张晨亮, 王建华, 万德成. 数值模拟船舶航行时船体间的相互作用[C]. 2015年船舶水动力学学术会议论文集. 中国造船工程学会船舶力学学术委员会, 2015: 491-496. ZhANG Chen-liang, WANG Jian-hua, WAN De-cheng. Computational simulation of the interaction between multiple ships[C]. Conference Proceedings of Ship Hydrodynamics of 2015. Ship Hydrodynamics Committee of China Shipbuilding Engineering Society, 2015: 491-496. |
| [3] |
段晔鑫, 刘源, 王毅, 等. 五体船侧体布局及兴波阻力优化[J]. 舰船科学技术, 2015, 37(3): 10-14. DUAN Ye-xin, LIU Yuan, WANG Yi, e tc. Research on the demihulls layout and wave resistance optimization of pentamaran[J]. Ship Science and Technology, 2015, 37(3): 10-14. DOI:10.3404/j.issn.1672-7649.2015.03.002 |
| [4] |
刘应中. 船舶兴波阻力理论[M]. 北京. 国防工业出版社. 2003.01. P78-107.
|
| [5] |
Insel M. An Investigation into the Resistance Components of High Speed Catamarans[D]. University of Southampton, 1990.
|
| [6] |
董文才, 夏翔, 左文锵, 等. 高速轻型穿浪双体船船型及性能试验研究[J]. 中国造船, 2008, 49(3): 118-126. DONG Wen-cai, XIA Xiang, ZUO Wen-qiang, et al. Experimental study on the form and the performance of high speed and light displacement wave piercing catamaran[J]. Ship Building of China, 2008, 49(3): 118-126. DOI:10.3969/j.issn.1000-4882.2008.03.016 |
| [7] |
许勇, 董文才. 波浪中多船近距离并行航行的水动力干扰研究[J]. 应用数学和力学, 2014, 35(4): 389-400. XU Yong, DONG Wen-cai. Hydrodynamic interactions between multiple ships advancing parallel in close proximity in waves[J]. Applied Mathematics and Mechanics, 2014, 35(4): 389-400. DOI:10.3879/j.issn.1000-0887.2014.04.005 |
| [8] |
况阳, 顾颖闽. 基于几何力学的水面无人艇艇群控制技术[J]. 舰船科学技术, 2019, 41(23): 123-126. DUAN Ye-xin, LIU Yuan, WANG Yi, et al. Control technology of USV group base on geometry mechanics[J]. Ship Science and Technology, 2019, 41(23): 123-126. |
 2020, Vol. 42
2020, Vol. 42
