近年来,人类在生存、发展及国家安全方面对海洋需求的日益增加,专业性极强的海洋工程作业平台不断涌现,颇具代表性的平台有:铺缆船,用于海底光缆(军用/民用)铺设和维护检修;打捞船,用于失事船舶、人员的打捞、救援;海上发射平台,用于导弹、运载火箭发射;海洋石油钻井平台,用于石油开采;科考船,用于海洋资源、地质勘探等。这类船舶需实现定点作业或者跟随预设航迹作业,为此动力定位(DP)系统应运而生。船舶DP系统主要功能是在船舶受到外界风浪流影响作用下,由控制模块生成控制指令,控制动力系统产生相应推力来实现船舶定点控位和航迹跟踪[1-3]。系统由测量系统、控制系统、电力推进系统和舵桨装置组成,其中控制系统最为核心,负责系统模型计算、控制策略选择、传感器数据融合等任务,而船舶DP系统是复杂的非线性系统,具有干扰不确定性、模型参数不确定性、状态变量测量噪声、执行机构受限等特点,因此其控制策略设计及应用研究是当今控制理论与应用领域的重要方向之一。
2011年Sorensen从DP系统数学模型、观测器控制器、推力分配等方面较系统地分析总结了近30年来用于DP控制系统的控制技术的发展情况[1]。近十年来,先进控制技术在DP控制系统设计领域取得较多成果,本文围绕DP系统核心控制策略,概括总结船舶DP系统的控制策略最新发展情况,并分析各种控制策略存在的优缺点,结合船舶DP系统的使命任务多样化,重点提出了DP系统控制策略的发展目标,以及下一步重点研究方向。
1 动力定位系统控制模型DP系统经典控制模型为Fossen提出的六自由度模型[4]:
| $\left\{\begin{aligned} & {{\dot{ \eta }} = R(\psi ){{\upsilon }}}{\text{,}} \\ & M{\dot{ \upsilon }} + {C_{RB}}({{\upsilon }}){{\upsilon }} + {C_A}({{{\upsilon }}_r}){{{\upsilon }}_r} + D({{{\upsilon }}_r}) + G({{\eta }}) = \\ & \quad \quad {\tau _{wind}} + {\tau _{wave2}} + {\tau _{moor}} + {\tau _{ice}} + {\tau _{thr}}{\text{。}} \end{aligned} \right.$ |
其中:
| $\left\{ {\begin{aligned} & {{\dot{\bf \eta }} = R(\psi ){\bf{\upsilon }}}{\text{,}} \\ & {M{\dot{\bf \upsilon }} = - D{\bf{\upsilon }} + \tau + \Delta (t)} {\text{。}} \end{aligned}} \right.$ |
其中:
DP控制策略经历了从经典的由低通滤波和PID控制结合的第1代过渡到以Kalman滤波和最优控制结合的第2代DP控制策略,并逐渐发展为以智能控制技术为基础的第3代DP控制策略。
2.1 基于PID算法的DP控制策略PID原理简单,易于工程应用,且鲁棒性强,适用于环境恶劣的工业控制过程,常用DP控制策略表达式为:
| $u(t) = {K_p}[e(t) + {1 / {{T_i}}}\int_0^t {e(t){\rm{d}}t} + {{{T_d}{\rm{d}}e(t)} / {{\rm{d}}t}}]{\text{。}}$ |
其中
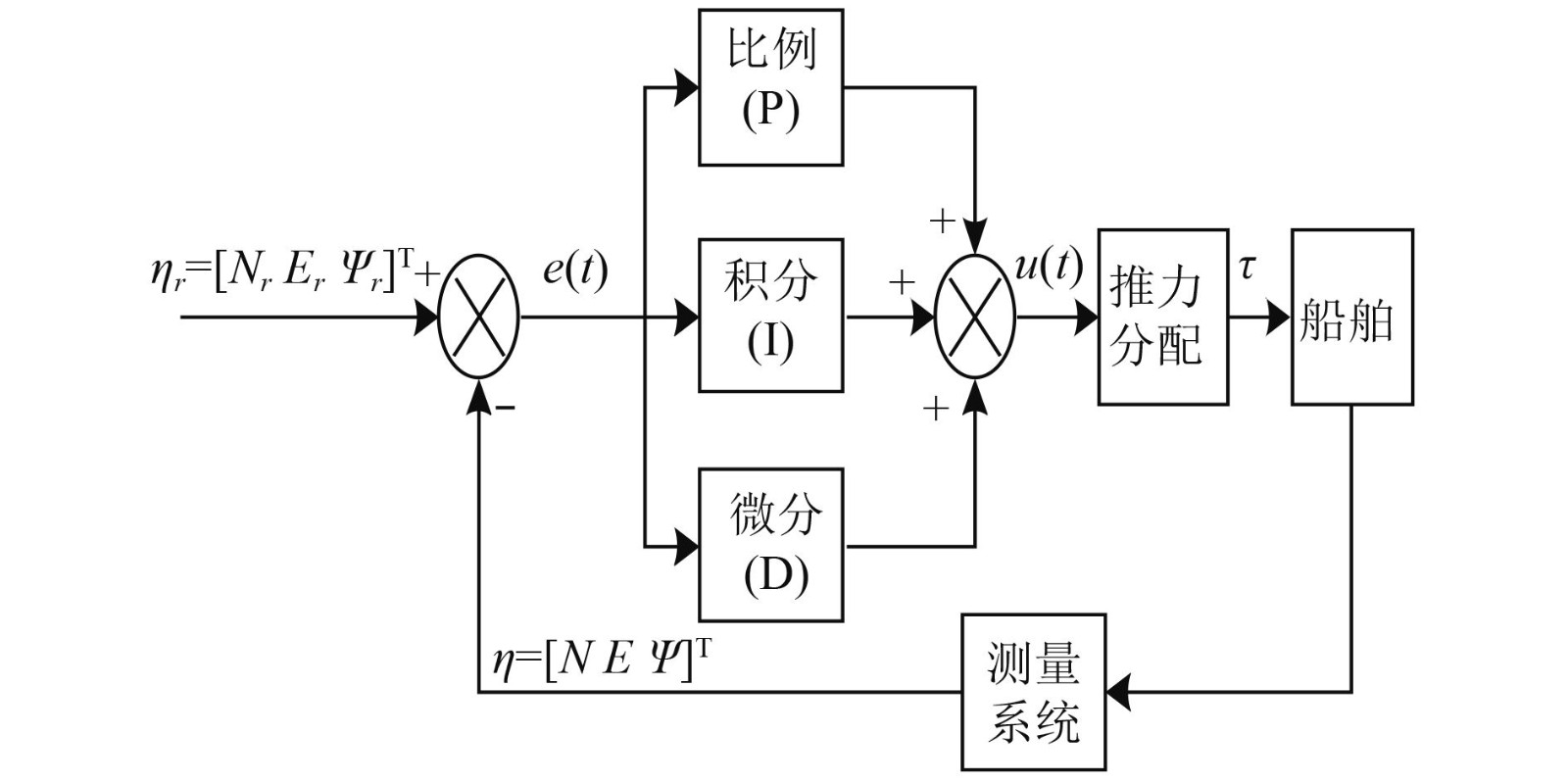
|
图 1 动力定位PID控制策略原理图 Fig. 1 The Schematic diagram of PID control strategy for dynamic positioning model |
考虑船舶存在对定位时间要求不高且控制过程中有异常外力影响系统的情况,Svenn[7]设计了一种基于PID的混合控制方法,当误差较大时,控制器中积分部分采用大数值作为调节参数,当接近期望值时,控制器切换为常规PID进行调节。直翼推进器响应速度足够高,可以保证定位的高精度、实时性,Philipp[8]针对配置直翼推进器的DP船舶设计PID控制器,并通过试验进行验证。作为未来船舶作业重点考虑的条件之一,极限海况的研究成果较少,Ole[9]将PID和滑模变结构策略设计的2种DP控制器进行了分析对比,结果表明基于滑模变结构的DP控制器在极限海况下更加有效。当船舶建模时考虑外界干扰频率差别如高频波浪力和低频海流漂移力,以及不同干扰的频率特性差异如风、冰载荷情况,传统PID控制将无法满足要求。为此,Awantha[10]提出一种基于小波多分辨率的PID控制策略,通过离散小波变化方法将位置误差和艏向误差分解成不同频率的组成部分,对各个部分分别设计PID控制器。为提高在环境干扰力影响下的船舶DP系统的精确性和稳定性,孙蓓蓓[11]建立了以动力模型和环境干扰模型为基础的动力定位数学模型,基于此提出模糊PID控制模型,并通过仿真进行分析验证。
由于PID控制策略只能针对线性系统,同时要求模型精确已知,因此,当被控系统为模型参数未知的线性系统,以及控制精度要求高的非线性系统,该方法将不再适用。
2.2 基于模糊/神经网络自适应算法的DP控制策略模糊逻辑系统(Fuzzy Logic Systems,FLS)与神经网络(Neural Network,NN)由于其特有的万能逼近特性,为解决复杂系统模型不确定性问题开辟了新的途径。将FLS或者NN的万能逼近特性与自适应控制方法的在线学习能力结合起来,可以保证被控系统在外界环境或系统本身发生变化情况下仍具有良好的控制性能[11-12]。船舶在航行作业过程中,受波浪、海流等外力作用影响船体会产生变形,事实上船舶DP控制系统为极其复杂的非线性模型,要实现高精度的动力定位能力,需要建立精确的数学模型,但是通常情况下船舶DP系统的精确数学模型却很难建立,因此,基于FLS/NN自适应控制策略为DP系统存在的上述问题提供了解决思路。以文献[6]为例,控制策略表达式为:
| $u(t) = - {R^{\rm{T}}}(\psi ){Z_1} - {K_2}{Z_2} + {{\bf{\theta }}^{\rm{T}}}\xi ({\bf{\bar x}}){\text{。}}$ |
其中:
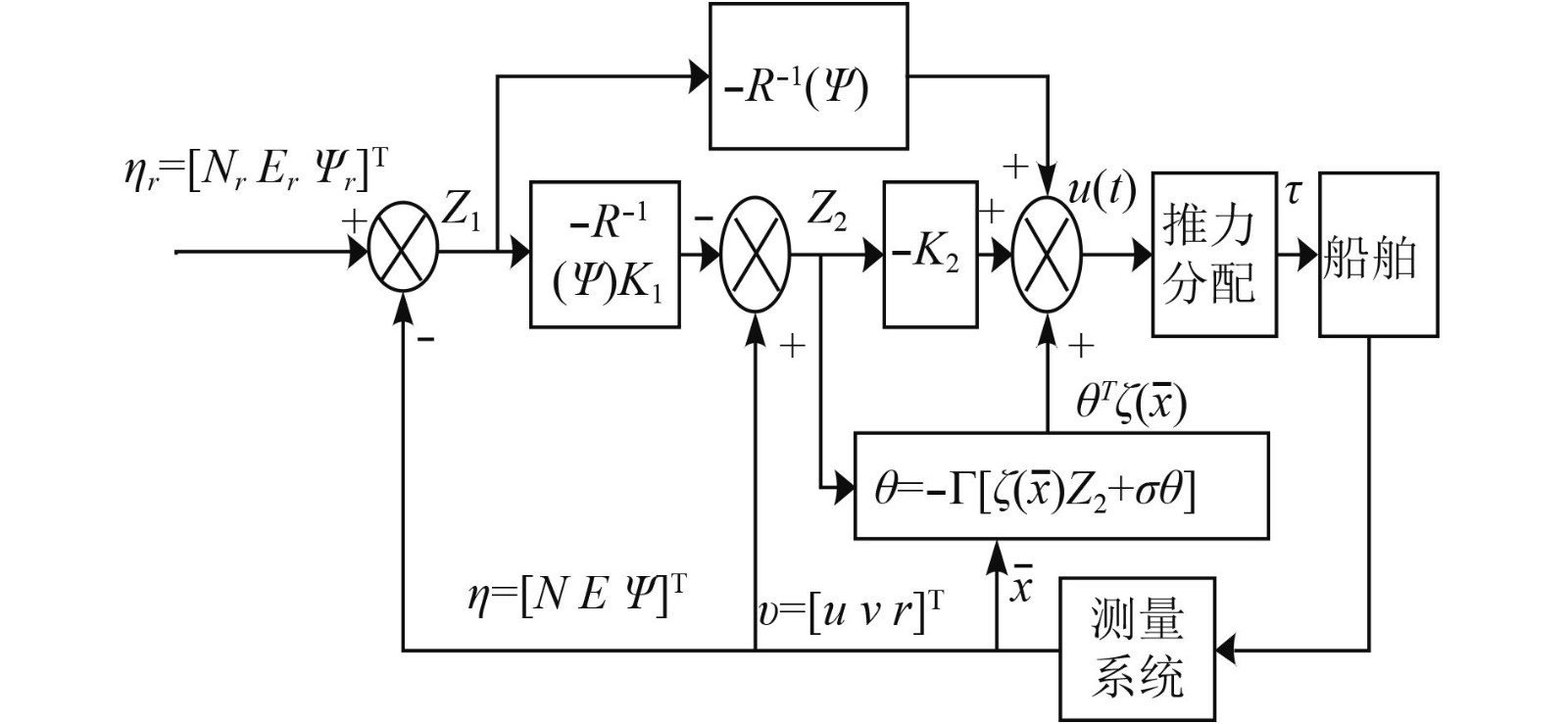
|
图 2 动力定位模糊自适应控制策略原理图 Fig. 2 The Schematic diagram of fuzzy adaptive control strategy for dynamic positioning model |
国内杜佳璐教授团队采用FLS/NN自适应控制方法,取得较多研究成果。文献[5]中针对存在外界干扰未知、参数不确定的系统提出鲁棒NN自适应控制器设计方法,通过Lyapunov稳定性理论证明了被控系统可跟踪给定的期望位置、首向,跟踪误差收敛,可满足DP系统控制精度要求,同时保证了所有自适应参数均有界。文献[14-15]分别考虑了实际工程中存在的控制输入饱和控制输入约束的情况,主要思路是先对控制输入数学模型进行合理的假设简化,再对模型不确定性和参数未知的被控系统设计控制器。上述成果中所提出的控制策略均通过了Lyapunov稳定性证明和仿真验证,然而在设计控制器时需假设系统所有状态变量是可测的,而实际情况却刚好相反,系统状态变量无法通过传感器进行测量。文献[16-17]针对这种制约条件,通过构造高增益状态观测器,设计了基于FLS/NN自适应的输出反馈控制器,理论证明和仿真试验证明方法的正确性和有效性。
基于FLS/NN自适应控制系统设计方法有如下优点:不需要建立系统精确地数学模型;对于未知干扰情况可通过构造干扰观测器解决。该方法虽然优点多,但目前尚无应用成果,主要原因在于:1)基于万能逼近器的自适应控制方法本身工程应用不成熟,船舶DP控制系统相对比较复杂,配置有特殊作业系统的船舶平台造价昂贵,应首选成熟可靠的控制方法;2)模型逼近过程需要根据反馈误差不断的调节参数,表现出控制量的不断调节,这与动力定位控制系统的绿色节能控制、推进器保护相冲突;3)在以往研究中,通常假设输出变量完全可测的,而实际中位置、首向变量测量值会存在随机干扰,即需要用先进的滤波算法如EKF,UKF等进行处理。
2.3 基于模型预测算法的DP控制策略模型预测控制(Model predictive control,MPC)又称为滚动时域控制,优化控制流程为:1)获取当前时刻系统状态测量值;2)求解一个优化控制问题得到预测控制时域控制率;3)将第1个控制量作为系统输入;4)下一时刻回到第1步。MPC优点在于控制输入变量可保证系统在预测控制时域内由跟踪误差等构成性能函数取得最优值,并且能够有效地处理复杂系统的约束问题,实现复杂目标控制,因此,MPC成功地应用于船舶DP控制系统[18-21],基本原理框图如图3所示。
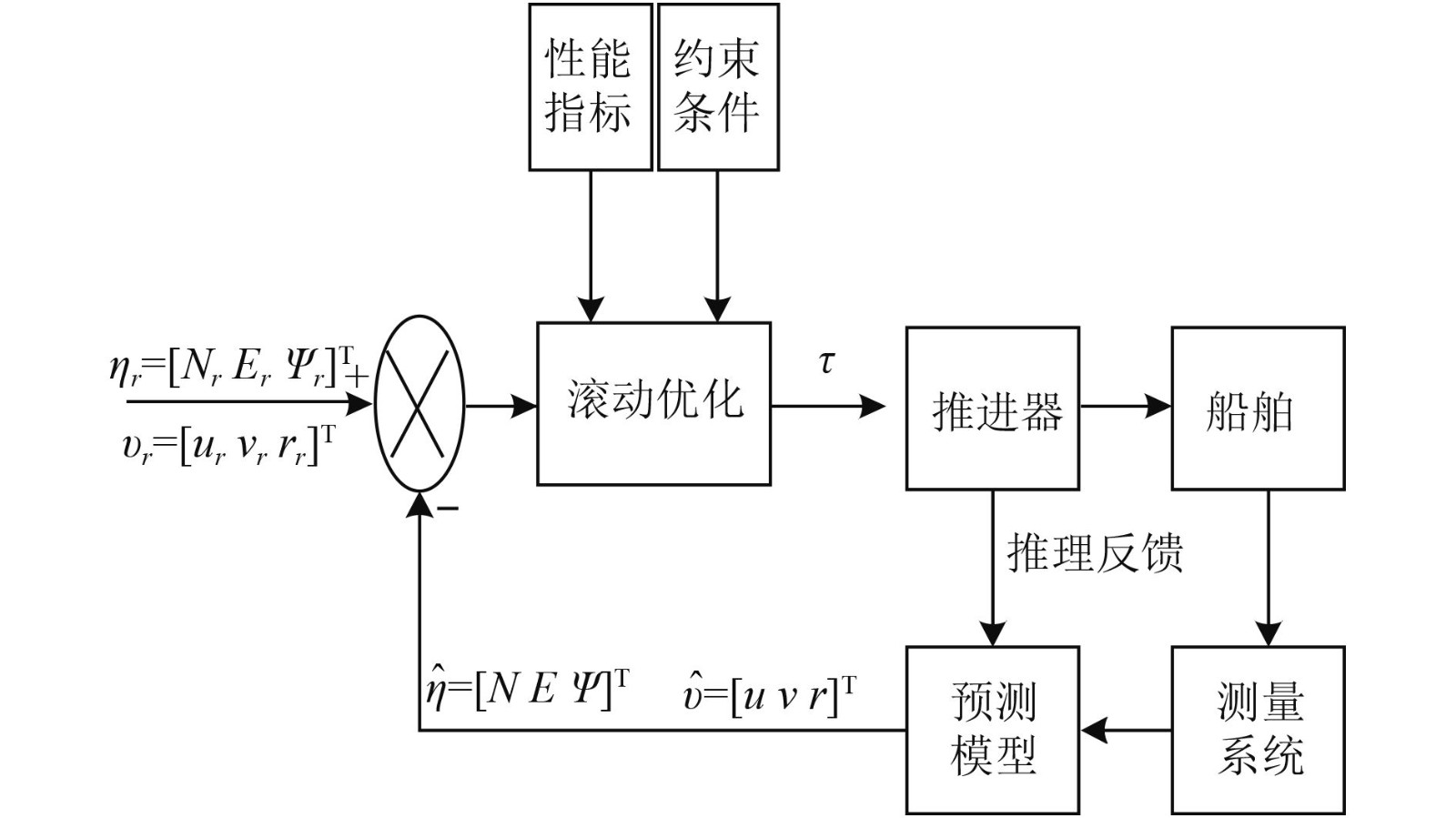
|
图 3 动力定位模型预测控制策略原理图 Fig. 3 The Schematic diagram of predictive control strategy for dynamic positioning model |
性能指标函数通常选用如下形式:
| $\begin{aligned} J =\; & \frac{1}{2}\int_0^T {\{ {\mu _1}{{[\eta (t + \tau ) - {\eta _r}(t + \tau )]}^{\rm{T}}}[\eta (t + \tau ) - {\eta _r}(t + \tau )]}+ \\ & {\mu _2}\Delta {u^{\rm{T}}}(t + \tau )\Delta u(t + \tau ){\rm{d}}\tau{\text{。}} \end{aligned} $ |
Margarita[22]研究了存在控制输入受限和外界干扰情况的DP预测控制系统设计方法,该方法包括非线性预测控制部分和线性控制部分,在临近期望值时通过设置切换函数实现2个阶段的自由切换,最终理论和仿真验证了策略的有效性。梁海志等[23]采用模型预测控制,将虚拟控制力直接由推力器推力显示表达,将性能指标中的控制力指标等效为推进器的能量消耗,并充分考虑了推进器物理性能和推力损失(桨-桨干扰等),同步实现了推力计算和推力分配。刘菊[24]针对实际动力定位控制系统设计工作复杂,作业时不能自定义修改最大导引速度的问题,提出一种基于模型预测控制的船舶动力定位导引控制系统。通过直接处理定位点之间的导引控制,保证控制系统不必要进行导引子系统设计,引入EKF滤波进行状态估计,保证了DP系统的控制精度。文献[25]详细分析了DP控制系统的整个工作流程,提出的预测控制策略的优点在于将推力分配模型引入系统控制模型,基于此建立的性能指标函数引入如推进器的转向角速度等因素,可更全面地评估控制策略,通过船模试验证明了控制策略的有效性。
2.4 基于容错控制算法的DP控制策略通常水面DP船舶推进系统配置2个全回转主推器和3个侧推器,钻井平台等则配置4个全回转主推器甚至更多。用于测量船舶位置、外界风浪力的传感器也根据DP等级进行冗余配置。这种设计上的冗余考虑可以保证船舶平台在单个或某几个执行器/传感器故障时船舶仍具备一定的DP能力,属于硬件冗余。而容错控制是在系统发生故障时可真正提高系统安全性和可靠性的另一种有效途径,属于软件冗余。目前船舶动力定位系统容错控制主要是针对推进系统及传感器故障情况进行DP控制系统设计研究[26-31]。宁继鹏[27]设计了基于虚拟传感器的控制重构方法,解决了几类传感器故障的船舶动力定位问题。文献[30]针对系统存在推进器故障发生和外部有界扰动情况,建立包含推进器失效、卡死、中断3种故障情形的模型,设计了一种不依赖故障检测模块和故障信息上下界的自适应滑模控制器。文献[31]针对过驱动近海供应船设计了基于故障容错鲁棒控制的动力定位系统,并与传统PID控制方法进行了对比。
动力定位船舶容错控制是十分复杂的课题,虽然针对推进器、传感器故障的容错控制取得了不少成绩,但是船舶自主容错控制方法并不完善,仍需进一步开展研究。
2.5 其他控制策略滑模变结构控制对含有不确定扰动和未建模动态的非线性系统具有鲁棒性强的特点,可以用来解决船舶DP所受的未知外界环境力的问题[9,32-35],但是滑模控制最大缺陷在于实现精确控制必然会引入输入震颤问题,而这将大大缩短推进系统使用寿命,因此解决这一矛盾需开展深入研究。
此外,传感器测量技术的发展,众多学者采用扩展卡尔曼滤波(EKF)[24]、无迹卡尔曼滤波(UKF)[10, 36-37]、容积卡尔曼滤波(CKF)[38-39]、粒子滤波(PF)等对状态变量测量值进行滤波处理,然后将滤波后的状态变量作为DP系统状态输入,这种方法可以保证DP控制系统具有精确的系统状态变量。近些年来,滤波算法取得较多研究成果,但应用于船舶DP系统产品的只有EKF算法,如何将先进的非线性滤波算法应用于船舶DP系统仍需进行长期研究。
3 船舶DP控制策略研究方向船舶DP控制系统未来研究方向可概括为两类:一类是从控制理论方法本身发展和创新;另一类是从满足新的需求方面研究,如水下平台、解决复杂环境(如极限海况、冰区)和高控制要求(如精度、响应时间)等问题。
3.1 模糊自适应控制策略模糊自适应控制方法由于对系统模型精确性要求不高,其万能逼近特性可以解决船舶运动控制模型难建立、任务过程中船舶状态变化导致模型的改变、未知外界环境力等问题。然而现今动力定位工程应用中尚无此控制方法,因此,基于模糊自适应控制策略的DP控制系统应首先实现工程应用,然后再解决控制输入受限、饱和等复杂问题。此外,如何在模糊自适应DP控制策略中解决传感器存在的量测噪声问题,也需要进一步研究。
3.2 模型预测控制策略基于预测控制策略的DP系统已成功应用于各类船舶,但目前所有DP系统船舶都对海况有严格要求,这主要受制于船舶排水量、推进器功率、船体型线、响应时间等因素。文献[9]表明基于PID控制和滑模变节构控制的动力定位控制系统均能满足极限海况条件,预测控制策略能否应用于极限海况仍需开展试验以及实船验证。预测控制核心在于滚动优化,保证每一步控制输出为最优,这不可避免地导致DP系统的调节时间变长,如何更加快速地完成动力定位,需开展更深入的研究工作。
3.3 水下平台DP控制策略当前DP系统主要针对水面船舶设计,控制对象为船舶的位置、首向或航迹,而对于水下无人潜器、潜艇尚无动力定位产品。事实上随着海洋作业的多样化发展,水下平台同样存在动力定位需求。如水下潜器从事某种特殊定点作业,潜艇悬停等,要实现水下动力定位,控制对象至少包括水深、纵倾和横倾。由此可见,水下平台动力定位控制比水面平台更加复杂,开展对水下平台的DP控制策略相关研究工作无论从理论方面还是从工程应用方面都将意义深远。
3.4 多DP船舶协同控制策略随着水面船舶DP技术迅速发展成熟,单艘船舶作业能力限制的问题越来越突出,而多艘DP船舶相互协调作业则具有更大的优势,可大幅提高作业的效率,具有容错性强和适应性强等优点[40-42]。如航行补给、资源勘探、移动式海上基地和破冰船护航等,往往需要多艘船舶相互协调才能共同完成任务。国内外目前已有较多学者进行过研究,但实际应用却很少,协调编队控制仍将是值得研究的方向。
4 结 语随着人类对海洋探索的不断深入,现有DP控制策略将无法满足使用需求。提升DP系统能力,首先要求测量系统提供更加精确位置、首向、风速风向、海浪等信息;其次要求推进系统配置更大功率的推进装置,同时电推系统的响应时间也需尽可能短。但是当前提升传感器设备的测量精度太难,而执行机构响应时间由桨叶加速过程、电气元件信号传递等物理因素决定,缩短响应时间几乎不可能,因此对DP系统的控制策略继续进行深入研究,是行之有效的方法。本文通过对近几年DP控制策略的研究情况进行梳理,分析了DP控制策略的发展方向,为今后DP系统研究工作提供思路。
| [1] |
SORENSEN A. J. A survey of dynamic positioning control systems[J]. Annual Reviews in Control, 2011, 35(1): 123-136. DOI:10.1016/j.arcontrol.2011.03.008 |
| [2] |
赵志高, 杨建民, 王磊, 等. 动力定位系统发展状况及研究方法[J]. 海洋工程, 2002, 2(1): 91-97. DOI:10.3969/j.issn.1005-9865.2002.01.017 |
| [3] |
吴德烽, 杨国豪. 船舶动力定位关键技术研究综述[J]. 舰船科学技术, 2014, 36(7): 1-6. DOI:10.3404/j.issn.1672-7649.2014.07.001 |
| [4] |
FOSSENT. I.. Marine control systems guidance, navigation and control of ships, rigs and underwater vehicles[M]. Trondheim, Norway, Marine Cyernetics AS, 2002.
|
| [5] |
DU Jialu, YANG Yang. A robust adaptive neural networks controller for maritime dynamic positioning system[J]. Neurocomputing, 110 (2013): 128–136.
|
| [6] |
HU Xin, DU Jialu, SHI Jiwei. Adaptive fuzzy controller design for dynamic positioning system of vessels[J]. Applied Ocean Research, 53 (2015): 46–53.
|
| [7] |
SVENN A. T., ROGER S.. Hybrid control to improve transient response of integral action in dynamic positioning of marine vessels[C]. IFAC-PapersOnLine 48–16 (2015) 166–171.
|
| [8] |
PHILIPP K., CHARLOTTE S., ADEL H., et al. Dynamic positioning with active roll reduction using voith schneider propeller[C]. IFAC-PapersOnLine 48-16 (2015) 178–183.
|
| [9] |
OLE M. R. R., ASTRID H. B., MORTEN B.. Comparing controllers for dynamic positioning of ships in extreme seas[C]. IFAC-PapersOnLine 49-23 (2016) 258–264.
|
| [10] |
AWANTHA J., SALIM A., SYED I.. Wavelet-based controller design for dynamic positioning of vessels[C]. IFAC paper, 2017.
|
| [11] |
孙蓓蓓. 动态不确定海况下的船舶动力定位控制算法. 舰船科学技术[J], 2016, 38(2A).
|
| [12] |
WANG. L. X.. Stable adaptive fuzzy control of nonlinear systems[J]. IEEE Transactions on Fuzzy System, 1993, 1(2): 146-155. DOI:10.1109/91.227383 |
| [13] |
ZHANG, T., GE, S. S. HANG, C. C.. Adaptive neural network control for strict-feedback nonlinear systems using backstepping design[J]. Automatica, 2000, 36(12): 1835-1846. DOI:10.1016/S0005-1098(00)00116-3 |
| [14] |
DU Jialu, HU Xin. Robust dynamic positioning of ships with disturbances under input Saturation[J]. Automatica, 2016, 73: 207-214. DOI:10.1016/j.automatica.2016.06.020 |
| [15] |
HU Xin, DU Jialu. Robust adaptive NN control of dynamically positioned vessels under input constraints[J]. Neurocomputing, 2018, 14: 1-12. |
| [16] |
LIN Xiaogong, NIE Jun, JIAO Yuzhao, et al.. Nonlinear adaptive fuzzy output- feedback controller design for dynamic positioning system of ships[J]. Ocean Engineering, 2018, 158: 186-195. DOI:10.1016/j.oceaneng.2018.03.086 |
| [17] |
DU Jialu, HU Xin. Adaptive robust output feedback control for a marine dynamic positioning system based on a high-gain observer[J]. IEEE Transactions on Neural Networks and Learning Systems, 2015, 1-12. |
| [18] |
王元慧, 施小成, 边信黔. 基于模型预测控制的船舶动力定位约束控制[J]. 船海工程, 2007, 29(3): 22-25. |
| [19] |
ÅSMUND V. F.. Dynamic positioning by nonlinear model predictive control[D]. Norwegian University of Science and Technology, 2008.
|
| [20] |
熊卫卫. 基于模糊预测控制的船舶动力定位系统控制器研究[D]. 镇江: 江苏科技大学, 2012.
|
| [21] |
王刚. 船舶动力定位系统模型预测控制研究[D]. 大连: 大连海事大学, 2016.
|
| [22] |
MARGARITA V. S., EVGENY I. V.. Dynamic positioning based on nonlinear MPC[C]. 9th IFAC Conference on Control Applications in Marine Systems, Osaka, Japan, September 2013: 17–20.
|
| [23] |
梁海志, 李芦钰, 欧进萍. 基于模型预测控制的动力定位过驱动控制设计[J]. 哈尔滨工程大学学报, 2014, 35(6): 701-706. |
| [24] |
刘菊, 熊晓东, 汪大鹏, 等. 基于EKF的船舶模型预测动力定位导引控制器设计[J]. 造船技术, 2016, 2: 18-23. DOI:10.3969/j.issn.1000-3878.2016.02.004 |
| [25] |
ALEKSANDER V., TOR A. J.. Dynamic positioning with model predictive control[J]. IEEE Transactions on Control Systems Technology, 2016, 1-14. |
| [26] |
胡明佳. 执行器故障的船舶动力定位系统容错控制[D]. 大连: 大连海事大学, 2016.
|
| [27] |
宁继鹏. 船舶动力定位容错控制方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2013.
|
| [28] |
张赞. 船舶动力定位测量系统智能故障诊断方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2017.
|
| [29] |
李鸣阳. 动力定位船推进器故障容错控制方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2018.
|
| [30] |
郝立颖, 韩金城, 郭戈, 等. 带有推进器故障的船舶动力定位系统的鲁棒滑模容错控制[J]. 控制与决策, 2019, 1-7. |
| [31] |
FLAVIA B., GIANLUCA I., SAURO L., et al.. Advanced control for fault-tolerant dynamic positioning of an offshore supply vessel[J]. Ocean Engineering, 2015, 472-484. |
| [32] |
谢文博, 付明玉, 施小成. 动力定位船舶自适应滑模无源观测器设计[J]. 控制理论与应用, 2013, 1(30): 131-136. |
| [33] |
付明玉, 刘佳, 吴宝奇. 基于扰动观测器的动力定位船终端滑模航迹跟踪控制[J]. 中国造船, 2015, 4(56): 33-45. |
| [34] |
和红磊, 王玉龙. 基于滑模自抗扰的半潜式海洋平台动力定位控制方法研究[J]. 船舶工程, 2016, 11(38): 72-77. |
| [35] |
关克平, 张新放. 滑模控制船舶动力定位控制系统研究[J]. 舰船科学技术, 2018, 3(40): 61-65. |
| [36] |
苏义鑫, 赵俊. 带有 UKF 滚动时域估计的动力定位控制器[J]. 哈尔滨工程大学学报, 2016, 10(37): 1381-1386. |
| [37] |
AWANTHA J., SALIM A., SYED I.. Wavelet-based controller design for dynamic positioning of vessels[C]. IFAC PapersOnLine 2017, 50 (1): 1133–1138.
|
| [38] |
徐树生, 李娟, 温利, 等. 强跟踪自适应CKF 及其在动力定位中应用[J]. 电机与控制学报, 2015, 2(19): 101-108. |
| [39] |
林孝工, 焦玉召, 梁坤, 等. 相关噪声下非线性滤波及在动力定位中的应用[J]. 控制理论与应用, 2016, 8(33): 1081-1088. |
| [40] |
焦建芳. 多动力定位船的协调编队控制方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2014.
|
| [41] |
王彬. 多艘动力定位船鲁棒自适应编队控制研究[D]. 哈尔滨: 哈尔滨工程大学, 2017.
|
| [42] |
骆伟. 多DP船协调编队有限时间控制方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2017.
|
 2020, Vol. 42
2020, Vol. 42
