在以现代高新技术为背景的电子战中,为了提高军事力量的突防能力和生存能力,就必须提高战斗平台的隐身能力,即控制和降低军用系统的雷达散射截面(Radar Cross Section,RCS)。雷达散射截面是基于平面波照射下目标各向同性散射的概念,在给定方向上返回或散射功率的一种量度,是定量表征目标散射强弱的物理量[1]。RCS的研究主要应用于隐身技术的提高,通过控制和降低军用目标的雷达特征,迫使敌方电子探测系统和武器平台降低其战斗效力,从而提高我方军事力量的突防能力和生存能力[2]。
战斗平台根据作战使命的不同,搭载不同的武器装备,以实现各自的作战效能。通常情况下,武器装备会裸露在舰船甲板面之上,以实现快速反应要求。当有雷达波对舰船进行探测时,武器装备就有可能形成较强的散射回波,通过与上层建筑的耦合作用,对舰船总体的雷达隐身性能产生较大影响[3],因此应采取有效措施对舰船上的武器装备进行隐身处理。
本文以某型舰及其导弹发射装置为研究对象,通过剖析影响导弹发射装置与舰船上层建筑耦合的因素,基于CST MWS的有限积分法(Finite Integration Technique,FIT),对某舰船近似三维模型进行电磁场仿真计算,研究导弹发射装置对舰总体雷达隐身性的影响。
1 基于CST MWS软件的有限积分法FIT算法原理CST MWS是以有限积分技术为基础的通用电磁场仿真软件。有限积分技术这种数值方法提供了一种通用的空间离散化方案,特点是将积分形式的麦克斯韦(Maxwell)方程离散化[4],通过时域求解预见电磁系统的瞬态响应,再将瞬态数据转换到频域,获得系统的宽频带响应,用于解决各种电磁场问题。
1.1 麦克斯韦方程组[1]麦克斯韦总结整合了法拉第、高斯、安培等前人发现的各种现象及其方程,引入了涡旋电场和位移电流的概念,把它们归纳到一起,用4个公式组成的方程组,涵盖了所有宏观的电磁现象,概况了宏观电磁场的基本规律。麦克斯韦积分方程组为:
| $\oint_{\partial S} {E \cdot {\rm{d}}l} = - \frac{\partial }{{\partial t}}\iint_S B \cdot {\rm{d}}S{\text{,}}$ | (1) |
| $\oint_{\partial S} H \cdot {\rm{d}}l = \iint_S J \cdot {\rm{d}}S + \frac{\partial }{{\partial t}}\iint_S D \cdot {\rm{d}}S{\text{,}}$ | (2) |
| $\mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\nolimits_{\partial V} B \cdot {\rm{d}}S = 0{\text{,}}$ | (3) |
| $\mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\nolimits_{\partial V} D \cdot {\rm{d}}S = \iiint_V \rho \cdot {\rm{d}}v = Q{\text{。}}$ | (4) |
式中:E为电场强度;B为磁通量强度;H为磁场强度;D为电通量密度;J为电流密度;ρ为电荷密度;Q为电量。
对于各向同性线性媒质来说,电磁场量之间的本构关系可以表示为以下媒质方程:
| $D = \varepsilon E{\text{,}}$ | (5) |
| $B = \mu H{\text{,}}$ | (6) |
| $J = \sigma E{\text{。}}$ | (7) |
式中:ε为媒质的介电常数;μ为媒质磁导率;σ为媒质的电导率。
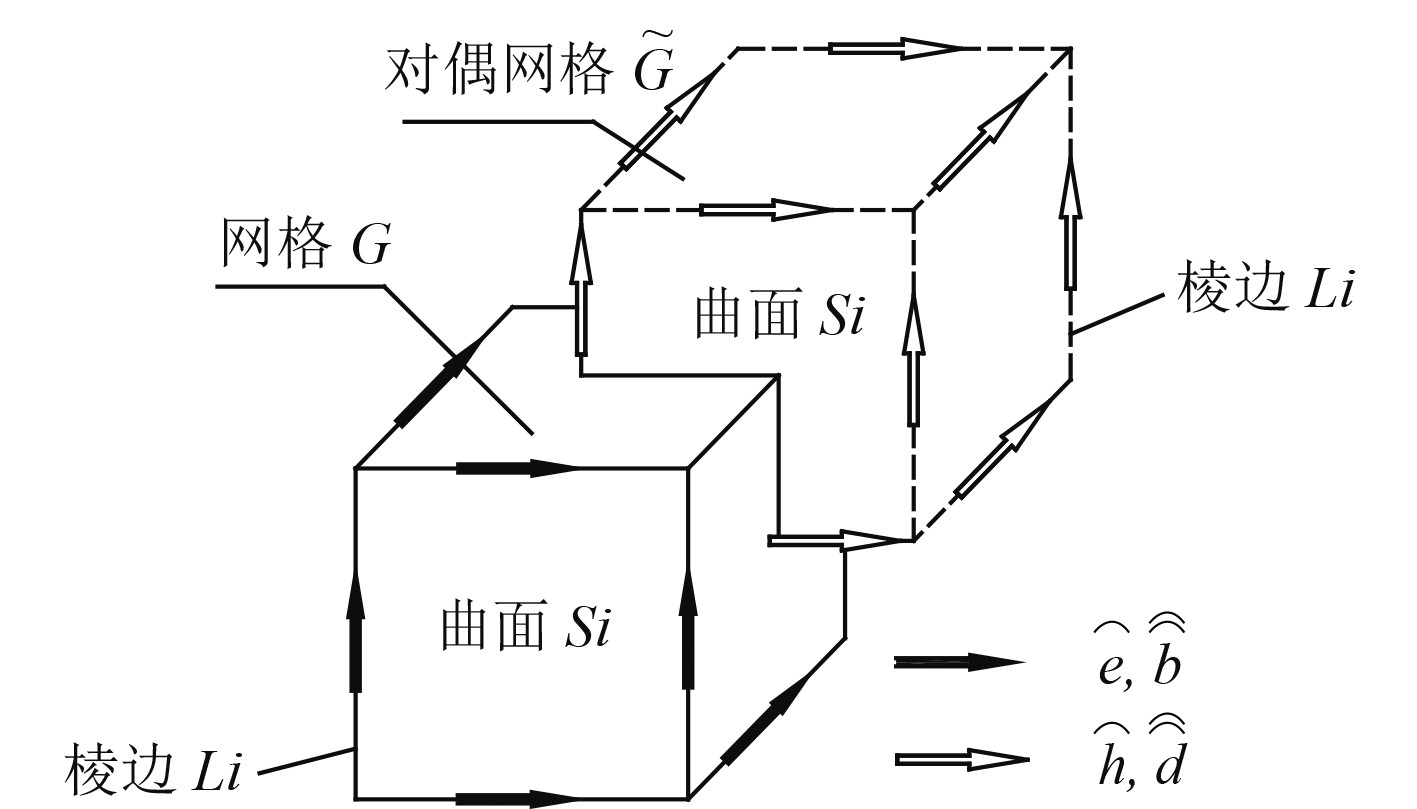
1.2 麦克斯韦方程空间离散求解在有限积分法中,首先将一个有限计算区域分割为许多小的网格单元,这类网格单元包含2套相互嵌套、相互正交的网格——网格G和对偶网格
|
图 1
网格G和对偶网格
|
将麦克斯韦方程组在每个网格面上离散,得到完整离散化的矩阵麦克斯韦方程为:
| $C{\overset{\frown} e} = - \frac{\rm d}{{{\rm d}t}}{\overset\frown{\overset\frown{b}}} {\text{,}}$ | (8) |
| $\tilde C{\overset{\frown} h} = {\overset\frown{\overset\frown{j}}} + \frac{\rm d}{{{\rm d}t}}{\overset\frown{\overset\frown{d}}}{\text{,}}$ | (9) |
| $S{\overset\frown{\overset\frown{b}}} = 0{\text{,}}$ | (10) |
| $\tilde S{\overset\frown{\overset\frown{d}}} = q{\text{。}}$ | (11) |
式中:C为离散旋度算子;
位于2个不同单元网格的积分电压和通量状态变量,可通过媒质矩阵联系起来。将媒质方程进行离散化处理可得矩阵关系式如下:
| ${\overset\frown{\overset\frown{d}}} = {{{M_\varepsilon}} }{\overset{\frown} e}{\text{,}}$ | (12) |
| ${\overset\frown{\overset\frown{b}}} = {{{M_\mu}} }{\overset{\frown} h}{\text{,}}$ | (13) |
| ${\overset\frown{\overset\frown{j}}} = {{{M_\sigma}} }{\overset{\frown} e}{\text{。}}$ | (14) |
式中:Mε为介电常数矩阵;Mμ为磁导率矩阵;Mσ为电导率矩阵。
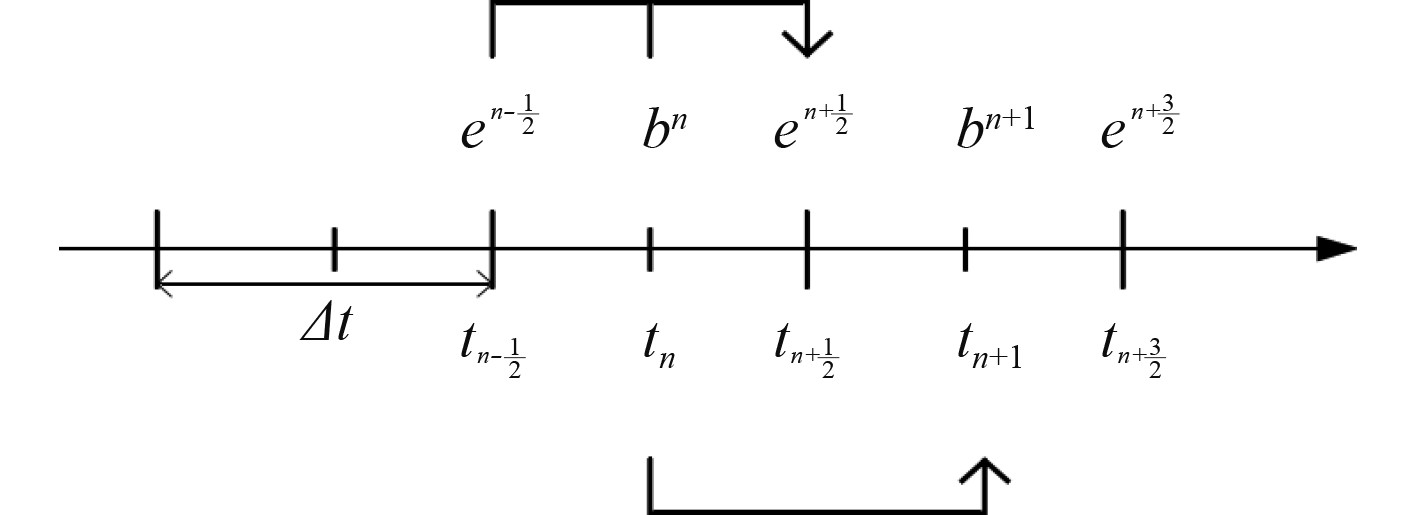
1.3 麦克斯韦方程时域离散求解麦克斯韦网格方程处理的仅为时间连续的,空间离散的情况,对于CST MWS的时域求解器设计的时域问题,还必须对时间离散化。本文采用蛙跃跳步法(Leap-Frog),如图2所示。
|
图 2 蛙跃跳步法图示 Fig. 2 Picture of leaping frog |
在时间轴上,每隔半个时间步长对电压e和磁通b按照时间顺序交替抽样,彼此相差半个时间步长。可得离散时间积分方程为:
| ${{\overset{\frown} e} ^{n + 1/2}} = {{\overset{\frown} e} ^{n - 1/2}} + \Delta t{{M_\varepsilon}} ^{ - 1}\left[{ {\tilde C{{M_\mu}} ^{ - 1}{{{\overset\frown{\overset\frown{b}}}} }^n} + {\overset\frown{\overset\frown{j}}} _S^n} \right]{\text{,}}$ | (15) |
| ${{\overset\frown{\overset\frown{b}}} ^{n + 1}} = {{\overset\frown{\overset\frown{b}}} ^n} - \Delta tC{{\overset{\frown} e} ^{n + 1/2}}{\text{。}}$ | (16) |
为保证时间积分过程的稳定性,时间步长Δt必须满足Courant稳定性条件,各单元网格的计算都必须满足如下稳定条件:
| $\Delta t \leqslant \frac{{\sqrt {\varepsilon \mu } }}{{\sqrt {\left[ {\frac{1}{{\Delta {x^2}}} + \frac{1}{{\Delta {y^2}}} + \frac{1}{{\Delta {z^2}}}} \right]} }}{\text{。}}$ | (17) |
式中:Δt为时间步长;Δx,Δy,Δz分别为3个方向的网格步长。
综上所述,有限积分法是一种通用的电磁算法,通过以上的数值方法,将离散化的麦克斯韦网格方程组按时间顺序在空间网格上依次求解,解算出相应的电场量和磁场量,在得到端口的场强值后,通过反射率的基本定义进行计算,可用于求解任意电磁场问题。
2 RCS仿真计算模型 2.1 对象模型参考国外某型导弹护卫舰安装了2座MK49型发射装置,分别位于导弹护卫舰的首部和尾部,实现该型舰艇全方位末端防御能力[5]。
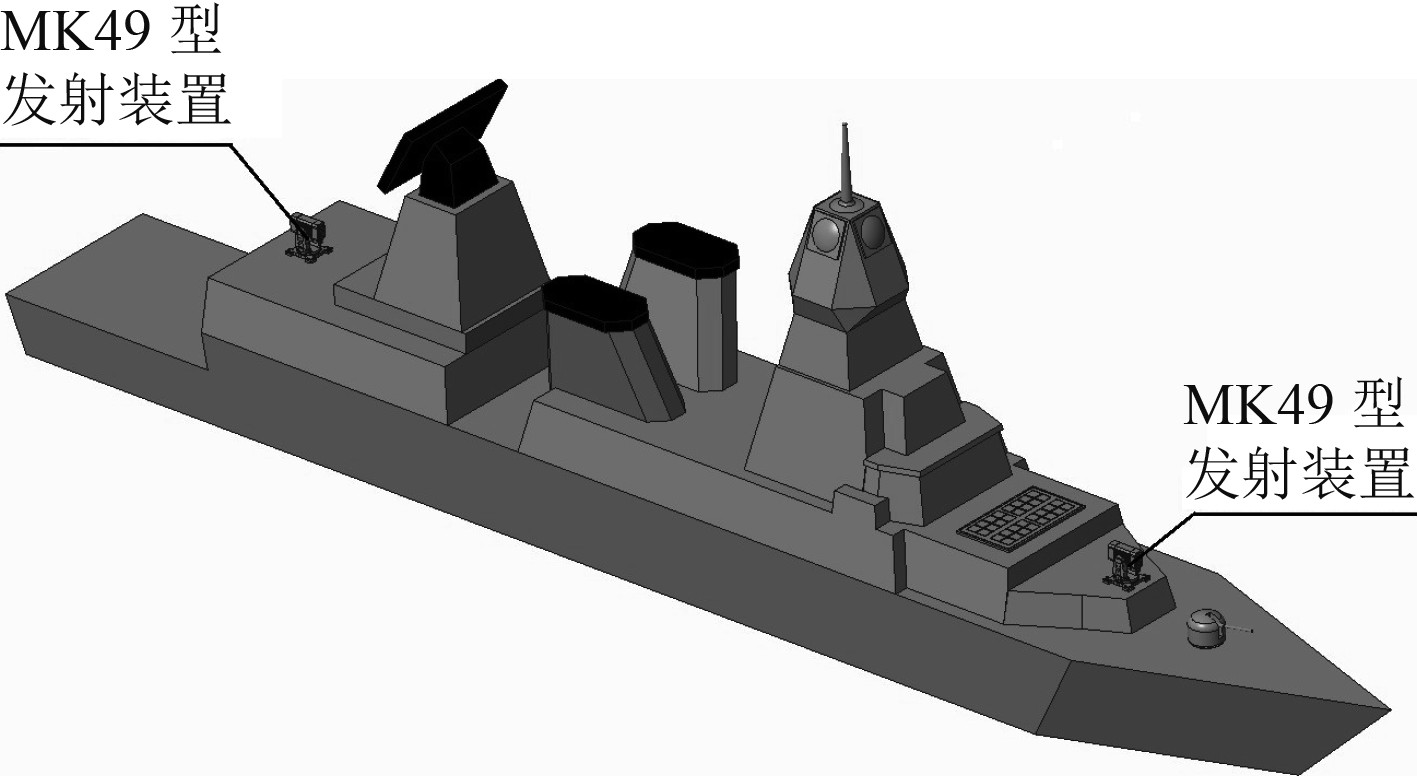
2.2 几何建模在搜集并整理了该型舰船大量资料的基础上,结合舰上装载的各种武器装备、雷达的表面特征,完成对舰炮、发射装置和雷达等部分的适当简化处理[6],基于CST微波工作室建立了完整的1:1舰船水线以上三维近似模型,该模型的外形特征及其布置全貌见图3所示。
|
图 3 舰船几何模型全貌布置 Fig. 3 Full-view arrangement of ship geometric model |
本文在进行RCS仿真分析时,选取前部MK49发射装置及相关舰体为研究对象,以突出典型武备的布置情况与舰体的耦合关系,提高计算的成功率和结果的置信度。
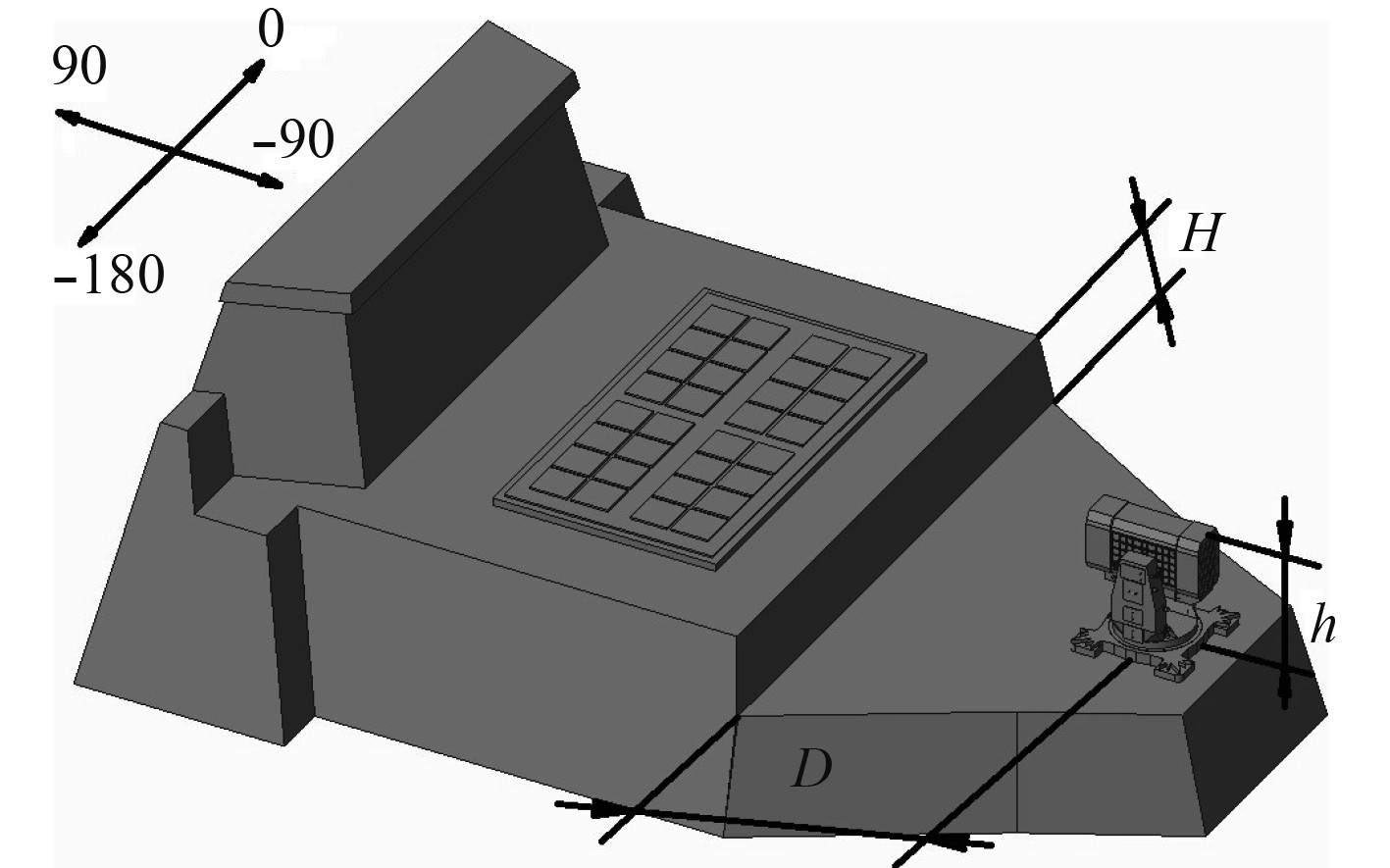
考虑到发射装置锁航状态为常态,因此选取发射装置在舰上的锁航位置为计算状态,即发射装置方向零位指向舰首(图4为−90°方向),高低角为0°。
选取的仿真计算模型如图4所示。
|
图 4 RCS仿真模型计算坐标系 Fig. 4 RCS simulation model calculation coordinate system |
图中:D为MK49发射装置中心面与后部上层建筑的距离;H为MK49发射装置底部安装面与上层建筑顶部的高度;h为MK49发射装置高度,舰体和发射装置设定为金属材质。
本文将发射装置高度h=2.8 m设置为定量;将发射装置中心面与后部上层建筑的距离D以及发射装置底部安装面与上层建筑顶部的高度H设置为变量,通过变量组合变换,研究发射装置对舰船RCS的影响。
3 仿真计算 3.1 耦合特性定义发射装置作为舰艇独立的舰面武器装备,安装在舰船平台上后,会与舰船平台产生一定程度的耦合,耦合后会出现多个散射中心,各个散射中心的散射特性及连接处的散射特性对舰船RCS有着不同的贡献[7],耦合后舰船整体RCS不等于简单地各个部分RCS代数和。如何通过对发射装置安装位置等变量进行有效控制以改善舰船的隐身性能,是本文研究的重点。
发射装置与舰船平台之间的耦合特性可以用下式表示:
| $ {{RCS}}_{\text{耦合}}={{RCS}}_{\text{舰船}}-({{RCS}}_{\text{平台}}+{{RCS}}_{\text{发射装置}})\text{。} $ | (18) |
式中:RCS耦合为发射装置与舰艇平台耦合后的RCS相对增加量;RCS舰船为发射装置安装在舰船平台上后整体RCS值;RCS平台为舰船平台自身的RCS值;RCS发射装置为发射装置自身的RCS值。
由式(18)可知,如果RCS耦合值大,说明发射装置对舰船RCS影响严重;如果RCS耦合值小,则说明发射装置对舰船RCS影响较小。
3.2 分析软件及参数设定本文使用基于CST MWS的有限积分法原理的CST Microwave Studio三维电磁场仿真软件,通过CST求解器求解出目标模型的雷达散射特性。
为保证分析结果的准确性,在进行分析时,发射装置和舰艇平台的RCS值均为相同测试条件下的数值。综合考虑仿真模型的尺寸量级和计算资源等条件,本文选择的测试条件如下:步长为0.5°,入射角为0°,入射平面波的频率为10 GHz和15 GHz,水平极化方式,取在0°~360°方位角范围内计算的仿真模型雷达散射截面RCS值。
3.3 求解计算及结果分析通过分别改变发射装置中心面与后部上层建筑的距离D以及发射装置底部安装面与上层建筑顶部的高度H的参数,得到一系列相应的仿真模型。将舰船平台、发射装置和发射装置安装在舰船平台后的仿真模型分别导入到CST软件中,进行网格剖分和求解计算。
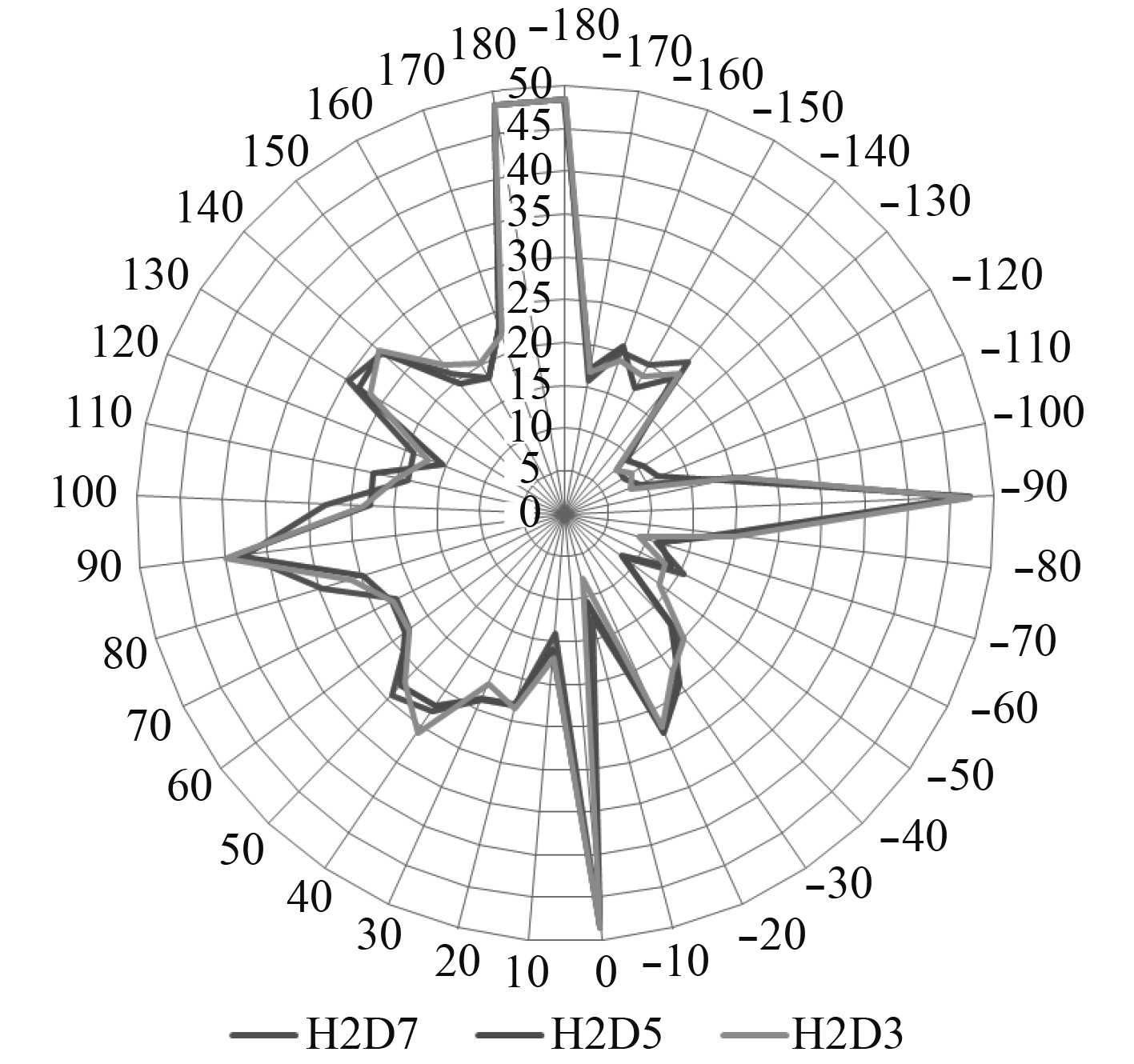
3.3.1 H为定量、D为变量条件下的求解及分析保持发射装置底部安装面与上层建筑顶部的高度H不变,通过改变发射装置中心面与后部上层建筑的距离D,得到不同仿真模型各测试点的RCS舰船和RCS耦合值的雷达图如图5~图8所示。
|
图 5 10 GHz条件下RCS舰船计算结果对比 Fig. 5 Comparison of RCSship calculations under 10 GHz condition |
|
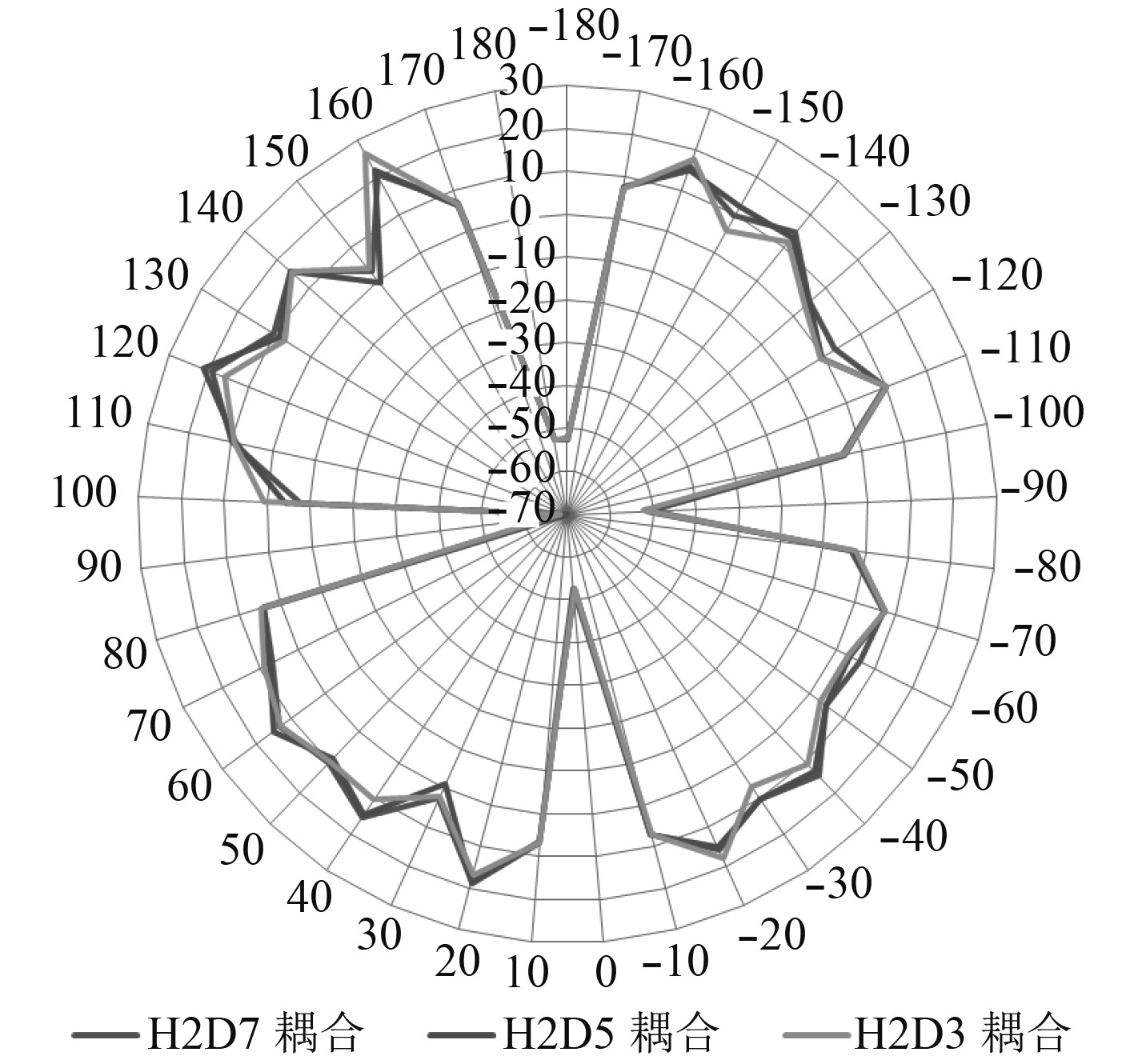
图 8 15 GHz条件下RCS耦合计算结果对比 Fig. 8 Comparison of RCScoupling calculations under 15 GHz condition |
为了进一步宏观比较RCS仿真结果和整体情况,对各测试点的仿真数据取周向平均值,计算结果见表1。
|
|
表 1 发射装置距舰船上层建筑不同距离条件下RCS计算结果(H=2) Tab.1 RCS calculation results of launcher at different distances from superstructure of ship(H=2) |
从以上仿真计算结果可以看出,在相同的入射平面波频率的测试条件下,保持发射装置底部安装面与上层建筑顶部的高度H不变,通过改变发射装置中心面与后部上层建筑的距离D,计算得到的RCS舰船值基本一致,如图5和图7所示。发射装置与舰艇平台RCS耦合值基本一致,如图6和图8所示。
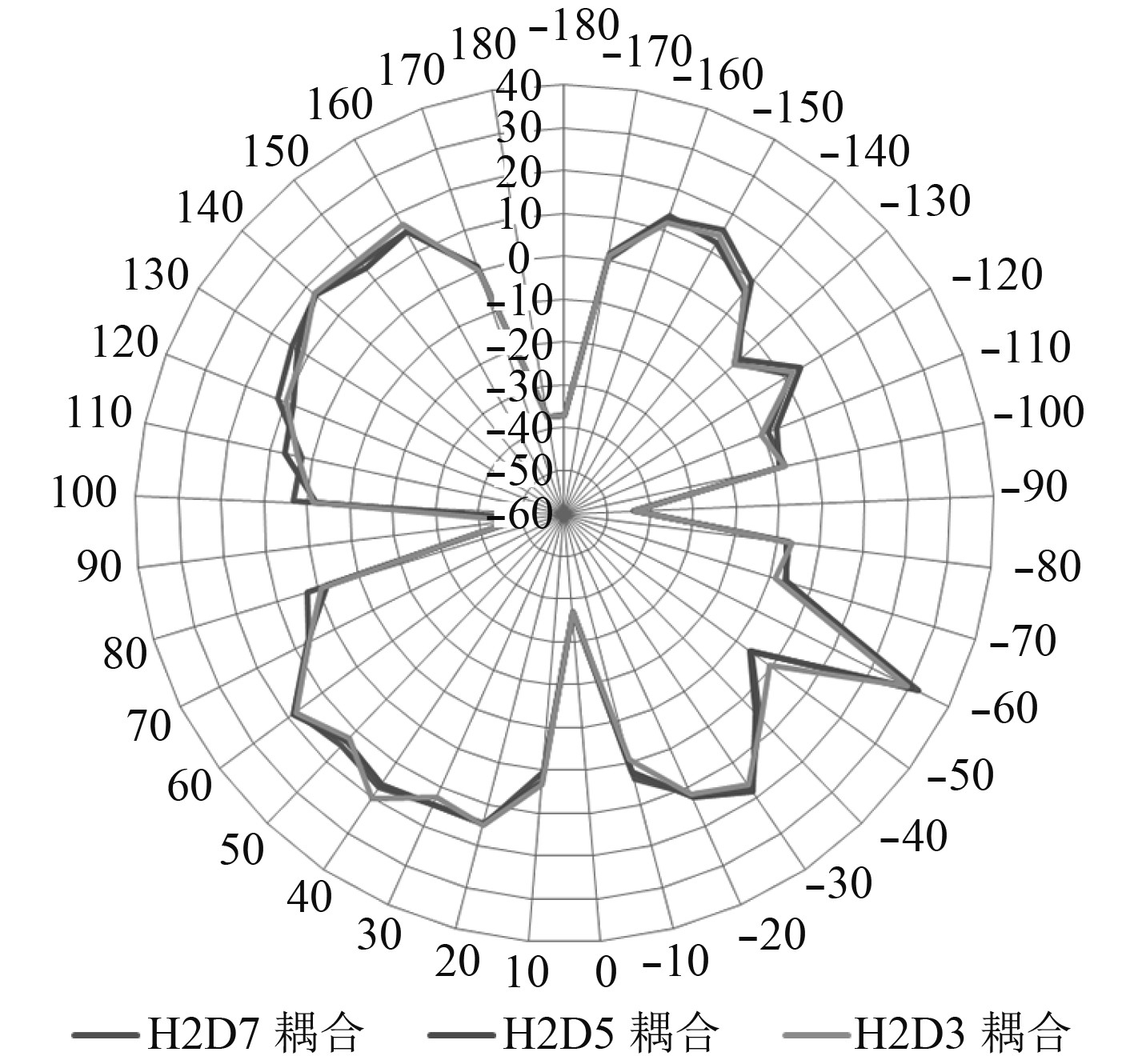
|
图 6 10 GHz条件下RCS耦合计算结果对比 Fig. 6 Comparison of RCScoupling calculations under 10 GHz condition |
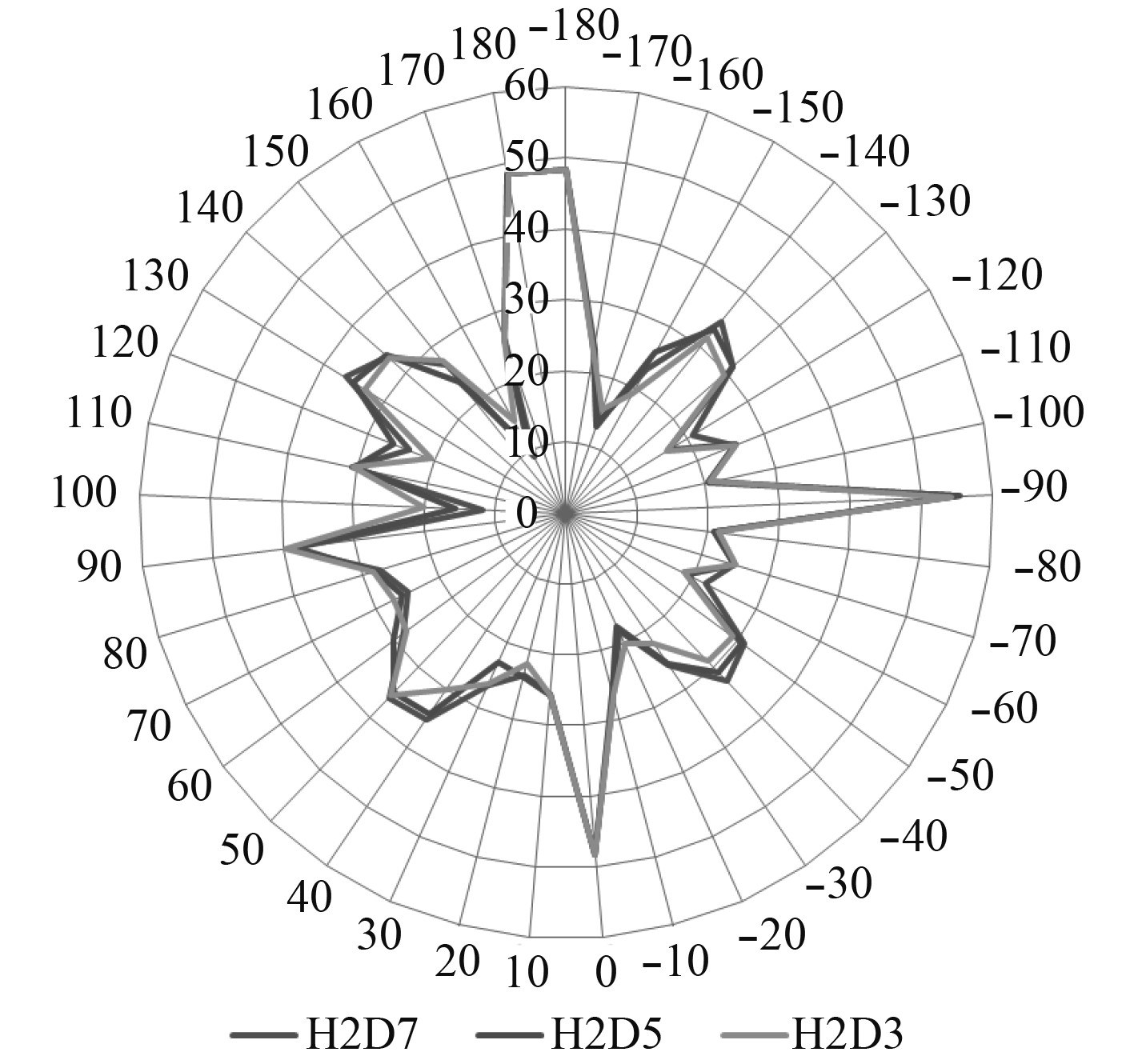
|
图 7 15 GHz条件下RCS舰船计算结果对比 Fig. 7 Comparison of RCSship calculations under 15 GHz condition |
由图5~图8的计算结果对比情况可知,在不同的入射平面波频率的测试条件下,保持发射装置底部安装面与上层建筑顶部的高度H不变,通过改变发射装置中心面与后部上层建筑的距离D,测试范围内各点RCS舰船值和RCS耦合值的变化趋势基本一致。
3.3.2 D为定量、H为变量条件下的求解及分析保持发射装置中心面与后部上层建筑的距离D不变,通过改变发射装置底部安装面与上层建筑顶部的高度H,得到不同仿真模型各测试点的RCS舰船和RCS耦合值的雷达图如图9~图12所示。
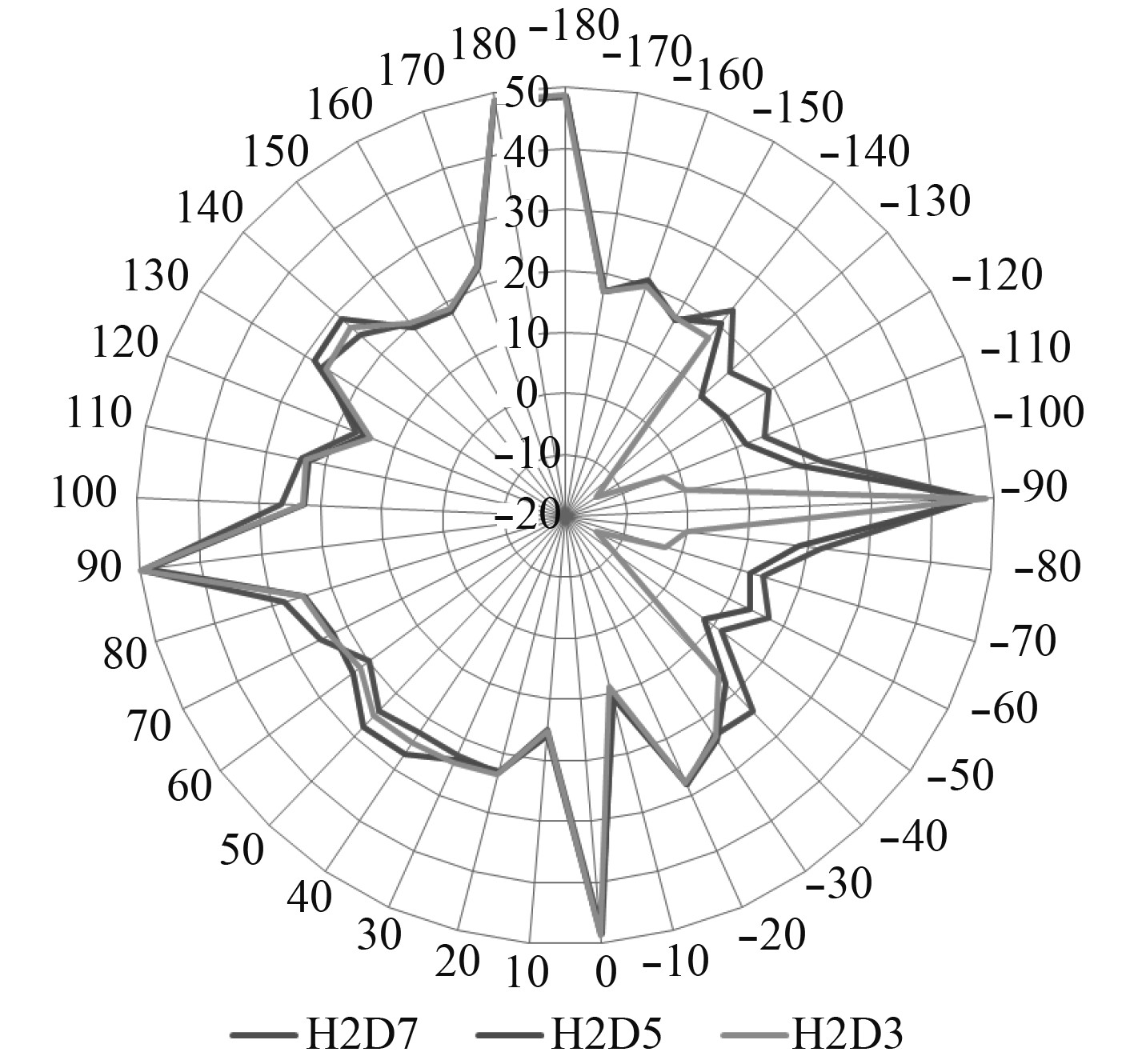
|
图 9 10 GHz条件下RCS舰船计算结果对比 Fig. 9 Comparison of RCSship calculations under 10 GHz condition |
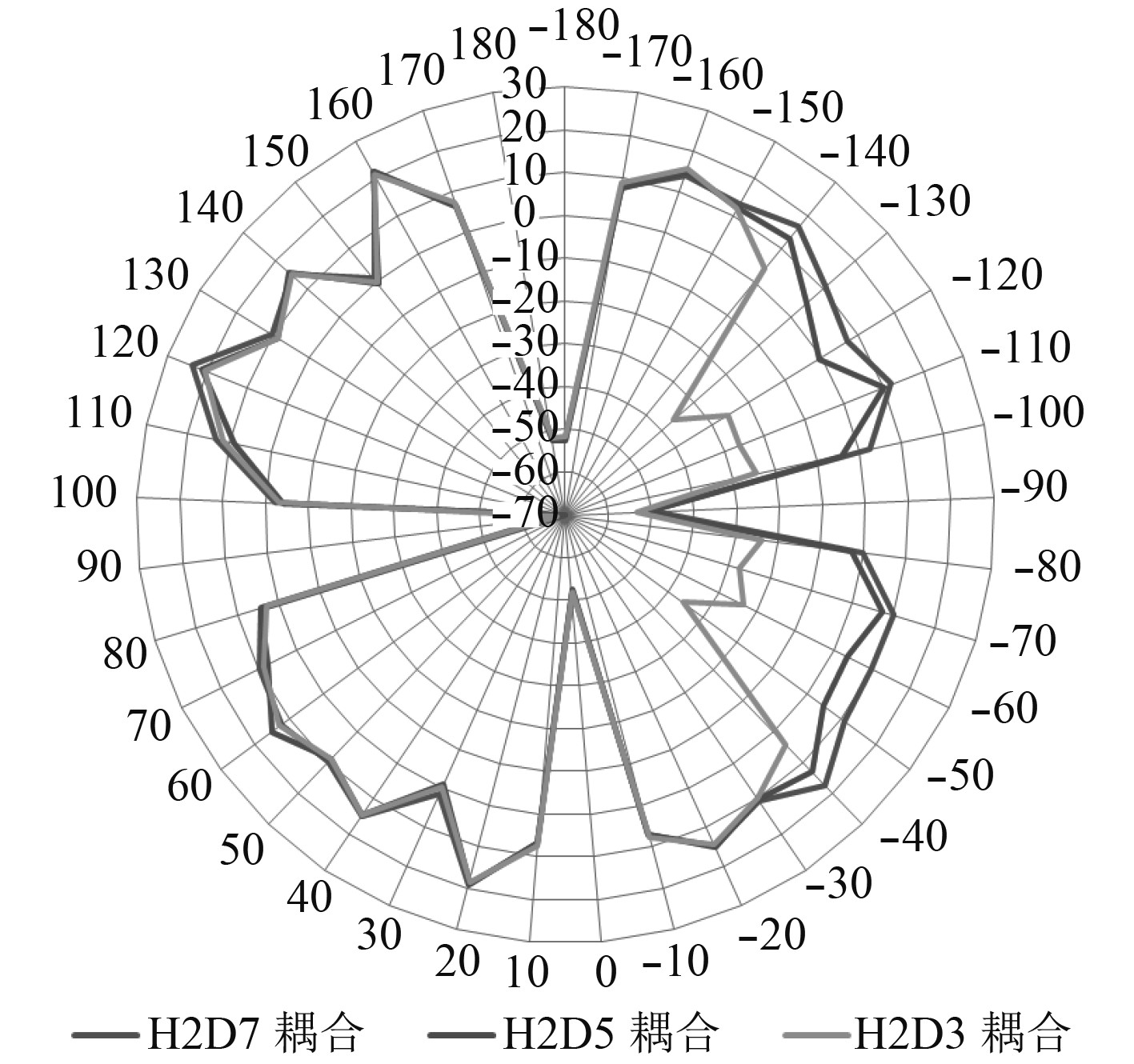
|
图 12 15 GHz条件下RCS耦合计算结果对比 Fig. 12 Comparison of RCScoupling calculations under 15 GHz condition |
为了进一步宏观比较RCS仿真结果和整体情况,对各测试点的仿真数据取周向平均值,计算结果见表2。
|
|
表 2 发射装置距舰船上层建筑不同高度条件下RCS计算结果(D=5) Tab.2 RCS calculation results of launcher at different height from superstructure of ship(D=5) |
可以看出,在相同的入射平面波频率的测试条件下,保持发射装置中心面与后部上层建筑的距离D不变,通过改变发射装置底部安装面与上层建筑顶部的高度H,计算得到的RCS舰船和RCS耦合值偏差较大,主要集中体现在计算坐标系中(−90°±45°)的范围内,即发射装置的正向左右各45°的区域(见图9~图12)。随着发射装置底部安装面与上层建筑顶部的高度H值的减小,RCS舰船和RCS耦合值却相应的增加,与发射装置底部安装面与上层建筑顶部的高度H值成反比关系。
从图10和图12的计算结果可知,当H>h时,发射装置正向左右各45°的区域内与舰船上层建筑的耦合效果更趋向于舰船平台的整体RCS水平;当H<h时,发射装置正向左右各45°的区域内与舰船上层建筑的耦合效果更趋向于发射装置自身的RCS水平,且随着高度H值的减少,耦合效果的趋势越明显。
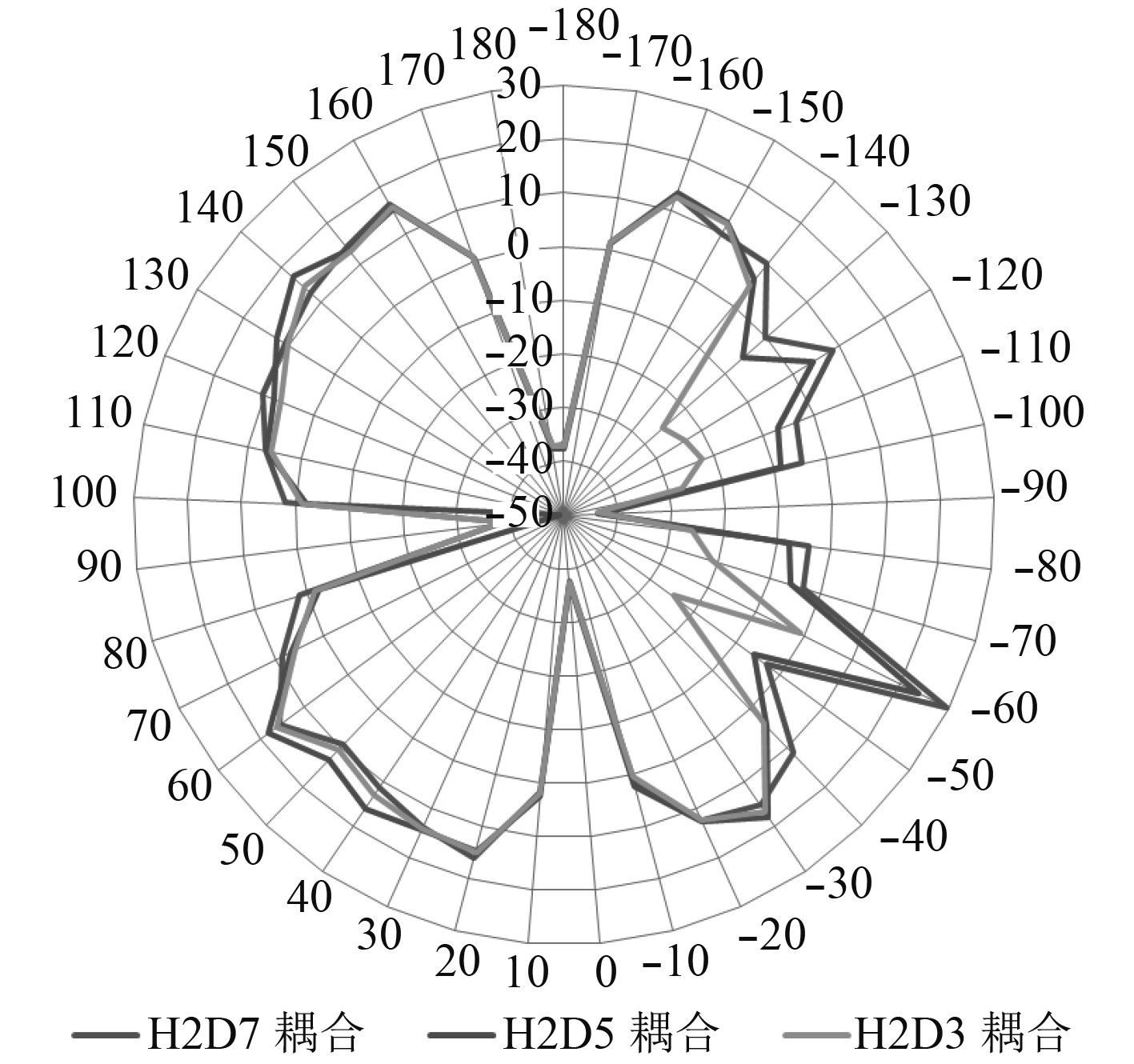
|
图 10 10 GHz条件下RCS耦合计算结果对比 Fig. 10 Comparison of RCScoupling calculations under 10 GHz condition |

|
图 11 15 GHz条件下RCS舰船计算结果对比 Fig. 11 Comparison of RCSship calculations under 15 GHz condition |
由图9~图12的计算结果对比情况可知,在不同入射平面波频率的测试条件下,保持发射装置中心面与后部上层建筑的距离D不变,通过改变发射装置底部安装面与上层建筑顶部的高度H,测试范围内各点RCS舰船值和RCS耦合值的变化趋势基本一致。
4 提高舰船隐身性能的方法 4.1 提高发射装置和舰船上层建筑隐身性能雷达隐身是通过控制和降低目标本身雷达特征信号,即缩减雷达散射截面RCS值,从而达到难以被发现、定位和识别的隐身目的。雷达隐身技术主要有外形隐身技术,雷达吸波材料隐身技术,无源对消技术和有源对消技术等。其中,最为常用和有效的是外形技术和吸波材料的应用。根据倾斜表面可以减小RCS的原理,在满足舰船及设备的稳定性和操控性等总体布置要求前提下,将舰船和设备所有的垂直表面改为倾斜表面,使反射回波不会回到入射波方向,尤其是针对目标的主要威胁区域和特征值进行外形优化设计,是舰船和发射装置外形隐身技术的最为行之有效的途径。如果所设计的几何结构不满足RCS的要求,则可以通过使用其它的隐身技术,如吸波材料技术进行进一步的改进优化,以达到有效缩减RCS的目标。
4.2 改善发射装置与舰船上层建筑的耦合效果发射装置安装在舰船上后,耦合后的整体散射特性是由发射装置和舰船上层建筑两种散射特性综合而成,二者贡献的大小将随着舰船上层建筑高度的不同而发生较大变化(见表2、图9~图12)。当发射装置高度超出相邻舰船上层建筑时,使发射装置形成了一个较强的反射源,耦合后的整体散射特性出现了一个较大的增加量,且与发射装置底部安装面与上层建筑顶部的高度H成反比关系。在舰船上层建筑自身具有较好的隐身性能前提下,当舰船上层建筑包络发射装置的高度后,耦合后的整体散射特性基本上趋于舰船平台自身的RCS水平,并且在一定范围内起到了有益的耦合效果。该方法也可为舰船隐身设计和舰船武备总体布置提供一种参考。
5 结 语本文针对某舰船上的导弹发射装置,建立发射装置与舰船上层建筑的RCS耦合模型,基于CST MWS的有限积分法原理,进行发射装置与舰船上层建筑的耦合分析,研究舰船上层建筑的结构变化以及发射装置在舰船上的布置形式对舰船雷达散射性能的影响,为提高舰船雷达散射性能提供了一种方法和思路[2],对研究对象的雷达散射截面缩减技术以及舰艇隐身结构优化具有一定的参考价值[8]。另外,本文是在发射装置处于舰上锁航状态条件下进行的RCS耦合分析,而发射装置处于作战跟踪状态条件下情况相对复杂,有待进一步开展相关研究工作。
| [1] |
庄钊文, 袁乃昌, 莫锦军, 等.军用目标雷达散射截面预估与测量 [M]. 北京: 科学出版社, 2007: 1-3.
|
| [2] |
王伟锋. 阵列天线结构变形与RCS耦合建模及综合性能分析 [D]. 西安: 西安电子科技大学, 2014.
|
| [3] |
朱英富, 张国良. 舰船隐身技术 [M]. 哈尔滨: 哈尔滨工程大学出版社, 2003: 8-10.
|
| [4] |
李明智, 熊章强, 张大洲. 有限积分法与有限差分法在弹性波数值模拟中的对比分析[J]. 中国科技论文, 2015, 10(3): 538-541. LI Ming-zhi, XIONG Zhang-qiang, ZHANG Da-zhou. Comparison of elastodynamic finite integration technique and finite difference method in numerical simulation of elastic wave[J]. China Sciencepaper, 2015, 10(3): 538-541. |
| [5] |
杨兴宝, 金钊, 朱传伟. 拉姆导弹武器系统近期发展及关键技术分析[J]. 飞航导弹, 2016(7): 25-29. |
| [6] |
刘鸿雁, 郑守铎. 反舰导弹标准靶标RCS仿真[J]. 海军航空工程学院学报, 2011, 26(1): 89-92. DOI:10.3969/j.issn.1673-1522.2011.01.021 |
| [7] |
程子君, 吴启华. 隐身桅杆与主船体耦合RCS特性研究[J]. 中国舰船研究, 2011, 6(3): 45-48, 54. CHENG Zi-jun, WU Qi-hua. The RCS characteristics of coupling between stealth mast and main hull[J]. Chinese Journal of Ship Research, 2011, 6(3): 45-48, 54. DOI:10.3969/j.issn.1673-3185.2011.03.010 |
| [8] |
宋广, 张德保, 李鸣. 水面舰船RCS统计模型分析[J]. 舰船电子对抗, 2011, 34(2): 73-74, 78. SONG Guang, ZHANG De-bao, LI Ming. Analysis of statistical model for RCS of surface ship[J]. Shipboard Electronic Countermeasure, 2011, 34(2): 73-74, 78. DOI:10.3969/j.issn.1673-9167.2011.02.019 |
 2020, Vol. 42
2020, Vol. 42
