0 引　言

捷联惯导系统静基座自主对准有外部信息依赖度低的特点，可直接利用惯导系统陀螺、加表输出和零速校正条件，完成粗对准和精对准^[1]。传统自对准算法一般依靠重力矢量及地球速率矢量直接估算导航坐标系到机体坐标系的姿态变换矩阵，这种方法对对准环境有严格的要求，一般只用于载体处于静止或微幅晃动条件下。对于系泊或漂浮状态的舰艇，由于受海浪影响，造成其装备的惯导系统测量结果受到严重干扰^[2]。在这种环境下，直接采用地球自转角速度作为参考信息计算初始姿态阵的方法已不再适用。但对于加速度计测量到的重力加速度信息，由于其干扰信息一般为谐波形式而且幅值小于重力加速度幅值，因此通过平滑处理可以消除，并提取出重力加速度信息，故地球重力加速度仍可直接作为粗对准的参考信息^[3-4]。

由于地球重力加速度在惯性坐标系中的运动轨迹为一圆锥面，因此，若取在惯性坐标系下重力加速度的投影，则其分量就能包含地球自转角速度信息，再结合陀螺和加速度计的输出，就可实现初始姿态阵的粗略估计。

1 粗对准算法设计 1.1 坐标系定义

定义如下坐标系：

1）导航坐标系（ $o{x_n}{y_n}{z_n}$ 系）

采用北天东地理坐标系。

2）载体坐标系（ $o{x_b}{y_b}{z_b}$ 系）

原点位于载体重心的前上右坐标系。

3）经线地球坐标系（ $o{x_{{e_0}}}{y_{{e_0}}}{z_{{e_0}}}$ 系）

原点在地球中心， ${y_{{e_0}}}$ 轴和地球自转轴重合， ${z_{{e_0}}}$ 轴在赤道平面内指向惯组所在点经线， ${x_{{e_0}}}$ 轴在赤道平面内， ${x_{{e_0}}}$ ， ${y_{{e_0}}}$ ， ${z_{{e_0}}}$ 轴构成前上右坐标系。

4）经线地心惯性坐标系（ $o{x_{{i_0}}}{y_{{i_0}}}{z_{{i_0}}}$ 系）

在粗对准的起始时刻 ${t_1}$ ，将 ${e_0}$ 系在惯性空间凝固后形成的坐标系。

5）载体惯性坐标系（ $o{x_{{i_{{b_0}}}}}{y_{{i_{{b_0}}}}}{z_{{i_{{b_0}}}}}$ 系）

在粗对准的起始时刻 ${t_1}$ ，将载体坐标系在惯性空间中凝固成为 ${i_{{b_0}}}$ 系。

1.2 算法设计

为隔离晃动对自主对准的影响，将姿态矩阵拆分为4个矩阵分别计算，设对准点纬度为 $L$ ，则姿态矩阵可写为：

${{C}}_b^n\left( t \right) = {{C}}_{{e_0}}^nC_{{i_0}}^{{e_0}}\left( t \right){{C}}_{{i_{{b_0}}}}^{{i_0}}{{C}}_b^{{i_{{b_0}}}}\left( t \right)\text{,}$

(1)

其中：

${{C}}_{{e_0}}^n = \left[ {\begin{array}{*{20}{c}} 0&{\cos L}&{ - \sin L} \\ 0&{\sin L}&{\cos L} \\ 1&0&0 \end{array}} \right]\text{,}$

(2)

${{C}}_{{i_0}}^{{e_0}}\left( t \right) = \left[ {\begin{array}{*{20}{c}} {\cos {\omega _{ie}}\left( {t - {t_0}} \right)}&0&{ - \sin {\omega _{ie}}\left( {t - {t_0}} \right)} \\ 0&1&0 \\ {\sin {\omega _{ie}}\left( {t - {t_0}} \right)}&0&{\cos {\omega _{ie}}\left( {t - {t_0}} \right)} \end{array}} \right]\text{。}$

(3)

式中： ${t_0}$ 为粗对准起始时刻。根据 ${i_{{b_0}}}$ 系的定义知 ${{C}}_b^{{i_{{b_0}}}}\left( {{t_0}} \right) = I$ ， ${{C}}_b^{{i_{{b_0}}}}\left( t \right)$ 可通过旋转矢量法解算获得。

${{C}}_{{e_0}}^n$ ， ${{C}}_{{i_0}}^{{e_0}}\left( t \right)$ ， ${{C}}_b^{{i_{{b_0}}}}\left( t \right)$ 可利用已知信息计算确定，因此只要能得到 ${{C}}_{{i_{{b_0}}}}^{{i_0}}$ 的估值就能完成 ${{C}}_b^n$ 的粗略估算，即粗对准的任务由对 ${{C}}_b^n$ 的估算问题转化为对 ${{C}}_{{i_{{b_0}}}}^{{i_0}}$ 的估算问题。而 ${{C}}_{{i_{{b_0}}}}^{{i_0}}$ 是载体惯性坐标系到经线地心惯性坐标系的姿态转换矩阵，因此可利用在这2个惯性空间内2个不共线矢量的测量来确定。受地球自转影响，重力在惯性坐标系会发生转动，所以重力在不同时间段内在这两个坐标系的积分所得矢量是不共线的，故可以利用重力信息进行 ${{C}}_{{i_{{b_0}}}}^{{i_0}}$ 的求取。

加表输出比力在 ${i_{{b_0}}}$ 系中的投影可以表示为如下形式：

${\tilde f^{{i_{{b_0}}}}} = \hat {{C}}_b^{{i_{{b_0}}}}{\tilde f^b}\text{。}$

(4)

式中： ${\tilde f^b}$ 为加速度计输出比力； $\hat {{C}}_b^{{i_{{b_0}}}}$ 为 $b$ 系与 ${i_{{b_0}}}$ 系间的变换矩阵，可根据陀螺输出计算得到。设加表含安装误差角、刻度系数误差及常值偏置误差，则加表输出的比力为：

$\begin{split} {{\tilde f}^b} = & \left( {I + \delta {K_A}} \right)\left( {I + \delta A} \right) \times\\ & \left( { - {g^b} + a_{LA}^b + a_D^b + a_{gor}^b} \right) + {\nabla ^b} = \\ {} & - {g^b} + a_{LA}^b + a_D^b + a_{gor}^b + \left( {\delta A + \delta {K_A}} \right)\times \\ & \left( { - {g^b} + a_{LA}^b + a_D^b + a_{gor}^b} \right) + {\nabla ^b} \text{。}\\ \\[-8pt]\end {split}$

(5)

式中： ${\nabla ^b} = {\left[ {\begin{array}{*{20}{c}} {{\nabla _x}}&{{\nabla _y}}&{{\nabla _z}} \end{array}} \right]^{\rm{T}}}$ 为加表常值偏置向量； $\delta {{{K}}_A} = {\rm{diag}}\left( {\delta {K_{Ax}},\delta {K_{Ay}},\delta {K_{Az}}} \right)$ 为加表刻度系数误差矩阵； $\delta {{A}} = \left[ {\begin{array}{*{20}{c}} 0&{\delta {A_z}}&{ - \delta {A_y}} \\ { - \delta {A_z}}&0&{\delta {A_x}} \\ {\delta {A_y}}&{ - \delta {A_x}}&0 \end{array}} \right]$ 为加表安装误差矩阵； $a_{LA}^b$ 为杆臂加速度； $a_D^b$ 为载体干扰加速度； $a_{gor}^b$ 为有害加速度，当载体处于漂浮状态时， $a_{gor}^b = 0$ ；

将式（5）代入式（4），得

$\begin{split} \hat C_b^{{i_{{b_0}}}}{{\tilde f}^b} = & - \hat C_b^{{i_{{b_0}}}}{g^b} + \hat C_b^{{i_{{b_0}}}}a_{LA}^b + \hat C_b^{{i_{{b_0}}}}a_D^b + \hat C_b^{{i_{{b_0}}}}{\nabla ^b} + \\ & \hat C_b^{{i_{{b_0}}}}\left( {\delta A + \delta {K_A}} \right)\left( { - {g^b} + a_{LA}^b + a_D^b + a_{gor}^b} \right) + \\ & \hat C_b^{{i_{{b_0}}}}{g^b} + \hat C_b^{{i_{{b_0}}}}a_{LA}^b + \delta {a^{{i_{{b_0}}}}} \hfill\text{。} \\ \\[-8pt]\end{split} $

(6)

式中：

$\begin{aligned} \delta {a^{{i_{{b_0}}}}} = & \hat C_b^{{i_{{b_0}}}}{\nabla ^b} + \hat C_b^{{i_{{b_0}}}}\left( {\delta A + \delta {K_A}} \right)\times \\ & \left( { - {g^b} + a_{LA}^b + a_D^b + a_{gor}^b} \right)\text{。} \\ \end{aligned} $

(7)

对（6）式两边在 $\left[ {{t_0},{t_k}} \right]$ 上积分，得

$\begin{split} {{\hat V}^{{i_{{b_0}}}}} = &\int_{{t_0}}^{{t_k}} {\hat C_b^{{i_{{b_0}}}}{{\tilde f}^b}} {\rm{d}}t =\\ & - \int_{{t_0}}^{{t_k}} {\hat C_b^{{i_{{b_0}}}}{g^b}} {\rm{d}}t + \int_{{t_0}}^{{t_k}} {\hat C_b^{{i_{{b_0}}}}a_{LA}^b} {\rm{d}}t + \int_{{t_0}}^{{t_k}} {\delta {a^{{i_{{b_0}}}}}} {\rm{d}}t= \\ & - \hat C_{{i_0}}^{{i_{{b_0}}}}\int_{{t_0}}^{{t_k}} {{g^{{i_0}}}} {\rm{d}}t + V_{LA}^{{i_{{b_0}}}} + \delta {V^{{i_{{b_0}}}}} \\ \\[-8pt]\end{split} $

(8)

式中: $V_{LA}^{{i_{{b_0}}}}$ 为杆臂速度在 ${i_{{b_0}}}$ 系中的投影，且 $V_{LA}^{{i_{{b_0}}}} = C_b^{{i_{{b_0}}}}\left( {{\bf{\omega }}_{ib}^b \times {r^b}} \right)$ ，若杆臂 ${r^b}$ 已知，则由陀螺输出计算得到 ${\hat C}_b^{{i_{{b_0}}}}$ 及 ${\bf{\hat \omega }}_{ib}^b$ ，可解算出杆臂速度 ${\hat V}_{LA}^{{i_{{b_0}}}}$ ，并且

$\hat V_{LA}^{{i_{{b_0}}}} = V_{LA}^{{i_{{b_0}}}} + \delta V_{LA}^{{i_{{b_0}}}}\text{，}$

(9)

式中， $\delta {\rm{V}}_{LA}^{{i_{{b_0}}}}$ 为杆臂速度计算误差。

由式（7）和式（8）可得：

$\begin{split} \tilde V_{}^{{i_{{b_0}}}} = & \hat V_{}^{{i_{{b_0}}}} - \hat V_{LA}^{{i_{{b_0}}}} = \\ & - \hat C_{{i_0}}^{{i_{{b_0}}}}\int_{{t_0}}^{{t_k}} {{g^{{i_0}}}{\rm{d}}t - \delta V_{LA}^{{i_{{b_0}}}} + \delta {V^{{i_{{b_0}}}}}} \approx\\ & C_{{i_0}}^{{i_{{b_0}}}}{V^{{i_0}}} {\text{。}} \end{split} $

(10)

式中， ${{{V}}^{{i_0}}} = \int_{{t_0}}^{{t_k}} {\left( { - {{\bf{g}}^{{i_0}}}} \right){\rm{d}}t}$ 。由于

$\begin{split} {g^{{i_0}}} = & C_{{e_0}}^{{i_0}}C_n^{{e_0}}{g^n} \hfill =\\ &\left[ {\begin{array}{*{20}{l}} { - g\cos L\sin {\omega _{ie}}\left( {t - {t_0}} \right)} \\ { - g\sin L} \\ { - g\cos L\cos {\omega _{ie}}\left( {t - {t_0}} \right)} \end{array}} \right]{\text{，}} \end{split} $

(11)

所以

${V^{{i_0}}}\left( {{t_k}} \right) = \left[ \begin{aligned} & \frac{{ - g\cos L\left( {\cos {\omega _{ie}}\Delta {t_k} - 1} \right)}}{{{\omega _{ie}}}} \\ & g\sin L\Delta {t_k} \\ & \frac{{g\cos L\sin {\omega _{ie}}\Delta {t_k}}}{{{\omega _{ie}}}} \\ \end{aligned} \right]{\text{，}} $

(12)

式中， $ \Delta {t_k} = {t_k} - {t_0}$ 。

由式（9）可知，在 ${t_{k1}}$ ， ${t_{k2}}$ 时刻（ ${t_0} < {t_{k1}} < {t_{k2}}$ ）有：

$\left\{ {\begin{array}{*{20}{c}} {{{\tilde V}^{{i_{{b_0}}}}}\left( {{t_{k2}}} \right) = C_{{i_0}}^{{i_{{b_0}}}}{V^{{i_0}}}\left( {{t_{k2}}} \right)} \text{,}\\ {{{\tilde V}^{{i_{{b_0}}}}}\left( {{t_{k2}}} \right) = C_{{i_0}}^{{i_{{b_0}}}}{V^{{i_0}}}\left( {{t_{k2}}} \right)} \text{,} \end{array}} \right.$

(13)

由式（12）可得：

$\hat{\rm{ C}}_{{i_{{b_0}}}}^{{i_0}} = {\left[ {\begin{array}{*{20}{c}} {{V^{{i_0}{\rm{T}}}}\left( {{t_{k1}}} \right)} \\ {{V^{{i_0}{\rm{T}}}}\left( {{t_{k2}}} \right)} \\ {{{\left[ {{V^{{i_0}}}\left( {{t_{k1}}} \right) \!\!\!\times {V^{{i_0}}}\left( {{t_{k2}}} \right)} \right]}^{\rm{T}}}} \end{array}} \!\!\right]^{ - 1}}\!\!\left[ {\begin{array}{*{20}{c}} {{{\tilde V}^{{i_{{b_0}}}{\rm{T}}}}\left( {{t_{k1}}} \right)} \\ {{{\tilde V}^{{i_{{b_0}}}{\rm{T}}}}\left( {{t_{k2}}} \right)} \\ \!\!\!{{{\left[ {{{\tilde V}^{{i_{{b_0}}}}}\left( {{t_{k1}}} \right) \times {{\tilde V}^{{i_{{b_0}}}}}\left( {{t_{k2}}} \right)} \right]}^{\rm{T}}}} \end{array}} \right]\text{。}$

(14)

上式即为粗对准时 $\hat{{C}}_{{i_{{b_0}}}}^{{i_0}}$ 估算式。将 ${{C}}_{{e_0}}^n$ ， ${{C}}_{{i_0}}^{{e_0}}\left( {{t_{k2}}} \right)$ 、 $\hat {{C}}_b^{{i_{{b_0}}}}\left( {{t_{k2}}} \right)$ 和 $\hat {{C}}_{{i_{{b_0}}}}^{{i_0}}$ 代入式（1）即可得到 ${t_{k2}}$ 时刻载体姿态的粗对准结果 $\hat C_b^n$ 。

2 精对准方案 2.1 精对准方案的选择

当惯导系统处于大幅度晃动条件下时，其相对地球的参考速度仍可视为0，因此，选择以速度误差作为观测量构建最优卡尔曼滤波来实现惯导系统的精对准。

2.2 捷联惯导系统误差模型的建立

1）捷联惯导系统误差方程

考虑到惯性元件误差以及系统导航参数误差等的影响，构建导航坐标系为 $n'$ 系，定义 $n'$ 系相对 $n$ 系的转角为姿态误差角 $\varphi = {\left[ {\begin{array}{*{20}{c}} {{\varphi _N}}&{{\varphi _U}}&{{\varphi _E}} \end{array}} \right]^{\rm{T}}}$ 。根据捷联惯导力学编排方程，可获得姿态误差方程如下：

${\dot \varphi ^n} = - \omega _{in}^n \times {\varphi ^n} + \delta \omega _{in}^n - C_b^n{\varepsilon ^b}\text{，}$

(15)

其中：

$\omega _{in}^n = \omega _{ie}^n + \omega _{en}^n$ ， $\delta \omega _{in}^n\delta \omega _{ie}^n + \delta \omega _{en}^n$ ， $\omega _{ie}^n = {\left[ {\begin{array}{*{20}{c}} {{\omega _{ie}}\cos L}& {{\omega _{ie}}\sin L}&0 \end{array}} \right]^{\rm{T}}}$ ， $\omega _{en}^n = {\left[ {\begin{array}{*{20}{c}} {\displaystyle\frac{{{V_E}}}{{{R_N} + h}}}&{\displaystyle\frac{{{V_E}}}{{{R_N} + h}}\tan L}&{ -\displaystyle \frac{{{V_N}}}{{{R_M} + h}}} \end{array}} \right]^{\rm{T}}}$ 。 ${R_N}$ ， ${R_M}$ 分别为子午面内曲率半径、卯酉圈内曲率半径、 ${\varepsilon ^b}$ 为载体系陀螺漂移。

根据捷联惯导速度解算方程，考虑系统误差影响，获得速度误差方程如下：

$\delta \dot V_e^n = {f^n} \times {\varphi ^n} - \left( {2\omega _{ie}^n + \omega _{en}^n} \right) \times \delta V_e^n + C_b^n{\nabla ^b}\text{.}$

(16)

其中： $\delta V_e^n = {\left[ {\begin{array}{*{20}{c}} {\delta {V_N}}&{\delta {V_U}}&{\delta {V_E}} \end{array}} \right]^{\rm{T}}}$ 。

2）捷联惯导系统状态空间模型

由式（14）和式（15），并设陀螺和加表的测量误差为随机常数，可得到SISN初始对准状态方程为：

$\dot X = Fx + Gwt\text{。}$

(17)

状态变量为：

$\begin{split} { X} = [{\varphi _N},{\varphi _U},{\varphi _E},\delta {V_N},\delta {V_U},\delta {V_E}, \\ {\varepsilon _x},{\varepsilon _y},{\varepsilon _z},{\nabla _x},{\nabla _y},{\nabla _z}{]^{\rm{T}}}{\text{，}} \end{split} $

(18)

随机噪声状态矢量为：

$ {{w}} = {\left[ {{w_{{V_n}}},{w_{{V_u}}},{w_{{V_e}}},{w_{{\varphi _n}}},{w_{{\varphi _u}}},{w_{{\varphi _e}}},{0_{1 \times 6}}} \right]^{\rm{T}}}{\text{，}} $

(19)

$ {{F}} = \left[ {\begin{array}{*{20}{c}} { - \omega _{in}^n \times }&A&{ - C_b^n}&{{0_{3 \times 3}}}\\ {{f^n} \times }&B&{{0_{3 \times 3}}}&{C_b^n}\\ {{0_{3 \times 3}}}&{{0_{3 \times 3}}}&{{0_{3 \times 3}}}&{{0_{3 \times 3}}}\\ {{0_{3 \times 3}}}&{{0_{3 \times 3}}}&{{0_{3 \times 3}}}&{{0_{3 \times 3}}} \end{array}} \right]{\text{，}} $

(20)

$A = \left[ {\begin{array}{*{20}{c}} 0&0&{\displaystyle\frac{1}{{{R_e}}}} \\ 0&0&{\displaystyle\frac{{\tan L}}{{{R_e}}}} \\ { - \displaystyle\frac{1}{{{R_n}}}}&0&0 \end{array}} \right]{\text{，}}$

(21)

$ B = \left[ {\begin{array}{*{20}{c}} { - \displaystyle\frac{{{V_u}}}{{{R_n}}}}&{ - \displaystyle\frac{{{V_n}}}{{{R_n}}}} \\ { - 2{\omega _{ie}}\sin L - \displaystyle\frac{{{V_e}}}{{{R_e}}}\tan L}&{} \\ {\displaystyle\frac{{2{V_n}}}{{{R_n}}}}&0 \\ {2{\omega _{ie}}\cos L + \displaystyle\frac{{{V_e}}}{{{R_e}}}}&{} \\ {2{\omega _{ie}}\sin L + \displaystyle\frac{{{V_e}}}{{{R_e}}}\tan L}&{ - 2{\omega _{ie}}\cos L - \displaystyle\frac{{{V_e}}}{{{R_e}}}} \\ {\displaystyle\frac{{{V_n}}}{{{R_e}}}\tan L - \displaystyle\frac{{{V_u}}}{{{R_e}}}}&{} \end{array}} \right]{\text{，}} $

(22)

取速度误差为观测量构建系统观测方程：

$Z = HX + V\text{。}$

(23)

其中， $H = \left[ {\begin{array}{*{20}{c}} {{I_{3 \times 3}}}&{{0_{3 \times 9}}} \end{array}} \right]$ ， $V$ 为量测噪声。

3 试验验证与结果分析 3.1 试验条件

为验证本文提出的晃动基座自对准算法，选用某中精度捷联惯导系统为试验对象，分别在静基座和晃动基座条件下进行自主对准验证试验。当地纬度信息39.81175º。

3.2 试验过程

每组试验对准时间为7 min，其中粗对准时间120 s，精对准滤波时间300 s。统计对准结束后纯惯性导航30 min的结果，以此来验证所提方法的可行性。

试验1：静基座自主对准验证试验。惯导系统静止于三轴转台上进行试验。

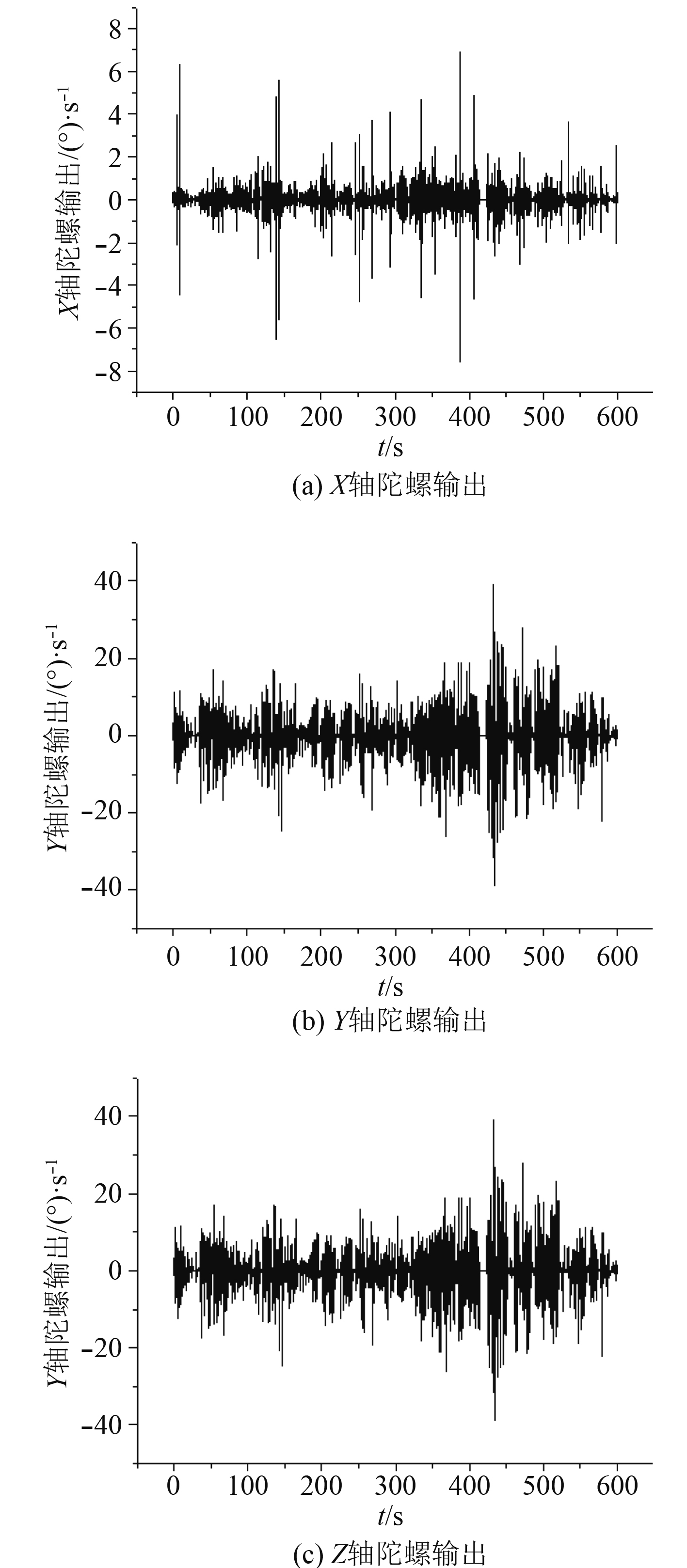
试验2：晃动基座自主对准验证试验。三轴转台进行晃动，试验过程中惯导系统晃动规律如图1所示。

3.3 试验结果及分析

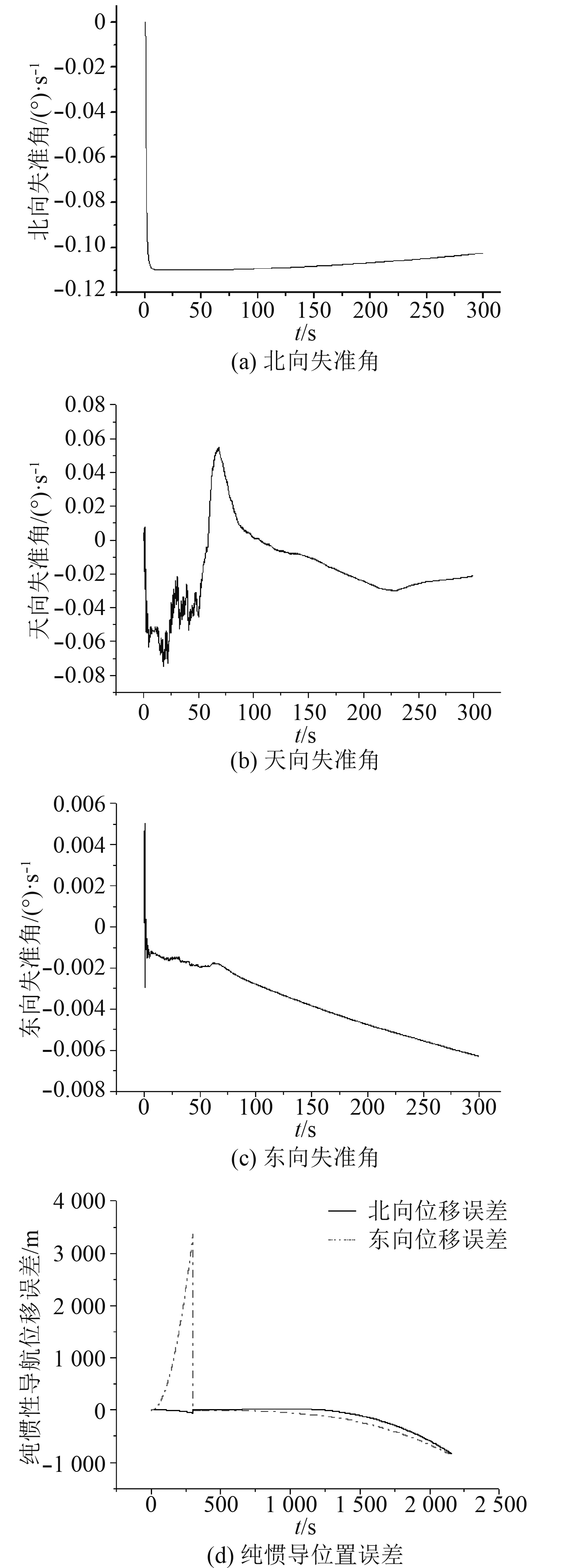
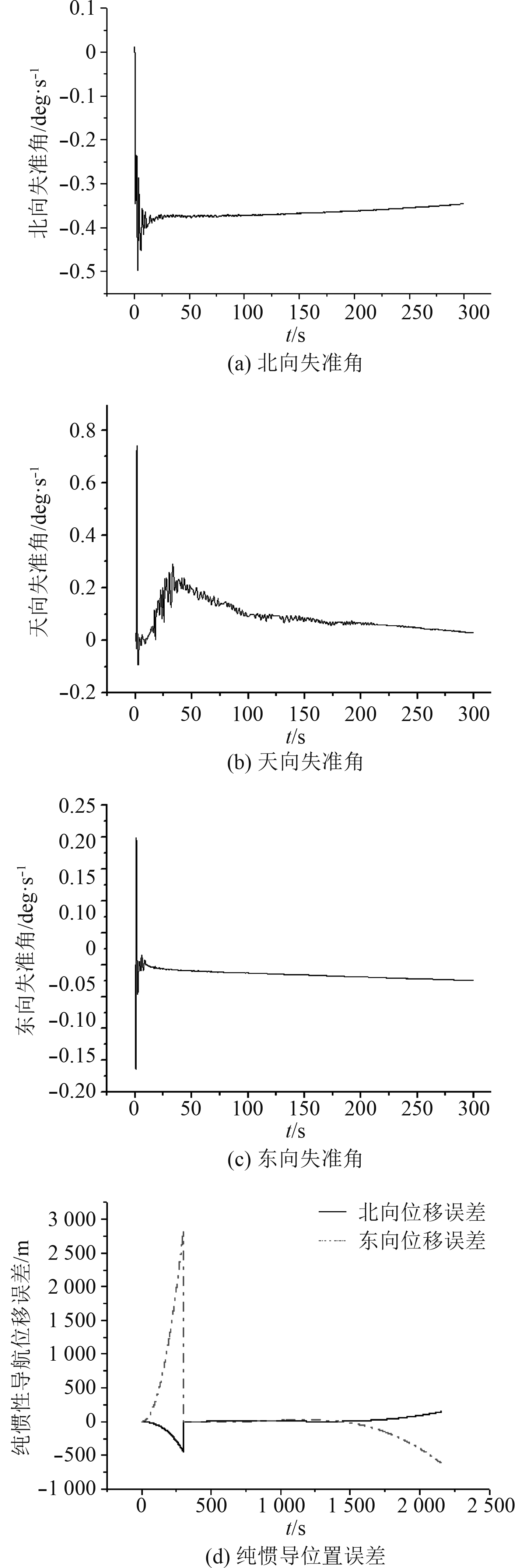
图2为静基座对准试验结果，图3为晃动基座对准试验结果。为比较2种情况下的对准效果，选用对准后自主导航30 min数据，表1为试验结果统计。

由图2可知，晃动基座自主对准方案对准效果与传统静基座自主对准方法差不多，由于可观测性和可观测度不高，方位失准角收敛速度很慢，在5 min的滤波过程中很难收敛，因而影响对准精度。

由图3可看出，晃动基座自主对准方案在晃动条件下，失准角收敛的很理想，方位失准角的收敛速度也快于静基座，从导航结果可以看出晃动条件下的对准效果明显好。

由表1统计的各项导航结果指标可以看出，晃动基座下自主对准方案对准精度较高。

4 结　语

本文利用惯性凝固假设，建立载体惯性坐标系，使载体坐标系相对载体惯性坐标系的姿态阵初值成为单位阵，从而可以进行姿态更新解算。所提方案通过将姿态阵拆分为4个矩阵，选用重力加速度在惯性空间的投影为参考信息，消弱了晃动的影响，保证晃动基座下的粗对准精度。利用高观测性的卡尔曼滤波进行状态估计，提高了算法精度。